Письма в ЖЭТФ, том 113, вып. 10, с. 697 - 703

Поглощение микроволнового излучения двумерными электронными

системами, связанное с возбуждением размерных резонансов

бернштейновских мод

С. И. Дорожкин⁺¹⁾, А. А. Капустин⁺, В. Уманский^∗, Ю. Х. Смет^×

⁺Институт физики твердого тела РАН, 142432 Черноголовка, Россия

^∗Department of Physics, Weizmann Institute of Science, 76100 Rehovot, Israel

^×Max-Planck-Institut für Festkörperforschung, Heisenbergstrasse 1, D-70569 Stuttgart, Germany

Поступила в редакцию 10 апреля 2021 г.

После переработки 21 апреля 2021 г.

Принята к публикации 22 апреля 2021 г.

На образцах гетероструктур GaAs/AlGaAs с двумерной электронной системой под микроволно-

вым излучением частоты 130-170 ГГц выполнены исследования зависимости амплитуд осцилляций

Шубникова-де Гааза от магнитного поля. Обнаружены две особенности подавления амплитуд осцил-

ляций излучением, имеющие резонансный характер по полю. Один из резонансов возникает в магнит-

ном поле, соответствующем второй гармонике циклотронного резонанса, в то время как существование,

положение и амплитуда второго резонанса более сложным образом зависят от частоты излучения. Об-

наруженное резонансное поглощение излучения на второй гармонике, по-видимому, является причиной

аномального пика магнетосопротивления, недавно наблюдавшегося около этой гармоники. Указанные

резонансы могут быть объяснены возбуждением в ограниченном образце стоячих магнитоплазменных

волн с одинаковым волновым вектором, но соответствующих двум различным областям их закона дис-

персии: почти бездисперсионному участку бернштейновской моды и циклотронной магнитоплазменной

моде.

DOI: 10.31857/S1234567821100116

Фотоотклик на микроволновое излучение, наблю-

системы при возбуждении в ней размерных магнито-

даемый в магнетосопротивлении двумерных элек-

плазменных резонансов (РМПР), связанных с фор-

тронных систем (ДЭС), демонстрирует целый ряд

мированием стоячих плазменных волн в образцах ко-

ярких эффектов. Прежде всего упомянем индуциро-

нечных размеров. РМПР сосуществуют с MIRO [1] и

ванные излучением осцилляции магнетосопротивле-

даже могут наблюдаться в состояниях с малой дисси-

ния (MIRO, microwave induced resistance oscillations

пацией [12]. Микроволновое поглощение при размер-

в англоязычной литературе) [1, 2], а также состо-

ных магнитоплазменных резонансах может быть за-

яния с близкими к нулю значениями диссипатив-

регистрировано по возрастанию температуры элек-

ных компонент тензоров магнетосопротивления [3-

тронного газа, например, при измерениях спектров

5] и магнетопроводимости [6], возникающие в ми-

фотолюминесценции [13, 14] или амплитуды осцил-

нимумах MIRO. Объяснение этих эффектов оказа-

ляций Шубникова-де Гааза (ОШДГ) [15], а также

лось возможным в терминах невзаимодействующих

по изменению добротности микроволновых резона-

электронов. Так, одним из механизмов возникнове-

торов [16, 17]. Регистрация резонансного поглощения

ния MIRO является формирование под облучени-

такими методами не связана с температурной зави-

ем неравновесной функции распределения электро-

симостью неосциллирующей части магнетосопротив-

нов, имеющей немонотонную зависимость от энергии

ления. В образцах с очень высокой подвижностью

[5, 7-9]. Возникновение MIRO считается не связан-

электронов и большим периодом ОШДГ несколько

ным с какими-либо резонансами в поглощении мик-

узких РМПР могут наблюдаться в пределах одной

роволнового излучения. Другим хорошо известным

осцилляции [18]. Наблюдавшиеся до сих пор РМПР

типом фотоотклика являются максимумы сопротив-

были связаны с магнитоплазменными волнами, опи-

ления [10, 1, 11], вызванные нагревом электронной

сываемыми широко известным законом дисперсии:

¹⁾e-mail: dorozh@issp.ac.ru

Письма в ЖЭТФ том 113 вып. 9 - 10

2021

697

698

С. И. Дорожкин, А. А. Капустин, В. Уманский, Ю. Х. Смет

√

2πe²n_sk

вязком течении сильновзаимодействующих двумер-

ω_mp = ω^2c +

(1)

ных электронов в магнитном поле. В данной работе

m^∗ǫ_eff

на основании измерений ОШДГ под микроволновым

Здесь ω_mp - круговая частота магнитоплазменной

облучением обнаружено сосуществование РМПР с

волны с волновым вектором k, ω_c = eB/m^∗c - цик-

резонансным поглощением излучения вблизи второй

гармоники ЦР. Показано, что объяснение двух резо-

лотронная частота электронов с эффективной мас-

сой m^∗ в магнитном поле B, n_s - плотность двумер-

нансов возможно на основании полного спектра маг-

нитоплазменных волн в ДЭС, образованного берн-

ных электронов, ε_eff - эффективная диэлектрическая

проницаемость среды, окружающей ДЭС. Во мно-

штейновскими модами [24]. Это объяснение состоит

гих случаях ε_eff неплохо описывается полусуммой ди-

в формировании размерных магнитоплазменных ре-

электрических проницаемостей подложки и вакуума.

зонансов двух типов: обычный РМПР, сформирован-

Для гетероструктур GaAs/AlGaAs обычно использу-

ный магнитоплазменными волнами со спектром (1),

ются значения m^∗ = 0.067m_e и ε_eff = 6.9. Возбужде-

и резонанс, соответствующий почти бездисперсион-

ния ДЭС со спектром (1) носят название циклотрон-

ным участкам спектра около второй гармоники ЦР

ных магнитоплазмонов (ЦМП). Для часто встреча-

(см. рис. 2a). Ниже мы будем называть этот резонанс

ющейся в эксперименте планарной геометрии образ-

размерным бернштейновским резонансом (РБР).

цов вида холловских мостиков ширины w в первом

Измерения были выполнены на двух образ-

приближении положения РМПР соответствуют зна-

цах, изготовленных из одной гетероструктуры

чениям волнового вектора k_n = nπ/w, где n = 1, 2, . . .

GaAs/AlGaAs, и показали одинаковые результаты.

(относительно отклонений от этого соотношения см.

Двумерные электронные системы создавались в

результаты численного расчета [19]). Отметим также

квантовых ямах GaAs шириной 30 нм за счет се-

недавнее наблюдение [20] стоячих магнитоплазмен-

лективного легирования кремнием в слой AlGaAs.

ных волн со спектром, отличным от (1) в силу нали-

После засветки от красного фотодиода при темпе-

чия на поверхности гетероструктуры металлической

ратуре около 4 К плотность электронов составляла

полоски, частично покрывающей ДЭС.

ns = 2.7 · 1011 см-2, а подвижность при темпера-

Неожиданным результатом [21, 22] оказалось на-

туре

0.5 К равнялась

6.8 · 10⁶ см²/В · с. Образцы

блюдение под микроволновым излучением частоты

имели планарную геометрию холловских мостиков

f узких пиков магнетосопротивления вблизи второй

шириной w

= 50 мкм и расстоянием между по-

гармоники циклотронного резонанса (ЦР), т.е., при

тенциальными контактами L = 300 мкм. Образцы

2πf = 2ω_c, где они накладываются на более плав-

помещались внутри сверхразмерного прямоуголь-

ные максимумы MIRO, расположенные примерно в

ного волновода сечением 6.5 × 13.0 мм² (WG19) и

тех же магнитных полях. Происхождение таких пи-

погружались в жидкий³Не, температура которого

ков связывается с сильной температурной зависимо-

во время измерений поддерживалась равной 0.5 К.

стью сопротивления исследованных образцов в соот-

Плоскость ДЭС ориентировалась перпендикулярно

ветствующей области магнитных полей и резонанс-

оси волновода, совпадавшей с направлением магнит-

ным нагревом электронной системы. Очевидно, что

ного поля. Непрерывное микроволновое излучение

при заданных n_s и k из формулы (1) можно полу-

диапазона частот 130-170 ГГц генерировалось лам-

чить совпадение частот РМПР и второй гармоники

пой обратной волны и проходило через аттенюатор

ЦР только для одного значения частоты f, тогда как

типа WG28, соответствующий диапазону частот

эффект наблюдается в довольно широком непрерыв-

90-140 ГГц. Мощность излучения менялась при из-

ном диапазоне частот. Для объяснения резонансно-

менении параметров аттенюатора, но это изменение

го поглощения микроволнового излучения на второй

для части использованного диапазона частот неточ-

гармонике циклотронного резонанса было предложе-

но соответствовало калибровке аттенюатора. Ниже

но несколько альтернативных механизмов. Это [23]

ослабление излучения характеризуется показаниями

возникновение плазменной неустойчивости при по-

аттенюатора.

падании частоты излучения в щель между первой и

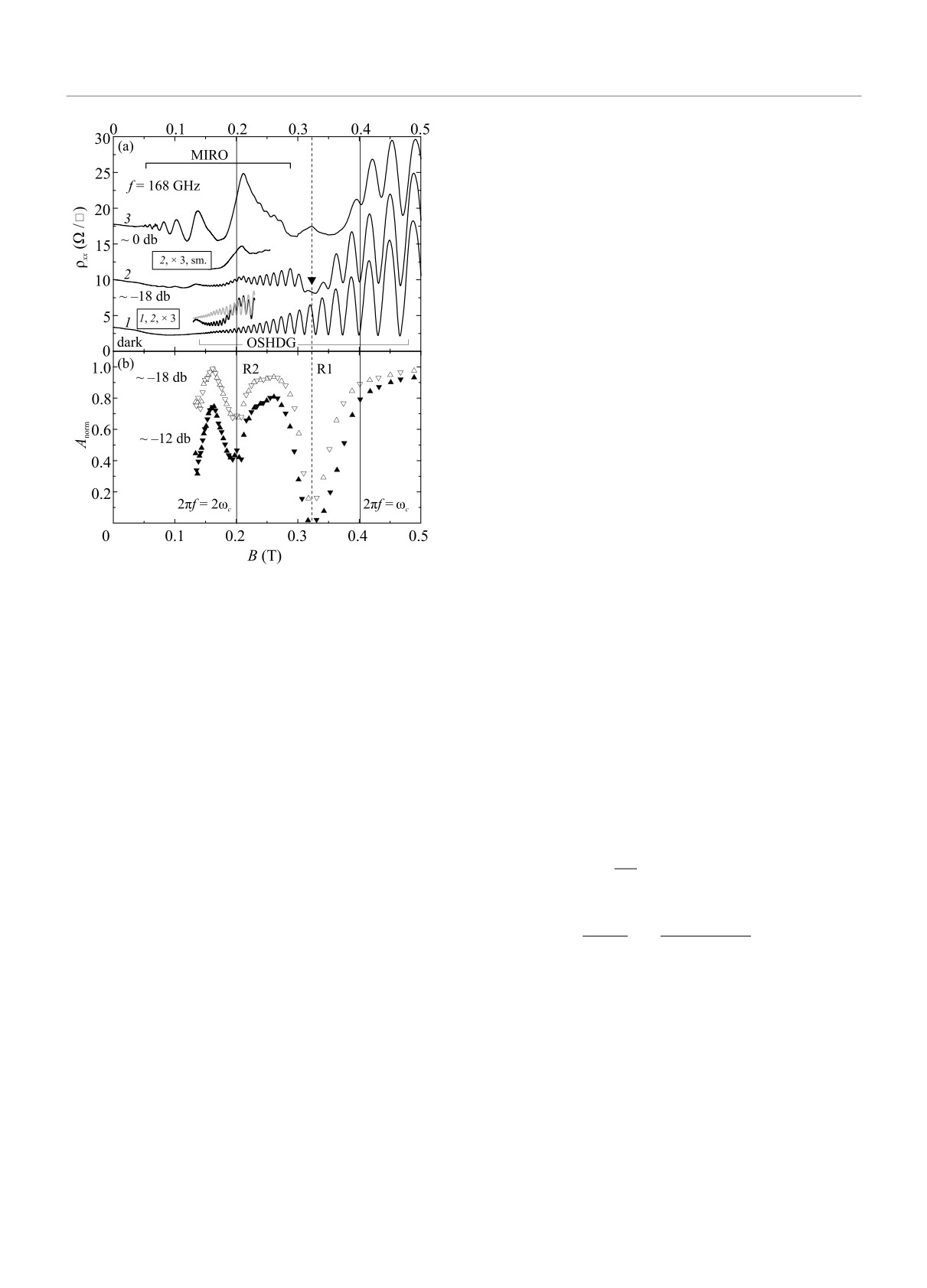
На рисунке 1a представлены кривые магнетосо-

второй бернштейновскими магнитоплазменными мо-

противления, измеренные в отсутствие микровол-

дами [24, 25], находящуюся вблизи удвоенной часто-

нового излучения и под облучением частоты f

ты ЦР. Реализация такой неустойчивости оказыва-

= 168 ГГц различной мощности. Высокочастотные

ется возможной вблизи металлического контакта к

осцилляции на всех кривых являются ОШДГ. Низ-

ДЭС. Другое недавно предложенное объяснение [26]

кочастотные осцилляции (MIRO) появляются под об-

связывается с высокочастотным резонансом [27] при

лучением (кривые 2 и 3) в более слабых полях. В дан-

Письма в ЖЭТФ том 113 вып. 9 - 10

2021

Поглощение микроволнового излучения двумерными электронными системами...

699

подавлении одной осцилляции, отмеченной треуголь-

ником на кривой 2. Результаты анализа подавления

других осцилляций показаны на рис. 1b. Для всех

наблюдаемых ОШДГ влияние облучения на их ам-

плитуды A_n характеризовалось отношением ампли-

туд осцилляций под облучением A^nω) и без облуче-

ния A⁰ⁿ. Нормированные значения A_norm,n = A^nω)/A⁰ⁿ

приведены на рис. 1b для двух значений мощности.

Из этого рисунка очевидно существование двух об-

ластей магнитных полей (R1 и R2), в которых про-

исходит наибольшее подавление амплитуды ОШДГ,

имеющее резонансный вид. Положение глубокого ми-

нимума (область R1), отмеченного пунктирной лини-

ей, будет обсуждаться ниже, левый же минимум (об-

ласть R2) расположен около второй гармоники ЦР,

где 2πf = 2ω_c. Отметим разное поведение под облу-

чением неосциллирующей части магнетосопротивле-

ния в этих областях. В области R1 она сначала резко

уменьшается (кривая 2), а при дальнейшем возрас-

тании мощности излучения образует максимум со-

противления (кривая 3). В области R2 на кривой 2

подавление амплитуды ОШДГ сопровождается воз-

никновением узкого пика, который при дальнейшем

Рис. 1. (a) - Удельное магнетосопротивление ρxx, из-

возрастании мощности сливается с ближайшим мак-

меренное в отсутствие облучения (кривая 1) и под об-

симумом MIRO (кривая 3). Два минимума на кри-

лучением частоты 168 ГГц двух различных мощностей

вых A_norm(B), очевидно, отражают две резонансные

(кривые 2 и 3, сдвинутые вверх на 7 и 14 Ом/квадрат

особенности в поглощении микроволнового излуче-

соответственно). Около кривых 2 и 3 указано номи-

ния. Мы связываем их с возбуждением двух размер-

нальное ослабление аттенюатора (подробнее см. текст).

ных магнитоплазменных резонансов, соответствую-

Между кривыми 1 и 2 показаны их фрагменты, рас-

тянутые в 3 раза вдоль вертикальной оси и наложен-

щих стоячим волнам с одним и тем же волновым

ные друг на друга для наглядности изменения ам-

вектором, но относящимся к разным частям спектра

плитуд ОШДГ в соответствующем интервале магнит-

магнитоплазмонов.

ных полей. Фрагмент кривой 2 в увеличенном в 3 ра-

В данной работе, интерпретируя наши экспери-

за масштабе, но со сглаженными ОШДГ показан над

ментальные результаты, мы рассмотрим более пол-

ней. (b) - Зависимости от магнитного поля амплитуд

ный по сравнению с (1) закон дисперсии магнито-

ОШДГ под облучением, нормированные на их величи-

плазменных волн в ДЭС, образованный бернштей-

ны в отсутствие облучения, для двух мощностей из-

новскими модами [24], который в квазистатическом

лучения. Треугольниками с вершинами вверх (вниз)

пределе (ω < ck/√εeff ) и отсутствии рассеяния элек-

представлены результаты для амплитуд осцилляций в

тронов является решением следующего уравнения:

их максимумах (минимумах). Сплошные вертикальные

линии отмечают положения циклотронного резонанса

∑

4e²m^∗

n²J²ⁿ(kR_c)

и его второй гармоники для электронов с эффективной

= 0.

(2)

ℏ²ǫ_effk

(ω/ω_c)² - n²

массой m^∗ = 0.067me. Пунктирная вертикальная пря-

n=1

мая отмечает магнитное поле, в котором наблюдается

Здесь J_n - функция Бесселя порядка n, R_c = V_F /ω_c -

максимальное подавление амплитуды ОШДГ и макси-

циклотронный радиус электронов на уровне Ферми

мум сопротивления при большой мощности излучения

вырожденной ДЭС, V_F - фермиевская скорость. Как

(кривая 3)

будет видно ниже, при наших экспериментальных

параметрах этот закон дисперсии фактически вклю-

ной работе мы прежде всего рассмотрим подавление

чает в себя дисперсию (1). Магнитодисперсия, полу-

ОШДГ в результате облучения. Этот эффект хоро-

ченная решением уравнения (2) для волнового век-

шо заметен уже при небольшой мощности излучения

тора k = π/w без использования свободных пара-

(кривая 2) и имеет резонансный характер. Этот ха-

метров, показана на рис. 2a. Она состоит из системы

рактер наиболее ярко проявляется в почти полном

непересекающихся ветвей (бернштейновских мод) с

Письма в ЖЭТФ том 113 вып. 9 - 10

2021

700

С. И. Дорожкин, А. А. Капустин, В. Уманский, Ю. Х. Смет

уравнении (2), существенен только первый член, а

функция Бесселя первого порядка заменяется глав-

ным членом ее разложения по малому параметру

kR_c. Можно показать, что для актуальных малых

значений волнового вектора горизонтальные участ-

ки магнитодисперсии на рис. 2а соответствуют по-

чти бездисперсионным зависимостям ω(k) в постоян-

ном магнитном поле. Для малых значений волново-

го вектора расщепления между бернштейновскими

модами очень малы. Они становятся существенны-

ми при kR_c ≳ 1, где они наблюдались эксперимен-

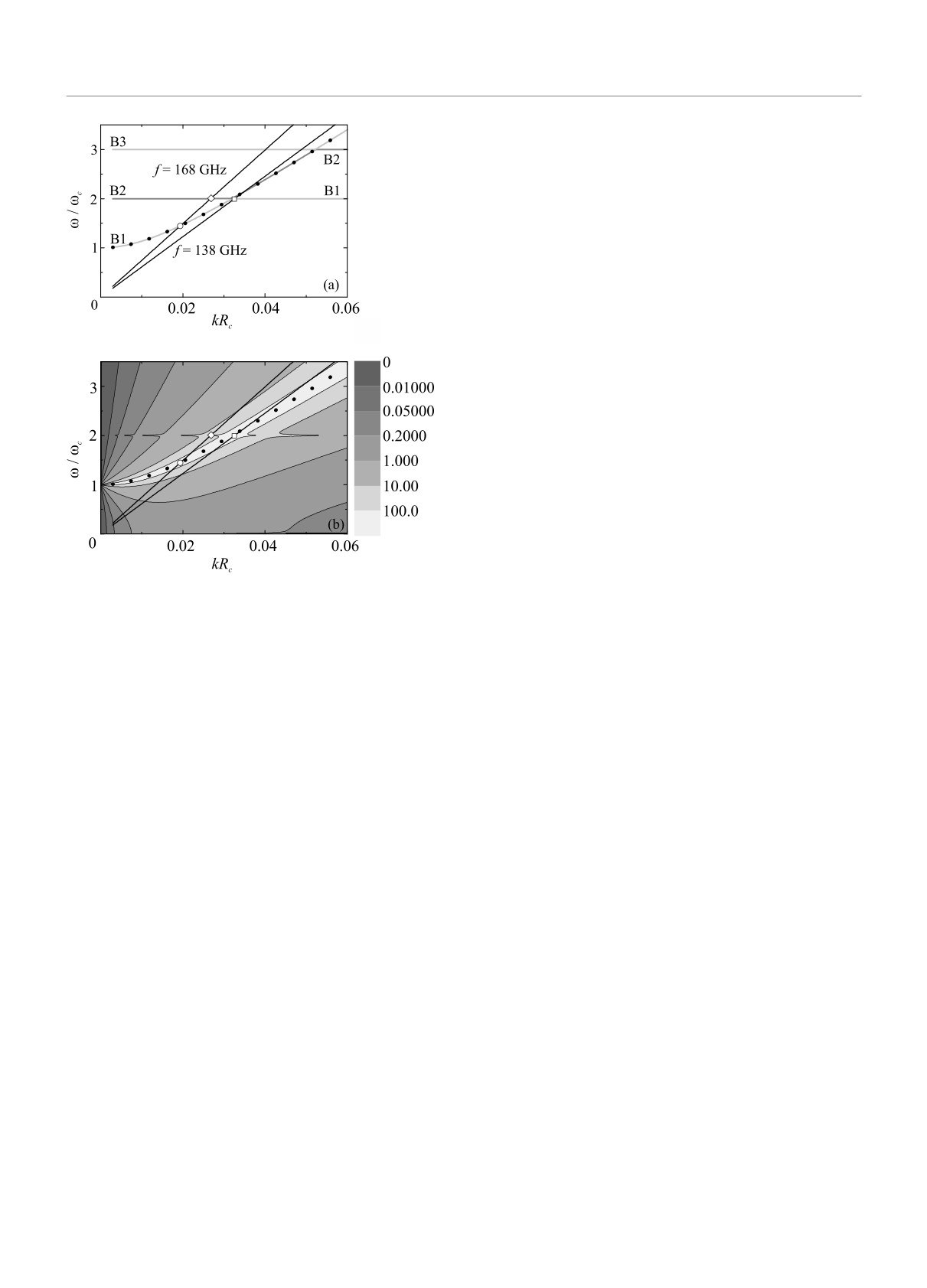
тально [28, 29]. В координатах (kR_c, ω/ω_c) на рис. 2a

развертка магнитного поля под облучением частоты

f = ω/2π, осуществляемая в эксперименте, соответ-

ствует движению в начало координат вдоль прямой

линии с наклоном 2πf/kV_F . Две такие линии (на-

грузочные прямые), соответствующие частотам 168

и 138 ГГц, также приведены на рис.2. Резонансное

поглощение ожидается в точках пересечения нагру-

зочных прямых и линий магнитодисперсии. Такое

предположение, однако, справедливо лишь в случае

полного отсутствия рассеяния электронов. Как бу-

дет обсуждаться ниже, для частоты 168 ГГц и до-

Рис. 2. (a) - Магнитодисперсия трех нижних бернштей-

стижимых в настоящее время значений подвижности

новских мод, полученная в результате численного ре-

электронов в рамках используемого анализа ожи-

шения уравнения (2) для значения волнового вектора

дается возникновение только двух резонансов, со-

k = π/w (серые кривые разной интенсивности, обо-

ответствующих пересечениям нагрузочной прямой с

значенные B1, B2 и B3). Черными точками показана

линиями магнитодисперсии второй бернштейновской

магнитодисперсия ЦМП для того же волнового векто-

моды в точке (0.02685, 2.0068) и циклотронного маг-

ра, определяемая уравнением (1). Сплошные прямые,

нитоплазмона в точке (0.0193, 1.45), где его магни-

описываемые соотношением ω/ωc = (2πf/kVF )kRc, со-

тодисперсия совпадает с дисперсией первой берн-

ответствуют движению по диаграмме при сканирова-

штейновской моды. Второе из указанных пересече-

нии магнитного поля для двух значений частоты из-

ний соответствует обычному размерному магнито-

лучения, указанных около прямых. Открытыми сим-

волами отмечены точки пересечения линии 168 ГГц с

плазменному резонансу. Первая же точка реализу-

модами B1 и B2, а также линии 138 ГГц с модой B1.

ет размерный бернштейновский резонанс. Очевидно,

(b) - Распределение интенсивности микроволнового по-

что в силу почти бездисперсионного поведения берн-

глощения по диаграмме (kRc, ω/ωc), вычисленное с ис-

штейновской моды около второй гармоники РБР в

пользованием уравнения (3) для τ = 2.6 · 10^-10 c, опре-

образцах типичных размеров будут реализовывать-

деленного из величины подвижности ДЭС, и k = π/w

ся именно около этой гармоники.

Расчетное положение РБР хорошо согласуется с

частотами ω, лежащими в интервалах n < ω/ω_c <

положением резонанса R2 около второй гармоники

n + 1. Зависимость, показанная темными точками,

ЦР. Расчетное же положение РМПР (ω/ω_c = 1.45)

представляет собой магнитодисперсию ЦМП со спек-

несколько отличается от положения резонанса R1 на

тром (1) и таким же волновым вектором k = π/w.

рис. 1 (ω/ω_c = 1.25). В связи с этим отметим, что

При использованном значении волнового вектора и

в экспериментах (см., например, [10, 11]) довольно

ω/ω_c = n эта дисперсионная зависимость почти пол-

часто наблюдается аналогичное незначительное (10-

ностью покрывается фрагментами бернштейновских

20 %) отклонение наблюдаемых положений РМПР

мод, отличными от их почти горизонтальных участ-

от рассчитанных для волнового вектора k = π/w.

ков. В общем случае закон дисперсии ЦМП (1) полу-

Это может быть связано со следующими факторами.

чается из уравнения (2) при малых значениях вол-

Во-первых, резонансы поглощения в полосках конеч-

нового вектора и частотах, достаточно удаленных

ной ширины могут быть сдвинуты от вычисленных

от гармоник ЦР, когда в сумме, фигурирующей в

в таком простом приближении [19]. Кроме того, зна-

Письма в ЖЭТФ том 113 вып. 9 - 10

2021

Поглощение микроволнового излучения двумерными электронными системами...

701

чение эффективной диэлектрической проницаемости

имеют только качественное значение для интерпре-

ε_eff может зависеть от реальной архитектуры гетеро-

тации наших результатов, так как сила осциллятора

структуры, особенно в случае наличия в ней сильно

для размерных резонансов вполне может отличать-

легированных слоев, и отличаться от обычно исполь-

ся [19] от рассчитанной для случая осциллирующе-

зуемого значения ε_eff = 6.9. Отметим, что положе-

го с координатой высокочастотного электрического

ние РБР около второй гармоники при актуальных

поля. Тем не менее, различие в микроволновом по-

значениях волнового вектора очень слабо зависит от

глощении при РМПР и РБР, ожидаемое на основа-

отклонений параметров образца от выбранных при

нии расчета, качественно коррелирует с наблюдени-

расчете значений, включая ширину w.

ем, что подавление амплитуды ОШДГ на рис. 1 мак-

Для качественного представления о сравнитель-

симально в области R1 и заметно меньше в обла-

ной силе наблюдаемых резонансов можно восполь-

сти R2.

зоваться формулой для поглощения волны, модули-

Из данных на рис.2a нетрудно видеть (см. нагру-

рованной по амплитуде вдоль плоскости ДЭС: E_x =

зочную прямую, соответствующую частоте 138 ГГц),

= E exp(i(kx-ωt)), полученной [30] для квазистати-

что изменение частоты излучения заметно сдвигает

ческого случая в квазиклассическом приближении:

положение РМПР по вертикальной оси ω/ω_c, не ме-

(

)_-1

няя положения РБР около второй гармоники ЦР. Ре-

m^∗e²ω

1 - iN/ω_cτ

2m^∗e

Q = E2 Im

зультаты измерений для частоты 138 ГГц приведены

2π(ℏk)²

1 - N(ω + i/τ)/ω_c

ℏ²kǫ_eff

на рис. 3. Как видно из этого рисунка, на этой час-

(3)

Здесь

∑

J^2l(kR_c)

N =

(ω + i/τ)/ω_c + l

l=-∞

τ - время релаксации электронов по импульсу. От-

метим, что эта формула приводит к максимумам по-

глощения на линиях закона дисперсии, получаемых

из уравнения (2), при ωτ → ∞. Более того, уравне-

ние (2) можно получить из уравнения (3), приравняв

нулю производную ∂Q/∂ω, а затем перейдя к преде-

лу ωτ → ∞. Результаты расчета поглощаемой мощ-

ности в соответствии с уравнением (3) представлены

на рис. 2b. Как следует из этих результатов, наиболее

сильное поглощение ожидается вдоль дисперсионной

кривой циклотронного магнитоплазмона и быстро

уменьшается при удалении от нее. Кроме того, как

показали более подробные численные расчеты, для

нашего значения подвижности электронов максиму-

мы поглощения вдоль нагрузочных линий возникают

в точках их пересечений с горизонтальными участ-

ками дисперсионных зависимостей только на второй

гармонике циклотронного резонанса. На рисунке 2b

этот факт проявляется в наличии около второй гар-

моники узких горизонтальных полос, соответствую-

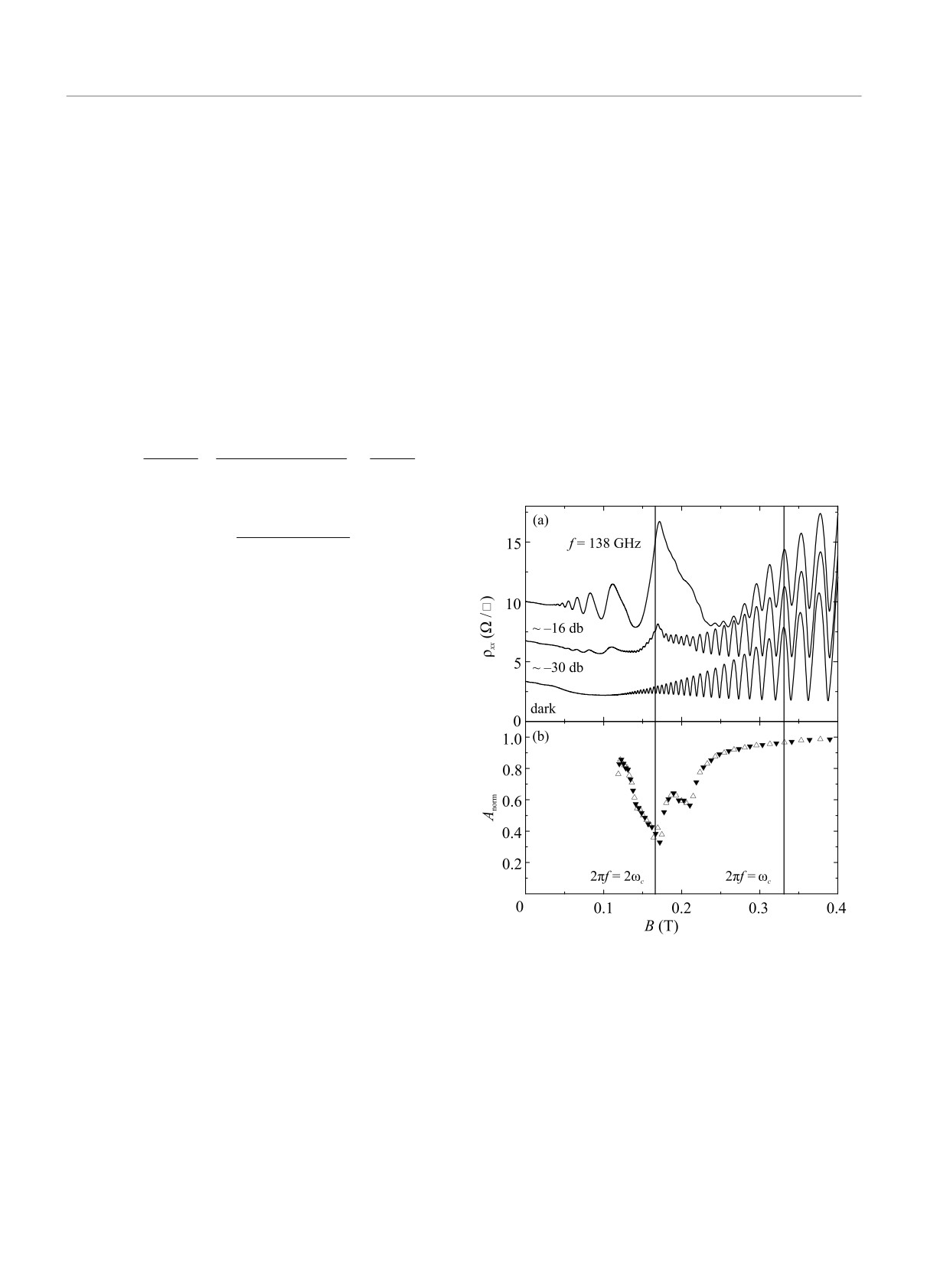
Рис. 3. Экспериментальные данные для частоты излу-

щих более высокому уровню поглощения излучения.

чения f = 138 ГГц, аналогичные приведенным на рис. 1

Уменьшение же подвижности в пять раз приводит

для f = 168 ГГц

к исчезновению максимума поглощения для часто-

ты 168 ГГц и на второй гармонике. Таким образом,

тоте доминирующим стал минимум A_norm(B) около

существование резонансов микроволнового поглоще-

второй гармоники, и исчез глубокий минимум в диа-

ния на гармониках циклотронного резонанса крити-

пазоне 1 < ω/ω_c < 2, что вполне коррелирует с ре-

ческим образом зависит от подвижности электронов

зультатом расчета для этой частоты на рис. 2а. От-

через параметр ωτ.

метим, что максимальное подавление ОШДГ около

Необходимо, однако, отметить, что приведенные

второй гармоники наблюдалось также в работе [31],

расчетные результаты для поглощаемой мощности

где не получило определенной интерпретации.

Письма в ЖЭТФ том 113 вып. 9 - 10

2021

702

С. И. Дорожкин, А. А. Капустин, В. Уманский, Ю. Х. Смет

Внимательное прочтение работ [21, 22] показы-

чае резонанс ожидается только на второй гармони-

вает, что пики сопротивления на второй гармони-

ке и отсутствует в области частот 1 < ω/ω_c < 2.

ке циклотронного резонанса наблюдались в области

Очевидно, что этот результат остается справедли-

частот 60-190 ГГц на образцах с подвижностью элек-

вым для волнового вектора k = π/w₂, соответству-

тронов, превышающей значение 10 · 10⁶ см²/В · с, и

ющего полоске шириной w₂ = w/2. Таким образом,

имеющих ширину проводящего канала холловских

представляется возможным наблюдение только од-

мостиков w ≤ 200 мкм. Как было отмечено выше,

ного резонанса - размерного бернштейновского ре-

высокая подвижность электронов может являться

зонанса на второй гармонике ЦР.

ключевым фактором для возникновения максимума

В заключение, полученные нами эксперименталь-

поглощения на второй гармонике. Небольшая вели-

ные и расчетные результаты свидетельствуют о ре-

чина ширины канала, очевидно, способствует фор-

зонансном поглощении микроволнового излучения

мированию стоячей волны при наличии рассеяния

двумерными электронами на второй гармонике цик-

электронов. Что касается частотного диапазона, как

лотронного резонанса в результате возбуждения сто-

следует из рис. 2b, максимального резонансного по-

ячих волн, соответствующих двум нижним берн-

глощения на второй гармонике следует ожидать для

штейновским модам магнитоплазменных колебаний.

частот, не слишком отличающихся от частоты, со-

Авторы благодарны В. А. Волкову и И. В. Кукуш-

ответствующей пересечению магнитодисперсии цик-

кину за полезные обсуждения.

лотронного магнитоплазмона и нагрузочной линии

Работа выполнена в рамках госзадания Инсти-

ω/ω_c = kR_cω/kV_F на второй гармонике. Нетрудно

тута физики твердого тела РАН. В.Уманский и

получить, что это происходит на частоте f = ω/2π =

Ю. Х. Смет благодарны German-Israeli Foundation

√

= (eV_F /ℏ)

m^∗/3πε_effw. Эта частота равняется 141

for Scientific Research and Development (GIF) за под-

ГГц при n_s = 2.7 · 10¹¹ см^-2, w = 50 мкм, т.е., ти-

держку.

пичных значениях параметров, при которых наблю-

дались пики магнетосопротивления на второй гар-

M. A. Zudov, R. R. Du, J. A. Simmons, and J. L. Reno,

монике. Необходимо отметить, что величина погло-

Phys. Rev. B 64, 201311(R) (2001).

щения на второй гармонике может усиливаться за

P. D. Ye, L. W. Engel, D. C. Tsui, J. A. Simmons,

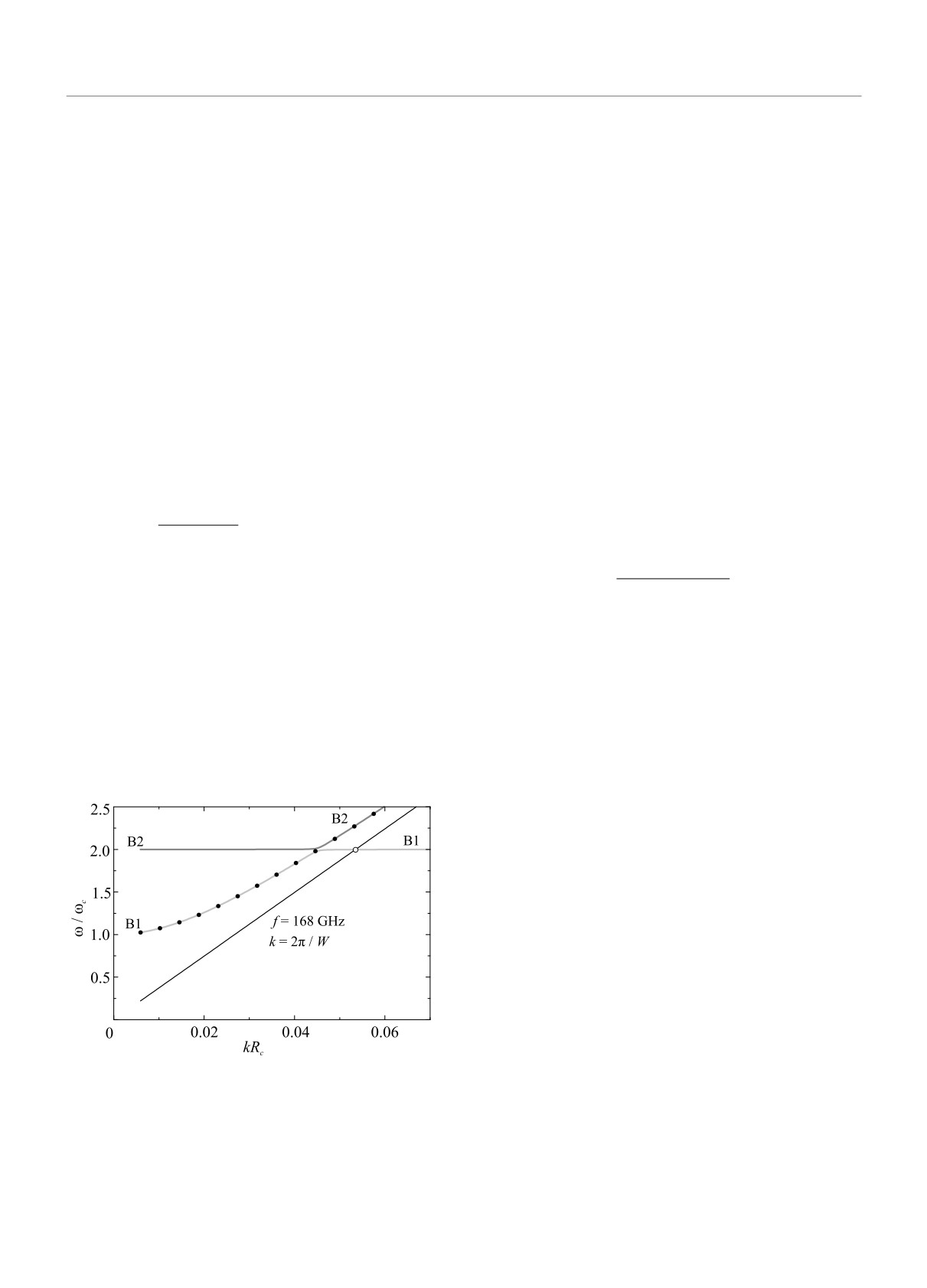
счет формирования РБР стоячими волнами с волно-

J. R. Wendt, G. A. Vawter, and J. L. Reno, Appl. Phys.

выми векторами k_(n+1) = (n + 1)π/w вследствие по-

Lett. 79, 2193 (2001).

чти бездисперсионной зависимости бернштейновской

R. G. Mani, J. H. Smet, K. von Klitzing,

моды около этой гармоники. Этот факт иллюстри-

V. Narayanamurti, W. B. Jonson, and V. Umansky,

руется результатами расчета магнитодисперсии для

Nature 420, 646 (2002).

k₂ = 2π/w и нагрузочной прямой для f = 168 ГГц,

M. A. Zudov, R. R. Du, L. N. Pfeiffer, and K. W. West,

приведенными на рис. 4. Действительно, в этом слу-

Phys. Rev. Lett. 90, 046807 (2003).

S. I. Dorozhkin, JETP Lett. 77, 577 (2003).

C. L. Yang, M. A. Zudov, T. A. Knuuttila, R. R. Du,

L. N. Pfeiffer, and K. W. West, Phys. Rev. Lett. 91,

096803 (2003).

I. A. Dmitriev, A.D. Mirlin, and D. G. Polyakov,

Phys. Rev. Lett. 91, 226802 (2003).

I. A. Dmitriev, M. G. Vavilov, I. L. Aleiner, A.D. Mirlin,

and D. G. Polyakov, Phys. Rev. B 71, 115316 (2005).

I. A. Dmitriev, A.D. Mirlin, D. G. Polyakov, and

M. A. Zudov, Rev. Mod. Phys. 84, 1709 (2012).

10.

E. Vasiliadou, G. Müller, D. Heitmann, D. Weiss,

K. von Klitzing, H. Nickel, W. Schlapp, and R. Lösch,

Phys. Rev. B 48, 17145 (1993).

11.

I. V. Kukushkin, V.M. Muravev, J. H. Smet, M. Hauser,

W. Dietsche, and K. von Klitzing, Phys. Rev. B 73,

Рис. 4. Результаты расчета для k = 2π/w магнитодис-

113310 (2006).

персии двух нижних бернштейновских мод и цикло-

12.

A. T. Hatke, M. A. Zudov, J. D. Watson, and

тронного магнитоплазмона, а также нагрузочной пря-

M. J. Manfra, Phys. Rev. B 85, 121306 (2012).

мой для f = 168 ГГц. Обозначения те же, что и на

13.

B. M. Ashkinadze, E. Linder, and V. Umansky, Phys.

рис. 2

Rev. B 62, 10310 (2000).

Письма в ЖЭТФ том 113 вып. 9 - 10

2021

Поглощение микроволнового излучения двумерными электронными системами...

703

14. I. V. Kukushkin, J. H. Smet, S. A. Mikhailov,

22. A. T. Hatke, M. A. Zudov, L. N. Pfeiffer, and

D. V. Kulakovskii, K. von Klitzing, and W. Wegscheider,

K. W. West, Phys. Rev. B 83, 121301(R) (2011).

Phys. Rev. Lett. 90, 156801 (2003).

23. V. A. Volkov and A. A. Zabolotnykh, Phys. Rev. B 89,

121410(R) (2014).

15. С. И. Дорожкин, А. А. Быков, И. В. Печенежский,

А.К. Бакаров, Письма в ЖЭТФ 85, 705 (2007).

24. I. B. Bernstein, Phys. Rev. 109, 10 (1958).

16. S. A. Studenikin, A. S. Sachrajda, J. A. Gupta,

25. K. W. Chiu and J. J. Quinn, Phys. Rev. B 9, 4724

Z. R. Wasilewski, O. M. Fedorych, M. Byszewski,

(1974).

D. K. Maude, M. Potemski, M. Hilke, K. W. West, and

26. P. S. Alekseev and A. P. Alekseeva, Phys. Rev. Lett.

123, 236801 (2019).

L. N. Pfeiffer, Phys. Rev. B 76, 165321 (2007).

27. P. S. Alekseev, Phys. Rev. B 98, 165440 (2018).

17. O. M. Fedorych, M. Potemski, S. A. Studenikin,

28. E. Batke, D. Heitmann, J. P. Kotthaus, and K. Ploog,

J. A. Gupta, Z. R. Wasilewski, and I. A. Dmitriev, Phys.

Phys. Rev. Lett. 54, 2367 (1985).

Rev. B 81, 201302(R) (2010).

29. И. В. Кукушкин, В. А. Волков, Двумерная электрон-

18. Q. Shi, M. A. Zudov, L. N. Pfeiffer, K. W. West,

ная жидкость в сильном магнитном поле. Маг-

J. D. Watson, and M. J. Manfra, Phys. Rev. B 93,

нитоплазмоны, магниторотоны, композитные фер-

165438 (2016).

мионы, Физматкнига, М. (2016).

19. S. A. Mikhailov and N. A. Savostianova, Phys. Rev. B

30. A. V. Chaplik and D. Heitmann, J. Phys. C: Solid State

71, 035320 (2005).

Phys. 18, 3357 (1985).

20. А. М. Зарезин, П. А. Гусихин, В. М. Муравьев,

31. Q. Shi, P. D. Martin, A. T. Hatke, M. A. Zudov,

И. В. Кукушкин, Письма в ЖЭТФ 111, 316 (2020).

J. D. Watson, G. C. Gardner, M. J. Manfra,

21. Y. Dai, R. R. Du, L. N. Pfeiffer, and K. W. West, Phys.

L. N. Pfeiffer, and K. W. West, Phys. Rev. B

92,

Rev. Lett. 105, 246802 (2010).

081405(R) (2015).

Письма в ЖЭТФ том 113 вып. 9 - 10

2021