Pis’ma v ZhETF, vol. 114, iss. 1, pp. 41 - 42

Two-impurity scattering in quasi-one-dimensional systems¹⁾

A. S. Ioselevich^+∗2), N. S. Peshcherenko^∗2)

⁺Condensed-matter physics laboratory, National Research University Higher School of Economics, 101000 Moscow, Russia

L. D. Landau Institute for Theoretical Physics, 119334 Moscow, Russia

Submitted 8 June 2021

Resubmitted 8 June 2021

Accepted 10

June 2021

DOI: 10.31857/S1234567821130097

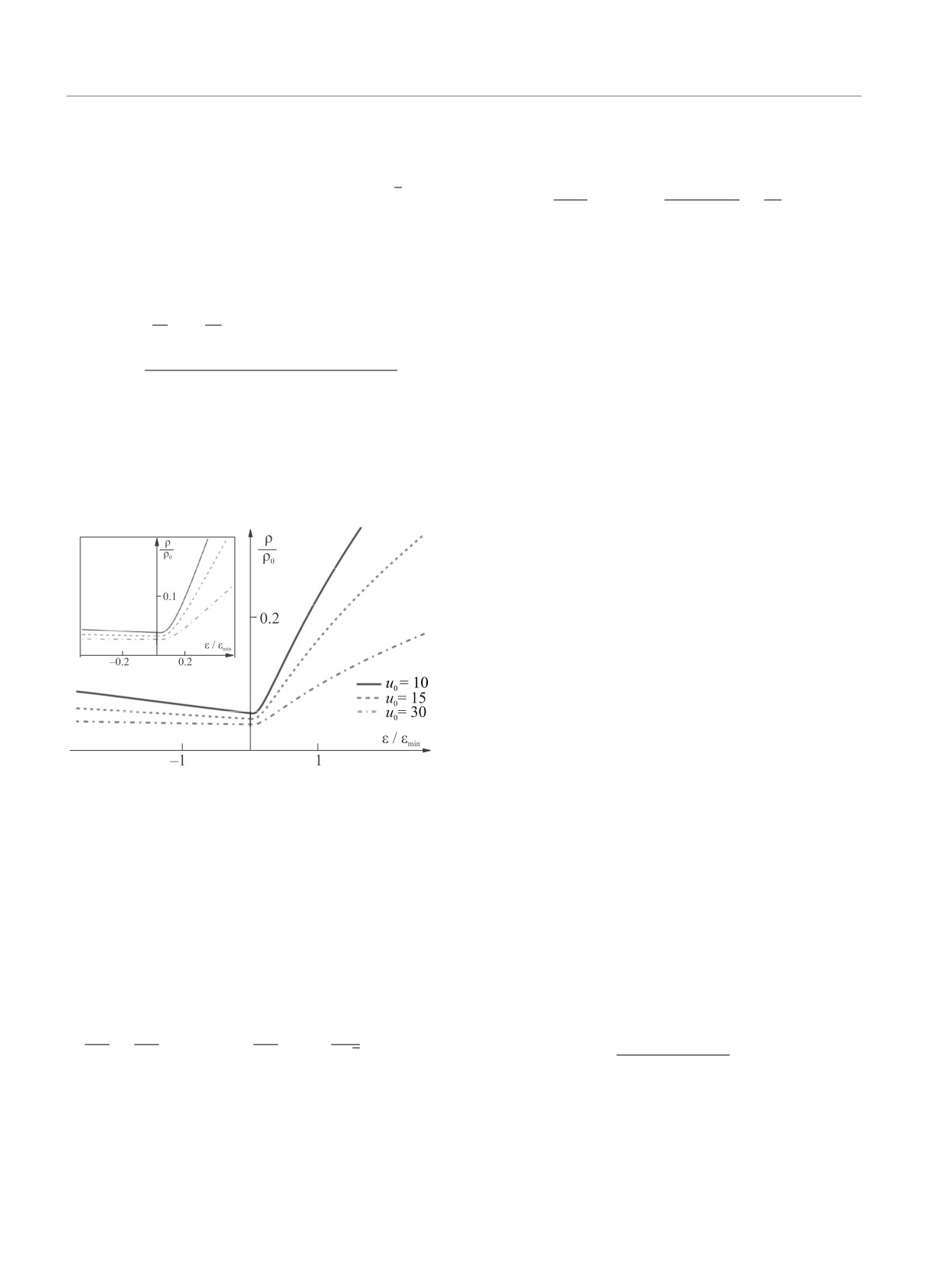
In quasi-one-dimensional systems with low concen-

ment is sufficient. For perturbative scattering amplitude

tration of impurities the quantization of transverse elec-

we have:

tronic motion is essential and the conductivity demon-

strates van Hove singularities when the Fermi level E_F

V(i)m

=V^(i)m

+V^(i)m

G_ε(z_i, z_i)V⁽ⁱ⁾

≡

1,m2

1,N

N,m2

{

}

approaches a bottom of some transverse quantization

≡

eiφi(m1-m2),

λ_i = λ

G_ε(z_i, z_i)

(1)

subband E_N . In our previous work [1, 2] we have demon-

π²

strated that for the case of a conducting tube of radius R

with weak disorder potential present on its surface, the

Here G_ε(z_i, z_i) is the exact multi-impurity Green func-

scattering at the central part of each singularity is sup-

tion of a strictly one-dimensional problem. In order to

pressed by single impurity non-Born effects. However,

take into account multiple scattering, we solve the fol-

single-impurity treatment of scattering breaks down at

lowing Dyson equation:

|ε| ∼ ε_min = (n/π)², where ε = 2m^∗R²(E_F -E_N ), m^∗ is

Λ(i)(ren)

λ(i)

Λ(i)(ren)

effective electron mass, n = n₂(2πR)² is dimensionless

g_ε(0)

concentration of point-like repulsing impurities. n and

π²

∑

dimensionless scattering amplitude λ are assumed to be

g_ε(0) =

g^(m)ε(0) ≈ -iπ², g^(m)ε(0) = -πiε^-1/2m, (2)

small: n, λ ≪ 1. For simplicity, in the present paper we

m=N

consider only the case of repulsing impurities λ > 0 and

develop a theoretical description of multi-impurity ef-

where g^εm)(0) is the free one-dimensional Green func-

fects in resistivity for |ε| ≲ ε_min. We show that these

tion in the m-th subband. The solution of (2) reads:

effects are effectively reduced to just two-impurity ones.

(ren)

= λ(q^-1i + 1 + iλ)^-1,

(3)

Scattering rate τ^-1mk for state with longitudinal mo-

[

]_-1

mentum k in an m-th subband of transversal quanti-

q_i = -

(λ/π²)G_ε(z_i, z_i)

- 1.

(4)

zation is related to corresponding self-energy Σ_mk(ε):

τ^-1mk = -2Im {Σ_mk}. The current-carrying states from

In order to proceed we need to evaluate G_ε(z_i, z_i).

(“nonresonant”) subbands with m = N are semiclassi-

One-dimensional Green function satisfies the following

cal, therefore the self-energies are formally additive:

Schroedinger equation:

{

}

d²

∑

(

)

+ U(z) - ε G(z,z_i) = -δ(z - z_i),

(5)

Σ_mk = Σ^(i)mk, Σ^(i)mk ≡ Σ⁽ⁱ⁾

E = ε_m + k²/2m^∗

(2π)² dz²

∑

U (z) = λ/π² δ(z - z_j ).

(6)

Our aim is to account for all scattering processes within

However, for |ε| ≪ ε_nB one can show that it is enough

the resonant subband (m = N) exactly while for nonres-

to consider only 3 impurities:

onant subband (m = N) processes perturbative treat-

∑

U (z) → U(z) = λ/π²

δ(z - z_j).

(7)

j=i,i±1

¹⁾Supplementary materials are available for this article at DOI:

??? and are accessible for authorized users.

Taking into account more distant impurities leads to

²⁾e-mail: iossel@itp.ac.ru; peshcherenko@itp.ac.ru

only small corrections to Re q_i and, at the same time,

Письма в ЖЭТФ том 114 вып. 1 - 2

2021

A. S. Ioselevich, N. S. Peshcherenko

to dramatic suppression of Im q_i. Therefore, for q_i we

from anomalously small L⁽⁺⁾ⁱ or L^(-)i: L^(±) ∼ 1/λ ≪

have: q_i = q⁽⁺⁾ⁱ + q^(-)i, where

1/n. For ρ_twin we have:

[

]

∫ ∞

ρ_twin

e^-nLdL

q^(±)i ≈ (k/4λ)cotk

L^±i + 1/4λ

k = 2π√ε,

≈ 2n

(11)

ρ₀

(4λL + 2)²

4λ

L⁽⁺⁾ⁱ = z_i+1 - z_i, L^(-)i = z_i - z_i-1.

(8)

Why the scattering at twin impurities is dominant

Averaging over impurities positions, for resistivity ρ(ε)

at low energy? There is no special enhancement for the

we arrive at the following result:

twin impurities scattering at low ε, but single-impurity

(ren)

scattering ampitude Λ

is suppressed by non-Born

Im 〈Λ^(ren)〉_L(±) =

effects for ε → 0 [2]. This screening effect is, however,

ρ₀

λ²

gradually destroyed, as a pair of impurities approach

∫ ∞

exp{-n(L⁽⁺⁾ + L^(-))}n²dL⁽⁺⁾dL^(-)

each other.

(9)

([q(L⁽⁺⁾) + q(L^(-))]^-1 + 1)² + λ²

However, at the first glance this observation is

counter-intuitive since the closer impurities are, the

where ρ₀ = (4π/e²E_F )n(λ/π)² is resistivity away from

more their pair resembles a solitary “composite impu-

van Hove singularity. In principle, (9) together with (8)

rity”, scattering at which is expected to be suppressed.

solve our problem: what is left is only to perform a dou-

The resolution to this paradox is as follows. Let us con-

ble integration in (9) (see numerical results at Fig. 1).

sider transitions between states from m, m^′ = N bands

Below we do it analytically in different energy domains.

due to scattering at a twin pair. In this case, the scat-

tering cross-section component that describes coherent

scattering at 2 impurities constituting the pair is pro-

portional to e^ikmm′ L, where L = |z_i - z_j| and typical

momentum transfer k_mm′ in a multi-channel system is

large: k_mm′ ∼ N ≫ 1. This contribution vanishes after

averaging over L and, therefore, twin pair of impurities

could be thought of as a “coherent” object for the pro-

cesses within resonant subband but it is “incoherent”

for scattering processes between states from current-

carrying nonresonant subbands.

To conclude, we have studied the behavior of ρ(ε)

in a tube in the vicinity of a van Hove singular-

ity. We have shown that in the range of energies

-(1/4)(ε_minε_nB)^1/2 < ε < ε_min ln^-2 λ the resistivity is

Fig. 1. (Color online) Plot of the total resistivity ρ(ε) for

dominated by scattering at rare “twin” pairs of close

λ = 0.2 (main plot) and λ = 0.05 (inset). In both cases

defects. The predicted effect is characteristic for multi-

three values of u0 = λ/n are used: u0 = 10, 15, 30

channel systems, it can not be observed in strictly one-

dimensional one.

For ε > 0 quasistationary states confined between

This work was supported by Basic Research Pro-

pairs of adjacent inpurities are present in the reso-

gram of The Higher School of Economics and by the

nant subband, and for not very low ε the principal

Foundation for the Advancement of Theoretical Physics

contribution to ρ(ε) comes from resonant scattering at

and Mathematics “Basis”.

these states. The corresponding resonance condition is

The authors are indebted to I. S. Burmistrov and P.

kL = πp, where p = 1, 2, . . . and L is either L⁽⁺⁾ⁱ or

M. Ostrovsky for valuable comments.

L^(-)i. As a result, we obtain:

Full text of the paper is published in JETP Letters

[

(

)

]_-1

ρ_res

πn

∑

πn

journal. DOI: 10.1134/S0021364021130038

e-nLp =

exp

-1

ρ₀

2λ²

2√ε

p=1

(10)

1. A. S. Ioselevich and N. S. Peshcherenko, JETP Lett.

108(12), 825 (2018).

However, ρ_res(ε) vanishes at ε → 0 and the finite con-

2. A. S. Ioselevich and N. S. Peshcherenko, Phys. Rev. B

tribution to ρ(ε = 0) has non-resonant character. The

99, 035414 (2019).

most important nonresonant contribution ρ_twin comes

Письма в ЖЭТФ том 114 вып. 1 - 2

2021