Письма в ЖЭТФ, том 114, вып. 11, с. 723 - 726
© 2021 г. 10 декабря
Численное исследование многочастичного рождения в теории φ4:
сравнение с аналитическими результатами
С. В. Демидов+∗, Д. Г. Левков+×, Б. Р. Фархтдинов+∗1)
+Институт ядерных исследований РАН, 117312 Москва, Россия
∗Московский физико-технический институт, 141700 Долгопрудный, Россия
×Институт теоретической и математической физики, МГУ им. М. В. Ломоносова, 119991 Москва, Россия
Поступила в редакцию
3 ноября 2021 г.
После переработки 8 ноября 2021 г.
Принята к публикации 9 ноября 2021 г.
Разработан численный метод для вычисления вероятностей многочастичного рождения в слабо свя-
занных скалярных теориях поля. Метод основан на квазиклассическом подходе Д.Т. Шона, использу-
ющем сингулярные классические решения. Мы применяем метод к процессам 1 → n в теории λφ4 с
ненарушенной симметрией и воспроизводим известные в литературе результаты при 1 ≪ n ≪ λ-1.
DOI: 10.31857/S1234567821230014
1. Введение. Как известно, теория возмущений
ным дальнейшее развитие надежных методов вычис-
не применима для вычисления амплитуд с большим
ления амплитуд многочастичного рождения.
количеством внешних ног n ≳ λ-1, где λ - малая
Некоторое время назад Д.Т.Шон предложил [16]
константа связи [1, 2]. Действительно, пересуммиро-
общий квазиклассический метод вычисления веро-
вание ряда теории возмущений в теории λφ4 [3, 4] по-
ятностей многочастичных процессов при λn ∼ O(1).
казывает [5], что вероятность многочастичного рож-
Метод основан на нахождении комплексных син-
дения экспоненциально подавлена при больших n. К
гулярных решений классических уравнений поля
примеру, инклюзивная вероятность рождения n ≫ 1
с определенными граничными условиями, см. так-
частиц из одной виртуальной частицы имеет вид
же [17, 18]. Несмотря на то, что этот метод явля-
ется достаточно общим, он до настоящего времени c
∑
P1→n (E) ≡
|〈f; E, n
S
φ(0)|0〉|2 ∝ eF1→n/λ,
(1)
успехом применялся только при λn ≪ 1, когда ква-
f
зиклассические конфигурации можно найти с помо-
щью полуаналитических соображений.
В данной работе мы впервые разрабатываем пол-
где
φ(0) создает виртуальное начальное состояние,
ную численную реализацию квазиклассического ме-
S обозначает S-матрицу, суммирование производится
тода сингулярных решений Д. Т. Шона. Наш алго-
по всем n-частичным конечным состояниям с энер-
ритм позволяет вычислять вероятность процессов
гией E, и мы опускаем все несущественные префак-
торы. При этом экспонента подавления F1→n < 0 в
1 → n в ненарушенной четырехмерной теории λφ4
при произвольных λn ∼ O(1) и λE ∼ O(m), где m
правой части выражения (1) является функцией ком-
бинаций λn и λE.
масса частиц в модели. В качестве первого этапа мы
приводим здесь численные результаты при λn ≪ 1 и
В последнее время значительно возрос интерес
демонстрируем, что они согласуются с предсказани-
к изучению многочастичных процессов [6-11]. Это
ями теории возмущений.
произошло из-за высказанной в статье [12] гипоте-
2. Квазиклассическое описание многоча-
зы о том, что, вопреки выражению (1), сечение мно-
стичного рождения. В данном разделе мы описы-
жественного рождения бозонов Хиггса растет фак-
ваем метод работы [16], рассматривая слабосвязную
ториально при высоких энергиях. Данный механизм
(3 + 1)-мерную теорию скалярного поля с действием
“Хиггсовского взрыва” впоследствии критиковался в
∫
работах [8, 13-15], и сейчас ситуация все еще далека
1
(
)
S =
d4x
-φ□φ - φ2 - φ4/2
,
(2)
от разрешения. Таким образом, представляется важ-
2λ
где λ ≪ 1 - константа связи, которая одновременно
1)e-mail: farkhtdinov@phystech.edu
играет роль параметра квазиклассического разложе-
Письма в ЖЭТФ том 114 вып. 11 - 12
2021
723
724
С. В. Демидов, Д. Г. Левков, Б. Р. Фархтдинов
ния. Здесь и далее мы используем единицы массы:
где мы опустили предэкспоненциальные множители
m = 1.
и ввели FJ , равный значению функционала
Удобно ввести источник J следующим образом:
FJ /λ = 2ET - nθ - 2ImS - 2J Reφ(0)/λ
(11)
∑
PJ(E, n) =
|〈f; n, E
Se-
φ(0)/λ|0〉|2.
(3)
на конфигурации φ(t, x).
f
Следует отметить, что в методе Д.Т. Шона ис-
пользуется нетривиальное предположение о том, что
Тогда вероятность (1) равна
экспонента подавления в формуле (1) универсальна,
т.е. не зависит от детальной структуры начально-
P1→n = λ2 lim
PJ/J2.
(4)
J →0
го состояния, если последнее содержит малое число
частиц n ≪ λ-1 [19-22]. В частности, эта экспонен-
В работе [16] величина (3) была представлена в ви-
та не чувствительна к выбору источника в выраже-
де функционального интеграла, который при малых
нии (3). При любом определении J, однако, квази-
λ вычислялся с помощью комплексной седловой кон-
классическое решение должно стать сингулярным в
фигурации φ(t, x). Седловые условия на φ включают
точке t = 0 при J → 0, поскольку его энергия равна
в себя классическое уравнение поля с источником,
нулю при t < 0 и равна E при t > 0, см. форму-
лы (6), (9), и работу [23].
□ φ(x) + φ(x) + φ3(x) = iJδ(4)(x),
(5)
В статьях [16, 24, 25] квазиклассические реше-
ния были получены аналитически при малых λn и ε.
и определенные граничные условия. А именно,
Было продемонстрировано, что в этой области ква-
квазиклассическая конфигурация должна быть
зиклассическая экспонента F1→n согласуется с од-
положительно-частотной в далеком прошлом:
нопетлевым пертурбативным результатом, получен-
∫
ным в работах [4, 26].
φ→ d3ke-ikx+iωkt ak
при
t → -∞,
(6)
3. Численные результаты. Кратко опишем
численный метод решения граничной задачи (5)-
где ak произвольны, а ωk = (k2 + 1)1/2. Кроме то-
(9), позволяющий найти седловые конфигурации при
го, ожидается, что решение линеаризуется также в
произвольных λn и ε. Мы аналитически продолжа-
бесконечном будущем, т.е. при t → +∞:
ем решение на контур комплексного времени, изоб-
∫
раженный на рис. 1. Вдоль этого контура фейнма-
d3k e
ikx
(
)
φ→
√
fke-iωkt + g∗-keiωkt
(7)
(2π)3/2
2ωk
Седловые условия в этом случае связывают друг
с другом положительно- и отрицательно-частотные
части поля φ:
fk = e-θ+2ωkT gk,
(8)
где T и θ представляют собой множители Лагранжа,
возникающие из-за фиксации энергии E и числа час-
тиц n в конечном состоянии. Значения этих величин
можно вычислить по стандартным формулам:
∫
∫
λE = d3k ωk fkg∗k, λn = d3k fkg∗k.
(9)
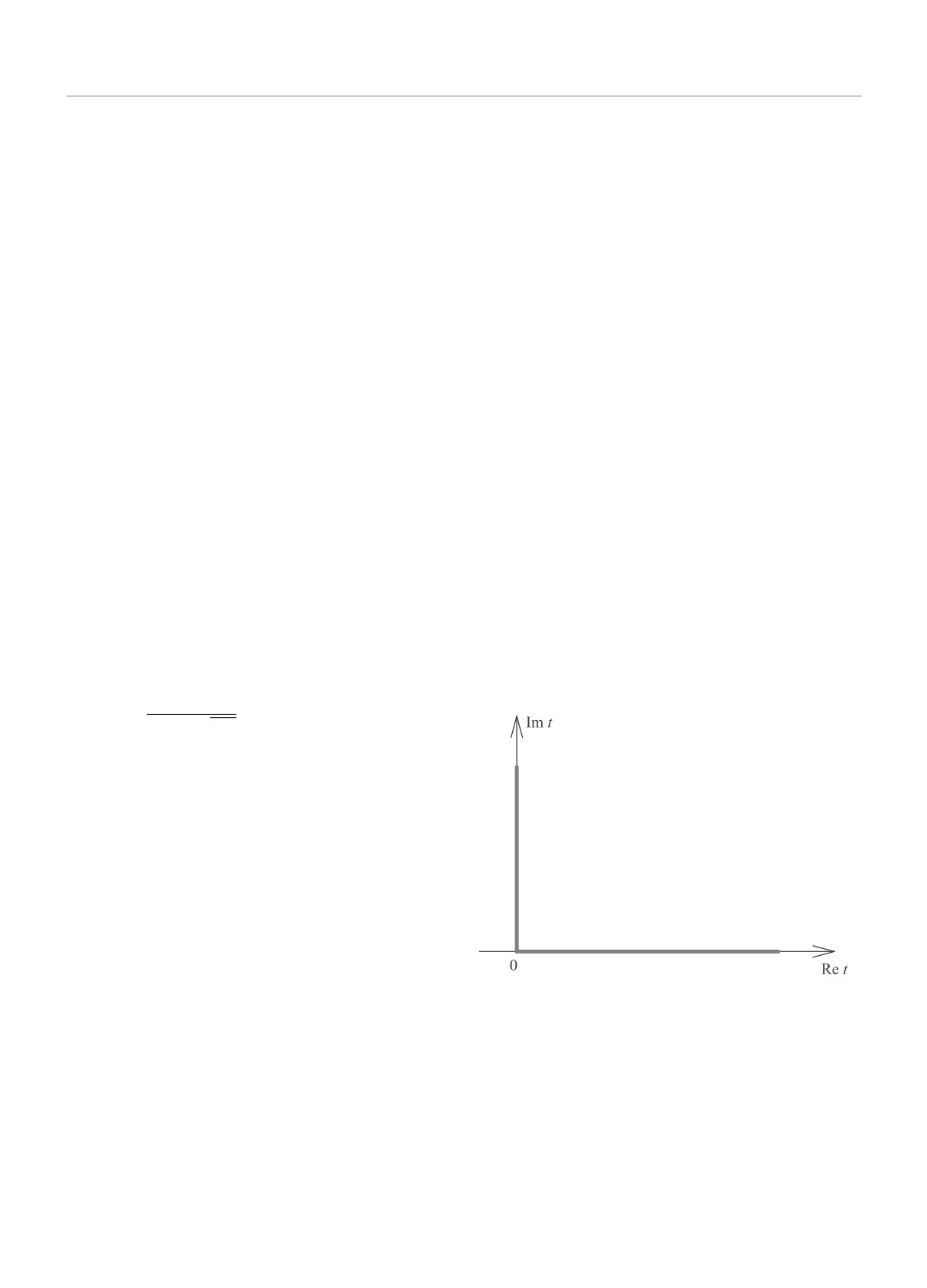
Рис. 1. (Цветной онлайн) Контур в комплексном
В дальнейшем мы будем параметризовать решения с
времени для решения квазиклассической граничной
помощью перемасштабированного числа родившихся
задачи (5)-(9)
частиц λn и средней кинетической энергии на части-
цу ε ≡ E/n - 1.
новское начальное условие (6) имеет вид:
После получения седловых конфигураций веро-
φ(t, x) → 0
при
Im t → +∞.
(12)
ятность (1) может быть вычислена как предел
Кроме того, мы регуляризуем источник, заменяя
P1→n ≈ lim
PJ ≈ lim
eFJ /λ,
(10)
Jδ(4)(x) → j e-x2/2σ2δ(t).
(13)
J →0
J →0
Письма в ЖЭТФ том 114 вып. 11 - 12
2021
Численное исследование многочастичного рождения в теории φ4. . .
725
В дальнейшем мы будем устремлять j и σ к
где ε ≃ O(1) и функция f(ε) неизвестна. Первые три
нулю одновременно. Мы подставляем сферически-
члена в выражении (14) и, в частности, f(ε), могут
симметричный анзац φ
= φ(t, r) в ур. (5) и в
быть найдены с помощью древесных диаграмм. Та-
граничные условия
(6)-(8), после чего дискре-
кое вычисление было проделано в работе [25] чис-
тизуем полученную систему на прямоугольной
ленно при произвольном ε. При ε ≤ 10 полученный
пространственно-временной решетке с узлами
ответ совпал с более простой оценкой снизу, основан-
(tj , rk). Полученная дискретная задача решается с
ной на O(4)-симметричных решениях [28]. Ниже мы
помощью метода Ньютона-Рафсона [27].
используем O(4) оценку для сравнения.
Изменяя малыми шагами значения T, θ, j и σ,
Наши результаты для f(ε) показаны на рис.3
мы находим все регуляризованные численные ре-
кругами с погрешностями, которые оценивают ве-
шения. Соответствующие им экспоненты подавле-
личину ошибки при экстраполяции j
→ 0. Чис-
ния FJ (ε, λn) вычисляются по формуле (11). При-
ленные данные покрывают ограниченный интервал
мер квазиклассической конфигурации φ(t, r) пред-
энергий 0.3 ≤ ε ≤ 6. При меньших ε седловые реше-
ставлен на рис. 2. На графике виден высокий острый
ния становятся нерелятивистскими и не помещают-
ся в доступный для вычислений пространственно-
временной объем. При ε ≥ 6 решение содержит вы-
сокочастотные волны, которые не удается разрешить
на имеющейся решетке.
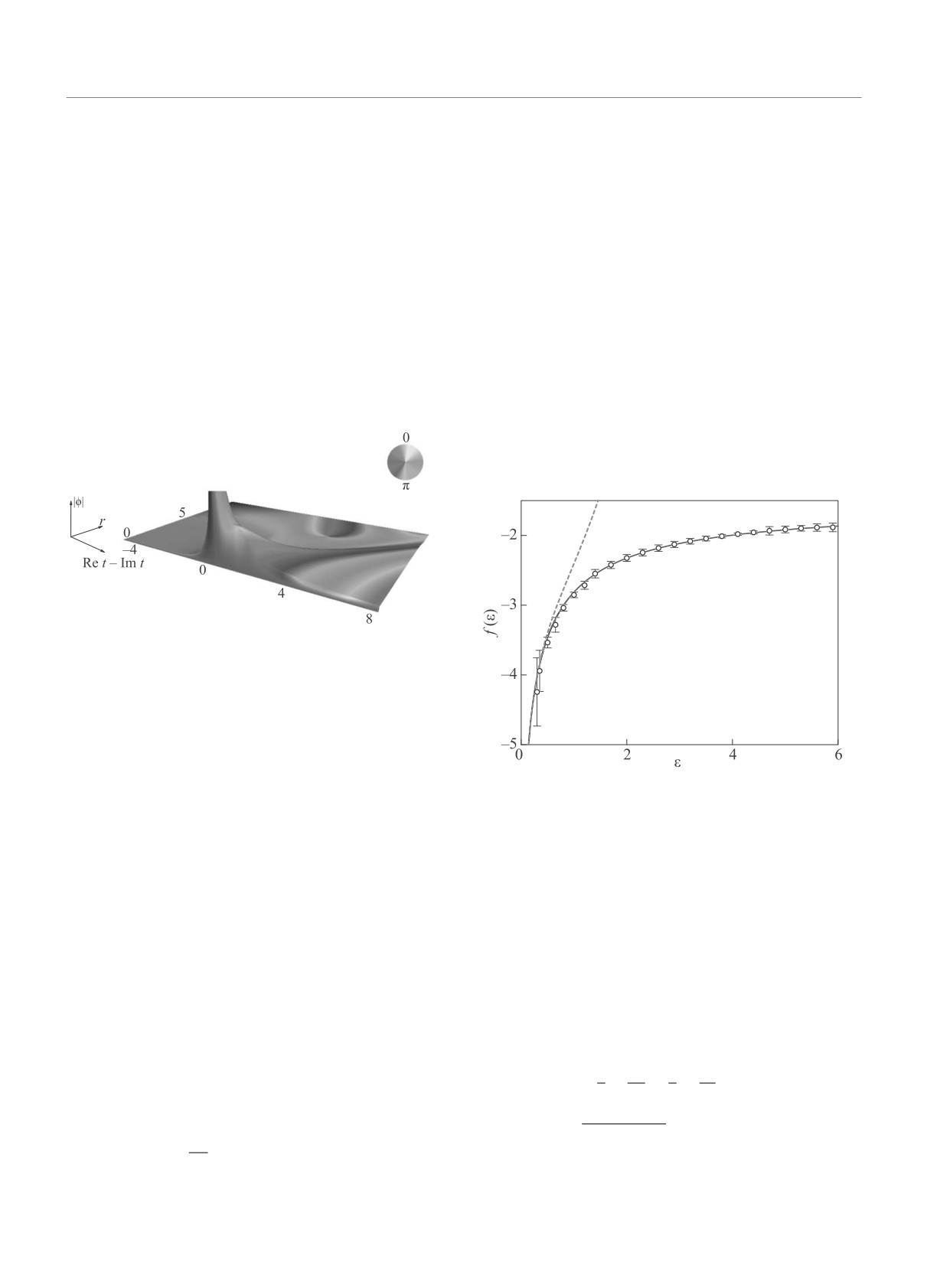
Рис. 2. (Цветной онлайн) Квазиклассическое решение
φ(t, r) с параметрами ε ≈ 1.35, λn ≈ 0.38, j = 0.3, и
σ ≈ 0.1. Цвет обозначает комплексную фазу поля φ
пик в окрестности точки t = r = 0, где находится
источник. Решение становится сингулярным в этой
точке при j, σ → 0. Вылетающие из источника вол-
Рис. 3. (Цветной онлайн) Численные значения f(ε)
ны описывают рожденные частицы конечного состо-
(круги с погрешностями) и древесные результаты:
яния.
O(4)-симметричная оценка из работ [28, 25] (сплошная
Вероятность P1→n ≈ exp{F1→n/λ} получается в
линия) и разложение (15) при малых ε (пунктирная
квазиклассическом выражении (10) в результате пре-
линия)
дельного перехода j, σ → 0. Однако седловые конфи-
гурации не могут быть вычислены непосредственно
Примечательно, что численные данные, пред-
при j = 0, так как в этом случае они сингулярны.
ставленные на рис. 3, согласуются с древесными ре-
Поэтому мы находим экспоненту подавления, экстра-
зультатами, полученными ранее в литературе. В
полируя значения FJ полиномами в точку j = σ = 0
частности, они совпадают с результатом, получен-
при j/σ = const. Технические детали этой процедуры
ным с помощью O(4)-симметричных седловых кон-
будут опубликованы в отдельной работе.
фигураций в работе [28] (сплошная кривая). Кроме
Для проверки нового алгоритма мы сравнили
того, наши результаты приближаются к асимптотике
полученную численно вероятность многочастичного
f (ε) при малых ε (пунктирная линия),
рождения P1→n с уже известными пертурбативными
3
ε
3
17
результатами при малых λn. В этой области квази-
f =
ln
+
-
ε+
2
3π
2
12
классическая экспонента F1→n имеет вид
1327 - 96π2
+
ε2 + O(ε3),
(15)
(
)
432
λn
F1→n = λn ln
- λn + λnf(ε) + O(λ2n2),
(14)
которая была вычислена в работе [24].
16
Письма в ЖЭТФ том 114 вып. 11 - 12
2021
726
С. В. Демидов, Д. Г. Левков, Б. Р. Фархтдинов
4. Заключение. В данной работе разработан
11.
S. Schenk, arXiv:2109.00549.
численный метод для квазиклассического вычисле-
12.
V. V. Khoze and M. Spannowsky, Nucl. Phys. B 926,
ния вероятностей процессов рождения n частиц при
95 (2018); arXiv:1704.03447.
n → +∞ и фиксированном λn, где λ - малая констан-
13.
A. Belyaev, F. Bezrukov, C. Shepherd, and D. Ross,
та связи. Мы проиллюстрировали метод с помощью
Phys. Rev. D 98, 113001 (2018); arXiv:1808.05641.
явного вычисления вероятности процесса 1 → n в
14.
A. Monin, arXiv:1808.05810.
четырехмерной теории λφ4 с ненарушенной симмет-
15.
M. Dine, H. H. Patel, and J. F. Ulbricht,
рией. При λn ≪ 1 наши численные данные согласу-
arXiv:2002.12449.
ются с древесными результатами, полученными ра-
16.
D. T. Son, Nucl. Phys. B
477,
378
(1996);
arXiv:hep-ph/9505338.
нее в литературе. Стоит подчеркнуть, что наш метод
также применим при λn ∼ O(1).
17.
S. Y. Khlebnikov, Phys. Lett. B 282, 459 (1992).
Работа выполнена при финансовой поддержке
18.
D. Diakonov and V. Petrov, Phys. Rev. D 50, 266
Российского фонда фундаментальных исследований
(1994); arXiv:hep-ph/9307356.
в рамках научного проекта # 20-32-90013.
19.
V. A. Rubakov, D. T. Son, and P. G. Tinyakov, Phys.
Lett. B 287, 342 (1992).
Численные вычисления были проведены на Вы-
20.
P. G. Tinyakov, Phys. Lett. B 284, 410 (1992).
числительном кластере Теоретического Отдела ИЯИ
РАН.
21.
G. F. Bonini, A. G. Cohen, C. Rebbi, and
V. A. Rubakov, Phys. Rev. D
60,
076004
(1999);
arXiv:hep-ph/9901226.
1. J. M. Cornwall, Phys. Lett. B 243, 271 (1990).
22.
D. G. Levkov, A. G. Panin, and S. M. Sibiryakov,
2. H. Goldberg, Phys. Lett. B 246, 445 (1990).
J. Phys. A 42, 205102 (2009); arXiv:0811.3391.
3. L. S. Brown, Phys. Rev. D
46, R4125
(1992);
23.
M. V. Libanov, V. A. Rubakov, and S. V. Troitsky, Phys.
arXiv:hep-ph/9209203.
Part. Nucl. 28, 217 (1997).
4. M. B. Voloshin, Nucl. Phys. B 383, 233 (1992).
24.
F. L. Bezrukov, M. V. Libanov, D. T. Son, and
5. M. V. Libanov, V. A. Rubakov, D. T. Son, and
S. V. Troitsky, in
10th International Workshop on
S. V. Troitsky, Phys. Rev. D
50,
7553
(1994);
High-energy Physics and Quantum Field Theory
arXiv:hep-ph/9407381.
(NPI MSU
95), Moscow, MSU
(1996), p. 228;
6. M. B. Voloshin, Phys. Rev. D
95,
113003
(2017);
arXiv:hep-ph/9512342.
arXiv:1704.07320.
25.
F. L. Bezrukov, Theor. Math. Phys. 115, 647 (1998);
7. J. Jaeckel and S. Schenk, Phys. Rev. D 98, 096007
arXiv:hep-ph/9901270.
(2018); arXiv:1806.01857.
26.
M. B. Voloshin, Phys. Rev. D
47, R357
(1993);
8. S. V. Demidov and B. R. Farkhtdinov, JHEP 11, 068
arXiv:hep-ph/9209240.
(2018); arXiv:1806.10996.
27.
W. Press, S. Teukolsky, W. Vetterling, and B. Flannery,
9. V. V. Khoze and J. Reiness, Phys. Rept. 822, 1 (2019);
Numerical Recipes: The Art of Scientific Computing, 3rd
arXiv:1810.01722.
ed., Cambridge University Press (2007).
10. J. Jaeckel and S. Schenk, Phys. Rev. D 99, 056010
28.
F. L. Bezrukov, M. V. Libanov, and S. V. Troitsky, Mod.
(2019); arXiv:1811.12116.
Phys. Lett. A 10, 2135 (1995); arXiv:hep-ph/9508220.
Письма в ЖЭТФ том 114 вып. 11 - 12
2021