Pis’ma v ZhETF, vol. 114, iss. 11, pp. 777 - 778
© 2021 December 10
Double quantum dot FET on graphene
H. Mohammadpour1)
Department of Physics, Azarbaijan Shahid Madani University, 53714-161, Tabriz, Iran
Submitted 16 October 2021
Resubmitted 26 October 2021
Accepted 5 November 2021
DOI: 10.31857/S1234567821230099
Applications of quantum dots (QD) in electronic and
the inside of conduction band only at the two quantum
optoelectronic devices rest beside the discrete energy
dots (QD-1 and QD-2).
levels of QDs [1-3]. Specially, QD-based nanoelectronic
Charge density of channel and current are computed
devices benefit from resonant tunneling of carriers via
by self-consistently solving 3-dimensional Poisson equa-
these levels that has wide applications in electronics [4-
tion and the non-equilibrium Green’s function (NEGF)
6]. Light-emitting FETs as well as phototransistors are
formalism [14]. Real space tight-binding Hamiltonian is
modern devices that exploit the discrete energy levels of
considered in nearest neighbor interaction approxima-
device [7-9]. Among the many devices are the graphene-
tion for atomistic pz -orbital; H = 2.7Σi,j δi,j±1 [15]. The
based FETs [2, 10, 11]. Its unique physical and electronic
retarded Green’s function of device is defined as:
properties, make graphene-based QDs promising candi-
G(E) = [(E + iη)I - H - U - Σs - Σd]-1,
(1)
dates for quantum devices. In our previous works QD-
channel on graphene FET was established by different
where E is energy with I being a unit matrix and
engineering of the FET [2, 3]. QDs are also of interest
η = 10-4 (eV) is a real number. U is the matrix of poten-
as potential logic elements in future quantum computers
tial energy. The Hamiltonian matrix contains channel
[12, 13].
region of GNR and some unit cells of source and drain.
In the novel graphene-based Metal-Oxide-
The effects of semi-infinite source and drain GNR are in-
Semiconductor (MOS) FET model of this research, the
cluded in left- and right-connected self-energies, ΣL(ors)
gate electrode is not directly attached to the dielectric
and ΣR(ord) which are calculated according to the iter-
layer on top of the channel, but two separate metallic
ative algorithm described in [16].
plates on top of dielectric layer cover two regions of
The channel energy level broadening due to the
channel. Then, a single metallic gate electrode is laid
source (drain) contact is Γs(d) = i(Σs(d) - Σ†s(d)).
on top of the plates. Hence, the single gate electrode is
The matrix of potential energy, U at Eq. (1) is
equi-potential with the plates and turn them into gate
achieved by solving Poisson equation
electrodes with equal voltages.
By this geometry implementations, the gate voltage
∇(ε∇U) = e2n.
(2)
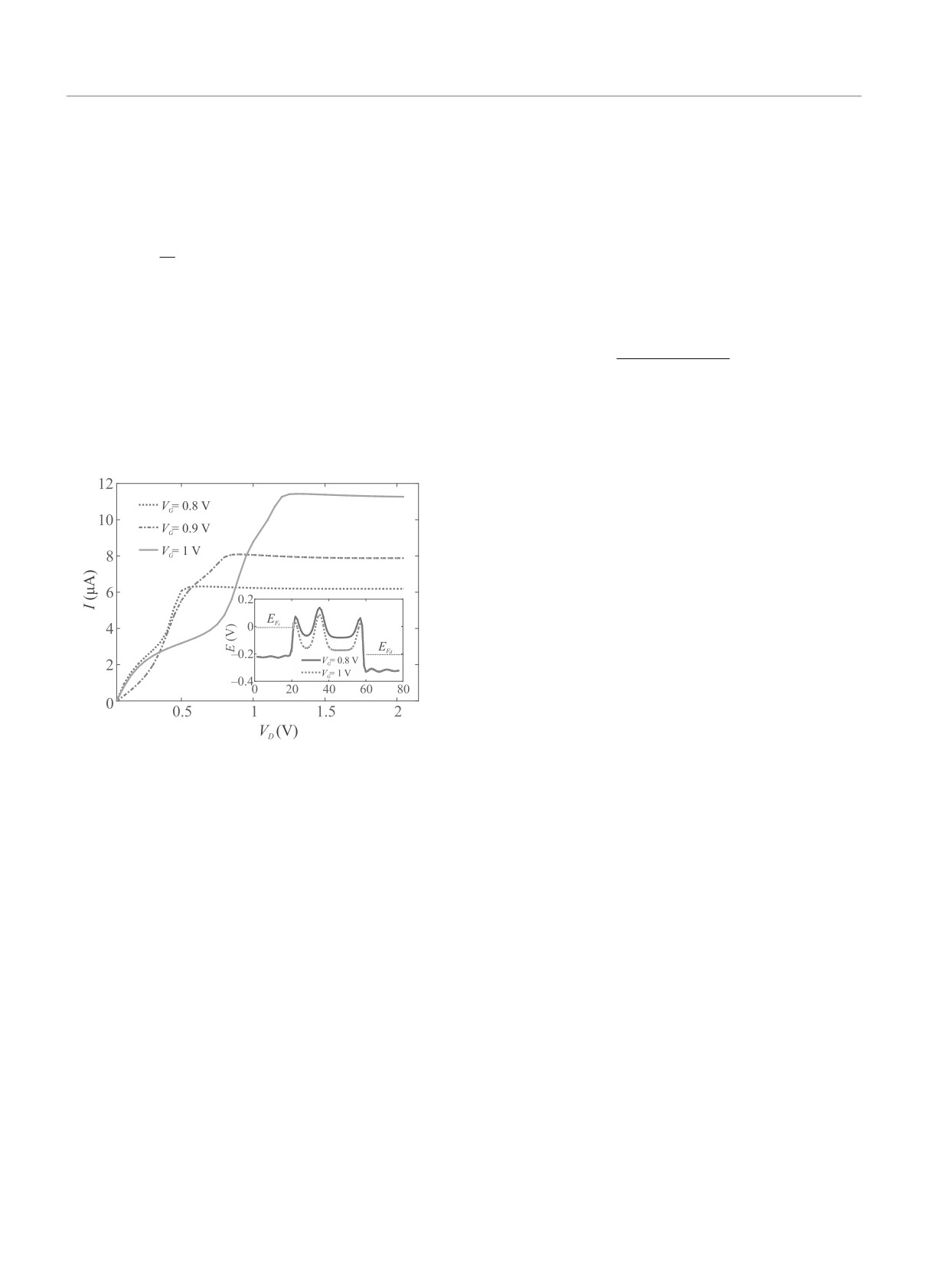
is applied to a set of two isolated QDs at the chan-
nel of the double-QD FET. The current-carrying re-
The electron density is calculated from electron corre-
gion of the double-QD FET is on a single armchair
lation function, Gn as:
graphene nanoribbon (A-GNR) with 13 carbon atoms
∫ +∞
dE
in the width direction that has a band gap of 0.72 eV.
n=2
Gn(E), Gn = GΣinG†
(3)
The channel of FET which is controlled by the gate volt-
-∞
2π
age is at the middle region of GNR and highly doped
with the in-scattering function of contacts, Σin, defined
conducting source and drain regions of GNR are at the
as:
two sides of channel. The GNR, is sandwiched between
two dielectric SiO2 layers of dielectric constant k = 3.9
Σin(E) = Γs(E)fs(E, EFs) + Γd(E)fd(E, EFd)
(4)
and 1 nm thickness.
The GNR-FET structure is symmetric at the top
fs(d)(E, EFs(d)) is the Fermi-Dirac distribution function
and bottom of GNR. The Fermi energy is transferred to
of source (drain) with Fermi energy equal to EFs(d).
Gn is defined in terms of retarded Green’s function
G(E) which is calculated from relation (1) using the
1)e-mail: mhmdpour@gmail.com
recursive Green’s function algorithm [17] provided that
Письма в ЖЭТФ том 114 вып. 11 - 12
2021
777