Письма в ЖЭТФ, том 114, вып. 6, с. 391 - 399

Решение уравнения Шредингера на квантовом компьютере

методом Залки-Визнера с учетом квантовых шумов

Ю. И. Богданов¹⁾, Н. А. Богданова, Д. В. Фастовец, В. Ф. Лукичев

Физико-технологический институт им. К. А. Валиева РАН, 117218 Москва, Россия

Поступила в редакцию 10 августа 2021 г.

После переработки 12 августа 2021 г.

Принята к публикации 12 августа 2021 г.

Рассмотрено моделирование квантовых систем на квантовом компьютере с использованием метода

Залки-Визнера с учетом квантовых шумов. Эффективность разработанных методов и алгоритмов проде-

монстрирована на примере решения нестационарного уравнения Шредингера для частицы в потенциале

Пешль-Теллера. Выполнено сравнение развитой аналитической теории влияния квантовых шумов на

точность моделирования с результатами численных расчетов методом Монте-Карло. Осуществлен про-

гноз точности решения уравнения Шредингера для многоэлектронной системы в зависимости от числа

электронов и для различных уровней шума.

DOI: 10.31857/S1234567821180099

1. Введение. Квантовые компьютеры позволя-

Визнера активно исследуется различными научны-

ют достичь экспоненциального ускорения при ре-

ми группами. Эффективность данного алгоритма на

шении определенных практически значимых задач.

небольшом числе кубитов была доказана и проде-

Одной из важнейших таких задач является задача

монстрирована численно [6], а также была проведена

моделирования квантовых систем. Необходимость в

апробация с использованием облачного квантового

проведении высокоточного моделирования эволюции

процессора IBM [7]. Универсальность данного алго-

квантовых систем различной природы возникает в

ритма позволяет применять его к самым различным

таких научных областях, как физика [1], квантовая

квантовым системам, включая системы многих тел с

химия [2] и компьютерные технологии [3]. Наибо-

кулоновским взаимодействием [8] и системы кванто-

лее прямой способ решения задач в случае квантово-

вых гармонических осцилляторов [9].

механических систем - это поиск решения нестацио-

Отметим, что было разработано несколько мо-

нарного уравнения Шредингера. Это уравнение, ко-

дификаций данного алгоритма. Например, описана

нечно, можно пытаться решать численно с исполь-

адаптация алгоритма Залки-Визнера к моделирова-

зованием классического компьютера. Однако, в этом

нию химических реакций [10]. Особое внимание авто-

случае, для проведения высокоточного моделирова-

ры этой работы уделяют приготовлению необходимо-

ния реальных практически важных задач, понадо-

го квантового состояния, что является важной про-

бится экспоненциально большое количество ресурсов

блемой при реализации ряда квантовых алгоритмов.

(по памяти и времени выполнения). С другой сторо-

В работе проводится апробация при моделировании

ны, для моделирования эволюции квантовой систе-

небольшого числа атомов (4-5), а также приводят-

мы можно использовать квантовый компьютер. По-

ся методы расчета химически значимых наблюдае-

казано, что квантовый компьютер способен эффек-

мых. Другое исследование [11] посвящено модифика-

тивно решать нестационарное уравнение Шредин-

ции алгоритма Залки-Визнера, которая превосходит

гера при использовании алгоритма Залки-Визнера

явную разностную схему по точности, однако требует

[4, 5], который является одним из основных методов

экспоненциальных затрат по памяти. Разработанный

анализа квантовых систем с использованием кванто-

алгоритм позволяет проводить моделирование дина-

вых вычислений.

мики в реальном времени, что было подтверждено в

Рассматриваемый алгоритм позволяет использо-

численных экспериментах.

вать ресурсы квантовых вычислений для модели-

Основное препятствие на пути развития кванто-

рования эволюции квантовой системы, описываемой

вых компьютеров и квантовых симуляторов связа-

произвольным гамильтонианом. Алгоритм Залки-

но с влиянием декогерентизации и квантовых шу-

мов на динамику многокубитных квантовых систем

¹⁾e-mail: bogdanov_yurii@inbox.ru

[12]. Учет влияния декогерентизации и квантовых

Письма в ЖЭТФ том 114 вып. 5 - 6

2021

391

392

Ю. И. Богданов, Н. А. Богданова, Д. В. Фастовец, В. Ф. Лукичев

(

)

шумов на эффективность работы алгоритма Залки-

exp

Δt

- оператор эволюции в импульсном

Визнера представляет собой актуальную и еще не

пространстве, определяемый оператором кинетиче-

исследованную задачу. Подобные исследования, на

; IQFT (Inverse Quantum Fourier

наш взгляд, критически важны для практической

Transform) - обратное квантовое преобразование Фу-

реализации рассматриваемого квантового алгорит-

рье, обеспечивающее переход от импульсного пред-

ма. Получаемые при этом результаты могут быть

ставления снова в координатное.

использованы для улучшения качества работы ал-

Прямое квантовое преобразование Фурье (QFT)

горитма как на программном, так и на аппаратном

волновой функции, обеспечивающее переход от ко-

уровнях. Данному исследованию алгоритма и посвя-

ординатного представления к импульсному, есть:

щена настоящая работа. В разделе 2 дается описание

∫

(

)

общей идеи метода Залки-Визнера. Важно отметить,

ψ(p) =

√

exp

px ψ(x)dx.

что каждый шаг эволюции квантового состояния ре-

2πℏ

ℏ

гистра кубитов связан с применением прямого и об-

Обратное квантовое преобразование Фурье (IQFT),

ратного преобразования Фурье и, таким образом,

обеспечивающее переход от импульсного представле-

точность преобразования Фурье в квантовом реги-

ния к координатному, есть:

стре лимитирует итоговую точность решения неста-

ционарного уравнения Шредингера. Оценка влияния

∫

(

)

квантовых шумов на квантовое преобразование Фу-

ψ(x) =

√

exp

ψ(p)dp.

2πℏ

ℏ

рье с использованием подхода на основе теории кван-

товых операций рассмотрена в разделе 3. В разде-

Наличие квантового регистра из n кубитов обеспе-

ле 4 представлена апробация разработанных мето-

чивает N = 2ⁿ точек дискретизации и отвечает эво-

дов и алгоритмов на примере рассмотрения динами-

люции соответствующей дискретизированной кван-

ки квантовой частицы в потенциале Пешль-Теллера.

товой системы в гильбертовом пространстве размер-

В разделе 5 представлены выводы по работе.

ности N.

2. Общая идея метода Залки-Визнера. Рас-

Представление эволюции в виде (1) является хо-

смотрим для простоты одномерную динамику кван-

рошим приближением при достаточно больших n_t в

товой частицы. Формальное обобщение на случай

силу формулы Троттера:

многомерной многочастичной системы производится

непосредственно. Полное время эволюции t разбива-

lim

[exp(-iAt/n_t) exp(-iBt/n_t)]nt = exp[-i(A+B)t].

nt→∞

ется на достаточное число интервалов n_t. Моделиро-

(2)

вание осуществляется на отдельном, малом интерва-

Известно, что если операторы A и B не коммутиру-

ле Δt = t/n_t и повторяется n_t раз.

ют, то

Работа алгоритма Залки-Визнера начинается с

учета влияния оператора потенциальной энергии в

exp[-i(A + B)t] = exp(-iAt)exp(-iBt)

координатном представлении, а затем, посредством

при конечных временах t. Однако, в силу формулы

преобразования Фурье, производится переход в им-

пульсное представление, в котором обеспечивается

Троттера (2), такого рода соотношение выполняет-

ся для малых времен Δt. В нашем случае в роли A

учет оператора кинетической энергии, после чего

происходит возврат в исходное координатное пред-

и B выступают операторы кинетической и потенци-

альной энергии соответственно. В данной работе бы-

ставление посредством обратного преобразования

Фурье. Таким образом, оператор унитарной эволю-

ли использованы две формы формулы Троттера [12],

отличающиеся порядком точности:

ции в координатном пространстве на малом интер-

вале времени Δt есть:

exp[-i(A + B)Δt] =

(

)

(

)

i p²

= exp[-iAΔt] exp[-iBΔt] + O((Δt)²),

U_Δt = IQFT exp

Δt QFT exp

V (x)Δt

ℏ 2m

ℏ

(1)

exp[-i(A + B)Δt] =

(

)

Здесь exp

-^iℏV (x)Δt

- оператор эволюции в ко-

= exp[-iAΔt/2] exp[-iBΔt] exp[-iAΔt/2]+O((Δt)³).

ординатном пространстве, определяемый потенциа-

лом V (x); QFT (Quantum Fourier Transform) - кван-

Первую из этих формул будем называть стан-

товое преобразование Фурье, обеспечивающее пере-

дартной, а вторую (более точную) - модифицирован-

ход от координатного представления в импульсное;

ной.

Письма в ЖЭТФ том 114 вып. 5 - 6

2021

Решение уравнения Шредингера на квантовом компьютере методом Залки-Визнера. . .

393





3. Влияние квантовых шумов на квантовое





преобразование Фурье: подход на основе тео-





U_θ = U^idealθ · V^noiseθ =



,

(4)

рии квантовых операций. Идеальная квантовая





 0



схема представляет собой последовательный набор

e^-i(θ+e·ξ)

унитарных квантовых преобразований {U_i}. Опера-

ции U_i обычно действуют на один, два или, что ре-

где U^idealθ - идеальный оператор поворота фазы, а

же, на три кубита. Для реальных физических си-

Vnoiseθ - соответствующий ему оператор шума. Для

стем реализация каждого преобразования U_i под-

простоты изложения мы характеризуем уровень шу-

разумевает наличие соответствующего гамильтони-

ма в формулах (3) и (4) одним и тем же параметром

ана H_i, осуществляющего операцию U_i за время t_i:

U_i = e-iHitⁱ/ℏ, однако для дальнейшего рассмотре-

Можно показать [15], что зашумляющее преобра-

ния достаточно ограничиться заданием операторов

зование V_noise для однокубитовых операторов (3) ста-

U_i. Задача моделирования работы квантовой схемы

тистически эквивалентно следующему набору опера-

состоит в нахождении итогового состояния системы

торов Крауса

U_s · U_s-1 · . . . · U₂ · U₁|ψ₀〉 по начальному состоянию

(

)

(

)

√

|ψ₀〉.

E₁ =

λ₁

, E₂ =

Для описания открытых квантовых систем, под-

-1

верженных влиянию квантовых шумов, необходи-

где

мо использовать формализм матриц плотности. При

этом преобразования квантовых состояний расширя-

λ₁ =

(1 + exp(-2e²)), λ₂ =

(1 - exp(-2e²)).

(5)

ются от унитарных до так называемых квантовых

операций [13, 14]. Действие произвольной квантовой

Аналогично, для зашумленного оператора контроли-

операции на квантовое состояние в виде матрицы

руемого сдвига фазы V^noiseθ из (4) имеем

плотности ρ может быть представлено в виде опе-





раторной суммы:









∑

E₁ =



,





ε(ρ) =

E_iρE^†i,

 0



√

(6)

где операторы E_i удовлетворяют условию нормиров-





∑

ки_i E^†iE_i = I (сохранение нормы) и называются









операторами Крауса.

E₂ =



,





В терминах векторов-состояний шум может быть

 0



√

введен при помощи метода Монте-Карло. Например,

1-P

произвольный однокубитовый вентиль U_ideal может

быть заменен на зашумленный аналог следующим

где P = exp(-e²).

образом:

Пусть начальное состояние системы, поступаю-

щей на вход моделируемой схемы, чистое. Тогда со-

ответствующая матрица плотности имеет единичный

U =U_ideal ·V_noise,

ранг. Каждый оператор Крауса задает один из аль-

(

)

(3)

тернативных путей эволюции квантовой системы, в

cos(eξ) sin(eξ)

V_noise =

связи с чем каждая квантовая операция увеличивает

- sin(eξ) cos(eξ)

ранг матрицы плотности в геометрической прогрес-

сии вплоть до максимально возможного ранга r = 2ⁿ,

где ξ - случайная величина с нормальным распре-

где n - число кубитов в системе. Для сокращения

делением N(0, 1), а e - уровень ошибки. Такое пред-

числа необходимых вычислительных ресурсов будем

ставление зашумленного преобразования оказывает-

на каждом шаге аппроксимировать полученную мат-

ся очень полезным и будет использоваться нами да-

рицу плотности матрицей плотности меньшего ран-

лее. Аналогичным образом может быть представ-

га (сохраняя лишь фиксированное число максималь-

лен зашумленный оператор контролируемого пово-

ных собственных значений и обнуляя остальные). Та-

рота фазы, используемый в квантовом преобразова-

кая аппроксимация сохраняет положительную опре-

нии Фурье:

деленность матрицы плотности; однако ее след при

Письма в ЖЭТФ том 114 вып. 5 - 6

2021

394

Ю. И. Богданов, Н. А. Богданова, Д. В. Фастовец, В. Ф. Лукичев

√

P +f

√1-P )²

этом уменьшается, что соответствует уменьшению

где

P_R =⁽

(1+f²)⁴

доли представителей, эволюционирующих по “пра-

Развитый приближенный подход позволяет про-

вильному” пути.

гнозировать влияние квантовых шумов на точность

Прямое применение аппроксимации единичным

многокубитовых квантовых схем, которые пока еще

рангом к квантовому преобразованию Фурье ведет

не реализованы “в железе” и которые не могут быть

к следующей оценке, задающей точность преобразо-

промоделированы ни на каких современных или пер-

вания для случайного состояния [15]:

спективных классических компьютерах.

Апробация на основе потенциала

F_QFT = P^nHP^n(n-1)/8R,

(7)

Пешль-Теллера. В настоящем разделе пред-

где P_H =¹² (1 + exp(-2e²)), P_R = exp(-e²) - вероят-

ставлены результаты численных экспериментов,

ности правильной работы преобразований Адамара

направленных на демонстрацию корректности при-

и условного сдвига фазы соответственно.

веденных выше формул и методов. Для этого было

Представленная формула использует тот факт,

осуществлено моделирование динамики квантовой

что преобразование Фурье содержит n преобразова-

частицы, находящейся в потенциале Пешль-Теллера.

ний Адамара и n(n - 1)/2 двухкубитовых фазовых

Данный потенциал задается следующей формулой

преобразований. При этом, для случайного состоя-

[16, 17]:

ния на входе, равномерно распределенного по ме-

V₀

ℏ²

λ(λ - 1)

ре Хаара, двухкубитовое фазовое преобразование на

V (x) = -

(10)

ch²(x/a)

2ma² ch²(x/a)

каждом шаге действует только на четвертую часть

от общего числа амплитуд случайного состояния,

Здесь безразмерный параметр λ характеризует глу-

поэтому двухкубитовый шум порождает показатель

бину потенциальной ямы. Параметры V₀ и a есть

степени n(n-1)/8. Данная формула задает довольно

величины, характеризующие глубину потенциальной

грубую оценку для вероятности совпадения.

ямы и ее пространственный масштаб.

Рассматриваемая оценка может быть существен-

Рассматриваемая задача допускает точное кван-

но улучшена приведением к главным осям операто-

товомеханическое решение [16,17]. Ограничимся рас-

ров Крауса для вентиля условного сдвига фазы (6).

смотрением состояний дискретного спектра (т.е. свя-

Хорошо известно, что операторы Крауса определе-

занных состояний, отвечающих отрицательной или

ны с точностью до широкого унитарного произвола.

нулевой энергии). Соответствующие энергетические

Путем подбора подходящего унитарного преобразо-

уровни есть:

вания диагонали матриц становятся ортогональны-

ℏ²

ми друг по отношению к другу. Операторы Крауса в

E_n = -

(λ - 1 - n)²,

(11)

2ma²

новом представлении имеют вид [15]:





где n = 0, 1, . . . , n_max. Заметим, что связанным состо-

яниям отвечает условие: n_max ≤ λ - 1.









Волновые (ненормированные) функции стацио-

E₁ =

√



,





нарных состояний, выраженные через гипергеомет-

1+f²

 0



√

рическую функцию, есть:

P +f

1-P

ψ_n(x) =

(8)

ch^λ-1-n(x/a)





-f

[

]





× F -n,2λ - 1 - n,λ - n,

(1 - th(x/a)) ,

(12)



-f





E₂ =

√

,





1+f²

-f

 0



где -∞ < x < ∞.

√

-f

P +

1-P

Другая форма записи (через полиномы Гегенбау-

эра, являющиеся частной формой полиномов Якоби)

√1+3P -P -1_√.

где P = exp(-e²), f =

P (1-P )

имеет вид:

Операторы Крауса (6) и (8) унитарно эквивалент-

ны, а следовательно, определяют одну и ту же кван-

ψ_n(x) =

Cn-n-2

(th(x/a)).

(13)

ch^λ-1-n(x/a)

товую операцию. Тогда улучшенная оценка для точ-

ности преобразования Фурье случайного состояния

В примерах, представленных ниже, проводится

есть:

сравнение результатов численных расчетов мето-

F_QFT = P^nHP˜^n(n-1)/8R,

(9)

дом Залки-Визнера с учетом квантовых шумов с

Письма в ЖЭТФ том 114 вып. 5 - 6

2021

Решение уравнения Шредингера на квантовом компьютере методом Залки-Визнера. . .

395

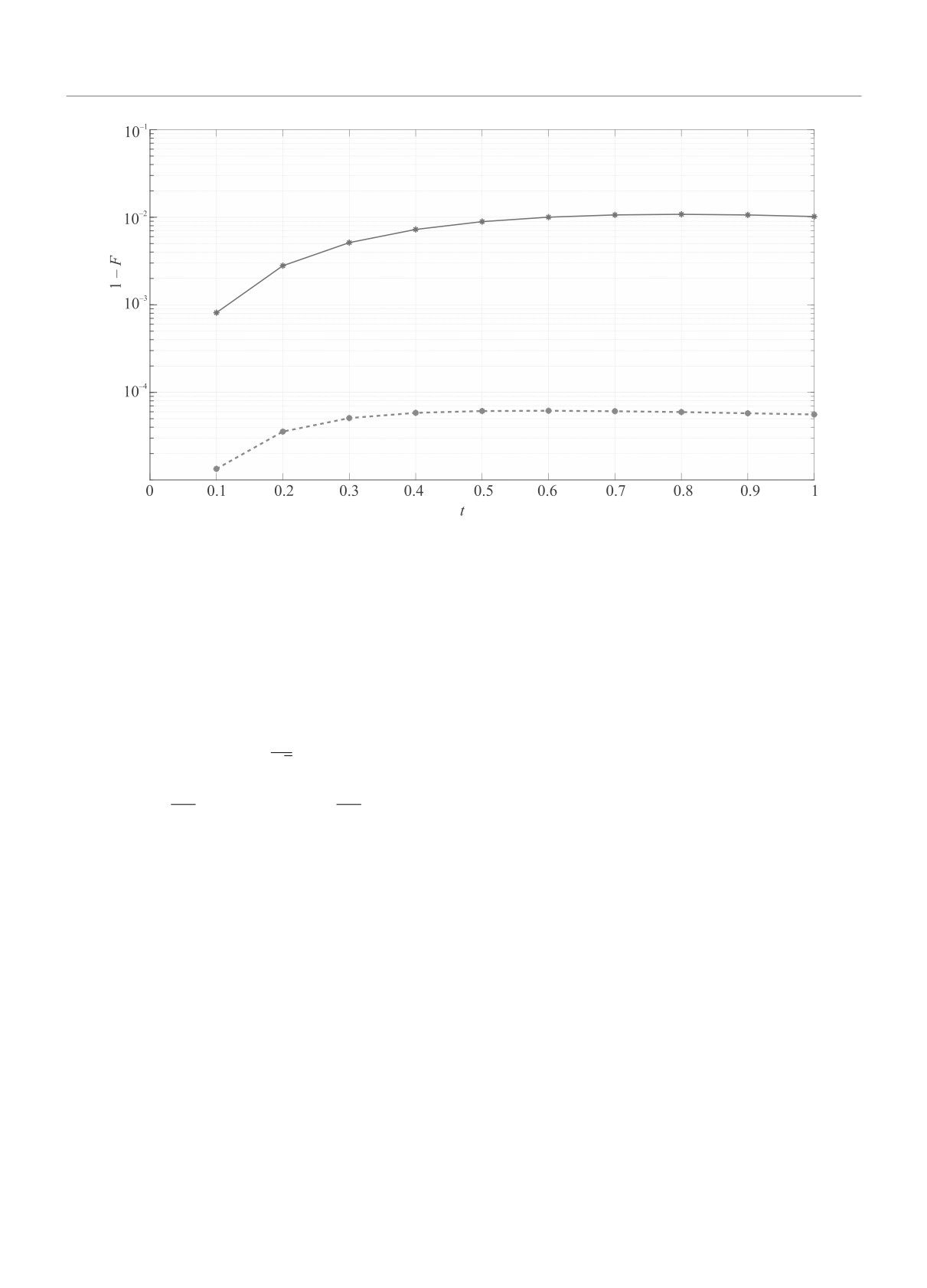
Рис. 1. (Цветной онлайн) Зависимость потерь точности от времени эволюции квантового состояния для стандартной

(верхняя сплошная кривая) и модифицированной формул Троттера (нижняя штриховая кривая)

точным аналитическим решением нестационарного

квантовом вычислителе. Рассматривалась эволюция

уравнения Шредингера.

квантового состояния регистра из

кубитов на

Рассматривалось следующее состояние, представ-

интервале времени 0 ≤ t ≤ 1 с шагом по времени

ляющее собой суперпозицию нулевой и первой мо-

Δt = 0.05 при уровне шума e = 0.01.

ды (глубина потенциальной ямы и пространствен-

Сравнение развитой теории влияния квантовых

ный масштаб были выбраны соответственно равны-

шумов на точность моделирования с результатами

ми λ = 4 и a = 1):

численных расчётов представлено на рис. 3 и 4.

Из рисунка 3 видно, что улучшенная оценка на

ψ(x, t) =

√ ×

(14)

основе формулы (9) имеет много лучшую точность

по сравнению с оценкой на основе (7) и визуально

[

(

)

(

)

]

E₀t

E₁t

совпадает с численными экспериментами. Рассмат-

× exp

-i

ψ₀(x) + i exp

-i

ψ₁(x)

ℏ

ривалась эволюция квантового состояния регистра

В качестве показателя точности рассматривалась ве-

из 7 кубитов на интервале времени 0 ≤ t ≤ 1 с ша-

роятность совпадения F (Fidelity), которая задает-

гом по времени Δt = 0.05 при уровне шума e = 0.01,

ся формулой F

= |〈ψ_noise|ψ_theor〉|² и характеризу-

было выполнено 30 экспериментов.

ет степень соответствия между зашумленной вол-

На рисунке 4 видно, что улучшенная оценка дает

новой функцией ψ_noise, полученной методом Залки-

адекватный прогноз точности для различного чис-

Визнера, и точным (но дискретизованным) решени-

ла кубитов в регистре. Рассматривалась эволюция

ем ψ_theor.

квантового состояния регистров из 7, 8 и 9 кубитов

На рисунке 1 представлено сравнение стандарт-

на интервале времени 0 ≤ t ≤ 1 с шагом по времени

ной и модифицированной формул Троттера для си-

Δt = 0.05 при уровне шума e = 0.01, для каждого

стемы из 7 кубитов при Δt = 0.1. Видно, что модифи-

регистра было выполнено по 30 экспериментов.

цированная формула Троттера в рассматриваемом

В представленных на рис. 3 и 4 случаях ошибка

примере обеспечивает ошибку, которая более чем на

дискретизации, обусловленная конечным числом ку-

2 порядка ниже, чем ошибка стандартной формулы

битов в регистре, оказалась пренебрежимо малой по

Троттера.

сравнению с ошибками, вызванными шумами в кван-

Рисунок 2 дает наглядное представление об

товом преобразовании Фурье. По этой причине уро-

уровне влияния квантовых шумов на точность

вень точности F оказался более низким для большего

получения решения уравнения Шредингера на

числа кубитов в регистре.

Письма в ЖЭТФ том 114 вып. 5 - 6

2021

396

Ю. И. Богданов, Н. А. Богданова, Д. В. Фастовец, В. Ф. Лукичев

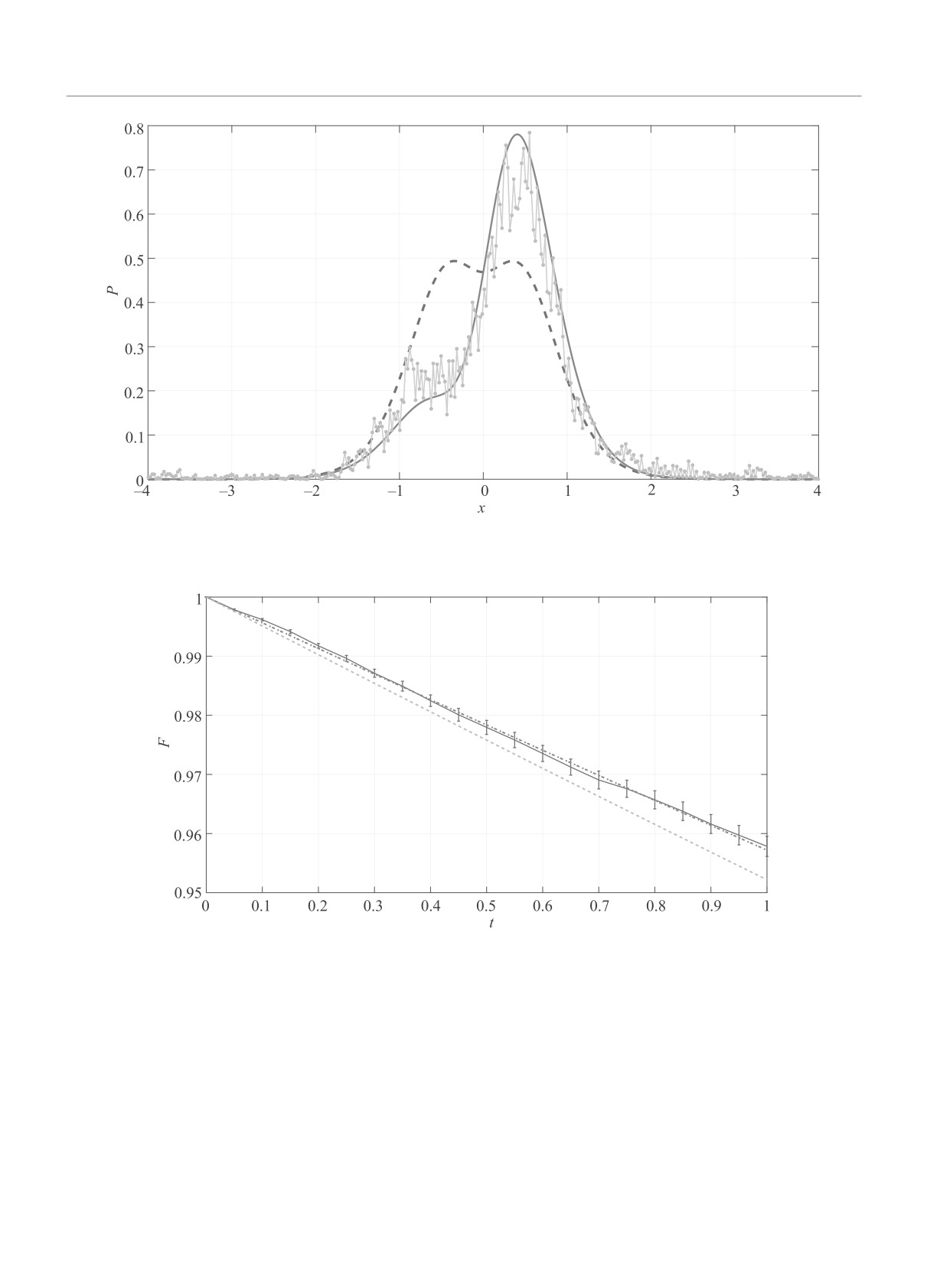
Рис. 2. (Цветной онлайн) Иллюстрация эволюции плотности распределения в координатном представлении. Начальное

состояние - штриховая кривая, конечное состояние в момент времени t = 1 - сплошная кривая, зашумленное решение

Залки-Визнера представлено набором точек

Рис. 3. (Цветной онлайн) Зависимость точности алгоритма Залки-Визнера моделирования движения частицы в по-

тенциале Пешль-Теллера от времени эволюции состояния. Исходная теоретическая оценка - штриховая линия, улуч-

шенная оценка - штрих-пунктирная линия, зашумленное численное решение Залки-Визнера - сплошная линия с

отмеченными среднеквадратичными ошибками

Теоретические кривые на рисунках 3 и 4 постро-

ле степени связан с тем, что на каждом шаге пре-

ены по следующей формуле, основанной на формуле

образование Фурье совершается дважды (прямое и

(9):

обратное преобразования).

F = (F_QFT)2t/Δt .

(15)

На рисунке 5 представлен прогноз точности ре-

В формуле (15) величина t/Δt представляет собой

шения уравнения Шредингера для многоэлектрон-

число шагов по времени, коэффициент 2 в показате-

ных систем с различным числом электронов и с уче-

Письма в ЖЭТФ том 114 вып. 5 - 6

2021

Решение уравнения Шредингера на квантовом компьютере методом Залки-Визнера. . .

397

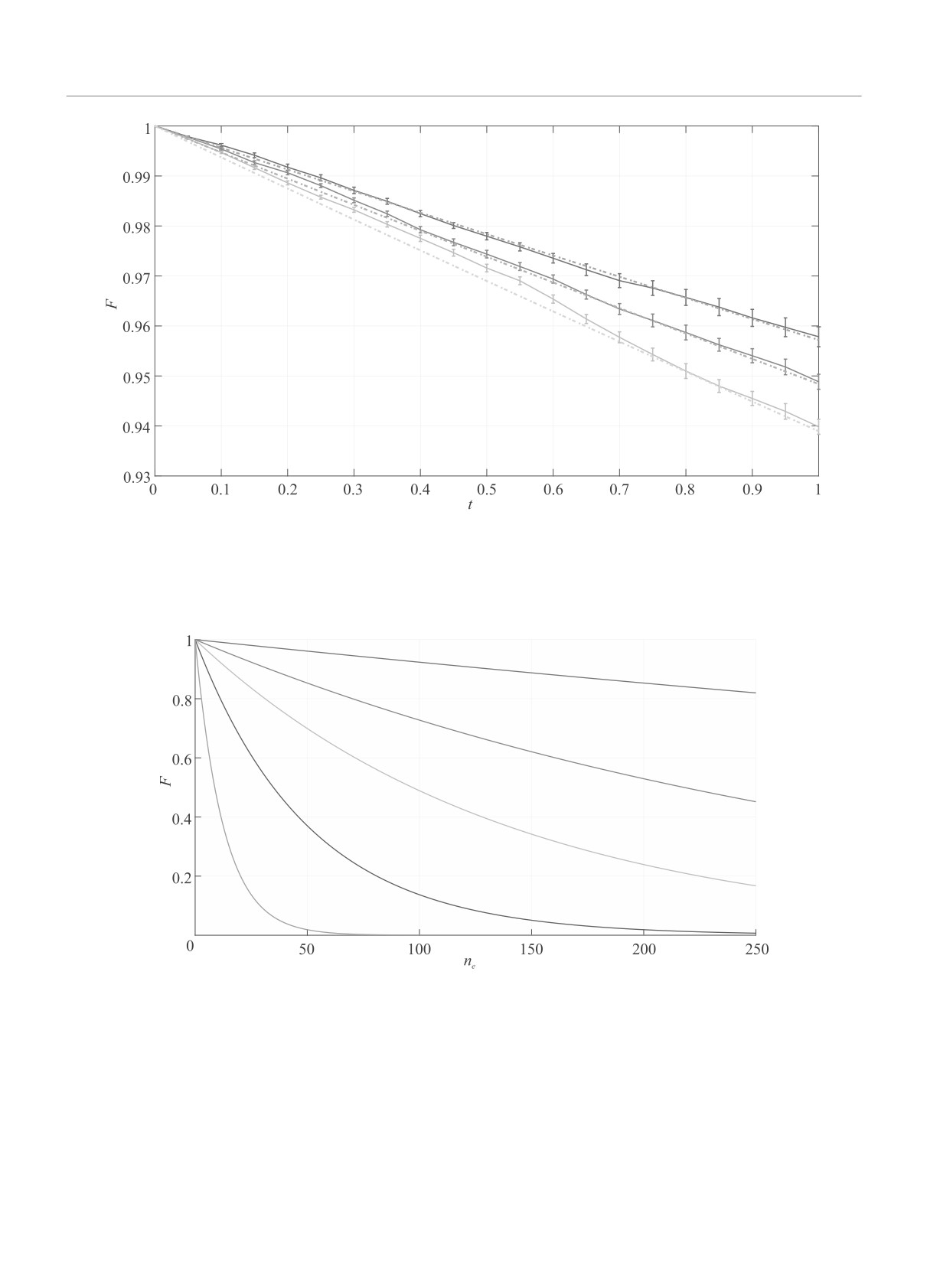
Рис. 4. (Цветной онлайн) Зависимость точности алгоритма Залки-Визнера моделирования движения частицы в по-

тенциале Пешль-Теллера от времени эволюции состояния при использовании различного числа кубитов в квантовом

регистре. Зашумленное численное решение Залки-Визнера - сплошные линии с отмеченными среднеквадратичными

ошибками, улучшенные теоретические оценки - штриховые линии, кривые сверху вниз отвечают соответственно 7-ми,

8-ми и 9-ти кубитам

Рис. 5. (Цветной онлайн) Зависимость точности моделирования алгоритма Залки-Визнера многоэлектронных систем

от числа электронов для различных уровней шума. Кривые сверху вниз отвечают увеличивающимся значениям уровня

шума, соответственно, e = 0.001, 0.002, 0.003, 0.005, 0.01

том различного уровня шумов. Прогноз получен по

ту было выделено n₀ = 8 кубитов, соответствующее

формуле (15) при t = 1, Δt = 0.1, считалось что

преобразование Фурье каждой координаты содержит

система из n_e электронов задана в 3n_e конфигураци-

в себе n₀ преобразований Адамара и n₀(n₀-1)/2 пре-

онном пространстве, при этом на каждую координа-

образований контролируемого фазового сдвига.

Письма в ЖЭТФ том 114 вып. 5 - 6

2021

398

Ю. И. Богданов, Н. А. Богданова, Д. В. Фастовец, В. Ф. Лукичев

Из рисунка 5 видно, что для адекватного моде-

Получены аналитические оценки для точности

лирования квантовых систем из десятков электронов

алгоритма Залки-Визнера, обусловленные ошибка-

требуется иметь уровень ошибки порядка e = 0.01 и

ми при реализации квантового преобразования Фу-

ниже, а для моделирования систем из сотен электро-

рье.

нов нужно обеспечить уровень e = 0.001 и ниже. При

Разработанные методы и алгоритмы апробирова-

этом вероятность ошибки отдельного вентиля долж-

ны на примере решения нестационарного уравнения

на достигать уровня e², т.е. порядка 10^-4-10^-6.

Шредингера для частицы в потенциале Пешль-

Заметим, что моделирование может оказаться

Теллера. Продемонстрировано хорошее согласие

успешным и при относительно невысоких уровнях

результатов численного моделирования методом

точности, когда F порядка 0.01 и даже ниже. В этом

Монте-Карло с аналитическими оценками.

Представлен метод прогнозирования точности ре-

случае искомый результат моделирования должен

шения уравнения Шредингера для многоэлектрон-

достигаться за счет большого объема статистики, по-

ных квантовых систем.

лучаемого в квантовых измерениях. Процесс отлад-

Авторы надеются, что результаты выполненного

ки экспериментальных и технологических процедур

исследования имеют существенное значение для раз-

требует широкого использования методов квантовой

работки методов моделирования квантовых систем с

томографии [18].

использованием квантовых компьютеров и симуля-

Заметим также, что задача моделирования кван-

торов, что критически важно для решения практи-

товой системы может быть совмещена с проведением

чески значимых задач в самых различных научных

квантовых измерений во взаимно-дополнительных

областях.

координатном и импульсном пространствах в рамках

Работа выполнена в рамках Государственного

томографического метода Монте-Карло, предложен-

задания ФТИАН им. К.А.Валиева РАН Минобр-

ного в [19].

науки РФ по теме # 0066-2019-0005 при поддержке

Реализация алгоритма Залки-Визнера может

Фонда развития теоретической физики и математи-

быть осуществлена на различных платформах,

ки “БАЗИС” (грант # 20-1-1-34-1).

включая ионы в ловушках [20], атомы в ловушках

[21, 22] и сверхпроводниковые кубиты [23]. Пред-

ставленные в настоящем исследовании результаты

1. R. Somma, G. Ortiz, E. Knill, and J. Gubernatis, Int.

могут быть использованы для различных экспе-

J. of Quant. Inf. 1, 189 (2003).

риментальных реализаций алгоритма на большом

2. I. Kassal, J. D. Whitfield, A. Perdomo-Ortiz,

числе кубитов в качестве базовой модели оценки

M.-H. Yung, and A. Aspuru-Guzik, Annu. Rev.

итоговой точности квантового алгоритма. Много-

Phys. Chem. 62, 185 (2011).

кубитная реализация рассматриваемого алгоритма

3. J. Diaz, K. Jansen, J. D. P. Rolim, and U. Zwick,

позволит находить решения уравнения Шредингера

Approximation, Randomization, and Combinatorial

Optimization. Algorithms and Techniques.

9th

для весьма сложных квантовых систем, радикально

International Workshop on Approximation

for

расширяя возможности современных аналитических

Combinatorial Optimization Problems (APPROX 2006)

и численных методов решения данного уравнения

and 10th International Workshop on Randomization

[24, 25].

and Computation (RANDOM

2006), Proceedings,

В настоящем исследовании мы сосредоточились

Barcelona, Spain (2006).

на анализе влияния шумов в квантовом преобразова-

4. C. Zalka, Fortschr. Phys. 46, 877 (1998);

нии Фурье на точность решения уравнения Шредин-

arXiv:quant-ph/9603026.

гера, отвлекаясь от ряда существенных факторов,

5. S. Wiesner, arXiv:quant-ph/9603028 (1996).

таких как конечная точность дискретизации, ошибки

6. G. Benenti and G. Strini, Am. J. Phys. 76, 657 (2008).

в фазовых преобразованиях, релятивистские поправ-

7. J. Abhijith, A. Adedoyin, J. Ambrosiano et al.

ки, фермионный характер многоэлектронных систем

(Collaboration), arXiv:1804.03719 (2020).

и др. Анализ влияния этих факторов на точность ре-

8. Y. Fan, Int. J. of Quant. Inf 10(05), 1250049 (2012).

шения уравнения Шредингера может стать предме-

9. R. D. Somma, Quantum Info. Comput. 16, 1125 (2016).

том отдельных исследований.

10. I. Kassal, S. P. Jordan, P. J. Love, M. Mohseni, and

5. Выводы. Разработан подход к моделированию

A. Aspuru-Guzik, Proc. Natl. Acad. Sci. 105, 18681

квантовых систем на квантовом компьютере с ис-

(2008).

пользованием метода Залки-Визнера с учетом кван-

11. Ю. И. Ожигов, Матем. моделирование 24(2),

109

товых шумов.

(2012).

Письма в ЖЭТФ том 114 вып. 5 - 6

2021

Решение уравнения Шредингера на квантовом компьютере методом Залки-Визнера. . .

399

12. М. Нильсен, И. Чанг, Квантовые вычисления и кван-

20. И. В. Заливако, И. А. Семериков, А. С. Борисенко,

товая информация, Мир, М. (2006), 824 с.

М. Д. Аксенов, К. Ю. Хабарова, Н. Н. Колачевский,

13. А. С. Холево, Квантовые системы, каналы, инфор-

Письма в ЖЭТФ 114(2), 53 (2021).

мация, МЦМНО, М. (2014), 311 с.

21. V. M. Porozova, L. V. Gerasimov, I. B. Bobrov,

14. Yu. I. Bogdanov, A. Yu. Chernyavskiy, A. S. Holevo,

S. S. Straupe, S. P. Kulik, and D. V. Kupriyanov, Phys.

V.F. Luckichev, and A. A. Orlikovsky, Proc. of SPIE

Rev. A 99, 043406 (2019).

8700, 87001A (2013); arXiv: 1207.3313 [quant-ph].

22. L. V. Gerasimov, R. R. Yusupov, I. B. Bobrov,

15. Yu. I. Bogdanov, A. Yu. Chernyavskiy, B. I. Bantysh,

V.F. Lukichev, A. A. Orlikovsky, I. A. Semenihin,

D. Shchepanovich, E. V. Kovlakov, S. S. Straupe,

D. V. Fastovets, and A.S. Holevo, Proc. of SPIE 9440,

S. P. Kulik, and D.V. Kupriyanov, Phys. Rev. A 103,

94401H (2014); arXiv:1412.2293 [quant-ph].

062426 (2021).

16. Л. Д. Ландау, Е. М. Лифшиц, Квантовая механика.

23. И. Н. Москаленко, И. С. Беседин, И. А. Цици-

Нерелятивистская теория, Наука, М. (1974), 752 с.

лин, Г. С. Мажорин, Н. Н. Абрамов, А. Григорьев,

17. З. Флюге, Задачи по квантовой механике, пер. с

И. А. Родионов, А.А. Доброносова, Д.О. Москалев,

англ. Б. А. Лысова, под ред. А. А. Соколова, Мир,

А. А. Пищимова, А. В. Устинов, Письма в ЖЭТФ

М. (1974), т. 1, 341 с.

110(8), 569 (2019).

18. Б. И. Бантыш, А. Ю. Чернявский, Ю. И. Богданов,

24. А. М. Дюгаев, П. Д. Григорьев, Письма в ЖЭТФ

Письма в ЖЭТФ 111(9), 615 (2020).

112(2), 107 (2020).

19. Ю. И. Богданов, Квантовая электроника 37(12), 1091

(2007).

25. А. Г. Кудрявцев, Письма в ЖЭТФ 111(2), 112 (2020).

Письма в ЖЭТФ том 114 вып. 5 - 6

2021