Письма в ЖЭТФ, том 114, вып. 9, с. 579 - 585

Температурная зависимость пропагаторов глюонов и духов

в подходе Дайсона-Швингенра в приближении радуги

Л.П.Каптарь⁺¹⁾, Б.Кэмпфер^∗×1),2)

⁺Лаборатория теоретической физики им. Н. Н. Боголюбова, Объединенный институт ядерных исследований, 141980 Дубна,

Россия

^∗Helmholtz-Zentrum Dresden-Rossendorf, PF 510119, 01314 Dresden, Germany

^×Institut für Theoretische Physik, TU Dresden, 01062 Dresden, Germany

Поступила в редакцию 26 августа 2021 г.

После переработки 26 августа 2021 г.

Принята к публикации 24 сентября 2021 г.

Исследуется температурная зависимость глюонных и дy´ховых пропагаторов в рамках модели, ос-

нованной на решениях уравнений Дайсона-Швингера в приближении радуги в калибровке Ландау.

Рассмотрение проводится в пространстве Евклида в мацубаровском формализме мнимого времени, в

рамках которого глюонный пропагатор больше не является О(4)-симметричной функцией, а приобре-

тает дискретный спектр по четвертой компоненте импульсов. Это приводит к необходимости различ-

ной трактовки поперечных и продольных (по отношению к термостату) составляющих пропагаторов.

Соответственно, уравнение Дайсона-Швингера для глюонов также расщепляется на два уравнения.

Полученная система связанных уравнений для продольных, поперечных и духовых пропагаторов реша-

ется численно в приближении радуги. Решения получены как функции температуры T , мацубаровской

частоты Ωn и квадрата пространственного импульса k². Эффективные параметры модели взяты из

предыдущего анализа уравнений Дайсона-Швингера при описании результатов решеточных расчетов

при нулевой температуре. Показано, что для нулевой частоты Мацубары поведение соответствующих

пропагаторов как функции пространственного импульса k² не чувствительно к температуре T, в то вре-

мя как при k² = 0 их зависимость от T довольно заметна. Также исследуется зависимость решений от

мацубаровской частоты Ωn.

DOI: 10.31857/S1234567821210011

I. Введение. В настоящее время изучение пове-

ми [10, 11], а также модели, основанные на прави-

дения адронов в горячей и плотной ядерной мате-

лах сумм КХД [12, 13] и на уравнениях Дайсона-

рии является одной из наиболее интересных и слож-

Швингера [14] (для более полного обзора различных

ных проблем, интенсивно исследуемых теоретика-

методов исследования калибровочных бозонов при

ми и экспериментаторами. Большая часть проводи-

нулевой и конечной температуре см., например, [15]).

мых и планируемых экспериментов в различных ис-

Несмотря на довольно строгую теоретическую ос-

следовательских центрах, например, в Belle (Япо-

нову, вышеуказанные подходы довольно сложны и

ния), BESIII (Пекин, Китай), LHC (ЦЕРН), GlueX

громоздки для дальнейшего применения при попыт-

(JLAB, США), NICA (Дубна, Россия), HIAF (Ки-

ках описания температурной зависимости физиче-

тай), FAIR (GSI, ФРГ) и т.д., включает в свои иссле-

ских связанных состояний, такие как мезоны и/или

довательские программы всесторонние исследования

глюболы. Поэтому появляется необходимость разра-

свойств адронов при высоких температурах и воз-

ботки более простых и прозрачных моделей, кото-

можный переход горячей ядерной материи в кварк-

рые, с одной стороны, являются простыми и фи-

глюонную плазму. Среди методов изучения свойств

зически понятными, с другой стороны, охватыва-

кварков и глюонов в вакууме и при конечных тем-

ют основные характеристики изучаемых явлений. С

пературах следует отметить подходы, основанные

этой целью, в этом письме мы обобщаем хорошо из-

на решеточных КХД расчетах [1-9], дополненные

вестное приближение радуги к уравнениям Дайсона-

функционально ренормгрупповыми (ФРГ) подхода-

Швингера в вакууме [16-19] для конечных темпера-

тур в евклидовом пространстве в формализме мни-

¹⁾e-mail: kaptari@theor.jinr.ru; kaempfer@hzdr.de

мого времени Мацубары [19-23].

²⁾B. Kämpfer.

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

579

580

Л.П.Каптарь, Б.Кэмпфер

Рис. 1. Схематическое представление рассматриваемых уравнений Дайсона-Швингера для пропагаторов глюона (верх-

няя строка) и духов (нижняя строка). Волнистые и пунктирные линии обозначают полные пропагаторы, отмеченые

черными кружками. Таким же образом отмечены и полные неприводимые одно-частичные вершины. В настоящем

подходе в уравнениях Дайсона-Швингера члены с четырьмя глюонными вершинами и кварковыми петлями были

опущены

II. Система уравнений Дайсона-Швингера

сается кварковых диаграмм, то они в инфракрасной

для духов и глюонов. Отметим, что в принци-

области существенно меньше лидирующих членов,

пе полная система связанных уравнений Дайсона-

см. [24], и могут быть игнорированы. В нашем слу-

Швингера для “одетых” кварковых, глюонных и

чае это может быть дополнительно оправдано тем,

духовых пропагаторов, а также вершинных функ-

что в tDSE их вклад в формировании динамиче-

ций может рассматриваться как точная интеграль-

ских кварковых масс пренебрежительно мал [5, 6,

ная формулировка КХД, полностью эквивалентной

25]. В глюонной же части tDSE вклад кварковых

теоретико-полевому подходу. Однако, очевидно, что

петель в собственно-энергетическую часть заметен

попытки точно решить (хотя бы численно) эту си-

только при значениях импульса вблизи максимума

стему, которая взаимосвязывает n-точечные и n + 1-

∼ 0.85-1.0 ГэВ/c, где эффект экранировки из-

точечные функции, образуя, таким образом, бес-

за рождения кварк-антикварковых пар из вакуума

конечную систему связанных уравнений, обречены

слегка уменьшает ее значение. В нашем подходе этот

на неудачу. Следовательно, для практических це-

эффект неявно учитывается при подборе феномено-

лей необходимы некоторые приближения. Обычно

логических параметров, которые находятся из срав-

бесконечная система уравнений на каком-то этапе

нения численного решения tDSE с полными решеточ-

обрезается, ограничиваясь лишь несколькими пер-

ными расчетами, учитывающими также кварковые

выми диаграммами Фейнмана. Как правило, такая

степени свободы (см., например, решеточные SU(2)

усеченная система включает только одно-петлевые

КХД расчеты [1, 2]).

диаграммы, однако с уже одетыми пропагаторами и

Прямое вычисление диаграмм Фейнмана на рис. 1

вершинами, как показано на рис.1 (см., например,

приводит к следующей системе связанных уравне-

[24]). Такая система известна как усеченные урав-

ний:

нения Дайсона-Швингера, tDSE (truncated Dyson-

Schwinger equations). Следует отметить, что набор

D^-1µν(k²⁴, k²) = Z₃D^-10µν(k²) +

диаграмм на рис. 1 уже сильно упрощен по сравне-

+ Σ^gluonµν(k²⁴, k²) + Σ^ghostµν(k²⁴, k²),

(1)

нию с набором диаграмм, обсуждаемом, в более ши-

роком контексте, например, в работе [14] и даже от-

D^-1G(k²⁴, k²) =

Z₃D^-1G0(k²) + S^ghost(k²⁴, k²),

(2)

носительно полной подсистемы одно-петлевых диа-

грамм. Этот набор не содержит независящие от им-

где Z₃ и

Z₃ обозначают глюоные и духовые констан-

пульса четырех-глюонные вершины (диаграммы ти-

ты перенормировки, D_0µν(k²) и D_G0(k²) обознача-

па “головастики”), а также кварк-глюонные петли.

ют соответствующие свободные пропагаторы, а че-

Как известно, диаграммы типа “головастики” пер-

тырехмерный импульс k в пространстве Евклида за-

турбативно исчезают в калибровке Ландау. Что ка-

писывается как k² = k²⁴ +k². Как упоминалось выше,

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

Температурная зависимость пропагаторов глюонов и духов. . .

581

∫

3T∑

G(Ω_m, q)

в евклидовом пространстве в формализме Мацубары

Σ^ghostµν(Ω_n, k) = -

d³q

духовые и глюонные пропагаторы обладают дискрет-

2π²

q²

]

ным спектром по четвертой составляющей импуль-

[g²

са, k₄ = Ω_n (n ⊂ Z), где Ω_n = 2πnT для бозонов и

× Γ^(0)µ(q)

D_G(Ω_n - Ω_m, p)Γ_ν(p) ,

(8)

4π

Ω_n = π(2n + 1)T для фермионов. В калибровке Лан-

дау пропагатор глюонов D^abµν (k₄, k) и духовой про-

пагатор D^abG(k₄, k) выражаются через “одевающие”

S^ghost(Ω_n, k) =

2π²

функции Z(k₄, k) и G(k₄, k) следующим образом:

∫

]

[g²

G(Ω_m, q)

× d³q

Γ^(0)µ(q)D_µν(p²)Γ_ν(k, q, p)

(9)

4π

q²

D^abµν(k) = δ^abD_µν(k₄, k) =

{

}

где термины, заключенные в квадратных скобках,

Z_T (k₄, k)

Z_L(k₄, k)

=δ^ab

P^Tµν(k) +

P^Lµν(k₄, k)

(3)

определяют ядро взаимодействия соответствующе-

k²

го интегрального уравнения. Явный вид уравнений

для функций Z_T,L получается из tDSE (1) подста-

G(k₄, k)

D^abG(k₄, k) = -δ^abD_G(k₄, k) = -δ^ab

(4)

новкой выражений (7)-(8) в уравнение (1), после-

k²

довательным умножением левых и правых частей

где a and b обозначают цветовые индексы, а

на P^T (Ω_n, k) и P^L(Ω_n, k) и, наконец, сворачиванием

P^Lµν(k₄, k), и P^Tµν(k) являются продольными и по-

всех Лоренц-индексов. В результате получается ска-

перечными (в

3-D пространстве) проекционными

лярная, не зависящая от Лоренц-индексов, система

операторами,

интегральных уравнений.

В принципе, константы перенормировки Z_3(T,L)



могут быть различными для поперечных и продоль-



µ и/или ν = 4,

ных пропагаторов и, соответственно, должны опре-

P^T

(k) =

µν

k_αk_β

 δ_αβ -

;

µ, ν = α, β = 1, 2, 3,

деляться независимо друг от друга. Однако, в на-

k²

стоящей работе для упрощения вычислений мы при-

k_µk_ν

P^Lµν = δ_µν -

- P^Tµν(k).

(5)

нимаем их одинаковыми как для поперечной, так и

k²

для продольной части. Более того, конкретные чис-

ловые значения для обеих констант Z₃ и

Z₃ берутся

Следует отметить, что оба эти проекционных опера-

тора являются поперечными в четырехмерном про-

из предыдущего фита [26] вакуумных решений tDSE

к решеточным КХД данным, Z₃ =

Z₃ ≈ 1.065.

странстве и обладают следующими полезными свой-

ствами

III. Приближение радуги для духов и глю-

онов. Попытки непосредственного решения полу-

ченной системы уравнений с использованием извест-

P^T P^T = P^T , P^LP^L = P^L, P^T P^L = P^LP^T = 0,

ных правил Фейнмана сталкиваются с трудностями,

(6)

(

)

(

)

P^TµνP^Tµν = Tr

P^T

= 2, P^LµνP^Lµν = Tr

P^L

= 1.

связанными с расходящимися петлевыми интеграла-

ми и симметрийными ограничениями, налагаемые на

глюон-духовых и глюон-глюонных вершинах, таки-

которые широко применяются при выводе уравнений

ми как, например, требование удовлетворения тож-

для Z_(T,L) из (3)-(4).

дества Славнова-Тейлора. Очевидно, что для кон-

Собственно-энергетические суммы Σ^gluonµν(k₄, k),

кретных вычислений необходимы дальнейшие при-

Σ^ghostµν(k₄, k) и S^ghost(k₄, k) в уравнениях (1)-(2) со-

ближения. Простейшее из них состоит в замене пол-

ответствуют трем петлевым диаграммам на рис.1.

ностью одетых вершин и пропагаторов на их голые

Свертка по цветовым индексам приводит к

значения, известное как приближение Мандельста-

ма [27-29]. К этому приближению возможны допол-

1 3T

Σ^gluonµν(Ω_n, k) =

нительные упрощения угловой зависимости Z(k²) и

2 2π²

∫

G(k²), которые позволяют вычислить интегралы по

∑

Z_T (Ω_m, q)P^Tαβ(q) + Z_L(Ω_m, q)P^Lαβ

d³q

углам в (7)-(9) аналитически. Полученные в этом

q²

случае одномерные интегральные уравнения реша-

ются численно. Такой подход известен в литературе

Γ^(0)µρα(k, p, -q)[D_T (Ω_n - Ω_m, p)P^Tρσ(q) +

4π

как y-max приближение [30]. В дальнейшем уравне-

]

ния Дайсона-Швиегера исследовались в рамках бо-

+ D_L(Ω_n - Ω_m, p)P^Lρσ(q)]Γ_βσν(q, -p, -k) ,

(7)

лее строгих подходов с учетом упомянутых выше

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

582

Л.П.Каптарь, Б.Кэмпфер

D₂₁

требований симметрий и регуляризаций расходящих-

F₂(p²) =

e-p2/ω21 +D22

e-p2/ω22 ,

(14)

ω⁴²¹

ω⁴

ся интегралов [31, 24] (см. также обзор [32] и приве-

денные в нем ссылки). Отмеченные подходы приво-

дят к довольно громоздким выражениям для систе-

F^T,L3(p²) = D^T,L p²³¹

e-p2/(ω

)² +

мы tDSE, которые вызывают трудности в нахожде-

(ω^T,L31)6

нии численных решений и их использования в даль-

p²

нейших применениях. Еще больше трудностей воз-

+D^T,L

e-p2/(ω

)² ,

(15)

(ω^T,L32)6

никает при попытках обобщения tDSE на конечные

температуры. Эти трудности можно преодолеть, ес-

где эффективные феноменологические параметры

ли допустить разумные приближения к ядрам взаи-

D_i и ω_i находятся из условия хорошего описания дан-

модействия в интегральных уравнениях, чтобы обес-

ных расчетов на SU(2) решетке при нулевой темпе-

печить сходимость интегралов и аналитическое ин-

ратуре (см. [26]).

тегрирование по углам. В настоящей заметке с этой

IV. Результаты и обсуждения. Использова-

целью мы используем хорошо известное приближе-

ние эффективного взаимодействия (10)-(15) позво-

ние радуги [16, 17, 21-23] для ядер в (7)-(9). Суть

ляет провести интегрирование по углам в аналити-

такого приближения состоит в замене в интеграль-

ческом виде [26], что в конечном итоге приводит к

ных ядрах взаимодействия полных одетых вершин,

системе линейных алгебраических уравнений отно-

совместно с обменными пропагаторами, их голыми

сительно частот Мацубары и одномерных интеграль-

аналогами, умноженными на некоторые эффектив-

ных уравнений относительно пространственных им-

ные форм-факторы:

пульсов |k| в евклидовом пространстве. Результат

]

интегрирования по углам включает в себя моди-

[g²

Γ^(0)µρα(k, p, -q)D_ρσ(p²)Γ_βσν(q, -p, -k)

фицированные функции Бесселя I_l(|q|, |k|) и экс-

4π

поненциальные интегральные функции Ei(1, |q|, |k|),

[

]

=Γ^(0)µρα(k, p, -q)

P^Tρσ(p)F^T1 (p²) + P^Lρσ(p)F^L1(p²)

умноженные на некоторые члены, зависящие от час-

тот Мацубары Ω_n и Ω_m, и пространственных момен-

× Γ^(0)βσν(q,-p,-k),

(10)

тов |q| и |k|. В дальнейшем эта система решается чис-

ленно. С этой целью одномерные интегралы аппрок-

]

[g²

симируются соответствующими гауссовыми квадра-

Γ^(0)µ(q)D_G(p²)Γ_ν(p)

= Γ^(0)µ(q)F₂(p²)Γ^(0)ν(p²), (11)

4π

турными формулами, что в конечном итоге приводит

к системе алгебраических уравнений относительно

]

частот Мацубары и узлов квадратурной формулы.

[g²

Затем такая система решается с помощью итераци-

Γ^(0)µ(q)D_µν(p²)Γ_ν(k, q, p)

4π

онной процедуры. В принципе, эффективные пара-

[

]

= Γ^(0)µ(q)

P^Tµν(p)F^T3 (p²) + P^Lµν(p)F^L3(p²)

Γ^(0)ν,

(12)

метры в уравнениях (13)-(15) могут различаться для

поперечных (T ) и продольных (L) частей. Кроме то-

где верхний индекс (0) у вершин Γ обозначает голые

го, все параметры, включая константы перенорми-

вершины взаимодействия 3-х глюонов и глюонов с

ровки

Z₃ и Z₃, могут зависеть от температуры T и

духами (более детальное обсуждение можно найти

частоты Мацубары Ω_n, см. работу [33]. Однако, как

в работе [26]). Как и в работе [26], в данном письме

было показано в работах [20, 34], при относительно

мы используем для форм-факторов F_1-3(p²) гауссов-

небольших температурах ядра взаимодействия в ин-

скую форму с двумя членами для каждого из них.

тегральных уравнениях слабо зависят от температу-

Этого вполне достаточно для получения надежного

ры, и в первом приближении они могут быть взяты

решения системы уравнений tDSE при T = 0, когда

такими же, как при T = 0 с D^T = D^L и ω^Ti = ω^Li.

O(4)-симметрия выполняется строго и, следователь-

При более высоких температурах такой выбор эф-

но, продольная и поперечная части пропагатора сов-

фективных параметров для поперечных и продоль-

падают. В явном виде, в евклидовом пространстве

ных частей менее оправдан. В настоящей заметке мы

эффективные форм-факторы выбираются как

используем одни и те же значения эффективных па-

раметров для всего диапазона рассмотренных тем-

F^T,L1(p²) = D^T,L

e-p2/(ω

)² +

ператур. Конкретные значения соответствуют набо-

(ω^T,L11)6

ру параметров, ранее найденных путем фитирова-

ния решений tDSE в вакууме, как указано в [26]:

+D^T,L p₁₂

e-p2/(ω

)² ,

(13)

D^T11 = D^L11 = 0.462 ГэВ², D^T12 = D^L12 = 0.116 ГэВ²,

(ω^T,L12)⁶

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

Температурная зависимость пропагаторов глюонов и духов. . .

583

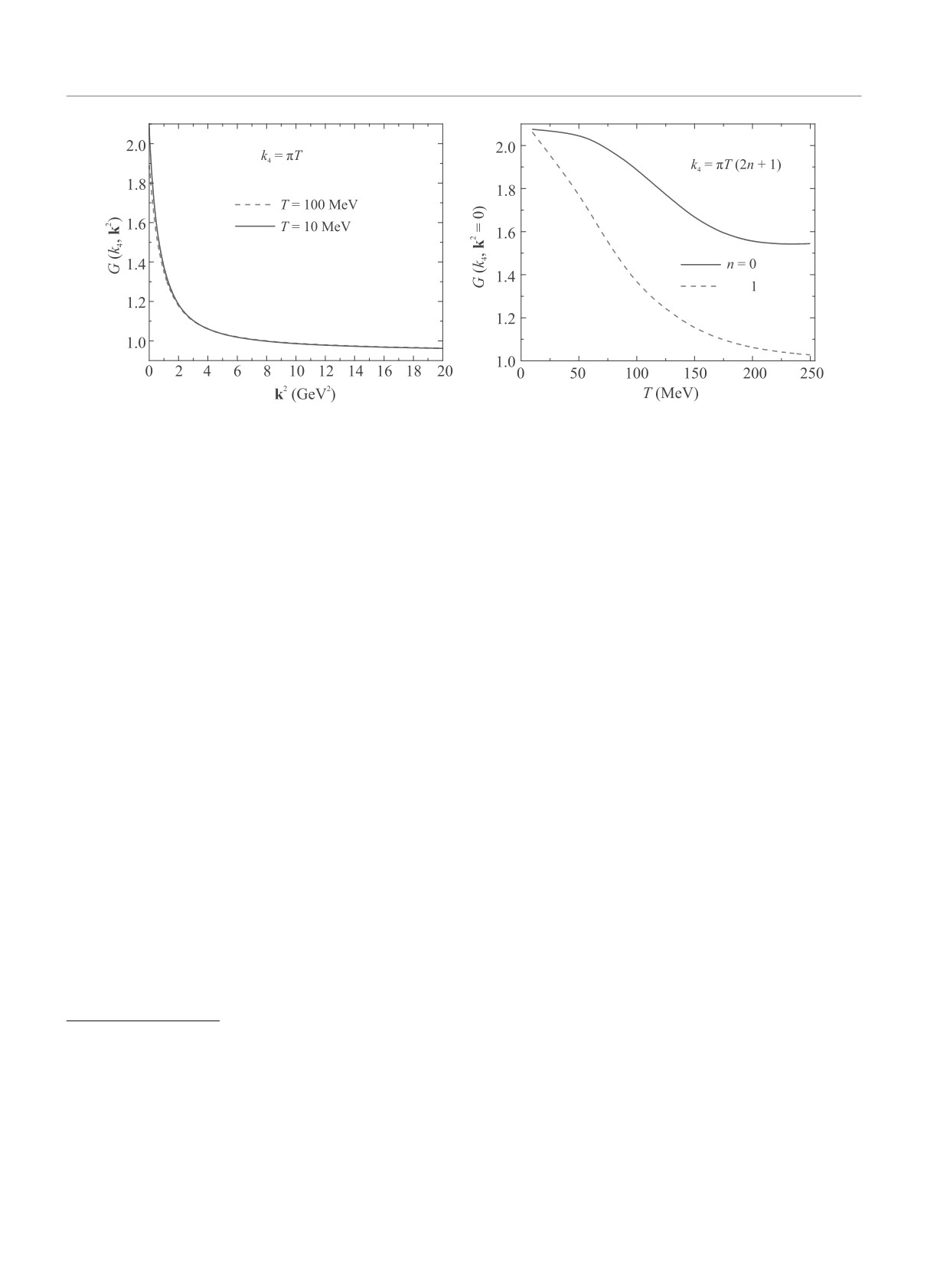
Рис. 2. (Цветной онлайн) Решение уравнения Дайсона-Швингера для духов G(k4, k²). Левая панель: зависимость

решения от квадрата пространственного импульса k² при нулевой частоте Мацубары, n = 0, для двух значений

температуры T = 10 МэВ (сплошная кривая) и T = 100 МэВ (штриховая кривая). Правая панель: температурная

зависимость G(k4, k²) при нулевом трехмерном импульсе k² = 0 и при двух значениях частоты Мацубары, n = 0

(сплошная кривая) и n = 1 (штриховая кривая)

ω^T11 = ω^L11 = 1.095 ГэВ, ω^T12 = ω^L12 = 2.15 ГэВ для

ная ограничивалась максимальным значением |k|² ∼

3-х глюонных петель, D^T21 = D^L11 = 7.7 ГэВ², D^T22 =

∼ 220 ГэВ²/c². Для получения более плотного рас-

= D^L22 = 0.25ГэВ², ω^T21 = ω^L21 = 0.58ГэВ, ω^T22 = ω^L22 =

пределения гауссовых узлов при низких |k|² была ис-

= 4.5 ГэВ для духовых петель и ω^T31 = ω^L31 = 0.73 ГэВ,

пользована масштабированная замена переменных,

ωT32 = ωL32 = 2.16ГэВ, DT31 = DL31 = 0.39πГэВ2,

см. [23].

D^T32 = D^L32 = 0.1π ГэВ² для дух-глюонной петли (см.

Результаты расчетов представлены на рис. 2 и 3.

три петлевые диаграммы на рис. 1).³⁾ Следует под-

На рисунке 2 приведена температурная зависимость

черкнуть, что при сохранении эффективных пара-

духвой функции G(k₄, k²). Левая панель иллюстри-

метров независимыми от температуры и по величине

рует ее поведение при нулевой частоте Мацубары,

такими же, как в вакууме, можно ожидать достаточ-

n = 0, как функция пространственных импульсов k²

но надежного решения tDSE лишь при низких и уме-

и двух значениях температуры, T = 10 МэВ и T =

ренных температурах, T ≤ 200 МэВ. Очевидно, что

= 100 МэВ. Как и ожидалось, температурная зависи-

при более высоких температурах эффективные пара-

мость довольно слабая для всех значений k² и очень

метры должны быть T - и n-зависимыми (см., напри-

похожа на поведение G(k²) при T = 0, см. работу [26].

мер, [22, 20, 33]) и, вероятно, совершенно разными

На правой панели мы показываем функцию G(k₄, k²)

для поперечных и продольных частей tDSE.

при k² = 0 и двух значениях частот Мацубары. По-

Полученная алгебраическая система уравнений

скольку четвертая составляющая импульса сильно

решалась итерационным методом. В конкретных

зависит от частоты Мацубары, k²⁴ = [π(2n + 1)T]²,

расчетах мацубаровские частоты брались в интер-

функция G(k₄, 0) довольно чувствительна к значе-

вале (-30 ≤ n ≤ 30), гауссовская сетка для инте-

ниям температуры T .

грирования по пространственной переменной |k|² со-

Аналогичный анализ для глюонного пропагатора

держала 72 узла, а сама пространственная перемен-

представлен на рис. 3, где для определенности рас-

сматривается только его поперечная часть (T ). По-

ведение продольного пропагатора качественно такое

³⁾Отметим, что в настоящей статье каждая из трех петель

же и в данной статье не приводится. На левой панели

на рис. 1 параметризуется двумя гауссовскими членами, в то

зависимость поперечного пропагатора отображается

время как в работе [26] духовая петля параметризовалась все-

го лишь одним. Введенный дополнительный член не влияет

как функция квадрата пространственного импульса

на качество фитирования вакуумных решеточных данных и в

k² при двух значениях частоты Мацубары, n = 0 и

настоящей работе используется исключительно для сохране-

n = 1, и двух значениях температуры, T = 10МэВ и

ния единообразия в параметризации петель. Соответственно,

нынешние обозначения слегка отличаются от обозначений, ис-

T = 100МэВ. Как и в случае духов, зависимость глю-

пользуемых в работе [26].

онного пропагатора от температуры довольно сла-

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

584

Л.П.Каптарь, Б.Кэмпфер

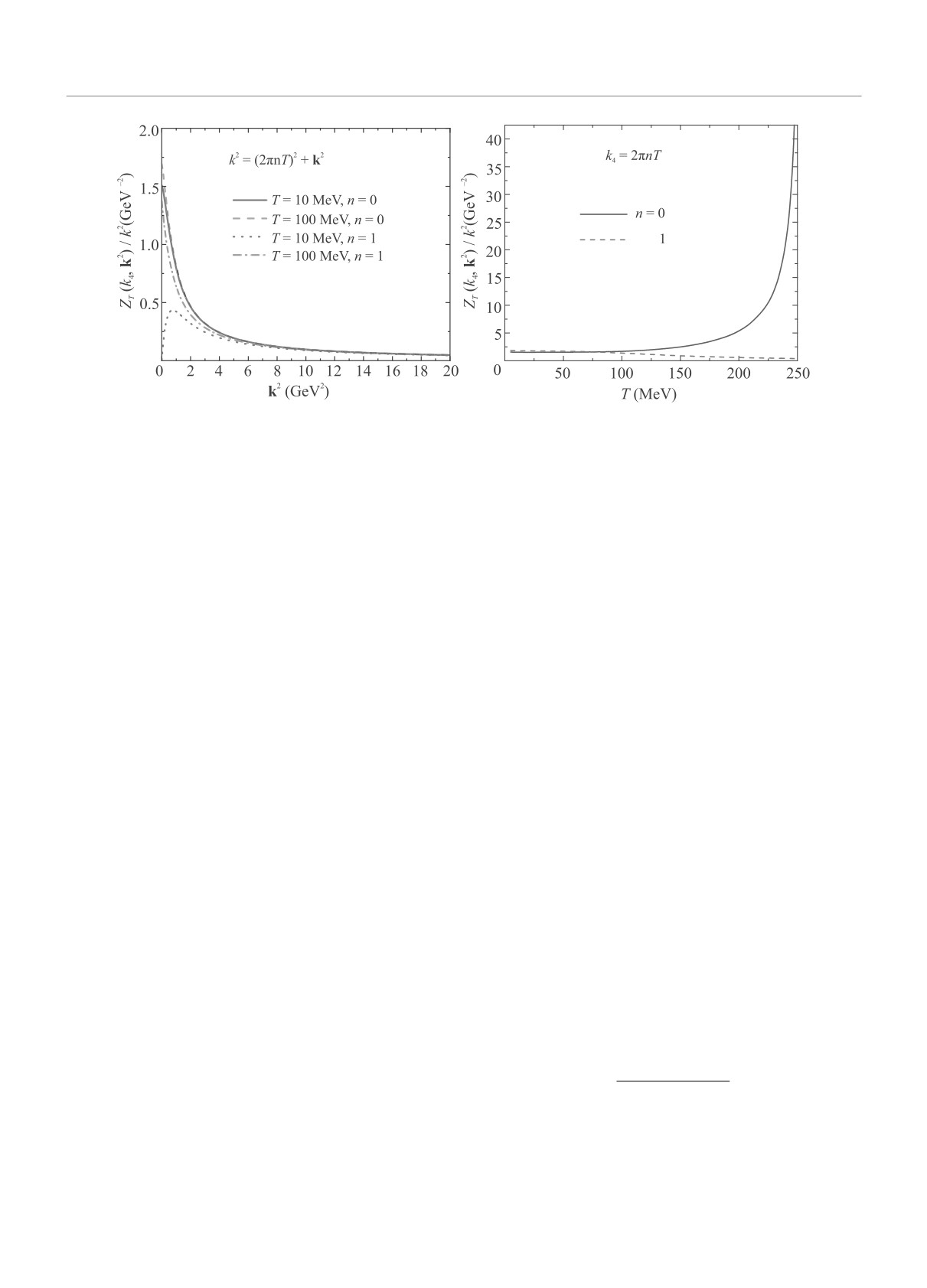
Рис. 3. (Цветной онлайн) Решение уравнения Дайсона-Швингера для поперечной части глюонного пропагатора

ZT (k4, k²)/k². Левая панель: зависимость от квадрата трехмерного импульса k² при двух значениях частоты Мацуба-

ры и двух значениях температуры. Сплошные и штриховые кривые соответствуют n = 0, T = 10 МэВ и T = 100 МэВ

соответственно. Пунктирные и штрих-пунктирные кривые соответствуют n = 1, T = 10 МэВ и T = 100 МэВ. Пра-

вая панель: температурная зависимость пропагатора глюонов при нулевом трехмерном импульсе k² = 0 и при двух

значениях частоты Мацубары, n = 0 (сплошная кривая) и n = 1 (штриховая кривая)

бая (ср. сплошную, T = 10 МэВ, и штрихованную,

полученными в рамках функционально ренормгруп-

T = 100МэВ, кривую). Зависимость от T более вы-

повых подходах (см. работы [10, 35, 11, 15] и приве-

ражена при малых значениях k² для ненулевой (на-

денные в них ссылки) или в подходах, основанных на

пример, для n = 1) частоты Мацубары, что хоро-

КХД решеточных расчетах [3, 4]. Здесь следует под-

шо видно из сравнения пунктирной (T = 10 МэВ)

черкнуть, что предложенный в этой статье упрощен-

с штрих-пунктирной кривой (T

= 100 МэВ). Это

ный подход с параметрами, независящими от темпе-

связано с тем, что при малых значениях простран-

ратуры, не может быть надежно применен для тем-

ственного импульса, k2 ∼ 0, значения 4-импульса

ператур T ≳ 200 МэВ, и поэтому сравнение с подхо-

k² ∼ k²⁴ становятся прямо пропорциональны квад-

дами ФРГ и/или решеточными расчетами при более

рату температуры, k²⁴ = 4π²T², и при T = 10 МэВ

высоких температурах затруднено.

и T = 100МэВ значения k² отличаются почти на

V. Резюме. Таким образом, в данной рабо-

два порядка. (Значение глюонного пропагатора при

те численно решена система усеченных уравнений

k² = 0 и n = 0 определяет эффективную массу глю-

Дайсона-Швингера для глюонов и духов в прибли-

она, Z_T /k² ∼ 1/(k² + m^2eff). Из наших расчетов мы

жении радуги при конечных температурах в рамках

делаем вывод, что в нашей модели m^2eff ∼ 0.6 ГэВ².)

формализма мнимого времени. Утверждается, что

На правой панели рис.3 приводится зависимость

для нулевых частот Мацубары, n = 0, поведение

от температуры T глюонного пропагатора при k² = 0

пропагаторов как функций квадрата пространствен-

и двух значениях частоты Мацубары, n = 0 и n = 1.

ного импульса k² не чувствительно к температуре

Отличие при средних и высоких температурах в по-

T практически во всем диапазоне k². Напротив, в

ведении пропагатора обусловлено величиной четвер-

самом начале координат, k² = 0, была обнаружена

той составляющей импульса k₄, которая равна ну-

существенная зависимость пропагаторов от n и T.

лю при n = 0 и конечна, k²⁴ = 4π²T², для n = 1.

Такие исследования открывают путь для изучения

Поскольку в уравнениях tDSE с гауссовыми ядра-

более сложных явлений, например, изменений харак-

ми взаимодействия (13)-(15) четвертые компоненты

теристих связанных состояний глюонов (глюболов) в

k4 входят как exp(-k24/ω2), значения соответству-

сильно нагретой ядерной материи.

ющих пропагаторов при ненулевых мацубаровских

частотах и больших температурах, T

∼ 250 МэВ

существенно подавляются. В интервале температур

1. V. G. Bornyakov, E.-M. Ilgenfritz, C. Litwinski,

0 ≤ T ≤ 250МэВ наши расчеты находятся в доволь-

M. Müller-Preussker, and V. K. Mitrjushkin, Phys. Rev.

но хорошем качественном согласии с результатами,

D 92, 074505 (2015).

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

Температурная зависимость пропагаторов глюонов и духов. . .

585

V.G. Bornyakov, V. K. Mitrjushkin, and M. Müller-

18.

P. Maris and P. C. Tandy, Phys. Rev. C 60, 055214

Preussker, Phys. Rev. D 81, 054503 (2010).

(1999).

R. Aouane, V. G. Bornyakov, E. M. Ilgenfritz,

19.

S. M. Dorkin, L. P. Kaptari, and B. Kämpfer, Phys. Rev.

V.K. Mitrjushkin, M. Muller-Preussker, and

C 91, 055201 (2015).

A. Sternbeck, Phys. Rev. D 85, 034501 (2012).

20.

S.-xue, L. Chang, Y.-x. Liu, and C. Roberts, Phys. Rev.

E. M. Ilgenfritz, J. M. Pawlowski, A. Rothkopf, and

D 84, 014017 (2011).

A. Trunin, Eur. Phys. J. C 78(2), 127 (2018).

21.

M. Blank and A. Krassnigg, Phys. Rev. D 82, 034006

P. O. Bowman, U. M. Heller, D. B. Leinweber,

(2010).

M. B. Parappilly, A. Sternbeck, L. von Smekal,

22.

S. Dorkin, L. P. Kaptari, and B. Kämpfer, Few Body

A.G. Williams, and J. Zhang, Phys. Rev. D

76,

Syst. 60, 20 (2019).

094505 (2007).

23.

S. Dorkin, M. Viebach, L. Kaptari, and B. Kämpfer,

P. O. Bowman, U. M. Heller, D. B. Leinweber,

J. Mod. Phys. 7, 2071 (2016).

M. B. Parappilly, and A. G. Williams, Phys. Rev.

24.

L. von Smekal, A. Hauck, and R. Alkofer, Ann. Phys.

D 70, 034509 (2004).

267, 1 (1998).

M. Albanese, F. Costantini, G. Fiorentini et al. (Ape

25.

C. S. Fischer, P. Watson, and W. Cassing, Phys. Rev. D

Collaboration), Phys. Lett. B 197, 400 (1987).

72, 094025 (2005).

Y. Chen, A. Alexandru, S. Dong, T. Draper, I. Horváth,

26.

L. P. Kaptari and B. Kämpfer, Few. Body Syst. 61, 28

F. X. Lee, K. F. Liu, N. Mathur, C. Morningstar,

(2020).

M. Peardon, S. Tamhankar, B. L. Young, and

J. B. Zhang, Phys. Rev. D 73, 014516 (2006).

27.

A. Hauck, L. von Smekal, and R. Alkofer, Comput.

Phys. Commun. 112, 149 (1998).

C. J. Morningstar and M. J. Peardon, Phys. Rev. D 60,

034509 (1999).

28.

S. Mandelstam, Phys. Rev. D 20, 3223 (1979).

10.

N. Dupuis, L. Canet, A. Eichhorn, W. Metzner,

29.

K. Buttner and M. R. Pennington, Phys. Rev. D 52,

J. M. Pawlowski, M. Tissier, and N. Wschebor, Phys.

5220 (1995).

Rep. 910, 1 (2021).

30.

D. Atkinson and J. C. R. Bloch, Phys. Rev. D 58, 094036

11.

A.K. Cyrol, M. Mitter, J. M. Pawlowski, and

(1998).

N. Strodthoff, Phys. Rev. D 97, 054015 (2018).

31.

L. von Smekal, A. Hauck, and R. Alkofer, Phys. Rev.

12.

M. A. Shifman, A. I. Vainshtein, and V. I. Zakharov,

Lett. 79, 3591 (1997).

Nucl. Phys. B 147, 385 (1979).

32.

R. Alkofer and L. von Smekal, Phys. Rept. 353, 281

13.

E. V. Shuryak, Nucl. Phys. B 203, 116 (1982).

(2001).

14.

C. Fischer, Progr. Part. Nucl. Phys. 105, 1 (2019).

33.

A. Maas, J. Wambach, and R. Alkofer, Eur. Phys. J. C

15.

A. Maas, Phys. Rept. 524, 203 (2013).

42, 93 (2005).

16.

R. Alkofer, P. Watson, and H. Weigel, Phys. Rev. D 65,

34.

A. Cucchieri, A. Maas, and T. Mendes, Phys. Rev. D

094026 (2002).

75, 07600 (2007).

17.

C. Roberts, V. Bnagwat, A. Holl, and S. Wringht, Eur.

35.

W.-j. Fu, J. M. Pawlowski, and F. Rennecke, Phys. Rev.

Phys. J. ST 140, 53 (2007).

D 101, 054032 (2020).

Письма в ЖЭТФ том 114 вып. 9 - 10

2021