Письма в ЖЭТФ, том 114, вып. 9, с. 615 - 619

Корреляция между коэффициентами сдвиговой вязкости

и теплопроводности в плотных простых жидкостях

С. А. Храпак, А. Г. Храпак¹⁾

Объединенный институт высоких температур РАН, 125412 Москва, Россия

Поступила в редакцию 7 сентября 2021 г.

После переработки 28 сентября 2021 г.

Принята к публикации 29 сентября 2021 г.

Отталкиваясь от зависимости транспортных коэффициентов от избыточной энтропии, исследована

корреляция между должным образом нормированными коэффициентами сдвиговой вязкости и тепло-

проводности плотных жидкостей. Продемонстрировано, что корреляция существует и может рассматри-

ваться как аналог соотношения Стокса-Эйнштейна между коэффициентами самодиффузии и сдвиговой

вязкости. Представленные результаты для четырех простых модельных систем с различными парными

потенциалами взаимодействия (Леннард-Джонс, Кулон, обратностепенной шестой степени и твердых

сфер), а также шести реальных атомарных и молекулярных жидкостей (Ar, Kr, Xe, CH4, O2 и N2)

поддерживают этот вывод и позволяют идентифицировать несколько универсальных классов. Предла-

гаются удобные для практических применений выражения для соотношения между коэффициентами

сдвиговой вязкости и теплопроводности.

DOI: 10.31857/S1234567821210072

1. Введение. Значительный прогресс в понима-

В отсутствие общей теории часто приходится по-

нии транспортных свойств жидкостей был достиг-

лагаться на феноменологические подходы, полуко-

нут в последние десятилетия [1-4]. Тем не менее, на-

личественные модели и масштабные соотношения.

ше понимание этих процессов остается неполным и

Среди наиболее полезных соотношений, предложен-

фрагментарным по сравнению с газами и тверды-

ных на данный момент, является связь между транс-

ми телами. Трудности с теоретическим описанием

портными коэффициентами и внутренней энтропи-

динамики жидкого состояния были недавно очень

ей простых систем, предложенная Розенфельдом [6].

хорошо сформулированы Бражкиным [5]. Твердые

Он продемонстрировал, что правильно приведенные

тела и газы можно рассматривать в некотором (ди-

транспортные коэффициенты являются приблизи-

намическом) смысле как “чистые” агрегатные состо-

тельно экспоненциальными функциями приведенной

яния. В твердых телах движение атомов чисто ко-

избыточной энтропии s_ex = (S -S_id)/Nk_B, где S - эн-

лебательное, в то время как в разреженных газах

тропия системы, S_id - энтропия идеального газа при

атомы свободно движутся по прямолинейным траек-

той же температуре и плотности, N - количество

ториям между столкновениями. Это упрощает раз-

частиц, а kB - постоянная Больцмана. Системно-

работку теорий транспортных процессов. С другой

независимая нормализация транспортных коэффи-

стороны, жидкости представляют собой “смешанное”

циентов, используемая Розенфельдом, имеет вид:

агрегатное состояние. Здесь присутствуют как коле-

ρ^1/3

ρ^-2/3

бательные, так и диффузионные движения атомов.

D_R = D

η_R = η

λ_R = λ

(1)

Их относительный вклад в атомную динамику зави-

v_T

mv_T

v_T

сит от термодинамического состояния. Вблизи фа-

где D, η и λ - коэффициенты самодиффузии, сдвиго-

зового перехода жидкость-твердое тело преоблада-

вой вязкости и теплопроводности, а индекс R указы-

ет колебательное движение, и более актуальны твер-

вает на нормализацию Розенфельда. Здесь ρ - кон-

√

дотельные подходы к транспортным свойствам. При

центрация атомов, v_T =

T/m - тепловая скорость,

более низкой плотности и более высоких температу-

T - температура в энергетических единицах (≡ k_BT)

рах преобладает баллистическое движение, и пере-

и m масса атома. Скейлинг, предложенный Розен-

нос аналогичен имеющему место в неидеальных га-

фельдом, имеет вид [7]

зах.

D_R ≃ 0.6e0.8sex , η_R ≃ 0.2e-0.8sex , λ_R ≃ 1.5e-0.5sex .

¹⁾e-mail: khrapak@mail.ru

(2)

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

615

616

С. A. Храпак, А. Г. Храпак

Отметим, что s_ex отрицательна, поскольку взаи-

Целью данной статьи является изучение корре-

модействия между атомами увеличивают степень

ляции между коэффициентами сдвиговой вязкости

структурного порядка по сравнению с невзаимодей-

и теплопроводности для плотных простых жидко-

ствующим идеальным газом. Было продемонстриро-

стей. Будет продемонстрировано, что корреляции

вано, что многие простые и не очень простые си-

действительно существуют. Это позволит нам пред-

стемы удовлетворяют приблизительному скейлингу

ложить приблизительную связь между коэффициен-

избыточной энтропии, хотя существуют и обратные

тами сдвиговой вязкости и теплопроводности, напо-

примеры. Современное состояние проблемы скейлин-

минающую соотношение SE. Этот подход потенци-

га с использованием избыточной энтропии можно

ально позволяет оценить все транспортные свойства

найти в обзоре [8].

только по одному известному (самодиффузии, вяз-

Еще одно полезное соотношение - соотношение

кости или теплопроводности).

Стокса-Эйнштейна (SE) между коэффициентами са-

2. Мотивация. В разреженных газах транспорт-

модиффузии и сдвиговой вязкости простых жидко-

ные свойства определяются столкновениями между

стей. Для плотных простых жидкостей оно имеет вид

составляющими их атомами. Коэффициенты пере-

носа можно оценить с помощью теории Чепмена-

Dη(Δ/T) = α_SE,

(3)

Энскога [24]. В первом приближении

где Δ = ρ^-1/3 - среднее межатомное расстояние, а

3√π vT

5√π mvT

α_SE - слабо зависящий от выбора системы коэффи-

η=

λ=

√π v_T , (4)

ρΩ₁

Ω₂

циент. Уравнение (3) также известно как соотноше-

где Ω₁ и Ω₂ - интегралы столкновений (сечения пере-

ние SE без гидродинамического диаметра (в действи-

тельности, роль гидродинамического диаметра игра-

дачи импульса и энергии, интегрированные с макс-

велловской функцией распределения по скоростям).

ет межатомное расстояние) [9].

Уравнение (3) выполняется для многих простых

Последние зависят от механизма взаимодействия

между атомами. Поскольку и сдвиговая вязкость, и

модельных и реальных жидкостей вблизи фазового

коэффициент теплопроводности обратно пропорци-

перехода жидкость-твердое тело [9-11]. Обоснование

было предложено в нескольких теоретических моде-

ональны Ω₂, соотношение между этими коэффици-

ентами не зависит от точного механизма взаимодей-

лях [12-14]. В частности, разработанная Цванцигом

теория, основанная на колебательном характере дви-

ствия:

λm

жения атомов в жидком состоянии на коротких вре-

(5)

менных масштабах [12], предсказывает коэффициент

Это соотношение является следствием процессов, ле-

SE как α_SE ≃ 0.13(1 + η/2η_l) = 0.13(1 + c^2t/2c^2t), где

жащих в основе переноса импульса и энергии в раз-

η_l - продольная вязкость, а c_t(l) - поперечная (про-

реженных газах, и не выполняется в жидком состо-

дольная) скорость звука. В результате коэффициент

янии [25].

α_SE теоретически может варьироваться от ≃ 0.13 до

С другой стороны, используя нормировку Розен-

≃ 0.18, что согласуется с результатами моделирова-

фельда (1) с соотношением SE без гидродинамиче-

ния и экспериментов для многих простых жидкостей

ского диаметра, мы получаем

[9-11].

Другие полезные приближения включают раз-

Dη(Δ/T) = D_Rη_R.

(6)

личные варианты скейлинга транспортных коэффи-

циентов по температуре замерзания (см., например,

В свою очередь из скейлинга избыточной энтропии

[15-21]). В нашей недавней статье было продемон-

(2) следует из α_SE = D_Rη_R ≃ 0.12. Это разумный

стрировано, что приведенные коэффициенты перено-

прогноз, хотя фактические значения коэффициен-

та α_SE немного выше (≃ 0.14 для однокомпонентной

са жидкостей Леннард-Джонса (LJ) демонстрируют

скейлинг по плотности замерзания, и этот скейлинг

плазмы и жидкостей Юкавы, ≃ 0.15 для жидкостей

LJ и ≃ 0.17 для жидкости твердых сфер [11]).

тесно связан со скейлингом по плотности коэффи-

циентов переноса жидкостей твердых сфер [22]. Ди-

Скейлинг по избыточной энтропии, примененный

к соотношению между коэффициентами сдвиговой

намическая эквивалентность между жидкостью LJ

и жидкостями твердых сфер также недавно обсуж-

вязкости и теплопроводности, дает

далась [23]. В литературе предлагались различные

λ_R ≃ 4.10η^5/8R.

(7)

простые модели для индивидуальных коэффициен-

тов переноса (самодиффузия, вязкость и теплопро-

Это указывает на аналогию с соотношением SE, хо-

водность).

тя она является неполной. Механизмы диффузии и

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

Корреляция между сдвиговой вязкостью и теплопроводностью...

617

сдвиговой вязкости в плотных жидкостях остаются

работе [22], где обсуждается скейлинг коэффициен-

тесно связанными, в то время как механизм тепло-

тов переноса по плотности замерзания в жидкостях

проводности имеет другую природу. Преобладающий

LJ. В данной статье мы рассматриваем достаточно

вклад в теплопроводность в плотных жидкостях вно-

плотные жидкости с плотностями выше, чем те, ко-

сят коллективные возбуждения (мы не рассматрива-

торые соответствуют минимумам в η_R и λ_R. Это со-

ем жидкие металлы, где преобладающий вклад вно-

ответствует жидкостному режиму на фазовой диа-

сят перенос и рассеяние электронов) [26]. Несмотря

грамме. В этом режиме и η_R, и λ_R монотонно воз-

на это различие, коэффициенты температуропровод-

растают с приближением к точке замерзания.

ности и кинематической вязкости некоторых благо-

Данные для сжиженных благородных газов, а

родных и молекулярных жидкостей демонстрируют

также кислорода и азота взяты из работы [28].

сходную (системно-зависимую) температурную зави-

Данные для метана взяты из работы [29]. Суще-

симость, а их минимумы относительно близки для

ствуют обширные наборы данных по транспортным

разных веществ [26]. Отношение mλ/η (равное 15/4

свойствам жидкостей LJ. Поскольку приведенные

в идеальном газе) демонстрирует немонотонную за-

коэффициенты переноса жидкостей LJ вдоль изо-

висимость от плотности, но мало отличается от ≃ 4

терм демонстрируют квазиуниверсальный масштаб-

(отклонения ∼ 50 % были получены для жидкости LJ

ный скейлинг по плотности замерзания [22], доста-

и ∼30% для модели однокомпонентной плазмы [25]).

точно рассмотреть только одну изотерму. Мы выбра-

Число Прандтля Pr = c_pη/mλ (где c_p - теплоемкость

ли изотерму T_∗ = T/ǫ = 2 (ǫ - энергетическая шкала

при постоянном давлении) увеличивается при при-

потенциала LJ) и использовали коэффициенты вяз-

ближении к точке замерзания, но не слишком силь-

кости и теплопроводности, указанные в таблицах в

но отличается от единицы [27]. Таким образом, поиск

работах [30, 31]. Для сильно неидеальной жидкост-

взаимосвязей между коэффициентами теплопровод-

ной однокомпонентной плазмы мы используем дан-

ности и вязкости не является неразумным.

ные моделирования методом молекулярной динами-

Ниже, используя литературные данные о сдвиго-

ки (MD) из работ [32, 33]. Кроме того, добавлены

вой вязкости и теплопроводности нескольких реаль-

две точки для потенциала отталкивания IPL6, кото-

ных и модельных систем, мы ответим на следующие

рые доступны в работе [34]. Наконец, транспортные

вопросы: (i) существует ли убедительная корреляция

данные для систем твердых сфер взяты из недав-

между этими коэффициентами переноса; (ii) универ-

них расчетов методом МД, представленных в рабо-

сальна ли эта корреляция; и (iii) насколько справед-

тах [35, 36].

лива форма скейлинга, описываемая уравнением (7).

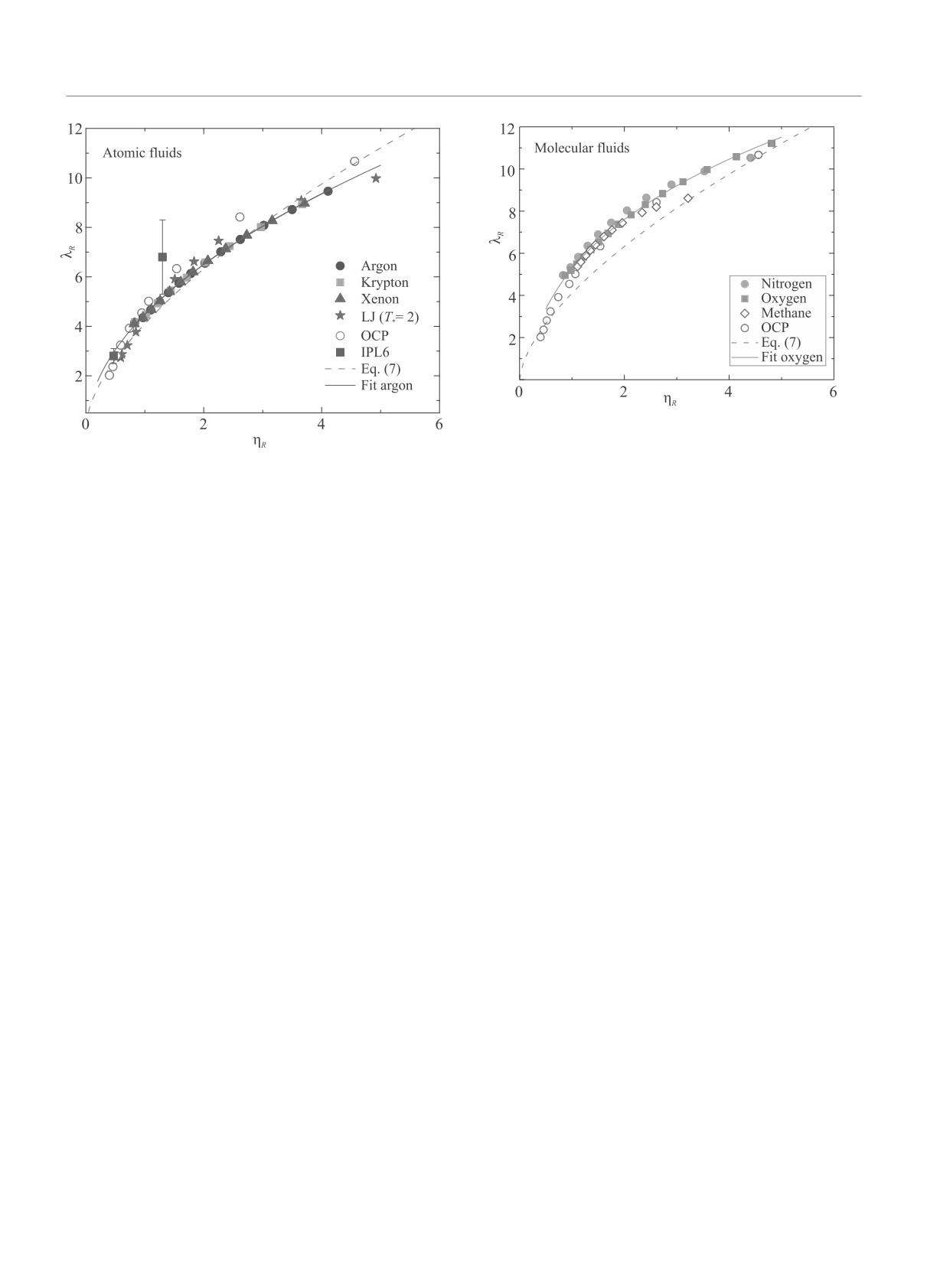
Результаты для сжиженных благородных газов,

3. Результаты. Нами проанализированы лите-

жидкостей LJ, OCP и IPL6 показаны на рис. 1. Вид-

ратурные данные для коэффициентов вязкости и

но, что коэффициенты вязкости и теплопроводности,

теплопроводности нескольких реальных и модель-

действительно, хорошо коррелируют. Точки данных

ных систем. Среди реальных исследуемых систем -

для рассмотренных различных одноатомных жидко-

сжиженные благородные газы (аргон, криптон и ксе-

стей имеют тенденцию группироваться вокруг ква-

нон), метан, кислород и азот. В данной работе рас-

зиуниверсальной кривой. Зависимость, описываемая

сматриваются также модельные системы: жидкости

уравнением (7), основанная на избыточной энтропии,

LJ, однокомпонентная плазма (OCP), жидкость с от-

показана пунктирной кривой. В целом наблюдает-

талкивающим обратно степенным ∝ 1/r⁶ (IPL6) за-

ся довольно хорошее согласие. Для сжиженных бла-

коном взаимодействия и модель твердых сфер (HS).

городных газов аргона, криптона и ксенона универ-

При рассмотрении зависимости приведенных ко-

сальная корреляция между λ_R и η_R особенно очевид-

эффициентов переноса D_R, η_R и λ_R от плотно-

на. На основе скейлинга по избыточной энтропии (7)

сти простых жидкостей имеется существенное каче-

может быть предложена следующая функциональ-

ственное различие. Коэффициент самодиффузии мо-

ная форма

нотонно убывает с приближением к точке замерза-

λ_R ≃ αη^βR + γ.

(8)

ния. Напротив, коэффициенты сдвиговой вязкости

и теплопроводности немонотонно зависят от плотно-

Анализируя данные для аргона, мы получили α ≃

сти. Они демонстрируют минимумы примерно при

≃ 4.88, β ≃ 0.50 и γ ≃ -0.40. Эта оценка приме-

одинаковой плотности системы, что указывает на пе-

нима также для криптона и ксенона. Точки данных

реход между газоподобным и жидкостным скейлин-

для жидкости LJ близки к таковым для сжиженных

гом коэффициентов переноса с ростом плотности.

благородных газов. При сильной неидеальности теп-

Хороший иллюстративный пример можно найти в

лопроводность ОСР лежит несколько выше. Тем не

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

618

С. A. Храпак, А. Г. Храпак

Рис. 2. (Цветной онлайн) Корреляция между λR и ηR

для молекулярных жидкостей N2, O2, и CH4. Символы

соответствуют имеющимся данным [28, 29] и числен-

Рис. 1. (Цветной онлайн) Корреляция между приведен-

ным результатам для OCP. Пунктирная кривая обо-

ным коэффициентом теплопроводности λR и коэффи-

значает скейлинг уравнения (7) на основе избыточной

циентом сдвиговой вязкости ηR для простых атомар-

энтропии. Сплошная кривая обозначает аппроксима-

ных жидкостей. Символы соответствуют имеющимся

цию, основанную на данных для кислорода

данным для различных реальных и модельных жидко-

стей (указаны на рисунке). Пунктирная кривая обозна-

дыми сферами в жидкостных возбуждениях и тер-

чает скейлинг уравнения (7) на основе избыточной эн-

тропии. Сплошная кривая обозначает аппроксимацию,

модинамике [37]. Недавние результаты скейлинга по

основанную на данных для аргона

шкале плотности замерзания транспортных свойств

леннард-джонсовских жидкостей продемонстрирова-

менее, все точки сгруппированы достаточно близко,

ли, что, хотя коэффициенты диффузии и сдвиговой

и мы можем рассматривать их как принадлежащие

вязкости могут быть довольно хорошо сопоставлены

к одному классу универсальности.

с коэффициентами диффузии и вязкости HS, коэф-

На рисунке 2 представлена зависимость λ_R от η_R

фициент теплопроводности плотных жидкостей HS

для молекулярных жидкостей: жидких азота, кис-

систематически больше, чем коэффициент теплопро-

лорода и метана. Здесь также наблюдается явная

водности LJ жидкости [22]. Поэтому мы демонстри-

универсальность, но класс универсальности отлича-

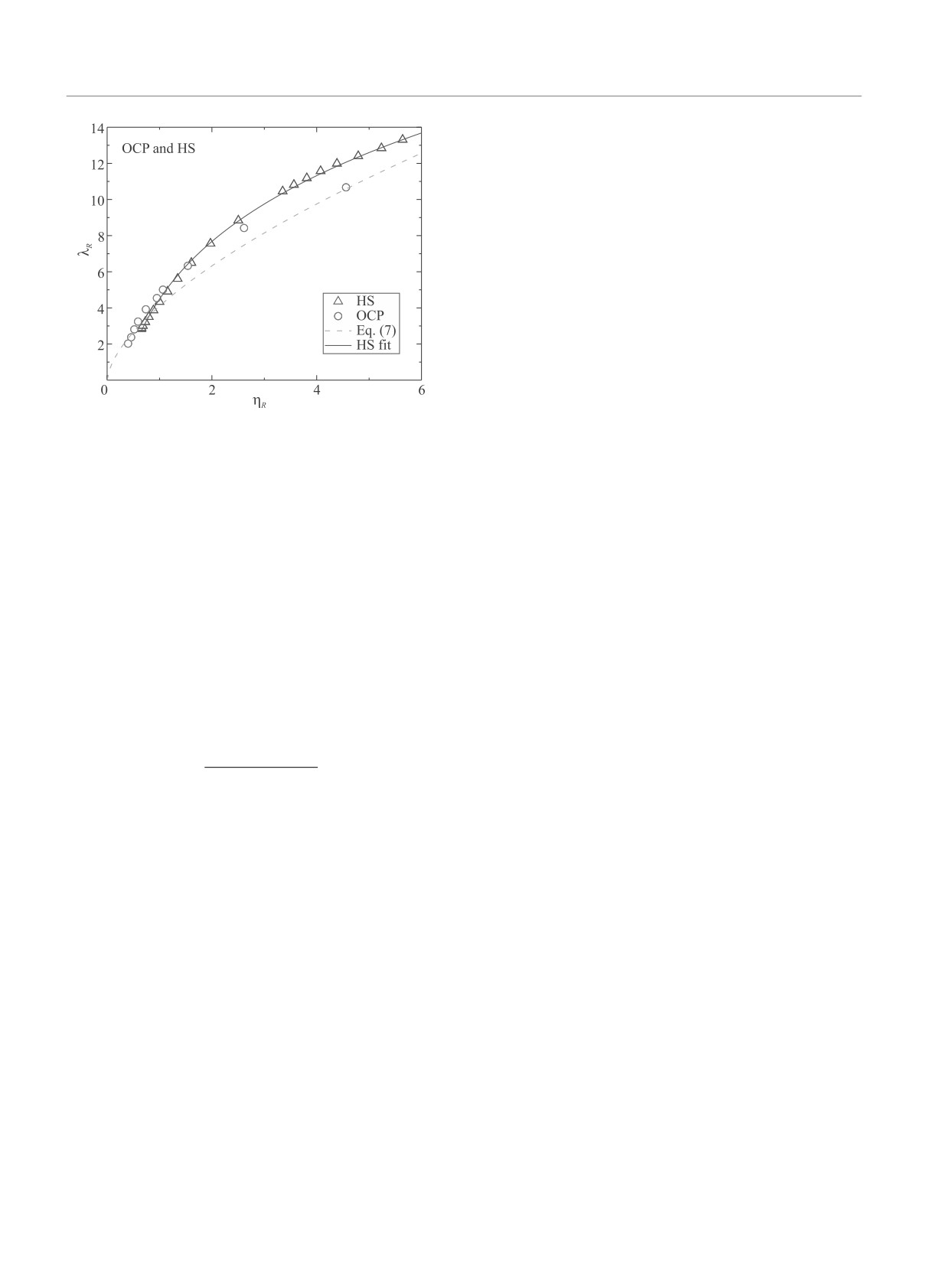
руем сравнение зависимости λ_R от η_R для особо мяг-

ется от класса жидких благородных газов. Скейлинг

кой жидкости OCP и жидкости HS отдельно, см.

уравнения (7) на основе избыточной энтропии не яв-

рис. 3. Теплопроводность жидкости HS систематиче-

ляется идеальным в этом случае. В то же время

ски выше, как и ожидалось. Подгонка с использо-

функциональная форма уравнения (8) остается при-

ванием уравнения (8) дает в пределе HS α ≃ 22.62,

менимой. Используя данные по кислороду, мы полу-

β ≃ 0.19 и γ ≃ -18.14. Это определяет класс универ-

чили α ≃ 10.51, β ≃ 0.29 и γ ≃ -5.25. Эти пара-

сальности твердых сфер.

метры справедливы и для азота. Данные для метана

4. Заключение. Основные выводы можно сфор-

демонстрируют некоторое отклонение по мере роста

мулировать следующим образом. Существуют опре-

плотности и увеличения приведенных коэффициен-

деленные корреляции между должным образом нор-

тов переноса. Интересно, что точки для жидкости

мированными коэффициентами сдвиговой вязкости

OCP лежат относительно близко к данным для рас-

и теплопроводности плотных жидкостей. Это явля-

сматриваемых молекулярных жидкостей.

ется аналогом соотношения Стокса-Эйнштейна меж-

Каноническая система отсчета в физике конден-

ду коэффициентами диффузии и вязкости. Однако

сированного состояния - это система твердых сфер.

взаимосвязь между вязкостью и теплопроводностью

Часто предполагается, что определенные структур-

не является полностью универсальной. Определен-

ные и динамические свойства систем мягких взаи-

ная системная зависимость имеет место (и это также

модействующих частиц могут быть интерпретирова-

напоминает ситуацию с соотношением SE [10, 11]).

ны по аналогии системам HS, даже несмотря на то,

Разные системы могут принадлежать к разным клас-

что существует кроссовер между мягкими и твер-

сам универсальности. В этом исследовании мы вы-

Письма в ЖЭТФ том 114 вып. 9 - 10

2021

Корреляция между сдвиговой вязкостью и теплопроводностью...

619

12.

R. Zwanzig, J. Chem. Phys. 79, 4507 (1983).

13.

U. Balucani, R. Vallauri, and T. Gaskell, Berichte der

Bunsengesellschaft für physikalische Chemie 94, 261

(1990).

14.

U. Balucani and M. Zoppi, Dynamics of the Liquid

State, Clarendon Press, Oxford (1994).

15.

Y. Rosenfeld, Phys. Rev. E 62, 7524 (2000).

16.

H. Ohta and S. Hamaguchi, Phys. Plasmas 7, 4506

(2000).

17.

O. S. Vaulina and S. V. Vladimirov, Phys. Plasmas 9,

835 (2002).

18.

G. Kaptay, Zeitschrift für Metallkunde 96, 24 (2005).

19.

O. S. Vaulina, X. G. Koss, Yu.V. Khrustalyov,

O. F. Petrov, and V. E. Fortov, Phys. Rev. E

82,

056411 (2010).

20.

L. Costigliola, U. R. Pedersen, D. M. Heyes,

Рис. 3. (Цветной онлайн) Корреляции между λR и ηR

T. B. Schrøder, and J. C. Dyre, J. Chem. Phys.

для систем HS и OCP. Пунктирная кривая соответству-

148, 081101 (2018).

ет скейлингу уравнения (7) на основе избыточной эн-

21.

S. Khrapak, AIP Adv. 8, 105226 (2018).

тропии. Сплошная кривая - аппроксимация на основе

22.

S. A. Khrapak and A. G. Khrapak, Phys. Rev. E 103,

данных для HS из работ [35, 36]

042122 (2021).

23.

L. L. Flores, J. M. Olais-Govea, M. Chávez-Páez, and

делили три таких класса: аргон (атомные жидко-

M. Medina-Noyola, Phys. Rev. E 103, 050602 (2021).

сти), кислород (молекулярные жидкости) и твердые

24.

S. Chapman and T. G. Cowling, The Mathematical

сферы. Если класс универсальности известен, знание

Theory of Non-uniform Gases - An Account of the

одного транспортного коэффициента позволяет оце-

Kinetic Theory of Viscosity, Thermal Conduction

нить два других. Это может быть очень полезным

and Diffusion in Gases, Cambridge University Press,

упрощением при описании различных явлений, от-

Cambridge (1990).

носящихся к жидкому состоянию.

25.

S. A. Khrapak, Phys. Rev. E 103, 013207 (2021).

Работа выполнена при финансовой поддержке

26.

K. Trachenko, M. Baggioli, K. Behnia, and

Министерства науки и высшего образования РФ (со-

V. V. Brazhkin, Phys. Rev. B 103, 014311 (2021).

глашение с ОИВТ РАН # 075-15-2020-785 от 23 сен-

27.

S. Khrapak and A. Khrapak, Molecules 26, 821 (2021).

тября 2020 г.).

28.

H. J. M. Hanley, R. D. McCarty, and W. M. Haynes,

J. Phys. Chem. Ref. Data 3, 979 (1974).

29.

D. G. Friend, J. F. Ely, and H. Ingham, Natl. Inst. Stand.

1. Y. Frenkel, Kinetic Theory of Liquids, Dover, N.Y.

Technol., Tech. Note 1325 (1989).

(1955).

30.

V. G. Baidakov, S. P. Protsenko, and Z. R. Kozlova,

2. J.-P. Hansen and I. R. McDonald, Theory of Simple

J. Chem. Phys. 137, 164507 (2012).

Liquids, Elsevier, Amsterdam (2006).

31.

V. G. Baidakov and S. P. Protsenko, J. Chem. Phys.

3. S. R. Groot and P. Mazur, Non-equilibrium

140, 214506 (2014).

Thermodynamics, Courier Corporation, N.Y. (1984).

32.

J. Daligault, K. Rasmussen, and S. D. Baalrud, Phys.

4. N. H. March and M. P. Tosi, Introduction to Liquid State

Rev. E 90, 033105 (2014).

Physics, World Scientific Pub Co Inc, River Edge, NJ

33.

B. Scheiner and S. D. Baalrud, Phys. Rev. E 100, 043206

(2002).

(2019).

5. V. V. Brazhkin, Phys.-Uspekhi 60, 954 (2017).

34.

R. Grover, W. G. Hoover, and B. Moran, J. Chem. Phys.

83, 1255 (1985).

6. Y. Rosenfeld, Phys. Rev. A 15, 2545 (1977).

35.

S. Pieprzyk, M. N. Bannerman, A. C. Branka,

7. Y. Rosenfeld, J. Phys.: Condens. Matter 11,

5415

M. Chudak, and D. M. Heyes, Phys. Chem. Chem.

(1999).

Phys. 21, 6886 (2019).

8. J. C. Dyre, J. Chem. Phys. 149, 210901 (2018).

36.

S. Pieprzyk, A. C. Branka, D. M. Heyes, and

9. L. Costigliola, D. M. Heyes, T. B. Schrøder, and

M. N. Bannerman, Phys. Chem. Chem. Phys.

22,

J. C. Dyre, J. Chem. Phys. 150, 021101 (2019).

8834 (2020).

10. S. Khrapak, Mol. Phys. 118, e1643045 (2019).

37.

S. Khrapak, N. P. Kryuchkov, L. A. Mistryukova, and

11. S. Khrapak and A. Khrapak, Phys. Rev. E 104, 044110

S. O. Yurchenko, Phys. Rev. E 103, 052117 (2021).

(2021).

Письма в ЖЭТФ том 114 вып. 9 - 10

2021