Письма в ЖЭТФ, том 115, вып. 12, с. 745 - 752

Модификация регуляризационного SVD-метода обратной свертки

Ю. В. Богомолов^+∗1), В. В. Алексеев^+∗, О. А. Леванова^+∗, А. Г. Майоров^∗, В. В. Малахов^∗, С. Г. Язынин⁺

⁺Ярославский государственный университет им. П. Г. Демидова, 150003 Ярославль, Россия

^∗Национальный исследовательский ядерный университет МИФИ, 115409 Москва, Россия

Поступила в редакцию 22 апреля 2022 г.

После переработки 3 мая 2022 г.

Принята к публикации 4 мая 2022 г.

Обратная свертка (unfolding) сегодня является важным этапом обработки экспериментальных дан-

ных, позволяя снижать влияние погрешностей и восстанавливать приближенные к истинным распре-

деления измеряемых физических величин. В настоящее время для решения этой задачи разработано

много подходов, в том числе широко используемых в современной физике атомного ядра и элемен-

тарных частиц, космофизике и других смежных научных направлениях. Однако многие применяемые

алгоритмы не предназначены или плохо адаптированы для восстановления многомерных распределе-

ний, когда, например, измеряются сразу несколько характеристик частиц. В работе предложен способ

адаптации SVD-алгоритма обратной свертки на многомерный случай. Для проверки построенный мо-

дифицированный метод применен к данным моделирования спектра космических лучей, измеряемого

в космофизическом эксперименте PAMELA. Метод не только позволил решить задачу восстановления

оценки истинного распределения многомерной величины (импульс и два угла, определяющих направле-

ние входа частицы в прибор), но и показал лучший результат в сравнении с классическим SVD-подходом

в одномерном случае (только импульс частицы).

DOI: 10.31857/S1234567822120011, EDN: imfewl

1. Введение. Экспериментальные возможности

чин, используются разные способы, которые можно

определения любой физической величины ограниче-

условно разделить на две большие группы:

ны характеристиками используемой научной аппара-

• гистограммные, где диапазон изменения физи-

туры, и по этой причине получаемые непосредствен-

ческой величины разделяется на дискретные

но при измерениях рапределения принято называть

интервалы (бины);

приборными. Однако интерес для анализа и физи-

ческих выводов представляют истинные распределе-

• безбиновые, не требующие такого разбиения.

ния физических величин или, по крайней мере, их

оценки. Отличия приборных и истинных спектров

В статье будут рассматриваться методы обрат-

могут быть связаны с конечными энергетическим,

ной свертки, применяемые к гистограммным спосо-

угловым или пространственным разрешениями при-

бам представления измерений, поскольку именно они

боров, наличием шумов и других источников лож-

широко применяются в различных областях совре-

ных или искаженных сигналов в научной аппарату-

менной экспериментальной физики, в том числе в

ре. Знание подобных инструментальных эффектов

экспериментах по физике частиц и космофизике, на-

и возможность их воспроизведения в математиче-

пример, в [9-12].

ской модели прибора позволяют строить качествен-

В гистограммном подходе при восстановлении

ные оценки истинных распределений с использова-

распределений множество значений непрерывной

нием специального математического подхода, в кото-

физической величины (или окрестность около иско-

ром формулируется так называемая задача обратной

мого значения дискретной величины) разбивается

свертки или анфолдинга (от англоязычного терми-

на интервалы. При этом описание измерительных

на “unfolding”) [1-3]. Подробные обзоры методов ре-

искажений сводится к определению вероятностей

шения этой задачи приведены, например, в работах

регистрации случайной величины в различных

[4-8].

бинах при условии, что истинное значение величины

Для построения статистических оценок, получен-

попадает в свой бин. Эти вероятности образуют так

ных в измерениях распределений изучаемых вели-

называемую матрицу миграций [1, 2]. Искажение

распределения, возникающее при измерении, пред-

¹⁾e-mail: yuribogomolov@gmail.com

полагает свертку истинного распределения с этой

Письма в ЖЭТФ том 115 вып. 11 - 12

2022

745

746

Ю. В. Богомолов, В. В. Алексеев и др.

матрицей. Тогда оценка истинного распределения

римента, детектированных аппаратурой в выделен-

определяется путем свертки измеренного распреде-

ных ячейках, обозначим как m = (m₁, m₂, . . . , m_n′)

ления с обратной матрицей миграции. Однако такая

и будем называть измеренным многомерным спек-

оценка оказывается неустойчивой [3, 13, 14], что

тром.

приводит к необходимости выбора других подходов.

Искажения, обусловленные конечным разрешени-

Некоторые методы обратной свертки позволяют

ем аппаратуры, шумами или другими приборными

не только учитывать информацию о характере ис-

эффектами, описываются матрицей миграций R, где

кажений, но также использовать априорные пред-

элемент R_ij вероятность того, что истинное значе-

положения об особенностях восстанавливаемого рас-

ние величины из j-й ячейки будет детектировано как

пределения физической величины (например, непре-

попавшее в i-ю ячейку. Тогда математические ожи-

рывность или гладкость) [15]. На этой идее основа-

дания ν

= (ν₁, ν₂, . . . , ν_n′ ) количества событий, де-

ны так называемые регуляризационные алгоритмы

тектированных в рассматриваемых ячейках, вычис-

[3, 5, 16], широко применяемые для корректировки

ляются следующим образом: ν = Rτ .

одномерных распределений в современных экспери-

Основной задачей является разработка методов

ментах [4, 17-20].

состоятельной статистической оценки неизвестных p

Однако рассматриваемая физическая величина в

или пропорциональных им математических ожида-

общем виде может являться многомерной, например,

ний τ по известному измеренному спектру m. Та-

ее компонентами может быть набор характеристик

кая задача носит название обратной свертки (также

элементарной частицы (энергия, масса, направление

используются термины деконволюция и unfolding).

движения и др.). В этом случае адаптация методов

Важный прикладной интерес представляют задачи

обратной свертки затруднительна, и такая задача се-

сравнительного анализа методов обратной свертки:

годня остается открытой, а для некоторых алгорит-

как сопоставления методов между собой, так и срав-

мов не решенной. В представленной статье предлага-

нения оценок истинного распределения, полученные

ется подход, позволяющий перенести хорошо зареко-

для разных реализаций одного метода (для различ-

мендовавшие себя алгоритмы обратной свертки, при-

ных параметров алгоритма, способов выделения би-

меняемые в одномерном анализе, на случай много-

нов и особенностей матрицы миграций) [16, 22].

мерного распределения. Также приводится его про-

Естественные допущения позволяют считать

верка с использованием данных моделирования ре-

последовательность зарегистрированных событий

гистрации космических лучей космофизической ап-

в каждом из бинов пуассоновским потоком [2], что

паратурой PAMELA [21], рассматривая три характе-

дает возможность построить статистическую оценку

ристики частицы - магнитную жесткость, полярный

истинного количества событий в рассматриваемых

и азимутальный углы входа в прибор.

бинах с помощью метода максимального правдопо-

добия. Решением соответствующей задачи является

2. Постановка задачи и обзор методов ее ре-

шения в одномерном случае. Пусть в ходе экс-

оценка τ

= R^-1m [3, 23], что также соответствует

“наивному” оцениванию истинного распределения

перимента наблюдаются N частиц, характеристики

(считать, что ν

= m, и решать систему уравнений

которых измеряются с помощью соответствующей

аппаратуры (факт детектирования частицы прибо-

Rτ

= m, инвертируя матрицу миграций). Такая

оценка истинного распределения является состо-

ром будем называть событием). Разобьем множество

истинных значений величины на n ячеек (много-

ятельной, несмещенной и имеющей наименьшую

дисперсию среди всех несмещенных оценок [3, 24].

мерных бинов) (Δ₁, Δ₂, . . . , Δ_n), где Δ_i ⊂ R^k. Дис-

кретизацией истинного распределения физической

Тем не менее, ее дисперсия зачастую является

достаточно высокой, а оценка оказывается неустой-

величины является набор вероятностей попадания

чивой (чувствительной к возмущениям измеренного

характеристик частицы в соответствующие бины:

распределения), что делает затруднительным ее

p = (p₁,p₂,...,p_n). Также истинным распределени-

использование на практике [3, 13, 14, 23].

ем будем называть математические ожидания коли-

Это требует искать другие пути построения оцен-

чества частиц в этих бинах: τ

= (τ₁, τ₂, . . . , τ_n), где

ки, в том числе основанные на искусственном введе-

τ_i = Np_i. Множество измеренных значений величи-

нии смещения. На практике особо выделяются такие

ны также разбиваем на интервалы (Δ^′1, Δ^′2, . . . , Δ^′n′ ),

два подхода [25].

где Δ^′i ⊂ R^k (зачастую для истинных и измеренных

значений используется одно и то же разбиение на

1. Итеративные методы, в которых последо-

бины, однако в общем виде такие разбиения могут

вательно производится уточнение статисти-

различаться). Количество частиц, по итогам экспе-

ческой оценки истинного распределения, с

Письма в ЖЭТФ том 115 вып. 11 - 12

2022

Модификация регуляризационного SVD-метода обратной свертки

747

ранней остановкой итеративного процесса.

1. Метод должен позволять использование в мно-

На этой идее основаны байесовский алгоритм

гомерном случае и учитывать миграцию между

д’Агостини [26] и некоторые его модификации,

ячейками (бинами), заданную матрицей R.

а также ряд других итеративных процедур [27].

2. Алгоритм должен учитывать непрерывность

или гладкость истинного многомерного распре-

2. Минимизация функции правдоподобия с вве-

денным “штрафным” слагаемым (идея регуля-

деления. Для этого естественным является под-

ризации). Такой подход применяется в SVD-

ход, основанный на регуляризации.

методе [28], использующем регуляризацию Ти-

3. Соответствующее этим особенностям спектра

хонова, алгоритме TUnfold [16, 29] и некоторых

регуляризационное слагаемое основывается на

других методах [30].

рассмотрении разностей значений величин в

пространственно близких ячейках (необходимо

Программные реализации метода д’Агостини,

учитывать, какие ячейки являются близкими

SVD-метода и алгоритма TUnfold включены в биб-

или соседними, а какие не являются).

лиотеки пакета программ ROOT [31], применяемого

в экспериментальных задачах физики высоких энер-

4. В предельном случае для одномерных измеря-

гий, а также связанного с ним пакета RooUnfold [32],

емых величин метод должен сводиться к ра-

предназначенного для решения задачи обратной

нее рассмотренным подходам (например, SVD-

свертки. Также авторы методов восстановления

алгоритму), особенности применения которых

спектра используют собственные программные

для восстановления спектра изучены.

разработки, содержащие реализации конкретных

алгоритмов решения задачи [33-37].

Оценку истинного распределения τ будем искать

Регуляризационный подход привлекателен воз-

как решение задачи минимизации:

можностью использовать для построения оценок

функции, отражающие предполагаемые особенности

Φ(τ ) = (Rτ - m)^T (Rτ - m) + αS(τ ) → min,

восстанавливаемого спектра. Например, регуляриза-

ция Тихонова, используемая в SVD-методе, отража-

где первое слагаемое соответствует функции прав-

ет гладкость распределения, однако существующие

доподобия без дополнительного смещения (минимум

реализации этого алгоритма применимы только для

этого слагаемого достигается при τ = R^-1m), а ре-

восстановления одномерных спектров, так как соот-

гуляризационная функция S(τ ) описывает заданные

ветствующая регуляризационная функция построе-

особенности искомого распределения [38]. При этом

на на основе разности значений в соседних линей-

числовой параметр α отражает вклад регуляризаци-

но занумерованных бинах. В то же время в мно-

онного слагаемого в функцию, используемую при по-

гомерном случае не существует нумерации бинов,

строении оценки спектра.

при которой пространственно близкие бины имели

В одномерном случае отношение близости бинов

бы близкие номера, поэтому применение упомянутых

вводилось естественным путем: бины нумеровались в

алгоритмов для восстановления многомерных рас-

порядке возрастания значения характеристики и со-

пределений в существующем виде невозможно. Тем

седними бинами считались те, номера которых отли-

не менее, можно поставить задачу модификации ре-

чаются на 1. В частности, это отношение позволяло

гуляризационной функции, основанной на степени

использовать при построении оценки спектра регу-

близости одномерных или многомерных бинов, что

ляризационную функцию

позволило бы адаптировать существующие алгорит-

мы на более широкий класс задач, а также повысить

∑

точность статистических оценок спектров и для од-

S(τ ) = (τ_i-1 - 2τ_i + τ_i+1)²,

номерного случая. Возможный вариант такой моди-

i=2

фикации, разработанный авторами, предлагается в

отражающую гладкость искомого распределе-

следующем разделе.

ния [28]. Она также может быть записана в виде

3. Многомерный регуляризационный ме-

тод. Перед описанием предлагаемого метода отме-

S(τ ) = (Cτ )^T (Cτ ),

тим некоторые основные положения, которые ис-

пользовались при адаптации описанных ранее под-

где матрица C отражает близость соседних бинов и

ходов.

имеет следующий вид:

Письма в ЖЭТФ том 115 вып. 11 - 12

2022

5^∗

748

Ю. В. Богомолов, В. В. Алексеев и др.





-1

С учетом этих обозначений для построения ре-







-1



гуляризационной функции будем использовать обоб-









щенную матрицу Кирхгофа (K), элементы k_ij кото-



-1



C =





рой вводятся так:











∑







w(Δ_i, Δ_v), при i = j;



-1



k_ij =

v=i



-1

-w(Δ_i, Δ_j), при i = j.

Соответственно, оценка истинного распределения

Предлагаемая модификация общего подхода ос-

будет получена как минимум функции

нована на использовании при построении регуляри-

зационной функции такой матрицы, которая позво-

Φ(τ ) = (Rτ - m)^T (Rτ - m) + α(Kτ )^T (Kτ ).

ляет отразить сложные виды отношения соседства

Для многомерного случая рассматривается по-

или близости бинов. Для бинарного отношения (два

следовательная (линейная) нумерация бинов. Поэто-

бина либо являются соседними, либо нет) в одномер-

му структура функции не меняется, но связи меж-

ном или многомерном случае в таком качестве будем

ду бинами определяются не их нумерацией, а видом

использовать матрицу Кирхгофа K = (k_ij ), где

матрицы K. И поскольку отношение близости теперь



вводится не только для соседних бинов, то появляет-



deg(Δ_i), при i = j;

ся возможность строить оценки распределения для

k_ij =

-1,

если i = j, а Δ_i и Δ_j соседние;

случая, когда параметры сильно коррелируют.



в остальных случаях.

Точка минимума получается как решение пере-

определенной расширенной системы уравнений:

[

]

[

]

Здесь через deg(Δ_i) обозначено количество бинов, со-

RK^-1

седних с бином Δ_i. Например, соседними можно счи-

Kτ =

√α · I

тать пространственные бины, имеющие общий уча-

сток границы. Несложно убедиться, что в одномер-

где I единичная матрица.

ном случае со стандартным бинарным отношением

Отметим, что матрица K является вырожденной,

соседства такая матрица K совпадает с описанной

поэтому для вычисления обратной матрицы и кор-

выше матрицей C, а построенная оценка истинного

ректного решения задачи ее нужно возмутить. Для

спектра будет соответствовать результатам упомяну-

этого прибавим константу ξ к диагональным элемен-

тых ранее регуляризационных алгоритмов [28, 29].

там, т.е. рассмотрим вместо K матрицу K +ξI. Далее

Для многомерных ячеек становится все более

при вычислении K^-1 будем предполагать, что эта по-

заметной ограниченность бинарного подхода: во-

правка уже сделана.

первых, можно считать соседними (близкими) не

Для решения системы воспользуемся подходом,

обязательно ячейки с общим участком границы, а

применяемым в исходном SVD-алгоритме обратной

во-вторых, степень близости даже для граничащих

свертки [28]. Пусть система линейных уравнений

ячеек может быть различной (и зависеть от разме-

имеет вид Aτ = m. Сингулярным разложением мат-

ра области касания, от размера самих ячеек и дру-

рицы A размера l × k называется ее представление

гих характеристик). Развивая предложенную идею,

в форме A = USV^T , где U и V ортогональные

можно перейти к небинарным отношениям близости

матрицы размером l × l и k × k соответственно, S

бинов. Для этого введем показатель w(Δ_i, Δ_j ) ≥ 0

диагональная матрица l × k (диагональные значе-

весовой коэффициент соседства ячеек Δ_i и Δ_j (при

ния s_i неотрицательны и называются сингулярными

i = j). Бинарный случай соответствует значениям

значениями), сама матрица S называется сингуляр-

w(Δ_i, Δ_j ) = 1 для соседних ячеек и w(Δ_i, Δ_j ) = 0

ной матрицей. Выбором U и V можно добиться того,

для ячеек, не являющихся соседними; однако мож-

чтобы сингулярные значения шли по убыванию. Для

но гибко настроить весовые коэффициенты, считая

l = k все матрицы будут квадратными.

их пропорциональными степени связи, определяемой

Точное решение системы линейных уравнений

заранее выбранным способом (по области соприкос-

Aτ = m с помощью сингулярного разложения вы-

новения, размеру ячеек, расстоянию между центра-

полняется по следующему алгоритму [28]:

ми масс ячеек и другим характеристикам). Общих

1. Составляется система USV^T τ = m.

жестких рекомендаций по выбору элементов матри-

цы K нет, выбор весов w(Δ_i, Δ_j ) может варьировать-

2. Выполняется замена z = V^T τ. Система приоб-

ся в зависимости от особенностей текущей задачи.

ретает вид USz = m.

Письма в ЖЭТФ том 115 вып. 11 - 12

2022

Модификация регуляризационного SVD-метода обратной свертки

749

3. Домножается слева на обратную матрицу

был разбит на две выборки: по одной из них стро-

U^-1 = U^T , получается система Sz = U^T m.

илась матрица миграций, а другая использовалась

для тестирования. Для выделенных трехмерных би-

4. Выполняется замена: d = U^T m. Система при-

нов строились трехмерные истинный и измеренный

обретает вид Sz = d.

спектры рассматриваемых величин, а также матри-

5. Матрица S является диагональной, поэтому

ца миграций.

компоненты решения строятся как z_i = d_i/s_i.

Восстановление спектра в трехмерном случае

производилось предложенным модифицированным

6. Записывается решение системы: τ = V z.

SVD-алгоритмом. Матрица Кирхгофа строилась на

Для плохо обусловленных матриц A значения d_i

основе бинарного отношения соседства трехмерных

и соответствующие s_i малы, поэтому малые возму-

бинов: w(Δ_i, Δ_j ) = 1, если бины Δi и Δj имеют

щения этих значений приводят к сильным погреш-

ненулевую площадь касания, и w(Δ_i, Δ_j ) = 0 в про-

ностям решений z_i и решений исходной системы τ.

тивном случае. Величина параметра регуляризации

Решение описанной выше расширенной системы

α выбиралась как квадрат наибольшего сингулярно-

уравнений производится приведенным способом на

го значения при разложении матрицы системы после

основе сингулярного разложения, однако промежу-

перенормировки (процедура выбора параметров опи-

точные решения z_i теперь выглядят так [28]:

сана в разделе 3).

Рассмотрим одномерные проекции трехмерного

d_i

s²ⁱ

z_i =

спектра, например, на область значений магнитной

s_i

s²ⁱ + α

жесткости для некоторого сегмента апертуры. На

При s²ⁱ ≫ α решения практически совпадают с

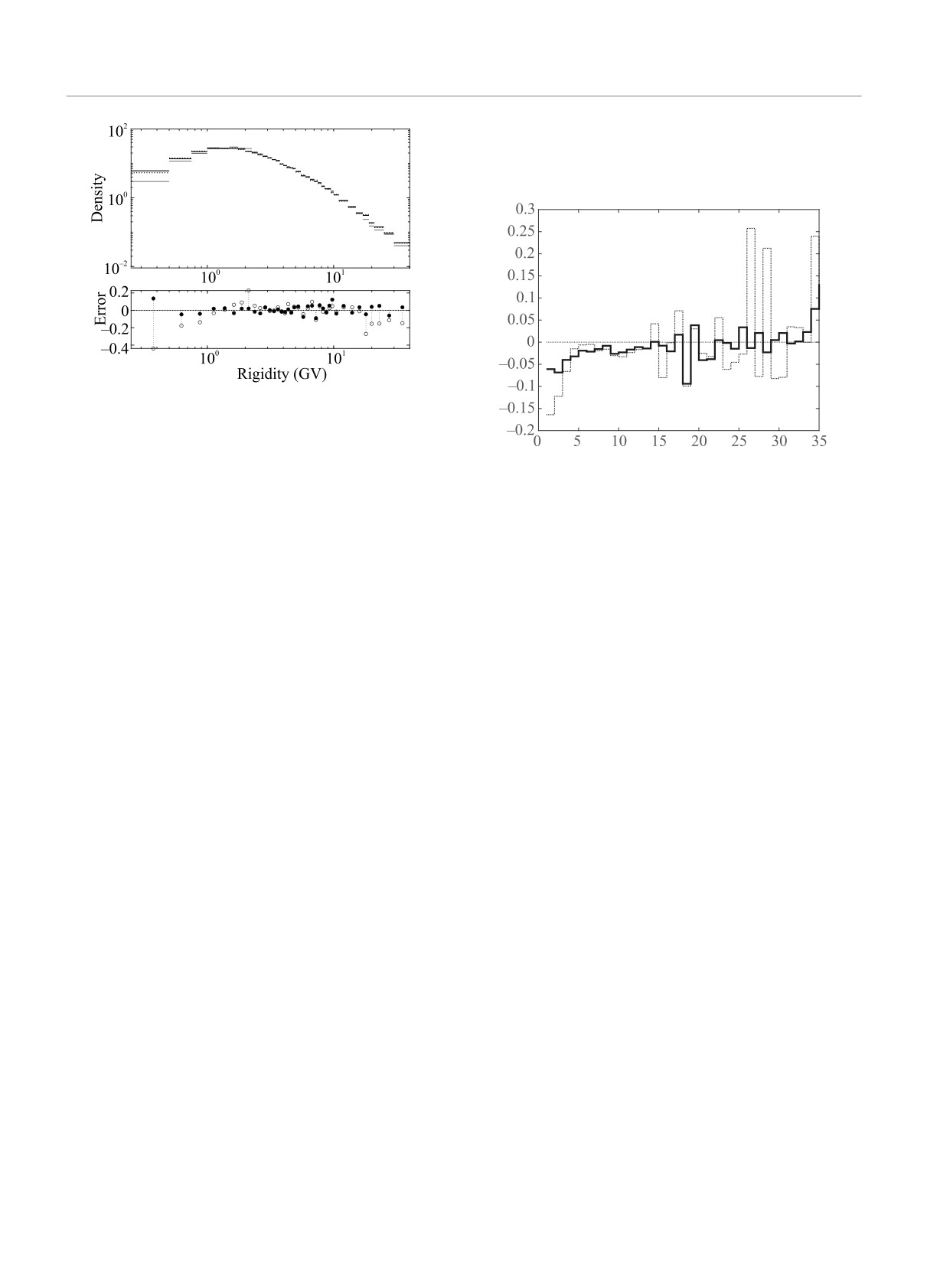
верхнем графике рис. 1 представлен пример вос-

рассмотренным прямым решением задачи. При ма-

становленного предложенным методом спектра (по-

лых сингулярных значениях s_i уже становится более

лужирная сплошная линия) в диапазоне азимута

заметным поправочный коэффициент. В качестве ко-

φ = 42^◦ и зенитного угла z = 17^◦. Для сравнения

эффициента регуляризации авторы SVD-алгоритма

приведены истинный и приборный спектры, пока-

рекомендуют выбирать квадрат “последнего большо-

занные соответственно пунктирной и тонкой сплош-

го” сингулярного значения [28]: расположить диаго-

ной линиями. В качестве показателя точности (по-

нальные элементы s_i матрицы S в порядке убывания

грешности) метода принимаем относительное откло-

и взять α = s^2k, где s_k ≫ s_k+1.

нение измеренного и восстановленного спектров от

Перед решением системы для уменьшения по-

истинного. Значения показателя точности для изме-

грешностей также производится перенормировка

ренного и восстановленного спектров приведены на

уравнений исходной линейной системы (чтобы

нижнем графике рис. 1 контурными и закрашенны-

каждое уравнение вносило одинаковый “вклад”) [28].

ми маркерами соответственно.

4. Результаты. В качестве исходных данных для

Из графика рис.1 следует, что предложенный ал-

анализа алгоритма использовано моделирование по-

горитм обратной свертки восстановил заниженный

тока протонов с характеристиками, соответствую-

спектр в области малых значений магнитной жест-

щими галактической компоненте космических лучей,

кости (до 1 ГВ) и завышенный спектр в диапазоне

который измеряется в космофизическом эксперимен-

жесткостей от 1.5 до 3 ГВ. Среднее значение погреш-

те PAMELA [21]. Для каждого события измеряет-

ности в рассматриваемом диапазоне от 0.35 до 40 ГВ

ся магнитная жесткость частицы, а также направ-

снизилось с δ_meas = 0.076 до δ_unf = 0.040. Для срав-

ление прилета, характеризуемое зенитным и азиму-

нения, использование прямого алгоритма восстанов-

тальным углами. В результате моделирования по-

ления спектра (применение обратной матрицы ми-

лучен набор пар истинных и измеренных значений

граций к измеренному спектру) приводит к средней

жесткости, зенитного угла и азимута. Область ис-

погрешности восстановленного спектра δ_inv = 0.088,

тинных значений величин (жесткость от 0.1 до 200

что выше не только средних погрешностей обратной

ГВ, зенитный угол от 0 до 45 градусов, азимуталь-

свертки для предложенного алгоритма, но и погреш-

ный угол произвольный) разбивалась на трехмерные

ностей при измерении (отклонении приборного спек-

ячейки (бины): по направлению прилета рассматри-

тра от истинного).

ваемый участок небесной сферы разбивался на близ-

Приведенная погрешность вычислялась для

кие по размеру области, в каждой такой области

результата работы алгоритма при однократном

рассматривалось неравномерное разбиение диапазо-

разбиении выборки на две подвыборки: для по-

на значений жесткости. Полученный набор данных

строения матрицы миграций и тестирования. Более

Письма в ЖЭТФ том 115 вып. 11 - 12

2022

750

Ю. В. Богомолов, В. В. Алексеев и др.

= 2). Для сравнения результатов рассмотрена

оценка, полученная исходным SVD- методом [28].

На рисунке 2 показаны относительные ошибки вос-

Рис. 1. Восстановление спектра в выбранном диапазоне

зенитного и азимутального углов. На верхнем рисун-

ке показаны истинный (пунктирная линия), прибор-

ный (тонкая сплошная линия) и восстановленный (по-

Рис. 2. (Цветной онлайн) Погрешность восстановле-

лужирная сплошная линия) спектры. На нижнем ри-

ния спектра для классического SVD-метода (штрих-

сунке показано относительное отклонение измеренного

пунктирная линия) и предложенного модифицирован-

(контурные маркеры) и восстановленного (закрашен-

ного SVD-метода (сплошная линия) в зависимости от

ные маркеры) спектров от истинного

номера бина (приборный спектр не представлен)

становленного спектра по отношению к истинно-

глубокий анализ систематических и статистических

му спектру (в каждом бине): сплошной линией

погрешностей может быть проведен в ходе серии

ошибки предложенного в статье алгоритма, штрих-

вычислительных экспериментов, в каждом из ко-

пунктирной линией ошибки SVD-алгоритма, ис-

торых проводится разбиение исходной выборки с

тинный спектр показан горизонтальной пунктирной

дальнейшим построением оценок отклонений восста-

линией на уровне 0. Для корректного отображения

новленного спектра от истинного. Это исследование

исключен первый бин, в котором для обоих алго-

предполагается вынести в отдельную работу.

ритмов характерна высокая относительная погреш-

Предложенный алгоритм позволяет решать за-

ность.

дачу восстановления спектра и в одномерном слу-

В области высоких значений магнитной жестко-

чае, более гибко учитывая отношение соседства меж-

сти (правая часть спектра) для предложенного алго-

ду бинами. Для каждой частицы в качестве изучае-

ритма отметим подавление больших колебаний оцен-

мой физической характеристики рассмотрена толь-

ки спектра. Среднее относительное отклонение так-

ко магнитная жесткость. Как и для многомерного

же снижено (по отношению к ошибке классического

случая, выполнено численное моделирование, в ре-

SVD-алгоритма). Таким образом, предложенный ал-

зультате которого получен набор пар истинных и из-

горитм показал более качественные результаты вос-

меренных значений жесткости. Далее построены ис-

становления спектра и в одномерном случае.

тинный и измеренный спектр в аналогично заданном

Стоит отметить, что разработанный алгоритм ба-

диапазоне значений жесткости, неравномерно раз-

зируется на использовании регуляризационного сла-

битом на интервалы. Для этого разбиения и дан-

гаемого, отражающего в том числе непрерывность

ных моделирования построена матрица миграций.

и гладкость по каждому из параметров многомер-

Алгоритм применяется к измеренному распределе-

ного распределения. Поэтому он может быть при-

нию жесткости в тестовой выборке, результат вос-

меним для подобных распределений, что подтвер-

становления спектра сопоставляется с соответствую-

ждается проведенным анализом. К распределениям,

щим истинным спектром (для тестовой выборки).

удовлетворяющим перечисленным свойствам, напри-

Восстановление спектра проводилось предложен-

мер, относятся и спектры космических лучей, в кото-

ным алгоритмом, в котором весовой коэффициент

рых наблюдаются изменения показателя при разных

связи между бинами экспоненциально уменьшает-

энергиях. Разработанный алгоритм при восстановле-

ся в зависимости от их удаленности (по номерам):

нии оценки истинного распределения сохраняет эту

w(Δ_i, Δ_j )

= cq^-|i-j| (рассмотрен случай c

= 2,

особенность (“излом” спектра).

Письма в ЖЭТФ том 115 вып. 11 - 12

2022

Модификация регуляризационного SVD-метода обратной свертки

751

5. Заключение. В работе изложен подход, поз-

10.

M. Aguilar, D. Aisa, D. Alpat et al. (AMS

воляющий адаптировать регуляризационные алго-

Collaboration), Phys. Rev. Lett. 114, 171103 (2015).

ритмы обратной свертки (в том числе распростра-

11.

F. P. An, A. B. Balantekin, H. R. Band et al. (Daya Bay

ненный в физике частиц SVD-алгоритм) для приме-

Collaboration), arXiv:2102.04614, Chin. Phys. C 45(7),

нения в более широком классе случаев. В частности,

073001 (2021).

можно отметить описание и применение алгоритма

12.

Д. Е. Карманов, И. М. Ковалев, И. А. Кудряшов,

обратной свертки, позволяющего восстанавливать

А. А. Курганов, А. Д. Панов, Д. М. Подорожный,

гладкие многомерные спектры, сохраняя возмож-

А. Н. Турундаевский, О. А. Васильев, Письма в

ность применения и в одномерном случае. Возмож-

ЖЭТФ 111(7), 435 (2020).

ность применения предложенного алгоритма к рас-

13.

H. W. Engl, M. Hanke, and A. Neubauer, Regularization

пределениям, для которых, например, характерны

of Inverse Problems, Kluwer Academic Publishers,

заметные немонотонные изменения по одной или

Dordrecht (2000).

нескольким переменным, требует отдельного изуче-

14.

J. Kaipio and E. Somersalo Statistical and

ния.

Computational Inverse Problems, Springer, N.Y.

На данном этапе отмечается, что для рассмотрен-

(2005).

ных в работе исходных данных представленный мо-

15.

G. Cowan, Statistical Data Analysis, Clarendon Press,

дифицированный алгоритм не уступает и даже пре-

Oxford (1998).

восходит исходные версии алгоритмов по точности

16.

T. Adye, Proceedings of the PHYSTAT 2011 Workshop,

восстановления спектра (например, по средней от-

CERN, Geneva, Switzerland, January 2011, CERN-

носительной погрешности в бинах). Также для мно-

2011-006; arXiv:1105.1160.

гомерного случая он позволяет строить достаточ-

17.

M. Arratia, A. Butter, M. Campanelli, V. Croft,

но точные оценки спектров для матрицы миграций,

A. Ghosh, D. Gillberg, K. Lohwasser, B. Malaescu,

не удовлетворяющих жестким требованиям диаго-

V. Mikuni, B. Nachman, J. Rojo, J. Thaler, and

нальности. Это дает возможность предполагать пер-

R. Winterhalder, arXiv:2109.13243.

спективность предложенного подхода и возможность

18.

G. Aad, B. Abbott, J. Abdallah et al. (ATLAS

его дальнейшей адаптации для решения актуальных

collaboration), Eur. Phys. J. C 72, 2039 (2012).

прикладных задач.

19.

V. Verzi, D. Ivanov, and Y. Tsunesada, Prog. Theor.

Исследование выполнено за счет гранта Россий-

Exp. Phys. 2017(12), 12A103 (2017).

ского научного фонда (проект # 19-72-10161).

20.

F. Li, Zh. Gu, L. Ge, H. Li, X. Tang, X. Lang, and

B. Hu, Results in Physics 13, 102211 (2019).

21.

O. Adriani, G. C. Barbarino, G. A. Bazilevskaya et

1. V. Blobel, in Proc. of the

1984

CERN School of

al. (PAMELA Collaboration), Phys. Rep. 544(4), 30

Computing, CERN 85-09, p. 88.

(2014).

2. V. Blobel, hep-ex/0208022.

22.

L. Brenner, P. Verschuuren, R. Balasubramanian,

3. G. Cowan, in Proc. Conf. on Advanced Statistical

C. Burgard, V. Croft, G. Cowan, and W. Verkerke,

Techniques in Particle Physics, ed. by M. R. Whalley

arXiv:1910.14654.

and L. Lyons, IPPP/02/39, Durham (2002).

23.

B. W. Rust, D. T. Ingersoll, and W. R. Burrus, A User’s

4. F. Span‘o, EPJ Web Conf. 55, 03002 (2013).

Manual for the FERDO and FERD Unfolding Codes,

5. S. Schmitt, arXiv:1611.01927v2, EPJ Web Conf. 137,

Oakridge National Laboratory, Oak Ridge (1983).

11008 (2017).

24.

P. Vischia, arXiv:2009.02913.

6. G. Zech, arXiv:1607.06910.

25.

M. Kuusela and P. B. Stark, arXiv:1512.00905.

7. Ю. В. Богомолов, В. В. Алексеев, О. А. Ле-

26.

G. D’Agostini, Nucl. Instrum. Methods Phys. Res. A

ванова,

А. Г.

Майоров,

В. В.

Малахов,

362, 487 (1995).

УФН

2022

(принята

печати);

doi:

27.

M. Kuusela and V. M. Panaretos, Annals of Appl. Stat.

https://doi.org/10.3367/UFNr.2022.05.039189 (english

9(3), 1671 (2015).

https://doi.org/10.3367/UFNe.2022.05.039189).

28.

A. Hoecker and V. Kartvelishvili, Nucl. Instrum.

8. А. Ю. Егоров, Я. А. Бердников, В. А. Бакаев,

Methods Phys. Res. A 372, 469 (1996).

И. М. Никитцина, Науч.-тех. ведомости СПбГПУ.

Физ.-мат. науки 12(3), 123 (2019).

29.

S. Schmitt, J. Instrum. 7(10), T10003 (2012).

9. S. Chatrchyan, V. Khachatryan, A. M. Sirunyan et al.

30.

P. Baron, Acta Phys. Pol. B 51(6), 1241 (2020).

(CMS Collaboration), Phys. Lett. B 709, 28 (2012).

31.

Офиц. сайт пакета ROOT https://root.cern.ch/.

Письма в ЖЭТФ том 115 вып. 11 - 12

2022