Письма в ЖЭТФ, том 115, вып. 5, с. 328 - 335

Эффект бабочки в системе квантовых точек в модели

Сачдева-Йе-Китаева

А. В. Лункин¹⁾

Институт теоретической физики им. Л. Д. Ландау РАН, 119334 Москва, Россия

Сколковский институт науки и технологий, 121205 Москва, Россия

Национальный исследовательский университет “Высшая школа экономики”, 101000 Москва, Россия

Поступила в редакцию 3 февраля 2022 г.

После переработки 3 февраля 2022 г.

Принята к публикации 3 февраля 2022 г.

В работе предложен способ вычисления аномально упорядоченного во времени коррелятора в обоб-

щении модели Сачдева-Йе-Китаева с ненулевой пространственной размерностью. Наш результат приме-

ним не только на малых временах, когда хаотичные свойства системы развиты слабо, но и на больших -

порядка времени Эренфеста. Мы показали, что информация о приложенном возмущении, которую опи-

сывает данный коррелятор, распространяется баллистически в виде фронта. Нами впервые была вы-

числена скорость фронта для моделей данного типа.

DOI: 10.31857/S123456782205010X

1. Введение. Чувствительность системы к на-

correlator (OTOC). Связь подобных корреляторов с

чальным условиям была отмечена А. Пуанкаре при

хаотичным поведением системы была впервые отме-

изучении неустойчивости в задаче трех тел. Позднее

чена в работе [1]. В общем случае мы можем рассмат-

эта задача изучалась А. Ляпуновым. Термин “Эф-

ривать не только сопряженные пары операторов, но

фект бабочки” был предложен Э.Лоренцом, кото-

и корреляторы вида

рый обнаружил подобную неустойчивость при моде-

лировании атмосферных явлений. Эффект выражен

F (t₁, t₂, t₃, t₄) = 〈X₁(t₁)X₂(t₂)X₃(t₃)X₄(t₄)〉,

(3)

в том, что расстояние между изначально очень близ-

кими траекториями системы со временем растет экс-

где X_i - произвольные операторы. Мы будем пола-

поненциально, т.е.

гать, что t₁ ≈ t₃ > t₂ ≈ t₄. Изучение таких корре-

ляторов позволяет характеризовать хаотичные свой-

∂q(t)

{q(t), p(0)} =

∼eλLt.

(1)

ства системы, а также понять распространение ин-

∂q(0)

формации в квантовой системе [2-4].

Для экспериментального изучения OTOC нам

Выше {. . . , . . .} - скобка Пуассона для данной си-

нужно “переместиться” в прошлое, создать возму-

стемы, p и q - канонически сопряженные импульс и

щение и посмотреть, к чему оно приведет по срав-

координата соответственно. Показатель λ_L называ-

нению с тем, что мы видели до этого. Подобный

ют экспонентой Ляпунова. Эта формула также мо-

опыт, для классической системы, был описан в рас-

жет быть обобщена на случай квантовых систем.

сказе Р. Брэдбери “И грянул гром”, главные герои

В таком случае экспонента Ляпунова может быть

которого, отправивишсь в далекое прошлое и убив

получена, по аналогии, из коррелятора следующего

там бабочку, увидели разительное отличие в их ми-

вида:

ре по возвращению назад. Современные управляе-

мые квантовые системы, имеющие большое число

〈[q(t), p(0)]²〉 ∼ eλLt.

(2)

степеней свободы, позволяют изучать подобные кор-

Из формулы (2) следует, что для вычисления экспо-

реляторы. Полностью контролируя систему, мы мо-

ненты Ляпунова нам необходимо вычислять корре-

жем изменить знак гамильтониана, определяющего

ляторы, аномально упорядоченные во времени. В ан-

эволюцию. После такой замены система эффективно

начнет двигаться назад во времени. Подобный экс-

глийской литературе их называют out-of-time ordered

перимент был поставлен группой Google Quantum

¹⁾e-mail: alunkin@itp.ac.ru

Ai [5].

328

Письма в ЖЭТФ том 115 вып. 5 - 6

2022

Эффект бабочки в системе квантовых точек в модели Сачдева-Йе-Китаева

329

Для достаточно большого класса систем указан-

гамильтонианом был описан в [2], при этом наличие

ный коррелятор (3) обладает универсальным поведе-

подобного фронта встречалось и в других моделях,

нием. А именно:

например, [10, 11].

F (t₁, t₂, t₃, t₄)

В данной работе мы исследуем поведение систе-

≈1-

eλL(t1-t2),

(4)

〈X₁(t₁)X₃(t₃)〉〈X₂(t₂)X₄(t₄)〉

мы, состоящей из гранул, динамика в каждой из них

описывается гамильтонианом модели SYK; при этом

где, как и раньше, параметр λ_L - экспонента Ляпу-

существует туннелирование между гранулами. Мы

нова данной квантовой системы. При этом C ≫ 1.

покажем, что сценарий, упомянутый выше, приме-

Для таких систем можно получить общую оценку на

ним для описания поведения OTOC в нашей систе-

экспоненту Ляпунова (далее ℏ = 1):

ме. Нами также впервые вычислена скорость распро-

λ_L ≤ 2πT.

(5)

странения фронта в обобщении модели SYK. Предло-

Это оценка была получена в работе [6]. Одним из

женный способ вычисления может быть также при-

менен и к другим моделям, основанным на модели

примеров, для которой эта оценка насыщается, яв-

ляется модель Сачдева-Йе-Китаева (SYK), [7], га-

SYK.

Отметим, что поведение OTOC в обобщении мо-

мильтониан которой будет введен далее.

дели SYK обсуждалось в работе [12]. Однако в ука-

Следующий вопрос, который естественно задать:

занной работе не исследовано поведение коррелятора

как ведет себя этот коррелятор в случае t₁ - t₂ ∼

на больших временах, соответственно понятие фрон-

∼ λ^-1LlnC? Время t_E = λ^-1LlnC называют временем

Эренфеста. В случае модели SYK ответ на этот во-

та было не определено. Также в работе [12] иссле-

довался лишь случай длинноволновых возбуждений,

прос был получен в работе [8], в которой было пока-

зано, что при t - t_E ≫ λ^-1L коррелятор F стремится

при этом, в ситуации общего положения, распростра-

нение фронта - баллистическое, т.е. результаты ра-

к 0. В работе [9] было рассмотрено поведение OTOC

для нульмерных фермионных систем на временах,

боты применимы лишь в ограниченной области па-

раметров. Методы, предложенные авторами этой ра-

больших чем время Эренфеста. В работе было по-

боты, существенно опираются на форму взаимодей-

казано, что такой коррелятор может быть вычислен

ствия между фермионами из разных гранул, которое

универсальным способом, исходя из поведения кор-

так же, как и гамильтониан, описывающий динамику

релятора на малых временах (4) и парных корреля-

внутри гранул - четвертого порядка по фермионным

ционных функций.

операторам.

В общем случае для нульмерных систем мы мо-

жем отметить, что на временах t ≪ t_E корреля-

Структура нашей работы следующая. В разделе 2

будет введена изучаемая модель и получено действие

тор изменяется экспоненциально, но этот рост по-

давлен фактором C^-1, таким образом система сла-

для ее описания. В разделе 3 будут описаны основ-

ные свойства модели SYK. В разделе 4 будет вычис-

бо демонстрирует хаотичное поведение. На временах

t - t_E ≫ λ^-1L хаотичные свойства проявляются пол-

лен OTOC, а также описаны основные его свойства.

2. Модель и основные свойства. Гамильтони-

ностью.

ан нашей модели имеет следующий вид:

Что следует ожидать для системы с ненулевой

пространственной размерностью? Предположим, что

{

}

∑

∑∑

операторы X₂ и X₄ приложены в точке r₂. Точку r₁

H =

H_r + i

w_r,i;r+δr,jχ_r,iχ_r+δr,j

и время приложения операторов X₁ и X₃ мы будем

δr i,j

менять, вычисляя при этом OTOC. В результате при

∑

H_r =¹

J_i,j,k,l;rχ_r,iχ_r,jχ_r,kχ_r,l.

(6)

фиксированной разнице времени t₁ - t₂ мы можем

i,j,k,l

разделить систему на две области: 1) область нераз-

витого хаоса с F = const; 2) область развитого хаоса

Здесь χ_r

- майорановские фермионы, ком-

с F → 0. В частности, точки на достаточно большом

мутационные соотношения которых имеют вид:

удалении относятся к области 1. Область 2 появля-

{χ_r,i, χ_r′_,i′ } = δ_i,i′ δ_r,r′ . Индекс i принимает значения

ется только при t₁ - t₂ ≥ t_E. Эти области разделяет

от 1 до N ≫ 1. Гамильтониан (6) описывает решетку

граница (фронт), которая со временем движется, что

из квантовых точек, имеющих радиус вектор r,

приводит к увеличению области 2. Скорость этого

δr - вектор между произвольной точкой и одним

движения, вообще говоря, зависит от направления,

из ее соседей. Член H_r описывает динамику внутри

так как информация о возмущении в системе распро-

точки, второй член в первой строчке описывает

страняется баллистически. Подобный сценарий рас-

туннелирование частиц между соседними точками.

пространения информации для систем с локальным

Гамильтониан H_r является гамильтонианом мо-

Письма в ЖЭТФ том 115 вып. 5 - 6

2022

4^∗

330

А. В. Лункин

∫

∑

дели SYK [7]. Качественно мы можем сказать, что

S = ε_σ dt₁dt₀δ^′(t₁ - t₀) ×

этот гамильтониан описывает систему, в которой





есть N вырожденных уровней, в таком случае эф-

∑



фекты взаимодействия становятся сильными и при-

χ^(σ)r,i(t₁)χ^(σ)r,i(t₀)

×



водят к неферми-жидкостному поведению, которое

r,i

∫

было описано, например, в работах [13, 14].

i∑∑

Тензоры w и J антисимметричны по индексам и

εσ1 εσ0

dt₁dt₀ ×

r σ

являются случайными гауссовыми независимыми ве-



]₄

личинами с нулевым средним и дисперсией, опреде-

[∑

 J²

χ(σ1)r,i(t₁)χ(σ0)r,i(t₀)

ляемой выражением:

× 4N3

3!J

w²

〈J^2i,j,k,l;r〉 =

〈w^2r,i;r+δr,j 〉 =

(7)

∑

∑w²

N³

χ(σ1)r,i(t₁)χ(σ0)r,i(t₀) ×

δr i,j

Мы предполагаем, что характерный масштаб взаи-

}

модействия внутри гранул много больше, чем харак-

× χ(σ1)r+δr,j(t₁)χ(σ0)r+δr,j(t₀)

терная амплитуда туннелирования, т.е. J ≫ w.

Для вычисления OTOC нам придется воспользо-

Определим поле G следующим образом:

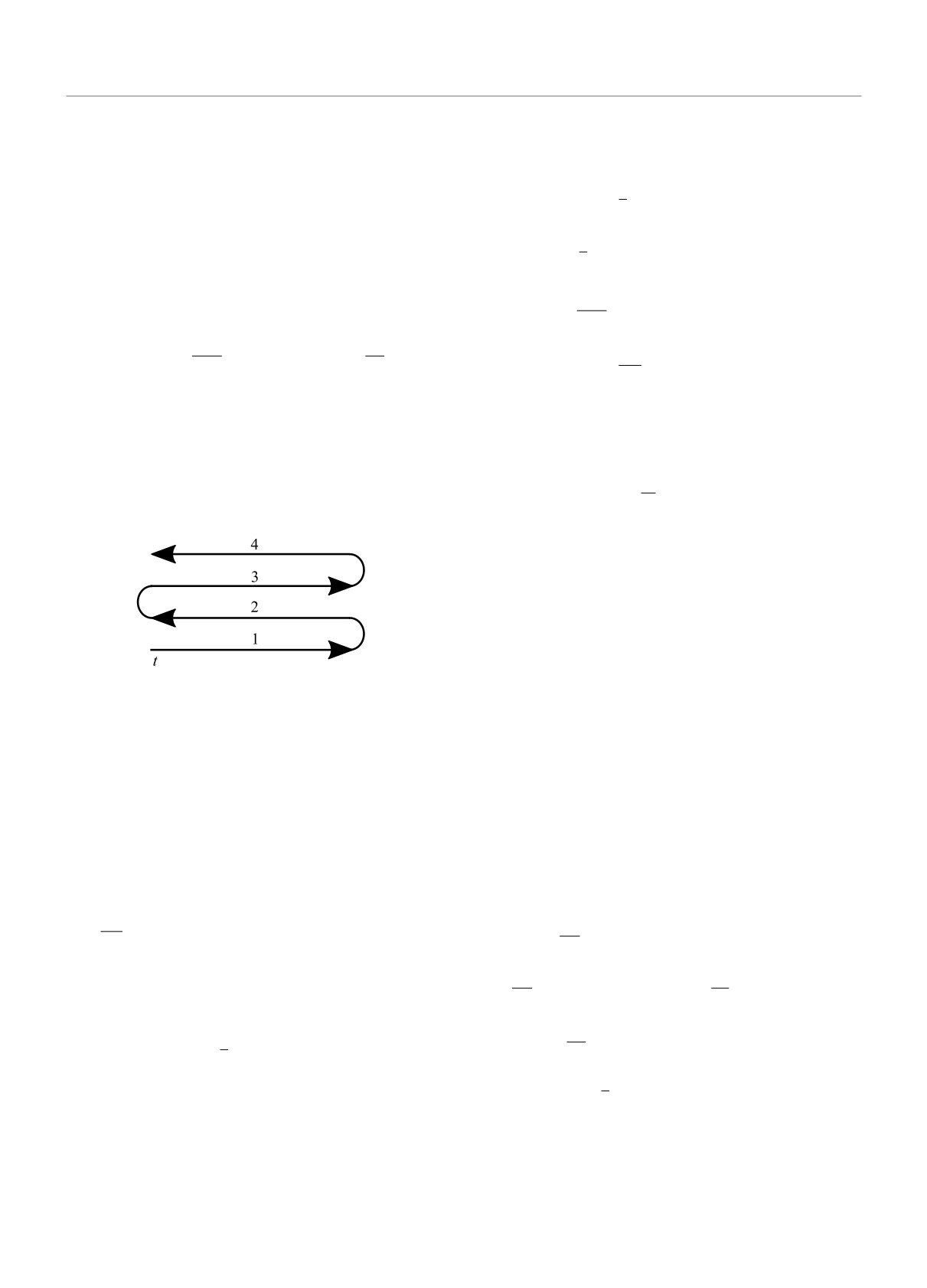
ваться двойным контуром Келдыша (рис.1). Техни-

1∑

ческие детали вычисления описаны в работах [2, 8,

χ(σ1)r,k(t₁)χ(σ0)r,k(t₀).

(10)

Gσ1σ0 (t1, t0|r) = -i

15].

Нам также потребуется ввести поле Σ, определен-

ное как множитель Лагранжа для поля G, тем самым

сделав последнее поле не обремененным никаким со-

отношением, кроме симметрий, связанных с переста-

новкой t₁ ↔ t₀.

Поскольку амплитуда туннелирования между

гранулами много меньше энергетического масштаба

взаимодействия внутри гранул, мы можем рассмот-

Рис. 1. Контур интегрирования для действия состоит

реть член с туннелированием как возмущение. А

из четырех частей, две из которых идут вперед во вре-

значит, мы можем ограничиться полями G, которые

мени, а две назад

зависят только от одной координаты, так как в

невозмущенной задаче гранулы никак друг с другом

Нам также понадобится различать поля, опреде-

не связаны. Также введем следующее обозначение

ленные на разных частях контура, для этого мы вве-

для удобства:

дем индекс σ ∈ {1, 2, 3, 4}. Например, фермионное

поле, определенное на части контура с номером σ,

Σ^(free)σ

(11)

1σ0

(t₁, t₀) = -εσ1 δσ1,σ0 δ^′(t1 - t0).

мы обозначим как χ^(σ)r,i. Тогда коррелятор, который

нас интересует будет иметь вид:

Используя новые поля и обозначение, запишем дей-

ствие в виде:

F (t₁, t₂, t₃, t₄) =

∑

∫

∑

〈T_Cχ^(1)r

(t₁)χ^(2)r

(t₂)χ^(3)r

(t₃)χ^(4)r

(t₄)〉.

(8)

1,i

2,i^′

1,i

2,i^′

S=-

dt₁dt₀Σ^(free)σ

N²

1σ0

(t₁, t₀)Gσ1 σ0 (t1, t0|r) +

i,i^′

r,σ1,σ

∫

Здесь символ T_C обозначает упорядочение опера-

iN∑∑

{J²

εσ1 εσ0

dt₁dt₀

G^4σ

(t₁, t₀|r) -

1 σ0

торов вдоль контура. Действие на контуре имеет вид:

r σ





}

∫

∑

∑



w²

ε_σ dt

χ^(σ)r,i(t)∂_tχ^(σ)r,i(t) - H^(σ)(t)

. (9)

Gσ1σ0 (t1, t0|r)Gσ1σ0 (t1, t0|r + δr)





δr

r,i

∫

1∑∑

dt₁dt₀Σσ1σ0 (t1, t0|r) ×

Здесь ε₁ = ε₃ = 1 = -ε₂ = -ε₄ - знак “направле-

r σ1,σ0

ния времени” соответствующей части двойного кон-

{

}

∑

тура. После усреднения по беспорядку действие при-

χ(σ1)r,k(t₁)χ(σ0)r,k(t₀)

.(12)

× iNGσ1σ0(t1, t0|r) -

мет вид:

Письма в ЖЭТФ том 115 вып. 5 - 6

2022

Эффект бабочки в системе квантовых точек в модели Сачдева-Йе-Китаева

331

Используя эти переменные, мы можем также

использовать седловые уравнения для полей G и Σ в

переписать наш коррелятор (8), который нужно

виде:

перенормировать, в результате он примет вид:

∑∫

|r) =

duΣσ1σ(u1, u|r)Gσσ0 (u, u0

F (t₁, t₂, t₃, t₄) =

〈T_CG₁₃(t₁, t₃|r₁)G₂₄(t₂, t₄|r₂)〉

= δσ1,σ0δ(u1 - u0),

(13)

〈T_CG₁₃(t₁, t₃|r₁)〉〈G₂₄(t₂, t₄|r₂)〉

(u₁, u₀|r).

(16)

Σσ1σ0 (u1, u0|r) = εσ1 εσ2 G^σ

σ0

Именно в таком виде коррелятор вычислен в работах

Тут мы ввели параметр q = 4, в конкретных вычис-

[8, 9].

лениях бывает полезным рассматривать этот пара-

Как мы видим, действие стало квадратичным от-

метр произвольным для размерной регуляризации.

носительно фермионных операторов, а значит, мы

Поэтому мы выпишем решения седловых уравнений

можем взять по ним интеграл и перейти к действию,

в общем виде.

записанному в терминах полей G и Σ. Однако перед

Уравнения выше имеют огромную группу сим-

этим нам удобнее перейти к безразмерной перемен-

метрий. Чтобы это увидеть, рассмотрим произволь-

ной u ≡ 2πT t, где T - температура системы, а также

ный набор монотонных функций f_σ,r(u), тогда мы

мы перемасштабируем поля следующим образом:

можем сделать преобразование по правилу:

)_3/2

[

]_Δ

(2πT

f^′σ

(u₁)f^′σ

(u₀)

Σ(t₁, t₀) ≡ J²

Σ(u₁, u₀),

Gσ1σ0 (u1, u0|r) →

1,r

0,r

× Gσ1σ0(fσ1,r(u1), fσ0,r(u0)|r),

(17)

)_1/2

(2πT

G(t₁, t₀) ≡

G(u₁, u₀).

(14)

где Δ =^1q . После подстановки новой функции G мы

получим тождество. Однако мы знаем, что исходный

В новых переменных действие будет иметь вид:

гамильтониан не зависит от времени, а значит, функ-

ция Грина, которую мы ищем, должна зависеть толь-

ко от разности времен. При этом матричные элемен-

∫

{

ты поля G не являются независимыми, так как свя-

∑

εσ1 εσ0

du₁du0 -

G^4σ

(u₁, u₀|r) ×

заны некоторыми соотношениями, одно из которых -

1 σ0

r σ1,σ0

флуктуационно-диссипационная теорема (связываю-

[

]

щая келдшевскую функцию Грина с запаздывающей

×Σ^(free)σ

1σ0

(u₁, u₀) + Σσ1σ0 (u1, u0|r) Gσ1σ0 (u1, u0|r)+

и опережающей). Поскольку мы работаем с систе-

(

)

∑

εσ1 εσ0

w²

мой, которая находится в равновесии, мы можем ука-

2πTJ

зать значение матричных элементов поля G лишь

δr

}

на первой части нашего двойного контура (соответ-

× Gσ1σ0(u1, u0|r)Gσ1σ0(u1, u0|r + δr)

ственно в формуле ниже σ ∈ {1, 2}). С учетом этого

комментария, трансляционно-инвариантное решение

- Tr ln(Σ).

(15)

седловых уравнений имеет вид:

При достаточно низкой температуре T ≪ T_FL ∼

Gσ0)1σ0 (u1, u0|r) = b^Δgσ1σ0 (u1 - u0),

∼ w²J^{последнийчлендействия(15)становитсядоми-}

[

]_Δ

s^′(0)(u₁)s^′(0)(u₀)

нирующим и поведение системы описываются обыч-

gσ1σ0 (u > 0) ≡ i

ной теорией ферми-жидкости. Мы будем работать

(s₍₀₎(u₁) - s₍₀₎(u₀))²

при T ≫ T_FL. В таком предположении, член с тун-

(

)

-e^-iπΔ e^iπΔ

(18)

нелированием можно рассматривать по теории воз-

-e^-iπΔ e^iπΔ

σ1σ

мущений. Пренебрегая им, мы приходим к действию

где b = (1-2Δ)tan(2πΔ)2π. Тут функция s0(u) = eu,

модели SYK, ниже мы остановимся на его свойствах.

такая форма записи обусловлена дальнейшими вы-

3. Основные свойства модели SYK. Вместо

кладками. Решение при u < 0 может быть восстанов-

вычисления функционального интеграла по полям G

лено, используя свойства симметрии функции Грина:

и Σ мы можем воспользоваться седловым приближе-

нием, так как S ∝ N, при этом N ≫ 1. Как было

gσ1σ0 (u) = -gσ0σ1 (-u). Группа симметрий уравнений

превосходит группу симметрий данного решения, ко-

отмечено выше, членом с w мы можем пренебречь

торая задана преобразованиями вида:

при T ≫ T_FL при выводе седловых уравнений. Член

с Σ^(free) важен при температурах порядка J и на ма-

as₀(u) + b

s₀(u) → s(u) =

(19)

лых временах. Полагая J ≫ T ≫ T_FL, мы можем

cs₀(u) + d

Письма в ЖЭТФ том 115 вып. 5 - 6

2022

332

А. В. Лункин

Обычно такое поведение свидетельствует о на-

ном случае наше рассмотрение ограничено времена-

личии мягкой (Голдстоуновской) моды. Однако на-

ми t ≪^NJ [19]. Далее мы займемся вычислением

ши уравнения являются приближенными, даже при

OTOC.

w = 0 мы пренебрегли членом Σ^(free), а значит, сим-

4. Поведение OTOC на больших временах.

метрия, которую мы обнаружили, является асимп-

Основная идея статьи состоит в рассмотрении следу-

тотической, подобное встречается при работе с σ-

ющего анзаца для поля f(u):

моделями [16]. В нашем случае это означает, что вме-

сто взятия всего функционального интеграла по по-

e^u + a(u)

e^f(u) =

(24)

лям G и Σ нам требуется проинтегрировать толь-

b(u)e^u + 1

ко по полям, которые являются решением седловых

уравнений. Многообразие таких полей можно задать

где a(u) и b(u) - медленные функции. Используя

следующим образом: все такие поля получены с по-

такую подстановку, мы можем написать выражение

мощью преобразования симметрии (17), которое при-

для поля g, которое следует из выражения ниже (мы

менили к седловому решению (18). Переход от ин-

пренебрегаем производными полей a и b в силу пред-

тегрирования по всем полям к интегрированию по

положения об их медленности):

полям, лежащим на определенном многообразии не

точен, он верен в силу того, что флуктуации в на-

(u₁ -u₀)

f^′σ

(u₁)f^′σ

(u₀)

0,r

правлении, перпендикулярном многообразию подав-

4 sinh²

(

) ≈

fσ1,r^(u1^)-fσ0,r^(u0⁾

лены в βJ раз [7].

4 sinh²

[

Это многообразие параметризовано функциями

aσ1,r(u1) - aσ0,r(u0)+

f_σ,r(u). Действие [7] на этом многообразии имеет вид

≈ 1+2

e^u1 - e^u

∑ ∫

]-1

S = -C_J ε_σ du Sch{efσ,r,u} -

bσ1,r(u1) - bσ0,r(u0)

(25)

r,σ

e^-u1 - e^-u0

∫

∑

-C_w

du₁du₀εσ1 εσ0 ×

В выражении выше мы оставили только линейные

δr,r,σ1,σ0

члены по a или b с экспоненциально растущими

×g^(f)σ

(u₁, u₀|r)g^(f)σ

(u₁, u₀|r + δr),

(20)

1σ0

коэффициентами, так как эти поля малы (a, b ∝

∝ N^-1/2). Однако, умножив их на экспоненциально

- теплоемкость моде-

πJT

большие множители, мы получим комбинацию, ко-

ли SYK и вклада в теплоемкость от возмущения со-

торая не мала. Для дальнейшей работы нам понадо-

ответственно, α_S ≈ 0.05. Поле g^(f) (при u₁ - u₂ > 0)

бится вспомогательный интеграл:

определено как:

[

]_Δ

∫

∞

gσf,1σ2 (u1, u0|r) =

f^′σ

(u₁)f^′σ

(u₀)

1,r

0,r

a^-γ

s^γ-1e^-sa

(26)

(21)

Γ(γ)

× gσ1σ0(fσ1,r(u1) - fσ0,r(u0)).

Символ Sch{s(u), u} обозначает производную Швар-

ца, которая определена как:

Используя (26) дважды, мы можем записать интере-

)_′

сующий нас коррелятор в виде:

′′

(s^′′)²

Sch{s(u), u} ≡

(22)

s^′

F (u₁, u₂, u₃, u₄) =

∞

∫

Одно из важных свойств производной Шварца сле-

ds_ods_e

дующее: при замене s на дробно-линейное преобразо-

(s_os_e)^(2Δ)-1e-se-so 〈eiSj 〉,

Γ(2Δ)²

вание от s величина производной не изменится. Кор-

∫

∑

(

)

релятор, который мы планируем вычислять, имеет

S_J =

a,r

(u)â_r(u) +jTb,r(u)br(u)

(27)

следующий вид, с учетом введенных обозначений:

(f)

〈T_Cg₁

(u₁, u₃|r₁)g^(f)2,4(u₂, u₄|r₂)〉

F (u₁, u₂, u₃, u₄)=

.(23)

Выше мы ввели столбцы â и

b, состоящие из полей a

〈g^(f)1,3(u₁, u₃|r₁)〉〈g^(f)2,4(u₂, u₄|r₂)〉

и b соответственно. Эти столбцы имеют по 4 компо-

Мы будем работать с квадратичным действием,

ненты в соответствии с ветвями контура. Столбец

которое применимо при w ≫^NJ [17, 18]. В против-

имеет следующий вид:

Письма в ЖЭТФ том 115 вып. 5 - 6

2022

Эффект бабочки в системе квантовых точек в модели Сачдева-Йе-Китаева

333





-2s_oδ(u - u₁)δ

r,r1

Имея квадратичное действие для полей a и b, мы мо-





e^u1 - e^u3

жем выполнить усреднение:







-2s_eδ(u - u₂)δ



r,r2







e^u2 - e^u4



〈eiSj 〉 ≈ exp{-s_es_oz},

(32)

ja = -i



(28)



2s_oδ(u - u₃)δr,r1









e^u1 - e^u3







2s_eδ(u - u₄)δr,r2

f_α(r₁ - r₂)

z≡

∑

(

) ×

π²

e^u2 - e^u4

4CJ + C_w

-1

δr

(_u

)

Вектор

jb определен аналогично.

4+u2-u1-u3

sinh

Теперь мы можем рассмотреть действие для по-

(_u

)

(_u

(33)

3-u1

sinh

4-u²2

лей a и b. Поскольку выбранное нами поле f (24)

локально близко к седловому, то мы можем вос-

∫

пользоваться квадратичным действием для вывода

d^dp

e^irp

f_α(r) ≡

(

(34)

действия для полей a и b. Квадратичное действие

∑

pδr

(2π)^d 1 + α_δr sin²

удобно записать, введя поле δf, определенное как

f = u+δf(u). Подобное квадратичное действие было

получено в работах [14, 20] и имеет вид:

∑ π²C_w8

∫

[

]_-1

δr

dΩd^dp

α≡

∑

(

) =

S₂ =

f^†p(Ω)

G(Ω, p) δfp(Ω),

π²

C_J + C_w

-1

(2π)^d+1

δr

[

]_-1

[

]_-1

[

]_-1

G(Ω, p)

G⁰(Ω)

- Σ(Ω, p),

(29)

8α_S

(2πT)2

+ (1 -

)

(35)

dπ²

где G - функция Грина мягких мод для нашего дей-

ствия, G⁰ - функция Грина мягких мод в модели

Знак ≈ в (32) означает, что мы выкинули члены,

SYK, Σ - собственная энергетическая часть, про-

пропорциональные s^2e и s^2o, так как они “локальны”,

порциональная w². Мы снова использовали матрич-

т.е. зависят от пары времен u₁, u₃ или u₂, u₄, в них

ное обозначение, объединив 4 поля δf с разных ча-

нет экспоненциального роста, и поэтому они малы.

стей контура в один вектор, мы также использу-

Как и ранее, d - размерность решетки. Функция z,

ем частотно-импульсное представление. Все матри-

с одной стороны, экспоненциально растет при увели-

цы выше имеют размер 4 × 4, однако они вычисля-

чении u₁ - u₂, с другой стороны, функция f экспо-

ются для равновесной системы, с учетом соотноше-

ненциально убывает при больших |r|. Наконец, мы

ния между запаздывающей и опережающей функ-

можем записать явную формулу для коррелятора:

циями Грина: G_R(Ω) = G_A(-Ω) и флуктуационно-

диссипационной теоремы, мы можем записать толь-

F (u₁, u₂, u₃, u₄) =

ко запаздывающую функцию Грина (все остальные

∞

∫

ds_ods_e

по ней восстанавливаются):

(s_os_e)^(2Δ)e-se-so e-ses^oz =

Γ(2Δ)²

[

]_-1

[G_R(Ω, p)]^-1 =

G^0R(Ω)

- Σ_R(Ω, p),

∫

∞

(

)

∑{

C_w

s^2Δ-1

e^-s

2Δ, 1,¹

Σ_R(Ω, p) =

Ω²ψ(Ω) +

ds =

Γ(2Δ) (1 + sz)^2Δ

z^2Δ

δr

}

{

( pδr)(

)

sin²

2(1 + Ω²) + (1 + 2Ω²)ψ(Ω)

1 - 4zΔ²

z ≪ 1,

(36)

ln(z)

(

)

(

)

z ≫ 1.

z^2ΔΓ(2Δ)

ψ(Ω) = Ψ

- iΩ

-Ψ -

Здесь U

- вырожденная гипергеометрическая

функция, однозначно определенная своими асимпто-

Ψ(z) = ∂_z ln Γ(z),

G^0R(Ω) =

(30)

C_J Ω²(Ω² + 1)

тиками.

Вместе с выражением для z (33) это выражение

Действие для полей a(Ω) и b(Ω) определено для Ω ≪

является главным результатом этой статьи. Отметим

≪ 1 в силу их медленности и имеет вид:

далее важные свойства полученного результата.

∫

[

]_-1

dΩd^dp

Во-первых, при C_w

= 0 мы получаем ответ для

S_2,ab =

â^†p(Ω)

G(i + Ω, p)

bp(Ω).

(31)

OTOC в модели SYK, это выражение совпадает с

(2π)^d+1

Письма в ЖЭТФ том 115 вып. 5 - 6

2022

334

А. В. Лункин

(√

)

формулой (6.10) работы [8] и совпадает с результа-

2 r

K₀

α a

том применения метода из статьи [9] к модели SYK.

f^(2D)α≫1(r) =

(40)

πα

Отметим, что предложенный нами метод вычисле-

ния отличается от методов в упомянутых работах,

Разберем зависимость параметра α от температу-

совпадение результатов - указание на возможность

ры. Используя формулу (35), мы можем отметить,

применения нашего (24) анзаца для задачи с w = 0.

что α не зависит от J и определяется только па-

Во-вторых, интеграл f_α(r) определяет зависи-

раметром^Tw . При достаточно высоких температурах

(_w)2

мость от расстояния между операторами в корре-

T ≫w,α∼

- зависит от температуры. В проти-

ляторе. Этот интеграл экспоненциально затухает с

−8

расстоянием, но вид затухания зависит не только от

принимает универсальное значение, которое не зави-

модуля r, но и направления, при не очень больших α

сит ни от параметров системы, ни от температуры.

(при больших α интеграл набирается на малых p и

Стоит отметить, что α₀ ≈ 5.27, и мы можем считать,

эта зависимость пропадает). Таким образом, мы де-

что α₀ ≫ 1.

лаем вывод, что информация о возмущении в систе-

Заключение. В представленной работе исследо-

ме распространяется баллистически, что качествен-

валось поведение OTOC для системы, состоящей из

но совпадает с поведением других систем [2, 10, 11].

квантовых точек. Динамика внутри точек описыва-

В-третьих, из формулы (36) следует, что в обла-

ется моделью SYK с характерным энергетическим

сти с z ≫ 1 коррелятор - мал,

F ≈ 0, мы будем

масштабом J. Между точками существует туннели-

говорить, что точки из этой области “знают” о при-

рование с характерной амплитудой w. Мы показали,

ложенном возмущении; область с z ≪ 1 “не знает”

что в такой системе ляпуновская экспонента имеет

о возмущении и в ней

F ≈ 1. Остановимся подроб-

свое максимальное значение λ_L = 2πT, аналогич-

нее на области c z ∼ 1. Зафиксировав направление,

но модели SYK. Из-за наличия ненулевой размер-

мы можем отметить, что z ∝ eλL(|t12|-rv2 )-ln(N), тут

ности изучаемый коррелятор имеет пространствен-

r₁₂ = |r₁ -r₂| ≫ 1 и t₁₂ = t₁ -t₂ ≈ t₃ -t₄, v - некото-

ную структуру: пространство можно разделить на

рый параметр с размерностью скорости. Из этого ви-

две области: 1) область, “знающая” о приложенном

да мы можем сказать, что со временем область z ∼ 1

возмущении с

F ≈ 0; 2) область, “не знающая” о воз-

распространяется со скоростью v, вдоль зафиксиро-

мущении с F ≈ 1. Эти области разделяет граница,

ванного ранее направления.

которая распространяется во времени. Детали рас-

В качестве примера приведем скорости для раз-

пространения, в общем случае, зависят от парамет-

ных случаев.

ров системы и деталей решетки. Однако при w ≫ T

В общем случае (произвольной размерности) уни-

границу можно считать сферической, а ее скорость

√_α

версальное поведение функции f из формулы (34)

распространения v_f = 2πT

a - зависит только от

наблюдается только приr2a^{≫α≫1,ту}

{ √

}

температуры и длины ребра решетки. Также отме-

2 r

ребра решетки. В таком случае f ∼ exp

тим, что несмотря на то, что вклад с w в седловое

α a

что соответствует скорости распространения фрон-

уравнение не существенен при T ≫ T_FL ∼^wJ

, свой-

та:

ства системы сильно меняются при T ∼ w. Подобный

эффект был также обнаружен в работах [14, 20].

√α

v = 2πT

(37)

Автор благодарен М. В. Фейгельману и

А. Ю. Китаеву за обсуждение работы на всех ее

которая не зависит от направления.

этапах. Также автор благодарен К. С. Тихонову за

В случае одномерной системы (r = (na)) асимп-

обсуждение свойств OTOC.

тотическое поведение функции f следующее:

Данное исследование было частично спонсирова-

(α)|n|



α ≪ 1,

но Фондом развития теоретической физики и мате-

f^(1D)(r) =

(

√

)_|n|

(38)

матики “БАЗИС”, программой фундаментальных ис-

 1√

1-_α

α ≫ 1.

2α

следований ВШЭ и грантом Российского фонда фун-

даментальных исследований # 20-32-90057.

В двумерном случае α ≪ 1:

(α

)|n|+|m|

f^(2D)α≪1(r) =

C^|m||n|+|m|.

(39)

1. A. I. Larkin and Yu. N. Ovchinnikov, Sov. Phys. JETP

Тут вектор r = (na, ma), как мы видим, эта функция

28(6), 1200 (1969).

сильно зависит от направления. При α ≫ 1 функция

2. I. L. Aleiner, L. Faoro, and L. B. Ioffe, Ann. Phys. 375,

f имеет вид:

378 (2016).

Письма в ЖЭТФ том 115 вып. 5 - 6

2022