Письма в ЖЭТФ, том 115, вып. 8, с. 500 - 504

Вычисление основных состояний спиновых стекол с использованием

ограниченной машины Больцмана

А. О. Король^+∗, В. Ю. Капитан^+∗1), А. В. Пержу⁺, М. А. Падалко^+∗, Д. Ю. Капитан^+∗, Р. А. Волотовский^+∗,

Е. В. Васильев^+∗, А. Е. Рыбин^+∗, П. А. Овчинников⁺, П. Д. Андрющенко^×, А. Г. Макаров^+∗,

Ю. А. Шевченко^+∗, И. Г. Ильюшин⁺, К. С. Солдатов^+∗

⁺Дальневосточный федеральный университет, 690922 Владивосток, Россия

^∗Институт прикладной математики Дальневосточного отделения РАН, 690041 Владивосток, Россия

^×Университет ИТМО, 197101 С.-Петербург, Россия

Поступила в редакцию 21 февраля 2022 г.

После переработки 17 марта 2022 г.

Принята к публикации 17 марта 2022 г.

В работе представлен нейросетевой метод вычисления конфигураций и значений энергий основных

состояний модели спинового стекла Эдвардса-Андерсона с периодическими граничными условиями. На-

блюдается макроскопическое вырождение основных состояний и нарушение трансляционной симметрии.

Достоверность результатов подтверждается сравнением с данными точных и приближенных вычисли-

тельных методов.

DOI: 10.31857/S1234567822080079, EDN: fnjsdl

Введение. Спиновое стекло характеризуется на-

только давно и широко используются для иссле-

личием беспорядка и фрустрации, которые возни-

дования различных физических систем [5-9], но и

кают из-за равного количества положительных и

продолжают активно развиваться и совершенство-

отрицательных взаимодействий в системе [1]. По-

ваться [10-13], благодаря развитию вычислительной

нятие фрустрации определяется как невозможность

техники.

удовлетворения всех совокупных взаимодействий в

Несмотря на то, что методы Монте-Карло явля-

системе из-за конкуренции между ними [2]. Реше-

ются часто используемыми инструментами при ис-

ние задач минимизации энергии и вычисления кон-

следовании классических систем, вблизи критиче-

фигураций основного состояния в моделях спиново-

ских точек эффективность резко снижается и воз-

го стекла связано с серьезными трудностями теоре-

никает так называемое “критическое замедление”, и

тического анализа и численных расчетов. Эти зада-

движение системы в фазовом пространстве становит-

чи относятся к классу недетерминистически полино-

ся очень медленным. Одним из алгоритмов, позволя-

миальных задач (NP-класс) [3]. По этим причинам

ющих преодолеть критическое замедление, являет-

создание эффективных алгоритмов для вычисления

ся гибридный мультиспиновый метод, который был

низкоэнергетических состояний является одной из

представлен и подробно описан в работе [12].

определяющих проблем в теории фрустрированного

В последнее время в физике начали применять-

магнетизма.

ся новые вычислительные подходы, такие как ма-

Методы Монте-Карло - группа математических

шинное обучение и нейронные сети [14, 15]. Мож-

методов вероятностного расчета для исследования

но выделить два основных подхода к применению

интегральных характеристик систем. Данные мето-

нейронных сетей для исследования спиновых систем.

ды позволяют исследовать системы взаимодейству-

Первый подход является альтернативой исследова-

ющих многих тел, для которых невозможно вы-

нию термодинамических средних физических вели-

полнить генерацию конфигураций, обладающих ми-

чин, когда изучение спиновых конфигураций состо-

нимальной энергией, из-за сложности и размера

ит в классификации неупорядоченных и упорядочен-

пространства состояний, поэтому используют при-

ных фаз с использованием алгоритмов машинного

ближенные методы [4]. Монте-Карло алгоритмы не

обучения. Использование такого подхода сводит про-

блему определения фаз и фазового перехода к задаче

¹⁾e-mail: kapitan.vyu@dvfu.ru

классификации [16-19].

500

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

Вычисление основных состояний спиновых стекол с использованием ограниченной машины Больцмана 501

Второй подход заключается в использовании ней-

ются различные модификации приближенных мето-

ронных сетей, например, машины Больцмана [20-22]

дов [27].

или авторегрессионной нейронной сети [23] для пред-

Ограниченная машина Больцмана. Ограни-

сказания спиновых конфигураций с наименьшей

ченная машина Больцмана - это стохастическая, ге-

энергией.

неративная модель нейронной сети, которая исполь-

В данной работе была рассмотрена модель спи-

зует идею “энергии” в качестве метрики для измере-

нового стекла Эдвардса-Андерсона [24] на квадрат-

ния качества обучения [21].

ной решетке спинов Изинга с бимодальным рас-

Как видно на рис.1, ограниченная машина

пределением связей и периодическими граничны-

Больцмана состоит из одного видимого слоя нейро-

ми условиями. Для численных расчетов исполь-

нов (v₁, . . . , v_n), одного скрытого слоя (h₁, . . . , h_m) и

зовалась комбинация гибридного мультиспинового

соответствующих коэффициентов смещения a и b.

метода (от англ. Hybrid Multispin Method (HMM))

[12] и ограниченной машины Больцмана (от англ.

Restricted Boltzmann Machine (RBM)) для предска-

зания основных энергетических состояний в модели

спинового стекла Эдвардса-Андерсона.

Для вычисления основных состояний мы исполь-

зовали данные гибридного мультиспинового метода

для обучения нейронной сети и прогнозирования со-

стояния спинового стекла с более низким уровнем

энергии, чем в наборах обучающих данных. На при-

мере небольших спиновых систем (4 × 4 и 6 × 6) бы-

ли проверены результаты работы нейронной сети и

проведено сравнение с результатами точного реше-

ния, рассчитанного методом исчерпывающего пере-

числения (от англ. Exhaustive Enumeration Method

Рис. 1. (Цветной онлайн) Архитектура ограниченной

(EEM)). Также для проверки был использован ал-

машины Больцмана

горитм, основанный на методе трансфер-матриц (от

англ. Transfer-Matrix Method (TMM)) [25, 26] для си-

Связи между слоями задаются с помощью матри-

стем до 20 × 20 спинов Изинга.

цы весов W = (w_i,j ) размера m × n и коэффициентов

Модель спинового стекла Эдвардса-

смещения a и b.

Андерсона. Эдвардс и Андерсон в 1975 г. в работе

Изначально связи и коэффициенты смещения

[24] предложили модель спинового стекла из L × L

инициализируются случайными значениями. В про-

спинов Изинга S_i

= ±1, расположенных в узлах

цессе обучения они меняются по алгоритму, описан-

квадратной решетки, с линейным размером L,

ному ниже. Входными данными для нейронной сети

периодическими граничными условиями и Гамиль-

являются конфигурации спинового стекла и количе-

тонианом:

ство нейронов видимого слоя соответствует количе-

∑

H =- J_ijS_iS_j,

(1)

ству спинов. Для обучения сети используются пря-

мой (от видимого слоя к скрытому) и обратный (от

〈ij〉

скрытого слоя к видимому) проходы по нейронам.

где S_i, Sj - спины Изинга в решетке, 〈i, j〉 означа-

В первую эпоху обучения на видимый слой сети

ет, что суммирование идет только по ближайшим

подаются входные данные v⁰. При прямом проходе

спинам; J_ij - связь между ближайшими соседними

нейроны видимого слоя обрабатывают эти данные и

спинами i и j. Важно отметить, что перед началом

передают результат нейронам скрытого слоя h⁰:

расчетов определяются все связи, и после этого они

остаются неизменными до конца исследования.

h⁰ ∼ p(h|v⁰) → p(h_j = 1|v) =

(2)

Одной из основных характеристик спинового

(

)

стекла является длительное время релаксации. При

∑

низких температурах релаксация системы становит-

σ b_j + w_i,jv_i

(3)

ся медленной, и трудно достичь равновесия даже для

i=1

систем небольшого количества частиц, в том чис-

ле в численных экспериментах, поэтому применя-

где σ - сигмоидная функция активации.

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

502

А. О. Король, В. Ю. Капитан, А. В. Пержу и др.

При обратном проходе обработанные в скрытом

Описанный выше способ обучения сети называет-

слое данные подаются обратно на видимый слой v¹:

ся алгоритмом контрастной дивергенции с выборкой

по Гиббсу [29].

v¹ ∼ p(v|h⁰) → p(v_i = 1|h) =





Нейросеть не различает связи и спины, по-

∑

(4)

этому для обучения используются только спины,

σa_i + w_i,jh_j.

значения которых масштабируются в диапазоне

j=1

[0; 1](-1 → 0, 1 → 1). Решетка спинов представля-

ется в виде бинарного одномерного массива длины

Для контроля переобучения сети сравниваются

L × L (где L - размер системы) и подается на вход

величины свободной энергии видимого слоя F(v) до

сети.

прямого и обратного проходов и после них [28]:

∑

Результаты и обсуждение. Для обучения ней-

F (v) = - v_ia_i - log(1 + exj ),

(5)

ронной сети и подтверждения результатов, методом

∑

исчерпывающего перечисления были сгенерированы

L = F(v¹) - F(v⁰),

(6)

системы спиновых стекол 4 × 4 и 6 × 6 спинов с бимо-

v¹

v⁰

дальным распределением связей J_ij . Для обучения

∑

выбирались 400 конфигураций из выбранных диапа-

где x_j = b_j +_i v_iw_i - входные данные для скры-

зонов энергий на один спин [1.5; 1.0] и [-0.5; -0.75]

того нейрона j, L - функция потерь (от англ. Loss

для системы 4 × 4, [1.33; 1.22] и [-0.67; -0.89] для

Function).

системы 6 × 6. Это было сделано с целью независи-

Если модель не переобучается - значение функ-

мого сравнения полученных результатов ограничен-

ции потерь L должно быть примерно равно нулю. В

ной машины Больцмана для каждой системы. При-

противном случае - средняя свободная энергия види-

меры систем для обучения 4 × 4 (E = -0.5) и 6 × 6

мого слоя увеличивается после прямого и обратного

(E = -0.89) показаны на рис. 3. Для численных рас-

проходов и эта разница представляет собой величину

четов использовались безразмерные величины в |J|

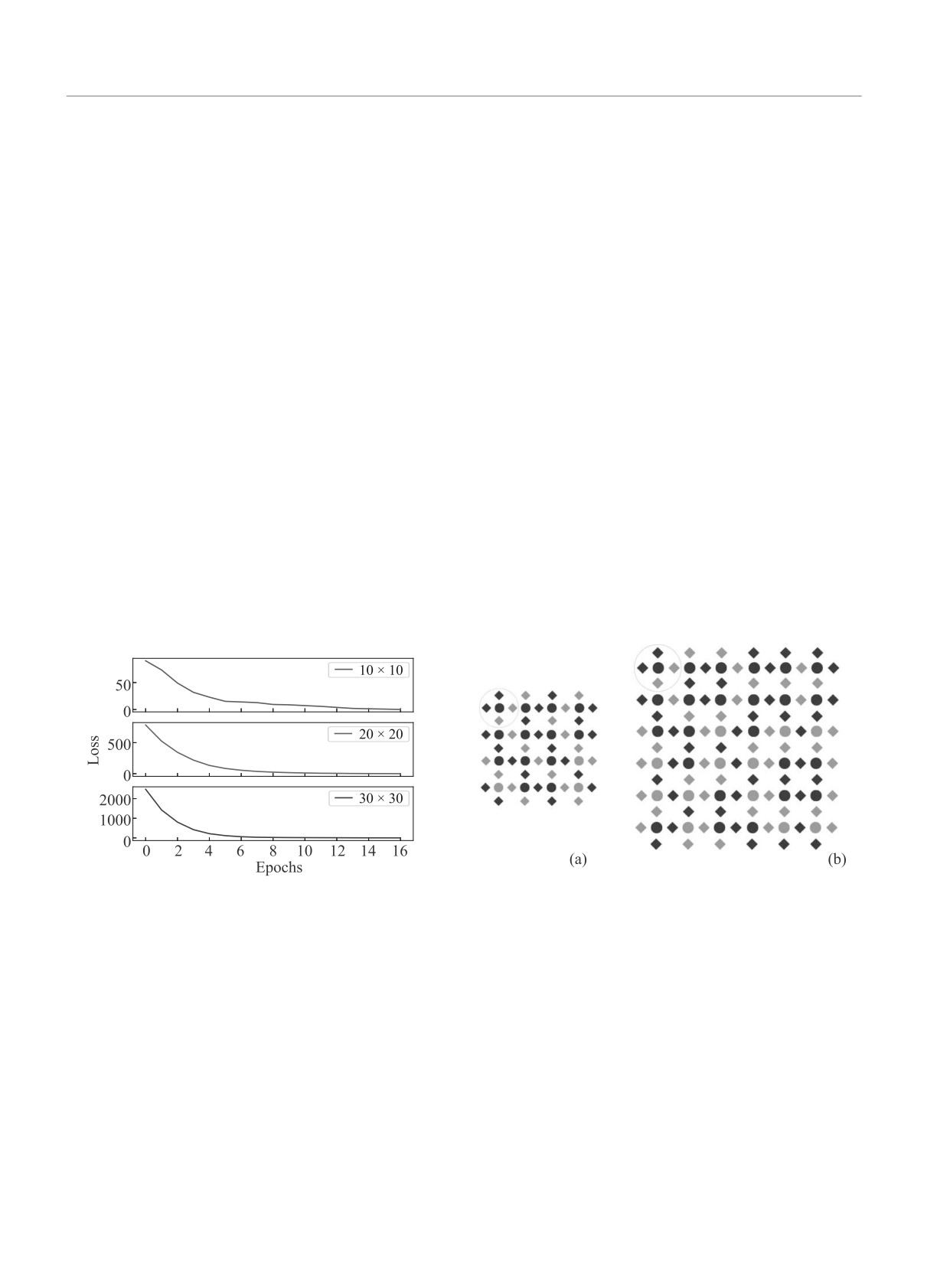
переобучения. На рисунке 2 представлены значения

единицах.

функции потерь L в зависимости от номера эпохи

обучения для систем различного числа спинов.

Рис. 2. (Цветной онлайн) Зависимость значения функ-

Рис. 3. (Цветной онлайн) Примеры систем для обуче-

ции потерь при обучении от порядкового номера эпохи

ния: (a) - 4 × 4 (E = -0.5); (b) - 6 × 6 (E = -0.89) с

заданным бимодальным распределением связей. Цвет

Далее обновляются значения весов и коэффици-

спинов (круг) или связей (ромб) зависит от координа-

енты смещения:

ты z между спином вниз S = -1 или J = -1 (синий) и

вверх S = +1 или J = 1 (оранжевый)

ΔW = v⁰[p(h = 1|v⁰)]^T - v¹[p(h = 1|v¹)]^T ,

(7)

Δa = v⁰ - v¹,

(8)

Исследование систем относительно небольшого

Δb = p(h = 1|v⁰) - p(h = 1|v¹),

(9)

числа спинов 4 × 4, 6 × 6 с помощью метода исчерпы-

W = W + αΔW,

(10)

вающего перечисления позволило получить точные

a = a + αΔa,

(11)

решения. Энергии и конфигурации основных состоя-

ний систем относительно большого числа спинов бы-

b = b + αΔb,

(12)

ли рассчитаны методами гибридного Монте-Карло и

где α - скорость обучения.

трансфер-матриц, см. табл. 1.

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

Вычисление основных состояний спиновых стекол с использованием ограниченной машины Больцмана 503

Таблица 1. Сравнение результатов, полученных различными

нение нейросетевых алгоритмов как перспективного

вычислительными подходами

вычислительного подхода.

EEM TMM HMM RBM

Для численных расчетов систем относитель-

Количество спинов E_min

E_min

но большого числа частиц ограниченная машина

4×4

-1.5

Больцмана вычислила конфигурации с меньшей

6×6

-1.3

энергией, чем гибридное Монте-Карло для 20 × 20

10 × 10

-1.4

30 × 30, и достигла минимума, который был

20 × 20

-1.38

-1.34

-1.38

30 × 30

-1.334

-1.342

рассчитан методом трансфер-матриц, см. табл. 1.

Также нейронная сеть позволяет вычислять не толь-

ко отдельные конфигурации в минимуме энергии,

Различные вычислительные методы показали

но и изучать грубый энергетический ландшафт

одинаковые результаты для системы 4 × 4: мини-

вырожденных основных состояний спиновых стекол.

мальная энергия составила E_min = -1.5, кратность

На примере системы 30 × 30 спинов было выявлено,

вырождения 14, половина конфигураций является

что в найденных низкоэнергетических конфигура-

антисимметричной, см. рис. 4.

циях невозможно выделить элементарную ячейку

спинов, трансляция которой позволила бы получить

такие состояния. В рамках данного исследования

ограниченная машина Больцмана показала более

высокую точность по сравнению с оптимизирован-

ным алгоритмом гибридного Монте-Карло.

Заключение. Нами было показано, что ос-

новные состояния систем спинового стекла можно

вычислять нейросетевыми методами. Работоспособ-

ность ограниченной машины Больцмана проверена

точными и приближенными вычислительными

методами, которые позволили подтвердить досто-

верность полученных результатов. Точно вычислена

Рис. 4. (a) - Пример системы для обучения: 4 × 4,

кратность вырождения основных состояний, их

(E = -0.5) с заданным бимодальным распределени-

энергия и конфигурации для систем с относительно

ем связей; (b)-(h) - основные состояния системы 4 × 4

малым числом спинов, для систем с относительно

при данном распределении связей

большим числом спинов вычислены значения мини-

При исследовании системы 6 × 6 с помощью

мальной энергии и некоторые соответствующие ей

метода исчерпывающего перечисления вычислены

конфигурации с разным спиновым избытком.

E_min = -1.3, 184-x кратное вырождение основно-

На основании этих результатов, с одной стороны,

го состояния. Результаты ограниченной машины

можно сделать вывод, что нейронные сети уже яв-

Больцмана: Emin = -1.3, 138-ми кратное вырож-

ляются полезными инструментами для решения за-

дение основного состояния, что несколько меньше,

дач, связанных с изучением сложных спиновых си-

чем в точном решении. 6 × 6 - максимальное ко-

стем и позволяют значительно улучшить результаты

личество спинов для расчета методом исчерпываю-

теоретических исследований, проводимых обычными

щего перечисления; системы относительно большо-

вычислительными методами. С другой стороны, мы

го числа частиц изучались гибридным Монте-Карло

столкнулись с проблемой определения числа вырож-

методом и методом трансфер-матриц. Метод исчер-

дений основного энергетического уровня из-за отсут-

пывающего перечисления позволяет получить все ос-

ствия точных решений для больших систем и, как

новные состояния, метод трансфер-матриц вычисля-

следствие, невозможностью проверки, смогли ли ис-

ет конфигурации этих состояний для систем мень-

пользуемые приближенные вычислительные методы

ше, чем 12 × 12, а для систем до 20 × 20 спинов он

достичь глобального энергетического минимума.

позволяет рассчитывать только значения минималь-

Авторы выражают благодарность проф.

ной энергии. В свою очередь, методы Монте-Карло,

К.В.Нефедеву и проф. В.И.Белоконю за сове-

в силу вероятностной специфики, позволяют вычис-

ты при планировании исследования и ценные

лять лишь малую часть вырожденных основных со-

замечания при работе над данной статьей.

стояний и не всегда достигают минимума, поэтому

Исследование фрустрированных магнитных си-

для решения такого класса задач актуально приме-

стем с применением ограниченной машины Больцма-

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

504

А. О. Король, В. Ю. Капитан, А. В. Пержу и др.

на выполнено за счет гранта Российского научного

12.

A. G. Makarov, K.V. Makarova, Yu.A. Shevchenko,

фонда #21-72-00058. Развитие гибридного мультис-

P. D. Andriushchenko, V. Yu. Kapitan, K. S. Soldatov,

пинового метода ведется в рамках Государственного

A. V. Perzhu, A. E. Rybin, D.Yu. Kapitan,

E. V. Vasil’ev, R. A. Volotovskii, Yu. V. Chubov,

задания Министерства науки и высшего образова-

and K. V. Nefedev, JETP Lett. 110, 702 (2019).

ния РФ # 0657-2020-0005. Исследования методом

13.

P. Mali, S. Radošević, P. Rakić, L. Stričević, M. Pavkov-

трансфер-матриц проведены при финансовой под-

Hrvojević, and M. Pantić, Chin. J. Phys. 59, 35 (2019).

держке гранта Президента Российской Федерации

14.

K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev,

для государственной поддержки ведущих научных

and A. Walsh, Nature 559, 547 (2018).

школ Российской Федерации # НШ-2559.2022.1.2.

15.

G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld,

Для проведения численных расчетов были ис-

N. Tishby, L. Vogt-Maranto, and L. Zdeborová, Rev.

пользованы вычислительные ресурсы ДВФУ.

Mod. Phys. 91, 045002 (2019).

16.

J. Carrasquilla and R. G. Melko, Nat. Phys. 13, 431

(2017).

1. P.

Nordblad, Disordered Magnetic Systems,

17.

P. Suchsland and S. Wessel, Phys. Rev. B 97, 174435

Encyclopedia of condensed matter physics, ed. by

(2018).

F. Bassani, G. L. Liedl, and P. Wyder, Elsevier,

Amsterdam (2005), p. 452.

18.

K. Shiina, H. Mori, Y. Okabe, and H.K. Lee, Sci. Rep.

10, 1 (2020).

2. M. J. Harris, S. T. Bramwell, D. F. McMorrow,

T. H. Zeiske, and K. W. Godfrey, Phys. Rev. Lett. 79,

19.

V. Kapitan, E. Vasiliev, A. Perzhu, D. Kapitan,

2554 (1997).

A. Rybin, A. Korol, K. Soldatov, and Yu. Shevchenko,

AIP Adv. 11, 015041 (2021).

3. A. Lucas, Front. Phys. 2, 5 (2014).

20.

D. H. Ackley, G. E. Hinton, and T. J. Sejnowski, Cogn.

4. D. Landau and K. Binder, A guide to Monte Carlo

Sci. 9, 147 (1985).

simulations in statistical physics, Cambridge University

press, Cambridge (2003).

21.

G. Torlai and R. G. Melko, Phys. Rev. B 94, 165134

5. V. I. Belokon, V. Y. Kapitan, and O. I. Dyachenko,

(2016).

J. Phys. Conf. Ser. 490, 012165 (2014).

22.

L. Huang and L. Wang, Phys. Rev. B 95, 035105 (2017).

6. V. V. Prudnikov, P. V. Prudnikov, A. N. Purtov, and

23.

B. McNaughton, M. V. Milosevic, A. Perali, and

M. V. Mamonova, JETP Lett. 104 776 (2016).

S. Pilati, Phys. Rev. E 101, 053312 (2020).

7. M.

Žukovič, Phys. Lett. A 404, 127405, (2021).

24.

S. F. Edwards and P. W. Anderson, Journal of Physics

F: Metal Physics 5, 965 (1975).

8. M. K. Ramazanov, A. K. Murtazaev, M. A. Magomedov,

and M. K. Mazagaeva, JETP Lett. 114, 693 (2021).

25.

B. Kaufman, Phys. Rev. 76, 1232 (1949).

9. K. Makarova, V. Strongin, Iu. Titovets, A. Syrov,

26.

M. A. Padalko, Yu. A. Shevchenko, V. Yu. Kapitan, and

I. Zinchenko, V. Samoylov, K. Hofhuis, M. Saccone,

K. V. Nefedev, Algorithms 15, 13 (2022).

A. Makarov, A. Farhan, and K. Nefedev, Phys. Rev.

27.

D. Kapitan, A. Rybin, P. Andriushchenko, V. Kapitan,

E 103, 042129 (2021).

E. Vasiliev, and K. Nefedev, Solid State Phenomena

10. K. S. Soldatov, K. V. Nefedev, V. Yu. Kapitan, and

312, 251 (2020).

P. D. Andriushchenko, J. Phys. Conf. Ser. 741, 012199

28.

R. Salakhutdinov, A. Mnih, and G. Hinton, Proceedings

(2016).

of the

24th International Conference on Machine

11. Yu. A. Shevchenko, A. G. Makarov, P. D. Andriushchen-

Learning (2007), p. 791.

ko, and K. V. Nefedev, JETP 124, 982 (2017).

29.

G. E. Hinton, Neural Comput. 14, 1771 (2002).

Письма в ЖЭТФ том 115 вып. 7 - 8

2022