Письма в ЖЭТФ, том 115, вып. 8, с. 512 - 519

О дифференциальных уравнениях для диаграмм Фейнмана

(Миниобзор)

В.Мишняков^+∗×◦1), П.Супрун^+◦

⁺Московский физико-технический институт, 141701 Долгопрудный, Россия

^∗Физический институт им. П. Н. Лебедева РАН, 119991 Москва, Россия

^×Институт теоретической и математической физики, МГУ им. М. В. Ломоносова, 119991 Москва, Россия

^◦Национальный исследовательский центр “Курчатовский институт”, 117218 Москва, Россия

Поступила в редакцию 10 марта 2022 г.

После переработки 21 марта 2022 г.

Принята к публикации 21 марта 2022 г.

Каким образом современный физик должен вычислять петлевые интегралы, задаваемые диаграм-

мами Фейнмана? Этот вопрос в последнее время привлекал к себе существенное внимание. Хотя его

исследование остается незавершенным, можно выделить основные направления, в которых ведется ак-

тивная работа. Одним из таких направлений является метод дифференциальных уравнений, основные

идеи и особенности которого мы попытаемся обозначить с целью выделения стоящих за ним принципов

в наибольшей общности.

DOI: 10.31857/S1234567822080122, EDN: fnljzp

1. Содержание метода. Типичный фейнманов-

2. Применить максимально возможное количе-

ский интеграл представляет из себя выражение вида

ство соотношений следующего типа (которые

после взятия всех производных и раскрытия

∫

d^dk₁ d^dk₂ . . . d^dk_l

скобок связывают между собой различные ин-

J (p₁, . . . p_M ; m₁, . . . m_N ) =

(1)

D₁ D₂ . . . D_n

тегралы, аналогичные по форме приведенным

выше):

где k_i - контурные импульсы, D - пропагаторы, за-

висящие от их сумм и разностей (конкретные ком-

∫

∂

P (k)q_j

бинации задаются графом Фейнмана по широко из-

d^dk₁d^dk₂ . . .d^dk_l = . . .

∂k_i Da11D22 ...D^e

вестным правилам). Основной задачей подобных ме-

(3)

тодов является установление зависимости функции

Основное содержание этих соотношений в том,

J от ее аргументов - масс частиц-переносчиков m_i

что “интеграл от полной производной зану-

и внешних импульсов p_j. Идея метода дифференци-

ляется”.

альных уравнений заключается в том, чтобы искать

и использовать соотношения между J и ее производ-

ными по параметрам [1]. Точнее, предлагаемый ал-

3. Из бесконечного числа возможных интегралов

горитм можно описать следующим образом:

фейнмановского типа (различающихся степе-

нями пропагаторов и одночленами в числи-

1. Продифференцировать исследуемый интеграл

теле) выбрать конечное подмножество, содер-

по параметрам, что дает (линейные комбина-

жащее исходный интеграл и обладающее тем

ции) выражений вида

свойством, что любая производная по пара-

метру любого выбранного интеграла является

∫

P (k)

рациональной линейной комбинацией интегра-

∂_iJ =

d^dk₁ d^dk₂ . . .d^dk_l,

лов, принадлежащих этому множеству. Ины-

Da11 D22 . . . D^e

(2)

ми словами, сумма интегралов, возникающая

где P (k) - скалярный многочлен от петлевых и

при дифференцировании любого выбранного,

внешних импульсов.

должна снова сводиться к выбранным интегра-

лам в силу тождеств типа (3) и их линейных

¹⁾e-mail: mishnyakovvv@gmail.com

комбинаций. Для поиска такого множества су-

512

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

О дифференциальных уравнениях для диаграмм Фейнмана

513

ществуют специальные методы, из которых мы

Напомним вкратце, как устроено уравнение

упомянем алгоритм Лапорты.

Пикара-Фукса в случае рода 1. Период эллиптиче-

ской кривой с “модулем” λ определяется следующим

4. В результате должна получиться система диф-

образом:

ференциальных уравнений следующего вида:

∮

∑

ω(λ) =

√

(8)

∂_iJ_α =

A_iαβ(t_j)J_β,

(4)

x(x - 1)(x - λ)

После двукратного дифференцирования по λ полу-

где в левой части стоят производные по параметрам

чаем три замкнутые дифференциальные формы. Так

функций J_α, входящих в конечный набор, выбран-

как пространство когомологий эллиптической кри-

ный на предыдущем шаге, так называемых “master

вой двумерно, должна существовать линейная ком-

integrals”. Коэффициенты A_iαβ (p_j , m_k) являются ра-

бинация ω(λ), ∂_λω(λ) и ∂^2λω(λ), являющаяся интегра-

циональными функциями своих параметров. Реше-

лом точной формы по замкнутому контуру, и, сле-

ние системы, заданной в подобной форме, может

довательно, равная нулю. Это условие эквивалентно

быть записано как:

дифференциальному уравнению на ω, коэффициен-

(∫

)

∑

ты которого могут быть вычислены и оказываются

∂_iJ_α =

A_iαβ(t_j)J_β → J = Pexp

A dx

(5)

следующими:

[

]

d²

1 - 2λ d

где Pexp - упорядоченная экспонента, причем в ее

ω=0

(9)

разложение входят интегралы A-матрицы (связно-

dλ²

(λ - 1) λ dλ

4 (λ - 1) λ

сти) вида

Заметим, что уравнение имеет форму (7) и означа-

ет, в сущности, что интеграл от полной производ-

∫x

ной (точной 1-формы) обращается в нуль, в полной

J_iterated =

dx_n-1A(x_n-1)×

аналогии с уравнением (3). Единственное отличие от

описанного выше метода состоит в том, что в данном

∫

случае мы начали с производных интеграла по пара-

× dx_n-2A(x_n-2) . . . A(x₀)dx₀.

(6)

метру и объединили их в полную производную, в то

время как выше мы сначала рассмотрели набор пол-

ных производных, которые затем выразили в форме

С другой стороны, эти соотношения между инте-

гралами фейнмановского типа могу быть сформули-

соотношений между интересующими нас интеграла-

ми. Заметим также, что в задачах квантовой теории

рованы в виде уравнения или системы уравнений бо-

лее высокого порядка на меньшее число базисных ин-

поля обычно требуется рассмотрение интегралов не

по замкнутому контуру, а по некоторому интерва-

тегралов. Система уравнений первого порядка при-

водится к такой форме взятием следующих произ-

лу. В этом случае соответствующее уравнение типа

водных и исключением дополнительных (к исход-

Пикара-Фукса может оказаться неоднородным, но

ному) мастер-интегралов. Например, для процессов,

после умножения на подходящий множитель и до-

включающих только один внешний импульс, таких

полнительного дифференцирования его можно сде-

лать однородным, увеличив порядок на единицу.

как диаграммы типа собственной энергии, система

сводится к единственному уравнению по переменной

Поскольку пространство первых когомологий

кривой рода g является 2g-мерным, порядок ана-

t=p²:

L[J] = 0,

(7)

логичных уравнений на периоды старших кривых

определяется их родом. Отсюда ясно, что задача

где L =

+... - дифференциальный оператор

определения порядка таких уравнений является

dtⁿ

вопросом теории когомологий. Построение соот-

априори неизвестного порядка, который может быть

ветствующей геометрической конструкции для

достаточно высоким, а сам оператор - иметь слож-

ную форму. В таком виде очевидно, что диффе-

интегралов Фейнмана является интересным откры-

тым вопросом, активно изучаемым в последнее

ренциальная структура семейства интегралов фей-

нмановского типа полностью аналогична структуре

время [2], а также [3].

Последнее замечание, которое мы хотим сделать

классических уравнений Пикара-Фукса для перио-

дов эллиптических кривых и кривых старшего рода.

в этом разделе, состоит в том, что обращение в

нуль интегралов от полных производных является

В следующем разделе мы приведем несколько при-

меров.

основным содержанием тождеств Уорда (условий

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

514

В.Мишняков, П.Супрун

Вирасоро) в теории матричных моделей [4, 5]. Со-

“Правильное” обобщение обозначенной иерар-

ответственно, возникает интригующий вопрос, мож-

хии, в которое входят, по всей видимости, про-

но ли поднять тождества на отдельные диаграммы,

извольно многократные полилогарифмы любо-

возникающие из интегрирования по частям на уро-

го рода, и ее связь с интегралами Фейнмана об-

вень точных статистических сумм и корреляторов.

щего вида в высших петлях, в настоящее время

Мы планируем уделить внимание этой проблеме в

неизвестны, относительно прогресса в этом на-

нашей дальнейшей работе.

правлении см. [11, 12].

2. Результаты. Свойства решений. Вышеопи-

санный метод дает возможность представить диа-

Определение многократных полилогарифмов (по

Гончарову) следующее:

граммы Фейнмана в виде некоторых новых интегра-

лов, не выражающихся в элементарных функциях.

I(a₀; a₁, a₂, . . . a_n; z) =

Однако иногда указанные интегралы могут быть вы-

ражены через известные специальные функции. Сле-

∫

dt₁

dt₂

dt_n

довательно, можно предположить, что те из них, ко-

(10)

t₁ - a₁

t₂ - a₂

t_n - a_n

торые не могут быть выражены подобным образом,

дают указание на “правильное” обобщение традици-

Наряду с функциями I, применение находят

онной системы спецфункций. Связь между диаграм-

функции типа Li, определяемые как:

мами Фейнмана и специальными функциями можно

грубо обозначить следующим образом:

Lim1,m2,...mn (x1, x2, . . .xn) =

∑

1. Однопетлевые диаграммы представляют собой

xk11x22 . . . xnn

(11)

функции, выражаемыми через полилогарифмы

km11k22 . . . kn

0<k1<k2<...<kn

Li_n [6, 7].

Эти два класса функций эквивалентны в силу

2. Некоторые двупетлевые диаграммы соответ-

следующего тождества:

ствуют многократным полилогарифмам, обоб-

щающим обычные [6], но этих функций недо-

Lim1,m2,...mn (x1, x2, . . .xn) =





статочно: существуют диаграммы с двумя пет-

лями, которые требуют для своего выраже-

=I 0|{z},

,...,

.

x₁

|{z}

x₁x₂

|{z}

x₁x₂ . . . x_n

ния повторных интегралов квадратных корней

m2-1

mn-1

и других эллиптических функций, иногда на-

(12)

зываемых эллиптическими полилогарифмами,

свойства которых на текущий момент остаются

(Еще не стандартное) определение эллиптических

до конца не изученными [8-10].

полилогарифмов:

∑

xj11

xj22

xjll

yk11

yk22

ykll

ELin1,...,n_l;m1,...,ml;a1,...,al^(xi^,yj^,q)=

·...·

kml

jm11

jm22

jmll

km11

km22

jr ,ks=0

j1k1+j2k2+...+jl kl

(13)

(j₁k₁ + j₂k₂ + j₃k₃ + . . . + j_lk_l)^a1 (j₂k₂ + j₃k₃ + . . . + j_lk_l)^a2 . . . (j_lk_l)l

Ниже мы приводим примеры, в которых эти

J_triangle(p₁, p₂, p₃) =

p²¹(z - z)

функции оказываются полезными.

(

)

1-z

× Li₂(z) - Li₂(z) +

ln(zz) ln

(14)

1-z

где

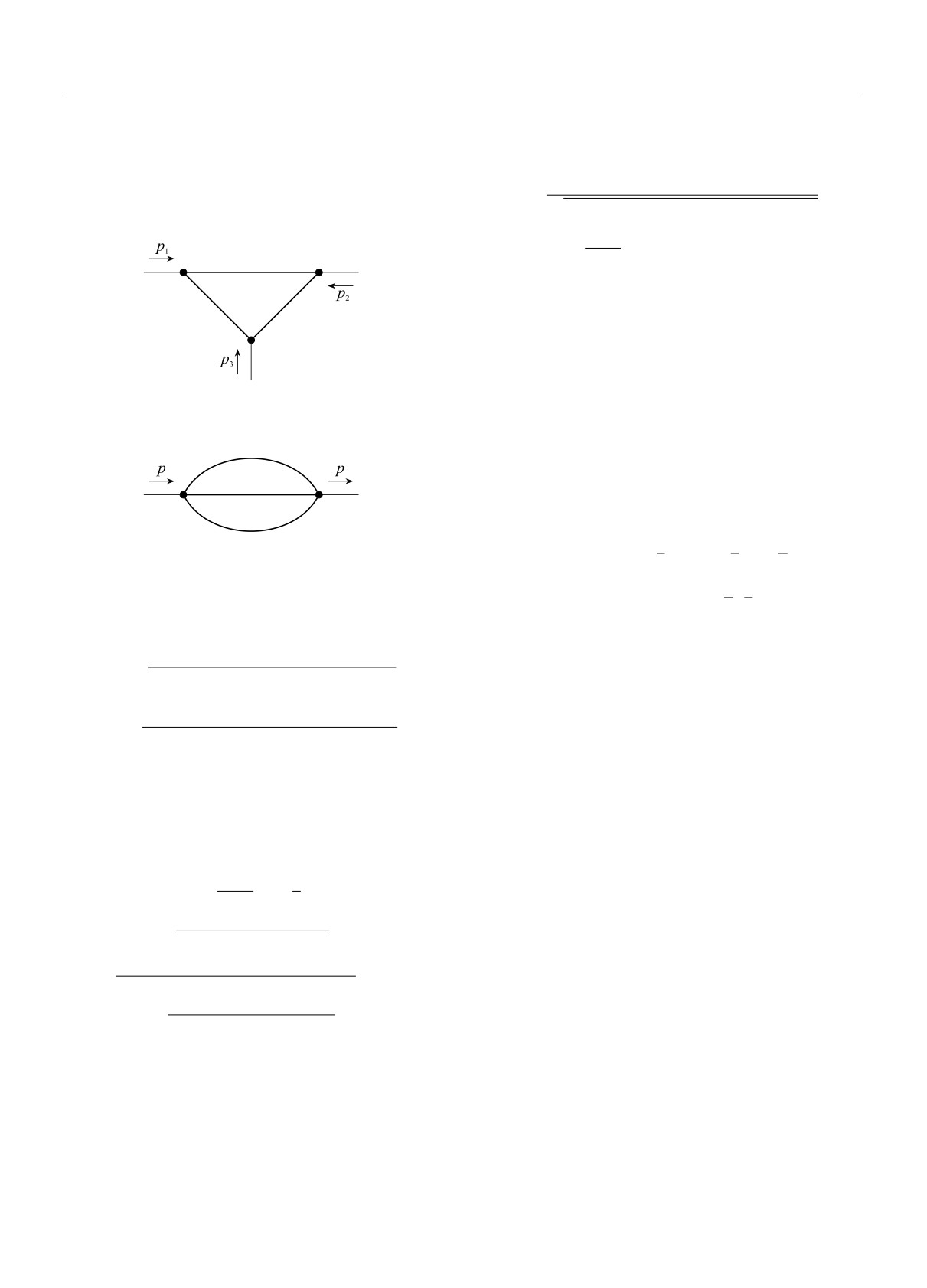
2.1. Пример на уровне одной петли. Описан-

p²² = p²¹|z|², p²³ = p²¹|1 - z|².

(15)

ный метод применительно к безмассовой треуголь-

ной диаграмме, изображенной на рис. 1, дает следу-

Хорошо видны полилогарифмы (в данном случае ди-

ющий результат:

логарифмы).

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

О дифференциальных уравнениях для диаграмм Фейнмана

515

2.2. Пример на уровне двух петель. Возмож-

моздкости и недостатка наглядности, см. [13]. Ответ,

но, самым простым примером, когда обычных (ро-

однако, мы приведем для общего случая [15]:

да нуль) кратных интегралов недостаточно, является

так называемая “sunrise”-диаграмма, изображенная

J₁ =

√

(p² - µ²¹)(p² - µ²²)(p² - µ²³)(p² - µ²)

на рис. 2. Система уравнений записана в терминах

∑

K(k)

E_2;0(w_j; -1; -q),

(19)

j=1

где µ = m₁ +m₂ +m₃, µ_i = µ-2m_i, q, k - стандартные

параметры эллиптической кривой

-p²x₁x₂x₃ + (x₁m²¹ + x₂m²² + x₃m²³)(x₁ + x₂ + x₃) = 0,

(20)

wi - комплексные (униформизованные) координа-

Рис. 1. Треугольная диаграмма

ты точек пересечения координатных осей (полюсов

подынтегральной функции) xi = xj = 0 с элли-

пической кривой, приведенной к нормальной форме

Якоби. Хорошо видны эллиптические дилогарифмы

(E_2;0). Их связь с функциями ELi, определенными

выше, дается формулой

(1)

E_2;0(x; y; q) = -i

Li₂(x) -

Li₂

Рис. 2. Двупетлевая диаграмма собственной энергии

))

четырех “master integrals” [13], но в случае равных

+ELi_2;0(x; y; q) - ELi_2;0

(21)

масс их количество сокращается до двух [14].

3. Алгебраическая природа петлевых инте-

∫

d^dk₁d^dk₂

гралов. Когда решение проблемы оказывается вы-

J₁ =

(16)

(k²¹ + 1)(k²² + 1)((p - k₁ - k₂)² + 1)

раженным в терминах специальных функций, воз-

никает обычный вопрос, делает ли это проблему “ре-

∫

d^dk₁d^dk₂

шенной” или предлагаемое решение не представляет

J₂ =

(17)

(k²¹ + 1)²(k²² + 1)((p - k₁ - k₂)² + 1)

из себя ничего сверх специального обозначения для

функции, остающейся при этом по-прежнему зага-

В этом случае зависимость от массы может быть

дочной. Разница между специальными функциями,

частично учтена заменой нормировочного коэффи-

решающими задачи, и специальными обозначениями

циента. Тогда дифференциальные уравнения фор-

для нерешенных задач заключается в том, что пер-

мулируются в терминах обезразмеренного импульса

вые обладают достаточно полным набором хорошо

z = p²/m²:

изученных свойств. К счастью, специальные функ-

d-3

ции, возникающие в фейнмановских вычислениях,

∂_zJ₁ =

J₁ +

J₂,

принадлежат к семейству, которое, по имеющимся

(d - 3)(8 - 3d)(z + 3)

данным, устроено “регулярно” с алгебраической точ-

∂_zJ₂ =

J₁ +

2z(z + 1)(z + 9)

ки зрения, что делает их весьма перспективными для

использования и исследования. К сожалению, про-

(d - 4)z² + 10(2 - d)z + 9(8 - 3d)

J₂ +

движения в изучении свойств этих функций можно

2z(z + 1)(z + 9)

считать существенными только для случая “рацио-

(18)

нальных” кратных полилогарифмов, в то время как

2(d - 4)²z(z + 1)(z + 9)

для эллиптических такие продвижения можно в луч-

С помощью подходящих операций дифференцирова-

шем случае только обозначить. По этой причине в

ния эта система может быть записана в эквивалент-

данном разделе обсуждаются только рациональные

ной форме одного уравнения для S в форме Пикара-

кратные полилогарифмы.

Фукса.

Многократные полилогарифмы являются обоб-

Система дифференциальных уравнений для слу-

щением классических, а классические полилогариф-

чая различных масс здесь не приводится из-за ее гро-

мы, как известно, удовлетворяют большому количе-

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

516

В.Мишняков, П.Супрун

ству функциональных тождеств. Простейшим при-

Во-вторых, это так называемое “перетасовочное

мером таких тождеств являются следующие:

произведение” допускает согласованное с ним копро-

изведение, так что эти две операции превращают се-

мейство полилогарифмов в биалгебру. Определение

Li₂(1 - z) = -Li₂(z) - ln(z)ln(1 - z) +

(22)

этого коумножения таково:

Δ (I(a₀; a₁, a₂, . . . a_n; a_n+1)) =

∑

ln²(-z)

Li₂(1/z) = -Li₂(z) -

(23)

I(a₀; a_i, a_j, . . . a_k; a_n+1) ⊗

∏

⊗

I(a_p; a_p+1, a_p+2, . . . a_q-1; a_q).

(25)

но, конечно, среди них существует и множество дру-

all the rest

гих, более сложных. Поэтому возникает естествен-

ный вопрос обобщения тождеств подобного рода на

Поскольку эта формула, вероятно, не отличается из-

бытком ясности, приведем более подробное объясне-

многократный случай, и возможное более или менее

систематическое решение основано на использовании

ние. Каждое слагаемое в копроизведении получается

следующим образом:

Хопф-алгебраических соотношений между исследуе-

мыми функциями [16], которые мы в общих чертах

1. Необходимо выбрать несколько переменных a_i,

описываем ниже.

a_j,. . ., a_k, идущих по порядку между a₀ и a_n+1.

Во-первых, произведение кратных полилогариф-

2. Тогда первый тензорный множитель равен

мов есть сумма полилогарифмов, что означает, что

I(a₀; a_i, a_j , . . . a_k; a_n+1). Другой множитель

их семейство является алгеброй. Лучше всего это

получается в результате следующих шагов.

видно на интегралах, начинающихся с одной и той

же точки:

3. Выбранные параметры a_i, a_j,. . ., a_k делят

всю последовательность a₀; a₁, a₂, . . . a_n; a_n+1 в

I(0, a₁, a₂, . . . a_n)I(0, b₁, b₂, . . . b_m) =

серию подпоследовательностей переменных a,

∑

идущих подряд, причем выбранные перемен-

I(0, a₁, b₁, b₂, a₃, a₄, a₅, b₃ . . .)

(24)

ные являются концами этих подпоследователь-

Sm+n/Sm×Sn

ностей. Каждой подпоследовательности соот-

(суммирование происходит по всем “перетасовкам” a_i

ветствует функция I(a_p; a_p+1, a_p+2, . . . a_q-1; a_q),

и b_j, сохраняющим порядок a и b между собой внут-

и все такие функции следует перемножить

ри каждого класса, но допускающим произвольное

по всем подпоследовательностям, тогда полу-

чередование самих классов букв).

ченное произведение будет являться вторым

Требование, чтобы первый аргумент I был ра-

тензорным множителем.

вен нулю, не приводит к ограничению общности, по-

Полученные тензорные объекты затем суммируют-

скольку

ся по всем возможным выборам, сделанным в п. 1.

Например, для n = 2 получается следующее выра-

I(a₀, a₁, a₂) = I(0, a₁, a₂) - I(0, a₁, a₀).

жение:

Δ(I(a₀; a₁, a₂, a₃)) = 1 ⊗ I(a₀; a₁, a₂; a₃) +

Путем дальнейшего интегрирования этого тожде-

+ I(a₀;a₁,a₂;a₃) ⊗ 1 + I(a₀;a₁;a₃) ⊗ I(a₁;a₂;a₃) +

ства, получаем его аналог для четырех аргументов,

+ I(a₀;a₂;a₃) ⊗ I(a₀;a₁;a₂).

(26)

I(a₀, a₁, a₂, a₃)

= I₀(0, a₁, a₂, a₃) - I(0, a₁, a₂, a₀) -

I(0, a₁, a₀)(I(0, a₂, a₃)

- I(0,a₂,a₀)) и т.д. для

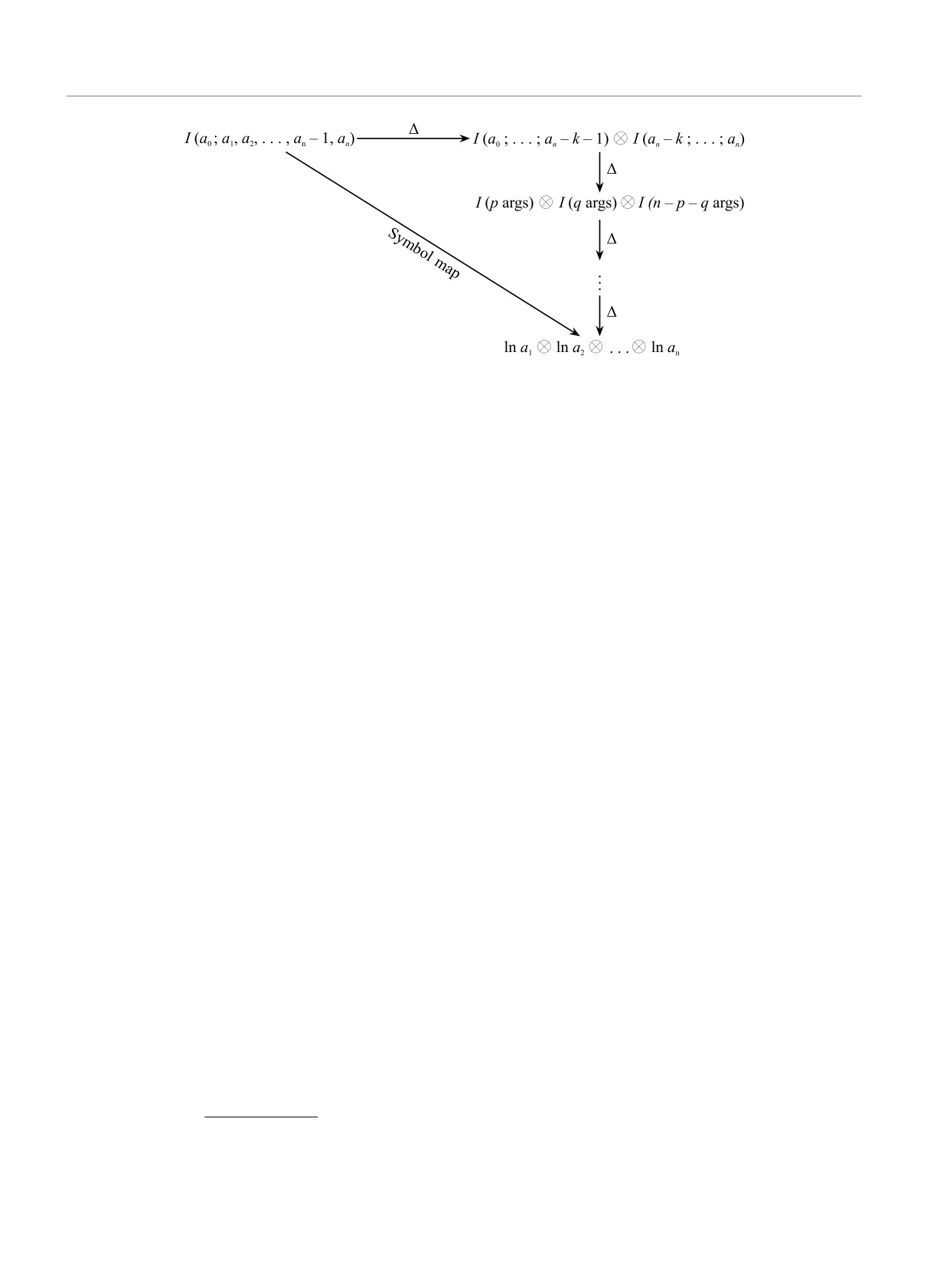
Эту процедуру можно проиллюстрировать гра-

всякого n. Из этого представления нетрудно видеть,

фически, см. рис. 3.

что число интегрирований в I-функциях является

Наконец, отображение антипода может быть од-

градуировкой, согласованной с умножением (если

нозначно определено из копроизведения для ал-

grd[a] = i и grd[b] = j, то ab строго однородна и

гебр этого класса[17], что делает рассматриваемое

grd[ab]

= i + j). Предполагается также, что эта

функциональное пространство настоящей алгеброй

градуировка должна сохраняться всеми функци-

Хопфа.

ональными отношениями между многократными

Копроизведение функции класса I - это сумма

полилогарифмами и остается верной для ограни-

тензорных произведений функций того же класса с

чений этих функций, т.е. при наложении условий

(как правило) меньшим трансцендентным весом; по-

на набор аргументов (например, если принять

следовательно применяя копроизведение к тензор-

все a_i равными z или 1). При таком подходе эта

ным множителям, можно сопоставить данной функ-

градуировка называется трансцендентным весом.

ции элемент тензорной алгебры над обсуждаемым

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

О дифференциальных уравнениях для диаграмм Фейнмана

517

Рис. 3. Правило коумножения в алгебре Хопфа полилогарифмов веса 2

функциональным пространством, все более и более

Li₂(1/z) = Li₂(z) -

(ln z)² + iπ ln z + Aζ(2).

(28)

высокой тензорной степени, но со все более и более

Сравнивая левую и правую части при z

низким трансцендентным весом сомножителей. Сле-

довательно, в некоторой степени Δ одной из однород-

получаем, что A = 2. Чтобы доказать равенство

ных компонент (относительно трансцедентного веса

Δ_1,1(ζ(2)) = 0, заметим, что

отдельных тензорных множителей, т.е. 3 ⊗ 1-, 2 ⊗ 2- и

∫

1⊗3-компоненты считаются имеющими разный вес)

dt₂

dt₁

Li₂(z) =

= I(0,1,0,z),

будет сумма произведений обычных логарифмов (ве-

t₂

1-t₁

са 1). Эта однородная компонента, называемая “сим-

следовательно,

волом” данной функции, ставится ей в соответствие

и содержит информацию о “наиболее трансцендент-

Δ(Li₂(z)) = I(0, 1, 0, z) ⊗ 1 + 1 ⊗ I(0, 1, 0, z) +

ной части” этой функции. Так как символы функций

являются произведениями обыкновенных логариф-

+ I(0,1,z) ⊗ I(1,0,z) + I(0,0,z) ⊗ I(0,1,0) =

мов, свойства последних определяют соотношения

= Li₂(z) ⊗ 1 + 1 ⊗ Li₂(z) - ln(1 - z) ⊗ ln(z).

между символами, которые, в свою очередь, являют-

ся отражением соотношений между их прообразами

Подстановкой z = 1 получаем

на уровне старшей трансцендентности. Отслеживая

Δ(ζ(2)) = 1 ⊗ ζ(2) + ζ(2) ⊗ 1.

ядра операторов коумножения, которые были при-

менены к данной функции, и рассматривая другие

В это выражение не входят члены с весовой струк-

однородные компоненты, можно восстановить менее

турой 1 ⊗ 1, следовательно, Δ_1,1(ζ(2)) = 0.

трансцендентные поправки. Описанная техника бы-

4. Обсуждение. В этой заметке нами обсужда-

ла с успехом применена при вычислении двупетлевой

лись наиболее базовые свойства петлевых интегра-

амплитуды двухпетлевого рассеяния в суперсиммет-

лов в квантовой теории поля. Из этих свойств мы

ричной теории Янга-Миллса [18]. Сказанное может

рассмотрели три основных сюжета. Во-первых, это

быть проиллюстрировано диаграммным образом, см.

структура D-модуля на петлевых интегралах. Вме-

рис. 4.

сто вычисления в явной форме, интегралы Фейн-

Приведем простой пример вычисления методом

мана представляются в виде решений систем диф-

символов. Допустим, что нам требуется выразить

ференциальных уравнений, имеющих когомологиче-

Li₂(1/z) через Li₂(z). Согласно приведенному вы-

ское происхождение в терминах некоторой внутрен-

ше описанию, мы должны взять n-е копроизведение

ней геометрии. Очень похожий подход использует-

Li₂(1/z) (в данном случае просто обычное копроиз-

ся при исследовании свойств статистических сумм

ведение) и взять его однородную компоненту транс-

в теории матричных моделей. С другой стороны,

цендентного веса (точнее, набора весов) 1⊗1⊗. . .⊗1

при анализе решений возникает интересная иерархия

(в данном случае 1 ⊗ 1). Обозначая через Δ_1,1 проек-

сложности решений этих уравнений как функций им-

цию копроизведения на эту однородную компоненту,

пульсов и масс, которая отсутствует (или, по край-

имеем:

ней мере, не видна при наивном походе) в нульмер-

ных моделях. Полная характеризация этой иерар-

Δ_1,1(Li₂(1/z)) = - ln(1 - 1/z) ⊗ ln(1/z) =

хичности в терминах топологии графа Фейнмана или

= ln(1 - z) ⊗ ln(z) - ln(z) ⊗ ln(z) + iπ ⊗ ln(z) =

каких-либо других параметров на сегодняшний день

неизвестна. Наконец, свойства алгебры Хопфа функ-

= Δ_1,1(Li₂(z) -

(ln z)² + iπ ln z),

(27)

ций на графах тесно связаны с общими свойствами

статистических сумм в КТП. Билинейный характер

поэтому (поскольку ядро Δ_1,1 веса 2 состоит только

хопфово-алгебраических соотношений позволяет, по-

из Li₂(1) = ζ(2))

видимому, перевести их на язык свойств, подобных

Письма в ЖЭТФ том 115 вып. 7 - 8

2022

518

В.Мишняков, П.Супрун

Рис. 4. Диаграмма для отображения символа

интегрируемости, для полных статистических сумм.

of Feynman Amplitudes, Springer Nature Switzerland,

Эта программа была исследована в наиболее общей

Cham (2021), v. 2; arXiv: 2102.07424 [hep-ph].

постановке [19-21] и в простейших КТП - матрич-

R. N. Lee and A.A. Pomeransky, JHEP 11, 165 (2013);

ных моделях [5]. Однако, как мы видим, подобны-

arXiv:1308.6676 [hep-ph].

ми свойствами обладают и основные строительные

S. Müller-Stach, S. Weinzierl, and R. Zayadeh,

блоки фейнмановских интегралов (см. также [22] и

Commun. Math. Phys.

326,

237

(2014);

ссылки в нем для более подробной информации о

arXiv:1212.4389 [hep-ph].

билинейных тождествах в контексте петлевых инте-

A. Mironov and A. Morozov, Phys. Lett. B 252, 47

гралов). Обычно интегрируемость матричных моде-

(1990).

лей не рассматривается с точки зрения соотношений

A. Morozov, Phys.-Uspekhi 37, 1 (1994);

между диаграммами. Однако и для теорий такого

arXiv:hep-th/9303139.

вида подобное рассмотрение возможно, и приводит

E. Panzer, Feynman integrals and hyperlogarithms,

к выводу, что билинейные уравнения на статистиче-

PhD thesis, Humboldt U. (2015); arXiv:1506.07243

[math-ph].

ские суммы на уровне теории возмущений задают ко-

умножение в алгебре Хопфа графов (см. также [23]).

G. ’t Hooft and M. J. G. Veltman, Nucl. Phys. B 153,

365 (1979).

В целом, активное изучение интегралов Фейнмана за

последние годы показывает, что и КТП в обычном

J. Broedel, C. Duhr, F. Dulat, B. Penante, and

L. Tancredi, JHEP 05, 120 (2019); arXiv:1902.09971

смысле проявляет свойства, аналогичные свойствам

[hep-ph].

матричных моделей, хотя и формулируемые в более

J. Broedel, C. Duhr, F. Dulat, and L. Tancredi, JHEP

сложном виде. Среди таких свойств отметим били-

05, 093 (2018); arXiv:1712.07089 [hep-th].

нейные соотношения общего вида и уравнения ти-

па Пикара-Фукса, аналогичные условиям Вирасоро.

10.

S. Weinzierl, Iterated Integrals Related to Feynman

Integrals

Associated to Elliptic Curves,

Следовательно, можно ожидать, что дальнейшие ис-

Antidifferentiation and the Calculation of Feynman

следования должны позволить нам установить наи-

Amplitudes, Springer Nature Switzerland, Cham (2020),

более общие свойства интегрируемости и для теорий

v. 12; arXiv:2012.08429 [hep-th].

поля в ненулевых измерениях.

11.

J. L. Bourjaily, A. J. McLeod, M. von Hippel, and

Мы благодарны А. Морозову за предложение

M. Wilhelm, Phys. Rev. Lett. 122(3), 031601 (2019);

подумать над этим кругом вопросов и полезные

arXiv:1810.07689.[hep-th].

замечания, а также участникам рабочего семина-

12.

K. Bönisch, C. Duhr, F. Fischbach, A. Klemm, and

ра ИТЭФ/МФТИ за ценные обсуждения. Рабо-

C. Nega, arXiv:2108.05310 [hep-th].

та Виктора Мишнякова частично финансировалась

13.

M. Caffo, H. Czyz, S. Laporta, and E. Remiddi, Nuovo

Российским фондом фундаментальных исследова-

Cim. A 111, 365 (1998); arXiv:hep-th/9805118.

ний и МОСТ, проект # 21-52-52004 и грант РФФИ

14.

S. Laporta and E. Remiddi, Nucl. Phys. B 704, 349

20-01-00644.

(2005); arXiv:hep-ph/0406160.

15.

L. Adams, C. Bogner, and S. Weinzierl, A walk on sunset

1. A. V. Kotikov, Differential Equations and Feynman

boulevard, RADCOR2015, UCLA, PoS, Los Angeles

Integrals, in Antidifferentiation and the Calculation

(2016), v. 096; arXiv:1601.03646 [hep-ph].

Письма в ЖЭТФ том 115 вып. 7 - 8

2022