Pis’ma v ZhETF, vol. 115, iss. 10, pp. 656 - 657
© 2022
May 25
Magnetic edge states in transition metal dichalcogenide monolayers
A. V. Chaplik+∗, L. I. Magarill+∗1), R. Z. Vitlina+
+Rzhanov Institute of Semiconductor Physics, Siberian Branch of Russian Academy of Sciences, 630090 Novosibirsk, Russia
∗Novosibirsk State University, 630090 Novosibirsk, Russia
Submitted 31 March 2022
Resubmitted 10 April 2022
Accepted 11
April 2022
DOI: 10.31857/S1234567822100093, EDN: dyvgbf
Magnetic edge states (MES) in a 2D system are
ficient at 1/√ω - ωmin is anomalously large if the spec-
quite similar to the magnetic surface states (MSS) in
imen width is much larger than the magnetic length.
a bulk specimen discovered experimentally in 1960 by
More complicate situation occurs for a half-plane of
Khaikin [1, 2] and theoretically described by Nee and
TMDC monolayer. As it is known in this case the Lan-
Prange [3-5]. Both those and others are formed by the so
dau levels for unbounded plane are additionally twofold
called “skipping orbits” of electrons: some electrons can-
degenerate in the valley index τ. Presence of an edge
not close their orbits in the magnetic field because center
lifts this degeneracy either: τ-doubling arises as one can
of the Larmour precession lies too close to the surface or
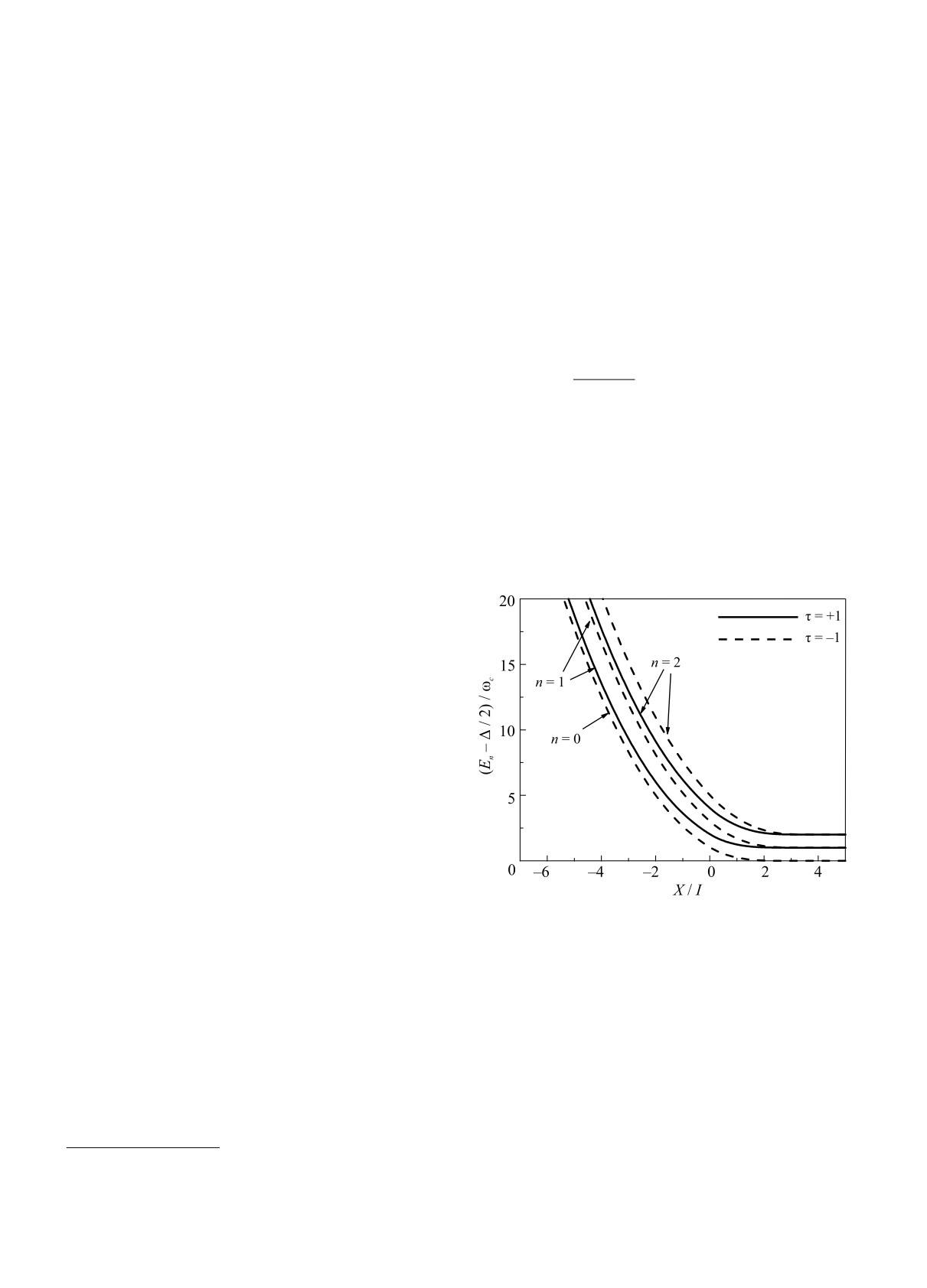
see in Fig.1, where Δ is the forbidden gap width, ωc
even beyond the specimen. In the last case the classically
is the cyclotron frequency, X is the suspension point
allowed for electrons area lies between a branch of “mag-
position and l is the magnetic length.
netic parabola” and the specimen boundary. Then the
separation between turning points can be significantly
less than the corresponding parameter of the bulk elec-
trons and that’s why the MSS energy quanta exceed the
Landau quantization intervals. As a result the Landau
levels in the bulk can be already blurred by temperature
and disorder while MSS are still observable in resonant
experiments. That’s how MSS were observed by Khaikin
when he measured the surface impedance of metals at
very weak magnetic fields. The Nee and Prange theory
was developed for weak fields either.
In the present paper we propose the theory of MESs
for conventional 2D semiconductor systems (like GaAs
quantum wells) and for monolayers of transition metal
dichalcogenides (TMDC) at arbitrary strong magnetic
fields. Effect of the monolayer boundary, e.g., edge of a
half-plane, results in lifting the degeneracy. The Landau
Fig. 1. Landau subbands for MoS2 in the conduction band
levels turn into 1D subbands in which energy depends
at the magnetic field 10 T
on the component of electron momentum parallel to the
edge of the half-plane. Optical interband magnetoab-
Unlike conventional semiconductors the selection
sorption of the conventional semiconductors is governed
rule Δn = 0 is violated for a semi-infinite TMDC mono-
by the same selection rule for the Landau level number
layer and, strictly speaking, any interband transition
that acts in case of unbounded plane Δn = 0 of the
is allowed though intensity of the forbidden in the un-
spectrum in position of the oscillator suspension point.
bounded plane transitions is much less than for allowed
The van Hove singularity of the M0 type (threshold of
ones. For suspension points both inside and outside the
absorption) remains square root behavior but the coef-
specimen at distances from the edge much greater than
the magnetic length analytical formulae for the 1D sub-
bands dispersion law are obtained; in the intermediate
1)e-mail: levm@isp.nsc.ru
region numerical calculations have been made.
656
Письма в ЖЭТФ том 115 вып. 9 - 10
2022
