Pis’ma v ZhETF, vol. 116, iss. 6, pp. 392 - 393

Mobility edge in the Anderson model on partially disordered random

regular graphs

O.Valba⁺¹⁾, A.Gorsky^∗×

⁺Department of Applied Mathematics, Tikhonov Moscow Institute of Electronics and Mathematics,

National Research University Higher School of Economics, 123458 Moscow, Russia

^∗Institute for Information Transmission Problems of the Russian Academy of Sciences (Kharkevich Institute), 127051 Moscow, Russia

^×Moscow Institute for Physics and Technology, 141700 Dolgoprudny, Russia

Submitted 28 July 2022

Resubmitted 23 August 2022

Accepted 28 August 2022

DOI: 10.31857/S1234567822180094, EDN: kggkzm

∑

Recently new mechanisms of ergodicity breaking in

IPR(i) =_n |ψⁿⁱ⁾|⁴, where ψⁿⁱ⁾ is the i-th eigenstate

the complicated interacting many-body systems have

of the matrix and n is the basis state index.

been uncovered. The combination of interaction and

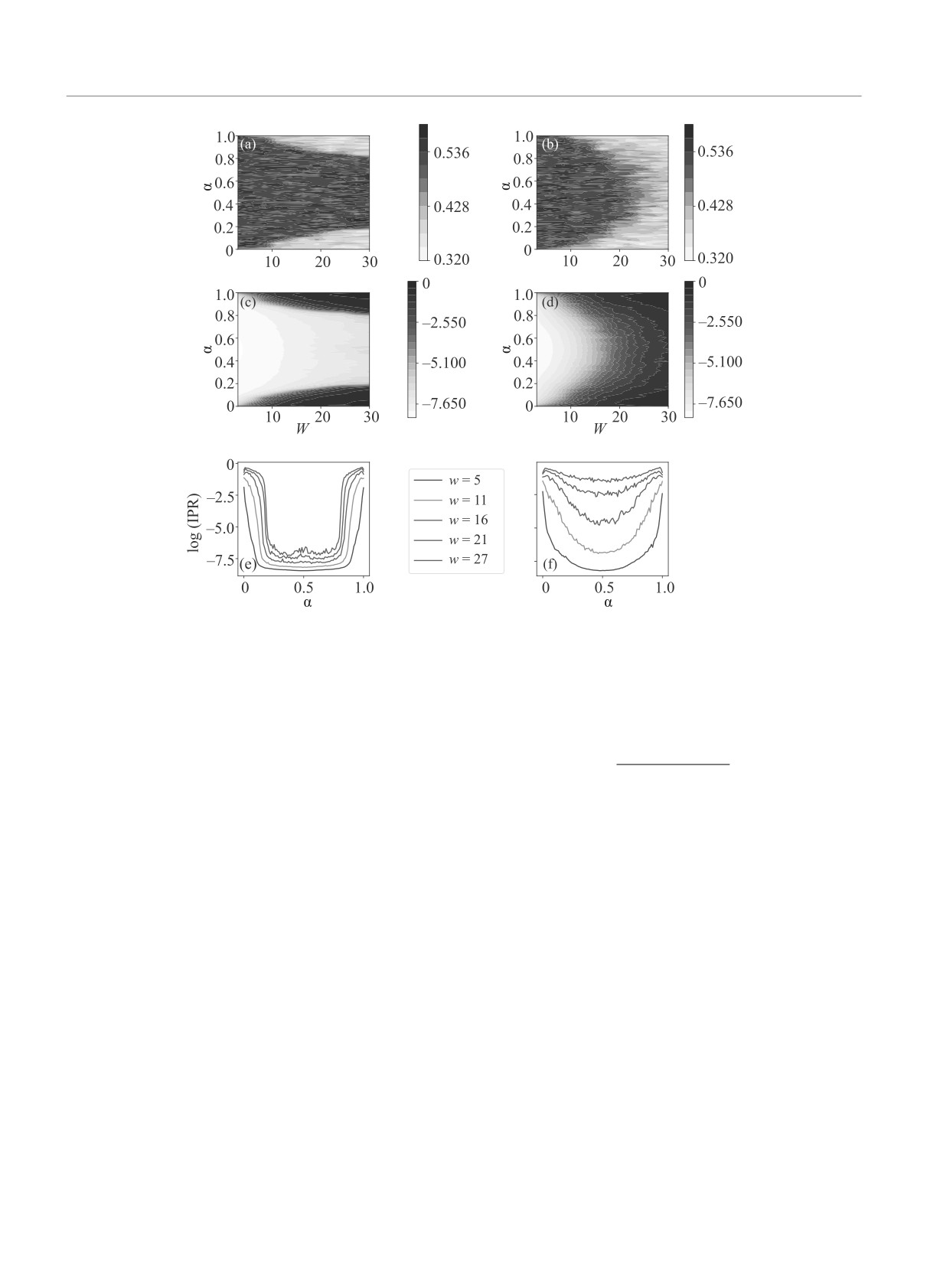
We analyze the ratio 〈r〉 and IPR for different parts

strong enough disorder amounts to the emergent many-

of the spectrum, dividing the sorting spectrum into

body localization (MBL) phase with full ergodicity

k = 100 equal parts and average the ratio 〈r〉 and

breaking [1-5]. The Anderson model on random regular

IPR over each window. The ordinate α = i/(N - 1)

graph (RRG) serves as the toy model for a identifica-

in Fig. 1 corresponds the normalized level position with

tion of MBL phase in the physical space, see [6] for the

i = 0,1,...,N-1, the energy level, the ordinate window

recent review. The many-body localization in the physi-

respectively is Δα = 1/k.

cal space presumably gets mapped into the one-particle

The heat maps Fig. 1a, c explicitly demonstrate, that

localization in a Hilbert space [7].

there is the mobility edge λ_m separating sharply the

We study non-interacting spinless fermions hopping

spectrum into two different regimes for RRG with par-

over RRG with connectivity p = 3 in a potential disor-

tial disorder in vertices. For |λ| > λ_m we observe local-

der described by Hamiltonian

isation state with the ratio 〈r〉 close to 〈r〉_P and inde-

pendence of IPR on N, while for central spectrum part

∑

(

∑

with |λ| ≤ λ_m the ratio 〈r〉 and IPP indicate on the de-

H =

c⁺ⁱc_j + c_ic^+j

+ ǫ_ic⁺ⁱc_i,

(1)

weakly

localized state. Note, that the mobility edge λ_m

〈i,j〉

i=1

depends on the disorder W and is observed even for

small W . Moreover, we do not observe the phase tran-

where the first hopping sum runs over the nearest-

sition at large W to completely localized phase which is

neighbor sites of the RRG, the second sum runs over

βN nodes with potential disorder. The energies ǫ_i are

familiar for completely disordered RRG (see Fig. 1b, d, f

with the same plots for β = 1.0).

independent random variables sampled from a uniform

distribution on [-W/2, W/2]. We consider gaps between

We consider partially disordered RRG as the toy

adjacent levels, δi = Ei+1 - Ei, where the eigenval-

model of a Hilbert space for some interacting disordered

ues of a given realization of the Hamiltonian for a

many-body system with the topologically protected sub-

given total number of particles, E_i, are listed in as-

sector. The nodes of RRG free from disorder correspond

cending order. The dimensionless quantity we have cho-

to topologically protected states in many-body system.

sen to characterize the correlations between adjacent

To some extend our model probes the effect of disorder

gaps in the spectrum is the ratio of two consecutive

on topologically protected states.

gaps: r_i = min(δ_i, δ_i+1)/ max(δ_i, δ_i+1). In turn, a direct

It is found that at some density of clean nodes in par-

measure of the (de)localization of the eigenfunctions

tially disordered RRG the sharp mobility edge emerges

is obtained by the inverse participation ratio (IPR),

in the spectrum of Anderson model and exists up to ar-

bitrarily large diagonal flat disorder W . We have studied

¹⁾e-mail: ovalba@hse.ru

the distribution of the eigenfunctions in RRG and have

392

Письма в ЖЭТФ том 116 вып. 5 - 6

2022

Mobility edge in the Anderson model on partially disordered random regular graphs

393

Fig. 1. (Color online) The ratio 〈r〉 in dependence on the disorder value W and the spectrum part α for β = 0.5 (a) and

β = 1 (b); the value log(IPR) in dependence on the disorder value W and the spectrum part α for β = 0.5 (c) and β = 1

(d); the dependencies of log(IPR) on the spectrum position α for different values of W and β = 0.5 (e) and β = 1 (f)

found that localized states are distributed almost solely

lar graphs”. Full text of the paper is published in JETP

within the dirty nodes while the delocalized part of the

Letters journal. DOI: 10.1134/S0021364022601750

spectrum mainly involves the clean nodes with small

disorder dependent contribution of the dirty nodes.

1. D. Basko, I. Aleiner, and B. Altshuler, Ann. Physics

The model certainly oversimplifies the issue, never-

321(5), 1126 (2006).

theless it can be considered as the indication that a

2. I. Gornyi, A. Mirlin, and D. Polyakov, Phys. Rev. Lett.

one-particle mobility edge in the hopping model in the

95(20), 206603 (2005).

Hilbert space and a mobility edge in the MBL phase

3. R. Nandkishore and D. A. Huse, Annu. Rev. Condens.

could be related. Indeed if the mechanism behind the

Matter Phys. 6(1), 15 (2015).

mobility edge in MBL involves density of highly degen-

4. F. Alet and N. Laflorencie, C. R. Phys. 19, 498 (2018).

erate zero-modes in the physical space then the density

5. D. A. Abanin, E. Altman, I. Bloch, and M. Serbyn, Rev.

of clean nodes in the Hilbert space is its relevant coun-

Mod. Phys. 91(2), 021001 (2019).

terpart.

6. K. S. Tikhonov and A. D. Mirlin, arXiv:2102.05930.

This is an excerpt of the article “Mobility edge in the

7. B. L. Altshuler, Y. Gefen, A. Kamenev, and L. S. Levi-

Anderson model on partially disordered random regu-

tov, Phys. Rev. Lett. 78(14), 2803 (1997).

Письма в ЖЭТФ том 116 вып. 5 - 6

2022