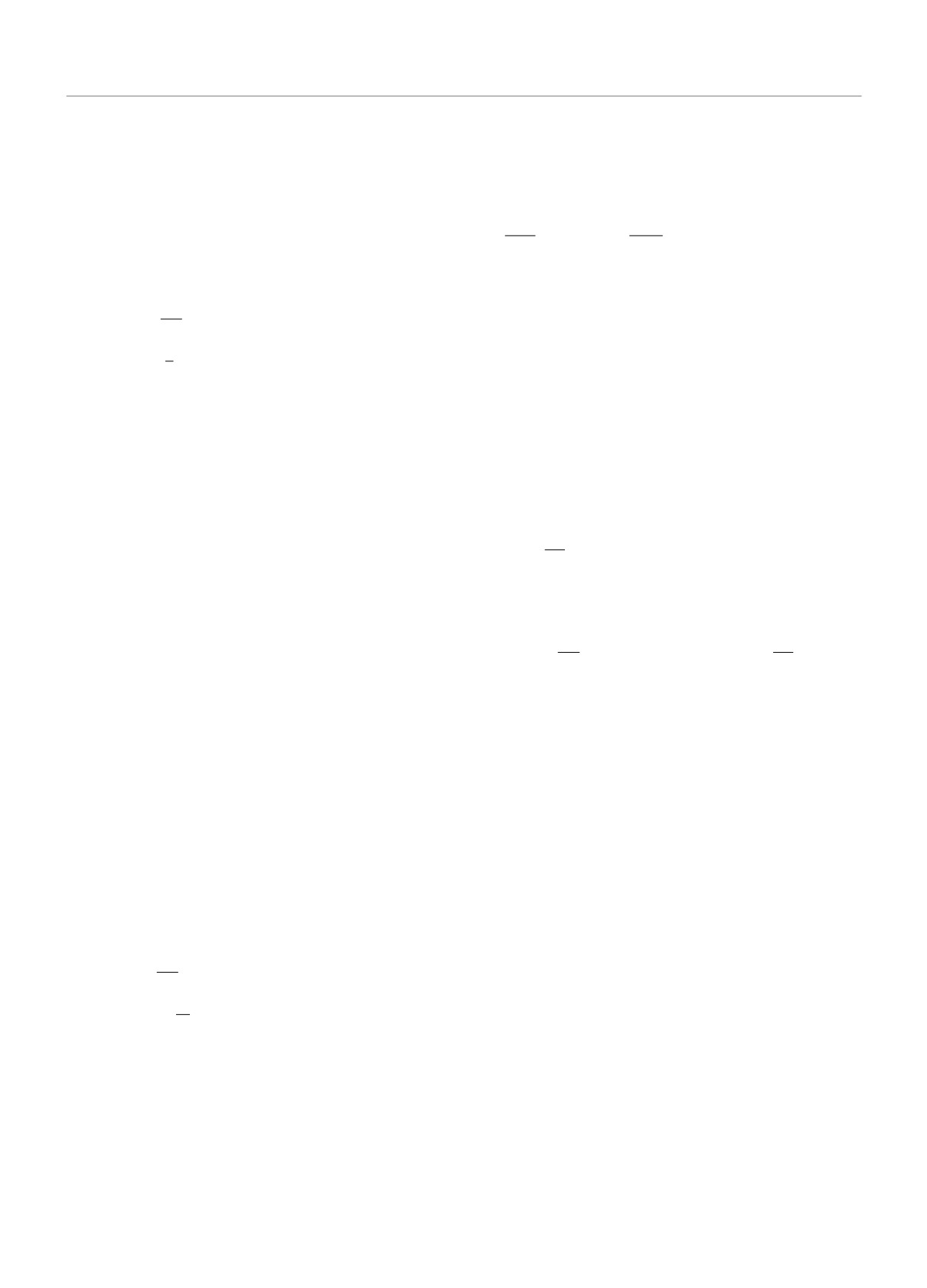Письма в ЖЭТФ, том 116, вып. 7, с. 443 - 449

Критическая температура наноструктуры

сверхпроводник/ферромагнетик вблизи магнитного скирмиона

В.А.Туманов¹⁾, В.Е.Зайцева, Ю.Н.Прошин

Казанский федеральный университет, 420008 Казань, Россия

Поступила в редакцию 1 июля 2022 г.

После переработки 26 августа 2022 г.

Принята к публикации 27 августа 2022 г.

Рассмотрен контакт сверхпроводника с киральным ферромагнетиком, содержащим сложные магнит-

ные структуры: спиральную или коническую текстуру, скирмион, киральный поплавок. Более подробно

рассмотрен случай одиночного скирмиона. Влияние таких магнитных неоднородностей на критическую

температуру становится существенным только для спиновых структур масштаба порядка 100 нм и ниже.

Решетки скирмионов и одиночные скирмионы такого размера недавно наблюдались экспериментально

в тонких магнитных слоях. В рамках теории эффекта близости в грязном пределе предлагается прибли-

женный подход, позволяющий рассчитывать критическую температуру в таких системах. Значительное

влияние наноразмерных спиновых вихрей на критическую температуру в сочетании с топологической

устойчивостью и малой плотностью тока, необходимой для их движения, позволяет эффективно исполь-

зовать такие системы в качестве сверхпроводящих спиновых вентилей.

DOI: 10.31857/S1234567822190065, EDN: khvfvw

Контакт сверхпроводника (S) с ферромагнитным

дальной фазе обсуждается в работах [15, 16]. Вли-

металлом (F) весьма привлекателен для исследова-

яние сверхпроводника на стабильность скирмиона в

ний из-за возможности сосуществования ферромаг-

S/F системе рассмотрено в работе [17]. В работе [18]

нитного и сверхпроводящего упорядочения в преде-

изучена возможность образования вихря Абрикосо-

лах одного образца [1-7]. Теоретически и эксперимен-

ва в сверхпроводнике на фоне скирмиона неелев-

тально исследуется возможность применения таких

ского типа в ферромагнитном слое с учетом спин-

систем в сверхпроводящей микроэлектронике [8-10].

орбитального взаимодействия. Связанное состояние

Куперовские пары при этом проникают в однород-

скирмиона и вихря рассмотрено в работе [19] и пока-

ный ферромагнитный слой на относительно неболь-

зано, что при определенных условиях возможно сме-

√

шую глубину порядка

D_f /I, где Df - коэффи-

щение вихря относительно центра скирмиона. В ра-

циент диффузии в ферромагнетике, I - эффектив-

боте [20], в числе прочих результатов, методом конеч-

ное обменное поле. Обменное взаимодействие сверх-

ных элементов рассчитано распределение сверхпро-

проводящих электронов с электронами в магнети-

водящего тока в S/F/S системе, содержащей скирми-

ке вызывает при этом большое количество интерес-

он. Теория эффекта близости в S/F системах, содер-

ных и практически важных явлений. В частности, в

жащих магнитные неоднородности, хорошо разрабо-

последние годы возрос интерес к изучению эффек-

тана [1-3], однако многие трехмерные задачи сложны

та близости сверхпроводника с киральным магнети-

в техническом отношении. Одна из таких задач - это

ком, в котором возможно существование стабильных

вычисление критической температуры S/F системы,

магнитных скирмионов. Такой интерес обусловлен,

содержащей магнитный вихрь или доменную стен-

в числе прочего, наблюдением в ряде эксперимен-

ку [21, 22]. В данной работе мы предлагаем прибли-

тальных работ [11-13] магнитных вихрей размером

женный подход к решению подобных задач. Подход

несколько нанометров [14]. В отличии от магнитных

основан на переходе к новому базису путем унитар-

неоднородностей микронного масштаба, такие маг-

ного преобразования в пространстве спина коллекти-

нитные структуры оказывают существенное влияние

визированного электрона. Как было показано ранее

на термодинамические и транспортные свойства S/F

[23], такой подход можно применить к гамильтони-

систем. Так, например, эффект близости сверхпро-

ану в приближении эффективного обменного поля,

водника с киральным ферромагнетиком в геликои-

в данной работе мы применим унитарное преобра-

зование к уравнениям Узаделя, полученным в рабо-

те [24] для неоднородной по направлению намагни-

¹⁾e-mail: tumanvadim@yandex.ru

Письма в ЖЭТФ том 116 вып. 7 - 8

2022

443

3^∗

444

В.А.Туманов, В.Е.Зайцева, Ю.Н.Прошин

ченности. Далее рассмотрим слои сверхпроводника

В обобщенных граничных условиях Куприянова-

и ферромагнетика в грязном пределе, когда длины

Лукичева [25] градиент также заменяется на удли-

когерентности в сверхпроводнике и ферромагнетике

ненную производную. Приведем для примера гра-

ξ_s(f) значительно превышают соответствующие дли-

ничные условия для двухслойной S/F системы

ны свободного пробега l_s(f) [1, 3]. Уравнение Узаделя

(

)

(

)

4D_s

4D_f

в этом случае для ферромагнитного слоя при произ-

∇Fs, n =

f,n

F_f -

F_s,

(6)

v_sσ_s

v_f σ_f

вольно направленной в пространстве намагниченно-

сти можно записать в виде [24]

где v_s(f) - скорости Ферми, σ_s(f) - параметры про-

зрачности границы со стороны S и F слоя [3]. Нор-

D_f

∇2 Fˆ

маль в данном случае направлена из S в F слой. От-

f (r, ω) - |ω|

f (r, ω)

(1)

метим, что при наличии двух и более внутренних

{

}

границ могут потребоваться повороты функции Уза-

−

sgnω (I, σ),F

f (r, ω)

= 0,

деля вида (3) для согласования базиса в спиновом

(

)

пространстве. На свободной границе ферромагнети-

-i(ϕ)

cos(θ)

sin (θ) e

(I, σ) = I

(2)

ка и сверхпроводника граничные условия имеют вид

sin (θ) e^i(ϕ)

- cos(θ)

(

)

(

)

∇Fs, n = 0,

f,n

= 0.

(7)

где

F - матричная функция Узаделя, D_f - коэффи-

циент диффузии в ферромагнитном слое, I - эффек-

В краевую задачу также входит уравнение Узаделя

тивное обменное поле, ω - мацубаровская частота. Δ

в сверхпроводящем слое

- сверхпроводящий параметр порядка. θ и ϕ - поляр-

D_s

ный и азимутальный углы, определяющие направле-

∇²

F (r, ω) - |ω|F (r, ω) = -Δs1.

(8)

ние намагниченности. Здесь и далее для простоты

принято, что k_B = µ_B = ℏ = 1, где k_B - постоянная

Краевая задача должна быть дополнена уравнением

Больцмана, µ_B - магнетон Бора.

самосогласования [1, 2]

Совершим локальный поворот в спиновом базисе:

(

)

T_c

∑ (

Δ_s

Δ_s ln

= πT_c

F (x, ω) -

(9)

F (r, ω) =

Û-1

F (r, ω)Û,

(3)

ω>0

где T_cs

- критическая температура уединенного

где

Û - унитарная матрица поворота, выбранная та-

сверхпроводника, ω_D - частота Дебая. Уравнение

ким образом, что

Û (I, σ)Û-1 = I σ₃ имеет вид

самосогласования оказывается инвариантным отно-

(

)

i(γ-ϕ)

сительно унитарных преобразований функции

F. В

cos(θ/2)e^iγ

sin (θ/2) e

U =

(4)

уравнениях (1), (7), (8) явно не учитывается магнит-

− sin(θ/2)e^-i(γ-ϕ) cos(θ/2)e^-iγ

ное поле, создаваемое ферромагнитным слоем. Внут-

ри ферромагнитного слоя его вклад мал по сравне-

а γ(r) - произвольная действительная функция ко-

нию с эффективным обменным полем. В сверхпро-

ординат. Произвольность γ(r) отвечает инвариант-

водящем слое его напряженность зависит от кон-

ности уравнения относительно локальных поворотов

фигурации намагниченности во всем образце, в том

вокруг оси z в пространстве спина коллективизиро-

числе от намагниченности в значительном удалении

ванного электрона. Для преобразованной матричной

от рассматриваемой области контакта. Как правило,

функции Узаделя

F уравнение принимает вид

поле, создаваемое достаточно тонкой ферромагнит-

D_f

ной пленкой, слабо и, по мнению большинства авто-

F (r, ω) - |ω|F (r, ω) -

ров (см., например, работу [26] или обзоры [1-3]), в

(5)

{

}

случае хорошего металлического контакта основное

sgnω

F (r, ω), σ₃

= 0.

влияние на критическую температуру имеет проник-

новение куперовских пар в ферромагнетик. Нужно

Удлиненная производная

D в данном случае опреде-

отметить однако, что при рассмотрении связанного

ляется как

f =

f + [Â,f ],

Â = Û∇Û^-1. Точно

состояния скирмиона и вихря Абрикосова магнитное

такой же вид она имеет для функций Грина в урав-

поле играет очень важную роль [18, 19]. Таким об-

нениях Горькова. Преобразованием (3) уравнение (1)

разом в нашей модели не описываются контакты с

можно привести к виду (5) для произвольной зависи-

сверхпроводниками 2 рода при магнитных полях вы-

мости направления намагниченности от координат.

ше H_c1.

Письма в ЖЭТФ том 116 вып. 7 - 8

2022

Критическая температура наноструктуры S/F вблизи магнитного скирмиона

445

Преобразования (3) позволяют значительно упро-

стить краевую задачу для многих магнитных фаз,

реализуемых в киральных магнетиках. Так, в част-

ности, если ферромагнетик находится в геликои-

дальной фазе, волновой вектор которой направлен

вдоль границы, все компоненты матричной функции

Узаделя зависят только от координаты, перпендику-

лярной границе. В работе [24] такой подход позволил

вычислить ток Джозефсона через слой неоднородно-

го ферромагнетика. Критическая температура S/F

системы для такой конфигурации намагниченности

была вычислена ранее в работе [15] методом фун-

даментального решения [27]. Рассматривалась кри-

тическая температура при двух различных ориен-

тациях магнитной спирали: вдоль и перпендикуляр-

но границе. Разница критических температур зави-

села от толщин слоев и качества контакта, а также

от периода магнитной спирали. Было показано, что

Рис. 1 (Цветной онлайн) Зависимость критической тем-

критическая температура оказывается выше в слу-

пературы S/F контакта для некоторых геометрий гели-

чае расположения спирали вдоль границы. Наши ре-

коидальной и конической фазы от толщины ферромаг-

зультаты для такой системы, приведенные ниже (см.,

нитного слоя d_f . Кривая 1 соответствует геликоидаль-

например, пунктирную и штрих-пунктирную кривые

ной намагниченности ферромагнитного слоя, волновой

на рис. 1), согласуются с результатами работы [15],

вектор магнитной структуры направлен вдоль S/F гра-

что усиливает доверие к использованию предложен-

ницы; 2 - коническая фаза, волновой вектор вдоль гра-

ного выше метода. Попробуем теперь найти критиче-

ницы; 3 - коническая фаза, волновой вектор перпен-

скую температуру контакта сверхпроводника с фер-

дикулярен границе; 4 - однородная намагниченность;

5 - геликоидальная намагниченность, волновой вектор

ромагнетиком в конической фазе. Локальное унитар-

перпендикулярен границе. Период магнитных текстур

ное преобразование в сочетании с произвольным вы-

LD = 52Å. Параметры системы: толщина сверхпро-

бором функции γ(r) в (4) позволяет свести краевую

водящего слоя ds = 113.5

Å, ls = 120

Å, ξs = 125

Å,

задачу к одномерной системе уравнений второго по-

2Iτ_f = 0.3, где τ_f - время свободного пробега в ферро-

рядка с постоянными коэффициентами. Дальнейшие

магнетике, σs = 6, nsf = (vsNs)/(vf Nf ) = 4, где Ns(f ) -

расчеты производятся стандартным способом в при-

плотность состояний на поверхности Ферми)

ближении постоянного в пределах слоя параметра

порядка [28-30]. Оно хорошо зарекомендовало себя

за сочетание простоты и хорошего совпадения с более

Вычисление критической температуры S/F систе-

строгим подходом фундаментального решения [27].

мы с произвольной конфигурацией намагниченности

Полученная функция Узаделя подставляется в урав-

представляет собой в общем случае существенно бо-

нение самосогласования (9), которое решается чис-

лее сложную задачу. Для таких спиновых текстур,

ленно. Приведем зависимость критической темпера-

как магнитные вихри и доменные стенки, уравнение

туры двухслойной S/F системы от толщины ферро-

(1) не сводится к уравнению с постоянными коэф-

магнетика для различных ориентаций намагничен-

фициентами преобразованием вида (3). Однако, пре-

ности в ферромагнетике относительно S/F границы.

образованная функция Узаделя значительно слабее

Наряду с уже изученными случаями магнитного ге-

меняется по фазе вдоль S/F границы. Это связано с

ликоида, волновой вектор которого направлен нор-

тем, что фаза компонент функций Узаделя задается

мально к S/F границе или лежит в ее плоскости [15],

преимущественно направлением намагниченности и

мы рассмотрели коническую фазу с полярным углом

толщиной ферромагнитного слоя на данном участке

π/6 (см. рис.1). Набор использованных параметров

границы. Для модифицированной функции

F (r, ω)

теории, выбранных нами в качестве примера, близок

направление намагниченности всегда одинаково в си-

к экспериментальным параметрам, полученным в ра-

лу определения. Это позволяет нам применить для

боте [31] для контакта ванадия (T_cs = 5.4) и железа

оценки критической температуры системы прибли-

с характерным значением эффективного обменного

женный подход. Иерархия слагаемых в уравнении

поля I порядка 1000 K.

(5) достаточно сложна. Наибольшими слагаемыми,

Письма в ЖЭТФ том 116 вып. 7 - 8

2022

446

В.А.Туманов, В.Е.Зайцева, Ю.Н.Прошин

как правило, являются член со второй производной

2γ = φ + π/2. После таких упрощений эффективное

от функции Узаделя (в перпендикулярном направле-

тензорное поле принимает вид

нии к границе) и выражение, содержащее произведе-

i sinθ

ние эффективного обменного поля с функцией Уза-

Â= -

σ₁∇θ +

σ₂∇ϕ.

(12)

деля. Для наиболее значимых в уравнении самосо-

Учитывая (11), дивергенция эффективного тензор-

гласования слагаемых, отвечающих небольшим ма-

ного поля

Â, входящая в выражение

D2F (r, ω), за-

цубровским частотам, соответствующее слагаемые в

пишется в виде

уравнении (5) также не слишком велики. Прочие сла-

гаемые в составе удлиненной производной являются

i sinθ

(∇,

Â) = -

σ₁Δθ +

σ₂Δϕ +

поправками по отношению к главным слагаемым для

практически реализуемых скирмионов. Изменение в

i sin2θ

σ₁(∇ϕ)².

(13)

функции Узаделя в плоскости границы в этом слу-

чае обусловлено изменением этих поправок от точ-

При решении уравнения Узаделя в сверхпроводящем

ки к точке. Соответствующие градиенты в силу вы-

слое здесь также удобно пользоваться приближением

ше сказанного достаточно малы, особенно для круп-

постоянного в пределах слоя сверхпроводящего па-

ных скирмионов (r ≫ ξ_s). Можно предложить так-

раметра порядка. Эти приближения позволяют нам

же оценку из более общих соображений, подходящую

разбить нашу задачу на одномерные краевые задачи

для мелкомасштабных магнитных вихрей. Сверхпро-

для каждой пары координат в плоскости границы

водящий параметр порядка в толще сверхпроводника

и решить их стандартным способом для систем вто-

может существенно меняться на расстояниях, превы-

рого порядка с постоянными коэффициентами. При

шающих сверхпроводящую длину когерентности ξ_s.

решении уравнения самосогласования (9), в рамках

Тогда, в силу уравнения самосогласования и гранич-

этого подхода, мы усредняем функцию Узаделя в S

ных условий (7), функция Узаделя в ферромагнит-

слое по координате, перпендикулярной границе и ре-

ном слое меняется по модулю в плоскости границы

шаем его численно. В плоскости границы мы усред-

столь же медленно. В уравнении (5) мы пренебрегаем

няем (сглаживаем) функцию Узаделя с гауссовым

производными от функции Узаделя в плоскости как

весом на масштабе ξ_s, так как на меньшем масштабе

величинами порядка 1/ξ_s. Здесь мы принимаем во

не представляется возможным определить критиче-

внимание, что изменения фазы в плоскости границы

скую температуру сверхпроводящего перехода. В до-

мы практически полностью учитываем за счет ло-

полнении к этому, входящий в уравнение самосогла-

кального унитарного преобразования (3). Такое до-

сования след матричной функции Узаделя меняется

статочно грубое приближение позволяет нам свести

вдоль границы очень слабо. Несмотря на грубость

уравнение (5) к системе обыкновенных дифференци-

данного подхода, так можно качественно оценить ло-

альных уравнений. Обратимся к величине

Â. В об-

кальное влияние магнитного вихря на критическую

щем случае она имеет вид

температуру. Для нахождения профиля намагничен-

ности мы воспользовались методом, описанным в ра-

боте [13], для экспериментально наблюдаемого мел-

Â= -

(sin(2γ - ϕ)σ₁ + cos(2γ - ϕ)σ₂)∇θ +

(

)

комасштабного одиночного скирмиона. Зависимость

(θ)

полярного угла от координаты можно найти из урав-

+ iσ₃

sin²

∇ϕ - ∇γ

нения

i sinθ

(

)

(cos(2γ - ϕ)σ₁ + sin(2γ - ϕ)σ₂)∇ϕ.

(10)

θ^′ρ

2 sin² θ

sin 2θ

θ^′′ρρ +

ρ²

В силу произвольности функции γ(r) это выражение

− hsinθ = 0; θ(0) = π;θ(∞) = 0,

(14)

можно упростить. Потребуем равенства нулю диаго-

где ρ =^2πrL, r - расстояние до центра скирмиона, LD

нальной компоненты эффективного тензорного поля

- период магнитного геликоида в отсутствии вешне-

)

го поля и анизотропии, k и h - параметры в функ-

(θ

sin²

∇ϕ = ∇γ.

(11)

ционале плотности микромагнитной энергии (см. по-

дробнее [13]). Поведение азимутального угла зависит

от типа скирмиона. Радиус скирмиона определяется

В нашем приближении каждая точка плоскости гра-

как [32]

ницы независима от других в рамках краевой зада-

θ₀

rs = r0 -

(15)

чи, и мы можем выбрать значение γ произвольно:

(θ′r)r=r0

Письма в ЖЭТФ том 116 вып. 7 - 8

2022

Критическая температура наноструктуры S/F вблизи магнитного скирмиона

447

где (r₀, θ₀) - точка перегиба профиля намагниченно-

S/F границы при размере скирмиона, близком к ξ_s.

сти θ(r).

Главный качественный результат выглядит вполне

Как и следовало ожидать, влияние на крити-

разумным: в области локализации скирмиона крити-

ческую температуру вблизи магнитной неоднород-

ческая температура оказывается выше, чем у осталь-

ности определяется ее масштабом по сравнению со

ных участков бислоя. Разница температур может

сверхпроводящей длиной когерентности. На рисун-

быть увеличена путем специального подбора тол-

ке 2 представлена критическая температура сверх-

щин сверхпроводника и ферромагнетика при условии

высокой прозрачности границ. Киральный поплавок

[33] оказывает качественно схожее влияние на сверх-

проводимость, но он может существовать только в

достаточно толстых ферромагнитных пленках.

Варьируя толщину сверхпроводящего слоя мож-

но добиться ситуации, когда сверхпроводимость бу-

дет проявляться в сверхпроводящем слое только

вблизи скирмиона. На рисунке 3 приведено схемати-

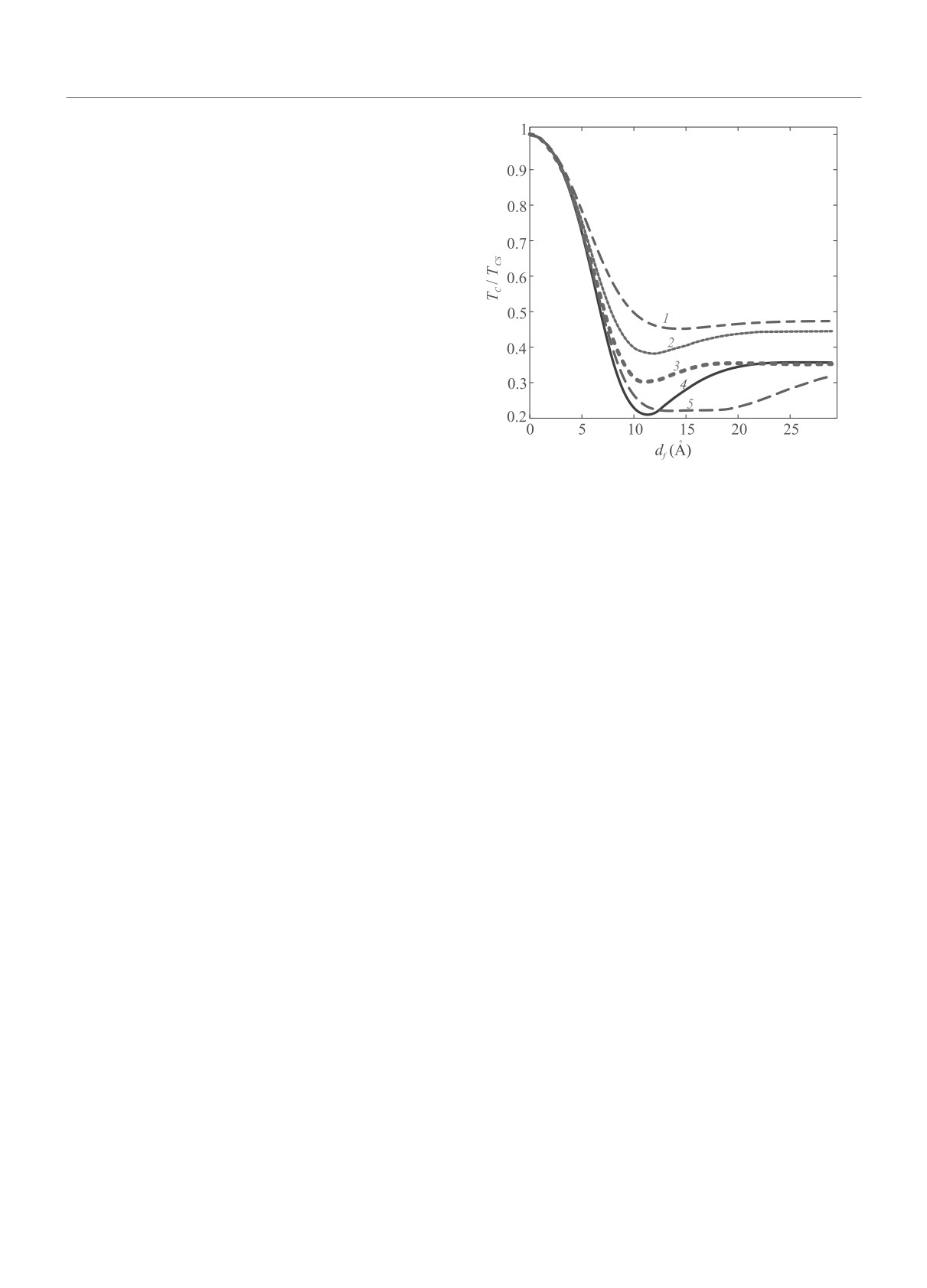
Рис. 2 (Цветной онлайн) Зависимость критической тем-

пературы Tc S/F системы от радиуса rs изолированно-

го скирмиона при различных толщинах ферромагнит-

ного и сверхпроводящего слоя. На вставке показана за-

висимость Tc контакта S/F от толщины df ферромаг-

Рис. 3. (Цветной онлайн) Схематическое изображение

нитного слоя при однородном намагничивании. Кривая

локализации сверхпроводящей фазы вблизи скирмиона

1 соответствует толщине S слоя ds = 112Å и толщине F

для плоского контакта S/F. Вдали от наноразмерного

слоя d_f = 10Å; 2 - S cлоя ds = 100Å, F слоя df = 25Å.

скирмиона намагниченность в F-слое однородна и над

Параметры системы: ls = 120Å, ξs = 125Å, 2Iτf = 0.3,

этими областями при значимых температурах сверх-

σs = 4, nsf = 4

проводимость в S-слое отсутствует

проводника вблизи одиночного скирмиона, локализо-

ческое представление своеобразного островка сверх-

ванного в соседнем слое ферромагнитного металла,

проводимости. Этот эффект проявляется при кон-

от радиуса скирмиона при различных толщинах S

такте с магнитными вихрями, характерный размер

и F слоев. Описанный эффект очень чувствителен к

которых порядка сверхпроводящей длины когерент-

толщине сверхпроводящего слоя и прозрачности гра-

ности. Нужно отметить, что при других параметрах

ницы. Согласно расчетам, наиболее яркий эффект

системы возможно связанное состояние скирмиона с

наблюдается при толщинах ферромагнетика (d_f ), со-

вихрем Абрикосова, эта ситуация рассмотрена в ра-

ответствующих первому минимуму T_c(d_f ). При та-

ботах [18, 35, 34]. Влияние скирмиона на критиче-

кой толщине ферромагнетика неоднородная намаг-

скую температуру в этом случае планируется рас-

ниченность меняет условия интерференции компо-

смотреть в дальнейших работах наряду с практиче-

ненты функции Узаделя, отвечающей парам, про-

ски важным случаем сильного внешнего магнитного

никшим в ферромагнитный слой из сверхпроводни-

поля. Необходимо отметить также, что рассмотрен-

ка, и компонентой, отраженной от свободной грани-

ный в данной работе эффект близости не единствен-

цы ферромагнетика. Это ожидаемо вызывает доста-

ный механизм взаимодействия вихря Абрикосова и

точно сложную зависимость критической темпера-

магнитного скирмиона. Как показано, в частности,

туры от размера скирмиона. Однако, мы не можем

в работах [17-19] электромагнитное взаимодействие

уверенно исключить небольших искажений, вызван-

играет в таких системах очень важную роль и яв-

ных методом усреднения функции Узаделя вдоль

ляется достаточным для формирования такого свя-

Письма в ЖЭТФ том 116 вып. 7 - 8

2022

448

В.А.Туманов, В.Е.Зайцева, Ю.Н.Прошин

занного состояния. В случае сверхпроводящего ост-

ровка, связанного с вихрем нанометрового масштаба,

критическая температура составляет примерно 10-

20 % критической температуры уединенного сверх-

проводника. При удалении от островка концентра-

ция куперовских пар убывает экспоненциально на

Рис. 5. (Цветной онлайн) Схематическое изображение

масштабе ξ_s. На рисунке 4 показана зависимость кри-

спинового клапана, основанного на повышении крити-

тической температуры островка от размеров скир-

ческой температуры сверхпроводника в области лока-

миона.

лизации скирмиона. Интенсивность заливки в сверх-

проводящем слое символизирует концентрацию купе-

ровских пар. Перемещение вихря в область между кон-

тактами создает условия для протекания сверхпрово-

дящего тока между сверхпроводящими берегами (ниж-

ний рисунок)

тиком в конической фазе и контакт с уединенным

скирмионом на фоне однородной намагниченности.

Наибольшее влияние на критическую температуру

скирмион ожидаемо оказывает в случае достаточно

тонких слоев ферромагнетика и высокой прозрачно-

сти интерфейса S/F. Путем специального подбора

толщин слоев можно добиться, чтобы сверхпроводи-

мость возникала только в области локализации спи-

нового вихря. Получившийся сверхпроводящий ост-

ровок, связанный с магнитным скирмионом, потен-

Рис. 4. (Цветной онлайн) Зависимость критической

циально может быть использован в качестве подвиж-

температуры Tc сверхпроводящего островка от радиу-

ного мостика для сверхтока.

са rs изолированного скирмиона для S/F контакта. На

Работа выполнена за счет средств Программы

вставке показана зависимость Tc от df при однород-

стратегического академического лидерства Казан-

ном намагничивании. Параметры системы: ds = 111Å,

ского (Приволжского) федерального университета.

= 120Å, ξs = 125Å, 2Iτf = 0.3, где τf , σs = 4,

n_sf = 4, k = 1.3, h = 0.01, d_f = 10Å

1. A. I. Buzdin, Rev. Mod. Phys. 77, 935 (2005).

Существенное влияние наноразмерных спиновых

2. K. B. Efetov, I. A. Garifullin, A. F. Volkov, and

вихрей на критическую температуру в сочетании с

K. Westerholt, Springer Tracts Mod. Phys. 227, 251

топологической защищенностью и низкой плотно-

(2008).

стью тока, необходимой для их движения [36-38],

3. Ю. А. Изюмов, Ю. Н. Прошин, М. Г. Хусаинов, УФН

позволяет эффективно использовать такие системы

172, 113 (2002).

в качестве сверхпроводящих спиновых клапанов [39-

4. Е. А. Кошина, В. Н. Криворучко, ФНТ 43, 754 (2017).

41]. Например, сверхпроводящий островок, локали-

5. B. Krunavakarn, Phys. Lett. A 383, 1341 (2019).

зованный между сверхпроводящими берегами, мо-

6. Р. Р. Гайфуллин, В. Н. Кушнир, Р. Г. Деминов,

жет выступать в качестве подвижного мостика для

Л. Р. Тагиров, М. Ю. Куприянов, А. А. Голубов, ФТТ

сверхпроводящего спинового клапана (см. рис.5).

61, 1585 (2019).

Толщина сверхпроводящего слоя и температура под-

7. C. В. Миронов, А. В. Самохвалов, А. И. Буздин,

бираются таким образом, чтобы S/F система была

А. С. Мельников, Письма в ЖЭТФ 113, 102 (2021).

близка к переходу в сверхпроводящее состояние. По-

8. R. Caruso, D. Massarotti, A. Miano, V. V. Bolginov,

явление скирмиона в этой области вызовет переход

A. B. Hamida, L. N. Karelina, G. Campagnano,

перемычки в сверхпроводящее состояние.

I. V. Vernik, F. Tafuri, V.V. Ryazanov, and

В рамках теории эффекта близости в грязном

O. A. Mukhanov, IEEE Trans. Appl. Supercond.

пределе предложен приближенный подход, позво-

28, 1 (2018).

ляющий рассчитать критическую температуру для

9. А. А. Максимовская, В. И. Ружицкий, Н. В. Кленов,

контакта сверхпроводника с неоднородным магне-

С. В. Бакурский, М. Ю. Куприянов, И. И. Соловьев,

тиком. Были рассмотрены контакт с ферромагне-

Письма в ЖЭТФ 115, 786 (2022).

Письма в ЖЭТФ том 116 вып. 7 - 8

2022

Критическая температура наноструктуры S/F вблизи магнитного скирмиона

449

10.

Л. Н. Карелина, Н.С. Шуравинa, А.С. Ионинa,

26.

F. S. Bergeret, K. B. Efetov, and A. I. Larkin, Phys. Rev.

С. В. Бакурскийc, С. В. Егоровa, И. А. Головчан-

B 62, 11872 (2000).

ский, В. И. Чичковe, В. В. Больгиновa, В. В. Рязано-

27.

Ya. V. Fominov, N. M. Chtchelkatchev, and

вa, Письма в ЖЭТФ 116, 108 (2022).

A. A. Golubov, Phys. Rev. B 66, 014507 (2002).

11.

S. Heinze, K. Bergmann, M. Menzel, J. Brede,

28.

М. В. Авдеев, Ю. Н. Прошин, ЖЭТФ 144, 1251

A. Kubetzka, R. Wiesendanger, G. Bihlmayer, and

(2013).

S. Blügel, Nature Phys. 7, 713 (2011).

29.

М. В. Авдеев, Ю. Н. Прошин, ЖЭТФ 102, 106 (2015).

12.

N. Romming, C. Hanneken, M. Menzel, J. E. Bickel,

30.

О. Н. Борисова, В. А. Туманов, Ю. Н. Прошин,

B. Wolter, K. von Bergmann, A. Kubetzka, and

Физика Металлов и Металловедение 121, 482 (2020).

R. Wiesendanger, Science 341, 636 (2013).

31.

I. A. Garifullin, D. A. Tikhonov, N.N. Garif’yanov,

13.

A.O. Leonov, T. L. Monchesky, N. Romming,

L. Lazar, Yu. V. Goryunov, S. Ya. Khlebnikov,

A. Kubetzka, A. N. Bogdanov, and R. Wiesendanger,

L. R. Tagirov, K. Westerholt, and H. Zabel, Phys. Rev.

New J. Phys. 18, 065003 (2016).

B 66, 020505-R (2002).

14.

И. Ф. Шарафуллин, Х. Т. Дьеп, Письма в ЖЭТФ

32.

A. Hubert and R. Schäfer, Magnetic domains:

114, 610 (2021).

the analysis of magnetic microstructures, Springer,

15.

N.G. Pugach, M. Safonchik, T. Champel,

Heidelberg (2008).

M. E. Zhitomirsky, E. Lähderanta, M. Eschrig,

33.

F. N. Rybakov, A. B. Borisov, S. Blügel, and

and C. Lacroix, Appl. Phys. Lett. 111, 162601 (2017).

N. S. Kiselev, New J. Phys. 18, 045002 (2016).

16.

N.G. Pugach, M. O. Safonchik, V. I. Belotelov,

34.

A. P. Petrović, M. Raju, X.Y. Tee, A. Louat, I. Maggio-

T. Ziman, and T. Champel, arXiv 2110.00369 (2021).

Aprile, R.M. Menezes, M. J. Wyszynski, N. K. Duong,

17.

V.L. Vadimov, M. V. Sapozhnikov, and A.S. Mel’nikov,

M. Reznikov, C. Renner, and M. V. Milosević, Phys.

Appl. Phys. Lett. 113, 032402 (2018).

Rev. Lett. 126, 117205 (2021).

18.

J. Baumard, J. Cayssol, F. S. Bergeret, and A. Buzdin,

35.

R. M. Menezes, J. F. Neto, C. C. de Souza Silva, and

Phys. Rev. B 99, 014511 (2019).

M. V. Milošević, Phys. Rev. B 100, 014431 (2019).

19.

E. S. Andriyakhina and I. S. Burmistrov, Phys. Rev. B

36.

J. Iwasaki, M. Mochizuki, and N. Nagaosa, Nat.

103, 174519 (2021).

Commun. 4, 1463 (2013).

20.

D. S. Rabinovich, I. V. Bobkova, and A.M. Bobkov,

37.

S. L. Zhang, W. W. Wang, D. M. Burn, H. Peng,

Phys. Rev. B 98, 184511 (2018).

H. Berger, A. Bauer, C. Pfleiderer, G. van Der Laan,

21.

M. Houzet and A. I. Buzdin, Phys. Rev. B 74, 214507

and T. Hesjedal, Nat. Commun. 9, 2115 (2018).

(2006).

38.

K. W. Moon, D. H. Kim, S. G. Je, B. S. Chun, W. Kim,

22.

В. А. Туманов, Ю. В. Горюнов, Ю. Н. Прошин, Пись-

Z. Q. Qiu, S. B. Choe, and C. Hwang, Sci. Rep. 6, 20360

ма в ЖЭТФ 107, 449 (2018).

(2016).

23.

V.A. Tumanov and Y.N. Proshin, J. Low Temp. Phys.

39.

S. Oh, D. Youm, and M. Beasley, Appl. Phys. Lett. 71,

185, 460 (2016).

2376 (1997).

24.

Ya. V. Fominov, A. F. Volkov, and K. B. Efetov, Phys.

40.

L. R. Tagirov, Phys. Rev. Lett. 83, 2058 (1999).

Rev. B 75, 104509 (2007).

41.

A. I. Buzdin, A. V. Vedyayev, and N. V. Ryzhanova,

25.

М. Куприянов, В. Лукичев, ЖЭТФ 94, 139 (1988).

Europhys. Lett. 48, 686 (1999).

Письма в ЖЭТФ том 116 вып. 7 - 8

2022