Письма в ЖЭТФ, том 117, вып. 6, с. 443 - 449

Измерение теплопроводности углеродных наностенок методом

третьей гармоники

Д.А.Чернодубов^a, Ю.В.Бондарева^b, М.В.Шибалов^c, А.М.Мумляков^c, В.Л.Жданов^d, М.А.Тархов^c,

К.И.Маслаков^e, Н.В.Суетин^f, Д.Г.Квашнин^g,h1), С.А.Евлашин^b

^aНациональный исследовательский центр “Курчатовский институт”, 123182 Москва, Россия

^bСколковский институт науки и технологий, 143025 Москва, Россия

^cИнститут нанотехнологий и микроэлектроники РАН, 119991 Москва, Россия

^dНациональный исследовательский университет “Высшая школа экономики”, 101000 Москва, Россия

^eМосковский государственный университет им. М. В. Ломоносова, 119991 Москва, Россия

^fНаучно-исследовательский институт ядерной физики им. Д. В. Скобельцына, 119991 Москва, Россия

^gИнститут биохимической физики им. Н. М.Эмануэля РАН, 119334 Москва, Россия

^hРоссийский национальный исследовательский медицинский университет им. Н. И. Пирогова, 117997 Москва, Россия

Поступила в редакцию 29 ноября 2022 г.

После переработки 8 февраля 2023 г.

Принята к публикации 8 февраля 2023 г.

Методом химического осаждения из газовой фазы в разряде постоянного тока были получены пленки

углеродных наностенок разной толщины. Впервые проведено измерение теплопроводности полученных

структур с использованием метода третьей гармоники (3-омега) в диапазоне температур от 280 до 310 К.

Показана зависимость теплопроводности стенок от их толщины. При толщине пленки 1 мкм значение

теплопроводности углеродных наностенок составляет 6.9 Вт м^-1 К^-1. Полученные результаты необходи-

мы для конструирования электрооптических приборов на основе углеродных наностенок.

DOI: 10.31857/S1234567823060083, EDN: qswcql

1. Введение. Тенденция к миниатюризации со-

лопроводности позволяют использовать углеродные

временных электронных устройств ставит актуаль-

структуры в качестве эффективных теплоотводящих

ную задачу увеличения эффективности процессов

материалов, способствующих улучшению характери-

теплоотвода, так как увеличение плотности тепло-

стик электронных устройств.

вой мощности при недостаточном теплоотводе мо-

Для достижения высоких значений теплопровод-

жет привести к ухудшению характеристик приборов,

ности углеродных материалов требуется обеспече-

снижению их работоспособности и даже выходу из

ние высокой чистоты и бездефектности выращива-

строя [1].

емых структур [3, 7-12]. Например, для аморфно-

Материалы на основе углерода обладают рекорд-

го углерода теплопроводность при комнатной тем-

ными значениями теплопроводности. Так, теплопро-

пературе может быть на три порядка меньше, около

водность алмаза при комнатной температуре до-

1 Вт м^-1 К^-1 [3].

стигает 2400 Вт м^-1 К^-1 [2], равно как и величина

Перспективным классом структур для использо-

теплопроводности низкоразмерных углеродных на-

вания в современной электронике являются углерод-

ноструктур, таких как графен и углеродные на-

ные наностенки (Carbon NanoWalls, УНС) [13-21],

нотрубки, превышает несколько тысяч Вт м^-1 К^-1

которые представляют собой углеродные структу-

[2, 3]. Стоит отметить, что последние теоретические

ры из преимущественно вертикально ориентирован-

исследования отмечают зависимость теплопроводно-

ных графитоподобных двумерных листов, напомина-

сти между слоями графена от наличия дефектов

ющих стенки. Толщина получаемых стенок варьиру-

и деформации [4-6]. Такие высокие значения теп-

ется от 1 до 10 нм [17-19]. Благодаря высокой удель-

ной площади поверхности [11] УНС используются в

¹⁾e-mail: dgkvashnin@phystech.edu

качестве светопоглотителей [20], элементов мемри-

Письма в ЖЭТФ том 117 вып. 5 - 6

2023

443

444

Д.А.Чернодубов, Ю.В.Бондарева, М.В.Шибалов и др.

сторов [15], в топливных ячейках [21], конденсаторах

ке при помощи метода химического осаждения из

и суперконденсаторах [16], электродах литий-ионных

газовой фазы в разряде постоянного тока (Direct

и солнечных батарей [22,23] и др. Эксперименталь-

Current Plasma Enhanced Chemical Vapor Deposition,

ные исследования показывают, что применение УНС

DC PECVD) [28]. Для синтеза структур использо-

и нановолокон увеличивает теплоотвод от чипа на

валась смесь газов CH₄ и H₂. Продолжительность

∼ 10 % и тем самым уменьшает температуру в “го-

роста составила 20 и 60 мин, что соответствует высо-

рячих точках” в ходе работы устройств, в том числе

те стенок 400 и 1000 нм. На рисунке 1а представле-

при высоких рабочих мощностях тока [24]. Однако

ны изображения синтезированных пленок УНС тол-

тепловые характеристики таких структур плохо изу-

щиной 400 нм, полученные с помощью сканирующей

чены.

электронной микроскопии (СЭМ). Для исключения

Измерение теплопроводности важно для модели-

шунтирования нагревателя при измерении теплопро-

рования процессов теплопереноса в УНС. Однако

водности после получения пленок, на их поверхность

процесс измерения теплопроводности в таких мате-

был нанесен слой оксида гафния толщиной 40 нм с

риалах является непростой задачей, в силу сложной

использованием атомно-слоевого осаждения (Atomic

морфологии и небольшой толщины УНС. В рабо-

Layer Deposition, ALD). Пленка оксида гафния оса-

те [25] при помощи метода лазерного импульса при

ждалась повторением реакционных серий, включа-

комнатной температуре была измерена теплопровод-

ющих в себя подачу металлоорганического прекур-

ность УНС, выращенных при помощи радиочастот-

сора TDMAH (tetrakis(dimethylamino)hafnium(IV)) и

ной плазмы с расширяющимся лучом на подложке из

паров H₂O в качестве неметаллического реактан-

плавленого кварца с буферным слоем нитрида алю-

та. Более подробно процесс осаждения диэлектриков

миния. Полученные значения теплопроводности со-

описан в работах [16, 29]. Следующим этапом была

ставили 5, 7, 12 и 18 Вт м^-1 К^-1 при толщинах 700,

нанесена пленка золота толщиной 100 нм в качестве

1000, 2200 и 4300 нм соответственно. В силу того, что

нагревателя-измерителя для проведения измерений

УНС являются пористыми, необходимо пересчиты-

теплопроводности при помощи метода 3-омега с ис-

вать эффективную теплопроводность k_CNW с учетом

пользованием установки магнетронного распыления

плотности структур. Соотношение истинной и кажу-

(рис. 1b). Детали процесса нанесения золотой плен-

щейся плотностей по результатам измерений соста-

ки на УНС подробно описаны в предыдущей работе

вило 0.22 и, таким образом, величины эффективной

[30]. На поверхность золота был нанесен фотополи-

теплопроводности были определены как 20, 32, 55 и

мер S1805 для создания структур нужной формы.

80 Вт м^-1 К^-1 соответственно толщинам пленок.

После было проведено экспонирование с исполь-

Ранее нами было исследовано изменение тепло-

зованием контактного шаблона и последующее трав-

проводности для пленок УНС на плавленом кварце

ление в 1М растворе КОН. Схема наносимых сло-

в диапазоне температур от 4.7 до 96 K. Полученные

ев показана на рис.1c. После создания шаблонов с

величины теплопроводности и их температурные за-

ширинами 2b = 5, 10, 20, 40 и 50 мкм и длиной

висимости подобны таковым для фуллеритов [26] и

около 2 мм было проведено травление в установке

фуллеренов [27]. При температурах около 90 К тепло-

с индуктивно-связанной плазмой (ICP-RIE) в сре-

проводность пленок УНС близка к теплопроводности

де Ar (30 см³/мин). Температура столика составляла

ультра-нано-кристаллических алмазных пленок [3], и

15^◦C, давление в камере 2.5 мТорр, мощность источ-

составляет 10 Вт м^-1 К^-1.

ников ICP и RF 900 Вт и 125 Вт соответственно. Вре-

Данная работа посвящена исследованию процес-

мя травления - 5 мин [16]. После создания структур

сов теплопереноса и измерению поведения теплопро-

фоторезистивный слой был удален с использовани-

водности УНС на кремниевой подложке в диапа-

ем растворителя. Схематическое изображение струк-

зоне комнатных температур, что крайне важно для

туры с нанесенными нагревателями-измерителями

практической реализации электронных устройств на

приведено на рис. 1d. На рисунке 1e показан боковой

их основе. Для измерения теплопроводности УНС

срез структур, а на рис. 1f показано соответствую-

впервые был использован метод третьей гармони-

щее распределение элементного состава внутри об-

ки (3-омега). Получены температурные зависимости

разца, измеренное при помощи энергодисперсионно-

теплопроводности для пленок УНС толщиной 400 и

го анализа.

1000 нм.

2.2. Характеризация морфологии и химическо-

2. Методы исследования.

го состава пленок УНС. Исследования полученных

2.1. Условия роста пленок. Исследуемые плен-

пленок были проведены с использованием сканирую-

ки УНС были выращены на кремниевой подлож-

щего электронного микроскопа SEM+ FIB Helios G4

Письма в ЖЭТФ том 117 вып. 5 - 6

2023

446

Д.А.Чернодубов, Ю.В.Бондарева, М.В.Шибалов и др.

та (Thermo Scientific DXR Raman Microscope) и рент-

баний от частоты приведено в работе [32]. Из изме-

геновской фотоэлектронной спектроскопии (РФЭС)

ренной амплитуды температурных колебаний опре-

Axis Ultra DLD (Kratos Analytical, UK) [28].

делялись тепловые сопротивления нагревателей как

2.3. Измерения теплопроводности пленок УНС.

R = ΔT/P, где P - тепловая мощность, подавае-

Измерения теплопроводности выполнены методом

мая на нагреватель. Эффективная теплопроводность

3-омега [31]. Его суть заключается в определении

k_eff тонких пленок в направлении, перпендикулярном

зависимости действительной части амплитуды тем-

слою структур, определялась как [33, 34]:

пературных колебаний нагревателя, нанесенного на

-^1b

поверхность образца, от частоты переменного тока,

k_eff =

(

)∕

(1)

проходящего через этот нагреватель. В качестве

2πlk_s

2l R₁ - R₂) - lnb2b1

нагревателей-термометров использовались пленки

золота толщиной 100 нм с ширинами 2b = 5, 10,

где t - толщина пленки, b_i - полуширины нагревате-

20, 40 и 50 мкм и длиной l = 2мм. Зависимость

лей, k_s - теплопроводность подложки, которая опре-

действительной части амплитуды температурных

делялась в этом же эксперименте по наклону зави-

колебаний от частоты тока, протекающего через

симости R_i (i = 1, 2 для нагревателей шириной 5 и

нагреватель-измеритель, позволяет определить

10 мкм соответственно) от натурального логарифма

как теплопроводность объемной подложки по ее

частоты тока через нагреватели. Поскольку в рам-

наклону, так и теплопроводность тонких слоев,

ках модели измерения теплопроводности методом 3-

поскольку их наличие изменяет характер теп-

омега тонкая пленка вносит постоянный вклад в ве-

лопереноса в структуре, увеличивая ее тепловое

личину амплитуды температурных колебаний, для

сопротивление. В случае, если толщина измеряе-

определения теплопроводности тонкой пленки нуж-

мой пленки много меньше ширины нагревателя,

но провести как минимум два измерения, варьируя

можно считать, что тепловой поток не успевает

один из геометрических параметров системы - про-

ушириться на пленке и проходит через нее прямым

ще всего это сделать, используя нагреватели разных

фронтом, увеличивая амплитуду температурных

ширин.

колебаний. Таким образом, задача измерения вели-

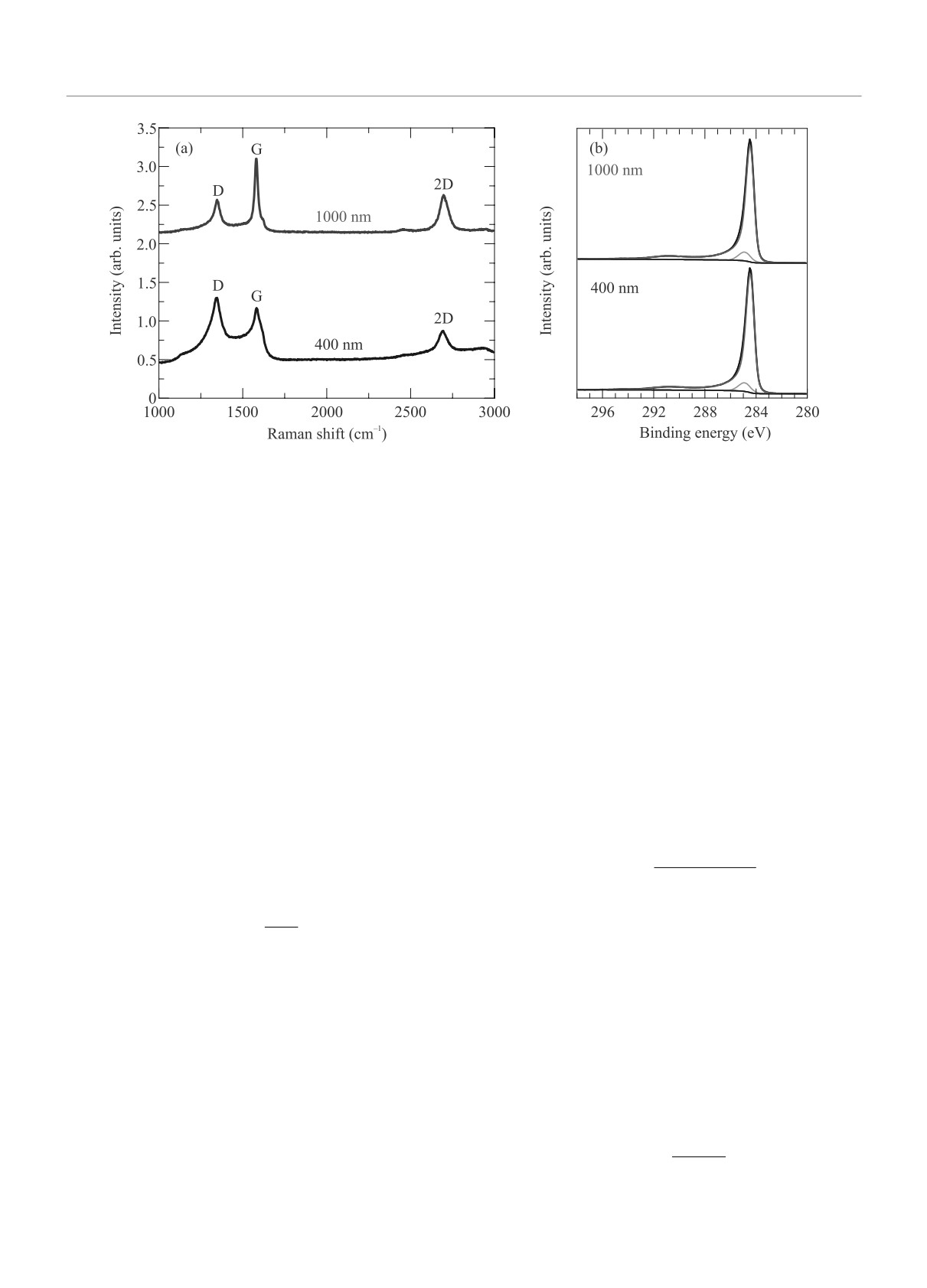
3. Результаты и обсуждения. На рисунке 2а

чины теплопроводности тонкой пленки может быть

приведены спектры КР для пленок УНС толщиной

решена при проведении измерений при помощи двух

400 нм (черная кривая, снизу) и 1000 нм (синяя кри-

нагревателей-термометров разной ширины.

вая, сверху). Для оценки размера нанокристалличе-

ских доменов L_a использовалась эмпирическая фор-

Достоинством методики 3-омега является воз-

мула из работы [35]:

можность прямого измерения теплопроводности

пленок малой толщины (от сотен нанометров)

)_-1

(I_D

в широком диапазоне температур. Классические

L_a = (2.4 × 10^-10)λ⁴

(2)

методики измерения теплопроводности, такие как

метод продольного теплового потока, не позво-

где λ_l - длина волны КР,I_D и I_G - интегральные

ляют проводить измерения тонких пленок из-за

интенсивности мод КР. На основе полученных спек-

конечного размера термопар или термометров

тров были определены интегральные соотношения

сопротивления, при помощи которых производит-

пиков I_D/I_G, которые составили 0.9 и 1.8 для образ-

ся измерение градиента температур на образце.

цов толщиной 400 и 1000 нм соответственно. Разме-

Существуют другие современные методики из-

ры кристаллических доменов составили 10 и 17 нм.

мерения теплопроводности тонких пленок, такие

Полученные различия в размерах доменов свиде-

как частотный или временной терморефлектанс

тельствуют о разном количестве дефектов на еди-

(frequency-domain thermoreflectance (FDTR), time-

ницу поверхности структур. Наличие дефектов мо-

domain thermoreflectance (TDTR)), но по сравнению

жет приводить к адсорбции функциональных групп.

с методом 3-омега они более сложны в реализации и

Для определения наличия и количества функцио-

проигрывают в точности измерений.

нальных групп на поверхности образцов использо-

Амплитуда температурных колебаний нагрева-

вали РФЭС. Полученные образцы, помимо углеро-

теля ΔT измерялась в диапазоне частот от 1 до

да (∼ 99.86 ат. %), содержали очень низкую концен-

33000 Гц при токе амплитудой 15 мА. Измерения про-

трацию кислорода (0.14 ат. %), которая является по-

водились в вакуумированной ячейке, охлаждаемой

рогом чувствительности метода. Образцы, получен-

парами азота. Подробное описание аппаратуры и ме-

ные при разных временах синтеза, имели идентич-

тодики измерений амплитуды температурных коле-

ные C1s спектры (рис. 2b). Основной вклад в РФЭС-

Письма в ЖЭТФ том 117 вып. 5 - 6

2023

Измерение теплопроводности углеродных наностенок методом третьей гармоники

447

Рис. 2. (Цветной онлайн) (a) - Спектры КРС и (b) - C1s РФЭС-спектры образцов толщиной 400 и 1000 нм

спектры дает ассиметричная компонента при энер-

1000 нм и 0.79 ± 0.11 Вт м^-1 К^-1 для образца толщи-

гии связи 284.5 эВ с характерными ароматически-

ной 400 нм.

ми сателлитами встряски, отвечающая sp²-углероду.

Следует отметить, что измеряемая методом

Доля sp²-углерода составляет 92.92 ат.%, также на-

3-омега амплитуда температурных колебаний опре-

блюдается компонента (около 6.88 ат. %) при энергии

деляется полным тепловым сопротивлением между

связи 284.9 эВ, которая соответствует sp³-углероду

нагревателем и подложкой. Помимо теплового

[28]. Полученные данные свидетельствуют о том, что

сопротивления тонкой углеродной пленки, в общее

в процессе синтеза не происходит изменение хими-

сопротивление вклады вносят также граничные

ческого состава УНС и количество функциональных

тепловые сопротивления между слоями структуры

групп на поверхности остается постоянным.

и сопротивления дополнительных слоев (изолиру-

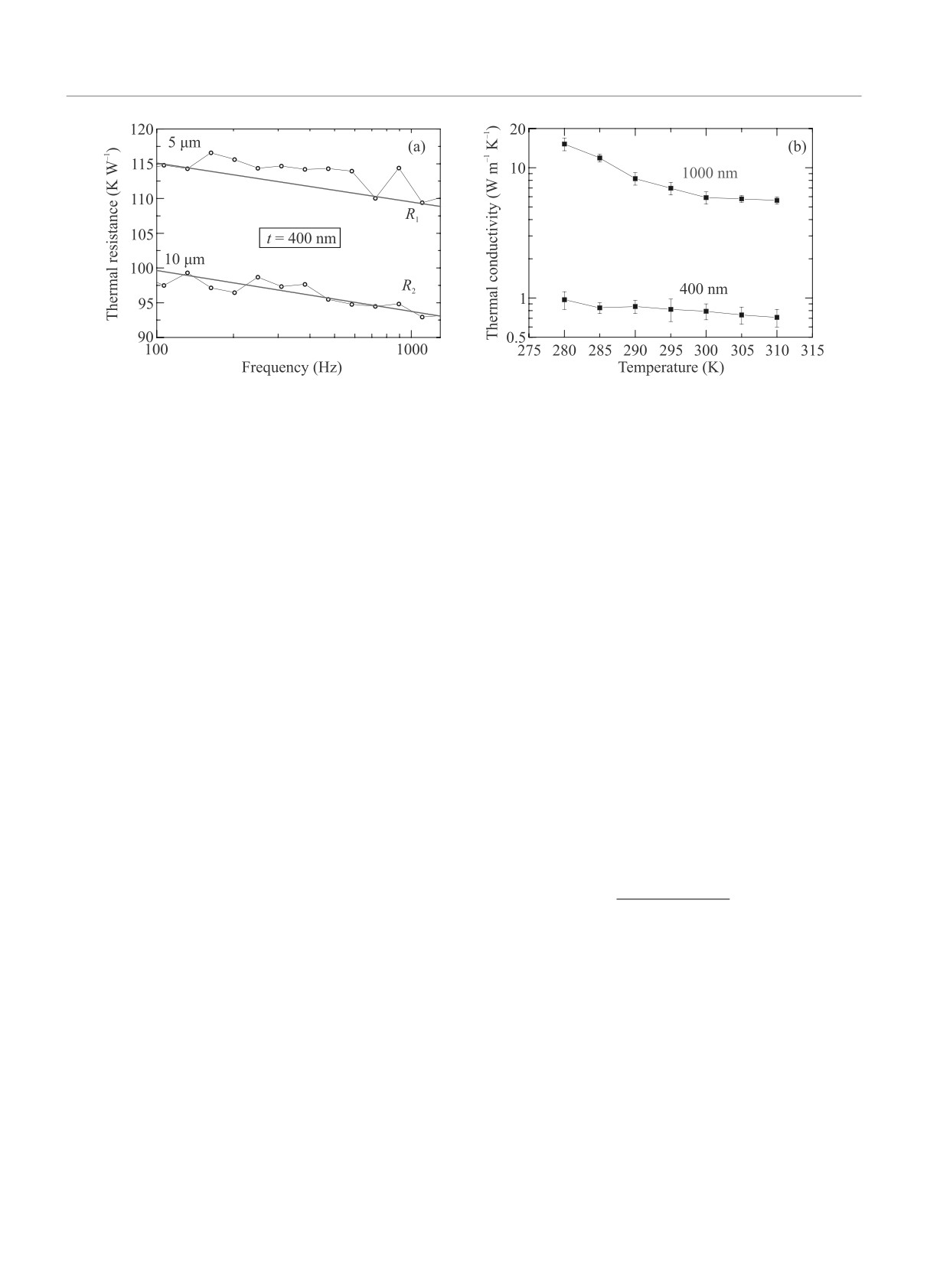
На рисунке 3а приведены частотные зависимости

ющий слой оксида гафния). Величину теплового

тепловых сопротивлений нагревателей шириной 5 и

сопротивления изолирующего слоя оксида гафния

10 мкм, нанесенных на пленку толщиной 400 нм. Из

толщиной 40 нм в нашем случае можно оценить

полученных зависимостей следует, что в диапазоне

как 25 м² К/ГВт [37]. Теплопроводность измеряемых

100-1300 Гц разность тепловых сопротивлений R₁ и

УНС c учетом вклада теплового сопротивления,

R₂ для двух нагревателей разной толщины постоян-

вносимого изолирующим слоем HfO₂, можно пере-

на, что позволяет определить величину теплопровод-

считать как [25]:

ности по наклону S зависимости амплитуды темпе-

κ_CNW

(4)

ратурных колебаний от частоты k_s как [36]

eff

R_meas - R_HfO

где R_meas = t/k_eff - измеренная величина полного

k_S = -

(3)

теплового сопротивления, а RHfO2 = 40 нм. Тогда ве-

2πlS

личины теплопроводности для двух пленок состав-

ляют 6.9 ± 0.7 Вт м^-1 К^-1 и 0.82 ± 0.12 Вт м^-1К^-1 со-

Величина k_s составила 120 ± 5 Вт м^-1 К^-1 при

ответственно. В случае пористого материала, каким

300 K. На рисунке 3 представлена температурная за-

является УНС, определенная величина эффективной

висимость теплопроводности k_eff двух пленок УНС

теплопроводности из-за наличия полостей отличает-

толщиной t = 400 и 1000 нм в диапазоне от 280 до

ся от величины теплопроводности непосредственно

310 К. Для измерений использовалась пара нагрева-

углеродной наноструктуры. Для учета вклада пори-

телей с ширинами 20 и 40 мкм для образца толщиной

стости в величину теплопроводности воспользуемся

1000 нм и ширинами 5 и 10 мкм для образца толщи-

приближением эффективной среды, в рамках кото-

ной 400 нм соответственно. При температуре 300 K

рой теплопроводность УНС определяется как [38]:

теплопроводность двух слоев отличается более чем

κ_CNW

eff

в 7 раз: 5.9 ± 0.6Втм^-1К^-1 для образца толщиной

κ_CNW =

(5)

Письма в ЖЭТФ том 117 вып. 5 - 6

2023

448

Д.А.Чернодубов, Ю.В.Бондарева, М.В.Шибалов и др.

Рис. 3. (Цветной онлайн) (a) - Зависимость теплового сопротивления R от частоты для пары нагревателей толщиной

5 и 10мкм на пленке толщиной 400нм при температуре 285К. (b) - Зависимость теплопроводности пленок толщиной

400 и 1000 нм от температуры

где Φ - доля твердой фазы УНС. В нашем слу-

перенос. Например, в графите теплопроводность в

чае она составила ∼ 0.3, тогда величины теплопро-

базисной плоскости и вдоль оси c отличаются на два

водности для двух пленок составляют 23 ± 2.4 и

порядка [40].

2.7 ± 0.4 Вт м^-1 К^-1 соответственно.

5. Выводы. В работе впервые измерена тепло-

проводность углеродных наностенок с использова-

Полученные результаты согласуются с резуль-

татами предыдущих работ. Так, в работе [25], где

нием метода 3-омега. Показано, что в случае плаз-

мохимического синтеза в разряде постоянного тока

измерения УНС проводились с использованием ла-

теплопроводность возрастает с увеличением толщи-

зерной методики, величина эффективной теплопро-

водности для слоя УНС толщиной 1000 нм соста-

ны структур, что связано с разным структурным со-

вершенством пленок, которое влияет на рассеяние

вила 7 Вт м^-1 К^-1. В нашем случае теплопровод-

ность структур такой же толщины составляет 6.9 ±

фононов на дефектах. При комнатной температу-

ре теплопроводность углеродных наностенок толщи-

±0.7 Вт м^-1 К^-1. Значение теплопроводности для бо-

лее тонких структур отличается: рассчитанная в [25]

ной 400 и 1000 нм составляет 0.82 ± 0.12 Вт м^-1 К^-1

и 6.9 ± 0.7 Вт м^-1 К^-1. Таким образом, теплопровод-

величина эффективной теплопроводности для слоя

толщиной 400 нм составляет около 2 Вт м^-1 К^-1, что

ность углеродных наностенок зависит от толщины

пленки. Соответственно, при использовании углерод-

примерно в 2 раза выше измеренного нами значе-

ния для подобных пленок. Такое отличие связано со

ных наностенок в качестве теплоотводов необходимы

более толстые структуры.

структурным совершенством УНС и их морфологи-

Получение и исследование дефектности углерод-

ей. Как показано выше, в нашем случае наблюдается

изменение размеров нанокристаллических доменов с

ных наностенок выполнено при поддержке гранта

Российского научного фонда # 22-73-10198.

10 до 17 нм для структур толщиной 400 и 1000 нм. Со-

отношение I_D/I_G в работе [33] составляет ∼ 1.2, что

соответствует размеру нанокристаллиических доме-

1. P. Lall, M. Pecht, and E. Hakim, Influence of Tempe-

нов ∼ 10 нм. Также имеются отличия в положении

rature on Microelectronics and System Reliability, CRC

мод 2D и G в соотношениях I_2D/I_G. Данное обсто-

Press, N.Y. (1997).

ятельство говорит о разном количестве графеновых

2. A. Inyushkin, A. Taldenkov, V. Ralchenko, A. Bolsha-

слоев в единичном листе УНС. Как показано в ра-

kov, A. Koliadin, and A. Katrusha, Phys. Rev. B 97,

боте [39], в случае углеродных наноструктур рассея-

144305 (2018).

ние фононов на границе в таких материалах не яв-

3. A. A. Balandin, Nature Mater 10, 569 (2011).

ляется полностью диффузным, что может заметно

4. А. И. Подливаев, К. С. Гришаков, К. П. Катин,

отразиться на зависимости теплопроводности от раз-

М. М. Маслов, Письма в ЖЭТФ 114, 172 (2021)

мера структуры. Помимо этого, структуры характе-

[JETP Lett. 114, 143 (2021)].

ризуются разной плотностью и ориентацией относи-

5. А. И. Подливаев, К. С. Гришаков, К. П. Катин,

тельно подложки. Ориентация и плотность структур

М. М. Маслов, Письма в ЖЭТФ 113, 182 (2021)

приводит к анизотропии свойств и влияет на тепло-

[JETP Lett. 113, 169 (2021)].

Письма в ЖЭТФ том 117 вып. 5 - 6

2023

Измерение теплопроводности углеродных наностенок методом третьей гармоники

449

А.И. Подливаев, Письма в ЖЭТФ 115, 384 (2022).

24.

Y. Zhang, L. Tan, H. Yin, G. Zhang, and J. Liu,

N.D. Orekhov, J. V. Bondareva, D. O. Potapov et al.

Experimental Measurements of Thermal Performances

(Collaboration), Carbon 191, 546 (2022).

of Carbon Nanomaterial with Vertical Structures

N. Orekhov and M. Logunov, Carbon 192, 179 (2022).

in Hotspot Heat Dissipation, in

2019

IEEE

19th

V.M. Egorov, A.K. Borisov, and V. A. Marikhin,

International Conference on Nanotechnology (IEEE-

Technical Physics Letters 48, 49 (2022).

NANO), Institute of Electrical and Electronics

10.

A.N. Enyashin, G. Seifert, and A. L. Ivanovskii, JETP

Engineers, Macao, China (2019), p. 370.

Lett. 80, 608 (2004).

25.

A. Achour, B. E. Belkerk, K. Ait Aissa, S. Vizireanu,

11.

H. Malekpour, P. Ramnani, S. Srinivasan,

E. Gautron, M. Carette, P.-Y. Jouan, G. Dinescu,

G. Balasubramanian, D. L. Nika, A. Mulchandani,

L. Le Brizoual, Y. Scudeller, and M.-A. Djouadi, Appl.

R.K. Lake, and A.A. Balandin, Nanoscale 8, 14608

Phys. Lett. 102, 061903 (2013).

(2016).

26.

A. Bilusic, S. Gradecak, A. Tonejc, A. Tonejc,

12.

T. Chen, Y. Huang, L. Wei, T. Xu, and Y. Xie, Carbon

J. Lasjaunias, and A. Smontara, Synth. Met. 121, 1121

203, 130 (2023).

(2001).

13.

Y. Wu, B. Yang, B. Zong, H. Sun, Z. Shen, and Y. Feng,

27.

J. Lasjaunias, M. Saint-Paul, A. Bilušić, A. Smontara,

J. Mater. Chem. 14, 469 (2004).

S. Gradečak, A. Tonejc, A. Tonejc, and N. Kitamura,

14.

M. Hiramatsu and M. Hori, Carbon Nanowalls:

Phys. Rev. B 66, 014302 (2002).

Synthesis and Emerging Applications, Springer Science

28.

S. A. Evlashin, F. S. Fedorov, P. V. Dyakonov et al.

& Business Media, Wien (2010).

(Collaboration), J. Phys. Chem. Lett. 11, 4859 (2020).

15.

S. Evlashin, M. Tarkhov, D. Chernodubov,

29.

A. M. Mumlyakov, M. V. Shibalov, I. V. Trofimov,

A. Inyushkin, A. Pilevsky, P. Dyakonov, A. Pavlov,

M. G. Verkholetov, A. P. Orlov, G. D. Diudbin,

N. Suetin, I. Akhatov, and V. Perebeinos, Phys. Rev.

S. A. Evlashin, P. A. Nekludova, Yu.V. Anufriev,

Appl. 15, 054057 (2021).

A. M. Tagachenkov, E. V. Zenova, and M. A. Tarkhov,

16.

A.M. Mumlyakov, M. V. Shibalov, E. R. Timofeeva,

J. Alloys Compd. 858, 157713 (2021).

I. V. Trofimov, N. V. Porokhov, S. A. Evlashin,

30.

P. Dyakonov, K. Mironovich, S. Svyakhovskiy,

P. A. Nekludova, E. A. Pershina, Yu. V. Anufriev,

O. Voloshina, S. Dagesyan, A. Panchishin, N. Suetin,

A.M. Tagachenkov, E. V. Zenova, and M. A. Tarkhov,

V. Bagratashvili, P. Timashev, E. Shirshin, and

Carbon 184, 698 (2021).

S. Evlashin, Sci. Rep. 7, 1 (2017).

17.

S. Evlashin, S. Svyakhovskiy, N. Suetin, A. Pilevsky,

31.

D. G. Cahill, Rev. Sci. Instrum. 61, 802 (1990).

T. Murzina, N. Novikova, A. Stepanov, A. Egorov, and

A. Rakhimov, Optical and IR Absorption of Multilayer

32.

D. A. Chernodoubov and A. V. Inyushkin, Rev. Sci.

Carbon Nanowalls, Carbon 70, 111 (2014).

Instrum. 90(2), 024904 (2019).

18.

H.J. Cho, H. Kondo, K. Ishikawa, M. Sekine,

33.

J. Alvarez-Quintana and J. Rodriguez-Viejo, Sensors

M. Hiramatsu, and M. Hori, Carbon 68, 380 (2014).

and Actuators A: Physical 142, 232 (2008).

19.

K. Kobayashi, M. Tanimura, H. Nakai, A. Yoshimura,

34.

D. A. Chernodubov, I. O. Maiboroda, M. L. Zanaveskin,

H. Yoshimura, K. Kojima, and M. Tachibana, J. Appl.

and A. V. Inyushkin, Phys. Solid State 62, 722 (2020).

Phys. 101, 094306 (2007).

35.

L. G. Cancado, K. Takai, T. Enoki, M. Endo, Y. A. Kim,

20.

V.A. Krivchenko, S. A. Evlashin, K. V. Miro-

H. Mizusaki, A. Jorio, L. N. Coelho, R. Magalhães-

novich, N. I. Verbitskiy, A. Nefedov, C. Wöll,

Paniago, and M. A. Pimenta, Appl. Phys. Lett. 88,

A.Ya. Kozmenkova, N.V. Suetin, S. E. Svyakhovskiy,

163106 (2006).

D. V. Vyalikh, A. T. Rakhimov, A. V. Egorov, and

36.

C. Dames, Annual Review of Heat Transfer 16, 7 (2013).

L. V. Yashina, Sci. Rep. 3, 1 (2013).

37.

M. A. Panzer, M. Shandalov, J. A. Rowlette, Y. Oshima,

21.

M. Hiramatsu, S. Mitsuguchi, T. Horibe, H. Kondo,

Y. W. Chen, P. C. McIntyre, and K. E. Goodson, IEEE

M. Hori, and H. Kano, Jpn. J. Appl. Phys. 52, 01AK03

Electron Device Letters 30, 1269 (2009).

(2013).

38.

M. T. Barako, A. Sood, C. Zhang, J. Wang, T. Kodama,

22.

W. Wei and Y.H. Hu, J. Mater. Chem. A 5, 24126

M. Asheghi, X. Zheng, P. V. Braun, and K. E. Goodson,

(2017).

Nano Lett. 16, 2754 (2016).

23.

V.A. Krivchenko, D.M. Itkis, S. A. Evlashin,

D. A. Semenenko, E. A. Goodilin, A.T. Rakhimov,

39.

D. L. Nika, A.S. Askerov, and A. A. Balandin, Nano

A.S. Stepanov, N. V. Suetin, A. A. Pilevsky, and

Lett. 12, 3238 (2012).

P. V. Voronin, Carbon 50, 1438 (2012).

40.

G. A. Slack, Phys. Rev. 127, 694 (1962).

Письма в ЖЭТФ том 117 вып. 5 - 6

2023