Письма в ЖЭТФ, том 118, вып. 3, с. 154 - 158

Поиск солнечных аксионов с энергией 8.4 кэВ, излучаемых

в М1-переходе ядер¹⁶⁹Tm

А. В. Дербин¹⁾, И. С. Драчнев, В. Н. Муратова, Д. А. Семенов, М. В. Трушин, Е. В. Унжаков

Петербургский институт ядерной физики им. Б. П. Константинова

Национальный исследовательский центр “Курчатовский институт”, 188300 Гатчина, Россия

Поступила в редакцию 28 июня 2023 г.

После переработки 29 июня 2023 г.

Принята к публикации 29 июня 2023 г.

Проведен поиск аксионов с энергией 8.4 кэВ, излучаемых в М1-переходе ядер¹⁶⁹Tm на Солн-

це, с помощью реакции резонансного поглощения ядрами¹⁶⁹Tm на Земле: A +¹⁶⁹Tm →¹⁶⁹Tm^∗ →

→¹⁶⁹Tm+(γ, e) (8.4 кэВ). В качестве детектора использовался кристалл тулиевого граната Tm3Al5O12,

который работал как болометрический детектор. Вычислен поток монохроматических 8.4 кэВ аксионов

и получены новые ограничения на константы связи аксиона с нуклонами и массу аксиона в KSVZ- и

DFSZ-моделях, которые составляют m^KSVZA ≤ 141 эВ и m^DFSZA ≤ 244 эВ (90 % у.д.) соответственно.

DOI: 10.31857/S1234567823150028, EDN: hweece

1. Введение. Вероятность рождения и регистра-

ленном виде соотношение m_A и f_A выглядит следу-

ции аксионов, гипотетических нейтральных псевдо-

ющим образом [17, 18]:

скалярных частиц, введенных в теорию для объяс-

нения отсутствия СР-нарушения в сильных взаимо-

(10⁶ ГэВ)эВ.

m_A = 5.69(5)

(1)

действиях [1-3] и являющихся хорошо мотивирован-

f_A

ными кандидатами на роль частиц темной материи,

Ограничения на массу аксиона возникают как

определяется эффективными константами связи ак-

следствие экспериментальных ограничений на кон-

сионов с фотонами g_Aγ , электронами g_Ae и нукло-

станты связи g_Aγ , g_Ae и g_AN , которые, в свою оче-

нами g_AN . Основными реакциями, предлагаемыми

редь, являются модельно зависимыми величинами.

для детектирования, являются конверсия аксионов

Монохроматические аксионы должны испус-

в фотоны в магнитном поле или в поле ядра, распад

каться в переходах магнитного типа в ядрах⁵⁷Fe

аксиона на два фотона, комптоновская конверсия и

(14.4 кэВ) и 83Kr (9.4 кэВ), низколежащие уровни

аксиоэлектрический эффект.

которых возбуждаются за счет высокой (1.3 кэВ)

В данной работе рассматривается только один

температуры в центре Солнца. Целью данной ра-

процесс - излучение и поглощение аксионов в ядер-

боты является поиск монохроматических аксионов

ном магнитном переходе, при этом излучение акси-

с энергией 8.4 кэВ, излучаемых в М1-переходе в

онов происходит на Солнце, а поглощение на Земле.

ядрах

¹⁶⁹Tm, с помощью реакции резонансного

Чувствительность эксперимента определяется толь-

поглощения, приводящей к возбуждению первого

ко константами связи аксиона с нуклонами. Экспери-

ядерного уровня 169Tm. Гамма- и рентгеновские

менты подобного рода были проведены ранее с ядра-

кванты и конверсионные и Ожэ электроны, возни-

ми⁵⁷Fe [4-6],⁷Li [7-9] и⁸³Kr [10-12].

После того как первоначальная модель “стандарт-

кающие при разрядке возбужденного уровня, могут

ного” PQWW-аксиона [1-3] была надежно закрыта

быть зарегистрированы. Вероятность испускания и

серией экспериментов, появились два класса моделей

последующего поглощения аксионов зависит только

“невидимого” аксиона - это модели KSVZ-аксиона

от константы связи с нуклонами и пропорциональна

(адронный аксион) [13, 14] и DFSZ-аксиона [15, 16].

g^4AN. Поиск аксионов с энергией 8.4 кэВ проводится

Масса аксиона m_A и его константа распада f_A в

впервые.

обоих моделях связаны с такими же характеристи-

Использовать изотоп¹⁶⁹Tm для поиска солнеч-

ками π⁰-мезона: m_AfA ≈ mπfπ(z1/2/(1 + z)), где

ных аксионов с непрерывным спектром, обусловлен-

z = m_u/m_d - отношение масс легких кварков. В чис-

ным константами g_Aγ (аксионы Примакова) и g_Ae

(тормозные и комптоновские процессы), было пред-

¹⁾e-mail: Derbin_AV@pnpi.nrcki.ru

ложено и реализовано в работах [19, 20].

154

Письма в ЖЭТФ том 118 вып. 3 - 4

2023

Поиск солнечных аксионов с энергией 8.4 кэВ, излучаемых в М1-переходе ядер¹⁶⁹Tm

155

Наиболее известны эксперименты по поиску сол-

ла. Более того, для протонного перехода отношение

нечных аксионов, возникающих в результате кон-

ω_A/ω_γ не обращается в нуль, как это может быть в

версии тепловых фотонов в поле солнечной плазмы.

случае нейтронных переходов.

Основываясь на взаимодействии аксиона с фотоном

Мы вычислили поток аксионов для стандартной

g_Aγ, аксионы пытаются обнаружить с помощью об-

солнечной модели BS05 [27] с высокой металлично-

ратной конверсии в лабораторном магнитном поле

стью [28] как сумму вкладов от отдельных сфериче-

[21, 22] или в поле кристалла [23, 24]. Ожидаемая

ских слоев толщиной dr, в которых использовались

скорость счета фотонов в данных экспериментах про-

конкретные значения температуры T и концентра-

порциональна g^4Aγ .

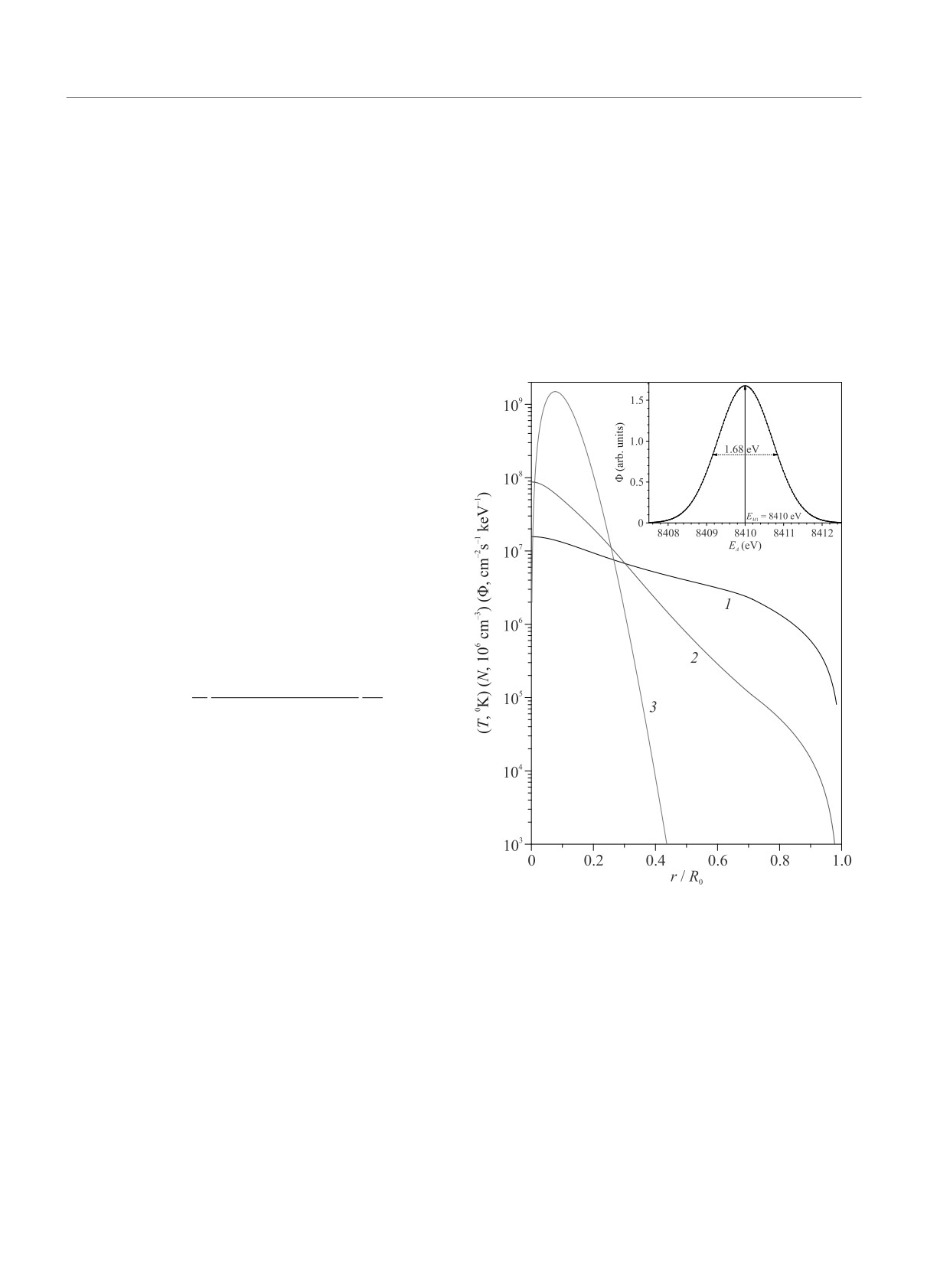
ции тулия N(r). На рисунке 1 показана зависимость

Подробные обзоры теоретических и эксперимен-

интегрального потока аксионов из слоя r²dr от ра-

тальных работ по аксионной тематике представлены

диуса r. Можно видеть, что 90 % потока аксионов

в [18].

излучается внутри r ≤ 0.2R_⊙.

2. Поток аксионов с энергией 8.4 кэВ от

Солнца. Первый уровень ядра¹⁶⁹Tm имеет энер-

гию E_γ = 8.410 кэВ, спин и четность J^π = 3/2⁺, при-

месь E2-перехода составляет 0.11 % (δ = 0.033) [25].

Для экспериментов проводимых по схеме мишень-

детектор, когда конверсионные и Ожэ-электроны по-

глощаются мишенью, важным является коэффици-

ент электронной конверсии. Для изучаемого перехо-

да он составляет e/γ = 264 (η = 3.79 × 10^-3) [25].

Поток аксионов от Солнца зависит от энергии

E_γ и времени жизни уровня τ_γ, от распространенно-

сти изотопа¹⁶⁹Tm на Солнце (N(r)), распределения

температуры внутри Солнца (T(r)), а также от от-

ношения вероятности испускания аксиона и фотона

ω_A/ω_γ [4, 26]:

2 exp(-E_γ/kT) ω_A

Φ_A(r) =

(2)

τ_γ (1 + 2 exp(-E_γ/kT)) ω_γ

Вследствие эффекта Доплера, вызванного теп-

ловым движением ядер в Солнце, спектр аксионов

представляет собой гауссово распределение с дис-

персией σ(T ) = E_γ (kT (r)/M)^1/2, где M - масса яд-

ра¹⁶⁹Tm. Полный спектр аксионов является суммой

гауссианов с дисперсиями σ(T ), определяемыми тем-

пературой в точке испускания аксиона на Солнце.

Наиболее интенсивный поток монохроматических

аксионов от Солнца связан с М1-переходом с перво-

Рис. 1. Распределение температуры (T,^◦K, кривая 1) и

го возбужденного уровня на основное состояние яд-

концентрации атомов¹⁶⁹Tm (N, в единицах 10⁶ см^-3,

ра⁵⁷Fe. Это обусловлено, в первую очередь, высо-

кривая 2) в зависимости от радиуса r. Поток акси-

кой распространенностью железа на Солнце. Тулий

онов из слоя r²dr для значения ωA/ωγ = 4 × 10-14

имеет на 7 порядков меньшую концентрацию, одна-

и dr = 5 × 10^-3R⊙ (Φ, см^-2 c^-1 кэВ^-1, кривая 3). На

ко такие факторы как более низкая энергия перехода

вставке показан энергетический спектр солнечных ак-

E_γ, меньшая величина доплеровского уширения σ(T)

сионов со средней энергией 8.41 кэВ

и 100 % распространенность изотопа¹⁶⁹Tm ведут к

увеличению ожидаемой скорости счета аксионов.

Дифференциальный спектр представляет собой

Принципиальное отличие М1-перехода в ядре

сумму отдельных гауссианов. Каждый вклад ха-

¹⁶⁹Tm от аналогичных переходов в ядрах⁵⁷Fe и⁸³Kr

рактеризовался величиной доплеровского уширения

состоит в том, что это, в основном, протонный пере-

σ(T ). Суммарный энергетический спектр аксионов

ход. Это особенно важно для поиска KSVZ-аксионов,

показан на вставке рис. 1, он хорошо описывается

у которых константа связи аксиона с нейтроном ма-

гауссовой функцией с дисперсией σ = 0.78 кэВ. Диф-

Письма в ЖЭТФ том 118 вып. 3 - 4

2023

156

А. В. Дербин, И. С. Драчнев, В. Н. Муратова и др.

ференциальный поток в максимуме распределения

аксионов σ(E_A) с энергией E_A дается выражением,

при E = 8.41 кэВ оказывается равным:

аналогичным выражению для сечения резонансно-

го поглощения γ-квантов с поправкой на отношение

Φ(E) = 3.73 × 10²²(ω_A/ω_γ) см^-2 с^-1 кэВ^-1.

(3)

ω_A/ω_γ:

Ширина полученного распределения существенно

[

√

4(E_A - E_M1)²

](ω_A)

превышает энергию ядра отдачи (2.2 × 10^-7 эВ), соб-

σ(E_A) = 2

πσ_0γ exp -

(6)

Γ²

ω_γ

ственную ширину ядерного уровня (Γ

= 1.12 ×

10^-7 эВ) и доплеровскую ширину уровня ядер¹⁶⁹Tm

где σ_0γ = 2.61×10^-19 см² - максимальное сечение ре-

мишени (3.3 × 10^-3 эВ), даже находящуюся при тем-

зонансного поглощения гамма-квантов ядром¹⁶⁹Tm.

пературе T = 300 К.

Полное сечение поглощения аксионов может быть

Отношение вероятностей аксионного и электро-

получено путем интегрирования выражения (6) для

магнитного переходов (ω_A/ω_γ ) было вычислено в ра-

σ(E_A) по спектру солнечных аксионов. Интегрирова-

ботах [29, 30]:

ние узкого распределения (6) по широкому спектру

[

]₂ (

)₃

аксионов дает значение, близкое Φ(E_M1) в выраже-

ω_A

g^0ANβ^∗ + g^3AN

p_A

нии (3). Ожидаемая скорость резонансного поглоще-

ω_γ

2πα(1 + δ²) (µ₀ - 0.5)β^∗ + µ₃ - η

p_γ

ния солнечных аксионов ядром¹⁶⁹Tm равна:

(4)

где p_γ и p_A - импульсы фотона и аксиона, δ - отно-

R_A = πσ_0γΓΦ_A(E_M1)(ω_A/ω_γ)²

(7)

шение вероятностей Е2 и М1 переходов, µ₀ ≈ 0.88 и

µ₃ ≈ 4.71 - изоскалярный и изовекторный ядерные

и может быть представлена в численном виде как:

магнитные моменты, β^∗ и η - параметры, которые

определяются конкретными ядерными матричными

R_A = 3.35 × 10^-6(ω_A/ω_γ)² c^-1.

(8)

элементами. Для ядра¹⁶⁹⁶⁹Tm с нечетным числом нук-

лонов и неспаренным протоном параметры β^∗ и η,

Отношение ω_A/ω_γ зависит от констант связи g^0AN

и g^3AN или C_p и C_n. В результате, скорость поглоще-

в одночастичном приближении, можно оценить как

β^∗ = 1 и η = 0.5 [26].

ния аксионов R_A ядром¹⁶⁰Tm, выраженная в еди-

ницах атом^-1 с^-1, в модельно независимом виде, т.е.

Изоскалярная g^0AN и изовекторная g^3AN части

зависящем только от значений констант связи, будет

константы связи аксиона с нуклонами являются мо-

выглядеть как:

дельно зависимыми величинами. Они могут быть вы-

ражены через эффективные константы связи аксио-

R_A = 3.55 × 10^-6(g^0AN + g^3AN )⁴(p_A/p_γ)⁶.

(9)

на с протонами C_p и нейтронами C_n [31, 32]:

Используя отношения, связывающие константы

g^0AN = (M_N /2f_A)(C_p + C_n);

g^0AN и g^3AN с массой аксиона m_A в KSVZ- и DFSZ-

(5)

g^3AN = (M_N /2f_A)(C_p - C_n),

моделях, скорость поглощения аксионов ядром

¹⁶⁹Tm в сутки можно представить как функцию

где M_N - масса нуклона. Эффективные константы

массы аксиона m_A, последняя выражена в единицах

C_p и C_n, в свою очередь, зависят от констант связи

эВ:

аксиона с кварками [18, 31]. Вычисления, выполнен-

ные в [31], дают для KSVZ модели следующие зна-

R^KSVZA = 4.88 × 10^-30m^4A(p_A/p_γ)⁶,

(10)

чения C^KSVZp = -0.47(3) и C^KSVZn = 0.02(3). Как

R^DFSZA = 5.41 × 10^-31m^4A(p_A/p_γ)⁶.

было отмечено ранее, взаимодействие аксиона с ней-

троном сильно подавлено. Для DFSZ аксион значе-

Общее число зарегистрированных аксионов зави-

ния C_p и C_n зависят от дополнительного парамет-

сит от числа ядер¹⁶⁹Tm в мишени, времени измере-

ра β [31]: CDFSZp = -0.617 + 0.435 sin2 β ± 0.025 и

ний и эффективности регистрации детектора, а веро-

C^DFSZn = 0.254 - 0.414 sin² β ± 0.025. Мы использо-

ятность наблюдения пика с энергией 8.41 кэВ опреде-

вали значения C^DFSZp = 0.2712 и C^DFSZn = 0.1248 при

ляется уровнем фона экспериментальной установки.

большом угле tanβ = 10, найденные в [32]. Исполь-

4. Экспериментальная установка. Для реги-

зуя отношение (1), можно выразить изоскалярную и

страции реакции резонансного поглощения солнеч-

изовекторную константы g^0AN и g^3AN через массу ак-

ных аксионов использовался детектор на основе кри-

сиона m_A.

сталла тулиевого граната Tm₃Al₅O₁₂, который был

3. Скорость поглощения 8.4 кэВ аксионов

специально изготовлен для данного эксперимента

ядрами¹⁶⁹Tm. Сечение резонансного поглощения

и работал как низкотемпературный болометр [33].

Письма в ЖЭТФ том 118 вып. 3 - 4

2023

Поиск солнечных аксионов с энергией 8.4 кэВ, излучаемых в М1-переходе ядер¹⁶⁹Tm

157

Кристалл был выращен в институте общей физики

где N_169Tm = 1.77 × 10²² - число ядер¹⁶⁹Tm в ми-

им. А. М. Прохорова РАН. Детектор имел форму ку-

шени, T = 3.34 × 10⁵ - время измерений в секундах

ба со стороной 10 мм, масса кристалла составляла

и ǫ = 1.0 - эффективность регистрации.

8.18 г, а масса тулия 4.97 г.

В соответствие с выражением (9), при условии

Для проведения измерений детектор был раз-

(p_A/p_γ )⁶

= 1, что справедливо для масс аксиона

мещен в вакуумном криостате в институте физи-

m_A ≤ 2 кэВ, получаем ограничение:

ки М. Планка и охлаждался до температуры око-

ло 10 мК. Установка была расположена на поверх-

|(g^0AN + g^3AN )| ≤ 8.89 × 10^-6,

(12)

ности земли. Для калибровки использовался стан-

дартный калибровочный источник⁵⁵Fe. Энергетиче-

для 90 % у.д. Ограничение (12) является модельно-

ское разрешение, полученное для линии с энергией

независимым ограничением на константы связи ак-

5.9 кэВ (K_α12 Mn), составило σ = FWHM/2.35 =

сиона или любой другой псевдоскалярной аксионо-

= 0.4 кэВ. Вследствии большого коэффициента элек-

подобной частицы с нуклонами. Используя выраже-

тронной конверсии e/γ эффективность регистрации

ния (10), легко получить ограничения на массу ак-

сиона в двух разных моделях, которые оказывают-

пика с энергией 8.4 кэВ c высокой точностью равна

ǫ= 1.0. Подробно характеристики детектора и экспе-

ся следующими: m^KSVZA ≤ 141 эВ в KSVZ-модели и

риментальная установка описаны в работах [33, 34].

m^DFSZA ≤ 244 эВ в DFSZ-модели.

Как было отмечено выше, при разрядке возбуж-

Результаты следует сравнить с пределами на мас-

денного уровня¹⁶⁹Tm испускаются конверсионные

су аксиона, полученными в экспериментах по поиску

и Ожэ электроны, рентгеновские и γ-кванты. Изо-

резонансного поглощения солнечных аксионов дру-

топ¹⁶⁹Tm входит в состав детектора, поэтому эф-

гими ядрами. В отмеченных выше работах с ядрами

фективность регистрации резонансного поглощения

⁵⁷Fe [4-6],⁷Li [7-9], и⁸³Kr [10, 11] получены верх-

в e/γ = 260 раз выше по сравнению с нашими преды-

ние пределы на массу для KSVZ-аксиона, которые

дущими экспериментами, выполненными по схеме

составляют величины 145 эВ, 13.9 кэВ и 65 эВ, соот-

“мишень-детектор” [19, 20].

ветственно.

Полученные результаты. Измерения

Более строгие астрофизические ограничения на

проводились

3.86

суток живого времени, полу-

константу связи аксиона с протоном основаны на из-

ченный спектр показан на рис. 3 в [34]. Уровень

менении температуры нейтронных звезд в присут-

фона в районе пика с энергией 8.4 кэВ составил

ствии аксионного излучения и составляют в KSVZ-

25 соб./0.1 кэВ сут.

модели - C^2p ≤ (1-6) × 10^-17 [35-37].

Измеренный спектр в интервале (4.6-20) кэВ под-

6. Заключение. Вычислен поток монохромати-

гонялся функцией для непрерывного фона с 4 па-

ческих солнечных аксионов с энергией 8.41 кэВ, свя-

раметрами и 4-мя гауссовыми пиками K_α1, K_α2, K_β

занный с разрядкой первого ядерного уровня¹⁶⁹Tm,

рентгеновских линий Mn от калибровочного источ-

возбуждаемого за счет высокой температуры Солн-

ника и ожидаемым аксионным пиком S₄ с энергией

ца. Проведен поиск резонансного поглощения дан-

8.4 кэВ. Положение и дисперсия гауссиана, описыва-

ных аксионов ядрами¹⁶⁹Tm, приводящего к возбуж-

ющего аксионный пик, были привязаны к парамет-

дения первого ядерного уровня¹⁶⁹Tm. Для регистра-

рам пика K_α1 марганца. “Аксионный” пик с энергией

ции частиц, возникающих при разрядке уровня, ис-

8.4 кэВ статистически не проявился.

пользовался кристалл Tm₃Al₅O₁₂, работающий как

Для установления верхнего предела на число от-

низкотемпературный болометр. В результате получе-

ны новые верхние пределы на массу аксиона в KSVZ-

счетов в пике использовался стандартный метод на-

хождения профиля χ²(S₄) и функции вероятности

и DFSZ-моделях, которые, для 90 % у.д., составляют

P (χ²(S₄)). Подгонка позволила установить верхний

m_A ≤ 141 эВ и m_A ≤ 244 эВ соответственно.

предел на число событий в пике S_lim = 128 собы-

Работа выполнена при поддержке Российского

тий для 90 % у.д. [34]. Определенный верхний предел

научного фонда, проект # 22-22-00017.

на число событий в пике с энергией 8.41 кэВ позволя-

ет ограничить константы взаимодействия аксиона C_p

1. R. D. Peccei and H. R. Quinn, Phys. Rev. Lett. 38, 1440

или (g^0AN + g^3AN ) и массу аксиона m_A в соответствии

(1977).

с выражениями (5), (9) и (10).

Ожидаемое число зарегистрированных аксионов

2. S. Weinberg, Phys. Rev. Lett. 40, 223 (1978).

составляет:

3. F. Wilczek, Phys. Rev. Lett. 40, 279 (1978).

S_A = R_AN_169TmTǫ ≤ S_lim,

(11)

4. S. Mariyama, Phys. Rev. Lett. 75, 3222 (1995).

Письма в ЖЭТФ том 118 вып. 3 - 4

2023

158

А. В. Дербин, И. С. Драчнев, В. Н. Муратова и др.

A.V. Derbin, A. I. Egorov, I. A. Mitropol’sky,

20.

A. V. Derbin, A.S. Kayunov, V.N. Muratova,

V.N. Muratova, D.A. Semenov, and E. V. Unzhakov,

D. A. Semenov, and E. V. Unzhakov, Phys. Rev.

Eur. Phys. J. C 62, 755 (2009).

D 83, 023505 (2011).

A.V. Derbin, V.N. Muratova, D. A. Semenov, and

21.

P. Sikivie, Phys. Rev. Lett. 51, 1415 (1983).

E. V. Unzhakov, Phys. At. Nucl. 74, 596 (2011).

22.

V. Anastassopoulos, S. Aune, K. Barth et al. (CAST

M. Krčmar, Z. Krečak, A. Ljubičić, M. Stipčević, and

collaboration), Nature Phys. 13, 584 (2017).

D. A. Bradley, Phys. Rev. D 64, 115016 (2001).

23.

F. T. Avignone, D. Abriola, R. L. Brodzinski et al.

A.V. Derbin, A. I. Egorov, I. A. Mitropol’skii, and

(Collaboration), The SOLAX Collaboration, Nucl.

V.N. Muratova, JETP Lett. 81, 365 (2005).

Phys. Proc. Supll. 72, 176 (1999).

P. Belli, R. Bernabei, R. Cerulli et al. (Collaboration),

24.

E. Armengaud, Q. Arnaud, C. Augier et al.

Nucl. Phys. A 806, 388 (2008).

(EDELWEISS Collaboration), JCAP 1311, 067 (2013).

10.

Yu. M. Gavrilyuk, A. N. Gangapshev, A. V. Derbin,

25.

C. M. Baglin, Nuclear Data Sheets 109, 2033 (2008).

I. S. Drachnev, V.V. Kazalov, V. V. Kobychev,

26.

W. C. Haxton and K. Y. Lee, Phys. Rev. Lett. 66, 2557

V.V. Kuz’minov, V. N. Muratova, S.I. Panasenkod,

(1991).

S. S. Ratkevicha, D. A. Semenov, D. A. Tekueva,

27.

J. N. Bahcall, A. M. Serenelli, and S. Basu, Astrophys.

E. V. Unzhakov, and S. P. Yakimenko, JETP Lett. 101,

J. 621, L85 (2005).

664 (2015).

28.

N. Grevesse and A. J. Sauval, Space Sci. Rev. 85, 161

11.

A.V. Derbin, I.S. Drachnev, A. M. Gangapshev,

(1998).

Yu. M. Gavrilyuk, V. V. Kazalov, V. V. Kobychev,

29.

T. W. Donnelly, S. J. Freedman, R. S. Lytel,

V.V. Kuzminov, V. N. Muratova, S. I. Panashenko,

R. D. Peccei, and M. Schwartz, Phys. Rev. D 18,

S. S. Ratkevich, D. A. Tekueva, E. V. Unzhakov, and

1607 (1978).

S. P. Yakimenko, J. Phys.: Conf. Ser. 934, 012018

(2017).

30.

F. T. Avignone, C. Baktash, W. C. Barker,

F. P. Calaprice, R. W. Dunford, W. C. Haxton,

12.

Yu. M. Gavrilyuk, A. N. Gangapshev, A. V. Derbin,

D. Kahana, R.T. Kouzes, H. S. Miley, and D. M. Moltz,

I. S. Drachnev, V.V. Kazalov, V. V. Kuzminov,

Phys. Rev. D 37, 618 (1988).

M. S. Mikulich, V. N. Muratova, D. A. Tekueva,

E. V. Unzhakov, and S. P. Yakimenko, JETP Lett. 116,

31.

G. G. di Cortona, E. Hardy, J. P. Vega, and G. Villadoro,

13 (2022).

JHEP 01, 034 (2016).

13.

J. E. Kim, Phys. Rev. Lett. 43, 103 (1979).

32.

F. T. Avignone III, R. J. Creswick, J. D. Vergados,

14.

M. Shifman, A. Vainshtein, and V. Zakharov, Nucl.

P. Pirinen, P. C. Srivastava, and J. Suhonen, JCAP 01,

021 (2018).

Phys. B 166, 493 (1980).

15.

M. Dine, W. Fischler, M. Srednicki, Phys. Lett. B 104,

33.

E. Bertoldo, A. V. Derbin, I. S. Drachnev et al.

199 (1981).

(Collaboration), Nuclear Instruments and Methods A

949, 162924 (2020).

16.

A. Zhitnitskii, Sov. J. Nucl. Phys. 31, 2 (1980).

34.

A. H. Abdelhameed, S. V. Bakhlanov, P. Bauer et al.

17.

M. Gorghetto and G. Villadoro, JHEP 03, 033 (2019).

(Collaboration), Eur. Phys. J. C 80, 376 (2020).

18.

R.L. Workman, V.D. Burkert, V. Crede et al. (Particle

Data Group), Prog. Theor. Exp. Phys. 083C01 (2022)

35.

J. Keller and A. Sedrakian, Nucl. Phys. A 897, 62

(2013).

and 2023 update.

19.

A.V. Derbin, S. V. Bakhlanov, A.I. Egorov,

36.

A. Sedrakian, Phys. Rev. D 93, 6, 065044 (2016).

I. A. Mitropol’sky, V. N. Muratova, D. A. Semenov, and

37.

K. Hamaguchi, N. Nagata, K. Yanagi, and J. Zheng,

E. V. Unzhakov, Phys. Lett. B 678, 181 (2009).

Phys. Rev. D 98(10), 103015 (2018).

Письма в ЖЭТФ том 118 вып. 3 - 4

2023