ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2019, том 45, № 11, с. 821-829

ОБНОВЛЕННЫЕ ЧИСЛЕННЫЕ ЭФЕМЕРИДЫ ГАЛИЛЕЕВЫХ

СПУТНИКОВ ЮПИТЕРА

Институт прикладной астрономии РАН, Санкт-Петербург, Россия

Поступила в редакцию 25.07.2019 г.; после доработки 04.09.2019 г.; принята к публикации 16.09.2019 г.

Представлены новые версии эфемерид галилеевых спутников Юпитера - Ио, Европы, Ганимеда и

Каллисто, построенные с использованием численного интегрирования уравнений движения спутников.

Модель движения спутников учитывает несферичность Юпитера, взаимные возмущения спутников

и возмущения от Солнца и больших планет. Начальные значения параметров движения спутников

уточнены по всем доступным рядам наземных оптических наблюдений, покрывающих интервал 1891-

2017 гг., наблюдениям космических аппаратов и радарным наблюдениям. В результате получены

коэффициенты разложения координат и скоростей спутников в ряды по полиномам Чебышева на

интервале 1891-2025 гг. Приведены среднеквадратические ошибки наблюдений и графики сравнения

построенных эфемерид, как с наблюдениями, так и с численными эфемеридами Лэнея. Построенные

эфемериды размещены в открытом доступе.

Ключевые слова: Солнечная система, эфемериды спутников.

DOI: 10.1134/S0320010819110044

ВВЕДЕНИЕ

EPM2015 (Питьева, 2017) для уточнения эфеме-

риды Юпитера. Предполагается, что новая версия

Эфемериды спутников больших планет необ-

эфемерид, описанная в настоящей работе, так же

ходимы при планировании наблюдений, а также

будет использована для этой цели.

планировании полетов космических аппаратов к

В настоящей работе представлена последняя

этим спутникам. Кроме того, наличие нескольких

версия численных эфемерид галилеевых спутников

независимых эфемерид позволяет проводить их

Юпитера — Ио, Европы, Ганимеда и Каллисто, по-

взаимный контроль.

строенных на интервале 1891-2025 гг. и уточнен-

В настоящее время наиболее точные эфемери-

ных по всем доступным рядам наземных астромет-

ды спутников, основанные на численном интегри-

рических наблюдений, проведенных на интервале

ровании уравнений движения, разрабатываются в

1891-2017 гг. Построение эфемерид проводилось

Лаборатории реактивного движения (JPL, США)

при помощи программного пакета ЭРА-7 (Эфеме-

(Джейкобсон, 2001) и Институте небесной механи-

ридные расчеты в астрономии) (Красинский, Ва-

ки в Париже (Лэней, 2004а, 2004б).

сильев, 1997), разработанного сотрудниками ИПА

Начиная с 2007 г. в ИПА РАН разрабаты-

РАН для решения различных задач динамической

ваются собственные численные теории движения

и эфемеридной астрономии. ЭРА-7 позволяет, как

естественных спутников планет с целью включения

использовать уже готовые эфемериды планет и

эфемерид этих объектов в приложения к “Астро-

спутников, так и самостоятельно строить числен-

номическому ежегоднику”, а также для уточнения

ные теории движения небесных тел.

орбит планет и самих спутников. Создание соб-

ственных независимых эфемерид позволяет свое-

ЧИСЛЕННАЯ МОДЕЛЬ

временно проводить их уточнение с появлением

новых наблюдений.

Теории движения спутников были построены

Предыдущие версии эфемерид галиллевых

методом дифференциального уточнения парамет-

спутников (Порошина и др., 2012; Космодамиан-

ров по нескольким последовательным итерациям,

ский, Порошина, 2014), были использованы при

на каждой из которых проводилось численное ин-

создании эфемерид EPM2011 (Питьева, 2013) и

тегрирование дифференциальных уравнений дви-

жения спутников методом Эверхарта 19-го поряд-

^*Электронный адрес: ga.kosmodamianskiy@iaaras.ru

ка. Улучшенные методом наименьших квадратов по

821

822

КОСМОДАМИАНСКИЙ

Таблица

1. Уточненные начальные планетоцентрические координаты (R) и скорости (V ) спутников на

2436204.5(TDB), на эпоху J2000.0

Координаты

Ио

Европа

Ганимед

Каллисто

R_x, км

304914.251

35946.405

-1021142.663

1850494.265

R_y, км

-264691.134

-607550.736

292563.013

249215.808

R_z, км

-121318.030

-293415.847

123479.391

141608.863

V_x, км/c

12.027

13.622

-3.226

-1.215

V_x, км/c

11.206

0.617

-9.388

7.373

Vx, км/c

5.529

0.591

-4.478

3.491

результатам сравнения с наблюдениями началь-

В табл. 1 приведены начальные значения коорди-

ные координаты и скорости служили начальными

нат и скоростей спутников, полученные в данной

данными при новом интегрировании в следующей

работе после уточнения по наблюдениям.

итерации. В результате интегрирования были полу-

В табл.

приведены гравитационные ха-

чены коэффициенты разложения координат и ско-

ростей спутников в ряды по полиномам Чебышева

рактеристики Юпитера и спутников, которые

на период 1891-2025 гг. Уравнения движения и ме-

были использованы в данной работе. Обозна-

тодика улучшения параметров подробно описаны в

чения в таблице: Gm — гравитационные массы

работе (Космодамианский, 2009).

объектов, R — экваториальный радиус Юпи-

тера, J₂, J₄, J₆ — вторая, четвертая и шестая

При интегрировании уравнений движения спут-

зональные гармоники разложения потенциала

ников были учтены следующие факторы: взаимные

Юпитера. Значения параметров взяты на сай-

возмущения спутников, возмущения от Солнца,

Сатурна, Урана и Нептуна, а также несферичность

те JPL (https://ssd.jpl.nasa.gov/?sat_phys_par,

Юпитера (J2, J4, J6). При вычислении возмущений

https://ssd.jpl.nasa.gov/?gravity_fields_op).

от Солнца и планет использовалась численная

теория EPM-2011, разработанная в ИПА РАН

При вычислении гравитационного потенциала

(Питьева, 2013). Для того чтобы минимизировать

Юпитера использовались экваториальные угловые

координаты северного полюса Юпитера на эпоху

численные ошибки, интегрирование велось “впе-

ред” и “назад” от даты 1 января 1958 г., близкой

JD2451545.0, которые были взяты из последнего

к середине интервала интегрирования. Начальные

отчета Рабочей группы по картографическим ко-

значения координат и скоростей спутников были

ординатам и элементам вращения (Арчинал и др.,

вычислены на эту дату по эфемериде Лиске (1977).

2018) и записаны в следующем виде:

.000938 sin Jb +

+ 0.001432 sin Jc + 0.000030 sin Jd + 0.002150 cos Je,

δ₀ = 64.495303 + 0.002413T + 0.000050cos Ja + 0.000404cos Jb +

+ 0.000617 cos Jc - 0.000013 cos Jd + 0.000926 cos Je,

W = 284.95 + 870.5360000d.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45

№ 11

2019

ОБНОВЛЕННЫЕ ЧИСЛЕННЫЕ ЭФЕМЕРИДЫ

823

Здесь

. 9605T,

. 2476T,

Je = 49◦.511251 + 64^◦3000T,

где d — интервал в днях от стандартной эпохи, T —

абсолютные позиционные наблюдения, отн. —

интервал в Юлианских столетиях (36 525 дней) от

относительные наблюдения), а также полученные

стандартной эпохи.

после улучшения эфемерид среднеквадратиче-

ское ошибки (СКО) по прямому восхождению и

склонению. В случае, если спутник не наблю-

НАБЛЮДЕНИЯ

дался, в колонках для прямых восхождений и

При уточнении параметров движения спут-

склонений стоит прочерк. Значительная часть

ников были использованы все опубликованные

использованных наблюдений опубликована на

на данный момент наземные фотографические

эпоху и равноденствие B1950.0. Была проведена

и ПЗС-наблюдения спутников. Всего было ис-

редукция этих наблюдений к эпохе и равно-

пользовано 17 647 астрометрических наблюдений

денствию J2000.0 по формулам, приведенным в

разных типов, полученных в период 1891-2017 гг.

работе Аоки и др. (1983). Большая часть на-

Информация об использованных наблюдениях,

блюдений была получена благодаря сайту Центра

краткое описание которых будет приведено ниже,

данных естественных спутников планет (NSDC,

дана в табл.

3-4, где для каждого спутника

и обсерватории приведены период, количество

http://nsdb.imcce.fr/obspos/obsindhe.htm) (Арло,

(числа в соответствующей колонке, соединенные

Емельянов, 2009).

знаком “+”, обозначают количество наблюдений

для каждого спутника) и тип наблюдений (абс. —

Наблюдения, проведенные в 1891-1936 гг. на

обсерваториях в Гельсингфорсе, Пулково, Гринви-

че, Дзо-Се (Китай), Париже, Бухаресте и Мысе

Таблица 2. Гравитационные параметры системы Юпи-

Доброй Надежды, а так же наблюдения, прове-

тера

денные в 1961-1978 гг. на обсерваториях в Бордо,

Ла Силле, Рио-де-Жанейро, в обсерватории Мак-

Параметр

Значение

Кормика, на Йеркской обсерватории и Королев-

ской обсерватории Бельгии в Уккле были взяты из

Gm_system, км³/с²

126712764.1 ± 2.7

каталога позиционных наблюдений спутников пла-

нет 1891-1978 гг., опубликованном Арло (1982).

Gm_Jupiter , км³/с²

126686536.1 ± 2.7

Всего в каталоге представлено 1138 наблюдений,

каждое из которых дает положение на один момент

R, км

71492

времени сразу нескольких спутников относитель-

но центра фотопластинки. Таким образом, всего

J₂ × 10-6

14695.62 ± 0.29

представлено 3916 положений спутников. Точности

этих наблюдений, в зависимости от обсерватории

J₄ × 10-6

-591.31 ± 2.06

и периода наблюдений, лежат в пределах 0.05^′′-

0.6^′′ Из-за сложностей с определением положения

J₆ × 10-6

20.78 ± 4.87

центра фотопластинки наблюдения были преобра-

зованы таким образом, что в каждом наблюдении

Gm_Io, км³/с²

5959.916 ± 0.012

(которое дает положение нескольких спутников на

один момент времени) был выбран опорный спут-

Gm_Europa, км³/с²

3202.739 ± 0.009

ник, относительно которого были получены диффе-

ренциальные координаты остальных спутников. В

Gm_Ganymede, км³/с²

9887.834 ± 0.017

результате были получены 3189 отдельных наблю-

дений дифференциального типа, которые и были

Gm_Callisto, км³/с²

7179.289 ± 0.013

использованы при улучшении теорий движения.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45

№ 11

2019

824

КОСМОДАМИАНСКИЙ

Таблица 3. Позиционные наблюдения Ио и Европы

Ио

Европа

Тип

Интервал

Количество

СКО, угл. сек

Обсерватория

набл.

наблюдений

Δα cos δ

Δδ

Δα cos δ

Δδ

Washington

абс.

1967-1998

1210 + 1248

0.12

0.11

Flagstaff

абс.

1998-2015

504 + 638

0.11

0.12

Nikolaev

абс.

1979-2014

303 + 330

0.18

0.17

0.16

Pulkovo

абс.

1974-1994

136 + 161

0.32

0.25

0.29

0.27

Pulkovo

абс.

2009-2017

260 + 302

0.08

0.09

0.08

Pulkovo

отн.

1976-2005

172 + 190

0.15

0.16

0.14

0.19

Pulkovo

отн.

1984-1986

37 + 50

0.13

0.21

0.10

0.20

Pulkovo

отн.

1974-1994

255 + 250

0.23

0.50

0.19

0.61

Pulkovo

отн.

1986-2005

9 + 61

0.04

0.07

0.08

0.11

Pulkovo

отн.

2013-2017

403 + 336

0.07

0.08

0.06

0.10

Itajuba

отн.

1995

122 + 122

0.09

0.03

0.17

0.05

Yunnan

отн.

2002-2010

435 + 20

0.03

0.04

0.02

HIPPARCOS

абс.

1990-1992

0.11

0.08

Hubble ST

отн.

1994-1997

32 + 4

0.07

0.04

0.08

PHEMU

отн.

1973-2015

779 + 625

0.05

0.07

0.04

0.06

Bourdeaux

отн.

1967-1974

142 + 144

0.35

0.34

Bucarest

отн.

1934

65 + 66

0.24

0.28

0.24

0.32

Cape

отн.

1924

84 + 86

0.09

0.14

0.11

0.16

Greenwich

отн.

1918-1919

91 + 92

0.08

0.17

0.08

0.24

Helsingfors

отн.

1891-1897

208 + 200

0.20

0.15

0.17

0.13

La Silla

отн.

1978

57 + 45

0.23

0.24

0.19

McCormick

отн.

1977-1978

162 + 179

0.22

0.11

0.17

0.14

Paris

отн.

1936

29 + 20

0.32

0.33

0.23

0.39

Pulkovo

отн.

1895-1910

332 + 319

0.16

0.15

Rio de Janeiro

отн.

1977

8 + 16

0.47

0.40

0.38

0.33

Uccle

отн.

1977-1978

35 + 37

0.34

0.43

0.35

0.39

Yerkes

отн.

1961-1963

30 + 33

0.32

0.39

0.28

0.29

Zo-Se

отн.

1917-1918

8 + 18

0.25

0.32

0.33

0.29

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ

том 45

№ 11

2019

ОБНОВЛЕННЫЕ ЧИСЛЕННЫЕ ЭФЕМЕРИДЫ

825

Таблица 4. Позиционные наблюдения Ганимеда и Каллисто

Ганимед

Каллисто

Тип

Интервал

Количество

СКО, угл. сек

Обсерватория

набл.

наблюдений

Δα cos δ

Δδ

Δα cos δ

Δδ

Washington

абс.

1967-1998

1324

0.13

0.12

Flagstaff

абс.

1998-2015

721 + 756

0.13

0.10

0.11

Nikolaev

абс.

1979-2014

339 + 339

0.17

0.15

0.14

La Palma

абс.

1992-1997

218 + 440

0.19

0.21

0.19

Pulkovo

абс.

1974-1994

161 + 155

0.28

0.22

0.27

Pulkovo

абс.

2009-2017

305 + 353

0.09

0.10

0.08

Pulkovo

отн.

1976-2005

187 + 162

0.15

0.20

0.16

0.25

Pulkovo

отн.

1984-1986

48 + 50

0.11

0.32

0.15

0.47

Pulkovo

отн.

1974-1994

216 + 252

0.24

0.63

0.27

0.86

Pulkovo

отн.

1986-2005

97 + 89

0.08

0.11

0.09

0.14

Pulkovo

отн.

2013-2017

207 + 35

0.06

0.09

0.10

Itajuba

отн.

1995

85 + 35

0.13

0.05

0.09

0.07

Yunnan

отн.

2002-2010

0.01

0.02

HIPPARCOS

абс.

1990-1992

16 + 13

0.11

0.04

0.09

0.06

Hubble ST

отн.

1994-1997

1 + 10

0.07

0.09

0.03

0.02

PHEMU

отн.

1973-2015

501 + 191

0.05

0.07

0.04

0.07

Bourdeaux

отн.

1967-1974

50 + 26

0.34

0.41

0.33

0.41

Bucarest

отн.

1934

17 + 39

0.24

0.26

0.31

0.34

Cape

отн.

1924

13 + 31

0.08

0.13

0.11

0.17

Greenwich

отн.

1918-1919

15 + 23

0.07

0.28

0.10

0.22

Helsingfors

отн.

1891-1897

43 + 56

0.19

0.17

0.14

0.15

La Silla

отн.

1978

15 + 9

0.24

0.22

0.20

McCormick

отн.

1977-1978

35 + 90

0.18

0.09

0.20

0.11

Paris

отн.

1936

5+5

0.23

0.34

0.28

0.52

Pulkovo

отн.

1895-1910

73 + 90

0.16

0.18

0.17

0.19

Rio de Janeiro

отн.

1977

5+2

0.32

0.54

0.21

0.42

Uccle

отн.

1977-1978

8 + 14

0.33

0.29

0.28

0.34

Yerkes

отн.

1961-1963

7+7

0.48

0.38

0.33

0.42

Zo-Se

отн.

1917-1918

2+3

0.08

0.10

0.09

0.30

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ

том 45

№ 11

2019

826

КОСМОДАМИАНСКИЙ

Таблица 5. Радарные наблюдения

Спутник

Дата

Время

τ,с

O - C, мс (E3)

O - C, мс

Ганимед

1992 02 20

05 57

4413.296899

0.849 ± 0.048

-0.169

Ганимед

1992 03 09

04 37

4417.270238

-0.729 ± 0.021

-0.023

Каллисто

1992 03 03

05 05

4394.993673

1.413 ± 0.087

0.747

Каллисто

1992 03 07

04 46

4402.260207

-1.386 ± 0.090

-1.189

3782 наблюдения получены на Военно-Морской

данных — 0.05^′′, получаемых из обработки кривых

обсерватории США в Вашингтоне в 1967-1998 гг.

блеска спутников. Астрометрическая обработка

при помощи длиннофокусного рефрактора. Точ-

фотометрических наблюдений взаимных затмений

ность этих наблюдений составляет 0.1^′′ (Арло и

и покрытий галилеевых спутников, полученных в

др., 2016).

1973, 1979-1980, 1985, 1990-1992 гг., проведена в

работах (Акснес и др., 1984; Франклин и др., 1991;

2619

наблюдений были получены в

1998-

2015 гг. на автоматическом транзитном телескопе

Каас и др., 1999). Оригинальный метод обработки

во Флагстаффе в рамках наблюдательной про-

фотометрических наблюдений взаимных явлений с

граммы планет и спутников FASTT (Flagstaff

целью получения из них астрометрических данных

Astrometric Scanning Transit Telescope). Точность

разработан Н.В. Емельяновым (2003). Получен-

этих наблюдений составляет 0.05^′′-0.1^′′ (Стоун,

ные по этому методу астрометрические данные из

Харрис, 2000; Стоун, 2000, 2001).

наблюдений, проведенных в 1997, 2002-2003, 2009

и 2014-2015 гг., приведены в работах (Емельянов,

4939 наблюдений 1974-2017 гг. были взяты в

Вашковьяк, 2009; Емельянов, 2009; Арло и др.,

базе наблюдений на сайте Пулковской обсерва-

2014; Сакет и др., 2018). В табл. 3 и 4 для этих

тории (http://puldb.ru/db2/sdb.php). Эти наблюде-

наблюдений в колонке “Обсерватория” стоит обо-

ния были выполнены на различных иструментах:

значение PHEMU.

26-дюймовом рефракторе, нормальном астрогра-

фе, лунно-планетном телескопе и двойном аст-

Помимо наземных наблюдений, в работе также

рографе. Точность фотографических наблюдений,

были использованы наблюдения, выполненные с

выполненных в период 1974-2005 гг., составля-

борта космических аппаратов: 47 положений спут-

ет 0.1^′′-0.5^′′. Необходимо отметить высокую точ-

ников относительно Юпитера, полученные при по-

ность современных пулковских ПЗС-наблюдений

мощи космического телескопа им. Хаббла (Мал-

спутников (Нарижная, 2015, 2016; Нарижная и

лама и др., 2004), точность которых составляет

др., 2018), которая составляет 0.08^′′.

0.04^′′ по обеим координатам, и 93 абсолютных

364 положения всех четырех спутников относи-

положения спутников, выполненные космическим

тельно Юпитера получены в Итаджубе (Бразилия)

аппаратом Hipparcos (Хестроффер и др., 1998;

в 1995 г. (Вейга, Виэйра, 1996). Точность этих

Пэрриман, 1997), точность которых составляет

наблюдений составляет порядка 0.1^′′.

0.03^′′-0.2^′′.

Использовано 526 относительных положений

Кроме того, были использованы четыре радар-

спутников, полученных в Юннаньской Обсерва-

тории в Китае в 2002-2010 гг. Эти наблюдения

ных наблюдения Ганимеда и Каллисто, получен-

представляют собой наблюдения близких пар спут-

ные в обсерватории Аресибо в 1992 г. (Хармон и

ников и обладают высокой точностью — 0.03^′′ по

др., 1994). Данные по этим наблюдениям приведе-

обеим координатам (Пенг и др., 2012).

ны в табл. 5 и включают дату и время получения

сигнала (в часах и минутах), время распростране-

В 1973 г. были начаты фотометрические на-

ния сигнала между радаром и спутником τ, а также

блюдения взаимных явлений и покрытий в системе

значения (O-C) с погрешностями, полученные ав-

спутников Юпитера, и с тех пор международные

торами этих наблюдений в сравнении с эфемеридой

кампании по наблюдениям этих явлений (PHEMU)

проводятся каждые шесть лет при участии обсер-

E3, разработанной Лиске. В последнем столбце

ваторий по всему миру. Данные наблюдения явля-

приведены значения (O-C) после улучшения, по-

ются источником очень точных астрометрических

лученные в данной работе.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45

№ 11

2019

ОБНОВЛЕННЫЕ ЧИСЛЕННЫЕ ЭФЕМЕРИДЫ

827

1.5

1.2

0.9

0.6

0.3

0.6

0.9

1.2

1.5

1900

1920

1940

1960

1980

2000

2020

1900

1920

1940

1960

1980

2000

2020

Дата, годы

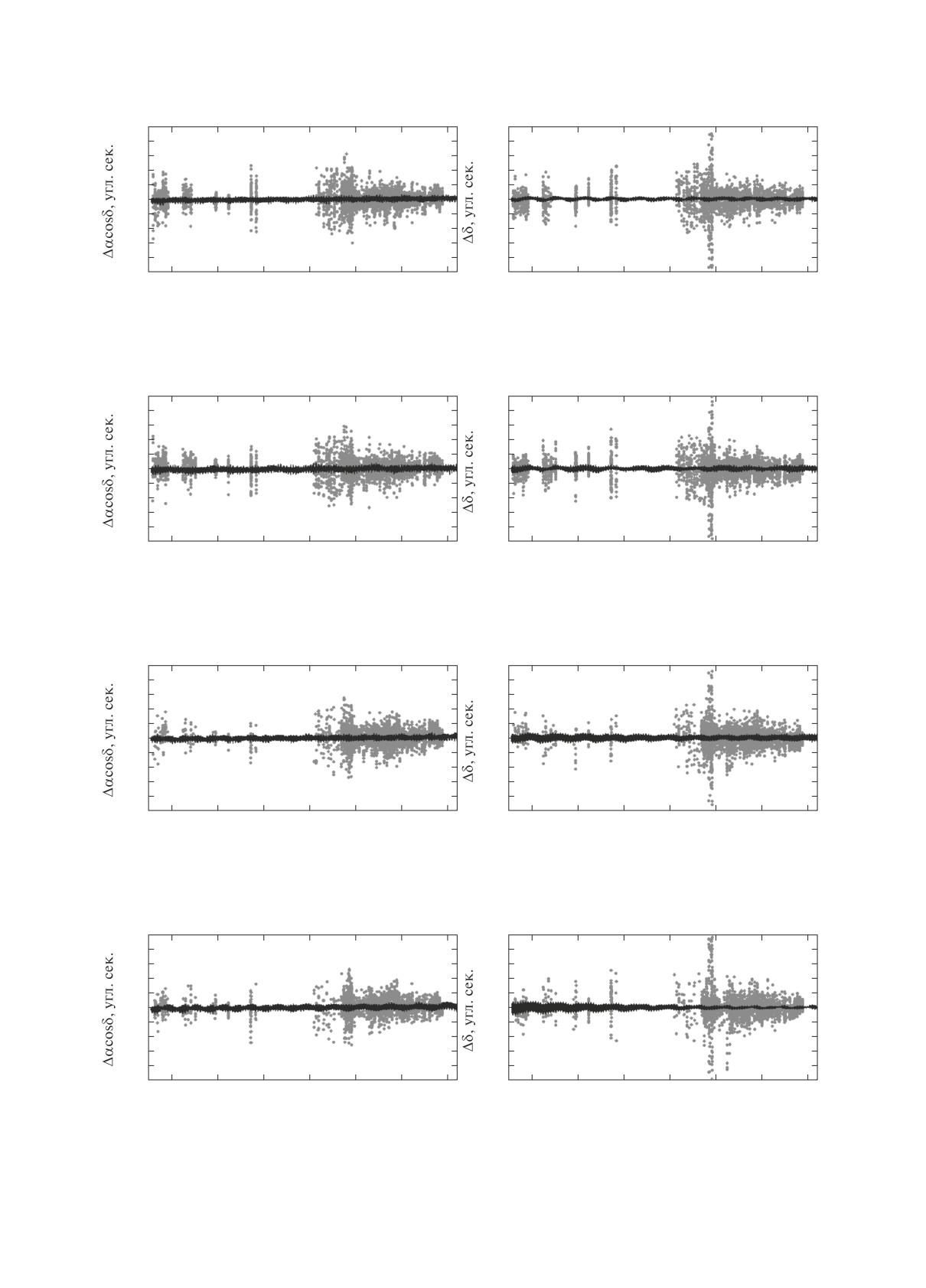
Рис. 1. Сравнение с наблюдениями и эфемеридой V. Lainey-V.2.0|V1.1 для Ио.

1.5

1.2

0.9

0.6

0.3

0.6

0.9

1.2

1.5

1900

1920

1940

1960

1980

2000

2020

1900

1920

1940

1960

1980

2000

2020

Дата, годы

Рис. 2. Сравнение с наблюдениями и эфемеридой V. Lainey-V.2.0|V1.1 для Европы.

1.5

1.2

0.9

0.6

0.3

0.6

0.9

1.2

1.5

1900

1920

1940

1960

1980

2000

2020

1900

1920

1940

1960

1980

2000

2020

Дата, годы

Рис. 3. Сравнение с наблюдениями и эфемеридой V. Lainey-V.2.0|V1.1 для Ганимеда.

1.5

1.2

0.9

0.6

0.3

0.6

0.9

1.2

1.5

1900

1920

1940

1960

1980

2000

2020

1900

1920

1940

1960

1980

2000

2020

Дата, годы

Рис. 4. Сравнение с наблюдениями и эфемеридой V. Lainey-V.2.0|V1.1 для Каллисто.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45

№ 11

2019

828

КОСМОДАМИАНСКИЙ

ОЦЕНКИ ТОЧНОСТИ

СПИСОК ЛИТЕРАТУРЫ

Аоки и др. (S. Aoki, M. Soma, H. Kanoshita,

В табл. 3 и 4 для каждого спутника и обсерва-

K. Inoue), Astron. Astrophys. 128, 263 (1983).

тории представлены среднеквадратические ошибки

Акснес и др. (K. Aksnes, F. Franklin, R. Mills,

представления наблюдений. В целом видно, что

P. Birch, C. Blanco, S. Catalano, J. Piironen), Astron.

для всех наблюдений полученные среднеквадрати-

J. 89, 280 (1984).

Арло (J.-E. Arlot), Amelioration des ephemerides

ческие ошибки соответствуют точностям, которые

des satellites galileens de Jupiter par l’analyse des

даются авторами наблюдений, и приведенным в

observations. These de Doctorat d’etat (Obs. de Paris,

разделе с описанием наблюдений. В частности, как

1982).

и следовало ожидать, наилучшим образом пред-

Арло, Емельянов (J.-E. Arlot and N.V. Emelyanov),

ставлены наблюдения взаимных явлений, наблю-

Astron. Astrophys. 503, 631 (2009).

дения, выполненные в рамках программы FASTT,

Арло и др. (J.-E. Arlot, N. Emelyanov,

современные пулковские наблюдения.

M.I. Varfolomeev, A. Amosse, C. Arena, M, Assafin,

L. Barbieri, S. Bolzoni, et al.), Astron. Astrophys.

На рис.

1-4

приведены значения (O-C)

572, A120 (2014).

после улучшения (серые точки) по прямому вос-

Арло и др. (J.-E. Arlot, N. Cooper, N. Emelyanov,

хождению и склонению для каждого спутника.

V. Lainey, L.E. Meunier, C. Murray, J. Oberst,

Кроме того, на этих же рисунках приведены

D. Pascu, et al.), Not. Sci. Tech. Inst. Mecan. Celest.

графики сравнения построенных эфемерид с

105 (2016)

численными эфемеридами Лэнея и др. (2004a,

Арчинал и др. (B.A. Archinal, C.H. Acton,

2004б) (черные линии). Сравнение проводилось

M.F. A’Hearn, A. Conrad, G.J. Consolmagno,

T. Duxbury, D. Hestroffer, J.L. Hilton, et al.), Celest.

на интервале 1891-2025 гг. по прямому вос-

Mech. Dyn. Astron. 130, 22 (2018).

хождению и склонению для каждого спутника.

Вейга, Виэйра (C.H. Veiga, M.R. Vieira), Rev. Mex.

Эфемериды Лэнея, а также эфемериды других

4, 118 (1996).

авторов, доступны благодаря серверу MULTY-

Джейкобсон (R.A. Jacobson), Bull. Am. Astron.

SAT (Емельянов, Арло, 2008) на сайте Службы

Soc. 33, 1039 (2001).

естественных спутников планет ГАИШ МГУ

10.

Емельянов Н.В. Астрон. вест.

37,

344

(2003)

(http://www.sai.msu.ru/neb/nss/nssephmr.htm).

[N.V. Emelyanov, Solar System Res. 37, 314 (2003)].

На рисунках видно, что расхождение между

11.

Емельянов Н.В., Вашковьяк С.Н. Астрон. вест. 43,

эфемеридами для Ио, Европы и Ганимеда на всем

251 (2009) [N.V. Emelyanov, S.N. Vashkovyak, Solar

System Res. 43, 240 (2009)].

интервале не превосходит 0.1^′′, а для Каллисто —

12.

Емельянов (N.V. Emelyanov), MNRAS, 394, 1037

0.15^′′.

(2009).

13.

Емельянов, Арло (N.V. Emelyanov, J.-E. Arlot),

Astron. Astrophys. 487, 759 (2008).

ЗАКЛЮЧЕНИЕ

14.

Каас и др. (A.A. Kaas, K. Aksness, F. Franklin and

Jay Lieske), Astron. J. 117, 1933 (1999).

Благодаря использованию всех доступных на

15.

Красинский, Васильев (G.A. Krasinsky and

данный момент наземных наблюдений галилеевых

M.V. Vasilyev), Proc. of IAU Coll. (Ed.

спутников Юпитера, покрывающих период 1891-

I.M. Wytrzyszczak, J.H. Lieske, R.A. Feldman,

Dordrecht, Kluwer, 1997), p. 239.

2017 гг., построены численные эфемериды этих

16.

Космодамианский Г.А. Астрон. вестн. 43, № 6, 483

спутников на интервале 1891-2025 гг. Сравне-

(2009)

[G.A. Kosmodamianskii, Solar System Res.

ние показало хорошее согласие как с наблю-

43, № 6, 483 (2009)].

дениями, так и с эфемеридами других авторов.

17.

Космодамианский Г.А., Порошина А.Л. Тр. ИПА

Построенные теории галилеевых спутников ис-

31, 39 (2014)

пользуются для вычисления эфемеридных таб-

18.

Лиске (J.H. Lieske), Astron. Astrophys. 56,

333

лиц, ежегодно публикуемых на сайте ИПА РАН

(1977)

в приложении к “Астрономическому ежегоднику”

19.

Лэней и др. (V. Lainey, L. Duriez, A. Vienne), Astron.

Astrophys. 420, 1171 (2004а).

(http://iaaras.ru/about/issues/yearbook/), а также

20.

Лэней и др. (V. Lainey, J.E. Arlot, A. Vienne), Astron.

доступны для пользователей на сайте ИПА РАН

Astrophys. 427, 371 (2004б).

благодаря Интерактивной службе расчета эфеме-

21.

Маллама и др. (A. Mallama, M. Aelion,

рид, разработанной в ИПА РАН и предостав-

C.A. Mallama), Icarus 167, 320 (2004)

ляющей доступ к различным эфемеридам с воз-

22.

Нарижная Н.В. Астрон. вестн. 49,

420

(2015)

можностью получения эфемеридных таблиц в раз-

[N.V. Narizhnaya, Solar System Res. 49, 383 (2015)].

личных единицах измерения и системах координат

23.

Нарижная Н.В. Астрон. вестн. 50,

364

(2016)

(http://iaaras.ru/dept/ephemeris/online/).

[N.V. Narizhnaya, Solar System Res. 50, 344 (2016)].

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45

№ 11

2019

ОБНОВЛЕННЫЕ ЧИСЛЕННЫЕ ЭФЕМЕРИДЫ

829

24. Нарижная Н.В., Ховричев М.Ю., Апетян А.А.,

30. Сакет и др. (E. Saquet, N. Emelyanov, V. Robert,

Бикулова Д.А., Ершова А.П., Беляев И.А.,

J.-E. Arlot, P. Anbazhagan, K. Bailli, J. Bardecker,

Куликова А.М., Оськина К.И. и др., Астрон. вестн.

A.A. Berezhnoy, et al.), MNRAS 474, 4730 (2018).

52, 316 (2018) [N.V. Narizhnaya, M.Y. Khovrichev,

31. Стоун, Харрис (R.C. Stone and F.H. Harris), Astron.

A.A. Apetyan, D.A. Bikulova, A.P. Ershova,

J. 119, 1985 (2000).

I.A. Balyaev, A.M. Kulikova, K.I. Os’kina, et al.,

32. Стоун (R.C. Stone), Astron. J. 120, 2124 (2000).

Solar System Res. 52, 312 (2018)].

25. Пенг и др. (Q.Y. Peng, H.F. He, V. Lainey, and

33. Стоун (R.C. Stone), Astron. J. 122, 2723 (2001).

A. Vienne), MNRAS 419, 1977 (2012).

34. Франклин и др. ( F. Franklin, J. Africano, W. Allen,

26. Питьева Е.В., Астрон. вестн.

47,

419

(2013)

K. Aksnes, P. Birch, C. Blanco, I. Coulson, J. Goguen,

[E.V. Pitjeva, Solar System Res. 47, 386 (2013)].

et al.), Astron. J. 102, 806 (1991).

27. Питьева Е.В., Тр. ИПА 43, 42 (2017).

35. Хармон и др. (J.K. Harmon, S.J. Ostro,

28. Пэрриман (M.A.C. Perryman), The Hipparcos and

J.F. Chandler, and R.S. Hudson), Astron. J. 107,

Tycho Catalogues. Vol. 1: Introduction and Guide

1175 (1994).

to the Data (Noordwijk, ESA Publications Division,

36. Хэстроффер и др. (D. Hestroffer, B. Morando,

1997).

E. Hog, J. Rjvalevsky, L. Lindegren, and F. Mignard),

29. Порошина и др. (A. Poroshina, M. Zamarashkina,

G. Kosmodamianskiy), Тр. ИПА 26, 75 (2012).

Astron. Astrophys. 334, 325 (1998).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45

№ 11

2019