ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2019, том 45, № 9, с. 666-672
ЦИРКУМБИНАРНЫЕ ПЛАНЕТНЫЕ СИСТЕМЫ В СОЛНЕЧНОЙ
ОКРЕСТНОСТИ: УСТОЙЧИВОСТЬ И ОБИТАЕМОСТЬ
© 2019 г. И. И. Шевченко1*, А. В. Мельников1,
Е. А. Попова1, В. В. Бобылев1, Г. М. Карелин1
1Главная (Пулковская) астрономическая обсерватория РАН, Санкт-Петербург, Россия
Поступила в редакцию 20.02.2019 г.; после доработки 07.05.2019 г.; принята к публикации 28.05.2019 г.
Для тесных двойных звезд в Солнечной окрестности, имеющих достаточные каталожные данные,
вычислены радиусы внутренней и внешней границ циркумбинарной зоны потенциальной обитаемости
(ЦЗО) и радиусы циркумбинарной зоны динамического хаоса (ЦЗХ). Впервые выделен подкласс
двойных, для которых граница ЦЗХ находится внутри границ ЦЗО (радиус ЦЗХ больше чем
внутренний радиус ЦЗО, но меньше чем внешний радиус ЦЗО): M4-V69, HATS551-027, EZ Aqr A-
C, 38 Cas, HD 2070, HD 15064, HD 28394, HD 160346 и HD 181602. Поскольку на границе
ЦЗХ, согласно современным теоретическим представлениям и наблюдательным данным, высока
вероятность нахождения планет, в планетных системах выявленных указанным образом двойных звезд
можно ожидать присутствия потенциально обитаемых циркумбинарных планет. Для звезд CM Dra,
WTS 19c-3-01405 и LP 661-13 радиус ЦЗХ меньше радиуса внутренней границы ЦЗО, однако у них
возможно наличие планет на внешних устойчивых орбитах, резонансных с орбитами планет у границы
ЦЗХ. Все впервые выявленные двойные указанных типов представляют поэтому существенный
интерес для будущих наблюдений.
Ключевые слова: двойные звезды, Солнечная окрестность, циркумбинарные планеты, обитаемость,
динамический хаос.
DOI: 10.1134/S0320010819080096
ВВЕДЕНИЕ
системах двойных звезд, среди них 73 являются
системами S-типа, а 22 — P-типа.
Поиск и исследования планет в системах двой-
ных звезд весьма актуальны хотя бы потому, что
К настоящему времени разработаны два ин-
терактивных интернет-ресурса, позволяющие
более 60% всех звезд Солнечного типа в Галак-
оценивать размеры зон устойчивости и обита-
тике входят в двойные системы (Дюкеннуа, Мей-
емости кратных звезд. Кунтц
(2014,
2015) и
ор, 1991). Несомненно, особый исследовательский
Кунтц и Брунц (2015) предложили теоретиче-
интерес представляют двойные звезды, у которых
ские алгоритмы и разработали систему BinHab
могут иметься потенциально обитаемые планеты,
при этом орбитальная динамика последних являет-
ся долговременно устойчивой.
обитаемости планетных систем P-типа и S-
типа. Первоначально (Кунтц, 2014) ресурс был
Планетные системы двойных звезд подразде-
ограничен случаем круговой орбиты двойной
ляются на два класса: системы S-типа (“satellite-
звезды, позднее было представлено (Кунтц, 2015)
type”), в которых планеты обращаются на ор-
обобщение на случай эллиптической орбиты.
битах вокруг одиночных звезд — компонентов
Задав в BinHab орбитальные и физические па-
двойной (циркумзвездные системы), и систе-
раметры звездной системы, можно вычислить
мы P-типа
(“planet-type”), в которых плане-
расположение границ зон обитаемости на основе
ты обращаются на орбитах вокруг центральной
модели Коппарапу и др. (2013, 2014) и границ
двойной (циркумбинарные системы). (Данные
зон устойчивости на основе эмпирических формул
обозначения введены в работе Дворака (1984).)
Хольмана и Вигерта (1999).
В каталоге Шварца и др. (2011, 2016) (http://
Мюллер и Хагигипур (2014) представили интер-
держится информация о 95 известных планетных
вычисления границ зон обитаемости и устойчиво-
*Электронный адрес: iis@gaoran.ru
сти как для двойных звездных систем, так и для
666
ЦИРКУМБИНАРНЫЕ ПЛАНЕТНЫЕ СИСТЕМЫ
667
звездных систем кратности больше двух. Границы
и ссылки в статье Шевченко, 2017.) Более того,
зон обитаемости определяются в рамках моделей
циркумбинарные скальные планеты двойных звезд
Кастинга и др. (1993), Селсиса и др. (2007) и
определенных классов являются фотоприливными
Коппарапу и др. (2013, 2014). Границы зон устойчи-
аналогами Земли в системе Солнце-Земля-Луна
вости определяются на основе критериев Хольмана
(имеют схожие с земными амплитудно-временные
и Вигерта (1999), как и в системе Кунтца и Брун-
параметры инсоляции и приливов) и, в общем
ца (2015). Система Мюллера и Хагигипура (2014)
случае, обладают рядом свойств, благоприятных
позволяет представить в удобном графическом ви-
для потенциальной обитаемости (Шевченко, 2017,
де конфигурацию зон обитаемости и устойчивости
2018). Таким образом, в планетных системах двой-
двойной звезды.
ных звезд указанного типа можно ожидать присут-
ствия потенциально обитаемых циркумбинарных
Джайме и др. (2012) составили и проанали-
планет. Выявленные двойные представляют поэто-
зировали выборку двойных звезд (161 объект) в
му существенный интерес для будущих наблюде-
ближайшей (радиусом менее 100 пк) окрестности
ний.
Солнца. В рамках теории Пичардо и др. (2005,
2009) для этих звездных систем были получе-
Среди наблюдательных проектов, которые в
будущем могут дать материал о подобных систе-
ны границы областей устойчивости для вероятных
мах, следует выделить миссию TESS. Цель мис-
планетных систем S- и P-типа. Позднее Джайме
и др. (2014) получили оценки размеров зон оби-
сии TESS (Transiting Exoplanet Survey Satellite,
таемости и устойчивости для 64 двойных звезд.
Критерием отбора служили принадлежность звезд
бой космический телескоп, успешно запущенный
к главной последовательности и наличие хорошо
на орбиту 18 апреля 2018 г., состоит в поиске по-
определенных физических и орбитальных парамет-
средством применения транзитного метода планет
ров. Границы зон устойчивости в работе Джайме
у ближайших (ближе 200 пк) ярких звезд. Важным
и др. (2014) получены в рамках теории Пичардо
отличием TESS от предшествовавшей ей миссии
и др. (2005, 2009), а зон обитаемости — на основе
Kepler является то, что поиск планет проводится
модели Коппарапу и др. (2013).
путем обзора всей небесной сферы, а не опре-
деленного ее сектора. Особое внимание миссии
В работе Поповой и Шевченко (2016), исхо-
TESS уделяется поиску планет у звезд спектраль-
дя из современных представлений о динамике и
ных классов G, K и M. Предполагается, что будут
архитектуре циркумбинарных планетных систем,
обнаружены около 20 тысяч экзопланет, и среди
наиболее вероятные циркумбинарные планетные
них будет несколько десятков планет, имеющих
орбиты определены как расположенные внутри
массы менее чем две земные и находящихся в зоне
главных резонансных ячеек на границе области
обитаемости родительской звезды (Барклай и др.,
динамического хаоса вокруг родительской двойной
2018). С TESS планируется открыть в ∼10 раз
звезды, что позволяет предсказать значения боль-
больше циркумбинарных планет, чем было открыто
ших полуосей орбит. Согласно Поповой и Шевчен-
в рамках миссии Kepler; см. Костов (2018).
ко (2016), в случае EZ Aqr (одной из ближайших к
Солнцу тесных двойных звезд) наиболее вероятная
орбита циркумбинарной планеты находится вблизи
МЕТОДИКА И ВЫБОРКА
зоны обитаемости и, с учетом неопределенности
границы этой зоны, может ей принадлежать.
Циркумбинарная зона динамического хаоса
Целью настоящей работы является выявление
(ЦЗХ) формируется вокруг гравитирующей двой-
таких двойных звезд в Солнечной окрестности,
ной из-за перекрытия орбитальных резонансов
у которых граница циркумбинарной зоны дина-
вида (p + 1)/1 (где p ≥ 1 — целые числа) между
мического хаоса (ЦЗХ) находится внутри границ
циркумбинарной “частицей” и центральной двой-
циркумбинарной зоны потенциальной обитаемости
ной, аккумулирующих при p → ∞ к параболиче-
(ЦЗО), то есть радиус ЦЗХ больше чем внутрен-
ской сепаратрисе
— границе между связанным
ний радиус ЦЗО, но меньше чем внешний радиус
эллиптическим и несвязанным гиперболическим
ЦЗО. Согласно современным теоретическим пред-
движением. (Вблизи этой границы резонансы (p +
ставлениям и наблюдательным данным, на границе
+ 1)/1 скапливаются и при определенном значении
ЦЗХ высока вероятность нахождения планет, по-
p начинают перекрываться, так как их ширина по
скольку миграция планет должна останавливаться
энергии убывает не так быстро, как расстояние
на границе центральной области хаоса (Пиренс,
между ними; см. Шевченко, 2015.) ЦЗХ форми-
Нельсон, 2007; Мескиари, 2012; Пардекопер и др.,
руется при μ = m2/(m1 + m2) ≳ 0.05, где m1 >
2012); эта граница может служить также и “ловуш-
> m2 —массы компонент двойной (Шевченко,
кой” для накопления протопланетного материала
2015). Радиальный размер ЦЗХ есть критиче-
(Массе и др., 2006; Мескиари, 2014) (см. обзор
ская величина большой полуоси планеты acr,
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45
№9
2019
668
ШЕВЧЕНКО и др.
соответствующая переходу от хаотической ди-
1000
намики к регулярной (при увеличении началь-
ного значения большой полуоси a). Далее мы
определяем эту величину посредством численно-
экспериментального соотношения, полученного
Хольманом и Вигертом (1999) для орбит в циркум-
100
бинарных системах:
aCZ
= 1.60 + 5.10e - 2.22e2 +
(1)
a
+ 4.12μ - 4.27eμ - 5.09μ2 + 4.61e2μ2,
10
где a и e — большая полуось и эксцентриситет
двойной системы. Начальный эксцентриситет ор-
биты планеты полагается равным нулю.
0.1
1
Масса m1[M(]
Для вычисления внутреннего и внешнего ради-
усов ЦЗО мы используем формулы модели Коп-
парапу и др. (2013), адаптированные для случая
1000
циркумбинарной иерархической планетной систе-
мы (Эггль, 2018):
(
)1/2
L1
L2
aHZ =
+
,
(2)
100
Seff,1
Seff,2
где
Seff,i = S⊙eff + aT⋆,i + bT2⋆,i + cT3⋆,i + dT4⋆,i
(3)
(i = 1, 2),
10
T⋆,i = Teff,i - 5780 K; Teff,i — эффективная темпе-
ратура i-го компонента двойной, а Li — его све-
0.1
1
тимость. Все расстояния здесь полагаются задан-
Масса m1[M(]
ными в а.е., светимости — в солнечных единицах.
Значения констант S⊙eff, a, b, c, d даны в статье
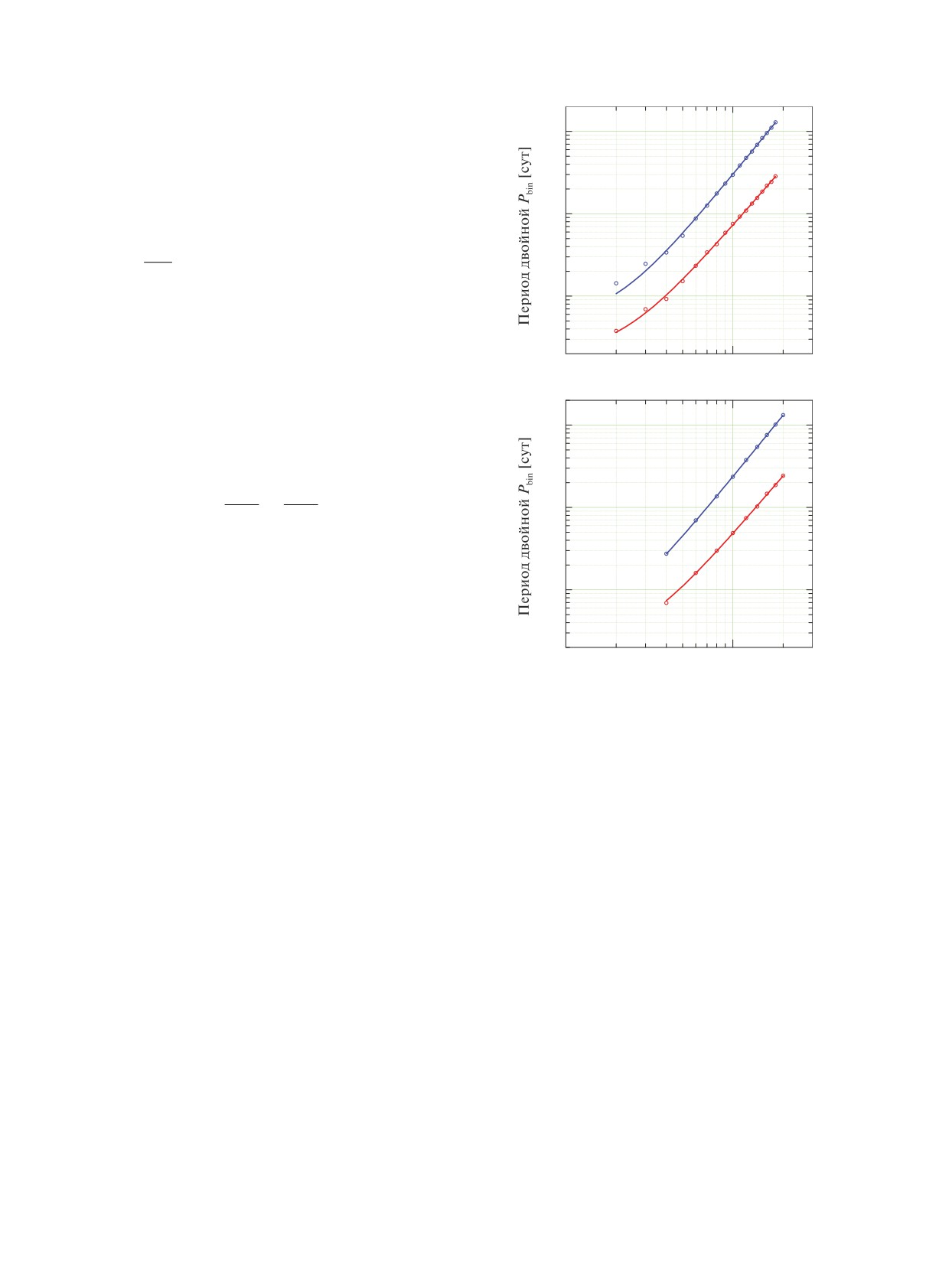
Рис. 1. Окно потенциальной обитаемости: верх-
Коппарапу и др. (2013). Для внутренней и внеш-
ний (синяякривая) и нижний(красная кривая) пределы
“окна обитаемости” для значений периодов двойной
ней границ ЦЗО значения констант различны. В
звезды, в зависимости от массы главного компонен-
случае, когда светимости L1 и/или L2 неизвестны,
та двойной. Внутри полосы, ограниченной синей и
их значения оцениваются нами посредством эмпи-
красной линиями, обеспечивается попадание границы
рического соотношения масса-светимость, приве-
ЦЗХ внутрь ЦЗО. Верхняя панель: случай двойных-
денного в Экер и др. (2015); Кунтц, Ванг (2018).
близнецов (μ = 1/2). Нижняя панель: случай двойных,
чьи компоненты отличаются по массе в два раза (μ =
Для предварительного грубого отбора потен-
= 1/3).
циально интересных объектов нами использован
критерий попадания объектов в окно потенци-
альной обитаемости (рис. 1). На рис. 1 пока-
двойных, чьи компоненты отличаются по массе
заны нижний (красная кривая) и верхний (синяя
в два раза (μ = 1/3). Предварительно разделив
кривая) пределы “окна обитаемости” для значений
двойные звезды в анализируемой выборке на двой-
периодов двойной звезды в зависимости от мас-
ные с компонентами примерно равных масс и на
сы m1 главного компонента двойной. У двойных,
двойные с компонентами сильно неравных масс,
попадающих внутрь полосы, ограниченной красной
можно легко установить, попадают ли они в “окно
и синей линиями, граница ЦЗХ находится внутри
обитаемости,” и таким образом предварительно
ЦЗО. Границы полосы, в которой обеспечивается
отождествить потенциально интересные объекты.
попадание границы ЦЗХ внутрь ЦЗО, найдены
Затем уже попадание границы ЦЗХ внутрь ЦЗО
численно с помощью формул (1) и (2). Синяя и
верифицируется с помощью приведенных выше
красная кривые представляют собой гладкую (по-
соотношений.
линомиальную) аппроксимацию дискретных чис-
При отборе потенциально интересных, с нашей
ленных данных, показанных точками.
точки зрения, двойных мы опираемся на рас-
На верхней панели представлен случай двойных
ширенную базу данных о спектрально-двойных
звезд-близнецов (μ = 1/2), а на нижней — случай
системах, построенную Экером и др. (2014). Ис-
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45
2019
№9
ЦИРКУМБИНАРНЫЕ ПЛАНЕТНЫЕ СИСТЕМЫ
669
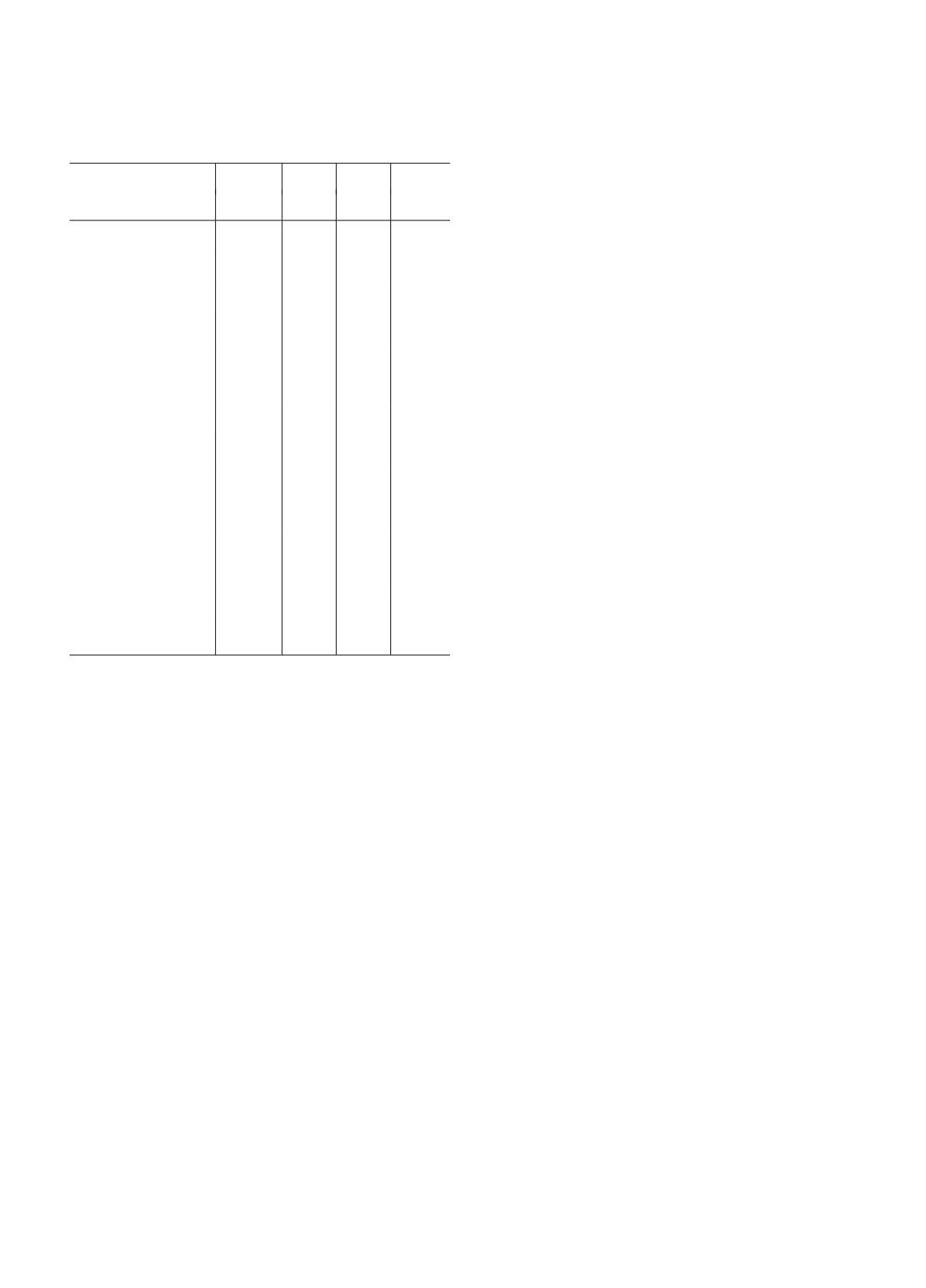
Таблица 1. Системы с потенциально обитаемыми циркумбинарными планетами: орбитальные и физические
параметры
V
d
a
Pbin
m1
m2
L1
L2
T1
T2
Система
HIP
e
μ
Ист.
m пк а.е.
сут
M⊙ M⊙
LSun
LSun
K K
M4-V69
-
15.54 1850.0 0.296 0.384
48.19 0.487 0.766 0.728
[1]
0.92062
0.71426 6084 5915
CM Dra
-
10.56
14.8 0.017 0.005
1.27 0.481 0.231 0.214
[1]
0.00550
0.00485 3130 3120
WTS 19c-3-01405
-
17.47
645.0 0.052 0.006
4.94 0.478 0.410 0.376
[1]
0.01702
0.01651 3309 3305
HATS551-027
-
12.74
39.2 0.040 0.000
4.08 0.423 0.244 0.179
[2]
0.00632
0.00340 3190 2990
EZ Aqr AC
-
9.41
3.4 0.029 0.000
3.79 0.440 0.122 0.096
[3]
0.00111
0.00046 2800 2500
LP 661-13
-
11.38
24.9 0.044 0.000
4.70 0.386 0.308 0.194
[4]
0.00978
0.00391 3200 3100
38 Cas
7078
6.05
28.6 0.640 0.310 135.32 0.366 1.210 0.700
[5]
2.27733
0.17331 6303 4287
HD 2070
1955
6.91
35.7 0.540 0.330 114.23 0.298 1.130 0.480
[5]
1.69377
0.02790 6045 3246
HD 15064
11231
6.85
28.6 0.640 0.290 143.85 0.402 1.010 0.680
[5]
1.02242
0.15062 5619 4196
HD 28394
20935
6.65
43.5 0.990 0.240 240.40 0.496 1.130 1.110
[5]
1.69377
1.56779 6045 5980
HD 160346
86400
6.67
11.1 0.390 0.230
84.44 0.351 0.720 0.390
[5]
0.19863
0.01021 4377 2785
HD 181602
95028
7.76
83.3 0.850 0.370 207.66 0.263 1.400 0.500
[5]
4.28128
0.03400 6888 3345
HIP 95110
95110
-
-
0.380
0.000
78.24 0.342 0.790 0.410
[6]
0.31126
0.01301 4687 2889
HIP 109951
109951
-
-
0.483 0.000 111.00 0.189 0.990 0.230
[6]
0.92806
0.00607 5536 3206
Примечание. Источники данных (столбец “Ист.”): [1] — Экер и др. (2014), [2] — Жу и др. (2015), [3] — Дельфосс и др. (1999),
[4] — Диттманн и др. (2017), [5] — Джайме и др. (2014), [6] — Токовинин (2018).
ходя из оценок фотометрического расстояния, мы
вычислений параметры звезд. Суммарная выборка
отобрали звезды, расположенные не далее 600 пк
включает в итоге 274 двойные звезды. Вычисления
от Солнца, согласно этой базе данных. Кроме
проведены для всех 274 звезд. Результаты расчетов
того, мы провели отождествление с каталогом Gaia
представлены только для тех из них, которые удо-
влетворяют предложенному нами критерию отбо-
DR1
ра, поскольку иначе объем статьи был бы слишком
Данный каталог построен из комбинации данных
первого года наблюдений космического телескопа
велик; кроме того, в рамках поставленной нами за-
дачи результаты для остальных звезд представляют
Gaia с положениями звезд Tycho-2; он обозначает-
лишь ограниченный интерес.
ся TGAS (Tycho-Gaia Astrometric Solution; Браун
и др., 2016; Линдегрен и др., 2016) и содержит
Данные об отобранных системах даны в табл. 1.
тригонометрические параллаксы и собственные
В ней приведены: названия системы (в том числе
движения около 2 млн звезд.
по классификации HIP, если они есть), V — на-
Исходя из имеющихся в литературе данных о
блюдаемая звездная величина, d — расстояние от
выборочных наблюдениях двойных звезд, в нашу
Солнца в пк, a — большая полуось орбиты двойной
выборку дополнительно включены пять потенци-
в а.е., e — ее эксцентриситет, Pbin — орбитальный
ально интересных двойных, чьи компоненты име-
период в сутках, m1, m2 — массы звезд в солнеч-
ют массы ≤0.5 M⊙: HATS551-027A (Жу и др.,
ных единицах M⊙, μ = m2/(m1 + m2), L1, L2 —
2015), WTS 19b-2-01387, 19c-3-01405, 19e-3-
светимости звезд в солнечных единицах L⊙, T1,
08413 (Биркби и др., 2012) и LP 661-13 (Диттманн
T2 — эффективные температуры звезд. Для каж-
и др., 2017). Ряд двойных взят из работы Джай-
дой системы дана ссылка на источник данных.
ме (2014).
Хотя в целом мы отбирали звезды, расположенные
Выбор перечисленных источников мотивирован
не далее 600 пк от Солнца, в табл. 1 включены
тем, что они содержат все необходимые для наших также две звезды, расположенные на большем
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45
№9
2019
670
ШЕВЧЕНКО и др.
x, a.u.
x, a.u.
x, a.u.
−2
-1
0
1
2
-0.2
-0.1
0
0.1
0.2
-0.4
-0.2
0
0.2
0.4
0.4
2
0.2
0.3
1
0.1
0.2
0.1
0
0
0
-0.1
-1
-0.1
-0.2
-0.3
-2
−0.2
-0.4
M4 V69
CM Dra
WTS 19c-3-01405
x, a.u.
x, a.u.
x, a.u.
−0.2
-0.1
0
0.1
0.2
-0.05
0
0.05
-0.2-0.1
0
0.1
0.2
0.2
0.075
0.2
0.050
0.1
0.1
0.025
0
0
0
-0.025
-0.1
-0.1
-0.050
-0.2
-0.2
−0.075
HATS551-027
EZ Aqr AC
LP 661-13
x, a.u.
x, a.u.
x, a.u.
−2
-1
0
1
2
-2
-1
0
1
2
-2
-1
0
1
2
2
2
3
2
1
1
1
0
0
0
-1
-1
-1
-2
-2
−2
-3
38 Cas
HD 2070
HD 28394
x, a.u.
x, a.u.
x, a.u.
−2
0
2
-1.0
-0.5
0
0.5
1.0
-1
0
1
3
1.0
1.5
2
1.0
0.5
1
0.5
0
0
0
-1
-0.5
-0.5
−2
-1.0
-3
−1.0
-1.5
HD 181602
HIP 95110
HIP 109951
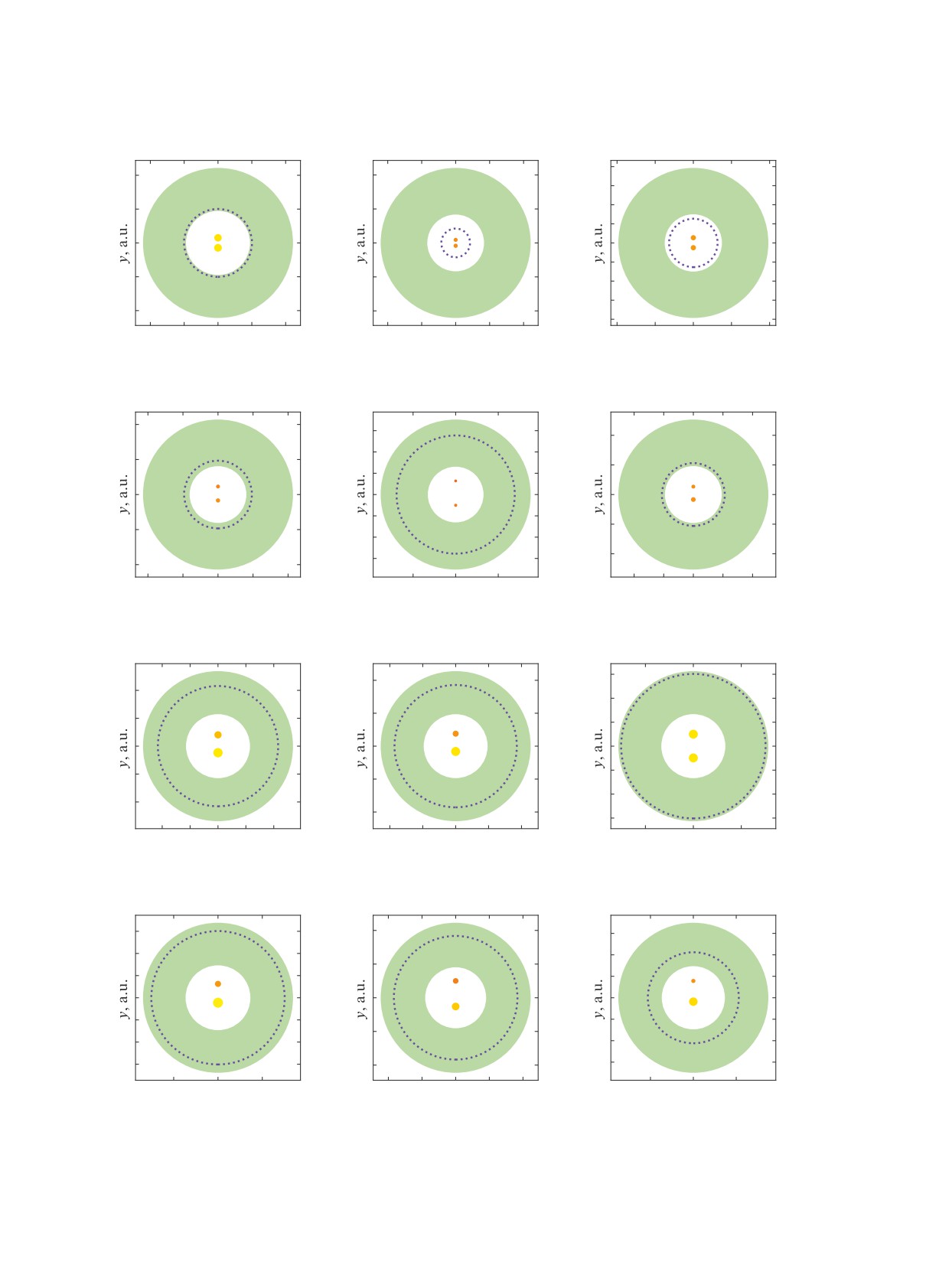
Рис. 2. ЦЗХ и ЦЗО двойных звездных систем из табл. 1 и 2. Граница ЦЗХ нанесена синей штриховой линией, ЦЗО
выделена зеленым цветом. В каждом случае двойная звезда и ее ЦЗХ и ЦЗО показаны в едином масштабе.
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45
№9
2019
ЦИРКУМБИНАРНЫЕ ПЛАНЕТНЫЕ СИСТЕМЫ
671
Таблица 2. Системы с потенциально обитаемыми цир-
Отметим, что первые четыре системы в табл. 1,
кумбинарными планетами: границы ЦЗО и ЦЗХ
2 и на рис. 1 являются затменными двойными,
остальные — либо спектрально-двойными, либо
визуально-двойными. Соответственно, первые
aCZ aHZ,in aHZ,ext
Система
HIP
четыре системы являются перспективными для
а.е.
а.е.
а.е.
наблюдений методом транзитов; остальные — для
наблюдений другими методами, если выяснится,
M4-V69
-
1.005
0.946
2.217
что их ориентация не позволяет использовать
транзитный метод.
CM Dra
-
0.042
0.084
0.221
WTS 19c-3-01405
-
0.127
0.150
0.393
ВЫВОДЫ
HATS551-027
-
0.097
0.081
0.214
Таким образом, для тесных двойных звезд в
EZ Aqr AC
-
0.069
0.033
0.088
Солнечной окрестности, имеющих достаточные ка-
таложные данные, нами вычислены радиусы внут-
LP 661-13
-
0.106
0.096
0.253
ренней и внешней границ циркумбинарной зоны
потенциальной обитаемости (ЦЗО) и радиусы цир-
38 Cas
7078
2.156
1.147
2.688
кумбинарной зоны динамического хаоса (ЦЗХ).
Нами установлено, что для двойных звезд M4-V69,
HD 2070
1955
1.858
0.971
2.278
HATS551-027, EZ Aqr A-C, 38 Cas, HD 2070,
HD 15064
11231
2.106
0.828
1.976
HD 15064, HD 28394, HD 160346 и HD 181602
граница ЦЗХ находится внутри границ ЦЗО (ра-
HD 28394
20935
3.015
1.336
3.130
диус ЦЗХ больше, чем внутренний радиус ЦЗО, но
меньше, чем внешний радиус ЦЗО).
HD 160346
86400
1.232
0.367
0.917
Для систем CM Dra, WTS 19c-3-01405 и
HD 181602
95028
3.011
1.463
3.385
LP 661-13 радиус ЦЗХ несколько меньше радиуса
внутренней границы ЦЗО; однако данные системы
HIP 95110
95110
0.918
0.453
1.114
все же представляют интерес, так как они могут об-
HIP 109951
109951
1.061
0.736
1.748
ладать планетами на внешних устойчивых орбитах,
резонансных с орбитами планет у границы ЦЗХ (в
том числе так называемыми twotino tatooines, см.
расстоянии, поскольку они представляют интерес
Шевченко, 2017).
для сопоставления с другими звездами из списка.
Авторы благодарны рецензенту за полезные за-
В табл. 2 приведены результаты расчетов границ
мечания. Работа И.И. Шевченко и А.В. Мель-
зон устойчивости и обитаемости. На рис. 2 зоны
никова частично поддержана Российским фондом
устойчивости и обитаемости для идентифициро-
фундаментальных исследований (проект № 17-02-
ванных систем представлены графически.
00028) и в рамках Программы фундаментальных
Согласно табл. 2 и рис. 2, для двойных звезд
исследований РАН КП19-270 “Вопросы проис-
M4-V69, HATS551-027, EZ Aqr A-C, 38 Cas,
хождения и эволюции Вселенной с применени-
HD 2070, HD 15064, HD 28394, HD 160346 и
ем методов наземных наблюдений и космических
HD 181602 граница ЦЗХ находится внутри границ
исследований”. Авторы заявляют об отсутствии
ЦЗО (радиус ЦЗХ больше, чем внутренний радиус
конфликта интересов.
ЦЗО, но меньше, чем внешний радиус ЦЗО). Для
системы EZ Aqr A-C данный факт был ранее уста-
СПИСОК ЛИТЕРАТУРЫ
новлен в работе Поповой и Шевченко (2016). Для
систем CM Dra, WTS 19c-3-01405 и LP 661-13
1. Барклай и др. (T. Barclay, J. Pepper, and
E.V. Quintana), Astrophys. J. Suppl. Ser. 239, 2
радиус ЦЗХ несколько меньше радиуса внутренней
(2018).
границы ЦЗО.
2. Биркби и др. (J. Birkby, B. Nefs, S. Hodgkin, et al.),
В случае системы HD
28394
внешний ра-
MNRAS 426, 1507 (2012).
диус ЦЗО лишь ненамного больше радиуса
3. Браун и др. (Gaia Collaboration, A.G.A. Brown,
границы ЦЗХ. Однако эта система, на наш
A. Vallenari, T. Prusti, J. de Bruijne, F. Mignard,
взгляд, все же потенциально интересна, поскольку
R. Drimmel, et al.), Astron. Astrophys. 595, 2 (2016).
определяемые границы ЦЗО в сильной степени
4. Дворак (R. Dvorak), Celest. Mech. 34, 369 (1984).
модельно-зависимы. Например, в модели Селсиса
5. Дельфосс и др. (X. Delfosse, T. Forveille, S. Udry, et
и др. (2007) внешний радиус ЦЗО для этой системы
al.), Astron. Astrophys. 350, 39 (1999).
больше, чем в использовавшейся здесь модели
6. Джайме и др. (L.G. Jaime, B. Pichardo, and
Коппарапу и др. (2013).
L. Aguilar), MNRAS 427, 2723 (2012).
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45
№9
2019
672
ШЕВЧЕНКО и др.
7.
Джайме и др. (L.G. Jaime, L. Aguilar, and
24.
Пардекопер и др. (S.-J. Paardekooper,
B. Pichardo), MNRAS 443, 260 (2014).
Z.M. Leinhardt, T. Th ´ebault, and C. Baruteau),
8.
Диттманн и др. (J.A. Dittmann, J.M. Irwin,
Astrophys. J. 754, L16 (2012).
D. Charbonneau, et al.), Astrophys. J. 836,
124
25.
Пиренс, Нельсон (A. Pierens and R. P. Nelson),
(2017).
Astron. Astrophys. 472, 993 (2007).
9.
Дюкеннуа, Мейор (A. Duquennoy and M. Mayor),
26.
Пичардо и др. (B. Pichardo, L.S. Sparke, and
Astron. Astrophys. 248, 485 (1991).
L.A. Aguilar), MNRAS 359, 521 (2005).
10.
Жу и др. (G. Zhou, D. Bayliss, J.D. Hartman, et al.),
27.
Пичардо и др. (B. Pichardo, L.S. Sparke, and
MNRAS 451, 2263 (2015).
L.A. Aguilar), MNRAS 391, 815 (2008).
11.
Кастинг и др. (J.F. Kasting, D.P. Whitmire, and
28.
Попова Е.А., Шевченко И.И., Письма в Аст-
R.T. Reynolds), Icarus 101, 108 (1993).
рон. журн. 42, 294 (2016).
[E.A. Popova and
12.
Коппарапу и др. (R.K. Kopparapu, R. Ramirez,
I.I. Shevchenko, Astron. Lett. 42, 260 (2016)].
J.F. Kasting, et al.), Astrophys. J. 765, 131 (2013).
13.
Коппарапу и др. (R.K. Kopparapu, R. Ramirez,
29.
Селсис и др. (F. Selsis, J.F. Kasting, B. Levrard, et
J. SchottelKotte, et al.), Astrophys. J. Lett. 787, L29
al.), Astron. Astrophys. 476, 1373 (2007).
(2014).
30.
Токовинин (A. Tokovinin), Astrophys. J. 156,
2
14.
Костов (V. Kostov)
“Discovering Circumbinary
(2018).
Planets with TESS.”
30th IAU GA, Vienna
31.
Хольман, Вигерт (M.J. Holman and P.A. Wiegert),
Astron. J. 117, 621 (1999).
ac.at/division-days/ddf/
32.
Шварц и др. (R. Schwarz, N. Haghighipour, S. Eggl,
15.
Кунтц (M. Cuntz), Astrophys. J. 780, A14 (2014).
et al.), MNRAS 414, 2763 (2011).
16.
Кунтц (M. Cuntz), Astrophys. J. 798, 101 (2015).
33.
Шварц и др. (R. Schwarz, B. Funk, R. Zechner, et
17.
Кунтц, Брунц (M. Cuntz and R. Bruntz), Cool Stars,
al.), MNRAS 460, 3598 (2016).
Stellar Systems, and the Sun: 18th Cambridge
34.
Шевченко (I.I. Shevchenko), Astrophys. J. 799, 8
Workshop (Ed. G. van Belle & H. Harris, Flagstaff:
(2015).
Proc. Lowell Observatory, 2014), p. 845.
18.
Кунц, Ванг (M. Cuntz and Z. Wang), Res. Not. Amer.
35.
Шевченко (I.I. Shevchenko), Astron. J. 153, 273
Astron. Soc. 2, 19 (2018).
(2017).
19.
Линдегрен и др. (L. Lindegren, U. Lammers,
36.
Шевченко (I.I. Shevchenko), Astron. J. 156,
52
U. Bastian, et al.), Astron. Astrophys. 595, 4 (2016).
(2018).
20.
Массе и др. (F.S. Masset, A. Morbidelli, A. Crida, and
37.
Эггль (S. Eggl), Handbook of Exoplanets (Ed. by
J. Ferreira), Astrophys. J. 642, 478 (2006).
H.J. Deeg and J.A. Belmonte, Springer International
21.
Мескиари (S. Meschiari), Astrophys. J. 752,
71
Publishing, 2018), p. 1.
(2012).
38.
Экер и др. (Z. Eker, S. Bilir, F. Soydugan, et al.),
22.
Мескиари (S. Meschiari), Astrophys. J. 790,
41
Publ. Astron. Soc. Australia 31, e024 (2014).
(2014).
23.
Мюллер, Хагигипур (T.W.A. M ¨uller and
39.
Экер и др. (Z. Eker, F. Soydugan, E. Soydugan,
N. Haghighipour), Astrophys. J. 782, 26 (2014).
et al.), Astron. J. 149, 131 (2015).
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 45
№9
2019