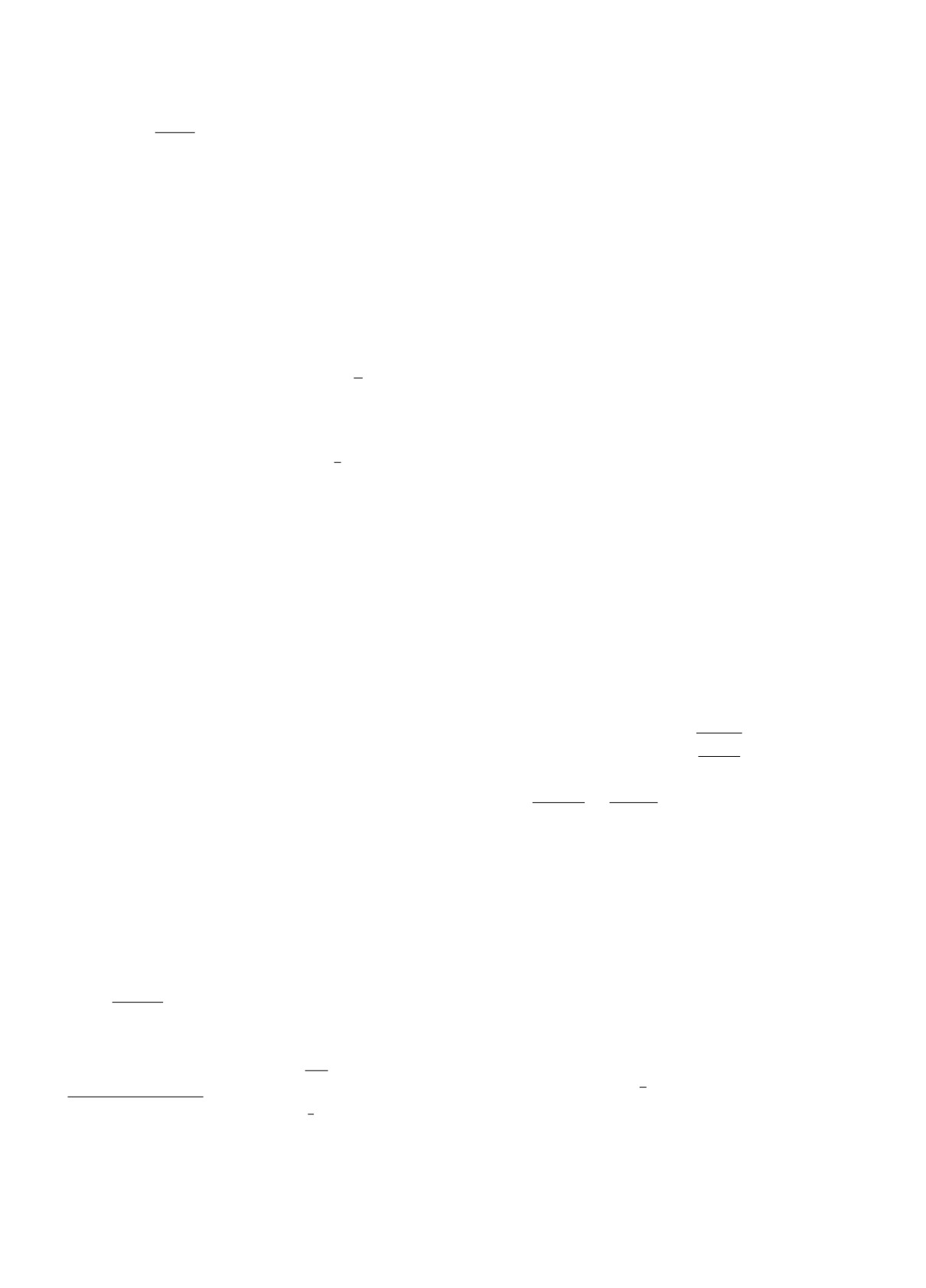ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2020, том 46, № 1, с. 15-26
О МЕХАНИЗМЕ ЛИНДЕН-БЕЛЛА ОБРАЗОВАНИЯ БАРОВ
В ГАЛАКТИЧЕСКИХ ДИСКАХ
© 2020 г. Е. В. Поляченко1*, И. Г. Шухман2**
1Институт астрономии РАН, Москва, Россия
2Институт солнечно-земной физики СО РАН, Иркутск, Россия
Поступила в редакцию 27.09.2019 г.
После доработки 13.11.2019 г.; принята к публикации 18.11.2019 г.
Один из возможных механизмов образования баров в дисках галактик был предложен Линден-Беллом
(1979). В его основе лежит предполагаемое усиление слабого затравочного овального возмущения
поверхностной плотности звезд в центральных областях галактики за счет выстраивания больших
осей прецессирующихэллиптических орбит. Согласно его качественным рассуждениям,выстраивание
орбит вдоль возмущения имеет место, если угловая скорость прецессии убывает с уменьшением
углового момента при постоянном значении адиабатического инварианта. Используя строгий подход,
основанный на нахождении устойчивых стационарных точек системы, мы показываем, что данное
условие не является единственным, определяющим ориентацию выстраивания орбит. Существенными
оказываются также направление прецессии орбиты в невозмущенном потенциале и скорость убывания
амплитуды потенциала бара с радиусом. В некоторых случаях последние даже могут быть более
важными.
Ключевые слова: звездные системы, звездная динамика.
DOI: 10.31857/S0320010819120052
ВВЕДЕНИЕ
потенциала Ωp, мала по сравнению с орбитальной
угловой скоростью звезды, Ω,
Вопрос о механизмах образования и поддер-
|Ωpr|
жания баров в центральных областях дисковых
≪ 1,
(1)
Ω
галактик является одним из ключевых вопросов
динамики галактик. Сейчас считается общеприня-
то звезда чувствует потенциал, усредненный по
тым, что большинство из них является результа-
орбите. Для такой орбиты в неаксиально-симмет-
том развития неустойчивости бар-моды аксиально
ричном потенциале угловой момент L и радиальное
симметричного диска (Поляченко, Фридман, 1976;
действие звезды I не сохраняются, но сохраняется
Бинни, Тримейн 2008; Селвуд, Уилкинсон, 1993).
адиабатический инвариант Jf = L/2 + I. Линден-
Это может быть справедливо также для галактик,
Белл обратил внимание, что если скорость пре-
имеющих в центре классический балдж (Поля-
цессии орбиты Ωpr уменьшается при уменьшении
ченко и др., 2016). Однако данный механизм не
углового момента при фиксированном Jf , то боль-
является единственным из возможных.
шие оси эллипсов прецессирующих орбит могут
оказаться запертыми в потенциале возмущения,
Альтернативный и очень изящный подход к об-
тем самым его усиливая и формируя бар. В случае
разованию баров был предложен Линден-Беллом
же, когда скорость прецессии растет с уменьше-
(1979), который не опирается на представление о
нием углового момента, большие оси орбит будут
неустойчивости, возникающей в самосогласован-
стремиться выстроиться поперек возмущения, и
ной системе. Пусть имеется случайное нарушение
тогда ожидать образования бара нельзя.
аксиальной симметрии или внешний затравочный
Ключевую роль в поддержании бара в механиз-
овальный потенциал. Если угловая скорость пре-
ме Линден-Белла играет знак производной угловой
цессии Ωpr звездной орбиты в системе отсчета, вра-
скорости прецессии по угловому моменту при фик-
щающейся со скоростью овального возмущения
сированном значении адиабатического инварианта
Jf , т.е. [∂Ωpr(L,I)/∂L]Jf . Эта величина получила
*Электронный адрес: epolyach@inasan.ru
**Электронный адрес: shukhman@iszf.irk.ru
в литературе название линден-белловской (ЛБ)
15
16
ПОЛЯЧЕНКО, ШУХМАН
(a)
(b)
i
i
p
p
CR
ILR
CR
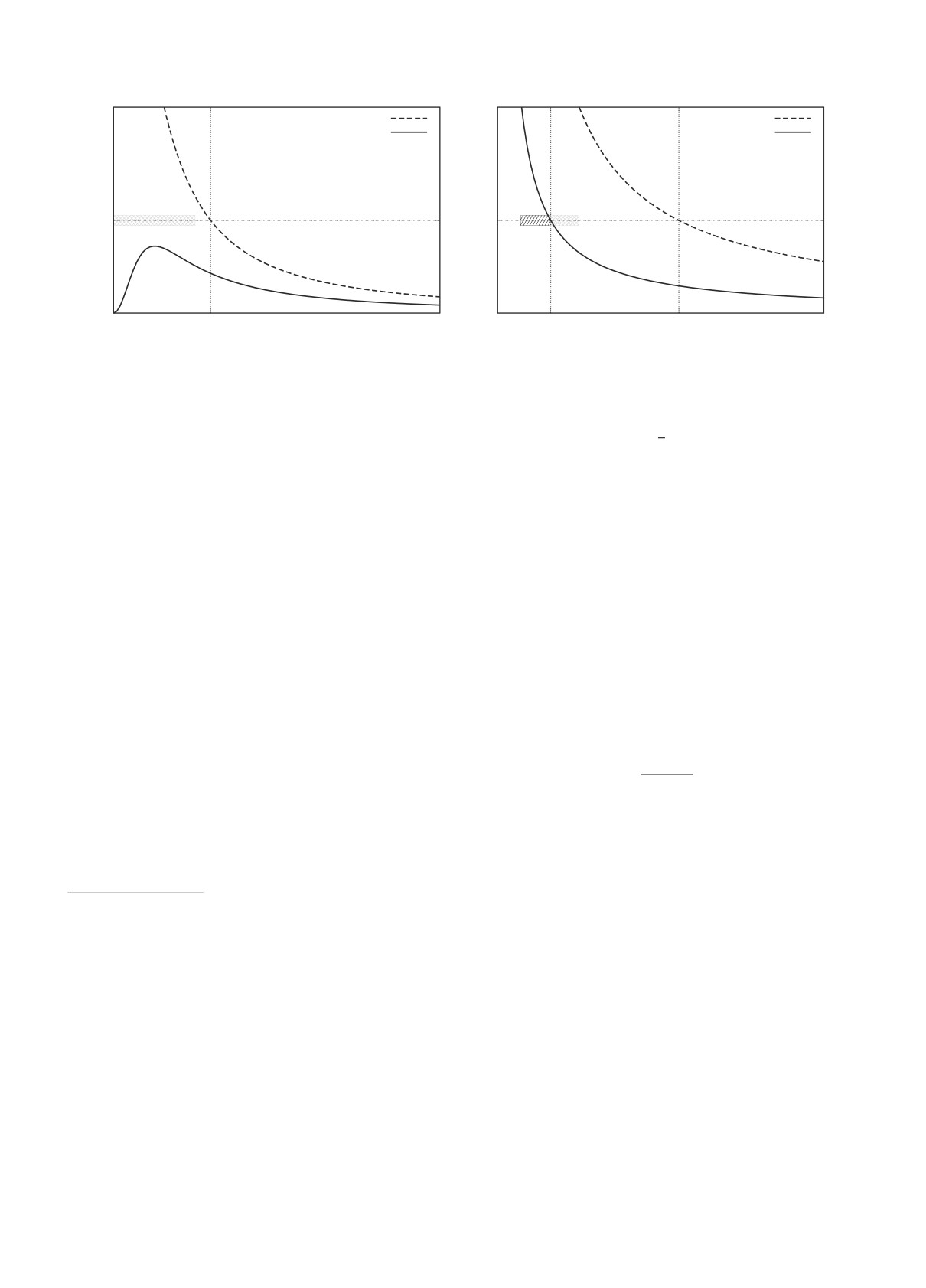
Рис. 1. Кривая вращения Ω(R) и кривая Ωi(R) для моделей с несингулярным (a) и сингулярным (b) потенциалами в
центре. Штриховые полоски показывают область применимости подхода, основанного на усреднении движения звезды
по орбите.
производной, и она широко используется не только
кривой Ωi(R) ≡ Ω(R) -12 κ(R), где κ — эпицикли-
в литературе по динамике дисков, но и при об-
ческая частота, определяющей скорость прецессии
суждении механизмов неустойчивости радиальных
почти круговых орбит в системе бара
орбит (НРО) в сферических системах [см., напри-
Ωpr = Ωi - Ωp,
(2)
мер, дискуссию в статьях Поляченко, Поляченко и
Шухмана (2015a) и Поляченко и Шухмана (2015b)
имеет невысокий максимум.
и цитированные там работы]. Следует отметить,
На рис. 1a показаны типичные кривые для угло-
однако, что положительный знак ЛБ-производной
вой скорости Ω(R) и кривая Ωi(R) для несингуляр-
в дисковых галактиках встречается довольно ред-
ных моделей.
ко. Гораздо чаще имеет место противоположная
Если max{Ωi(R)} ≪ Ω(R), то при Ωp ≳ max Ωi,
ситуация, когда эта производная отрицательна.
условие (1) будет выполнено. В этом случае адиа-
Поэтому орбиты с отрицательной ЛБ-производной
батический подход действительно оправдан в ши-
называют нормальными, а с положительной ЛБ-
рокой области по радиусу (почти до радиуса ко-
производной — аномальными1 . Подчеркнем, что
ротации), то есть можно работать с усредненным
важность роли ЛБ-производной скорости прецес-
вдоль орбиты потенциалом и считать, что сохра-
сии жестко связана с условием (1), означающим
няется адиабатический инвариант Jf . Для приме-
медленность скорости прецессии в системе бара по
ра потенциала с аномальными орбитами Линден-
сравнению с динамической частотой звезды. Од-
Белл (1979) использовал изохронный потенциал:
√
нако такое условие может выполняться не всегда.
Φ0(r) = -GM/[b +
r2 + b2]. Согласно его расче-
Есть два очевидных случая, когда оно может быть
там, для этой модели max{Ωi} ≈ 0.05(GM/b3)1/2
выполнено.
и достигается при R ≈ 1.5b (угловая скорость на
Первый — когда угловая скорость вращения
этом радиусе Ω ≈ 0.3(GM/b3)1/2 ≫ max{Ωi}), а
Ω(R) соответствует несингулярным в центре рас-
область, в которой почти круговые орбиты ведут
пределениям потенциала. В этом случае профиль
себя аномально, простирается примерно до R =
1 В этом, кстати, отличие почти круговых орбит в дис-
= 4b. В этой области все орбиты могут выстроиться
ках от почти радиальных орбит в сферических звездных
вдоль возмущения, вращающегося с угловой ско-
системах, которые в основном являются аномальными.
ростью Ωp ≳ 0.05(GM/b3)1/2.
Аномальность почти радиальных орбит в сферических
системах породила гипотезу, впервые сформулированную
Второй случай, для которого адиабатический
Мерриттом (1987), а затем поддержанную рядом других
подход оправдан, это область вблизи внутренне-
авторов (Вайнберг, 1991, Саха, 1991; Палмер, 1994), что
го линдбладовского резонанса (ILR), R = RL, где
НРО имеет ту же природу, что и линден-белловский
скорость прецессии в системе бара, равна нулю,
механизм выстраивания орбит вдоль бара в дисках. В
Ωpr(RL) = 0. Почти круговые орбиты, радиус ве-
работе Поляченко и Шухмана (2015b) показано, что
дущего центра которых, R, равен RL представляют
справедливость такой гипотезы верна лишь отчасти, а
именно только для некоторого класса функций распреде-
собой слабо эксцентричные 2:1 эллипсы, покоящи-
ления звезд, для которых НРО достаточно медленная по
еся в системе бара. Орбиты, с радиусом ведущего
сравнению с характерным динамическим временем Tdyn ∼
центра, слегка отличающегося от RL, прецессиру-
∼ (GM/R3)-1/2. В противном случае представление об
ют со скоростью
орбите как отдельном объекте, которое эксплуатируется
в этой гипотезе, становится неоправданным.
Ωpr(R) ≈ Ω′i(RL)(R - RL) .
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
О МЕХАНИЗМЕ ЛИНДЕН-БЕЛЛА
17
Поскольку для моделей с сингулярным потенци-
ГАМИЛЬТОНИАН ЯКОБИ И УСРЕДНЕНИЕ
алом (см. рис. 1b) Ωi везде убывает с радиусом,
ПОТЕНЦИАЛА
dΩpr/dR < 0, прецессия орбит в области снаружи
Пусть на фоне равновесного аксиально-сим-
метричного потециала диска Φ0(r) имеется слабое
от ILR (R > RL) является ретроградной (враще-
овальное возмущение потенциала δΦ, вращающее-
ние орбиты в системе бара в сторону, противо-
ся с угловой скоростью Ωp, которое в этой системе
положную вращению самой звезды по орбите в
отсчета имеет вид
покоящейся системе отсчета), а в области внутри
δΦ(r,ϕ) = A(r)cos(2ϕ).
(3)
ILR (R < RL) — прямой, т.е. в сторону вращения
звезды по орбите. Ниже мы увидим, что наряду с
Будем считать, что A < 0. Тогда впадины потен-
ЛБ-производной скорости прецессии, решающее
циала вытянуты вдоль оси OX, а гребни — вдоль
значение для установления направления выстраи-
оси OY. Соответственно большая ось овального
вания орбит имеет знак прецессии, определяющий
возмущения поверхностной плотности σ (то есть,
направление прецессии орбит в невозмущенном
бара, порождающего этот потенциал), ориентиро-
потенциале.
вана вдоль оси OX.
Исследуем орбиты звезд, близких к круговым, в
Ниже для удобства будем обозначать модели и
потенциале Φ(r, ϕ) = Φ0(r) + δΦ(r, ϕ). Поскольку
кривые Ωi(R), подобные изображенным на рис. 1a,
потенциал стационарен в системе отсчета бара, при
движении звезды сохраняется интеграл Якоби
типом I, а подобные изображенным на рис. 1b,
типом II.
HJ(L,I,r,φ) = H0(L,I) + δΦ(r,φ),
(4)
— невозмущенный гамильтониан, записан-
где H0
Цель предлагаемой статьи — детально проана-
ный в системе отсчета, вращающейся со скоростью
лизировать качественные рассуждения, касающи-
Ωp, который в эпициклическом приближении (I ≪
еся важности ЛБ-производной скорости прецес-
≪ L) имеет вид
сии для нахождения ориентации больших осей
1
эллипсов запертых орбит. Для этого мы найдем
H0(L,I) =
Ω2(R)R2 + Φ0(R) +
(5)
2
устойчивые стационарные точки гамильтониана
+ κ(R)I + β(R)I2 - ΩpL.
Якоби на фазовой плоскости переменных (I, φ) при
фиксированном Jf , где φ — угол, характеризую-
Здесь
щий ориентацию эллипса, и выясним, при каких
R = R(L), L = L(R) = Ω2(R)R,
условиях этот угол соответствует выстраиванию
1 dΦ0(R)
орбит вдоль, а при каких — поперек бара. Мы
Ω2(R) =
,
рассмотрим оба упомянутых выше вида потенциала
R dR
(
)1/2
при выполнениии условий применимости усред-
dΩ2
κ(R) =
4Ω2 + R
,
нения потенциала по орбите и покажем, что хотя
dR
для типа I характерно выстраивание аномальных
R —радиус ведущего центра. Далее в зависимости
орбит вдоль бара, главной причиной этого явля-
от удобства, мы будем в качестве независимой пе-
ется не положительный знак ЛБ-производной, а
ременной использовать либо угловой момент L, ли-
ретроградность прецессии в системе бара, которая
бо R. Малое слагаемое β(R)I2, соответствующее
имеет место для достаточно быстрых баров, Ωp ≳
пост-эпициклическому приближению, включено в
≳ max{Ωi}. То же касается и моделей типа II.
гамильтониан для того, чтобы можно было учесть
Орбиты снаружи от ILR благодаря ретроградности
c одинаковой точностью зависимость от I ради-
прецессии в этой области, выстраиваются вдоль
альной Ω1(L, I) и азимутальной Ω2(L, I) частот,
бара, а внутри ILR — перпендикулярно бару. Знак
отвечающих переменным действия I1 ≡ I и I2 ≡ L
ЛБ-производной играет второстепенную роль, так
соответственно:
что даже нормальная орбита может оказаться ори-
∂H0(L,I)
Ω1(L,I) =
= κ + 2βI + O(I2),
(6)
ентированной вдоль бара. Мы покажем также, что
∂I
если скорость убывания на периферию амплитуды
∂H0(L,I)
dκ
потенциала бара достаточно велика, это может
Ω2(L,I) =
=Ω-Ωp +
I + O(I2).
∂L
dL
привести к изменению полученных результатов,
Явный вид β можно получить, пользуясь вычис-
касающихся ориентации орбит, на противопо-
лениями, приведенными, например, в работах Шу
ложные (ориентация вдоль бара поменяется на
(1969), Марка (1976) или Бертина (2014):
ориентацию поперек бара и наоборот при тех же
(
)
знаках прецессии и ЛБ-производной скорости
1
1
1
dq
β =
3q -
q2 +
R
,
(7)
прецессии).
8R2
3
2
dR
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
18
ПОЛЯЧЕНКО, ШУХМАН
d ln(κ2)
≡ b(R)I1/2 > 0,
q=
d ln R
в отличие от знака амплитуды A. Здесь I =
В дальнейшем будем считать, что условие (1)
= I(Jf,L) = Jf - 12L. В результате мы получаем
выполнено. Это означает возможность усреднить
усредненный потенциал Якоби
потенциал δΦ по быстрому движению:
(
)
HJ
L,I(L,Jf ),φ
=
(14)
V (L, Jf , φ) =
(8)
∮
= H0(L,I) + B(L,I)cos(2φ).
1
=
δΦ (r(L,Jf ,w1),ϕ(L,Jf ,w1,φ)) dw1,
Согласно (10), направлению большой оси ор-
2π
биты отвечает значение w1
= π, и из (9) видно,
где мы, аналогично Поляченко (2004, 2005), ввели
что соответствующее значение угловой переменной
∮
вместо переменных действия I1 = (2π)-1
rdr и
φ сдвинуто относительно азимута апоцентра ϕ на
I2 = L, и соответствующих им угловых переменных
π/2. Поэтому положению апоцентров орбиты на
w1 и w2, новые переменные действие-угол, а имен-
оси OX, т.е. вдоль бара, отвечают значения φ =
но, угловые переменные
=12π;32π. В следующем разделе мы исследуем ста-
1
ционарные точки гамильтониана и найдем возмож-
w1,φ = w2 -
w1,
(9)
ные стационарные ориентации орбит. Положение
2
стационарных точек зависит, в том числе, от знака
которые являются сопряженными переменным
величины B.
действия Jf (=12 L + I) и L соответственно. Смысл
введения этих переменных в том, что таким образом
СТАЦИОНАРНЫЕ ТОЧКИ
отделяется быстрое орбитальное движение, w1, от
ГАМИЛЬТОНИАНА ЯКОБИ
медленного прецессионного, φ. Действительно,
Cтационарные точки определяются из условия
dw1
dφ
1
[
(
)
]
=Ω1,
= (Ω2 - Ωp) -
Ω1 ≪ Ω1.
∂HJ
L,I,φ
dt
dt
2
= 0,
(15)
∂L
Величина dφ/dt представляет собой (малую) ско-
Jf
рость прецессии орбиты в невозмущенном потен-
(
)
∂HJ
L,I,φ
циале во вращающейся системе отсчета или, что
= 0,
то же самое, скорость изменения угла ориентации
∂φ
большой оси эллиптической орбиты φ.
что дает
Используя эпициклическую связь между пере-
(∂B)
менными в реальном пространстве (r, ϕ) и пере-
Ωpr(L,I) +
cos 2φ = 0,
(16)
∂L
Jf
менными в пространстве действие-угол (cм., на-
пример, Бинни, Тримейн, 2008)
sin(2φ) = 0,
2Ω ρ
где
r = R - ρcosw1, ϕ = w2 +
sin w1,
(10)
κ R
1
Ωpr(L,I) = Ω2(L,I) - Ωp -
Ω1(L,I).
(17)
найдем явный вид усреденного вдоль орбиты по-
2
тенциала:
Учитывая, что (∂/∂L)Jf = (∂/∂L)I -12 (∂/∂I)L,
V = B(L,Jf)cos(2φ),
(11)
и что для орбит, близких к круговым, (∂/∂L)I ≪
где
≪ (∂/∂I)L, запишем условия (16) в виде
)
A(R)( ρ)(R dA
4Ω
1
B(L, Jf ) = -
+
,
(12)
Ωpr(L,I) = ±
I-1/2b(L);
(18)
2
R A dR
κ
4
√
1
3
ρ=
2I/κ — размер эпицикла. Если абсолютная
φ = 0;π; φ =
π;
π.
(19)
2
2
величина амплитуды потенциала бара убывает с
радиусом не слишком быстро, так что
Верхний знак, (+), в правой части (18) соответ-
dln|A|
ствует случаю φ = 0; π, т.е., как мы установили
4Ω
,
выше, выстраиванию орбиты перпендикулярно ба-
<
dlnR
κ
ру, а нижний знак, (-), соответствует случаю φ =
то знак амплитуды усредненного потенциала B
=12π;32π, т.е. выстраиванию орбиты вдоль бара.
положителен, B > 0:
Дальнейшая задача состоит в том, чтобы выяснить,
[√
]
при каких условиях реализуется тот или иной из
2I
2Ω
B(L, Jf ) ≈ -A(R)
≡
(13)
этих двух случаев. Рассмотрим модели I и II по
κR2 κ
отдельности.
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
О МЕХАНИЗМЕ ЛИНДЕН-БЕЛЛА
19
Стационарные точки для моделей типа I
есть не что иное, как ЛБ-производная скорости
прецессии в пределе малых I. Таким образом, урав-
Имеем из (6) для скорости прецессии в невозму-
нение для стационарных точек (18) приобретает
щенном потенциале в системе бара:
вид
1
1
Ωpr ≡ Ω2 - Ωp -
Ω1 =
(20)
QI1/2 - 2PI3/2 = ±
b,
(24)
2
[
]
4
dκ
= Ω(L) +
I-Ωp
-
где Q = Ωpr (L0 + 2Jf ) — скорость прецессии ор-
dL
[
]
биты в невозмущенном потенциале в системе бара
1
и пределе I → 0, с радиусом ведущего центра,
-
κ(L) + β(L)I
,
2
соответствующим угловому моменту L0 + 2Jf . Для
или
моделей типа I в случае, когда Ωp ≳ max{Ω(R) -
1
-
κ(R)}, величина Q везде отрицательна, т.е.
Ωpr = Ωp
(21)
2
r (L) + μ(L)I,
прецессия всегда ретроградная. Однако, знак P
может быть как положительным (аномальная ор-
где введены новые обозначения Ωpr (L) ≡ Ωi(L) -
бита), так и отрицательным (нормальная орбита).
− Ωp = [Ω(L) - Ωp] - 12κ(L) для скорости прецес-
Заметим, что усредненный гамильтониан Якоби
сии в системе бара в пределе I → 0 и величина
HJ в переменных (I,φ) при фиксированном Jf
μ(L) ≡ dκ/dL - β.
(в котором опущен постоянный вклад, зависящий
Для слабо-эллиптических орбит с ведущим
центром в окрестности некоего радиуса R = R0
только от Jf и L0) можно представить в виде2 :
(с соответствующим угловым моментом L = L0 =
HJ = -2QI + 2PI2 + bI1/2 cos(2φ).
(25)
= Ω(R0)R20) имеем
Проанализируем решения уравнения (24). Име-
Ωpr(L,I) ≈ Ωpr (L0) +
(22)
(
)
ем f(I1/2) = ±14 b, где
dΩp
r
+
ΔL + μ(L0)I,
f (z) = Qz - 2Pz3.
(26)
dL
L0
Положение стационарных точек зависит от относи-
ΔL = L - L0.
тельных знаков и Q и P.
Вместо адиабатического интеграла Jf удобно вве-
(i). В случае Q < 0, P < 0 кривая f(I1/2) имеет√
сти его “усеченный” вариант:
1
отрицательный минимум при I1/2 =
Q/P, рав-
6
1
1
ный
Jf ≡ I +
ΔL = Jf -
L0,
2
2
2Q
( Q)1/2
полагая, что ΔL и I — величины одного порядка.
fmin =
< 0.
3
6P
Подставляя вместо ΔL его выражение через Jf и
I, найдем:
В этом случае возможны либо одна, либо три ста-
ционарных точки в зависимости от величины ам-
Ωpr(L,I) ≈ Ωpr (L0) +
плитуды b (пока считаем ее положительной). При
(
)
b < bcrit ≡ 4|fmin| имеем три стационарные точки:
dΩp
r
+2
(Jf - I) + μ(L0)I,
dL
2 Запись гамильтониана в виде (25) означает, что мы при-
L0
нимаем следующий скейлинг малых величин по отно-
или
шению к малой амплитуде потенциала бара A, которую
мы полагаем величиной порядка ε ≪ 1: b = O(ε), I1/2 =
Ωpr(L,I) ≈ Ωpr (L0 + 2Jf ) -
(23)
[(
)
]
= O(ε1/3), Q ≡ Ωpr = O(ε2/3), P ≡ (∂Ωpr/∂L)Jf = O(1),
dΩpr)
1
Jf = O(I) = O(ΔL) = O(ε2/3), так что HJ = O(ε4/3) +
-2
-
μ(L0) I =
+ ..., где многоточие означает вклады более высокого по-
dL
2
L0
рядка по ε. Выбранное упорядочение позволяет избежать
необходимости учета более высоких порядков эпицикли-
=Ωp
r (L0 + 2Jf ) - 2PI.
ческого приближения (выше, чем O(I1/2)) при вычис-
лении невозмущенных орбит и усредненного потенциала
Из (21), легко видеть, что величина
бара V (L, I, φ), что привело бы к гораздо более гро-
(
)
моздким вычислениям и формулам (см., например, работу
dΩp
1
r
Контопулоса (1975), в которой рассчитаны траектории
P =
dL
-2μ(L0)
орбит вблизи внутреннеголиндбладовскогорезонанса для
L0
случая возмущающего потенциала в виде спирали).
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
20
ПОЛЯЧЕНКО, ШУХМАН
f
b < 4|fmin|
b/4
1/2
I
(4/63)1/2
I1/2(4/23)1/2
I1/2
1
2
3
0
I1/2
-b/4
fmin
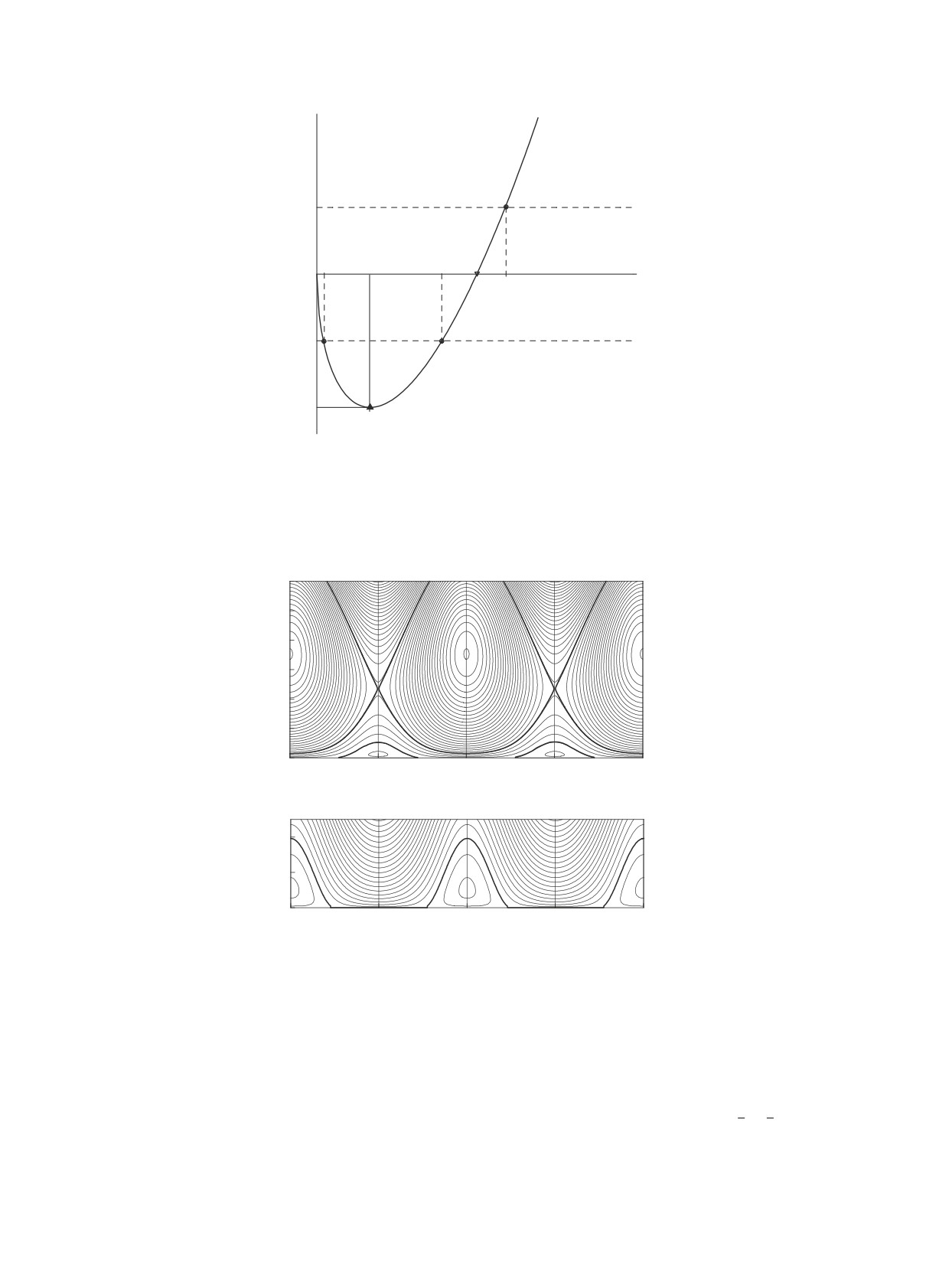
Рис. 2. Функция f(I1/2) для случая Q < 0, P < 0 и b < 4|fmin|. Здесь возможны 3 стационарныеточки: две для знака - и
одна для знака + в правой части (24). Из них устойчивыми являются только две, I1 и I3. Первая из них дает ориентацию
вдоль бара, вторая — поперек бара. Точка I2 соответствует седловой точке гамильтониана и является неустойчивой. При
b > 4|fmin| = bcrit возможнатолькоодна стационарнаяточка, соответствующаязнаку +(в областиf > 0). Она устойчива
и дает ориентацию поперек бара.
4 < 0, 3 < 0, b < bcrit
(a)
I
0
π/2
π
3π/2
2π
φ
4 < 0, 3 < 0, b > bcrit
(b)
I
0
π/2
π
3π/2
2π
φ
Рис. 3. Изолинии гамильтониана Якоби HJ (I,φ) (25) для кривых вращения типа I для случая нормальных орбит,
ЛБ-производная cкорости прецессии отрицательна, P < 0. (a) — b < bcrit, (b) — b > bcrit.
I1 < I2 < I3, причем, две из них, I1 и I2, соответ-
линии HJ (I, φ)) для случая нормальных орбит,
ствуют выбору знака минус в правой части (24),
P < 0, для кривых вращения типа I. Видно, что
а третья, I3 соответствует выбору знака плюс. На
если b < bcrit существуют два вида стационарных
рис. 2 показано взаимное расположение точек в
орбит, соответствующих экстремумам гамильтони-
случае b < bcrit.
ана — вытянутые вдоль бара (φ =12 π;32 π), и вытя-
При b > bcrit есть только одна стационарная
точка, соответствующая знаку плюс.
нутые, перпендикулярно бару (φ = 0; π). Имеется
На рис. 3a показаны фазовые портреты (изо- две сепаратриссы (показаны жирными линиями),
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
О МЕХАНИЗМЕ ЛИНДЕН-БЕЛЛА
21
4 < 0,
3 > 0
I
0
π/2
π
3π/2
2π
φ
Рис. 4. То же, что на рис. 3 для случая аномальных орбит,P >
0. Стационарные точки соответствуют орбитам, вытянутым
вдоль бара: (φ =1π;3π).
2
2
разделяющие области либрирующих (запертых) и
внутреннего линдбладовского резонанса. Имеем
циркулирующих (пролетных) орбит. Верхняя се-
из (21) вблизи R = RL, или, что то же самое, вбли-
паратрисса состоит из двух ветвей, пересекаю-
зи LILR, где [Ω(RL) - Ωp] -12κ(RL) = 0, LILR =
щихся в седловых точках, которые соответству-
= (ΩR2)R=RL :
ют неустойчивым стационарным точкам I = I2, φ =
(
)
=12π;32π (см. рис. 2). Нижняя сепаратрисса соот-
dΩp
r
ветствует HJ = 0. При b > bcrit (рис. 3b) сепара-
Ωpr =
ΔL + μILRI,
(27)
dL
трисса состоит из одной ветви, соответствующей
ILR
HJ = 0. Замкнутые изолинии, окружающие экс-
где нижний индекс означает, что соответствующая
тремальные точки, отвечают орбитам, запертым в
величина берется при L = LILR. Подставляя сюда
потенциале бара.
ΔL = 2Jf - 2I, получим уравнение для нахожде-
(ii). В случае аномальной орбиты, Q < 0, P > 0
ния стационарных точек:
кривая f(I1/2) везде отрицательна и монотонно
(
)
убывает. Здесь, вне зависимости от величины b
dΩp
r
1
возможна только одна стационарная точка, соот-
2
Jf - 2PI = ±
bI-1/2,
(28)
dL
4
ветствующая выбору знака минус в (24), т.е. ори-
ILR
(
)
ентации вдоль бара. Фазовый портрет для случая
dΩp
r
μ
аномальных орбит Q < 0, P > 0 показан на рис. 4.
P =
-
,
Видно, что здесь единственная возможная ори-
dL
2
ILR
ентация периодических орбит — вдоль бара (φ =
где P снова означает ЛБ-производную скорости
=12π;32π).
прецессии. Если теперь переобозначить величину
Таким образом, аномальные орбиты действи-
Q:
тельно ориентируются вдоль бара, в согласии с
(
)
идеей Линден-Белла (1979). Однако, как мы виде-
dΩp
r
ли выше, даже в случае нормальной орбиты, P < 0,
Q≡2
Jf,
(29)
если амплитуда бара ниже критической, наряду со
dL
ILR
стационарными периодическими орбитами, вытя-
нутыми перпендикулярно бару, существуют стаци-
мы снова получим уравнение вида (24), как и для
онарные периодические орбиты, вытянутые вдоль
случая кривых типа I. Однако теперь Q: имеет
несколько иной смысл и она может иметь как отри-
бара. Их эксцентриситет, e ∝ I1/2, меньше, чем
у орбит, ориентированных перпендикулярно бару:
цательный, так и положительный знак. Несложно
видеть, что эта величина представляет собой ско-
I1/21 < I1/23. Но если в диске нет или мало орбит
рость прецессии орбит в невозмущенном потенци-
с достаточно большими эксцентриситетами, един-
але в пределе I → 0 с радиусом ведущего центра,
ственно возможной ориентацией орбит остается
соответствующим угловому моменту LILR + 2Jf .
ориентация вдоль бара.
Поскольку 2Jf = ΔL + 2I, то при ΔL ≳ 2I имеем
(
)
Стационарные точки для моделей типа II
dΩp
r
Как мы уже отмечали выше, для кривых ти-
Q≈
ΔL =
dL
па II адиабатический подход возможен вблизи
ILR
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
22
ПОЛЯЧЕНКО, ШУХМАН
(
)
dΩp
r
Этот результат согласуется также с результатом
=
ΔR ≈ Ωpr (RL + ΔR).
Голдрейха и Тримейна (1981), которые пытались
dR
RL
объяснить появление конечного эксцентриситета
орбит частиц, вращающихся вблизи ILR в кольцах
Отсюда видно, что величина Q фактически пред-
Урана, за счет возмущающего воздействия грави-
ставляет скорость ретроградной прецессии невоз-
тационного потенциала спутника.
мущенной орбиты снаружи от ILR, т.е. при ΔR > 0
и прямой прецессии внутри ILR, т.е. при ΔR < 0,
Если же амплитуда потенциала бара превышает
критическую, b > bcrit, возможна только единствен-
поскольку dΩp
r
/dR < 0.3 Кроме того, в отличие
ная стационарная точка, отвечающая знаку (+)
от случая кривых типа I, для любых реальных
в правой части (30), т.е. периодическим орбитам,
кривых типа II знак ЛБ-производной P всегда
ориентированным поперек бара. Фазовый портрет
отрицателен, а орбиты всегда нормальны.
для этого случая показан на рис. 3b.
Аналогично (24), имеем
В области внутри ILR, где прецессия в невоз-
1
f (I1/2) ≡ QI1/2 + 2|P|I3/2 = ±
b,
(30)
мущенном потенциале проградная, Q > 0, кривая
4
f (I1/2) везде положительна и монотонно растет
В области снаружи от ILR, где Q < 0, кривая
от нуля. В этом случае критической амплитуды
f (I1/2) имеет тот же вид, что и на рис. 2. Это
не существует. При любой амплитуде возможна
(
)1/2
стационарная точка, отвечающая знаку (+). Это
значит, что и здесь при b < bcrit =23
|Q|3/6|P|
значит, что внутри ILR орбиты выстраиваются пер-
существуют три стационарные точки, I1 < I2 < I3
пендикулярно бару. В случае малой амплитуды этот
две из которых, I1 и I3 соответствуют экстремумам
результат также сшивается с результатом линейной
гамильтониана (25), т.е. устойчивы, а точка I2 яв-
нерезонансной теории Сандерса и Хантли (1976).
ляется седловой точкой, т.е. неустойчива. При этом
Фазовый портрет для этого случая показан на
стационарная точка с I = I1 отвечает знаку (-)
рис. 3b.
в правой части (30), т.е. периодическим орбитам,
вытянутым вдоль бара, а точка I = I3 отвечает
знаку (+), т.е. орбитам, ориентированным поперек
Роль знака амплитуды B усредненного потенциала
бара. Фазовый портрет в этом случае совпадает с
бара
изображенным на рис. 3a.
Итак, мы установили, что если невозмущен-
Выше мы везде считали, что знак амплитуды
ные орбиты всех звезд системы очень близки к
B = b(L)I1/2 усредненного потенциала
круговым, то единственно возможными стационар-
V (L, I, φ) = B(L, I) cos(2φ), где
ными периодическими орбитами являются орбиты
√
с I = I1, вытянутые вдоль бара. Это полностью
1
b(L) = -A(R)
×
(31)
согласуется с результатом, впервые полученным
2κR2
]
Сандерсом и Хантли (1976) (изложенном также в
[dln|A|
4Ω(R)
обзоре Селвуда и Уилкинсона, 1993, и моногра-
×
+
cos(2φ), R = R(L),
d ln R
κ
фии Бинни и Тримейна, 2008), которые в рамках
линейной нерезонансной теории показали, что
положителен, предполагая, что скорость измене-
в диске с почти круговыми орбитами с кривыми
ния потенциала достаточно мала. Однако, если
вращения типа II для любого R в области между
α ≡ dln|A|/dlnR < 0 и по абсолютной величине
радиусом внутреннего линдбладовского резонанса
превосходит отношение 4Ω/κ, т.е., если в какой-то
RL и радиусом коротации RC (но не слишком
области по R
близко к ним) существует периодическая орбита,
|α(R)| > 4Ω(R)/κ(R),
(32)
ориентированная вдоль бара. Можно даже пока-
зать, что если (средний) радиус этой орбиты при-
то амплитуда b становится отрицательной. Смена
ближается к ILR, ее эксцентриситет e = 2ρ/R =
знака амплитуды усредненного потенциала бара
√
приводит к изменению всех выводов, касающихся
=2
I/κR2 точно соответствует I1, получаемому
ориентации стационарных периодических орбит, на
из уравнения (30) в пределе очень малых I:
противоположные. Действительно, поскольку V ∝
∝ bcos(2φ), то смена знака b эквивалентна замене
I1/2 = I1/21 ≈ -b
[
]
4Q
1
cos(2φ) → cos
2(φ +
π)
. Это означает, что при
2
тех же самых соотношениях между P и Q, при
3 В принципе, знак величины Jf(= 1ΔL + I) может поло-
2
которых в случае b > 0 стационарными являлись
жительным даже для отрицательных ΔL, если |ΔL| < 2I.
Тогда знак Q окажется отрицательным не только снаружи,
точки φ = 0; π, соответствующие орбитам, ориен-
но и внутри ILR, хотя и в очень узкой области.
тированным перпендикулярно бару, в случае b < 0
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
О МЕХАНИЗМЕ ЛИНДЕН-БЕЛЛА
23
3
стационарными станут точки φ =12 π;
π, соот-
Из рис. 5a следует, что скорость убывания аб-
2
ветствующие орбитами, вытянутым вдоль бара. И
солютной величины |A(r)| зависит от распреде-
наоборот. В частности, для модели изохронного по-
ления поверхностной плотности. Однако асимпто-
тенциала, рассмотренного Линден-Беллом (1979),
тически, при r/a ≫ 1, она одинакова для хорошо
то есть для кривых вращения типа I, где возможны
локализованных баров (т.е. таких баров, плот-
нормальные орбиты, P > 0, они окажутся ориенти-
ность σB(r) которых спадает быстрее, чем 1/r4).
рованы поперек, а не вдоль бара.
Несложно показать, что для хорошо локализован-
ных баров асимптотика A(r) есть
Проанализируем теперь возможность выпол-
нения неравенства (32) для достаточно разумных
∫
∞
3π
распределений поверхностной плотности бара
A(r) ≈ -
G σB(r′)r′3dr′.
σ(r). Поскольку для любой возможной кри-
4r3
0
вой вращения галактики Ω < κ < 2Ω, то отно-
шение 4Ω/κ может варьироваться в пределах
В частности, для (I) и (II), имеем при r ≫ a:
2 < 4Ω/κ < 4. Так, для модели Местеля (1963),
√
3
A(I)(r)/(Gσ0a) ≈ -
π(a/r)3,
Ω(r) ∝ 1/r, κ =
2Ω и 4Ω/κ = 23/2 = 2.83.
8
Рассмотрим несколько естественных моделей
9
распределения поверхностной плотности бара
A(II)(r)/(Gσ0a) ≈ -
π(a/r)3.
σ(r, φ) = σB(r) cos(2ϕ), и найдем соответству-
2
ющие им распределения потенциала δΦ(r, ϕ) =
Для модели (III) с пограничной асимптотикой,
= A(r) cos(2ϕ). Можно показать, что A(r) и σB(r)
σ(III)B ∼ r-4, получим
связаны следующим интегральным соотношением:
9
∫∞
A(III)(r)/(Gσ0a) ≈ -
π(a/r)3 ln(1.862r/a),
4
r′σB(r′)
16
A(r) = -
G
×
(33)
3
r>
т.е. она спадает немного медленней, чем для моде-
0
лей I и II.
[(
)
(
)
]
2
1
Для плохо локализованной модели плотности IV
×
+1
K(z) - 2
+1
E(z) dr′,
z2
z2
скорость спадания самая медленная, ∼1/r:
где z = r</r>, r< = min(r, r′), r> = max(r, r′), а
A(IV)(r)/(Gσ0a) ≈ -π(a/r).
K(z) и E(z) — полные эллиптические интегралы
На рис. 5b видно, что самое большое отрица-
первого и второго рода соответственно. Мы чис-
тельное значение α(r) ≡ d ln |A(r)|/d ln r для экс-
ленно4 рассчитали амплитуды потенциала A(r) для
поненциальных моделей I и II приходится не на их
четырех достаточно плавно спадающих распреде-
далекий асимптотический хвост, где оно равно -3,
лений σB(r):
а на область, следующую за минимумом A(r), и
достигается не на периферии диска, а в области,
(i) — σ(I)B(r) = σ0 exp(-r2/a2),
примыкающей к минимуму амплитуды потенциала.
(ii) — σ(II)B(r) = σ0 exp(-r/a),
Для модели I оно равно примерно αmin ≈ -3.56 и
достигается при r/a ≈ 2.35. Для модели II αmin ≈
σ0
(iii) — σ(III)B(r) =
,
≈ -3.29 и достигается при r/a ≈ 8.5. Это означает,
(1 + r2/a2)2
по-видимому, что при достаточно резкой границе
σ0
поверхностной плотности бара возможны довольно
(iv) — σ(IV)B(r) =
1 + r2/a2
большие отрицательные значения α(r) в окрестно-
сти этой границы.
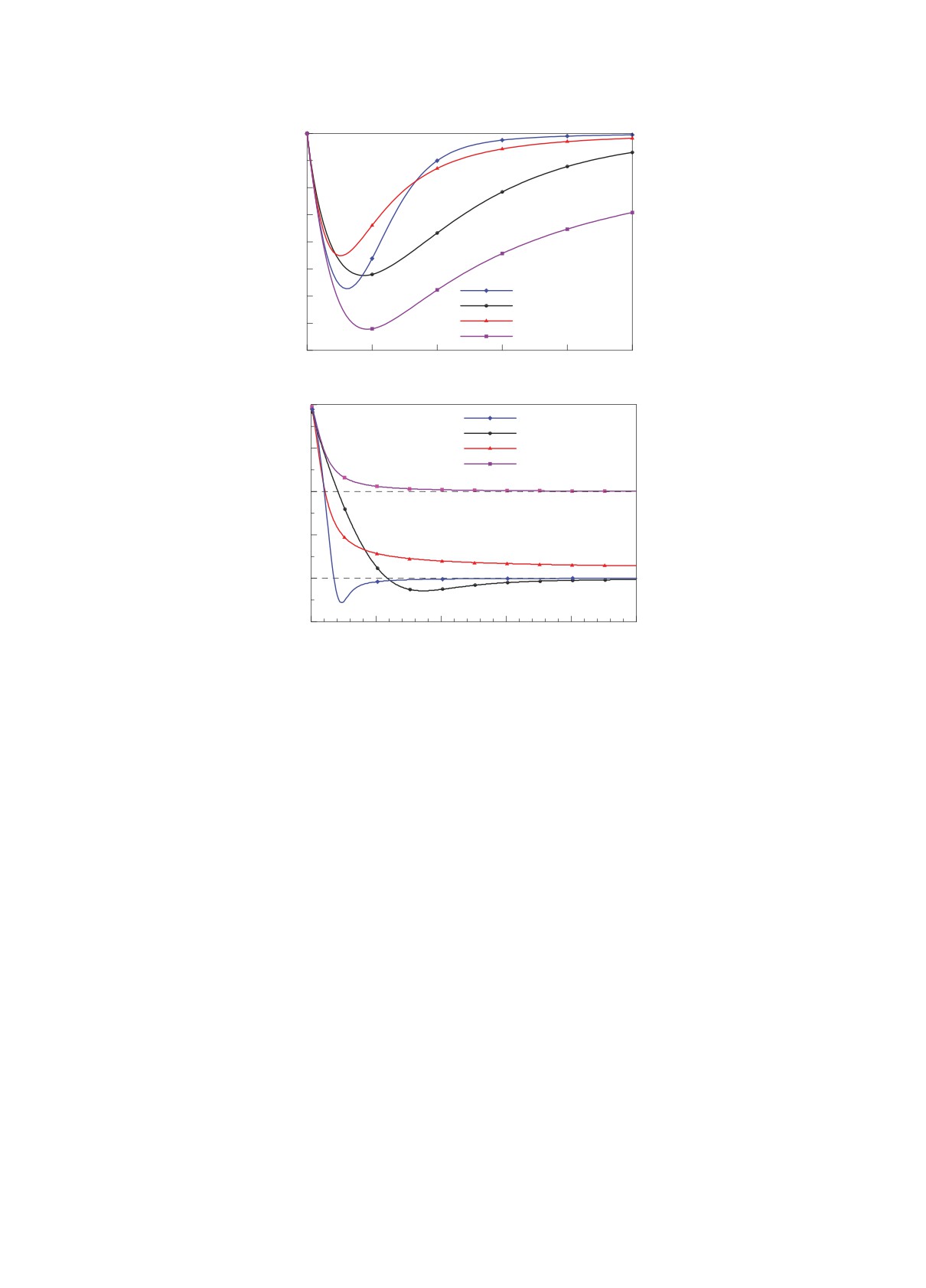
На рис. 5a показаны профили амплитуд A(r)
для этих распределений, а на рис. 5b — их ло-
Мы проверили это утверждение, рассмотрев
ступенчатую модель распределения плотности.
гарифмические производные α(r) = d ln |A|/d ln r.
Ступенька предполагалась с небольшим сглажи-
ванием:
4 Для гауссовой модели σ(I)B удается найти аналитическое
{
[
]}
выражение для потенциала:
√
σ(V)B(r) = σ0/
1 + exp
(r - a)/δ
(34)
√
{
[
4
1
A(r) = -
πGσ0a
2ζ
1-e-ζ
πζ I0(ζ) +
3
2
На рис. 6 показаны профили амплитуды потен-
]}
1
1
циала A(r) для пяти значений параметра δ =
+ I1(ζ) +
I1(ζ)/ζ
,
ζ =
(r/a)2,
4
2
= 0.025a; 0.05a; 0.1a; 0.2a; 0.4a. Видно, что чем
меньше δ, там больше по абсолютной величине
где In(z) — модифицированные функции Бесселя 1-го
рода.
значение α в области, примыкающей к краю бара
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
24
ПОЛЯЧЕНКО, ШУХМАН
A/G0a
0
(a)
0.2
0.4
0.6
0.8
1.0
= 0exp( r2/a2)
1.2
= 0exp( r/a)
1.4
= 0exp(1 + r2/a2)2
= 0exp(1 + r2/a2)
1.6
0
1
2
3
4
5
r/a
d(ln|A|)/d(lnr)
1
(b)
= 0exp( r2/a2)
= 0exp( r/a)
0
= 0exp(1 + r2/a2)2
= 0exp(1 + r2/a2)
1
2
3
4
0
5
10
15
20
25
r/a
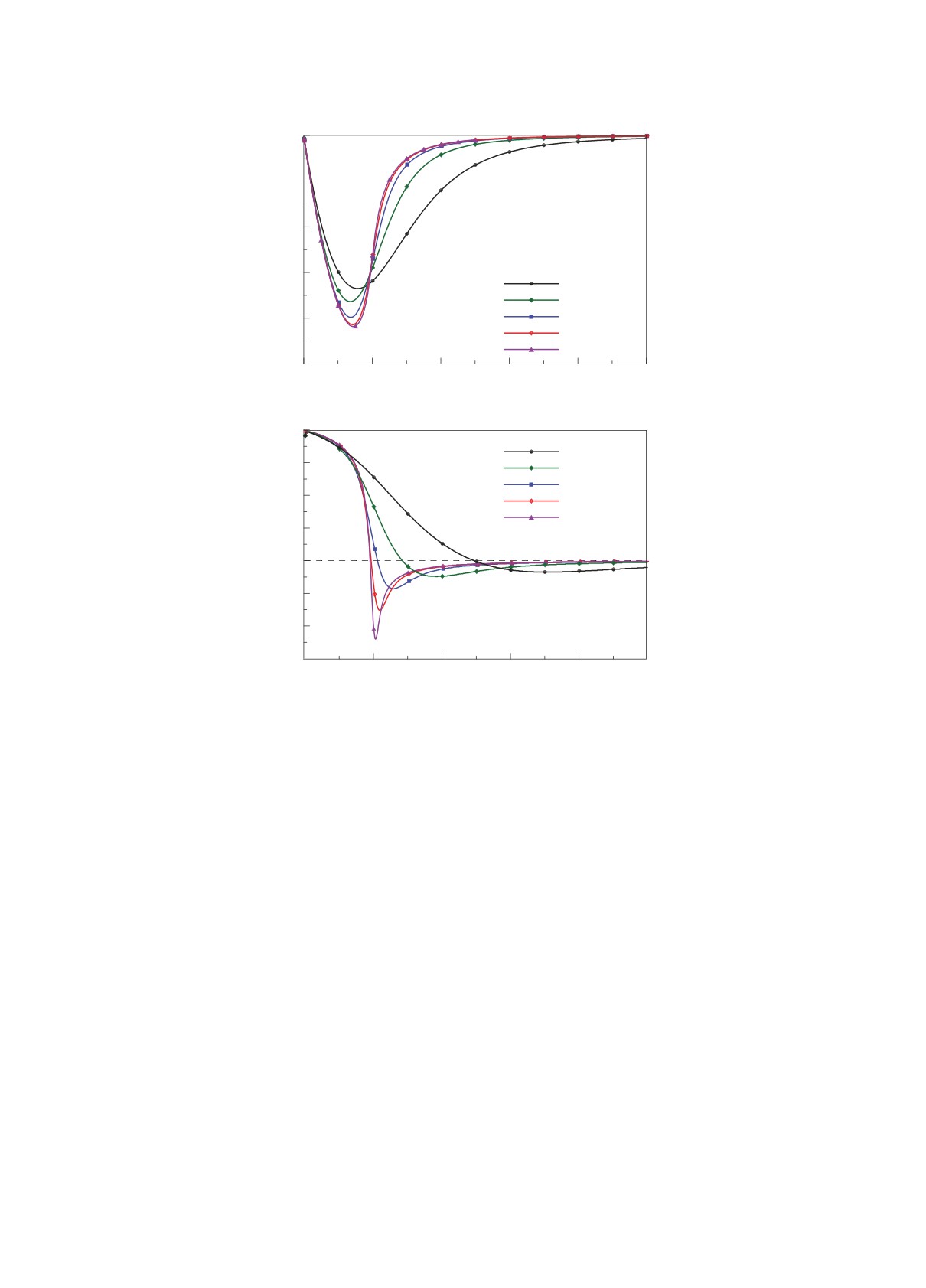
Рис. 5. (a) — Амплитуда потенциала A(r), создаваемая барообразным возмущением поверхностной плотности диска
σ(r,ϕ) = σB(r) cos(2ϕ) для четырех моделей σB(r), (b) — логарифмическая производная амплитуды потенциала α =
= dln|A|/dlnr для этих профилей.
r ≈ a. Так, для δ = 0.025a αmin = α(r = 1.03a) =
= A(r) cos[2(ϕ - Ωpt)], A < 0, создаваемого вра-
= -5.4. Однако видно также, что с уменьшением δ
щающимся c угловой скоростью Ωp барооб-
происходит одновременное сужение по радиусу об-
разным возмущением поверхностной плотности
ласти больших отрицательных α. Вся эта область
σ(r, ϕ) = σB(r) cos[2(ϕ - Ωpt)] на фоне аксиально-
сосредоточена вблизи скачка плотности.
симметричного потенциала галактик может при-
Таким образом, отрицательные значения ампли-
водить к запиранию прецессирующих орбит звезд
туды усредненного потенциала бара b = |A|(α +
и выстраиванию их вдоль бара, приводя к его
+ 4Ω/κ), в принципе, возможны, поскольку отри-
усилению. Продемонстрировано, что хотя при
цательные значения α могут превышать по абсо-
положительном знаке ЛБ-производной угловой
лютной величине характерные значения отношения
скорости прецессии, [∂Ωpr(L, I)/∂L]Jf > 0, запер-
4Ω/κ, которые, как правило, не выше трех. Однако
тые орбиты, действительно, могут выстраиваться
такое превышение происходит либо довольно дале-
вдоль бара, этот знак не является единственным,
ко от границ бара, r ≫ a, где α = -3, либо в узкой
и даже не является доминирующим фактором,
области вблизи границы, если она очень резкая.
определяющим ориентацию запертых орбит (как
В области, где сосредоточено основное тело бара,
считалось ранее). Важную роль играют знак самой
r ≲ a, амплитуда усредненного потенциала бара
прецессии орбит в невозмущенном потенциале, Ωpr,
b, действительно, положительна, как мы (и, по-
а также величина амплитуды бара.
видимому, Линден-Белл, 1979) полагали выше.
Так, в случае, когда (положительная) амплитуда
ЗАКЛЮЧЕНИЕ
b усредненного по быстрому орбитальному дви-
Мы показали, что слабое овальное возму-
жению потенциала бара V = bI1/2 cos(2φ) суще-
щение гравитационного потенциала δΦ(r, ϕ) = ственно ниже критической, а прецессия орбит в
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
О МЕХАНИЗМЕ ЛИНДЕН-БЕЛЛА
25
A
0
(a)
0.4
0.8
1.2
= 0.4a
= 0.2a
1.6
= 0.1a
= 0.05a
= 0.025a
2.0
0
1
2
3
4
5
r/a
d(ln|A|)/d(lnr)
1
(b)
= 0.4a
0
= 0.2a
= 0.1a
1
= 0.05a
= 0.025a
2
3
4
5
60
1
2
3
4
5
r/a
{
[
]}
Рис.
6. Амплитуда потенциала A(r), соответствующая ступенчатой функции σ(V)B(r) = σ0/
1 + exp
(r - a)/δ
(a), и ее логарифмическая производная α = d ln |A|/d ln r (b), для пяти значений параметра сглаживания δ/a =
= 0.025; 0.5; 0.1; 0.2; 0.4.
невозмущенном потенциале ретроградная, Ωpr < 0,
и ее ЛБ-производной, если спадание плотности
выстраивание запертых орбит происходит вдоль
бара σB(r) на периферию диска достаточно быст-
бара, независимо от знака ЛБ-производной. При
рое. В этом случае в области границы, r ∼ a, а
этом, если ЛБ-производная отрицательна, наряду
в некоторых случаях и далее к периферии диска,
с орбитами, вытянутыми вдоль бара, присутствуют
амплитуда усредненного потенциала бара b < 0, в
также более эксцентричные орбиты, вытянутые по-
отличие от b > 0 в области основного тела бара,
перек бара, при условии, что популяция звезд диска
r ≲ a, что приводит к смене ориентации орбит в
содержит такие орбиты (см. рис. 2 и рис. 3a).
этих областях.
Ориентация запертых орбит, действительно,
Проведенное рассмотрение справедливо в об-
определяется знаком ЛБ-производной, но только
ласти, где эпициклическое движение звезд можно
при условии, что амплитуда бара достаточно
разделить на быстрое (орбитальное) и медленное
велика. Тогда при отрицательной ЛБ-производной
(прецессионное). Мы рассмотрели два типа ха-
запертые орбиты вытянуты перпендикулярно ба-
рактерных кривых вращения, в одном из которых
ру (см. рис.
3b), а при положительной ЛБ-
такое разделение возможно в широкой по радиусу
производной — вдоль бара, как это и следует из
области (вплоть до радиуса коротации), а в дру-
качественных рассуждений Линден-Белла (1979).
гом — в окрестности внутреннего линдбладовского
Мы показали также, что ориентация больших
резонанса.
осей орбит может поменяться на противополож-
ную в определенных областях диска при тех же
Работа поддержана КП19-270 “Вопросы про-
соотношениях между знаками скорости прецессии исхождения и эволюции Вселенной с применением
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020
26
ПОЛЯЧЕНКО, ШУХМАН
методов наземных наблюдений и космических ис-
9. Местель (L. Mestel), MNRAS 126, 553 (1963).
следований” (подпрограмма II “Астрофизические
10. Палмер (P.L. Palmer), Stability of collisionless
объекты как космические лаборатории”), грантом
stellar systems: mechanisms for the dynamical
Немецкого исследовательского фонда DFG —
structure of galaxies (Astrophys. Sp. Sci. Library,
Project-ID
138713538 — SFB 881 (“The Milky
Dordrecht; Boston: Kluwer Acad. Publ., 1994).
11. Поляченко В.Л. и Фридман А.М., Равновесие
Way System”, subproject A06), грантом фонда
и устойчивость гравитирующих систем (М.:
“Volkswagen Foundation” No.
90411, а также
Наука, 1976).
в рамках базового финансирования программы
12. Поляченко (E.V. Polyachenko), MNRAS 348, 345
ФНИ II. 16 (И.Ш.).
(2004).
13. Поляченко (E.V. Polyachenko), MNRAS 357, 559
(2005).
СПИСОК ЛИТЕРАТУРЫ
14. Поляченко В.Л., Поляченко Е.В., Шухман И.Г.,
1. Бертин (G. Bertin), Dynamics of Galaxies (2nd ed.,
Письма в Астрон. журн.
41,
3
(2015a).
Cambridge Univ. Press, Cambridge, UK, 2014).
[V.L. Polyachenko et al., Astron. Lett. 41, 1 (2015a)].
2. Бинни, Тримейн (J. Binney and S. Tremaine),
15. Поляченко, Шухман (E.V. Polyachenko and
Galactic Dynamics (2nd ed., Princeton Univ. Press,
I.G. Shukhman), MNRAS 451, 5120 (2015b).
NJ, 2008).
16. Поляченко, Берцик, Юст (E.V. Polyachenko,
3. Вайнберг (M.D. Weinberg), Astrophys. J. 368, 66
P. Berczik, and A. Just), MNRAS 462, 3727 (2016).
(1991).
17. Сандерс, Хантли (R.H. Sanders and J.M. Huntley),
4. Голдрейх, Тримейн (P. Goldreich and S. Tremaine),
Astrophys. J. 209, 53 (1976).
Astrophys. J. 243, 1062 (1981).
18. Саха (P. Saha), MNRAS 248, 494 (1991).
5. Контопулос (G. Contopoulos), Astrophys. J. 201,
19. Селвуд,
Уилкинсон (J.A. Sellwood and
566 (1975).
A. Wilkinson), Rep. Progress Phys. 56, 173 (1993).
6. Линден-Белл (D. Lynden-Bell), MNRAS 187, 101
20. Спарк, Селвуд (L.S. Sparke and J.A. Sellwood),
(1979).
MNRAS 225, 653 (1987).
7. Марк (J.W-K. Mark), Astrophys. J. 203, 81 (1976).
8. Мерритт (D. Merritt), IAUS 127, 315 (1987).
21. Шу (F.H. Shu), Astrophys. J. 158, 505 (1969).
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46
№1
2020