ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2020, том 46, № 7, с. 520-532

ГРАФОДИНАМИКА АКТИВНЫХ ОБЛАСТЕЙ СОЛНЦА: КОМПЛЕКСЫ

МОРСА-СМЕЙЛА И МУЛЬТИМАСШТАБНЫЕ ГРАФЫ

МАГНИТОГРАММ

¹Ярославский государственный университет им. П.Г. Демидова, Ярославль, Россия

²Главная (Пулковская) обсерватория РАН, Санкт-Петербург, Россия

³Институт информационных и вычислительных технологий КН МОН РК, Алматы, Казахстан

⁴Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

Поступила в редакцию 14.02.2020 г.

После доработки 26.05.2020 г.; принята к публикации 26.05.2020 г.

Обсуждается модель эволюции Активной Области (АО), в которой граф, построенный на особых

точках поля, кодирует магнитные паттерны АО. При этом динамические сценарии АО отображаются

дискретной структурой сети, сформированной на максимумах, минимумах и седловых точках магнит-

ного поля. Динамика АО приводит к перестройке графа, графодинамике. В работе обсуждаются два

графа. Первым из них является граф комплекса Морса-Смейла. Он представляет собой клеточную

градиентную модель магнитного поля, каждая клетка которого содержит максимум, минимум и две

седловых точки. Комплекс Морса-Смейла допускает упрощение (редактирование) с предписанной

детальностью, которое сохраняет топологию поля. Второй граф кодирует динамику АО сразу на

разных масштабах, в так называемом Scale-Space. Это пространство образовано последовательно-

стью сверток исходной магнитограммы с гауссовским ядром, так что масштаб размытия является его

дополнительной координатой. В каждом слое Scale-Space рассматриваются неморсовские особые

точки, с вырожденным гессианом и лапласианом. Кривые, соединяющие эти точки в разных мас-

штабах, образуют критические пути, вершины которых называют топ-точками. Полученный на этих

точках граф кодирует структуру вырожденных структур поля АО на разных масштабах. В статье

предлагается эффективный способ вычисления критических путей с помощью множества Якоби.

Можно полагать, что предвспышечные режимы связаны со значительным изменением топологии

поля, которая управляет графодинамикой. Следовательно, они должны сопровождаться заметными

вариациями спектра собственных значений дискретного лапласиана графа (матрицы Кирхгофа-

Лапласа). В качестве примера приводится эволюция спектров этих графов, построенных по магни-

тограммам вспышечно-активной области АО12673. Данными служили SDO/HMI магнитограммы

АО для скалярной LOS-компоненты. Обсуждается возможная связь больших вариаций спектра с

последующими Х-вспышками.

Ключевые слова: комплекс Морса-Смейла, дискретный лапласиан, графодинамика, активные обла-

сти, магнитограммы, солнечные вспышки.

DOI: 10.31857/S0320010820070013

ВВЕДЕНИЕ

ную феноменологию, дополненную теоретическими

соображениями, позволяющими “арифметизовать”

Динамика магнитных полей в активных обла-

магнитограммы, т.е. приписать меру ее отдельным

стях (АО) отслеживается в изменениях геометрии и

паттернам. Объемы наборов дескрипторов, охва-

топологии наблюдаемых паттернов магнитограмм.

тывающих и векторные магнитограммы, варьиру-

Выделение предвспышечных режимов основано,

ются в широких пределах: от 171, где включе-

как правило, на выборе подходящих признаков

ны спиральность, фрактальная размерность и да-

(дескрипторов), описывающих сложность наблю-

же энергия Изинга магнитограммы (Кемпи и др.,

даемых паттернов в пространстве и во време-

2019), до 10 параметров АО, которые отбирались

ни. Выбор опирается на богатую наблюдатель-

по значению их корреляций со вспышечной про-

^*Электронный адрес: ng-makar@mail.ru

дуктивностью, для восьмилетней истории выборки

520

ГРАФОДИНАМИКА АКТИВНЫХ ОБЛАСТЕЙ СОЛНЦА

521

(Лим и др., 2019). Корректный выбор лучших

зованных ребрами, мы получим симплициальный

дескрипторов из смеси разнородных и коррелиро-

комплекс (cм., например, Эдельсбруннер, Харер,

ванных претендентов по критерию их корреляций

2010). В физике Солнца можно найти примеры

со вспышками на большой временной истории вряд

применения таких конструкций, (см., например,

ли полезен на практике для предсказания вспышки

Ашванден, 2010). Так, диаграмму Вороного и ду-

в конкретной АО на интервале 1-3 дня. Тем не

альную к ней триангуляцию Делоне использова-

менее популярные в настоящее время 18 так назы-

ли для описания тонкой структуры фотосферных

ваемых SHARP параметров выделены как раз по

полей (Шрийвер и др., 1997), марковского мо-

их прогностической эффективности (Бобра и др.,

делирования хромосферных структур и машинной

2014). Однако при построении авторегрессионных

идентификации АО (Турмон, Мухтар, 1997, 1998).

нелинейных предикторов 18-мерное пространство

признаков также может оказаться чрезмерно боль-

Уточним теперь смысл, в котором граф мо-

шим вследствие эффекта концентрации меры (см.

жет аппроксимировать АО. Рассмотрим сперва эту

Приложение А1).

проблему на примере конечного облака точек S =

Итоги численных экспериментов эпигноза¹,

= {x_i}Ni=1, случайно выбранных из компактной об-

основанные на большом числе дескрипторов и

ласти в R². Существует несколько способов при-

методах машинного обучения (Лиу и др., 2019),

писать “форму”, точнее набор форм, такому обла-

указывают пока на избыточность коррелиро-

ку. Можно, например, использовать альфа-формы

ванных характеристик и порождают сомнения в

(Эдельсбруннер и др., 1983), которые описыва-

эффективности стандартных подходов к прогно-

ют облако с разной степенью детальности. Самой

зу (Лим и др., 2019). В последней дискуссии

рафинированной формой будет оригинальное мно-

по прогнозу было указано на важность учета

жество точек. Конечной, наиболее грубой, явля-

паттернов предвспышечной эволюции АО (Лека

ется минимальная выпуклая оболочка, натянутая

и др.,

2019). Возможно, ключевым моментом

на все точки облака методом “аркана” (Препарата,

успешного предсказания является диагностика

Шеймос, 1989). Последовательную детализацию

переходов от спокойного режима “вспышки нет и

можно получить, используя триангуляцию Делоне

не будет” к режиму “вспышечный режим начался”.

облака. Из нее последовательно извлекаются те

Возможно, что наиболее эффективным окажется

ребра, которые являются максимальным диамет-

подход, комбинирующий предсказания времени

ром пустого диска, не превышающего величины

начала вспышечного процесса с прогнозом общего

2/α. Аналогичные идеи переменной окрестности

сценария развития вспышечной активности АО

точек лежат в основе построения топологического

(Пак и др., 2020). Таким образом, важны методы,

комплекса. Если B (x_i, ε) — замкнутый шар (диск)

позволяющие параметризовать эволюционную

радиуса ε с центром в точке x_i ∈ S, тогда их_⋃

картину магнитограммы АО “в целом”.

объединениеxi∈SB(xi,ε)⊃Sслужитпокрыти-

Для этого удобно вообще отказаться от “по-

ем Минковского для S (Макаренко и др., 2001).

точечной” арифметизации магнитограммы, кодируя

Нервом покрытия называют общую часть объеди-_⋂

ее паттерны глобально, графом или сетью, накры-

вающей всю АО. Сеть в определенном смысле,

нения N (ε, S) =xi∈SB(xi,ε)=0(Эдельсбрун-

который мы определим ниже, аппроксимирует поле

нер, Харер, 2010). При дилатации покрытия, т.е.

АО, являясь его дискретной моделью — остовом

синхронном увеличении радиусов всех дисков, воз-

или скелетоном. Эти термины имеют строгие

никают их пересечения. Заменим каждую пару

определения, но в этом месте мы используем их

пересекающихся дисков ребром, соединяющим их

как метафору: описание динамической геометрии

центры. Пересечение трех дисков заменим гранью

скачущей лошади предлагается заменить движе-

треугольника, построенного на их центрах. Реб-

нием некоторого ее остова из ребер, соединяю-

ра и грани можно получить непрерывной дефор-

щих информативные точки формы. В математике

мацией — гомотопией³ — элементов нерва. Кон-

такие конструкции называют неориентированным

струкция, которая получится в итоге, содержит

графом. В R² это непустое множество вершин

вершины, ребра и грани. Ее называют комплексом

или 0-симплексов² и множество соединяющих их

Чеха или нервом покрытия. Если пространство,

ребер или 1-симплексов (Молитьерно, 2016). До-

из которого выбраны точки, допускает триангу-

полнив его гранями, т.е. 2-симплексами, заполня-

ляцию, и его можно стягивать к его же точкам,

ющими пустоты внутри замкнутых циклов, обра-

то теорема о Нерве утверждает, что нерв облака

¹Таким образом, “предсказания” событий, которые уже

³Гомотопия — это семейство непрерывных по параметру,

произошли в истории АО.

но необязательно однозначных отображений двух про-

²Simplex — простейший.

Нульмерные

или

странств. В нашем примере это пересекающиеся диски и

симплексы— просто точки, 1-симплексы— ребра.

ребро, к которому они стягиваются.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

522

АЛЕКСЕЕВ и др.

гомотопически эквивалентен его покрытию Мин-

поля будет изменять его конфигурацию для АО.

ковского (Эдельсбруннер, Харер, 2010).

Таким образом, можно говорить о динамике графа

или графодинамике. Сам термин был введен в

Комплекс Чеха меняется с изменением мас-

штаба ε. Поэтому описанную выше процедуру его

1997 г. Марком Айзерманом и др. для описания

сложных систем в автоматике.

построения называют фильтрацией (Эдельсбрун-

нер, Харер, 2010). Ее можно представить себе

Предположим, что эволюция АО содержит

как последовательность вложенных друг в дру-

детерминированную компоненту, которая опи-

га комплексов, визуализирующих точки облака с

сывается гладкой моделью, заданной в форме

возрастающим масштабом разрешения. Конечным

системы дифференциальных уравнений или, в

итогом фильтрации будет комплекс, состоящий из

общем случае, — группой диффеоморфизмов⁴. Для

одной “закрашенной” грани. На языке топологии

реконструкции таких моделей из наблюдений могут

фильтрация позволяет описывать свойства много-

оказаться полезными градиентные динамические

образия, используя так называемые группы гомо-

системы и относящийся к ним граф связно-

логий комплекса, которые характеризуются чис-

сти Морса (Аллили, Корриво,

2007; Аллили

лами Бетти (β_i, i = 0, 1, 2, . . . ). Строгие определе-

и др., 2007), построенные на магнитограммах.

ния можно найти в монографиях (Эдельсбруннер,

Он получается из комплекса Морса-Смейла

Харер, 2010; Кнудсон, 2015), а здесь ограничимся

(MS-комплекса), который разбивает поле на

простыми примерами. Числа Бетти подсчитывают

простые структуры — клетки (Эдельсбруннер,

число i-мерных циклов, которые нельзя стянуть

Харер, 2010). Каждая клетка такого комплекса

в точку: они ограничивают “дыру”. Рассмотрим

содержит максимум, минимум и две седловые

“пустой” треугольник [abc] ∈ R². Мы имеем один

точки⁵. MS-комплексы с успехом применяются

связный объект, все точки которого эквивалент-

для топологического анализа космологических

ны. Это обстоятельство реферируем как β₀ = 1.

данных (см., например, Cоусби, 2011; Пранав и

Граница треугольника является 1-циклом, который

др., 2017; Фельдбрюгге и др., 2019). Очень важно,

нельзя стянуть в точку, поэтому полагаем β₁ = 1.

что комплексы допускают топологическое редак-

Все остальные числа Бетти β_i = 0, i ≥ 2. Если тре-

тирование, т.е. упрощение, основанное на идеях

угольник [abc] является заполненным, т.е. является

персистентности (Эдельсбруннер, Харер,

2010;

границей 2-симплекса, то β₀ = 1, но β₁ = 0, пото-

Гюнтер и др., 2014). Первые примеры построения

му что грань позволяет стянуть границу в точку.

MS-комплексов для АО по LOS (line of sight)

Определим границу ориентированного симплекса

компонентам HMI/SDO магнитограмм приведены

как ∂ [ab] = b - a. Таким образом, граница обра-

в нашей работе (Макаренко и др., 2016).

зована двумя точками, причем начальная берется

со знаком минус. Точки являются 0-циклами, их

Другим интересным графом является конструк-

граница равна нулю. На этом примере легко по-

ция, построенная в пространстве масштабов Scale-

нять идею эквивалентности двух циклов, а именно:

Space на критических точках с использованием

два 0-цикла гомологичны друг другу, b ∼ a + ∂ [ab]

теории катастроф. Это пространство получается

потому, что различаются на границу 1-симплекса,

итеративным размытием (блюрингом) оригиналь-

который и позволяет их совместить. Числа Бетти

ного изображения гауссовским ядром (Линдеберг,

дают важную информацию о топологии случайных

2013). Степень размытия, которое определяется

полей, поскольку связаны с числом критических

числом итераций, позволяет определить допол-

точек поля так называемыми неравенствами Морса

нительную координату в Scale-Space, задающую

(Фельдбрюгге и др., 2019). Первые применения

масштаб. В этом пространстве, кроме Морсовских

гомологий к магнитограммам вспышечных АО опи-

особых точек, появляются и другие, связанные

саны в работах Макаренко и др. (2013), Князева и

с вырождением Гессиана, матрицы вторых про-

др. (2015), Дешмук и др. (2020).

изводных изображения. Их можно использовать

Выберем теперь на компактной области поля

для построения мультимасштабных графов, свя-

множество критических (особых) точек поля, в

занных с глубинными свойствами изображения и

которых градиент обращается в нуль. Их роль в

дифференциально-геометрическими инвариантами

компактном описании полей была отмечена еще

Джеймсом Максвеллом (1870) на примере земной

⁴Взаимно-однозначное дифференцируемое отображение

топографии. В физике Солнца критические точки

двуx пространств, обратное к которому также гладкое,

представляют интерес в прогностических задачах

снабженное структурой 1-параметрической группы отно-

сительно времени.

вспышечных АО (см., например, Ванг, Ванг, 1996)

⁵Интересно, что сами комплексы можно рассматривать

и для теории фотосферных полей (Жужома и др.,

как дискретные мультизначные динамические системы и

2017). Если построить некоторый граф на особых

использовать для анализа критических областей изобра-

точках магнитограммы, то эволюция магнитного

жения (Аллили и др., 2007).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

ГРАФОДИНАМИКА АКТИВНЫХ ОБЛАСТЕЙ СОЛНЦА

523

высокого порядка (K ¨eйпер, 2002). Критические пу-

образуют MS-комплекс (Кнудсон, 2015). Тополо-

ти, соединяющие последовательность критических

гия каждой клетки предельно простая: она содер-

точек на каждом масштабе, позволяют восстано-

жит два седла, максимум и минимум. Напомним,

вить скалярное поле в смысле обратной задачи

что характеристика Эйлера определяется форму-

(Кантерс и др., 2005).

лой χ = #(max) - #(saddles) + #(min), в кото-

Для того чтобы отследить перестройку графов

рой символ # означает “целое число”. (Эдельс-

в процессе динамической эволюции АО, можно

бруннер, Харер, 2015). Поскольку седла и экстре-

использовать методы спектральной геометрии. Из-

мумы имеют топологические идексы разных зна-

вестно, что каждому графу соответствуют несколь-

ков, общий индекс клетки равен нулю. Аналогом

ко матриц, описывающих взаимные связи вершин и

может служить гауссовское поле, для которого

число седел в среднем равно сумме максимумов и

ребер. Одной из них является матрица Кирхгофа-

минимумов.

Лапласа, которую часто называют дискретным ла-

пласианом графа (Молитьерно, 2016). Спектр соб-

MS-комплекс получил свое название по име-

ственных значений этой матрицы легко вычислить

нам двух математиков: Стивена Смейла, который

(Чунг, Грахам, 1997). В итоге графы и их спектры

изучал топологию динамических систем, и Мар-

дадут нам графодинамические модели магнитного

стона Морса, который исследовал связи топологии

поля АО, которые могут оказаться полезными в

гладких многообразий и свойства функций, на них

прогностических задачах.

заданных.

Целью данной статьи является описание схемы

Формально пусть f : M → R — гладкая веще-

построения разных графодинамических моделей

ственнозначная функция, определенная на гладком

АО. Мы собираемся сделать это на примере двух

компактном многообразии M, dim M = 2. Рас-

упомянутых выше графов следующим образом:

смотрим ее градиентное поле: ∇f ≡ grad f. Кри-

вая γ : [0, 1] → M называется интегральной кри-

вой, если для каждой точки p ∈ γ ее касательный

• привести краткий обзор идей построения

вектор совпадает с градиентом. Точки lim_t→-∞ γ(t)

MS-комплексов для магнитограмм;

и limt→+∞ γ(t) называют начальной и конечной

• изложить оригинальную схему построения

точкой интегральной кривой γ (t), соответственно,

критических кривых в Scale-Space и графа

в том случае, если пределы существуют (Кнудсон,

на топ-точках;

2015). Точку p, в которой ∇f |_p = 0, называют

критической. Она является невырожденной, если

{

}

• привести примеры графов Морса и графов

детерминант ее гессиана H(p) =

∂²f/∂x_i∂x_j

|_p

по топ-точкам с их спектральными характе-

не равен нулю. Тип невырожденной особой точ-

ристиками для вспышечной АО.

ки — минимум, максимум или седло — определяют

собственные значения гессиана. Точнее, число от-

В тексте статьи используются лишь минимальные

рицательных собственных значений гессиана на-

математические сведения на уровне определений,

зывают индексами Морса для критических точек.

необходимые для понимания текста. Подробности

В случае двумерного поля индексы совпадают с

можно найти в цитируемой литературе. В Прило-

числом неустойчивых направлений в окрестности

жении статьи приводятся некоторые математиче-

критической точки. Для максимума оба направ-

ские детали.

ления неустойчивы; для седла неустойчивым яв-

ляется одно направление, и, наконец, минимум не

имеет неустойчивых направлений. Поэтому индек-

ТЕОРИЯ МОРСА И MS-КОМПЛЕКСЫ

сы Морса равны 0, 1 и 2 для минимума, седла и

максимума соответственно. Функция f называется

Эвристическая идея MS-комплекса заключает-

морсовской, если все ее критические точки невы-

ся в построении сети кривых, касательными к ко-

рождены (Кнудсон, 2015). Интегральные кривые

торым являются градиенты поля. Линии соединяют

морсовской функции имеют следующие свойства

критические точки поля так, что образуются два се-

(Cоусби, 2011):

мейства: восходящее многообразие, согласованное

с возрастанием градиента, и нисходящее многооб-

разие, линии которого согласованы с убыванием

• каждая интегральная кривая начинается и

градиента. Первое семейство можно представить

кончается в критической точке.

себе интегральными линиями, которые соединяют

седловые точки и максимумы поля. Второе семей-

• Существует единственная интегральная кри-

ство соединяет интегральными линиями минимумы

вая, проходящая через каждую точку p ∈

и седла. Пересечение этих линий, называемых кри-

∈ M; две различные интегральные кривые не

тическими, разбивает поле на клетки, которые и

пересекаются, но могут иметь общее начало

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

524

АЛЕКСЕЕВ и др.

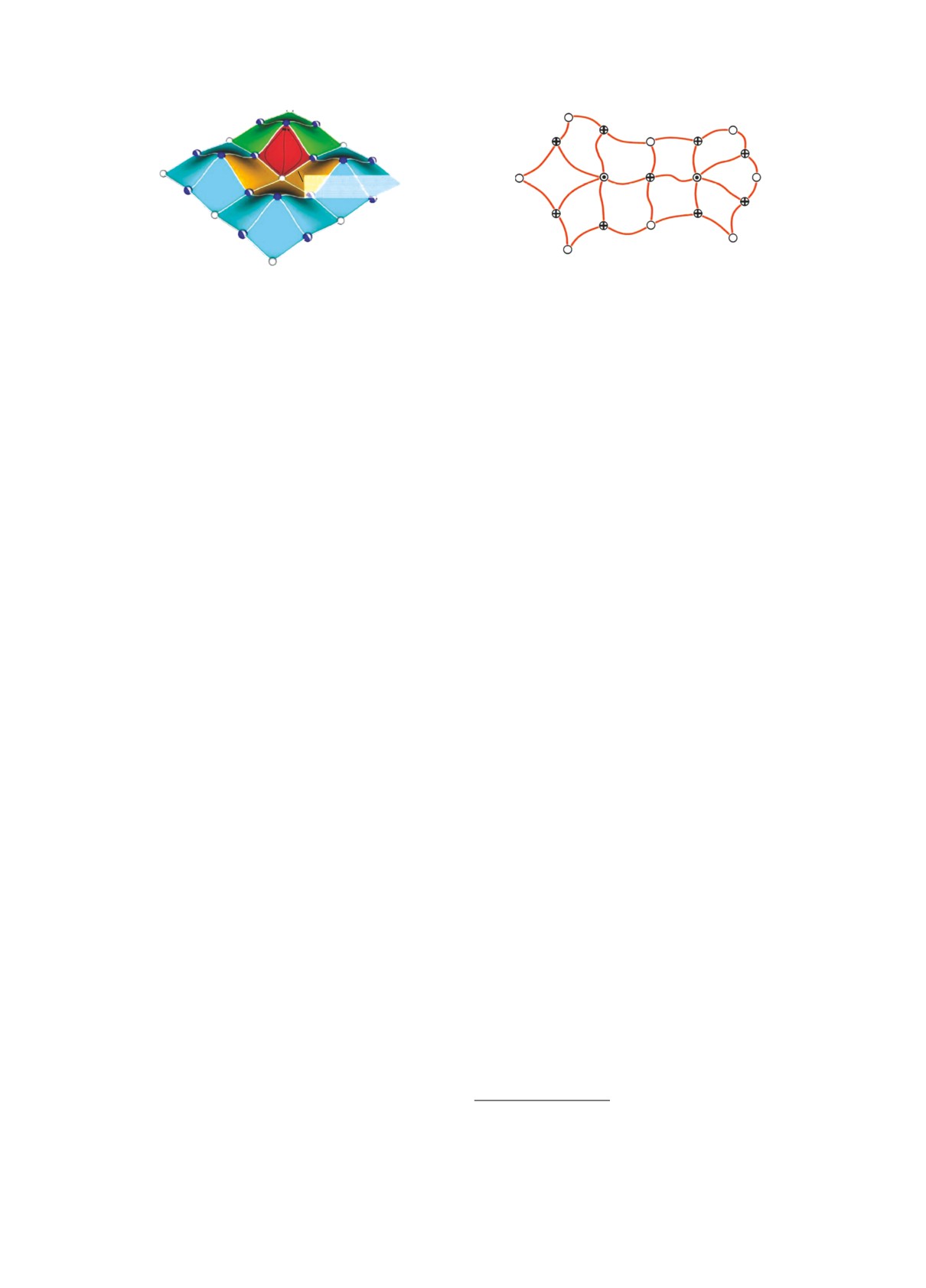
Cell of the Morse-Smale

complex

Рис. 1. Клетки MS-комплекса (слева) и скелетон (справа) (рисунок из работы Cоусби, 2011). Седла маркированы

кружком с крестом.

и/или конец. Интегральная кривая, прохо-

адаптированный к биполярным полям, программ-

дящая через критическую точку, вырождена

ный комплекс, который доступен в репозитории

в этой точке.

https://github.com/thekindbeetle/topology.

Введем теперь формализм, поясняющий идею

• Множество всех интегральных кривых по-

топологической персистентности, на которой осно-

крывают все M и индуцируют отношение эк-

вано упрощение MS-комплекса (Эдельсбруннер,

вивалентности на M: p, p^′ ∈ M эквивалент-

Харер, 2011). Пусть M_t = f-1 ((-∞; t]), подуров-

ны, тогда и только тогда, если интегральные

ни множества уровней функции f. Когда t увели-

кривые γ_p и γ_p′ , проходящие через p и p^′,

чивается, топология множеств M_t изменяется при

имеют общие начало и конец.

переходе уровня t тогда и только тогда, если f (p) =

= t для некоторой критической точки p (Кнудсон,

Перечисленные условия определяют разбиение

2015). В случае dim M = 2 топологическими свой-

ствами, или особенностями, являются только ком-

многообразия M на клетки, которые образуют MS-

поненты связности и “дыры”, т.е. циклы, не явля-

комплекс. Интегральные кривые, соединяющие

ющиеся границами поверхности. Если какое-либо

максимумы с седлами и седла с минимумами,

из свойств появляется на уровне t₀, то говорят, что

образуют 1-мерный скелетон MS-комплекса и

свойство “родилось в момент t₀”. Например, при

называются дугами комплекса (рис. 1).

прохождении седла, разделяющего два максиму-

Численные алгоритмы для реализации MS-

ма, рождается вторая компонента⁶. Точно также,

комплекса основаны на дискретном варианте тео-

если дыра или компонента связности исчезают на

рии Морса (Кнудсон, 2015), в котором критические

уровне t₁, то говорят, что свойство “умерло в мо-

точки функции Морса кодируются симплексами

мент t₁”. Время жизни топологического свойства,

с размерностью, совпадающей с ее индексом

выраженное в единицах уровня t₁ - t₀, называют

Морса m_{i}, {i} = min, max, sad. Так, минимумы

его персистентностью (рис. 2, слева). Пару кри-

(m_min = 0) кодируются вершинами, седла (m_sad =

тических точек (рождение — смерть) реферируют

= 1) — ребрами, а максимумы (m_max = 2) — гра-

как персистентную пару. Основной идеей то-

нями комплекса. Функция Морса задается таким

пологического упрощения или редактирования яв-

образом, что в вершинах ее значения меньше,

ляются сохранение свойств с высокой персистент-

чем на ребрах, а на ребрах меньше, чем на

ностью и удаление свойств с ее низкой величиной

гранях. У этого правила в каждом симплексе

(Эдельсбруннер и Харер, 2010). Так, персистент-

бывает не больше одного исключения, которое и

ность пары критических точек (x₁, x₄) на рис. 2 со-

позволяет проводить “стрелки” дискретных гради-

ставляет |f(x₄) - f (x₁)| > |f(x2) - f (x3)|. По-

ентов. Симплексы, которые не являются началами

этому пару (x₂, x₃) можно сократить, “выпрямив”

стрелок, называют критическими. Подчеркнем,

склон на графике от x₁ до x₄.

что в дискретном варианте седла и максимумы

Топологическое упрощение содержит два шага

являются не точками, а симплексами (Кнудсон,

(Гюнтер и др., 2014):

2015). Дискретное векторное поле удовлетворяет

определенным условиям, являющимся дискретны-

• Найти персистентную пару с наименьшим

ми аналогами перечисленных выше для непрерыв-

значением персистентности.

ных полей. Известны алгоритмы для вычисления

MS-комплексов по цифровым “серым” изобра-

⁶Представим горизонтальную плоскость, пересекающую

жениям (Робинс и др., 2011), и доступны готовые

две горы, разделенные седлом. Ниже седла в сечении

пакеты программ, например, DisPerSE (Cоусби,

только одна компонента связности. При пересечении сед-

2011). Мы использовали для вычислений свой,

ла и выше их уже две.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

ГРАФОДИНАМИКА АКТИВНЫХ ОБЛАСТЕЙ СОЛНЦА

525

f(x)

M₂

f(x₄)

f(x₂)

m₁

s m₂

m₁

f(x₃)

M₁

f(x₁)

x₁

x₂ x₃

x₄

Рис. 2. Левая панель: персистентность пары критических точек (x1, x4) больше, чем для пары (x2, x3). Поэтому пару

(x2, x3) можно сократить (пунктир). Правая панель: сокращение пары (s, m2) седло-минимум не меняет топологию.

1500

350

1000

300

500

250

200

-500

150

-1000

100

-1500

-2000

100

200

300

100

200

300

Рис. 3. Пример MS-комплекса одной из магнитограмм АО 12673 для разных уровней упрощения, сохраняющего

χ = 0. Минимумы—синие точки, седла— зеленые, максимумы— красные точки. Слева: #(max) = 23; #(min) = 29;

#(sadd) = 52. Справа: #(max) = 10; #(min) = 16; #(sadd) = 25.

• Изменить значения функции f таким об-

часовыми интервалами. Хорошо заметно измене-

разом, чтобы результат имел те же кри-

ние конфигурации критических точек комплекса и

тические точки, за исключением удаленной

границ клеток.

персистентной пары (см. рис. 2, справа, где

Для полученного графа можно выписать мат-

значение f изменено локально, только на

рицу Кирхгофа-Лапласа, и тогда графодинамику

дуге и смежных ей клетках комплекса).

можно описывать изменением ее спектра.

Упрощение проводится до достижения заданного

SCALE-SPACE, ТОП-ТОЧКИ

И МНОЖЕСТВА ЯКОБИ

порога персистентности, которым может быть

естественное ограничение. Например, функция

Основная идея масштабируемого пространства

Морса на сфере не может иметь меньше двух

или Scale-Space заключается в последователь-

критических точек, а на торе меньше четырех.

ном размытии деталей изображения, при кото-

Пример топологического редактирования магнито-

ром отслеживаются уровни исчезновения харак-

граммы приведен на рис. 3. Две панели отличаются

терных деталей. Тем самым выявляется “глубин-

разным уровнем персистентности, сохраняющим

ная” структура изображения, связанная с инва-

характеристику Эйлера.

риантами высокого порядка (K ¨eйпер, 2002). Раз-

мытие реализуется (Линдеберг, 2013) итерацией

Можно показать, что MS-комплекс позволяет

сверток оригинального изображения I(x), x ∈ R² с

восстановить скалярное поле в PL приближении

и, следовательно, аппроксимирует поле АО в

гауссовским ядром g_t(x) шириной t = σ²:

∫

смысле обратной задачи (Аллеманд-Джоржис и

др., 2015).

I_t(x) = I(x) ∗ g_t(x) = I(y)g_t(y - x)dy;

(1)

На рис. 4 приведена графодинамика АО на

R²

(

)

примере трех редактированных, с фиксированной

g_t(x) =

√ exp

-x²/2t

персистентностью, MS-комплексов, разделенных

2πt

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

526

АЛЕКСЕЕВ и др.

Рис. 4. Три эпизода графодинамики MS-комплекса АО

12673 с фиксированным уровнем персистентности после

упрощения, разделенные часовым интервалом времени.

Свертка обладает свойством полугруппы: g_t ∗ g_s =

нему по величине максимумом (Гу и др., 2010).

= gt+s, так что число итераций или, что то же самое,

Такой граф нетрудно построить для магнитограмм

ширина ядра определяет масштаб деталей, которые

вспышечных АО (Князева и др., 2016; Лукьянов

еще сохраняются на изображении. Важным явля-

и др., 2017). Его прогностическая эффективность

ется принцип причинности, который утверждает,

еще не исследована детально. Заметим, однако, что

что высота максимумов с масштабом уменьшается,

временная последовательность критических сетей

а минимумов, напротив, увеличиваются — изобра-

для магнитограмм АО будет неоднородна по мас-

жение “уплощается”. Новые элементы не могут

штабам, поскольку трудно выбрать для них “об-

возникнуть, не имея своих мелкомасштабных про-

щий” бета-устойчивый уровень сглаживания. Кро-

образов. Для случая 2D матрица вторых производ-

ме того, эта сеть не содержит седловых точек,

ных (гессиан) I(x, y) содержит диагональ (I_xx, I_yy),

которые особенно важны для описания сложности

I_xx ≡ ∂²I/∂x∂x. Так, что след Гессиана I_xx + I_yy =

магнитных полей (Жужома и др., 2017).

= ΔI дает лапласиан, который равен сумме двух

Рассмотрим поэтому способ построения другого

собственных значений. Из принципа причинности

графа также в Scale-Space. Идея его построения

следует, что в максимумах ΔI < 0 и ∂I/∂t < 0, по-

восходит к классическим результатам Джеймса

тому что их высота убывает с масштабом. В мини-

Дэймона (1995) о связи гауссовского блюринга и

мумах неравенства меняют знаки, так что в общем

теории катастроф. Рассмотрим, как и выше, одно-

случае (∂I/∂t) ΔI > 0. В предположении линейно-

параметрическое семейство (см. (1)) магнитограмм

сти этому условию можно удовлетворить, положив

I_t (Линдеберг, 2013). Критические точки при каж-

∂I/∂t = αΔI, α > 0. Таким образом, свертка (1)

дом фиксированном масштабе t, очевидно, удовле-

с учетом принципа причинности эквивалентна для

компактной области второй краевой задаче для

творяют условию ∇I_t(x, y) = 0. Вырожденными

называют точки (x, y, t), в которых, кроме гради-

уравнения диффузии⁷ (Линдеберг, 2013):

ента, в нуль обращается и гессиан: det HIt (x, y) =

∂I_t/∂t = (1/2)ΔI_t, I₀ = I(x,0) = I(x),

(2)

= 0. В вырожденных особенностях поля происхо-

где ширина ядра t играет роль времени.

дит либо появление, либо слияние пары критиче-

ских точек с противоположными знаками гессиана.

Для Морсовских точек масштаб t называют

Кроме того, в силу уравнения (2) в Scale-Space

бета-устойчивым, если его изменение в неболь-

шом интервале приблизительно сохраняет число

возникают точки, для которых обращается в нуль

экстремумов (Гу и др., 2010). На этом уровне

производная по масштабу ∂I_t/∂t = 0 или, что то

уравнение (2) позволяет оценить лапласиан как

же самое, ΔI_t = 0. Понятно, что в этом случае

разность двух изображений:

след Гессиана обращается в нуль, а вторая диаго-

наль должна содержать смешанные производные с

ΔI_t = 2∂I_t/∂t ≈ It+1 - I_t.

(3)

разными знаками. Этой ситуации, следовательно,

Ранжируя экстремумы лапласиана по величине,

будут соответствовать седловые точки.

начиная с самого глубокого минимума, можно по-

Мы ограничиваемся случаем det HIt (x, y) = 0,

строить в Scale-Scape двудольный граф. Он на-

∇I_t(x,y) = 0. При непрерывном изменении мас-

зывается критической сетью и образован ребрами,

штаба последовательность таких особых точек об-

соединяющими каждый минимум с ближайшим к

разует критические пути (K ¨eйпер, 2002; Линдеберг,

2013). Вершины критических путей называют топ-

⁷Другой способ доказать эквивалентность (1) и (2) запи-

сать решение (2) через функцию Грина, используя преоб-

точками, которые служат вершинами графа, опи-

разование Фурье.

сывающими мультимасштабную структуру поля.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

ГРАФОДИНАМИКА АКТИВНЫХ ОБЛАСТЕЙ СОЛНЦА

527

Рис. 5. Множество критических путей трех магнитограмм АО 12673, разделенных 3-часовыми интервалами. Черные

линии — критические пути, т.е. траектории критических точек при изменении масштаба.

Вычисление критических путей в общем случае

Мы реализовали алгоритм для построения крити-

связано с вычислением вторых производных на

ческих путей, основанных на этих идеях.

дискретном носителе. Разумеется, можно исполь-

На рис. 5 приведен пример построения крити-

зовать соотношение I^′(x) ∗ g_t(x) = I(x) ∗ g^′t(x), ко-

ческих путей для трех магнитограмм АО, после-

торое называют слабым дифференцированием, но

довательных во времени. Заметим, что множество

мы поступим иначе. В этой работе мы используем

критических путей аппроксимирует поле в смысле

оригинальный способ построения критических пу-

обратной задачи (Кантерс и др., 2005).

тей с помощью множеств Якоби.

Существует несколько способов построения

Формально пусть f, g — функции Морса на R².

графа по топ-точкам. Один из них заключается

Множеством Якоби (Эдельсбрунер, Харер, 2004)

в следующем. Будем спускаться вниз по кри-

этих двух функций называют множество точек, в

тическому пути, уходящему в бесконечность, и

которых градиенты этих функций коллинеарны, т.е.

последовательно подключать критические точки

векторное произведение |∇f × ∇g| = 0. Формаль-

в порядке уменьшения масштаба. Точнее, ребра,

но пусть f, g определены на компактном многооб-

соединяющие точки, подключаются в соответствии

разии M ⊂ R² и допускают вычисление градиентов.

с триангуляцией Делоне, которая постоянно пере-

Тогда множество Якоби J определяется как

страивается при движении вниз по масштабам.

J = {x ∈ M|∇f(x) + λ∇g(x) = 0

(4)

В качестве примера на рис. 6 показан граф,

или λ∇f(x) + ∇g(x) = 0}.

построенный согласно описанной схеме для кри-

тических путей одной из магнитограмм АО 12673.

Отсюда следует, что множество J образовано

Каждому такому графу соответствует матрица Ла-

критическими точками функций f(x) + λg(x) либо

пласа, для которой и вычисляется спектр.

λf(x) + g(x). Можно показать, что множество

Якоби двух морсовских f, g : M → R является

гладким вложением 1D многообразия (т.е. набора

ДИСКРЕТНЫЙ ОПЕРАТОР ЛАПЛАСА

кривых) в M (Эдельсбрунер, Харер, 2004).

И ЕГО СПЕКТР

Определим пару функции в Scale-Space:

Пусть G = {V, E} — неориентированный граф,

F (x,y,t) = f_t(x,y), G(x,y,t) = t,

(5)

имеющий |V | = n вершин. Ради простоты обозна-

где f_t(x, y) = f(x, y) ∗ g_t(x, y), как и прежде,

чим его вершины натуральной последовательно-

свертка исходной функции с гауссовским ядром

стью чисел V = {x₁, x₂, ..., x_n}. Говорят, что две

(1). Нетрудно убедиться, что множество Якоби

вершины смежны, x_i ∼ x_j, или i ∼ j, если они инци-

функций F , G совпадает с множеством крити-

дентны одному ребру, т.е. являются его граничными

ческих путей мультимасштабного представления

точками. Число ребер, инцидентных вершине x_i,

функции f(x, y). Действительно, ∇G = (0,0,1).

называют ее степенью deg x_i. Матрица смежности

Множество Якоби состоит из точек, в которых

AидиагональнаяматрицастепенейD определяют-

градиенты функций F , G коллинеарны. Следо-

ся выражениями (Молитьерно, 2016):

вательно, множество Якоби образуют точки, для

{

которых ∇F_t = 0, т.е.

если x_i ∼ x_j ,

A_ij =

(7)

∂F/∂x = 0;

∂F/∂y = 0.

(6)

иначе,

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

528

АЛЕКСЕЕВ и др.

300

280

260

240

100

220

200

180

160

140

120

300

100

200

100

300

Рис. 6. Граф, построенныйна топ-точках для одной из магнитограмм АО 12673. Слева 3D изображение,справа проекция

на плоскость.

AR12673, Morse graph connectivity

0.20

0.18

0.16

0.14

0.12

x2.2

x9.3

0.10

Рис. 7. Изменение сглаженной алгебраической связности дискретного лапласиана MS комплексов в интервале 3-

6 сентября 2017 г. Вспышки показаны вертикальными линиями. Приблизительно за сутки до события наблюдается

уменьшение алгебраической связности с последующим ее возрастанием.

{

deg x_i если i = j,

где сумма берется по всем вершинам j ∼ i, инци-

D_ij =

дентным x_i. Такое определение согласуется с клас-

иначе.

сическим, где лапласиан определяется усреднени-

ем функции по ее границе (см. Приложение А2).

Дискретный лапласиан или матрица Кирхгофа-

Нетрудно убедиться, что матрица (8) действитель-

Лапласа (Молитьерно, 2016; Чунг, Грахам, 1997)

но определяет лапласиан (9) в каждой вершине.

является разностью L = D - A или определяется

К аналогичному выражению можно прийти ре-

выражением:

шением второй краевой задачи для дискретного

⎧

⎨deg i если i = j,

набора точек (см. Приложения А3, А4).

L_ij =

-1

если i = j и i ∼ j,

(8)

Множество λ₀ ≤ λ₁ ≤ . . . ≤ λn-1 собственных

⎩

значений графа L, полученных как решение урав-

иначе.

нения Lu = λu, называют спектром дискретного

лапласиана. Напомним, что для связного графа

Предположим, что в каждой вершине x_i графа

λ₀ = 0. Поэтому мы использовали первое нетриви-

задана функция f(x_i). В простейшем случае можно

альное собственное значение λ₁, которое называют

положить f(x_i) = i. Тогда лапласианом функции в

алгебраической связностью (Чунг, Грахам, 1997).

этой точке называют выражение:

Отметим, что спектр позволяет “услышать” пере-

∑

стройку графа, в смысле задачи Вейля-Каца (см.

-Δf(x_i) = (deg x_i)-1

[f(x_j) - f(x_i)],

(9)

j∼i

Приложение А5).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

ГРАФОДИНАМИКА АКТИВНЫХ ОБЛАСТЕЙ СОЛНЦА

529

AR12673

1.8

0.3

1.7

0.2

1.6

1.5

0.1

1.4

1.3

1.2

0.1

1.1

x2.2

x9.3

x2.2

x9.3

1.0

0.2

Рис. 8. Графики изменений сглаженной алгебраической связности АО 12673 (cлева) и ее первой производной (справа)

для графов, построенныхпо топ-точкам в Scale-Space. Значительные вариации кривых наблюдаются приблизительноза

1.5 сут до X-вспышек.

РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ

В первом случае по временной последователь-

ЭКСПЕРИМЕНТОВ

ности HMI/SDO магнитограмм выбранной АО

12673 для каждой из них вычислялся клеточный

Для численных экспериментов мы использова-

комплекс Морса-Смейла.

ли LOS магнитограммы области АО 12673 (сен-

тябрь, 2017 г.). Она имела наибольшую вспышеч-

Полученные для ее магнитограмм MS-комплексы

ную продуктивность из всех АО цикла № 24 (Сан,

топологически редактировались для того, чтобы

Нортон, 2017). Активная Область продуцировала

убрать незначимые (в смысле персистентности)

восемь вспышек класса М и четыре вспышки клас-

флуктуации поля. Они рассматривались как гра-

са X, самой мощной из которых была вспышка

диентные модели магнитной динамики АО, которые

Х9.3 (SOL2017-09-06T11:53). За 4 ч до этого

сохраняют ее топологические свойства.

события произошла вспышка Х2.2 (SOL2017-09-

Во втором случае для той же последователь-

06T08:57).

ности магнитограмм с помощью множества Якоби

Для последовательности HMI/SDO магнито-

строились критические пути в Scale-Space и граф

грамм этой области с дискретом 30^m были вы-

по топ-точкам. Такой граф отражает “глубинную”

числены MS-комплексы и графы по топ-точкам.

структуру магнитограммы, суммируя информацию

Для каждого графа Морса был вычислен спектр

о критических точках на всех доступных масшта-

дискретного лапласиана. На рис. 7 приведен гра-

бах.

фик изменения алгебраической связности λ₁ этого

Эволюция АО продуцирует перестройку гра-

графа за период 3-6 сентября 2017г.

фа. Для количественного описания графодинамики

Заметное уменьшение алгебраической связно-

обоих графов использовался спектр дискретного

сти, предваряющее события приблизительно за

лапласиана. График изменения первого нетриви-

сутки, хотелось бы связать с предвспышечной ди-

ального собственного значения λ₁ — алгебраиче-

намикой. Однако такой вывод нуждается в про-

ской связности — демонстрирует сложное поведе-

верке на состоятельной статистической выборке

ние для двух вариантов графов. На рис. 7 мож-

вспышечных АО.

но выделить интервалы депрессии, которые хо-

Для сравнения на рис. 8 приведены графики

телось бы считать предшествующими вспышкам

изменения алгебраической связности графов на

приблизительно за сутки. Аналогичные колебания

топ-точках для той же области АО12673 (слева) и

связности демонстрируют графы, построенные по

ее первой производной (справа).

топ-точкам как в связности, так и в ее первой

производной (рис. 8).

Вопрос, имеют ли обнаруженные эффекты про-

ЗАКЛЮЧЕНИЕ

гностическую значимость, конечно, требует тести-

В этой работе мы использовали методы дис-

рования на статистически представительной вы-

кретной теории Морса и теории катастроф для

борке вспышечных АО. Заметим, что перестрой-

построения топологической модели АО в форме

ка графа, а следовательно, и изменение спектра,

графа Морса и мультимасштабного графа по топ-

вызывается не только движением критических то-

точкам в Scale-Space.

чек, но и возникновением новых точек, связанных,

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

530

АЛЕКСЕЕВ и др.

1 ,B

Рис. 9. Полный граф {x1, x2, x3} образованный вершинами треугольника (слева), его матрицу Лапласа-Кирхгофа L и

граничную матрицу В ≡ ∂ (справа).

}

например, со всплытием магнитного потока. Это

+ [f (x₀ - h) - f (x₀)]

усложняет задачу сравнения графов: они становят-

Практически очевидна аналогия с (9): лапласиан

ся не изометричны. Одним из вариантов решения

вычисляется как арифметическое среднее разно-

этой проблемы может быть вычисление дискрет-

стей функции в x₀ и ее значений на границах

ной кривизны Оливье-Риччи для графа (Самал,

интервала.

2018), которая связана как со спектром дискретно-

го лапласиана, так и числами Бетти. Она является

A3. Рассмотрим полный граф {x₁, x₂, x₃}, об-

глобальной геометрической характеристикой поля,

разованный вершинами треугольника, его матрицу

вычисляется на ребрах графа и более устойчива к

Лапласа-Кирхгофа L и граничную матрицу В ≡

изменению числа вершин.

≡ ∂ (рис. 9). Последняя описывает вершинно-

Наша главная цель заключалась в построении

реберные отношения. Пусть p = (x, e) — функ-

топологических моделей эволюции АО, которые

ция, определенная на парах вершина-ребро e =

допускают регулируемое упрощение, сохраняющее

= [x_a, x_b] ≡ [a, b], так что p = (x_a, e) = +1, p =

характеристику Эйлера. Так, MS-комплекс, как

= (x_b, e) = -1, где знак зависит от того, является

градиентная модель, позволяет отслеживать эво-

ли вершина началом или концом ребра. Тогда

люцию АО в инвариантных переменных. Граф, по-

{

строенный на топ-точках, отслеживает мультимас-

p(x_i, e_j ),

штабную динамику, опирающуюся на неморсов-

B_ij =

ские особые точки. Таким образом, мы предлага-

если x_i ∈ e_j .

ем графодинамику АО, снабженную интерфейсом

Легко убедиться, что: ∂ ≡ B; ∂ · ∂^T = Δ = L. Ко-

дискретной римановой геометрии, как универсаль-

ную модель для описания и диагностики эволюции

граничный оператор ∂ является аналогом операто-

активных магнитных паттернов.

ра ∇для функций.

Умножение вектора (x₁, x₂, x₃)^T на полный

ПРИЛОЖЕНИЕ А

граф {x₁, x₂, x₃}, образованный вершинами тре-

угольника, его матрицу Лапласа-Кирхгофа L и

A1. В пространствах большой размерности лю-

граничную матрицу В ≡ ∂, действительно дает

бая пара векторов, почти наверное, является ор-

дискретные лапласианы (9) функции f(x_i) = i в

тогональной (Горбань, Тюкин, 2018). Рассмотрим

вершинах графа:

функцию f(x₁, x₂,

,x_n) ≡ f (x), n ≫ 1 большого

числа слабо связанных переменных. Ее первый

-2x₁ + x₂ + x₃ = (x₂ - x₁) + (x₃ - x₁) = Δ(x₁),

член разложения в ряд Тейлора f (x + h) - f (x) ≈

x₁ - 2x₂ + x₃ = (x₁ - x₂) + (x₃ - x₂) = Δ(x₂),

≈ (∇f (x) · h) + . . . равен нулю, поскольку два век-

тора, градиент и смещение, почти наверное, ор-

x₁ + x₂ - 2x₃ = (x₁ - x₃) + (x₂ - x₃) = Δ(x₃).

тогональны. Следовательно, f (x + h) = f (x), т.е.

наша функция — постоянная (Зорич, 2014), и лю-

А4. Покажем теперь, что (9) является дискрет-

бой нелинейный многомерный предиктор, реализу-

ным аналогом классического уравнения диффузии

емый, например, с помощью нейросети, приведет к

∂

инерционному прогнозу.

Δu(x, t) =

u(x, t)

(A4.1)

∂t

A2. Пусть f(x) дважды дифференцируема в

окрестности точки x₀. Используя ее разложения

с начальными условиями u(x, 0) = f(x). Решение

в ряд Тейлора в окрестностях x₀ для f(x₀ + h) и

удобно записать (Розенберг, 1997), используя теп-

f (x₀ - h), легко получить выражение для второй

ловой оператор (ядро)

производной (одномерный лапласиан):

∫

{

u(x, t) =

H^t(x,y)f(y)dμ(y);

(A4.2)

f^′′(x₀) = lim

[f (x₀ + h) - f (x₀)] +

h→0 h²

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

ГРАФОДИНАМИКА АКТИВНЫХ ОБЛАСТЕЙ СОЛНЦА

531

∫

Работа выполнена при поддержке Российского

H^t(x,y)dμ(y) = 1.

фонда фундаментальных исследований (грант

мол-нр

№ 19-32-50023) и гранта МОН РК

Здесь интеграл берется по подходящей мере Ле-

№ AP05134227.

бега, H^t(x, y) — обычно гауссовское ядро, а u(x, t)

измеряет температуру в точке x в момент t > 0 вы-

званной единицей тепла, помещенной в начальный

СПИСОК ЛИТЕРАТУРЫ

момент в точку y. Перепишем уравнение (А3.2) в

Аллеманд-Джоржис и др. (L. Allemand-Giorgis,

виде

G.P. Bonneau, S. Hahmann), Topological Methods

∫

∂

in Data Analysis and Visualization. (Springer,

Δu(x, t) =

H^t(x,y)f(y)dμ(y)

(A4.3)

Cham, 151, 2015).

∂t

Ашванден (M.J. Aschwanden), Solar Phys. 262, 235

(2010).

и аппроксимируем производную справа, разностью

Аллили, Корриво (M. Allili, D. Corriveau), Computer

решения (А3.2) и начального значения:

Vision and Image Understanding 105, 188 (2007).

Δu(x, t) =

(A4.4)

Аллили и др. (M. Allili, D. Corriveau, S. Derivi `ere,

⎞

⎛∫

T. Kaczynski, A. Trahan), J. Math. Imaging and

1_⎝

Vision 28, 99 (2007).

= lim

H^t(x,y)f(y)dμ(y) - f(x)⎠ =

t→∞

Айзерман M.A., Гусев Л.А., Петров C.B., Смир-

нова И.M., Автоматика и телемеханика 7,

135

∫

(1997).

= lim

H^t(x,y)(f(y) - f(x)) dμ(y).

Бобра и др. (M.G. Bobra, X. Sun, J.T. Hoeksema,

t→∞ t

M. Turmon, Y. Liu, K. Hayashi, G. Barnes,

K.D. Leka), Solar Phys. 289, 3549 (2014).

Здесь использовано условие нормировки ядра и тот

Ванг, Ванг (H.N. Wang, J. Wang), Astron.

факт, что f(x) не зависит от переменной интегри-

Astrophys. 313, 285 (1996).

рования. Тогда для дискретного набора точек (вер-

Горбань, Тюкин (A.N. Gorban, I.Y. Tyukin),

шин) графа и гауссовского ядра нетрудно получить

Philosoph. Trans. Royal Soc. A: Mathem., Phys.

(Розенберг, 1997):

and Engin. Sci. 376, 20170237 (2018).

∑

|x-y_i|²

Гуткин, Смиланский (B. Gutkin, U. Smilansky), J.

Δu(x) ≈

e^-

(f(y_i) - f(x)) , (A4.4)

Phys. A: Mathemat. and General. 34, 6061( 2001).

y_i∼x

10.

Гу и др., (S. Gu, Y. Zheng, C. Tomasi), European

Conference on computer vision, (Springer Berlin

где сумма включает все вершины y_i, инцидентные

Heidelberg, 663, 2010).

x: y_i ∼ x. Это выражение совпадает с (9) с точ-

11.

Гюнтер и др. (D. G ¨unther, J. Reininghaus,

ностью до весового множителя, которым является

H-P. Seidel, T. Weinkauf), Topological Methods

гауссовское ядро.

in Data Analysis and Visualization III (Springer,

А5. Пусть Ω ∈ R² — компактная область с ме-

Cham, 135, 2014).

рой Лебега |Ω|и гладкой границей ∂Ω. Пусть далее

12.

Деймон (J. Damon), J. Different. Equat. 115, 368

Spec(Δ) = {λ_k}∞0 — спектр собственных значе-

(1995).

ний первой краевой задачи для уравнения Лапласа:

13.

Дешмук и др. (V. Deshmukh, V. Berger, T.E. Bradley,

Δu + λu = 0; u|∂Ω = 0. Герман Вейль в 1911 г.

E.J.D. Meiss), J. Space Weath. and Space Climate

получил для числа собственных значений, меньших

10, 13 (2020).

λ, асимптотическую формулу N (λ) ∼ |Ω| λ. В свя-

14.

Жужома и др. (Е.В. Жужома, В.С. Медведев,

Н.В. Исаенкова), Нелинейная динам.

13,

399

зи с этим результатом Марк Кац (1966) предло-

(2017).

жил следующую задачу. Предположим, что Ω —

15.

Зорич В.А., Теория вероятностей и ее применения

мембрана или барабан и вы обладаете идеальным

59, 436 (2014).

слухом, т.е. “слышите” весь спектр Spec (Δ) ее

16.

Кантерс и др. (F. Kanters, M. Lillholm, R. Duits,

тонов. Формально свойство называется слыши-

B. Janssen, B. Platel, L. Florack, B. ter Haar

мым, если оно полностью определяется Spec (Δ).

Romeny,), Internat. Conf. on Scale-Space Theories

Какие геометрические и топологические свойства

in Computer Vision (Springer, Berlin, Heidelberg,

Ω можно “услышать”? Вейль показал, что мож-

431, 2005).

но услышать площадь барабана. Оказывается, за

17.

Кац (M. Kac), Аm. Mathem. Mon. 73, № 4P2, 1

исключением экзотических случаев, слышимыми

(1966).

являются периметр |∂Ω|и число дыр в барабане.

18.

Кемпи и др. (C. Campi, et al.), Astrophys. J. 883, 150

Более сложной оказалась проблема изоспектраль-

(2019).

ности. Аналог этой задачи для графов обсуждается

19.

Князева и др. (I.S. Knyazeva, N.G. Makarenko,

в работе (Гуткин, Смиланский, 2001).

F.A. Urt’ev), Geomagnet. Aeronomy 55, 1134 (2015).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020

532

АЛЕКСЕЕВ и др.

20.

Князева и др. (I.S. Knyazeva, N.G. Makarenko,

34.

Препарата Ф., Шеймос М. Вычислительная гео-

I. Makarenko, A Vdovina, F.A. Urtiev), Phys.

метрия: введение (Мир, 1989).

Procedia 738, 012070 (2016).

35.

Пранав и др. (P. Pranav, H. Edelsbrunner, R. Van

21.

K ¨eйпер (A. Kuijper) The deep structure of Gaussian

de Weygaert, G. Vegter, M. Kerber, B.J. Jones,

scale space images (PhD thesis, Utrecht Univer.,

M. Wintraecken), MNRAS 465, 4281 (2017).

2002).

36.

Робинс и др. (V. Robins, P.J. Wood, A.P. Sheppard),

22.

Кнудсон (K.P. Knudson), Morse theory: smooth and

IEEE Transactions on pattern analysis and machine

discrete (World Scientific Publ. Co., 2015).

intelligence 33, 1646 (2011).

23.

Лека и др. (K.D. Leka, S-H. Park, K. Kusano,

37.

Розенберг (S. Rosenberg). The Laplacian on a

J. Andries, G. Barnes, S. Bingham, D.Sh. Bloomfield,

Riemannian manifold. (London Math. Soc. Student

A.E. McCloskey, et al.), Astrophys. J. 881(2), 101

Texts, V. 31, Cambridge 1997).

(2019).

38.

Cоусби (T. Sousbie), MNRAS 414, 350 (2011).

24.

Лим и др. (D. Lim, Y.J. Moon, J. Park, E. Park,

39.

Сан, Нортон, (X. Sun, A.A. Norton), Res. Not. AAS

K. Lee, J.Y. Lee, and S. Jang), arXiv preprint

1, 24 (2017).

arXiv:1907.11373 (2019).

25.

Лиу и др. (H. Liu, C. Liu, J.T. Wang, H. Wang),

40.

Самал и др. (A. Samal, R.P. Sreejith, J. Gu, S. Liu,

Astrophys. J. 877, 121 (2019).

E. Saucan, J. Jost), Scientific Rep. 8, 8650 (2018).

26.

Линдеберг (T. Lindeberg) Scale-space theory in

41.

Турмон и Мухтар (M. Turmon, S. Mukhtar), Proc.

computer vision, (Springer Science&Business

IEEE Intl. Conf. Image Processing, vol. III, (CL 97-

Media, 2013).

1147), 320-323 (1997); Proc. Compstat-98, Bristol,

27.

Лукьянов и др. (A.D. Lukyanov, N.G. Makarenko,

UK. (CL 98-0761), 473-478 (1998).

I. Knyazeva), Phys. Procedia 798, 012181 (2017).

42.

Фельдбрюгге и др. (J. Feldbrugge, M. van Engelen,

28.

Макаренко Н.Г., Малкова Д.Б., Мячин М.Л., Кня-

R. van de Weygaert, P. Pranav, G. Vegter), J.

зева И.С., Макаренко И.Н., Фундаментальная и

Cosmology Astropart. Phys. 2019, 052 (2019).

прикладная математика, 18(2), 79 (2013).

43.

Чунг, Грахам (F.R. Chung, F.C. Graham), Spectral

29.

Макаренко и др. (N.G. Makarenko, D.O. Park,

graph theory (No. 92). (American Mathemat. Soc.

V.V. Alexeev), Phys. Procedia 675, 032026 (2016).

1997).

30.

Макаренко и др. (N.G. Makarenko, L. Karimova,

44.

Шрийвер и др. (C.J. Schrijver, A.A. van Ballegooijen,

A. Terekhov, M. Novak), Physica A: Statist. Mech.

H.J. Hagenaar, R.A. Shine), Astrophys. J., 487, 424

Appl. 289, 278 (2001).

(1997).

31.

Максвелл (J. Clerk Maxwell), Phil. Mag. Ser. 4 40,

45.

Эдельсбруннер, Харер, (H. Edelsbrunner, J. Harer)

421 (1870).

Computational topology: an introduction,

32.

Молитьерно (J.J. Molitierno), Applications of

(American Mathematical Soc., 2010).

combinatorial matrix theory to Laplacian

46.

Эдельсбрунер и Харер, (H. Edelsbrunner, H. Harer),

matrices of graphs. (Chapman and Hall / CRC,

in Foundations of Computational Mathematics

2016).

(Cambridge, 37-57, 2004).

33.

Пак Сун Хонг и др. (S-H. Park, K.D. Leka,

47.

Эдельсбруннер и др. (H. Edelsbrunner,

K. Kusano, J. Andries, G. Barnes, S. Bingham,

D. Kirkpatrick, R. Seidel), IEEE Trans. Inform.

D.Sh. Bloomfield, A.E. McCloskey, et al.), Astrophys.

Theory 29, 551(1983).

J. 890(2), 124 (2020).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 46

№7

2020