ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2021, том 47, № 1, с. 53-65
ВЛИЯНИЕ ДИСПЕРСИИ СКОРОСТЕЙ ПЫЛИ В МЕЖЗВЕЗДНОЙ
СРЕДЕ НА ЕЕ РАСПРЕДЕЛЕНИЕ ВНУТРИ ГЕЛИОСФЕРЫ
© 2021 г. Е. А. Годенко1,2,3*, В. В. Измоденов1,2,3
1Институт проблем механики им. А.Ю. Ишлинского РАН, Москва, Россия
2Московский государственный университет им. М.В. Ломоносова, Московский центр фундаментальной
и прикладной математики, Москва, Россия
3Институт космических исследований РАН, Москва, Россия
Поступила в редакцию 27.08.2020 г.
После доработки 18.11.2020 г.; принята к публикации 26.11.2020 г.
Межзвездная пыль проникает в гелиосферу из-за относительного движения Солнца в локальной
межзвездной среде. На частицы межзвездной пыли в гелиосфере действуют электромагнитные силы,
сила гравитационного притяжения и сила радиационного давления. Внутри гелиосферы и на ее
границах, где солнечный ветер взаимодействует с плазмой межзвездной среды, распределение частиц
межзвездной пыли меняется из-за действия этих сил и становится существенно неоднородным. В
нашей предыдущей работе было продемонстрировано существование особенностей в распределении
концентрации межзвездной пыли на расстоянии ∼0.03-10 а.е. от плоскости гелиосферного токового
слоя. В настоящей статье исследуется влияние дисперсии в распределении частиц межзвездной
пыли по скоростям и показано, что она сильно влияет на упомянутые особенности в распределении
концентрации. Даже относительно небольшие величины дисперсии оказывают значительное влияние
на распределение концентрации и сглаживают области повышенной концентрации, обнаруженные
ранее.
Ключевые слова: пыль, гелиосфера, численные методы.
DOI: 10.31857/S0320010821010046
ВВЕДЕНИЕ
др., 1992). В силу того, что длина свободного про-
бега межзвездных атомов гелия намного больше
Локальная межзвездная среда движется отно-
характерного размера гелиосферы, по измерениям
сительно Солнца со скоростью ∼26 км/c (Витте,
межзвездных атомов гелия можно получать мак-
2004, МакКомас, 2015). Помимо плазменной и
роскопические параметры локальной межзвезд-
нейтральной компонент, локальная межзвездная
ной среды. В настоящее время прямые измерения
межзвездных атомов водорода, кислорода и гелия
среда содержит также пылевую компоненту (Манн,
2010). В отличие от частиц плазмы, нейтральные
проводятся на КА Interstellar Boundary Explorer
и пылевые частицы могут проникать в гелиосфе-
(IBEX) с помощью прибора IBEX-Lo (см., напри-
ру из-за относительного движения. Так, напри-
мер, Мёбиус и др., 2009; Катушкина и др., 2015;
мер, длина свободного пробега атомов водорода
Балюкин и др., 2017). Также на КА SOHO (прибор
по перезарядке ∼50-100 а.е. (Измоденов и др.,
SWAN) продолжаются измерения интенсивности
и спектральных характеристик рассеянного сол-
2000), что сопоставимо с характерным размером
нечного Лайман-альфа излучения (см., например,
гелиосферы.
Кюэмэра и др., 2013). Для анализа эксперимен-
Присутствие межзвездных частиц в гелиосфе-
тальных данных в настоящее время используются
ре было впервые экспериментально подтверждено
различные модели гелиосферы (см., например, Из-
в работе Берто, Бламонт (1971) на основе ана-
моденов, Алексашов, 2015, 2020; Погорелов и др.,
лиза рассеянного солнечного излучения в линии
2011; Зирнштейн и др., 2016).
Лайман-альфа (Lα). На космическом аппарате
(КА) Улисс были впервые проведены прямые изме-
Частицы межзвездной пыли — частицы, харак-
рения потоков межзвездных атомов гелия (Витте и
терные размеры которых находятся в диапазоне
от сотен нанометров до нескольких микрометров
*Электронный адрес: eg24@yandex.ru
(Матис и др., 1977). По химическому составу в
53
54
ГОДЕНКО, ИЗМОДЕНОВ
гелиосфере обычно выделяют углеродные и крем-
пыли для двух различных конфигураций гелио-
ниевые частицы (Дрэйн, 2009). Массовая доля
сферного магнитного поля (фазы фокусировки
межзвездной пыли от общей массы локальной
и дефокусировки отдельно). Также в этой ра-
межзвездной среды составляет ≈1% (Манн, 2010).
боте учитываются турбулентность межзвездного
Из-за различных физических процессов (напри-
магнитного поля (благодаря которой у пылинок
мер, из-за фотоионизации или из-за столкнове-
появляются дополнительные компоненты скоро-
ния с электронами) частицы межзвездной пыли
сти) и зависимость поверхностного потенциала
приобретают положительный электрический заряд.
частиц пыли от гелиоцентрического расстояния.
Будучи заряженными, пылевые частицы испыты-
Современные исследования межзвездной пыли
вают влияние гелиосферного магнитного поля, что
связаны с работами Стеркен и др. (2012), Стеркен
сильно усложняет динамику движения этих частиц
и др. (2019), Страб и др. (2015), Страб и др. (2019).
по сравнению с динамикой движения межзвездных
Используемые в этих работах модели распре-
атомов (без учета перезарядки атомов с протона-
деления межзвездной пыли являются развитием
ми).
более ранней модели Ландграфа и др.
(2000).
Трудность обнаружения частиц межзвездной
Они используют более совершенную технику
пыли была связана с наличием в гелиосфере
численного счета, а также актуальные параметры
межпланетной пыли, которая образуется из асте-
межзвездной среды и гелиосферы, полученные из
роидов, комет и других крупных объектов. Поэтому
последних экспериментальных данных. Мищен-
для обнаружения межзвездных пылевых частиц
ко и др. (2020) применили лагранжевый метод
на космическом аппарате Улисс (Грюн и др.,
(Осипцов, 2000) для изучения особенностей в
1994) необходимо было использовать направление
распределении концентрации межзвездной пыли
потока межзвездной среды, которое к тому моменту
в гелиосфере. В упрощенной стационарной по-
уже было известно (по измерениям межзвездных
становке, в которой гелиосферный токовый слой
атомов гелия). Более того, миссия Улисса была
представляет собой плоскость, совпадающую с
замечательна тем, что это был первый космиче-
плоскостью солнечного экватора, было проде-
ский аппарат, траектория которого выходила из
монстрировано существование сингулярностей в
плоскости эклиптики, и, следовательно, процесс
распределении концентрации. Они показали, что
отделения частиц межзвездной пыли от частиц
эти сингулярности образуют несколько плотных
межпланетной пыли становился проще, поскольку
слоев частиц межзвездной пыли по обе стороны
межпланетная пыль находится преимуществен-
от плоскости токового слоя. Данные особенности
но в плоскости эклиптики (например, частицы,
не были обнаружены в предыдущих работах, по-
образующие зодиакальный свет). Впоследствии
священных изучению распределения межзвездной
параметры межзвездной пыли также определялись
пыли в гелиосфере, поскольку в этих работах
по измерениям, проведенным на космических
моделирование проводилось методом Монте-
аппаратах Галилео (Алтобелли и др., 2005) и
Карло, при использовании которого для поиска
Кассини (Алтобелли и др., 2007).
особенностей требуются сетки расчетной области
Теоретическое моделирование распределения
чрезвычайно высокого разрешения. В этой работе
межзвездной пыли началось с пионерских работ
мы используем сетку расчетной области, ячейки
которой по одному из направлений имеют размер
Берто, Бламонт (1976) и Леви, Йокипи (1976). Они
исследовали отдельное влияние гравитационной и
10-3 а.е., а для исследования эффектов вблизи
электромагнитной силы на распределение пылевых
сингулярностей использовались ячейки размера
частиц в гелиосфере. Следующая волна интереса
10-6 а.е.
к изучению межзвездной пыли была связана с
Мищенко и др. (2020) использовали предполо-
измерениями, полученными на КА Улисс. В серии
жение, что в локальной межзвездной среде все ча-
работ Ландграф и др. (2000), Ландграф и др.
стицы межзвездной пыли имеют одинаковую ско-
(2003) были проанализированы эти измерения с
рость. Однако из-за того, что пылевые части-
помощью моделирования методом Монте-Карло.
цы имеют положительный электрический заряд,
Они рассматривали совместное влияние грави-
они вступают во взаимодействие с межзвездным
тационной силы, силы радиационного давления и
магнитным полем. Неоднородности межзвездного
электромагнитных сил на частицы межзвездной
магнитного поля ведут к ускорению заряженных
пыли в присутствии нестационарного гелиосфер-
частиц (Хоанг и др., 2012), которое нарушает од-
ного магнитного поля. Распределение межзвездной
нородность в распределении частиц межзвездной
пыли и эффект фильтрации пылевых частиц на
пыли по скоростям в локальной межзвездной среде
границе гелиосферы были исследованы в работах
и вносит в это распределение дисперсию. Цель
Чеховски, Манн (2003), Алексашов и др. (2016).
данной работы — исследовать влияние дисперсии
В работе Славин и др. (2012) была построена
в распределении частиц межзвездной пыли по ско-
трехмерная модель распределения межзвездной
ростям на возникновение особенностей в распре-
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
ВЛИЯНИЕ ДИСПЕРСИИ СКОРОСТЕЙ ПЫЛИ
55
делении концентрации в гелиосфере. В работе Сла-
вин др. (2012) также рассматривается дисперсия в
невозмущенном потоке межзвездной пыли, однако
z
V_ISM
ее влияние на возникновение особенностей они не
исследуют, поскольку для вычислений использует-
ся сетка расчетной области гораздо более низко-
го разрешения, чем в настоящей работе — ячейки
размером в 5 а.е. по каждому направлению.
r
y
ОПИСАНИЕ МОДЕЛИ
Математическая постановка задачи
HCS
Для описания движения частиц межзвездной
x
пыли в гелиосфере мы используем кинетический
подход, который состоит в вычислении функции
распределения межзвездной пыли по скоростям
fd(t,r,v). Кинетическое уравнение для поиска
функции распределения fd(t, r, v):
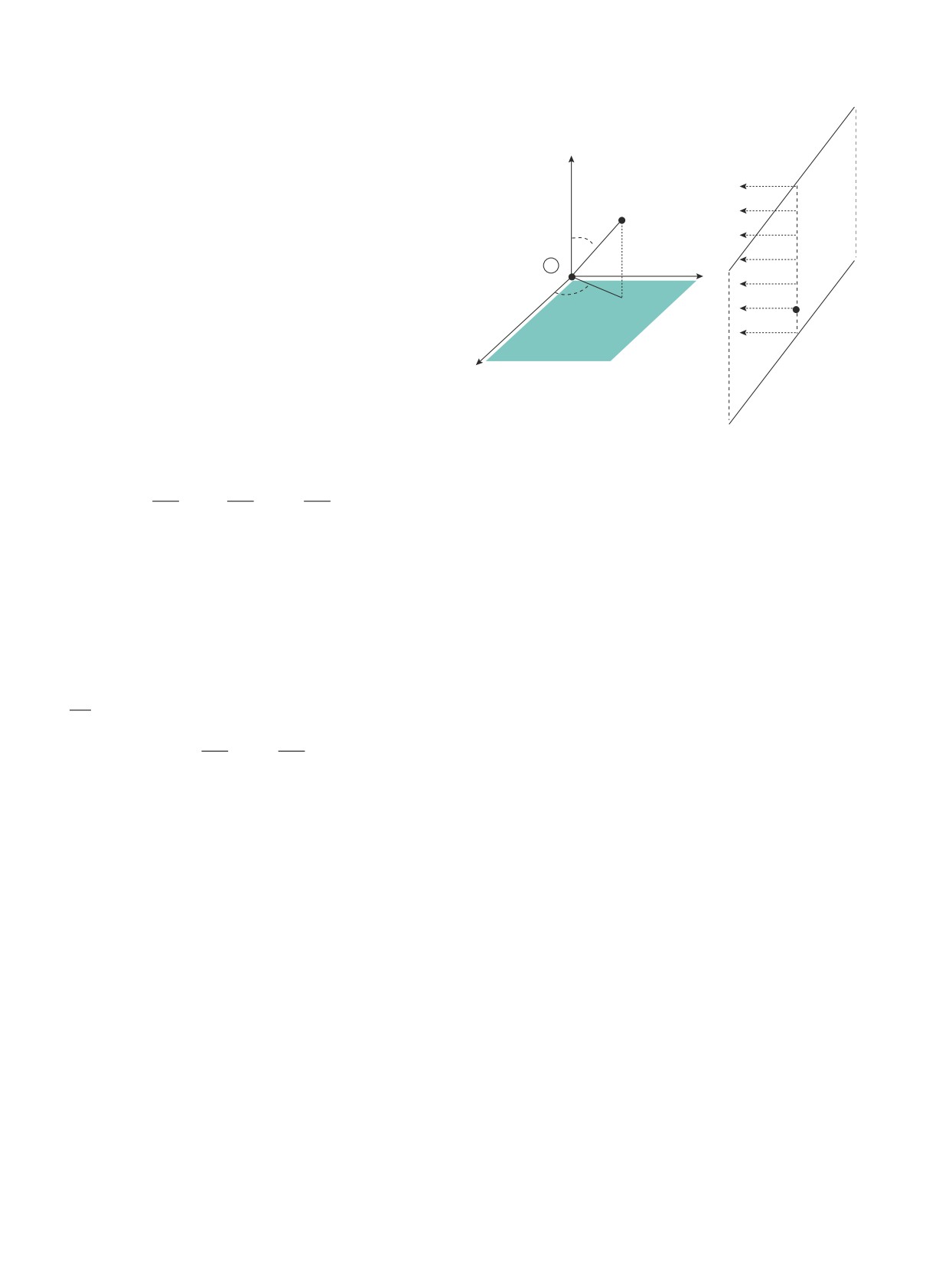
Рис. 1. Декартова система координат Oxyz. Нача-
ло координат O соответствует положению Солнца.
∂fd
∂fd
∂fd
Ось Oy направлена противоположновектору скорости
+v·
+F·
= 0,
(1)
∂t
∂r
∂v
движения локальной межзвездной среды относительно
Солнца vISM. Ось Oz совпадает с осью вращения
где F — результирующая сила, действующая на ча-
Солнца. Сферические координаты вводятся стандарт-
стицы пыли. В правой части (1) стоит 0, поскольку
ным способом.
мы пренебрегаем упругими столкновениями частиц
между собой и их взаимодействием с протонами
и электронами в гелиосфере (Густафсон, 1994). В
где fTS(v) — функция распределения межзвезд-
данной работе мы рассматриваем стационарную
ной пыли за пределами TS, en — вектор единич-
модель гелиосферного магнитного поля и стацио-
ной внутренней нормали к сфере радиуса rTS . В
нарные граничные условия, поэтому решение ки-
дальнейшем мы обсудим детально конкретный вид
нетического уравнения также будет стационарным,
функции fTS(v).
∂fd
= 0:
∂t
Для завершения математической постановки
∂fd
∂fd
задачи нужно также сформулировать граничное
v·
+F·
= 0.
(2)
условие в пространстве скоростей:
∂r
∂v
fd(r,v)|v→∞ = 0.
(4)
Для корректной математической постанов-
ки нужно сформулировать граничные условия.
Заметим, что каждая конкретная задача, которую
В данном случае для того, чтобы понять, как
можно описать с помощью математической по-
распределение межзвездной пыли изменяется
становки (2)-(4), будет определяться полем ре-
внутри области сверхзвукового солнечного ветра,
зультирующей силы F(r, v) и граничной функцией
мы предполагаем, что поток межзвездной пыли
распределения fTS(v).
является невозмущенным за пределами внутрен-
ней ударной волны (Termination Shock, TS) —
ударной волны, которая ограничивает область
Анализ действующих сил
распространения сверхзвукового солнечного ветра
в модели взаимодействия солнечного ветра с
Введем декартову систему координат, как пока-
межзвездной средой. В дальнейшем это поможет
зано на рис. 1. На частицы пыли основное влияние
нам отделить изменения распределения пыли
оказывают четыре силы (Катушкина, Измоденов,
в области взаимодействия солнечного ветра с
2019): центрально-симметричные силы гравитаци-
межзвездной средой (Алексашов и др., 2016) от
онного притяжения Fgrav и радиационного дав-
изменений в области сверхзвукового солнечного
ления Frad, электромагнитная сила Fel, а также
ветра. Поэтому граничное условие в физическом
сила трения Fdrag пылевых частиц с протонами,
пространстве поставим на сфере радиуса rTS , где
электронами и нейтральными атомами. Оценки по-
rTS — кратчайшее расстояние от Солнца до TS:
казывают, что в гелиосфере силой Fdrag можно
fd(r,v)|r=rTS , v·en>0 = fTS(v),
(3)
пренебречь (Густафсон, 1994).
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
56
ГОДЕНКО, ИЗМОДЕНОВ
Здесь vrel = v - vp, q — заряд частицы, c0 — ско-
рость света в вакууме, md — масса частицы, vp —
скорость солнечного ветра, B — гелиосферное
магнитное поле. Заряд частицы выражается через
поверхностный потенциал Ud и радиус частицы:
q = Uda. Потенциал Ud всверхзвуковом солнечном
Z
O
ветре изменяется несущественно (рис. 2 из Алек-
сашов и др., 2016, рис. 2 из Славин и др., 2012),
поэтому для простоты мы полагаем его посто-
r_TS
янным. При моделировании траекторий пылинок
вне области сверхзвукового солнечного ветра,
конечно, нужно учитывать изменения величины
потенциала с гелиоцентрическим расстоянием,
Y
однако это выходит за рамки данной работы.
4
Масса сферической частицы md =
ρdπa3, где
3
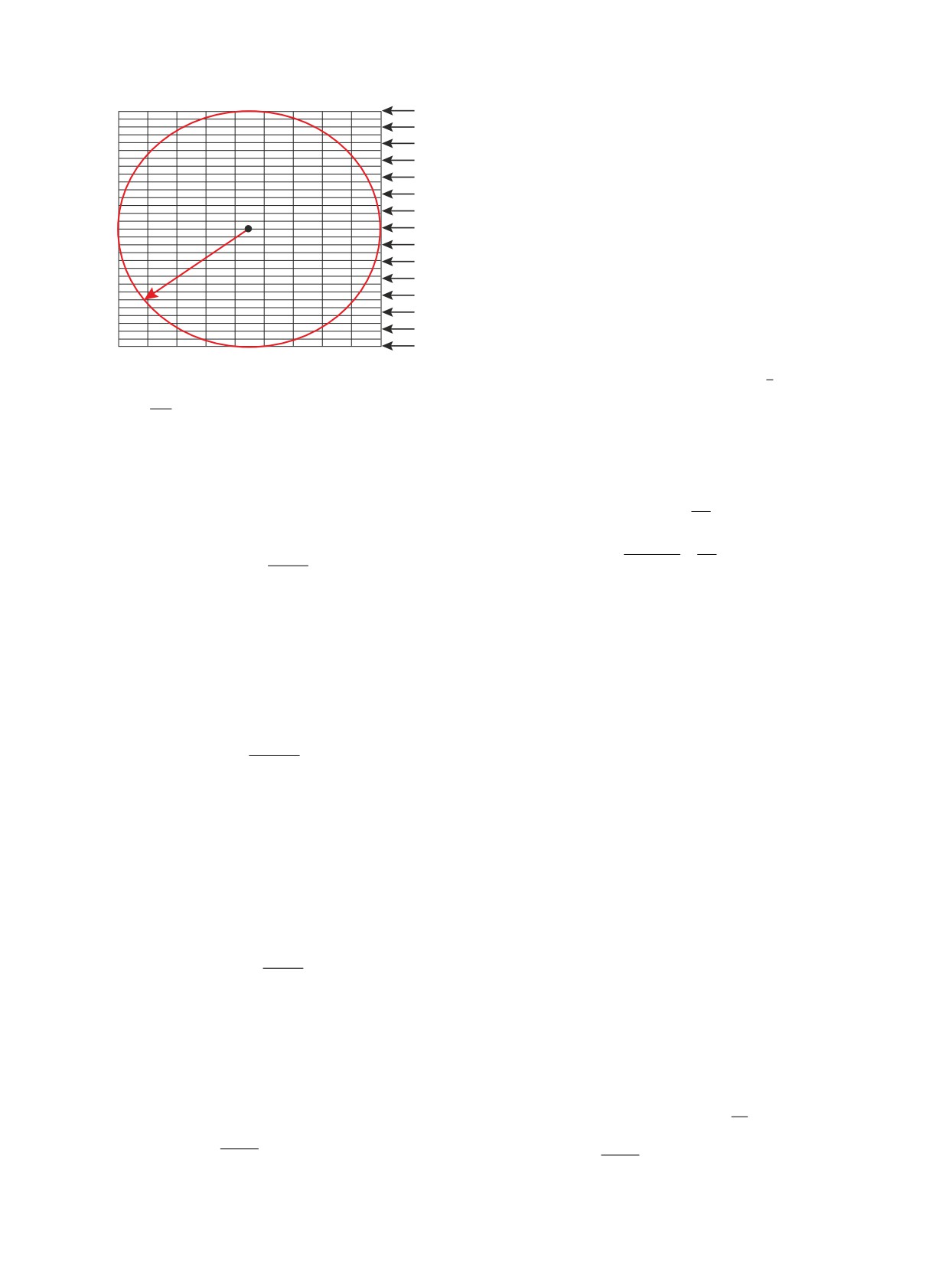
Рис. 2. Расчетная область — квадрат со стороной
ρd — массовая плотность частиц. Солнечный ветер
2rT S = 2rTS , описанный около окружности радиусаL
1
полагается сферически-симметричным, распро-
r = rTS в плоскости x = 0, где rTS — расстояние от
страняющимся с постоянной скоростью vp =
Солнца до TS. Ячейки расчетной области — прямо-
угольники размера Δŷ × Δz.
= vswer. Для гелиосферного магнитного поля
используется паркеровская модель:
)2
(rE
Сила гравитационного притяжения Fgrav имеет
Br = ±BE
,
(9)
r
следующий вид:
BEΩrE
(rE)
GMS
Bφ = ∓
sin θ,
Fgrav = -
er,
(5)
vsw
r
r2
Bθ = 0,
где G — гравитационная постоянная, MS — масса
Солнца.
где BE — усредненная величина магнитного поля
на орбите Земли, rE — астрономическая единица,
Поскольку вектор Fgrav коллинеарен вектору
Ω —угловая скорость вращения Солнца. Знак ±
Frad, и абсолютные величины этих векторов про-
характеризует полярность магнитного поля в зави-
порциональны r-2, удобно ввести безразмерный
симости от положения относительно гелиосферно-
параметр β, который является отношением абсо-
го токового слоя. Здесь для простоты мы полагаем,
лютных величин этих векторов:
что гелиосферный токовый слой является плоским
|Frad|
(плоскость Oxy на рис. 1). В реальности это не
β=
(6)
|Fgrav|
так, поскольку существует ненулевой угол между
осью вращения Солнца и его магнитной осью,
В данной работе для простоты мы рассматри-
поэтому гелиосферный токовый слой из-за вра-
ваем частицы сферической формы. В этом случае
щения Солнца вокруг своей оси принимает форму
параметр β зависит только от характеристик звез-
“юбки балерины” (ballerina skirt). Также в данной
ды и от массы частицы (см. Катушкина, Измоденов,
работе мы предполагаем, что магнитное поле яв-
2019). Здесь мы используем зависимость β = β(m)
ляется стационарным, т.е. плоскость токового слоя
из Стеркен и др. (2012) (зеленая сплошная линия
в данной системе координат покоится, и в области
на рис. 14 из этой работы). Выражение для силы
z > 0 компонента магнитного поля Br < 0, Bφ > 0,
радиационного давления следующее:
а в области z < 0, наоборот, Br > 0, Bφ < 0. Од-
GMS
нако на самом деле гелиосферное магнитное поле
Frad = β
er.
(7)
изменяется в течение 22-летнего цикла солнечной
r2
активности и, в частности, изменяет свою поляр-
Силовые линии гелиосферного магнитного поля
ность каждые 11 лет. В будущем мы планируем
вморожены в солнечный ветер, поэтому если пе-
развить нашу модель на случай нестационарного
рейти в систему координат, связанную с солнечным
магнитного поля.
ветром, то можно записать выражение для элек-
Таким образом, можем записать поле результи-
тромагнитной силы (в Гауссовой системе единиц),
рующей силы, действующей на частицы пыли:
используя скорость пылевых частиц относительно
er
солнечного ветра vrel:
F(r, v) = (β - 1)GMs
+
(10)
r2
q
q
Fel =
(vrel × B) .
(8)
+
[(v - vp) × B].
c0md
c0md
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
ВЛИЯНИЕ ДИСПЕРСИИ СКОРОСТЕЙ ПЫЛИ
57
Граничное условие
Славин и др. (2012) моделируют дисперсию с
помощью добавления дополнительной скорости,
В данной работе мы предполагаем, что вне TS
лежащей в плоскости, перпендикулярной направ-
частицы межзвездной пыли представляют из себя
лению межзвездного магнитного поля в области,
однородный поток частиц, движущийся со средней
откуда начинают свое движение пылевые части-
скоростью vISM , в который внесена дисперсия по
цы. Эта добавочная компонента скорости имеет
компоненте скорости vz. Межзвездное магнитное
поле имеет пространственные и временные неодно-
фиксированную величину (3 км/c), но случайное
родности, которые служат источником ускорения
направление в указанной плоскости. В настоящей
заряженных частиц в межзвездной среде (Хоанг и
работе мы моделируем дисперсию только по одной
др., 2012). Вследствие этого ускорения и возникает
компоненте скорости vz, однако за счет использо-
дисперсия в распределении межзвездной пыли по
вания нормального распределения, величина доба-
скоростям. Ниже будет показано, что относительно
вочной компоненты будет отличаться для разных
маленькие значения дисперсии только лишь по
пылинок.
одной компоненте скорости vz уже существенно
влияют на результаты. Вид граничной функции
распределения fTS(v):
Безразмерная постановка задачи
fTS(v) = nISMδ(vx) ×
(11)
(
)
1
v2z
× δ(vy + vISM)
√
exp
-
,
В качестве характерной длины в данной зада-
σz
2π
2σ2z
че рассмотрим величину L1 =GMS
, а в качестве
где δ — дельта-функция Дирака, σz — дисперсия
v2
ISM
по компоненте скорости vz. При σz → 0 выраже-
характерной скорости — величину скорости дви-
ние (11) вырождается в функцию распределения,
жения локальной межзвездной среды vISM . По-
соответствующую случаю, когда все частицы пыли
скольку задача является линейной и однородной по
имеют одинаковую скорость vISM :
fd(r,v), то заменой fd →fd мы избавимся отn
ISM
fTS(v) = nISMδ(vx)δ(vy + vISM )δ(vz),
(12)
параметра nISM , возникающего в (11). Тогда после
и постановка задачи становится идентичной поста-
обезразмеривания постановка задачи (2)-(4), (10),
новке задачи в работе Мищенко и др. (2020).
(11) примет вид
⎧
⎪
fd
fd
v·
+F·
= 0,
⎨
∂r
∂v
(
)
1
√
)δ(vy + 1)
exp
- vz
,
(13)
fd(r, v)|r=rTS, v·en>0=δ(vx
2σ2z
⎪
σz
2π
⎩
fd(r, v)|v→∞ = 0,
где r =rL
,
v=vv
,
fd =fd
,
F= FL1
,
σz =
v2em
3UdBE R2E Ω
vISM
1
ISM
v3ISM
v2
=
=
,
,
LΩ .
ISM
v2ISM
4πc0ρda2v2ISM
vsw
L1
L1
результирующей силы в безразмерном виде:
F= (β - 1)er
+
(14)
r2
)
Плоские траектории
v2em
+ sgn(z)
(vISM v-er
×
v2
vsw
ISM
Рассмотрим проекцию выражения (14) на ось
(
)
LΩ er
sinθ
Ox:
× -
+
eϕ
,
L1 r2
r
x
xz
где LΩ =vswΩ,vem=q
c0md
Fx = (β - 1)
+ sgn(z)ε
+
(16)
r3
r3
размерная постановка задачи содержит пять без-
(
)
размерных параметров:
vISM
LΩ vy z - vz ŷ
vz x
+ sgn(z)ε
-
-
vsw
L1
r3
r2
σz,β,ε =
(15)
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
58
ГОДЕНКО, ИЗМОДЕНОВ
Поскольку значение безразмерного параметра
в расчетную область через границу в единицу
vISM ≈ 0.05 ≪ 1, то можем пренебречь соответ-v
времени в безразмерном виде:
sw
ствующим членом в (16), и тогда в упрощенном ви-
F0 =
(21)
де проекция безразмерной силы на ось Ox примет
⎛
⎞
π
следующий вид:
∫
2
∫
⎜
⎟
x
xz
=
(v·en
fTS(v)dv
⎝
⎠ rT S dϕ = 2rT S .
Fx = (β - 1)
+ sgn(z)ε
(17)
r3
r3
π
−
(v·en)>0
2
Значит, частицы, которые при пересечении TS име-
ют следующие начальные условия:
x|TS = 0,
vx|T S = 0,
(18)
Технические детали
не покинут плоскость x = 0 во время своего движе-
В данной работе мы рассматриваем частицы
ния в гелиосфере, согласно теореме существования
радиуса 0.37 мкм. Для этих частиц β = 1, следова-
и единственности решения задачи Коши. Для про-
тельно, гравитационная сила и сила радиационного
стоты и наглядности в настоящей работе мы будем
давления в (14) взаимно уничтожаются.
рассматривать только такие частицы, траектории
которых целиком лежат в плоскости x = 0.
Для расчетов мы использовали следующие
численные значения параметров: rTS = 100 а.е.,
=
vISM = 26.4 км/c, MS = 2 × 1030 кг, vsw
Метод решения
= 400 км/c, RE = 1 а.е., Ud = +3 В, BE = 30 мкГ,
Для решения кинетического уравнения мы ис-
ρd = 2500 кг/м3, Ω = 2.9 × 10-6 с-1.
пользуем метод Монте-Карло. Расчетная область
Размер ячеек сетки расчетной области, если он
разбивается на прямоугольные ячейки Δŷ × Δz
не указан отдельно, составляет 0.1 а.е. × 0.001 а.е.
(рис. 2), причем Δz ≪ Δŷ, потому что слои с осо-
по направлениям Oy и Oz соответственно. Для
бенностями в распределении концентрации, най-
решения системы обыкновенных дифференциаль-
денные в Мищенко и др. (2020), ориентированы
ных уравнений, описывающих динамику движения
горизонтально. Более того, поскольку эти слои
пылевых частиц, используется метод Рунге-Кутты
имеют приблизительно нулевую толщину, необхо-
четвертого порядка.
димо сильно уменьшать величину Δz для того,
чтобы обнаружить эти особенности с помощью
Заметим также, что выбранное фиксированное
моделирования методом Монте-Карло.
положение гелиосферного токового слоя соответ-
Для каждой частицы межзвездной пыли ее на-
ствует фазе фокусировки гелиосферного магнитно-
чальное положение на сфере радиуса rTS и на-
го поля, т.е. случаю, когда траектории частиц меж-
чальная скорость генерируются случайным обра-
звездной пыли прижимаются к плоскости токового
зом по функции распределения fTS (v) из (13).
слоя. Для этого выпишем проекцию на ось z силы,
При движении каждой конкретной частицы пыли
действующей на пылинки:
в гелиосфере мы фиксируем промежутки време-
z
ни ti, которые эта частица провела в ячейках сетки
Fz = (β - 1)
+
(22)
r3
расчетной области (ti = 0, если данная частица не
[
попала в ячейку). Таким образом, согласно кине-
x2 + ŷ2
+ sgn(z)ε
-
+
тическому определению функции распределения и
r3
(
)]
концентрации, а также по закону больших чисел:
v
ISM
LΩ vxŷ - vy x
vx x + vy ŷ
+
-
+
,
∑
vsw
L1
r3
r2
F0
ti
→ fd(rc, vc),
(19)
N
ΔrcΔvc
i=1
где вновьvISM ≈ 0.05 ≪ 1, поэтому на большихv
sw
гелиоцентрических расстояниях ведущим членом
∑
будет
F0
ti
→ nd(rc).
(20)
N
Δrc
x2 + ŷ2
i=1
-sgn(z)ε
(23)
r3
Здесь N — количество рассмотренных частиц,
Видно, что в таком случае при z > 0 компонен-
rc, vc — координаты центра ячейки в фазовом
пространстве, Δrc — объем ячейки в физическом
та силы
Fz < 0, поэтому на частицы пыли будет
пространстве, ΔrcΔvc — объем ячейки в фазовом
действовать притягивающая к токовому слою сила.
пространстве,
F0 — поток частиц пыли, входящих
Аналогично при z < 0 имее
Fz > 0.
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
ВЛИЯНИЕ ДИСПЕРСИИ СКОРОСТЕЙ ПЫЛИ
59
Density, σ = 0 m/s, a = 0.37 mcm
15
2
V_ISM
13
1
11
9
0
HCS
Sun
7
N/N_0
2
9.310
-1
8.276
5
1
7.241
6.207
0
5.172
4.138
3
-1
3.103
2.069
-2
-2
1.034
0
-10
0
10
20
30
40
50 Y, a.u.
1
−10
0
10
20
30
40
50
60
Y, a.u.
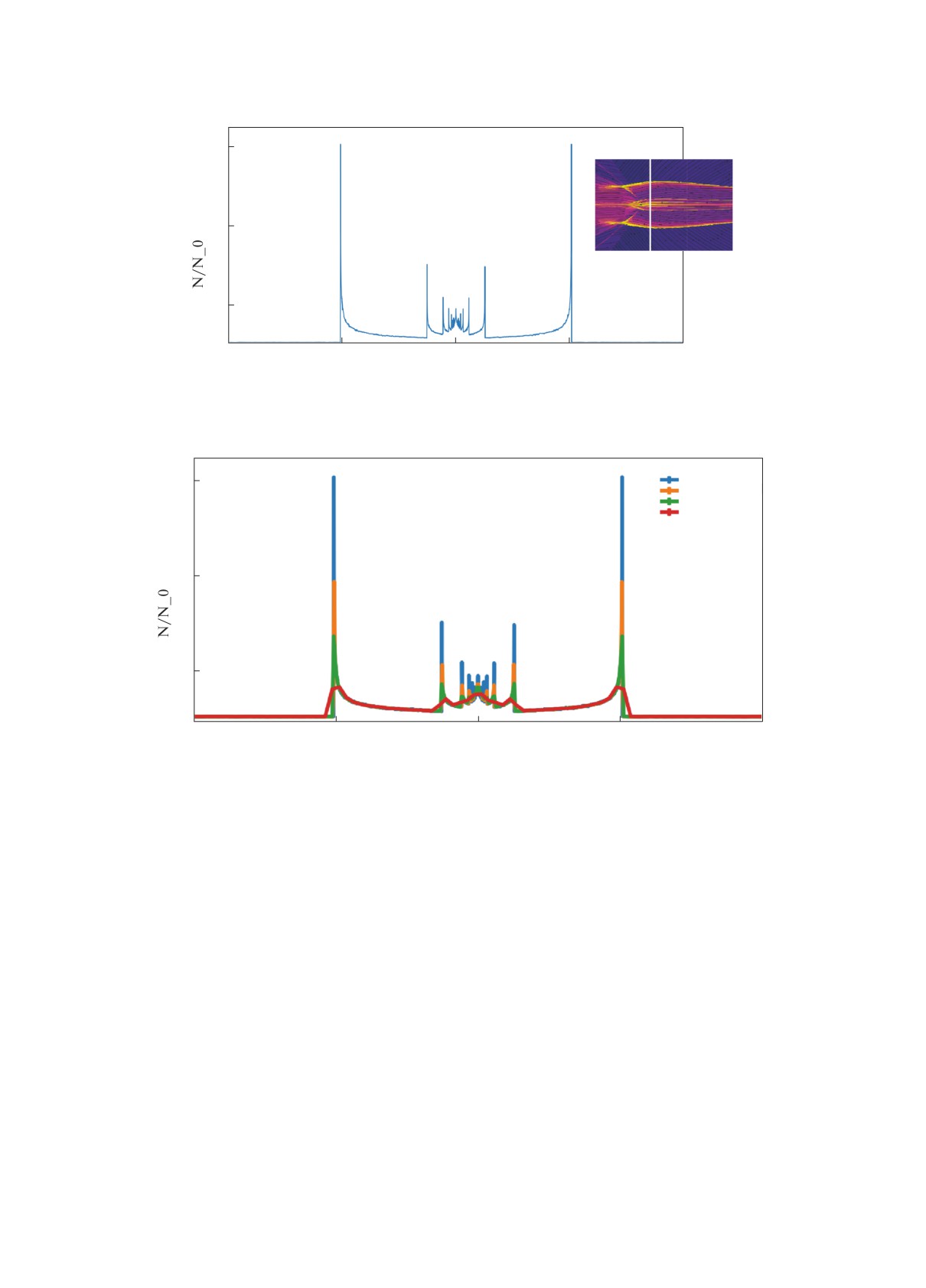
Рис. 3. Карта распределения концентрации (плоскость x = 0) при отсутствии дисперсии в граничном распределении.
Тонкие структуры желтого цвета соответствуют каустикам. В правом нижнем углу аналогичное распределение из
Мищенко и др. (2020). Относительная статистическая ошибка в каждой точке не превышает 2-3%. Размер частиц
a = 0.37 мкм. Количество траекторий N = 2000000.
РЕЗУЛЬТАТЫ
сложная структура, состоящая из множества ло-
кальных максимумов в распределении концентра-
Особенности в распределении концентрации
ции.
В работе Мищенко и др. (2020) было показано,
Поскольку сетка расчетной области состоит из
что при отсутствии дисперсии в граничном распре-
ячеек конечного размера, для обнаружения осо-
делении траектории частиц межзвездной пыли об-
бенностей в распределении концентрации при мо-
разуют каустики, на которых расположены осо-
делировании методом Монте-Карло необходима
бенности в распределении концентрации. Каустика
сетка очень высокого разрешения. На рис. 5 пока-
представляет собой огибающую семейства траек-
зано, как распределение концентрации межзвезд-
торий пылевых частиц. По определению, каустика
ной пыли вдоль линии (x = 0, y = 2) изменяется
каждым своим сегментом касается бесконечного
при варьировании размера ячейки расчетной сет-
числа траекторий частиц, что и является причи-
ки Δz. Концентрация межзвездной пыли в ячейке,
ной возникновения особенностей. Эти особенности
содержащей точку каустики, увеличивается при
можно относительно легко находить с помощью
уменьшении параметра Δz, поэтому в этой ячейке
лагранжевого подхода (который использовался в
расположена особенность в распределении кон-
работе Мищенко и др., 2020), однако в данном
центрации.
разделе мы покажем, что упомянутые особенно-
Механизм формирования каустик можно уви-
сти можно находить и с помощью метода Монте-
деть на следующем примере. Рассмотрим частицы,
Карло, хотя с вычислительной точки зрения это
вылетающие из узкой щели на границе расчетной
будет менее эффективно.
области (рис. 6). Трубка тока, образованная траек-
На рис. 3 продемонстрирована карта распре-
ториями этих частиц, при приближении к Солнцу
деления концентрации межзвездной пыли вместе с
начинает сужаться, и в точке каустики ее ширина
линиями тока. Показана окрестность гелиосферно-
достигает минимального значения (ширина при-
го токового слоя. Симметричные структуры желто-
близительно в тысячу раз меньше, чем на границе
го цвета, которые ограничивают область повышен-
расчетной области). Из закона сохранения массы
ной концентрации, соответствуют каустикам. При
nvΣ = const
(24)
моделировании методом Монте-Карло они пред-
ставляют собой тонкие области, где происходит
концентрация n достигает своего максимального
резкое увеличение концентрации (рис. 4). Внут-
значения в точке, где ширина Σ является мини-
ри области, ограниченной каустиками, образуется
мальной, поскольку v (компонента скорости по
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
60
ГОДЕНКО, ИЗМОДЕНОВ
Density at y = 2.0 a.u.
100
60
20
-2
-1
0
1
2
Z, a.u.
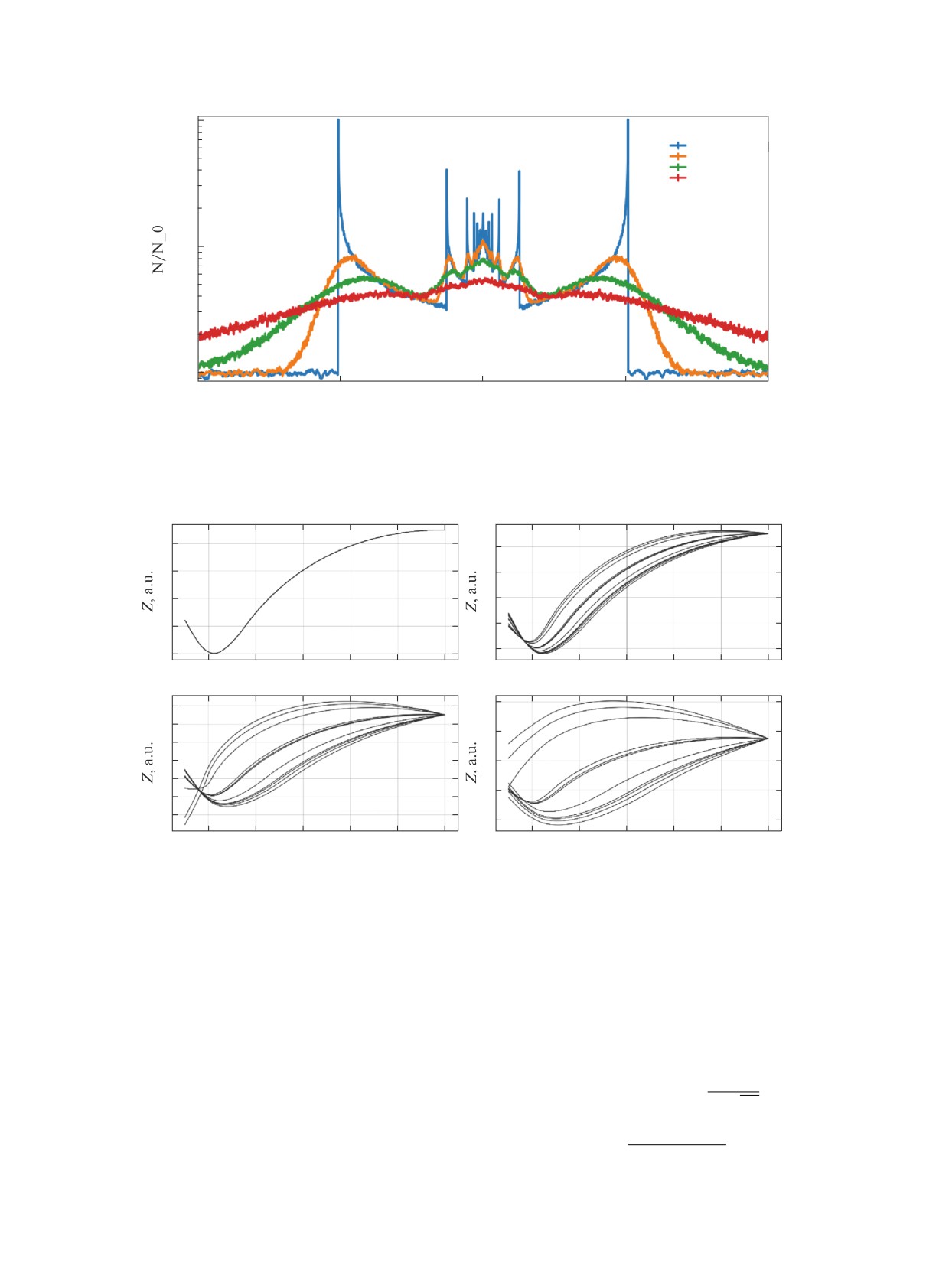
Рис. 4. Распределение концентрации вдоль линии (x = 0, y = 2). Относительная статистическая ошибка в каждой точке
не превышает 2-3%. Размер частиц a = 0.37 мкм. Количество траекторий N = 2 000 000.
100
Δz = 0.001
Δz = 0.005
Δz = 0.01
Δz = 0.05
60
20
-2
-1
0
1
2
Z, a.u.
Рис. 5. Распределение концентрации вдоль той же линии, что и на рис. 4. Четыре линии разного цвета со-
ответствуют различным значениям размера ячеек расчетной сетки в направлении оси Oz (Δy = 0.1 а.е., Δz =
= {0.05 а.е., 0.01 а.е., 0.005 а.е., 0.001 а.е.}). Относительная статистическая ошибка в каждой точке не превышает 2-3%.
Размер частиц a = 0.37 мкм. Количество траекторий N = 2 000 000.
оси y) практически не изменяется вдоль траекто-
вычисления для нескольких различных значений
рии.
параметра σz: 0, 0.01, 0.02, 0.04. На рис. 7 пред-
ставлены карты распределения концентрации для
четырех различных значений σz. C увеличением
Влияние дисперсии в граничном распределении
значения параметра σz каустики размываются, и
В данной работе мы рассматриваем главным
особенности в распределении концентрации про-
образом дисперсию по компоненте скорости vz, по-
падают. Области повышенной концентрации оста-
скольку мы моделируем траектории лишь в плос-
ются только в окрестности токового слоя. Данные
кости симметрии x = 0 (поэтому дисперсию по
области образуются за счет увеличения амплитуды
компоненте скорости vx мы не учитываем), а из
электромагнитной силы при уменьшении гелио-
рис. 11 (см. ниже) видно, что дисперсия по ком-
центрического расстояния. Увеличение амплиту-
поненте скорости vy оказывает меньшее влияние
ды электромагнитной силы ведет к уменьшению
на распределение, чем дисперсия по компоненте
амплитуды осцилляций частиц вокруг плоскости
скорости vz.
токового слоя, и, следовательно, общий поток ча-
Для того чтобы исследовать влияние дисперсии
стиц межзвездной пыли начинает прижиматься к
на распределение межзвездной пыли, проводились плоскости токового слоя, образуя области повы-
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
ВЛИЯНИЕ ДИСПЕРСИИ СКОРОСТЕЙ ПЫЛИ
61
3
2
1
0
1
0
20
40
60
80
100
Y, a.u.
Рис. 6. Трубка тока из траекторий частиц, вылетающих из узкой щели на границе расчетной области. Показано, как
ширина этой трубки изменяется при приближениик Солнцу. Точка минимальной ширины трубки тока лежит на каустике.
Размеры вставок 0.6 (а.е.) × 0.025 (а.е.). Размер частиц a = 0.37 мкм.
2
2
15
15
σ = 0
σ = 0.01
13
13
1
1
11
11
9
9
0
0
Sun
7
Sun
7
5
5
-1
-1
V_ISM
3
V_ISM
3
1
1
-2
-2
−10
0
10
20
−10
0
10
20
Y, a.u.
Y, a.u.
2
2
15
15
σ = 0.02
σ = 0.04
13
13
1
1
11
11
9
9
0
0
Sun
7
Sun
7
5
5
-1
-1
V_ISM
3
V_ISM
3
1
1
-2
-2
−10
0
10
20
−10
0
10
20
Y, a.u.
Y, a.u.
Рис. 7. Сравнение карт распределения концентрации для различных значений дисперсии σz: 0, 0.01, 0.02, 0.04. Особен-
ности в распределении концентрации пропадают при появлении дисперсии в граничном распределении. Относительная
статистическая ошибка в каждой точке не превышает 2-3%. Размер частиц a = 0.37 мкм. Количество траекторий
N = 2000000.
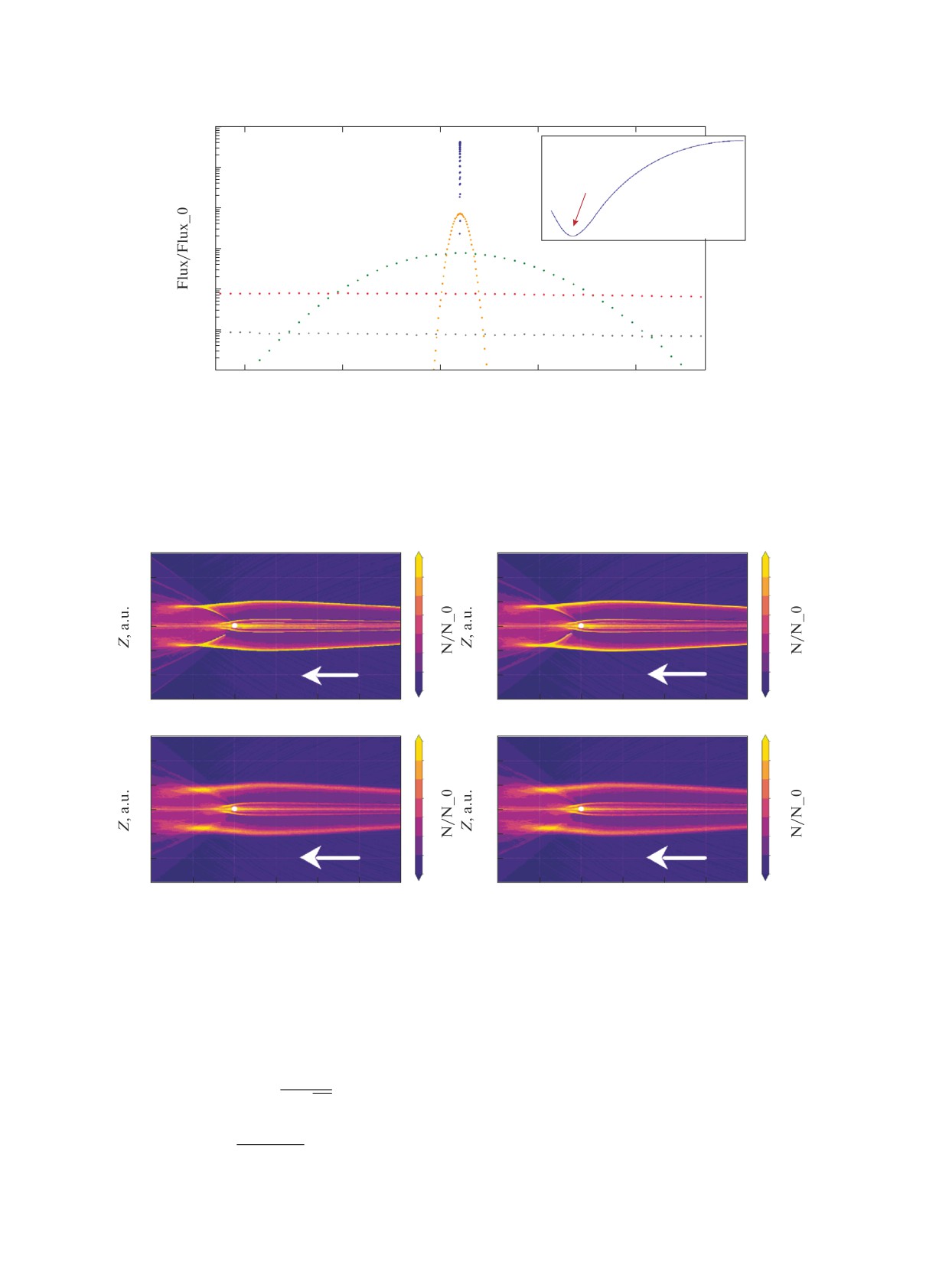
шенной концентрации. Из рис. 8 хорошо видно, как
Причины исчезновения особенностей можно
сильно концентрация в ячейках, содержащих точки
увидеть на рис. 9, 10. На рис. 9 продемонстрирова-
каустики при σz = 0, уменьшается при появлении
ны траектории частиц, запущенных из тонкой щели
дисперсии в граничном распределении, а также при
на границе расчетной области, для разных значений
дальнейшем увеличении этой дисперсии. При дис-
параметра σz. Как было упомянуто выше, резкое
персии в 4% уже не наблюдается никаких призна-
уменьшение ширины такой трубки тока при σz = 0
ков ранее существовавших особенностей, а поток
служило причиной возникновения особенностей в
частиц межзвездной пыли все больше становится
распределении концентрации. В данном случае при
похож на невозмущенный.
ненулевой дисперсии траектории частиц начинают
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
62
ГОДЕНКО, ИЗМОДЕНОВ
102
σ = 0
σ = 0.01
σ = 0.02
σ = 0.04
101
100
-2
-1
0
1
2
Z, a.u.
Рис. 8. Сравнение распределений концентрации вдоль линии (x = 0, y = 2) для различных значений дисперсии σz: 0,
0.01, 0.02, 0.04. Структура распределения концентрации резко изменяется при изменении дисперсии σz . Относительная
статистическая ошибка в каждой точке не превышает 2-3%. Размер частиц a = 0.37 мкм. Количество траекторий
N = 2000000.
3
3
2
2
1
1
0
0
= 0
= 0.01
1
1
0
20
40
60
80
100
0
20
40
60
80
100
Y, a.u.
Y, a.u.
6
4
3
4
2
1
2
0
0
1
2
= 0.02
= 0.04
2
0
20
40
60
80
100
0
20
40
60
80
100
Y, a.u.
Y, a.u.
Рис. 9. При появлении дисперсии в граничной функции распределениятраектории частиц, вылетающих из узкой щели на
границе расчетной области, расходятся. Размер частиц a = 0.37 мкм.
разлетаться, и, следовательно, концентрация в
пыли существенно влияют на ее распределение
точках, являющихся точками каустики при σz =
внутри гелиосферы.
= 0, перестает неограниченно возрастать. На
Для того чтобы показать влияние дисперсии,
рис.
10
представлены распределения потоков
внесенной по компоненте скорости vy, можно вме-
концентрации в окрестности точки, являющейся
сто граничного условия (11) рассмотреть следую-
точкой каустики при σz = 0, для разных значений
щее:
параметра
σz. Можно заметить, что максимум
1
потока от траекторий, запущенных из тонкой щели
fTS(v) = nISMδ(vx)
√
×
(25)
на границе расчетной области, приблизительно об-
σy
2π
[
]
ратно пропорционален величине дисперсии σz. Та-
(vy + vISM )2
ким образом, даже маленькие значения дисперсии
× exp -
δ(vz ),
2σ2y
в начальном распределении частиц межзвездной
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
ВЛИЯНИЕ ДИСПЕРСИИ СКОРОСТЕЙ ПЫЛИ
63
Flux distribution at y = 1.245 a.u.
105
0
104
103
0.00004
102
0.0004
0.004
101
0.04
100
101
1.02
1.01
1.00
0.99
0.98
Z, a.u.
Рис. 10. Распределение потоков концентрации в окрестности точки каустики (при σz = 0) для различных значений
дисперсии σz: 0, 0.00004, 0.0004, 0.004, 0.04. Для построения данного рисунка необходимо было добиться сходимости по
размерам ячейки расчетной сетки, количеству рассмотренных частиц и шагу интегрирования. Для случая σz = 0 размер
ячейки Δz выбирался равным 0.000001 (а.е.), что в 1000 раз меньше, чем соответствующий размер ячеек сетки, на
которой проводилось большинство расчетов в данной работе. Относительная статистическая ошибка в каждой точке
не превышает 5%. Размер частиц a = 0.37 мкм.
3
3
15
15
σ = 0
σ = 0.01
2
13
2
13
11
11
1
1
9
9
0
0
Sun
7
Sun
7
-1
5
−1
5
V_ISM
V_ISM
3
3
-2
-2
1
1
-3
-3
−10
-5
0
5
10
15
20
−10
-5
0
5
10
15
20
Y, a.u.
Y, a.u.
3
3
15
15
σ = 0.02
σ = 0.04
2
13
2
13
11
11
1
1
9
9
0
0
Sun
7
Sun
7
-1
5
-1
5
V_ISM
V_ISM
3
3
-2
-2
1
1
-3
-3
−10
-5
0
5
10
15
20
−10
-5
0
5
10
15
20
Y, a.u.
Y, a.u.
Рис. 11. Сравнение карт распределения концентрации для различных значений дисперсии σy, внесенной по компоненте
скорости vy : 0, 0.01, 0.02, 0.04. Вид областей повышенной концентрации практически не изменяется с увеличением
дисперсии. Относительная статистическая ошибка в каждой точке не превышает 5-6%. Размер частиц a = 0.37 мкм.
Количество траекторий N = 200 000.
которое в безразмерном виде выглядит так:
На рис. 11 представлено сравнение двумерных
распределений концентрации при различных зна-
1
чениях дисперсии
σy, внесенной по компоненте
fTS(v) = δ(vx)
√
×
(26)
σy
2π
скорости vy. Видно, что при тех же величинах дис-
[
]
персии (σy: 0, 0.01, 0.02, 0.04), которые выбирались
(vy + 1)2
× exp -
δ(vz).
и для моделирования с дисперсией, внесенной по
2σ2y
компоненте скорости vz, вид области повышенной
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
64
ГОДЕНКО, ИЗМОДЕНОВ
концентрации при увеличении дисперсии практиче-
2010) на протяжении всего времени движения пы-
ски не изменяется. Особенности в распределении
левых частиц в гелиосфере). Эффект нестацио-
концентрации так же, как и прежде, пропадают
нарности магнитного поля является важным эф-
при появлении дисперсии. Однако для того, что-
фектом, который оказывает существенное влияние
бы добиться того же эффекта устранения обла-
на распределение межзвездной пыли и который,
стей повышенной концентрации, что и для случая
соответственно, необходимо учитывать при моде-
дисперсии, внесенной по компоненте скорости vz,
лировании.
необходимо использовать более высокие значения
дисперсии. Связано это с тем, что области повы-
шенной концентрации вытянуты вдоль оси Oy, и,
следовательно, в силу стационарности постановки
Авторы признательны правительству Россий-
задачи, относительно маленькие изменения компо-
ской Федерации и Министерству высшего образо-
ненты скорости vy не могут существенно повли-
вания и науки РФ за поддержку по гранту 075-
ять на распределение концентрации межзвездной
15-2020-780 (N13.1902.21.0039). Мы благодарим
пыли.
Д.Б. Алексашова, И.И. Балюкина, А. Грановского
за конструктивное обсуждение результатов данной
ЗАКЛЮЧЕНИЕ
работы и за помощь в подготовке текста статьи, а
также Фонд “Базис” за поддержку в рамках гранта
В данной работе мы показали, что особенности
18-1-1-22-4 .
в распределении концентрации межзвездной пыли
в гелиосфере, найденные в работе Мищенко и др.
(2020) с помощью лагранжевого подхода, можно
СПИСОК ЛИТЕРАТУРЫ
также находить при помощи моделирования мето-
1.
Алексашов и др. (D.B. Alexashov, O.A. Katushkina ,
дом Монте-Карло. Однако это сопряжено с ис-
V.V. Izmodenov, and P.S. Akaev), MNRAS 458, 2553
пользованием ячеек сетки расчетной области очень
(2016).
маленького размера. В наших расчетах необходимо
2.
Алтобелли и др. (N. Altobelli, S. Kempf, H. Kr ¨uger,
было использовать в окрестности точек каустики
M. Landgraf, M. Roy, and E. Gr ¨un), J. Geophys. Res.
ячейки, размеры которых в направлении оси Oz
110, 7102 (2005).
не превышают 10-3 а.е. С вычислительной точки
3.
Алтобелли и др. (N. Altobelli, V. Dikarev, S. Kempf,
зрения разбить всю расчетную область на ячейки
R. Srama, S. Helfert, G. Moragas-Klostermeyer,
такого размера невозможно, а более слабое разре-
M. Roy, and E. Gr ¨un), J. Geophys. Res. 112, 7105
шение по сетке (т.е. ячейки большего размера) не
(2007).
позволяет улавливать точки каустики.
4.
Балюкин и др. (I.I. Baliukin, V.V. Izmodenov,
E. M ¨obius, D.B. Alexashov, O.A. Katushkina, and
Моделирование дисперсии в граничном распре-
H. Kucharek), Astrophys. J. 850, 119 (2017).
делении было проведено с помощью нормального
5.
Берто, Бламонт (J.L. Bertaux and J.E. Blamont),
распределения по одной из компонент скорости.
Astron. Astrophys. 11, 200 (1971).
Было установлено, что появление дисперсии ведет
6.
Берто, Бламонт (J.L. Bertaux and J.E. Blamont),
к исчезновению каустик и сглаживанию областей
Nature 262, 263 (1976).
повышенной концентрации. Известно (Хоанг и др.,
7.
Витте и др. (M. Witte, H. Rosenbauer, E. Keppler,
2012), что дисперсия межзвездной пыли по ско-
H. Fahr, P. Hemmerich, H. Lauche, A. Loidl, and
ростям может достигать 15% в межзвездной среде
R. Zwick), Astron. Astrophys. 92, 333 (1992).
ввиду неоднородностей межзвездного магнитного
8.
Витте (M. Witte), Astron. Astrophys. 426,
835
поля по пространству и по времени. Однако из ре-
(2004).
зультатов моделирования ясно, что значительные
9.
Грюн и др. (E. Gr ¨un, B. Gustafson, I. Mann,
качественные и количественные изменения в рас-
M. Baguhl, G.E. Morfull, P. Staubach, A. Taylor, and
пределении концентрации наблюдаются даже при
H.A. Zook), Astron. Astrophys. 286, 915 (1994).
значениях дисперсии, не превышающих 5%. Таким
10.
Густафсон (B.A.S. Gustafson), Ann. Rev 22, 553
образом, эффект дисперсии скоростей необходимо
(1994).
учитывать при поиске областей повышенной кон-
11.
Дрэйн (B.T. Draine), Space Sci. Rev. 143,
333
центрации в гелиосфере.
(2009).
12.
Зирнштейн и др. (E.J. Zirnstein, J. Heerikhuisen,
В будущем мы планируем развить нашу модель
H.O. Funsten, G. Livadiotis, D.J. McComas, and
на случай нестационарного гелиосферного маг-
N.V. Pogorelov), Astrophys. J. Lett. 818, 30 (2016).
нитного поля, в котором учитываются 22-летние
13.
Измоденов и др. (V.V. Izmodenov, Y.G. Malama,
циклы солнечной активности (в данной работе
A.P. Kalinin, M. Gruntman, R. Lallement, and
мы рассматривали стационарное магнитное поле,
I.P. Rodionova), Astrophys. Space Sci. 274,
71
которое находилось в фазе фокусировки (Манн,
(2000).
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021
ВЛИЯНИЕ ДИСПЕРСИИ СКОРОСТЕЙ ПЫЛИ
65
14. Измоденов, Алексашов (V.V. Izmodenov and
25. Мёбиус (E. M ¨obius, P. Bochsler, M. Bzowski,
D. B. Alexashov), Astrophys. J. Suppl. Ser. 220:32
G.B. Crew, H.O. Funsten, S.A. Fuselier,
(2015).
A. Ghielmetti, D. Heirtzler, et al.), Science 326,
15. Измоденов, Алексашов (V.V. Izmodenov and
969 (2009).
D.B. Alexashov), Astron. Astrophys. 633:12 (2020).
26. Мищенко и др. (A.V. Mishchenko, E.A. Godenko,
16. Катушкина и др. (O.A. Katushkina, V.V. Izmodenov,
and V.V. Izmodenov), MNRAS 491, 2808 (2020).
D.B.
Alexashov,
N.A.
Schwadron,
and
27. Осипцов (A.N. Osiptsov), Astrophys. Sp. Sci. 274,
D.J. McComas), Astrophys. J. Suppl. Ser. 220:33
377 (2000).
(2015).
28. Погорелов и др. (N.V. Pogorelov, J. Heerikhuisen,
17. Катушкина, Измоденов (O.A. Katushkina and
G.P. Zank, S.N. Borovikov, P.C. Frisch, and
V.V. Izmodenov), MNRAS 486, 4947 (2019).
D.J. McComas), Astrophys. J. 742, 104 (2011).
18. Кюэмэра и др. (E. Qu ´emerais, B.R. Sandel,
29. Славин и др. (J.D. Slavin, P.C. Frisch, H.-R. M ¨uller,
V.V. Izmodenov, and G.R. Gladstone), Cross-
J. Heerikhuisen, N.V. Pogorelov, W.T. Reach, and
Calibration of Far UV Spectra of Solar System
G.P. Zank), Astrophys. J. 760, 46 (2012).
Objects and the Heliosphere 141 (2013).
30. Стеркен и др. (V.J. Sterken, N. Altobelli, S. Kempf,
19. Ландграф и др. (M. Landgraf, W.J. Baggaley,
G. Schwehm, R. Srama, and E. Gr ¨un), Astron.
E. Gr ¨un, H. Kr ¨uger, and G. Linkert), J. Geophys. Res.
Astrophys. 538, A102 (2012).
105, 10343 (2000).
31. Стеркен и др. (V.J. Sterken, A.J. Westphal,
20. Ландграф и др. (M. Landgraf, H. Kr ¨uger, N. Altobelli,
N. Altobelli, D. Malaspina, and F. Postberg),
and E. Gr ¨un), J. Geophys. Res. 108, 8030 (2003).
Space Sci. Rev. 215, 7, 43 (2019).
21. Леви, Йокипи (E.H. Levy and J.R. Jokipii), Nature
32. Страб и др. (P. Strub, H. Kr ¨uger, and V.J. Sterken),
264, 423 (1976).
Astrophys. J. 812, 140 (2015).
22. МакКомас и др. (D.J. McComas, M. Bzowski,
33. Страб и др. (P. Strub, V.J. Sterken, R. Soja,
P. Frisch, S.A. Fuselier, M.A. Kubiak, H. Kucharek,
H. Kr ¨uger, E. Gr ¨un, and R. Srama), Astron.
T. Leonard, E. M ¨obius, et al.), Astrophys. J. 801, 28
Astrophys. 621, A54 (2019).
(2015).
34. Хоанг и др. (T. Hoang, A. Lazarian, and
23. Манн (I. Mann), Ann. Rev. Astron. Astrophys 48, 173
R. Schlickeiser), Astrophys. J. 747, 54 (2012).
(2010).
35. Чеховски, Манн (A. Czechowski and I. Mann),
24. Матис и др. (J.S. Mathis, W. Rumpl, and
K.H. Nordsieck), Astrophys. J. 217, 425 (1977).
Astron. Astrophys. 410, 165 (2003).
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№1
2021