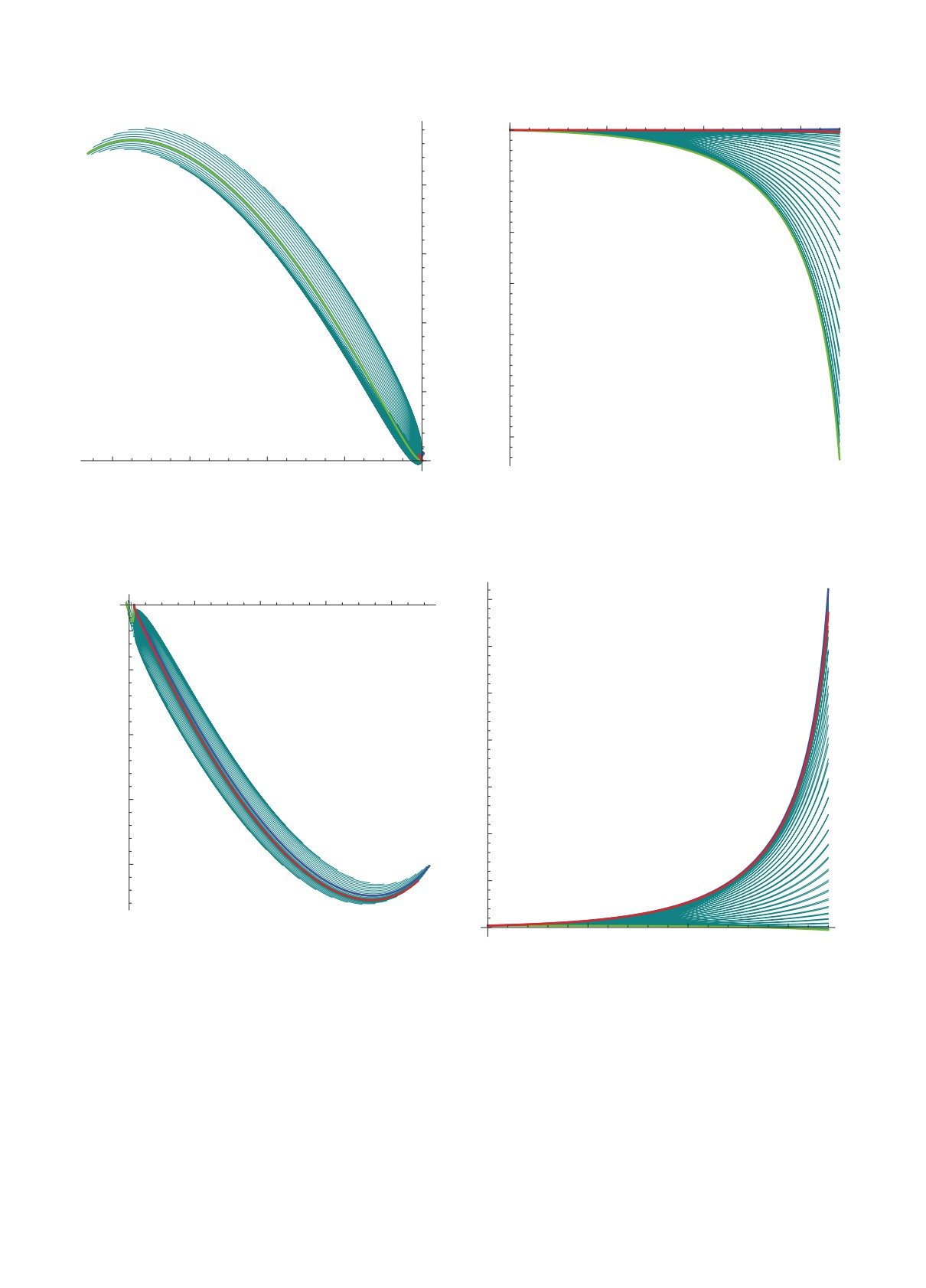ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2021, том 47, № 10, с. 733-742

ОРБИТАЛЬНОЕ МАНЕВРИРОВАНИЕ В ОКРЕСТНОСТЯХ

КОЛЛИНЕАРНЫХ ТОЧЕК ЛИБРАЦИИ С ИСПОЛЬЗОВАНИЕМ СИЛ

СВЕТОВОГО ДАВЛЕНИЯ

¹Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

Поступила в редакцию 02.07.2021 г.

После доработки 02.07.2021 г.; принята к публикации 05.08.2021 г.

Исследуется управляемое движение космического аппарата с солнечным парусом в межпланетном

космическом пространстве вблизи окрестностей коллинеарных точек либрации L₁ и L₂ системы

Солнце-Земля. Для описания орбитального движения используются уравнения круговой ограни-

ченной задачи трех тел и их модификации. В работе представлена методика построения законов

управления орбитальным движением и дана оценка области управляемости при решении задачи

стабилизации или длительного удержания космического аппарата в окрестности L₁ и L₂. Эта методика

основана на решении задачи управления для линеаризованной модели уравнений орбитального

движения и перенесения результатов на нелинейный случай. Такая методика построения управлений

расширяет возможности как при решении задач стабилизации движения, так и при решении задач

маневрирования в окрестности коллинеарной точки либрации. Для космического аппарата с солнеч-

ным парусом дана оценка области управляемости, представлены траектории возможного движения

космического аппарата, которые обеспечиваются ориентацией солнечного паруса, при перелете из

окрестности коллинеарной точки либрации. Именно в данных областях космического пространства,

ввиду относительно небольшой величины силы гравитации, сила светового давления может иметь

существенную эффективность. В качестве примера рассмотрена модель космического аппарата с

солнечным парусом, парусность которого соответствует аппарату из реализованного проекта IKAROS

и на порядок меньше парусности аппарата стандарта CubeSat из реализованного проекта LightSail-2.

Ключевые слова: ограниченная задача трех тел, точка либрации, солнечный парус, управляемое

движение, инвариантное многообразие, маневрирование.

DOI: 10.31857/S0320010821100077

ВВЕДЕНИЕ

паруса для удержания космического аппарата на

квазипериодической орбите. В работе (Шиманчук

Использование окрестности коллинеарной точ-

и др., 2020) рассматривалась задача удержания КА

ки либрации (L₁ или L₂) системы Солнце-Земля

вблизи инвариантного многообразия в окрестности

в межпланетном космическом пространстве Земли

коллинеарной точки либрации. В данной работе

уже давно имеет практическое значение в связи с

мы приводим результаты численного исследования

проектами, реализуемыми NASA и ESA (ISEE-3,

орбитального маневрирования с использованием

SOHO, WIND, ACE, Genesis и т.д.). При этом для

солнечного паруса, которое позволяет оценить воз-

корректировки и управления движением исполь-

можности такого управления и охарактеризовать

зуются различные системы двигателей. В работе

область управляемости.

будем рассматривать движение космического ап-

парата (КА) под действием сил светового давления.

Под солнечным парусом будем понимать КА с

установленной и развернутой на нем отражающей

Идея использования солнечного паруса для

поверхностью, которая, поглощая и отражая сол-

удержания КА в окрестности коллинеарной точки

нечный свет, сообщает КА управляющее ускоре-

либрации была сформулирована в работе Бук-

ние.

лесса, Макиннеса (2008). В этой работе были

изучены возможности использования изменения

Движение КА с солнечным парусом рассматри-

площади паруса, а также изменение ориентации

вается в межпланетном космическом пространстве

во вращающейся геоцентрической системе коорди-

^*Электронный адрес: d.shimanchuk@spbu.ru

нат в рамках хилловского приближения круговой

733

734

ШИМАНЧУК и др.

ограниченной задачи трех тел Солнце-Земля-КА

||x||²

+x₂y₁ - x₁y₂.

(Шмыров, 2005).

Гамильтониан

(2) на траекториях движения

неуправляемой системы (1) сохраняет свое значе-

ДИНАМИЧЕСКАЯ МОДЕЛЬ

ние, т.е. является интегралом для системы (1). Это

свойство можно использовать для оценки точности

В качестве основной динамической модели дви-

численного интегрирования.

жения для построения законов управления ори-

ентацией солнечного паруса и численного моде-

Система линеаризованных уравнений неуправ-

лирования будем использовать упрощенные урав-

ляемой системы (1) в окрестности коллинеарной

нения, так называемое хилловское приближение

точки либрации L₁ имеет вид

уравнений движения. Эти уравнения получаются из

⎧

⎪x1 = x2 + y1,

круговой ограниченной задачи трех тел, если пе-

⎪

рейти от барицентрической вращающейся системы

⎪x2 = -x1 + y2,

⎪

координат к относительной вращающейся системе

⎨

x₃ = y₃,

координат с началом в центре массы Земли и оста-

(3)

⎪y1 = 8(x1 - 1) + (y2 - 1),

вить два первых члена в разложении солнечного

⎪

потенциала. Такой прием применил Хилл в своей

y₂ = -4x₂ - y₁,

⎪

теории движения Луны.

⎩

y₃ = -4x₃,

Уравнения управляемого движения КА во вра-

а в окрестности L₂

щающейся системе координат при использовании

⎧

хилловского приближения для солнечного потен-

⎪x1 = x2 + y1,

циала могут быть представлены в виде (Шмыров,

⎪

x₂ = -x₁ + y₂,

2005)

⎪

⎨

⎧

x₃ = y₃,

⎪x1 = x2 + y1,

(4)

⎪

⎪y1 = 8(x1 + 1) + (y2 + 1),

⎪

⎪x2 = -x1 + y2,

⎪

⎪y2 = -4x2 - y1,

⎪x3 = y3,

⎩

⎨

y₃ = -4x₃.

3x₁

y₁ = -

+ 2x₁ + y₂ + u₁,

(1)

⎪

||x||³

Матрицы неуправляемых линеаризованных си-

⎪

3x₂

⎪

стем (3), (4) имеют одинаковый спектр (Шмыров,

y₂ = -

-x₂ -y₁ +u₂,

⎪

||x||³

2005):

⎪

3x₃

√

⎩y3 = -

-x₃ +u₃,

√

||x||³

λ1,2 = ±

1+2

7 = ±l,

√

где x = (x₁; x₂; x₃) — вектор координат КА, y =

λ3,4 = ±i

7 - 1 = ±iω_e,

= (y₁; y₂; y₃) — вектор сопряженных импульсов,

λ5,6 = ±2i = ±iω_n.

центр инерции Земли совпадает с началом си-

стемы координат, а ось Ox₁ направлена вдоль

Из положительности собственного значения λ₁ =_√

оси, соединяющей центры масс Земли и Солн-

√

1+2

следует неустойчивость координат

ца. u = (u₁; u₂; u₃) — вектор управляющего воз-

точек либрации L₁, L₂, т.е. координаты коллинер-

действия. В случае, когда u = 0, будем иметь

ных точек либрации — неустойчивые положения

неуправляемую систему (1), которой будет отве-

равновесия типа седло, центр, центр.

чать неуправляемое движение. В принятой модели

единицы времени и расстояния выбраны таким

образом, что единица расстояния приблизительно

ПОСТАНОВКА ЗАДАЧИ

равна 10-2 а.е., а единица времени — 58.0916 сут

Коллинеарная точка либрации является неустой-

(год, деленный на 2π). Точки либрации L₁ и L₂

чивой по Ляпунову (Маркеев, 1978). Поэтому если

во вращающейся системе неподвижны и имеют

требуется обеспечить длительное пребывание КА

координаты x^∗ = (1; 0; 0), y^∗ = (0; 1; 0) и x^∗∗ =

в окрестности точки либрации, то необходимо ре-

= (-1; 0; 0), y^∗∗ = (0; -1; 0) соответственно.

шать задачу стабилизации орбитального движения

(Шмыров, 2005). С другой стороны, неустойчи-

Неуправляемая система (1) — гамильтонова с

вость точки либрации может быть использована

Гамильтонианом

как положительный фактор при задаче маневриро-

||y||

3x²

вания небесного тела в околоземном космическом

H =

(2)

||x||

пространстве (Шмыров и др., 2015; Шмыров,

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 10

2021

ОРБИТАЛЬНОЕ МАНЕВРИРОВАНИЕ

735

Шиманчук, 2015). Такие задачи возможны, на-

где

пример, при разработке способов противодей-

ствия астероидно-кометной опасности. Ударный

a₁ =

управляемый объект перемещается в окрестность

√(l2 + 3)2

коллинеарной точки либрации и удерживается

там длительное время. Затем, при приближении к

(

)

Земле опасного астероида или кометы, этот объект

l² - 3

l²

× l² + 5;

; 0;

; 2; 0

отправляется на перехват. Из-за неустойчивости

такой маневр можно реализовать с помощью

малых управляющих воздействий (в частности,

— собственный вектор-строка, соответствующий

солнечного паруса).

собственному значению l, z = (x₁ ∓ 1; x₂; x₃; y₁; y₂ ∓

∓ 1; y₃) — вектор-столбец, где верхний знак (ниж-

В этом случае и возникает задача исследования

ний знак) соответствует окрестности коллинеарной

движения солнечного паруса в межпланетном кос-

точки либрации L₁ (L₂). Вектор a₁ определяется с

мическом пространстве Земли при использовании

точностью до множителя, для определенности по-

окрестностей коллинеарных точек либрации L₁ и

лагаем, что первая, четвертая и пятая компоненты

L₂.

удовлетворяют условиям:

Пусть солнечный парус с заданными характе-

ристиками (m — масса солнечного паруса, S — его

a₁₁ > 0, a²¹⁴ + a²¹⁵ = 1.

(5)

площадь) находится в окрестности коллинеарной

точки либрации L₁ или L₂ с начальными данными

На траекториях неуправляемой линеаризован-

x₀ = (x₁₀,x₂₀,x₃₀), y₀ = (y₁₀,y₂₀,y₃₀). Требуется

ной системы (3) и (4) функция опасности как функ-

дать представление о возможностях маневрирова-

ция времени имеет вид

ния и движения солнечного паруса в зависимости

от его ориентации и характеристик в межпланетном

d₁(t) = ce^lt,

космическом пространстве Земли.

где c — действительное число, определяемое на-

Исследуется вопрос возможностей солнечного

чальными данными.

паруса в задаче управляемого движения КА в меж-

У линейных неуправляемых систем уравне-

планетном космическом пространстве окрестности

ний (3) и (4) имеется инвариантное 5-мерное

коллинеарных точек либрации L₁ и L₂. При этом

многообразие, заполненное ограниченными тра-

очень важно иметь качественную характеристику

екториями, асимптотически приближающимися к

траекторий орбитального движения в окрестно-

двухчастотным колебаниям с частотами ω_e и ω_n.

сти точки либрации, по которой можно судить

о перспективах дальнейшего движения — уход в

Это многообразие, определяемое уравнением

околоземное пространство, переход на гелиоцен-

d₁(x,y) = 0.

трическое движение или длительное пребывание в

окрестности точки либрации. Такой характеристи-

В общем случае для неуправляемой нелинейной

кой может служить текущее значение специаль-

системы (1) знак функции опасности определяет

ной функции от фазовых переменных (координат и

направление ухода КА из окрестности коллинеар-

сопряженных импульсов) — “функции опасности”.

ной точки либрации L₁ к Земле или к Солнцу, а

Эта функция строится на основе линейного при-

из окрестности коллинеарной точки либрации L₂ к

ближения. Мы провели численные исследования,

Земле или от направления к Земле. Этот результат

из которых видно, что эта характеристика остается

получен из численных экспериментов.

справедливой и в нелинейном случае.

Для управляемой линеаризованной системы

уравнений движения (3) поведение функции опас-

ПРИНЦИП ПОСТРОЕНИЯ

ности d₁ на траекториях описывается уравнением

УПРАВЛЯЕМОГО ДВИЖЕНИЯ

1 = ld1 + a14u1 + a15u2.

(6)

Важной характеристикой поведения решения

как систем (3), (4), так и самой нелинейной систе-

Уравнение (6) позволяет строить управления

мы (1) в окрестности коллинеарной точки либрации

по методу оптимального демпфирования функции

L₁ или L₂, является линейная форма фазовых

опасности. Эти управления могут использоваться

переменных — функция опасности (Шмыров и др.,

как для стабилизации (Шмыров, 2005; Шиманчук

2015; Шмыров, Шиманчук, 2015; Поляхова и др.,

и др., 2020), так и для маневрирования (Шмыров и

2018; Шиманчук, Шмыров, 2013):

др., 2015; Шмыров, Шиманчук, 2015; Поляхова и

d₁ = a₁z,

др., 2018; Шиманчук, Шмыров, 2013).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 10

2021

736

ШИМАНЧУК и др.

x₁

M₂

M₁

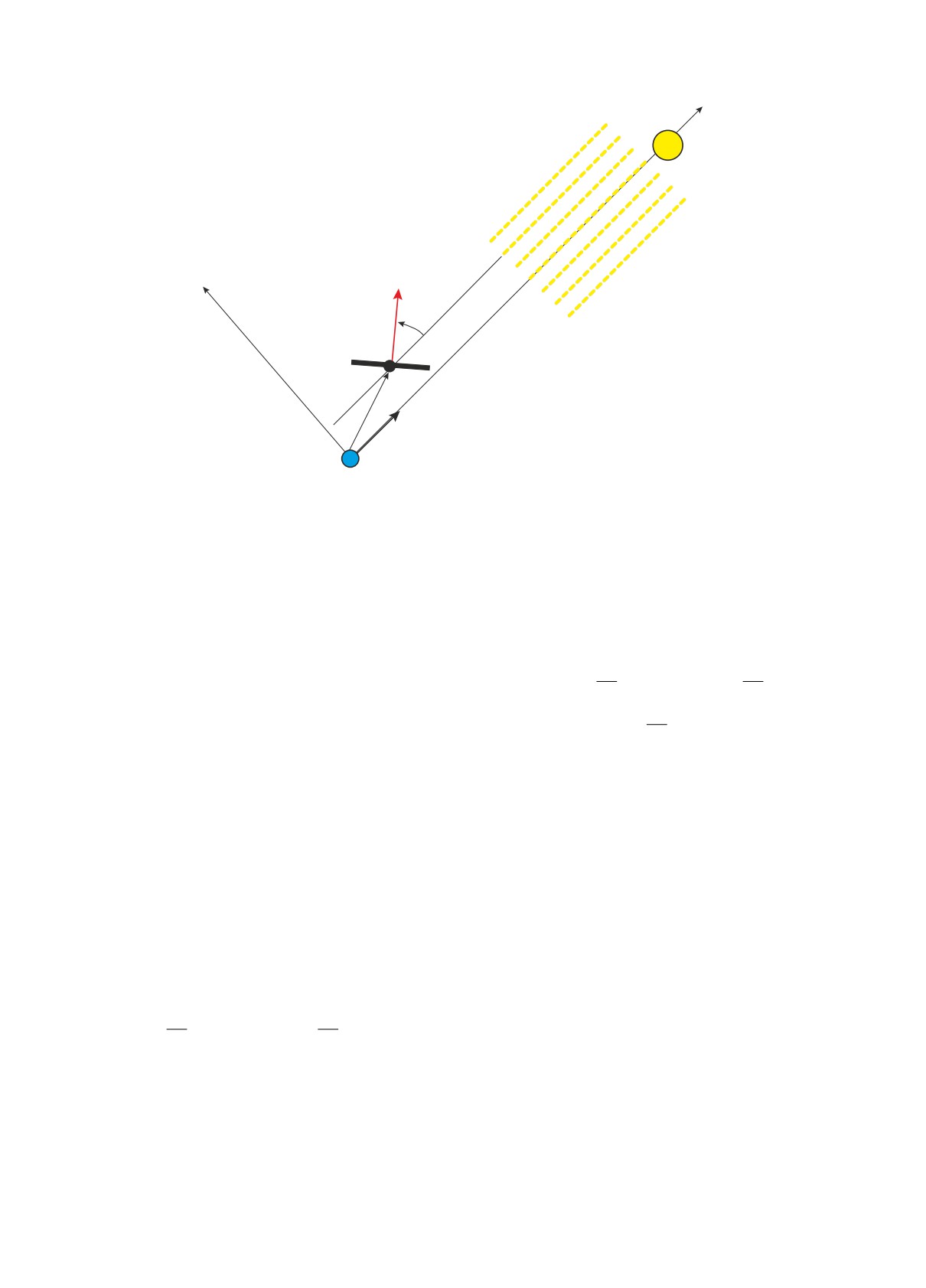
Рис. 1. Солнечный парус во вращающейся системе координат Oxyz.

УПРАВЛЯЕМОЕ ДВИЖЕНИЕ

верхности); i — орт направления от Земли к Солн-

С ПОМОЩЬЮ СИЛ

цу (рис. 1).

СВЕТОВОГО ДАВЛЕНИЯ

В таком случае можно определить компоненты

вектора управления, создаваемого солнечным па-

Как видно из линеаризованных уравнений (3)

русом:

и (4), а также из численного исследования (Ши-

манчук и др., 2020), поведение нормальной (к плос-

u₁ = -2k

cos³ ϕ - (1 - k)

cos ϕ,

(7)

кости эклиптики) составляющей движения носит

колебательный характер. Поэтому основное вни-

мание мы обратим на орбитальное движение в

u₂ = -2k

cos² ϕ sin ϕ,

плоскости эклиптики. Именно здесь и проявляют-

u₃ = 0,

ся свойства неустойчивости, позволяющие суще-

ственно изменять траектории орбитального движе-

где при условии k= const имеем один управляющий

ния с помощью малых управляющих воздействий.

параметр ϕ — угол между векторами i и e. Угол ϕ

В связи с этим мы предполагаем, что солнечный

при движении солнечного паруса в достаточно ма-

парус движется таким образом, что орт вектора

лой окрестности точки либрации можно принять

нормали паруса e все время параллелен плоскости

равным углу между направлением на Солнце и

эклиптики. В этом случае управляющее ускоре-

вектором нормали паруса.

ние, создаваемое направленным потоком фотонов

Следует заметить, что реализация закона управ-

от Солнца, также будет лежать в плоскости, па-

ления (7) отвечает плоскому развороту паруса во-

раллельной плоскости эклиптики. Отраженный и

круг нормали к плоскости эклиптики. Если па-

поглощенный потоки посредством солнечного па-

рус обладает односторонней отражающей поверх-

руса сообщают небесному телу ускорение, которое

ностью, то, согласно (7), управляющий параметр

определяется по формуле

лежит в отрезке ϕ ∈ [-π/2, π/2]. При ϕ = ±π/2

силы светового давления на КА не действуют.

-2k

〈i, e〉²e - (1 - k)

〈i, e〉i,

Исследуем вопрос возможностей управляемого

где p — давление солнечного света; 〈∗, ∗〉 — опе-

движения КА с солнечным парусом. Движению к

рация скалярного произведения векторов; k — ко-

Солнцу из окрестности L₁ соответствует траекто-

эффициент отражающей способности паруса, удо-

рия с d₁ > 0, а движению к Земле — траектория

влетворяющий ограничениям 0 ≤ k ≤ 1 (при k = 1

с d₁ < 0. Движению к Земле из окрестности L₂

имеем случай идеально отражающей поверхности

соответствует траектория с d₁ > 0, а движению от

паруса, при k = 0 — случай абсолютно черной по-

направления к Земле — траектория с d₁ < 0. Для

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 10

2021

ОРБИТАЛЬНОЕ МАНЕВРИРОВАНИЕ

737

f(k,

)

0.8

0.6

0.4

0.2

1.5

1.0

0.5

1.0

1.5

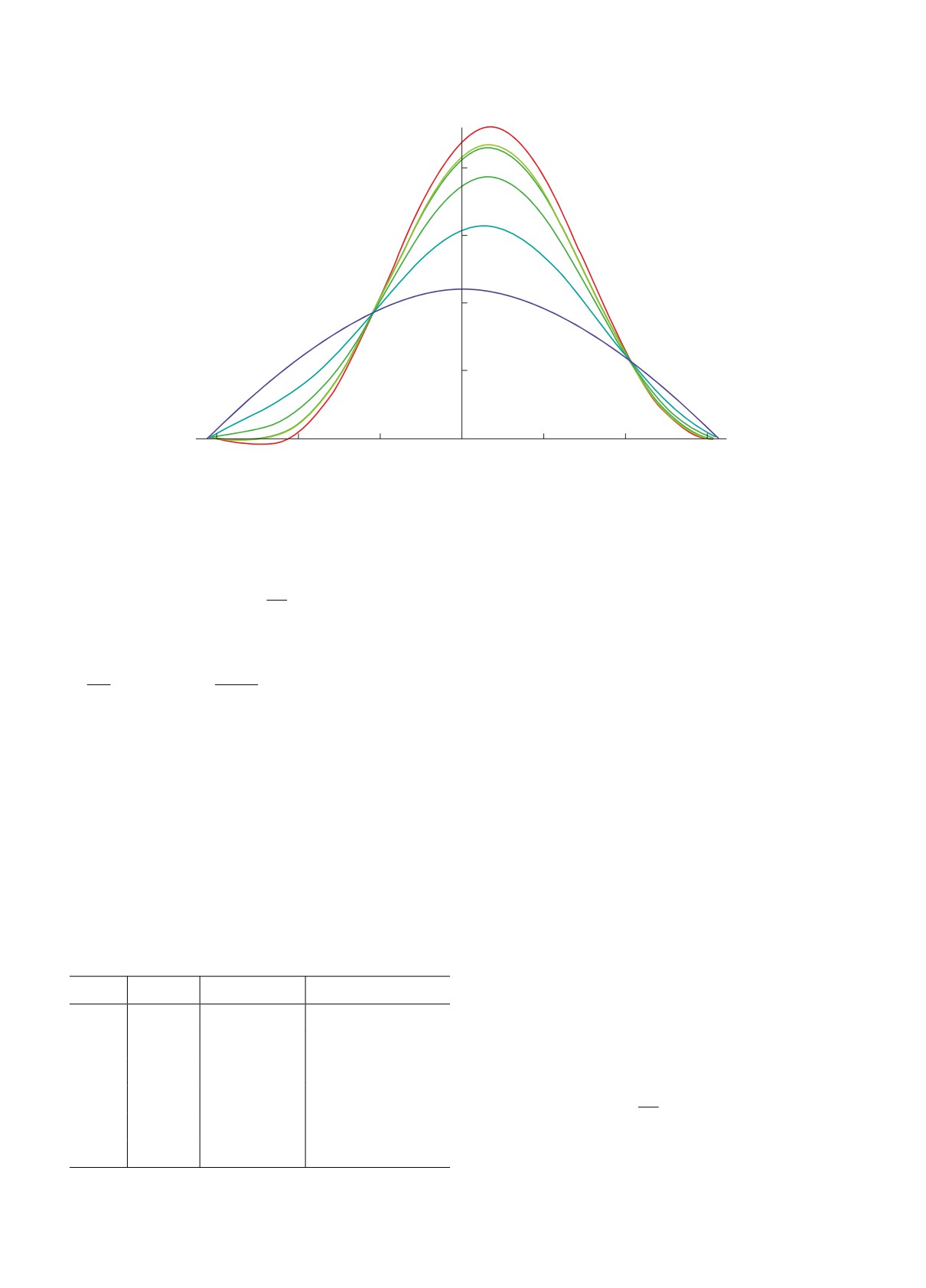
Рис. 2. Графики функции f(k, ϕ): k = 1 (красная кривая), k = 0.9, 0.88, 0.7, 0.4 (зеленые кривые), k = 0 (синяя кривая).

производной функции опасности (6), учитывая (5)

ближенно описывает область управляемости при

и (7), тогда можем записать

решении задачи удержания и дает представление о

возможностях солнечного паруса.

1 = ld1 - 2

f (k, ϕ),

(8)

Прежде всего отыщем максимум и минимум

[

функции f(k, ϕ) по ϕ при различных значениях k

где f(k, ϕ) = cos ϕ k cos ϕ sin(ϕ + ϕ₀) + (1 - k) ×

(см. табл. 1).

]

Из рис. 2 следует, что эффективность управле-

a₁₄

l² + 3

, ϕ₀ = arctg

≈ 1.076 рад.

ния в области d₁ < 0 уменьшается при уменьшении

коэффициента k, т.е. сама возможность управле-

При решении задачи удержания (стабилизации)

ния в области d₁ < 0 обеспечивается достаточно

значение функции опасности не слишком отлича-

высокой отражающей способностью паруса, по-

ется от нуля. Поэтому управляющий параметр ϕ

скольку при k ≤ k_cr ≈ 0.88 функция f(k, ϕ) ≥ 0 для

выбираем так, чтобы правая часть (8) была по-

любого ϕ ∈ [-π/2, π/2]. Параметр k, если позволя-

ложительной, если d₁ < 0, и отрицательной, если

ют отражающие свойства паруса, можно использо-

d₁ > 0. Однако сделать это не всегда возможно.

вать как управляющий параметр совместно или при

Мы опишем область фазового пространства, в

фиксированном значении угла ϕ. Однако можно

которой этот выбор возможен. Эта область при-

заметить, что имеются такие значения угла ϕ: -

-0.537866 и 1.03293, для которых f(k, ϕ) равняет-

ся соответственно 0.377847 и 0.225398 при любом

Таблица 1. Значения угла ϕ, которые обеспечивают

экстремум функции f(k, ϕ) (α — максимум, β — мини-

значении k ∈ [0, 1], что характеризует ограничен-

мум), при фиксированных значениях отражающей спо-

ность использования только отражающей способ-

собности паруса k

ности солнечного паруса при данных значениях

угла ориентации.

Пусть рассматривается случай движения пару-

са в окрестности точки либрации L₁ или L₂, тогда

0.168016

-1.24375

для удержания паруса в области d₁ < 0 из равен-

0.9

0.165262

-1.30361

ства (8) и условия оптимального демпфирования

функции опасности получаем

0.88

0.164649

±π/2,-1.3232

0.7

0.157865

±π/2

ld₁ - 2

f (1, β) > 0.

(9)

0.4

0.137104

±π/2

Это условие может быть обеспечено, если отра-

±π/2

жающая способность паруса k > k_cr, иначе управ-

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 10

2021

738

ШИМАНЧУК и др.

1.1

1.2

1.3

1.4

x₁

d₁

2.0

(б)

0.05

1.5

0.10

0.15

1.0

0.20

0.5

0.25

(a)

0.30

0.5

1.0

1.5

x₂

Рис. 3. Траектории движения солнечного паруса из окрестности L1 (а) и график значений функции опасности (б) с

начальными данными (11) при d1 > 0 на промежутке времени около 100 сут.

ление с целью удержания в области d₁ < 0 не

Далее, на примере паруса с идеально отражаю-

представляется возможным.

щей способностью приведем численные примеры,

Аналогично для удержания солнечного паруса в

которые демонстрируют возможности управления

области d₁ > 0 можно получить

орбитальным движением солнечного паруса.

ld₁ - 2

f (1, α) < 0.

(10)

ЧИСЛЕННЫЕ ПРИМЕРЫ ДВИЖЕНИЯ КА

Если условия (9), (10) не выполняются для α

С СОЛНЕЧНЫМ ПАРУСОМ

и β, то они не выполняется для любого другого

угла ϕ, что во многом обусловлено начальными

Проведем компьютерное моделирование дви-

данными и характеристикой солнечного паруса —

жения солнечного паруса с идеально отражающей

парусностью S/m. В этом случае солнечный парус

способностью в окрестности коллинеарных точек

будет просто уходить из окрестности коллинеарной

либрации L₁ и L₂. Для моделирования движе-

ния используем параметры солнечного паруса m =

точки либрации L₁ к Земле или к Солнцу, для

окрестности L₂ — от направления к Земле или к

= 300 кг, S = 225 м², которым будет соответство-

Земле.

вать значение парусности, равное 7.5 см²/г. Это на

Из условий (9) и (10) можно получить оценку

порядок меньше парусности солнечного паруса из

снизу и сверху для значения функции опасности,

реализованного проекта LightSail-2, для которого

а следовательно, и оценку области управляемости

она равна 64 см²/г.

для задачи стабилизации орбитального движения в

Результаты численного моделирования управ-

окрестности коллинеарной точки либрации L₁ или

ляемого движения солнечного паруса с начальны-

L₂:

ми данными

d^min1 ≤ d₁(x,y) ≤ d^max1,

2pS

• для окрестности L₁:

где d^min1 =

f (1, β), d^max1 =

f (1, α). Ясно,

x₁₀ = 1.015, x₂₀ = 0, x₃₀

= 0,

(11)

что в случае k < k_cr можно принять d^min1 = 0. Такой

y₁₀ = 0, y₂₀ = 1, y₃₀ = 0 (d₁ > 0),

анализ случая идеально отражающей поверхно-

сти паруса в работе (Шиманчук и др., 2020) был

x₁₀ = 0.9998, x₂₀ = 0, x₃₀ = 0,

использован для построения законов управления

y₁₀ = 0, y₂₀ = 1, y₃₀ = 0 (d₁ < 0);

орбитальным движением паруса с целью его удер-

жания в окрестности точки либрации L₁.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 10

2021

ОРБИТАЛЬНОЕ МАНЕВРИРОВАНИЕ

739

0.5

1.0

1.5

x₂

0.20

0.15

0.10

0.05

(a)

(б)

d₁

0.2

0.4

0.6

0.8

Рис. 4. Траектории движения солнечного паруса из окрестности L1 (а) и график значений функции опасности (б) с

начальными данными (11) при d1 < 0 на промежутке времени около 100 сут.

d₁

0.8

0.6

0.4

0.2

x₁

(б)

0.05

0.10

0.15

0.20

x₂

(a)

0.5

1.0

1.5

Рис. 5. Траектории движения солнечного паруса из окрестности L2 (а) и график значений функции опасности (б) с

начальными данными (12) при d1 > 0 на промежутке времени около 100 сут.

• для окрестности L₂:

при ϕ ∈ [-π/2, π/2) на промежутке времени поряд-

ка ста земных суток месяца приведены на рис. 3-6,

x₁₀ = -0.985, x₂₀ = 0, x₃₀ = 0,

(12)

где также проиллюстрированы значения функции

y₁₀ = 0, y₂₀ = -1, y₃₀ = 0 (d₁ > 0),

опасности на траекториях движения. Выделенные

на рисунках красным цветом кривые относятся к

x₁₀ = -1.0002, x₂₀ = 0, x₃₀ = 0,

неуправляемому движению КА, зеленым — к дви-

y₁₀ = 0, y₂₀ = -1, y₃₀ = 0 (d₁ < 0)

жению КА при ϕ = α, синим — к движению КА

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 10

2021

740

ШИМАНЧУК и др.

0.5

1.0

1.5

0.30

0.25

0.5

0.20

1.0

0.15

1.5

0.10

0.05

2.0

(a)

(б)

d₁

1.5

1.4

1.3

1.2

1.1

x₁

Рис. 6. Траектории движения солнечного паруса из окрестности L2 (а) и график значений функции опасности (б) с

начальными данными (12) при d1 < 0 на промежутке времени около 100 сут.

при ϕ = β (см. табл. 1, случай k = 1). Выбор на-

параметра (ϕ ∈ [-π/2, π/2), в каждом из примеров

чальных данных в окрестности точки либрации с

строятся 64 траектории).

точностью до линейного приближения обусловлен

Заметим также, что совместно с углом ориента-

областью управляемости -0.00079 < d₁(x₀, y₀) <

ции паруса ϕ при движении КА следует рассмат-

< 0.04221. Кроме этого, выбор таких начальных

ривать управляющий параметр τ, который соот-

данных связан с близостью к границе управляемо-

ветствует моменту времени переориентации пару-

сти, тогда можно сказать, что найдутся значения

са. Так, пусть для первого и второго численных

угла ϕ, для которых обеспечивается движение,

примеров (рис. 3, 4) КА на промежутке времени τ,

при котором функция опасности меняет знак, т.е.

приблизительно равном пятидесяти суткам, совер-

солнечный парус не уходит в ту область, которой

шал неуправляемое движение, а далее происходит

соответствует знак функции опасности в началь-

переориентация паруса, согласно уже проведен-

ный момент времени. Также заметим, что если ϕ =

ным ранее численным экспериментам. На рис. 7 и 8

= 0 (нормаль паруса направлена на Солнце), то

представлены результаты такого моделирования.

ускорение от солнечного паруса будет равно 6.84 ×

Численные примеры демонстрируют возможно-

× 10-6 м/c², т.е. под действием только сил свето-

сти управляемого движения КА с солнечным па-

вого давления КА из состояния покоя за сто суток

русом при фиксированном значении управляющего

отклонится на расстояние порядка 255.3 тыс. км.

параметра ϕ, что и позволяет перейти к решению

Вопрос о том, каким образом КА оказался в

вопроса управляемого движения КА с солнечным

точке с фазовыми координатами (11), (12), в дан-

парусом с целью удержания КА в окрестности точ-

ной работе не исследуется, формулировка идеи и

ки либрации или решения задач, связанных с ма-

возможный алгоритм решения такой задачи пред-

неврированием в межпланетном космическом про-

ставлены в работе Шиманчука, Шмырова (2013).

странстве Земли. Также численное исследование

На рис. 3 и 4 представлены траектории движе-

подтверждает принятую гипотезу о соответствии

ния солнечного паруса из окрестности точки L₁ и

поведения функции опасности и траектории ор-

соответствующие графики значений функции опас-

битального движения — когда функция опасности

ности на этих траекториях. Аналогично на рис. 5

возрастает, наблюдается переход к гелиоцентриче-

и 6 представлены траектории движения солнечного

скому движению из окрестности L₁ и к геоцентри-

паруса из окрестности точки L₂ и соответствующие

ческому движению из окрестности L₂. Если зна-

графики значений функции опасности на траекто-

чение функции опасности убывает, то это соответ-

риях. Здесь каждой траектории соответствует по-

ствует переходу к геоцентрическому движению из

стоянное значение — узел равномерного разбиения

окрестности L₁ и к гелиоцентрическому движению

рассматриваемого промежутка для управляющего

из окрестности L₂.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

2021

№ 10

ОРБИТАЛЬНОЕ МАНЕВРИРОВАНИЕ

741

1.1

1.2

1.3

1.4

x₁

d₁

(б)

2.0

0.05

1.5

0.10

0.15

1.0

0.20

0.5

0.25

(a)

0.30

x₂

0.5

1.0

1.5

Рис. 7. Траектории движения солнечного паруса из окрестности L1 (а) и график значений функции опасности (б) с

начальными данными (11) при d1 > 0 на промежутке времени около 100 сут.

0.5

1.0

1.5

0.030

(б)

0.05

0.025

0.10

0.020

0.15

0.015

0.20

0.010

0.25

0.30

0.005

(a)

0.35

d₁

0.94

0.95

0.96

0.97

0.98

0.99

Рис. 8. Траектории движения солнечного паруса из окрестности L1 (а) и график значений функции опасности (б) с

начальными данными (11) при d1 < 0 на промежутке времени около 100 сут.

ЗАКЛЮЧЕНИЕ

го паруса существенно выше в области d₁ > 0

по

сравнению с управлением в области d₁ < 0. При

Предложенные законы управления движением

этом такая возможность и максимальная эффек-

КА с солнечным парусом, построенные для модели

тивность маневрирования в области d₁ < 0 обес-

хилловского приближения круговой ограниченной

печиваются достаточно большой отражающей спо-

задачи трех тел, показали в ходе численных экс-

периментов свою эффективность и в более общей

собностью паруса k. Показано, что при k < k_cr ≈

модели движения — круговой ограниченной зада-

≈ 0.88 такая возможность теряется, т.е. парус с

че трех тел (Шиманчук и др., 2020). Эффектив-

невысокой отражающей способностью не может

ность управления для задачи удержания солнечно-

обеспечить движение “против солнечного ветра”.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 10

2021

742

ШИМАНЧУК и др.

Предложенная методика управления ориента-

остается справедливым и для нелинейной системы

цией с различной отражающей способностью сол-

уравнений.

нечного паруса позволяет решать как задачи удер-

жания солнечного аппарата в окрестностях кол-

линеарных точек либрации, так и задачи ухода из

СПИСОК ЛИТЕРАТУРЫ

этих окрестностей. Задача удержания или стаби-

1. Буклесс, Макиннес (J. Bookless and C. McInnes),

лизации заключается в обеспечении близости в

Acta Astronautica 62, 159 (2008).

фазовом пространстве КА к инвариантному мно-

2. Маркеев А.П., Точки либрации в небесной меха-

гообразию. При решении задачи маневрирования

нике и космодинамике (М.: Наука, 1978).

в межпланетном космическом пространстве Земли

3. Поляхова и др. (E. Polyakhova, A. Shmyrov, and

из условия оптимального демпфирования функции

V. Shmyrov), AIP Conf. Proceed. (Ed. E.V. Kustova,

опасности определяется направление скорейшего

G.A. Leonov, M.P. Yushkov, N.F. Morosov,

выхода из окрестности точки либрации (для пред-

M.A. Mekhonoshina, St. Petersburg, AIP, 2018).

ставленных численных примеров движения КА с

4. Шиманчук Д.В., Шмыров А.С., Вестн. С.-Петерб.

солнечным парусом эти направления определяют-

ун-та. Сер. 10: Прикладная математика, информати-

ся значениями угла ориентации — α и β). Такой

ка, процессы управления 2, 76 (2013).

подход был использован в работе Шмырова и др.

5. Шиманчук Д.В., Шмыров А.С., Шмыров В.А.,

(2015). В настоящем исследовании для оценки об-

Письма в Астрон. журн.

46,

193

(2020)

ласти достижимости на конечном промежутке вре-

[D.V. Shymanchuk, et al., Astron. Lett. 46,

185

мени рассмотрены движения при фиксированных

(2020)].

различных значениях угла ориентации солнечного

6. Шмыров В.А., Вестн. С.-Петерб. ун-та. Сер. 10.

паруса.

Прикладная математика. Информатика. Процессы

Приведенное численное исследование показало,

управления 2, 193 (2005).

что силы светового давления могут существенно

7. Шмыров,

Шиманчук (A. Shmyrov and

повысить эффективность орбитального маневри-

D. Shymanchuk), Inter. Conf. on Mechanics -

рования в окрестности коллинеарной точки либ-

Seventh Polyakhov’s Reading (Ed. A.A. Tikhonov,

рации системы Солнце-Земля. Это исследова-

St. Petersburg, IEEE, 2015).

ние позволяет сделать вывод: знак специальной

8. Шмыров и др. (A. Shmyrov, D. Shymanchuk, and

функции — функции опасности в окрестности точ-

L. Sokolov), Inter. Conf. on “Stability and Control

ки либрации может служить в качестве харак-

Processes” in Memory of V.I. Zubov, SCP 2015

теристики орбитального движения. Этот теорети-

- Proceedings (Ed. L.A. Petrosyan, A.P. Zhabko,

ческий результат для линеаризованных уравнений

St. Petersburg, IEEE, 2015), p. 129.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 10

2021