ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2021, том 47, № 11, с. 782-792

ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНЫХ ЗВЕЗД КАТАЛОГА П. КУТО,

ОПРЕДЕЛЕННЫЕ С УЧЕТОМ ДАННЫХ GAIA DR2 И GAIA EDR3

¹Московский государственный технологический университет “СТАНКИН”, Москва, Россия

Поступила в редакцию 22.10.2021 г.

После доработки 02.11.2021 г.; принята к публикации 02.11.2021 г.

Впервые определены орбиты десяти звезд, открытых П. Куто: COU 99, 357, 610, 850, 1346, 1531,

1642, 1752, 1845, 2459. У двух из них (COU 850 и 1752) наблюдениями охвачена дуга более

половины оборота, орбиты остальных звезд определялись по коротким дугам (5-50^◦). Орбиты COU

99, 610, 1346, 1531 и 1845 вычислены с использованием сумм масс компонент, оцененных по

фотометрическим данным и тригонометрическим параллаксам каталогов Gaia, Hipparcos и Tycho.

Кроме того, произведено уточнение орбит COU 66, 169, 773, 1006 и 1897.

Ключевые слова: визуально-двойные звезды, орбиты.

DOI: 10.31857/S0320010821110036

ВВЕДЕНИЕ

по коротким дугам является метод параметров ви-

димого движения (ПВД) (Киселев, Кияева, 1980;

В данной работе исследуются визуально-

Быков, Холшевников, 2013; Кияева, Романенко,

двойные звезды, открытые П. Куто и вошедшие

2020), для его работы необходимо знать относи-

в составленный им каталог (Куто, 1995). Ранее

тельные лучевые скорости и суммы масс. В нашем

нами были опубликованы 20 орбит звезд этого

методе в зависимости от особенностей имеющихся

каталога (Байдин, Кречет, 2021). В настоящий

данных можно как использовать V_rBA и MAB(ph),

момент мы представляем десять орбит, опреде-

так и не использовать.

ленных впервые: COU 357, 850, 1642, 1752, 2459

Первоначально делается попытка определить

вычислены без использования фотометрических

орбиту без дополнительных данных (V_rBA и

сумм масс, остальные (COU 99, 610, 1346, 1531,

MAB(ph)). Если после вычислений динамическая

1845) получены с учетом фотометрических данных.

Кроме того, мы производим уточнение пяти орбит

и фотометрическая суммы масс или вычисленная

и измеренная относительные лучевые скорости не

(COU 66, 169, 773, 1006, 1897), вычисленных ра-

согласуются, орбита вычисляется с использова-

нее другими исследователями (Харткопф, Мэйсон,

нием дополнительных данных. У представленных

2021).

в данной работе звезд измерения относительных

Для определения орбит использовался метод

лучевых скоростей не проводились. Для пяти звезд

(Байдин, 2015; Байдин и др., 2018), который поз-

не удалось получить орбиты с динамическими

воляет вычислить орбиту по наблюдениям, рас-

массами, удовлетворяющими данным каталогов

пределенным на короткой дуге. Этот метод можно

Gaia (Браун и др., 2018, 2021), Hipparcos и Tycho

отнести к одной из модификаций метода Харткопфа

(ESA, 1997), поэтому мы использовали фотомет-

и др. (1989). В последнем для определения трех

рические массы для уточнения элементов орбит.

величин (P , T_p, e) использовался метод подбора,

Еще для одной звезды (COU 66) представлены

мы же применяем генетический алгоритм. Также

две орбиты: первая вычислена без использования

для повышения точности результатов наш метод

фотометрической суммы масс, вторая — с учетом

позволяет использовать дополнительные данные:

значения суммы масс.

относительные лучевые скорости (V_rBA) и суммы

масс компонент (MAB(ph)), оцененные по фотомет-

Применение фотометрических сумм масс при

рическим данным и спектральным классам. Одним

определении орбит долгопериодических пар (P

из наиболее известных методов определения орбит

> 500 лет) можно считать вынужденной мерой.

Достаточно надежные орбиты подобных объектов

^*Электронный адрес: al.baidin@yandex.ru

встречаются очень редко, так как для этого пара

782

ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНЫХ ЗВЕЗД

783

должна находиться на малом расстоянии от Солн-

способами. В методе И.С. Измайлова (2019) зада-

ца (π_t ∼ 100 мсд) и наблюдаться около 200 лет, в

ча разбита на два этапа: 1) имея первые приближе-

качестве примера можно привести STT 547 (Ки-

ния величин P , T_p, e, которые заранее были опреде-

яева и др. 2001, 2020; Измайлов, 2019). В работе

лены методом Тиле-Иннеса, методом наименьших

(Байдин и др., 2018) орбита этой пары вычислена

квадратов вычисляются A, B, F , G; 2) зная A, B,

тремя способами: описанным ниже методом без

F, G, с помощью нелинейного метода наименьших

использования дополнительных данных, с исполь-

квадратов уточняются P , T_p, e.

зованием относительной лучевой скорости, взятой

В работе Харткопфа и др. (1989) предложен

из работы А.А. Токовинина (1994), и модифици-

другой подход. Если приведенные координаты из-

рованным методом ПВД (Байдин, 2018). Орбиты

вестны, то уравнения (1) являются линейными от-

STT 547, полученные разными авторами и различ-

носительно величин A, B, F , G. Для вычисления

ными методами, мало отличаются друг от друга.

приведенных координат необходимо знать P , T_p и

В большинстве случаев для долгопериодических

e, тогда с помощью (3) можно найти эксцентриче-

пар вычисляются предварительные орбиты, ис-

скую аномалию и подставить в (2). Харткопф и др.

пользование фотометрических масс в ходе вычис-

(1989) предложили P , T_p и e определять подбором,

лений позволяет повысить точность результатов.

а величины A, B, F , G находить методом наи-

Полученные предварительные орбиты долгоперио-

меньших квадратов. В этом подходе одновременно

дических пар можно использовать для проведения

определяются P , T_p, e, A, B, F , G, для которых

статистических исследований (Токовинин, 1998,

сумма взвешенных квадратов невязок минимальна.

2020; Токовинин, Кияева, 2016; Кияева и др., 2018).

В настоящей работе орбиты определены моди-

фицированным методом Харткопфа и др. (1989).

Вместо подбора в нем используется генетический

МЕТОД ОПРЕДЕЛЕНИЯ ОРБИТ

алгоритм (ГА), такой подход был предложен в

работе (Байдин, 2015). Время, затрачиваемое на

Основные уравнения метода следующие:

определение орбиты, при использовании генетиче-

x = AX + FY, y = BX + GY,

(1)

ского алгоритма в сравнении с методом подбора

уменьшается. Еще одно преимущество использо-

X = cosE - e, Y = (1 - e²)1/2 sinE,

(2)

вания ГА связано с тем, что вместо первых прибли-

жений задаются интервалы возможных значений

P, T_p и e, одинаковые для всех исследуемых звезд.

E - esinE - n(T - T_p) = 0,

(3)

Для вычисления орбит, представленных в данной

где x и y — декартовые координаты звезды-

работе, наиболее удобными являются следующие

спутника относительно главной компоненты в

интервалы: P ∈ [10; 10 000], T_p ∈ [1800; 11 800], e ∈

картинной плоскости, X, Y — приведенные коор-

∈ [0.001; 0.95].

динаты, E — эксцентрическая аномалия.

Как правило, наблюдениям, распределенным на

В качестве неизвестных (элементов орбит) у нас

малой дуге, могут одинаково хорошо удовлетво-

выступают A, B, F , G — элементы Тиле-Иннеса,

рять заметно отличающиеся друг от друга орбиты

P — период (он связан со средним движением n =

(Киселев, 1989; Байдин, 2018). Исключение из

= 2π/P ), e — эксцентриситет, T_p — момент про-

этого правила составляют только орбиты, опре-

деляемые по современным высокоточным наблю-

хождения периастра. От перечисленных элементов

дениям, например, звездного интерферометра PTI

с помощью стандартного алгоритма (Куто, 1981)

(Колавита и др., 1999). В наших исследованиях

можно перейти к элементам орбит (P , a, i, Ω, T_p,

используются в основном визуальные и спекл-

e, ω), которые входят в современный каталог орбит

интерферометрические наблюдения, имеющие бо-

двойных звезд (Харткопф, Мэйсон, 2021).

лее низкую точность. Поэтому в случае обработки

С учетом количества наблюдений N, используя

наблюдений на малых дугах при повторных запус-

(1), можно составить 2N уравнений и решить их

ках ГА получаются различные орбиты. Проблема

методом наименьших квадратов. В качестве ис-

повторяемости результатов исследования решена

комых величин выступают элементы орбит, урав-

посредством многократного запуска ГА (обычно

нения получаются нелинейными, поэтому нужно

20 повторений) и выбора орбиты с элементами,

задавать первые приближения, и могут возникнуть

наиболее близкими к средним. Кроме средних зна-

проблемы со сходимостью. Последнее затрудняет

чений элементов орбиты было принято решение

определение орбит по наблюдениям на короткой

определять среднеквадратичные отклонения эле-

дуге и наблюдениям, неоднородно покрывающим

ментов орбит. Последние характеризуют “разброс”

дуги порядка или более половины оборота. Про-

орбит, хорошо удовлетворяющих используемой со-

блему со сходимостью можно решать различными

вокупности относительных положений.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 11

2021

784

КИССЕР, КРЕЧЕТ

Эксперименты с модельными и реальными дан-

Веса наблюдений (p_i) определялись по форму-

ными (Байдин, 2018) показали, что при работе

лам (Байдин, Кречет, 2021)

с наблюдениями, распределенными на малых ду-

√

p_int = 50D1.5

N, p_vis =D0.5

(8)

гах (20-50◦) и имеющими погрешность σρ/ρ ∈

∈ (0.01-0.1), довольно часто вычисленные орбиты

где D — апертура телескопа, N — количество

сильно отличаются от истинных. Такие результа-

измерений, с помощью которых определены сред-

ты сопровождаются более чем на порядок завы-

ние относительные координаты звезды-спутника,

шенными динамическими суммами масс и завы-

p_vis — веса визуальных наблюдений разделения

шенными значениями эксцентриситетов, которые

(веса позиционных углов в четыре раза больше).

устремляются к верхнему граничному значению (в

При использовании условия (5) совместно с

программе задано 0.95). Эти два критерия хоро-

(4), (6)-(8) завышенные динамические суммы масс

шо подходят для оценки качества получаемых ор-

получаются редко, эксцентриситеты также редко

бит: фотометрические и динамические суммы масс

устремляются к верхнему граничному значению.

должны быть примерно равны, и значения экс-

Требования к точности определения фотометриче-

центриситета не должны устремляться к заданной

ских сумм масс и точности значений тригонометри-

верхней границе (вместо 0.95 можно задать 0.99

ческих параллаксов (они используются для опре-

или более).

деления динамической и фотометрической суммы

Если по наблюдениям относительных положе-

масс) при этом возрастают, так как эти величины

ний орбиту, удовлетворяющую описанным выше

теперь, наравне с относительными положениями,

двум критериям, получить не удается, то для уточ-

влияют на сумму квадратов невязок (5).

нения элементов орбит можно применить допол-

Описанный метод с коэффициентами (4) позво-

нительные данные: фотометрические суммы масс

ляет определить эллиптическую орбиту независимо

MAB(ph) и относительные лучевые скорости V_rBA.

от качества наблюдений и реальных особенностей

В работе (Байдин и др. 2018) предложено изменить

движения пары, т.е. в отдельных случаях может

условие отбора решений в генетическом алгоритме,

получиться эллиптическая орбита с удовлетвори-

минимумы сумм квадратов невязок умножить на

тельной динамической суммой масс, хотя пара яв-

коэффициенты

ляется оптической. Подобные результаты необхо-



_M



димо исключить из рассмотрения. Для этого в ходе

MAB(d)

k_M = 1 +AB(ph) -

(4)

наших исследований определялись элементы пря-

MAB(ph)

молинейного движения (Харткопф и др., 2006.5)



_V



всех звезд, у которых наблюдениями охвачены дуги

rBA(obs) - VrBA(cal)

k_V = 1 +

менее 100^◦, и форма этих дуг близка к прямоли-

V_BA

нейной. Из вычисленных величин использовались

где MAB(ph) — фотометрическая сумма масс,

видимая относительная скорость и среднеквадра-

тичное отклонение, определяемое с учетом весов

MAB(d) — динамическая сумма масс, VrBA(obs)

√

и VrBA(cal) —наблюдаемая и вычисленная по

μ_BA =

x² + y², S(p)lin =

χ²/N,

(9)

элементам орбит относительная лучевая скорость,_√

где x, y — проекции относительной скорости, N —

V_BA = μ2BA + V2rBA(obs) — скорость

звезды-

количество наблюдений, используемых в вычисле-

спутника относительно главной компоненты,

ниях, χ² — сумма взвешенных квадратов невязок

μ_BA — проекция относительной скорости на кар-

(5) для модели прямолинейного движения.

тинную плоскость (вычисляется с помощью разло-

О наличии физической связи говорит выполне-

жений относительных координат по времени).

ние хотя бы одного из неравенств

Основное условие для выбора элементов орбит

μ_BA < μ, S(p)el < S(p)lin,

(10)

с учетом коэффициентов (4) следующее

где μ_BA — видимая скорость звезды-спутника

χ² = χ^2int + χ^2vis = min,

(5)

относительно главной компоненты (9), μ — соб-

где

ственное движение пары, S(p)el и S(p)lin — сред-

∑

(

неквадратичные отклонения

(9), определенные

χ^2int = k_M k_V

pi(int)

(xi(obs) - xi(cal))² +

(6)

с учетом весов наблюдений, для моделей эл-

)

липтического и прямолинейного относительных

+ (yi(obs) - yi(cal))²

движений. Условие μ_BA < μ может выполняться

∑

(

и для оптической пары, поэтому вывод о наличии

χ^2vis = k_M k_V

pi(vis)

(ρi(obs) - ρi(cal))² +

(7)

физической связи можно сделать, если μ_BA как

)

минимум в несколько раз меньше μ. Выполнение

+ 4 ∗ ρ2i(cal)(θi(obs) - θi(cal))²

условия S(p)el < S(p)lin показывает, что модель

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 11

2021

ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНЫХ ЗВЕЗД

785

Таблица 1. Элементы орбит

COU

66^∗

99^∗

169

357

610^∗

773

850

P, год

255.6

143.2

321.3

92.7

393.8

361.1

165.3

48.00

σ_P

21.4

3.3

38.0

4.2

42.8

76.8

7.7

0.07

a,^′′

0.930

0.727

0.599

0.457

0.369

0.826

0.232

0.2774

σa

0.050

0.011

0.048

0.005

0.027

0.118

0.007

0.0005

i,^◦

155.9

147.0

146.2

134.1

123.0

100.5

76.5

45.3

σ_i

2.8

0.4

5.1

0.9

3.2

0.2

0.1

Ω,^◦

132.8

12.0

39.7

50.2

128.9

26.9

45.2

101.6

σΩ

5.4

5.1

4.0

4.6

1.4

2.5

0.1

0.5

T_p, год

2025.9

2031.3

1902.0

1964.5

2360.8

1943.0

2019.5

1944.75

σ_Tp

1.0

3.8

13.1

0.4

46.4

0.7

2.1

0.07

0.493

0.497

0.128

0.676

0.253

0.780

0.213

0.495

σe

0.017

0.019

0.052

0.033

0.050

0.054

0.008

0.004

ω,^◦

102.2

25.5

58.6

259.7

316.0

66.5

86.6

60.3

σω

9.9

4.0

29.0

1.8

7.1

8.8

7.2

0.6

COU

1006

1346^∗

1531^∗

1642

1752

1845^∗

1897

2459

P, год

221.0

139.6

203.5

433.8

71.4

619.2

82.3

633.6

σ_P

44.7

28.6

40.8

52.8

8.0

109.1

1.7

98.6

a,^′′

0.743

0.212

0.448

0.247

0.182

1.000

0.138

1.833

σa

0.083

0.030

0.057

0.020

0.019

0.120

0.001

0.140

i,^◦

52.2

119.2

123.8

59.3

50.3

64.5

31.7

120.9

σi

1.6

6.3

1.3

1.0

3.4

3.3

1.1

Ω,^◦

16.6

62.9

11.9

101.3

125.6

178.2

133.0

95.9

σ_Ω

2.7

5.6

3.8

1.0

7.6

0.4

0.5

1.7

T_p, год

1980.2

2029.9

2024.3

2026.0

2006.4

1932.8

2017.3

2586.0

σ_Tp

3.0

0.8

0.7

5.8

0.3

1.7

0.2

103.5

0.384

0.479

0.758

0.277

0.477

0.663

0.408

0.445

σe

0.083

0.096

0.013

0.055

0.051

0.036

0.001

0.039

ω,^◦

201.1

109.2

70.3

11.9

83.6

56.0

200.9

223.6

σ_ω

8.5

13.8

2.4

6.9

10.8

10.6

1.6

12.3

^∗ Орбита определена с учетом фотометрической суммы масс.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 11

2021

786

КИССЕР, КРЕЧЕТ

эллиптического движения лучше согласуется с

к настоящему моменту накоплено большое коли-

имеющимися наблюдениями, чем модель прямоли-

чество спекл-интерферометрических наблюдений

нейного.

этой пары.

В табл. 2 и 3 представлены следующие вели-

чины: N_int и N_vis — количество спекл-интерферо-

ОСНОВНЫЕ РЕЗУЛЬТАТЫ

метрических и визуальных наблюдений, использу-

Для определения орбит использовались наблю-

емых для окончательного определения орбиты (по-

дения относительных положений с сайта обсерва-

сле исключения с помощью правила 3σ), T₁ и T_N —

моменты первого и последнего используемых на-

тории в Ницце (Контэль и др., 2001), из четвертого

блюдений, ρ — разделение, вычисленное на эпоху

интерферометрического каталога (Харткопф и др.,

2022 г., Δθ — угол поворота с момента открытия

2020), каталогов Gaia DR2 (Браун и др., 2018)

по 2022 г., π_t — тригонометрический параллакс,

и Gaia EDR3 (Браун и др., 2021) и из работ

MAB(d) и MAB(ph) — фотометрическая и динамиче-

последних лет, имеющихся в свободном доступе¹.

ская суммы масс в единицах M_⊙, величины μ_BA,

В случае данных Gaia относительные координаты

μ, S(p)el и S(p)lin были введены выше. Погрешности

вычислялись при наличии координат обеих компо-

нент пары.

μ_BA и μ в табл. 3 не указаны, в большинстве слу-

чаев они невелики (менее 1 мсд/год), исключение

Фотометрические данные и параллаксы брались

составляют COU 169 и 1642, у первой собственное

из каталогов Gaia DR2 (Браун и др., 2018) и Gaia

движение взято из каталога Hipparcos, стандарт-

EDR3 (Браун и др., 2021), при отсутствии этих дан-

ные ошибки собственных движений по прямому

ных использовались каталоги Hipparcos и Tycho

восхождению и склонению σμα∗ = 3.08 мсд/год,

(ESA, 1997; Фабрициус, Макаров, 2000; Фабрици-

ус и др. 2002; Ван Лейвен, 2007). Для определения

σμδ = 3.19 мсд/год, у второй — из каталога Gaia

фотометрических масс звезд осуществлялся пере-

DR2, σμα∗ = 1.740 мсд/год, σμδ = 1.618 мсд/год.

ход к фотометрической системе (UBV ) с помощью

Дуги, охваченные наблюдениями, у COU 169, 773,

отношений, представленных в работах Буссо и др.

850 и 1897 заметно отличаются от прямолинейных,

(2019), Риелло и др. (2021), затем использовались

поэтому элементы прямолинейного движения для

эволюционные треки (Жирарди и др., 2000) и зави-

этих звезд не вычислялись, и в табл. 3 отсутствуют

симость масса-светимость.

значения μ_BA и S(p)lin.

В табл. 1 представлены вычисленные элементы

Разделение (ρ), представленное в табл. 2, по-

орбит. У звезд COU 99, 357, 610, 850, 1346,

казывает, насколько сложна пара для наблюде-

1531, 1642, 1752, 1845, 2459 орбиты определены

ния в настоящий момент, угол поворота (Δθ) —

впервые. У пяти из них (COU 357, 850, 1642,

насколько она перспективна для исследования в

1752, 2459) фотометрические и динамические сум-

ближайшем будущем. Примерное равенство фото-

мы масс получились близкими по величине, поэто-

метрических и динамических сумм масс говорит,

му мы не производили уточнение элементов орбит

что имеющиеся данные о паре (эпохи и наблю-

с учетом фотометрических сумм масс, остальные

денные относительные координаты, тригонометри-

(COU 99, 610, 1346, 1531, 1845) определены с

ческие параллаксы и фотометрические данные) не

учетом фотометрических сумм масс. Также мы про-

находятся в противоречии, величины (μ_BA, μ, S(p)el

извели уточнение пяти орбит (COU 66, 169, 773,

иS(p)lin) используются для доказательства того,что

1006, 1897), полученных ранее другими исследо-

пара физическая.

вателями, у COU 66 представлены две орбиты,

отличие этих орбит в том, что в одном случае

В каталоге Gaia EDR3 у нескольких изучаемых

фотометрическая сумма масс использовалась, в

пар (COU 66, 99, 169, 610, 850, 1845, 2459) име-

другом — не использовалась.

ются координаты обеих компонент на эпоху 2016,

аналогичные данные в каталоге Gaia DR2 на эпоху

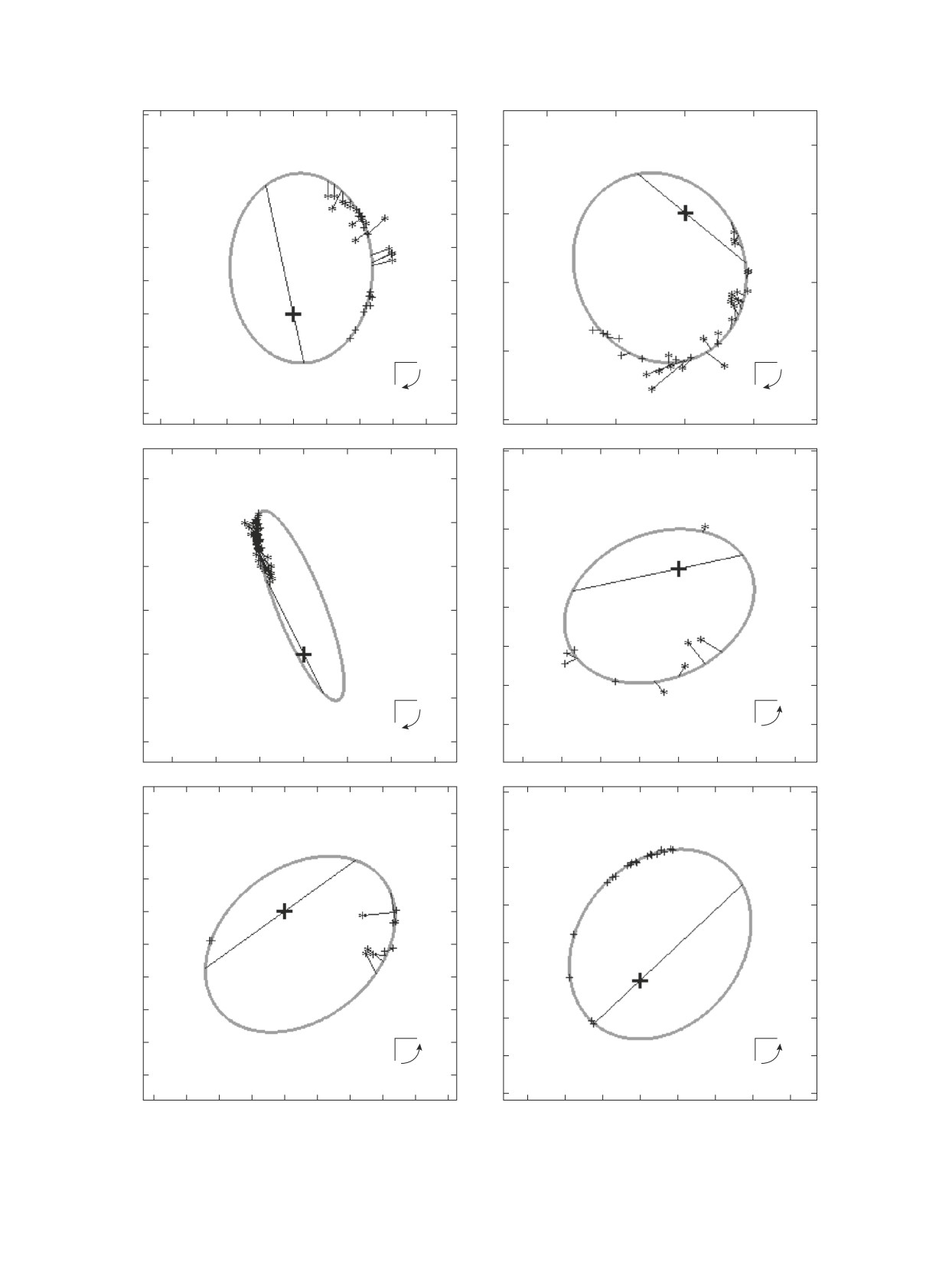
На рис. 1 изображены орбиты звезд COU 66,

2015.5 представлены у COU 169, 2459. У пере-

169, 610, 850, 1752 и 1897 в картинной плоскости.

численных звезд были вычислены относительные

Эти звезды, по нашему мнению, являются наиболее

координаты звезд-спутников, полученные наблю-

актуальными для исследования в ближайшие годы.

дения использовались для определения орбит.

У COU 66, 169, 850, 1752 и 1897 при наличии

современных точных наблюдений через два или три

Фотометрические данные раздельно для каж-

десятилетия можно определить надежные орби-

дой компоненты в каталоге Gaia EDR3 имеются у

ты, а COU 610 является довольно яркой звездой

следующих объектов: COU 66, 99, 169, 610, 850.

(видимая звездная величина примерно равна 4),

У остальных звезд имеется либо фотометрия глав-

ной компоненты (A), либо объединенная фотомет-

¹https://ui.adsabs.harvard.edu

рия пары (AB). Фотометрия AB использовалась

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 11

2021

788

КИССЕР, КРЕЧЕТ

Таблица 2. Вспомогательная информация об исследуемых парах

COU

WDS

N_int

N_vis

T₁

T_N

ρ,^′′

Δθ,^◦

15465 + 1957

1965.47

2018.2362

0.429

115.7

14432 + 2246

1966.32

2016.296

0.642

48.9

169

10140 + 2227

1967.24

2018.288

0.511

119.8

357

02250 + 2529

1968.99

2013.805

0.290

44.8

610

15329 + 3122

1971.523

2016.520

0.842

7.0

773

08539 + 1958

1972.16

2006.310

0.046

121.6

850

00360 + 3708

1972.97

2016.0

0.290

364.2

1006

18130 + 3318

1973.45

2009.4404

0.611

150.6

1346

23239 + 3456

1974.74

2009.7505

0.096

66.0

1531

05085 + 3755

1978.02

2010.8925

0.111

98.9

1642

22268 + 4033

1977.89

2011.858

0.178

38.6

1752

12017 + 4728

1980.09

2012.1000

0.184

273.3

1845

23267 + 4103

1978.73

2016.8712

0.991

12.4

1897

08585 + 3548

1984.0554

2015.1851

0.079

220.5

2459

04245 + 5051

1989.07

2016.0

1.117

43.8

Таблица 3. Вспомогательная информация об исследуемых парах

COU π_t, мсд MAB(d), M_⊙ MAB(ph), M_⊙ μ_BA, мсд/год μ, мсд/год

S(p)el,^′′

S(p)lin,^′′

25.7243

1.1

27.0

165.6

0.111

0.556

11.2753

1.45

9.3

64.5

0.085

0.095

169

12.83

5.3

1.5

117.7

0.075

357

5.7226

1.7

≈2

3.9

9.7

0.049

0.073

610

8.2139

7.8

5.3

23.8

0.105

0.182

773

4.7733

4.2

20.6

0.047

850

16.5902

2.0

1.3

90.5

0.062

1006

15.8418

2.1

1.6

24.9

126.2

0.068

0.117

1346

5.5825

2.8

4.1

36.5

0.051

0.055

1531

10.0395

2.15

8.1

40.3

0.080

0.117

1642

3.3171

2.2

≈4

2.6

9.3

0.063

0.069

1752

5.8047

6.0

2.2

10.5

78.7

0.081

0.505

1845

10.0066

2.6

8.5

36.8

0.160

0.172

1897

4.4505

4.4

4.9

9.9

0.048

2459

20.3228

1.8

1.9

24.3

65.4

0.108

0.115

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ

том 47

№ 11

2021

ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНЫХ ЗВЕЗД

789

для проверки данных других каталогов (сравнива-

2017) и наблюдениями Gaia (DR2 c эпохой 2015.5

лась светимость LbolAB, определенная по данным

и EDR3 с эпохой 2016).

Gaia, со светимостью LbolA + LbolB, определенной

2. Пары, вычисленные с учетом фотометриче-

по данным других каталогов).

ских сумм масс (COU 99, 610, 1346, 1531, 1845).

Для определения фотометрических и динамиче-

Для перечисленных пар при вычислении орбит

ских сумм масс использовались параллаксы ката-

без использования фотометрических сумм масс

лога Gaia EDR3. У двух звезд (COU 169 и COU

были получены плохие результаты. Фотометриче-

1642) параллакс в Gaia EDR3 отсутствует, парал-

ские и динамические суммы масс отличались зна-

лакс и собственное движение COU 169 взяты из

чительно, а вычисленные эксцентриситеты были

каталога Hipparcos (Ван Лейвен, 2007), параллакс

примерно равны верхнему граничному заданному в

и собственное движение COU 1642 — из каталога

ГА значению. В табл. 1 представлены элементы ор-

Gaia DR2.

бит этих пяти пар, определенные с использованием

Ниже мы даем комментарии по некоторым па-

значений фотометрических сумм масс. В табл. 3

рам, связанные с особенностями определения их

представлены величины, доказывающие в силу вы-

орбит.

полнения условий (10), что все пары являются

1. Пары, вычисленные без использования фото-

физическими.

метрических сумм масс (COU 357, 850, 1642, 1752,

Более подробно остановимся на звезде COU

2459).

610, так как она является достаточно яркой (ви-

COU 357. Наблюдениями покрыта дуга менее

димая звездная величина около 4) и видна нево-

40^◦. Последнее наблюдение выполнено Харшоу и

оруженным глазом. Наблюдениями охвачена ду-

др. (2016). Невязки (o - c)_ρ почти всех визуальных

га менее 10◦, но они покрывают значительную

наблюдений прошлого века положительны, поэто-

часть видимого эллипса (рис. 1). Невязки (o - c)_ρ

му окончательно орбита определялась без исполь-

всех визуальных наблюдений 70-х годов, кроме

зования разделений (ρ) визуальных наблюдений.

MLR 1971.56 (Контэль и др., 2001), отрицательные

(из-за этого часть наблюдений оказалась внутри

COU 850. С учетом последнего наблюдения

видимого эллипса, см. рис. 1). Окончательно ор-

Gaia EDR3 наблюдениями охвачен почти полный

бита определялась без использования разделений

оборот, но распределены они неравномерно. Очень

визуальных наблюдений. Эта пара интенсивно на-

важным для определения орбиты является наблю-

дение Куто 1992.564 (Куто и др., 1993), его неслож-

блюдалась Макалистером с 1976 по 1989 г. (в чет-

но найти на рис. 1, так как оно заметно отстоит от

вертом интерферометрическом каталоге представ-

лено 48 наблюдений). Последние наблюдения пары

остальных наблюдений.

выполнены Хорчем и др. (2020), Серо (2017) и

COU 1642. Наблюдениями охвачена дуга менее

Скардия и др. (2019). В каталоге Gaia EDR3 ко-

40^◦, но фотометрическая и динамическая суммы

ординаты звезды-спутника определены с заметной

масс (табл. 3) хорошо согласуются. Последние

погрешностью (∼0.03^′′), относительное положе-

наблюдения пары выполнены Герреро и др. (2018).

ние, вычисленное по координатам, плохо согласу-

COU 1752. Наблюдениями охвачена дуга более

ется с остальной совокупностью данных, поэтому

половины оборота, но распределены они неравно-

не использовалось в вычислениях.

мерно: имеются наблюдения с 1980 по 1993 г. на

3. Пары, у которых производилось уточнение

дуге 30^◦, два последних наблюдения Хорча и др.

орбит (COU 66, 169, 773, 1006, 1897).

(2017) отстоят от них более чем на половину оборо-

В табл. 4 мы описали причины, из-за которых

та. Невязки (o - c)_ρ всех визуальных наблюдений

решили уточнить орбиты из шестого каталога.

80-х годов отрицательные, поэтому окончатель-

но орбита определялась без использования раз-

У двух пар (COU 66 и 169) замечены несоот-

делений (ρ) визуальных наблюдений. Завышенное

ветствия между астрометрическими и фотометри-

значение динамической суммы масс в сравнении с

ческими данными, поэтому ниже даны пояснения.

фотометрической (см. табл. 3) можно объяснить

COU 66. В ходе первых пробных вычислений

наличием относительной погрешности параллакса

обнаружено, что невязки (o - c)_ρ всех визуальных

Gaia EDR3 порядка 30%. Стоит отметить, что со

наблюдений 60-х и 70-х годов отрицательны, по-

значением параллакса из каталога Gaia DR2 полу-

этому представлена орбита, вычисленная без ис-

чается динамическая сумма масс 3.6M_⊙, которая

пользования разделений визуальных наблюдений.

неплохо согласуется с фотометрической суммой

Значение динамической суммы масс получилось

масс.

заниженным (0.72M_⊙), погрешностью параллакса

COU 2459. Наблюдениями охвачена дуга менее

Gaia EDR3 ее не объяснить, так она дает σ_M ∼

40^◦, но дуга длиной 20^◦ довольно плотно покрыта

∼ 0.01M_⊙. Фотометрическая сумма масс опреде-

наблюдениями Хорча и др. (2002, 2008, 2010, 2012,

лена достаточно надежно, поэтому орбита была

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 11

2021

790

КИССЕР, КРЕЧЕТ

Таблица 4. Информация об орбитах, которые ранее были определены другими исследователями

COU

Авторы

Причины, по которым принято решение уточнить орбиту

66 Рика Ромеро (2013)

Последние наблюдения Хорча и др. (2017), Токовинина и др. (2019) и Gaia EDR3

имеют заметные невязки: (o - c)_ρ < -0.015^′′, (o - c)_θ ∈ (-3.5^◦; -0.8^◦).

169 Куто (1999)

Почти все наблюдения после 2000 г. имеют большие невязки: (o - c)_ρ > 0.015^′′,

(o - c)_θ < -2^◦.

773 Куто (1999)

Наблюдения после 2000 г. имеют большие невязки: (o - c)_ρ < -0.025^′′,

(o - c)_θ > 2^◦.

1006 Куто (1999)

Невязки спекл-интерферометрических наблюдений очень велики:

(o - c)_ρ > 0.2^′′, (o - c)_θ < -20^◦.

1897 Докобо, Тамазян (2013) У последних наблюдений Хорча и др. (2020) (o - c)_ρ > 0.015^′′. С учетом данных

Gaia EDR3 динамическая и фотометрическая суммы масс отличаются более чем

в три раза (MAB(d) = 17.5M_⊙, MAB(ph) = 4.9M_⊙).

также определена с учетом фотометрической сум-

Вычисление орбит выполнено модифицирован-

мы масс, именно она изображена на рис. 1.

ным методом Харткопфа и др., в котором вместо

подбора для определения P , T_p и e применяется

COU 169. Использовалась фотометрия Gaia

генетический алгоритм (ГА). Основное преимуще-

EDR3. Спектр пары K5 (Мэйсон и др., 2001), а аб-

солютная звездная величина M_v обеих компонент

ство метода подбора и ГА связано с отсутствием

примерно как у звезд K0. Значение динамической

проблем со сходимостью. Генетический алгоритм в

суммы масс получилось завышенным (табл. 3).

сравнении с методом подбора значительно умень-

Возможно, все перечисленное связано с занижен-

шает время, затрачиваемое на определение орбиты.

Кроме того, появляется возможность использова-

ным значением параллакса в каталоге Hipparcos

ния некоторых особенностей ГА для повышения

(Ван Лейвен, 2007). Фотометрические данные Gaia

точности получаемых результатов, это в первую

EDR3 компонент пары, спектральный класс K5

очередь актуально при работе с наблюдениями,

и динамическая и фотометрическая суммы масс

покрывающими малые дуги или неравномерно рас-

хорошо согласуются при параллаксе около 20 мсд.

пределенными на дуге. У таких пар имеется множе-

ство орбит, одинаково хорошо удовлетворяющих

ЗАКЛЮЧЕНИЕ

накопленным к настоящему времени данным. ГА, в

силу его стахостической природы, как раз позволя-

В работе определены орбиты пятнадцати визуально-

ет вычислить не одну, а множество орбит.

двойных звезд, открытых П. Куто. У десяти из

Далее, имея большую совокупность орбит,

них орбиты вычислены впервые, для пяти было

можно вычислить средние значения орбитальных

произведено уточнение орбит. Представленные

элементов и выбрать орбиту, которая наилучшим

результаты являются предварительными. Надеж-

образом им соответствует. Здесь, как и в любых ис-

ные орбиты в ближайшее время при наличии

следованиях, справедливо то, что средние значения

современных точных наблюдений относительных

оказываются точнее отдельно взятого результата

положений можно получить для COU 66, 169, 850,

(ранее, работая с отдельными двойными звездами,

1752 и 1897.

мы доказали справедливость этого утверждения

Орбиты COU 850 и 1752 были определены

для элементов орбит).

впервые, у первой из них наблюдениями покрыт

В генетическом алгоритме можно изменить

целый оборот, у второй — более половины оборота,

условие отбора решений в новую популяцию с

но в обоих случаях наблюдения распределены на

учетом дополнительных данных. В представленном

дуге очень неравномерно. Орбиты COU 66, 169 и

методе определения орбит в качестве дополни-

1897 были уточнены, актуальность этих пар связа-

тельных данных выступают относительные лучевые

на с двумя причинами: 1) COU 169 и 1897 имеют

скорости и фотометрические суммы масс. Условие

периоды обращения менее 100 лет; 2) COU 66 и

отбора изменяется таким образом, что орбиты,

1897 проходят в настоящий момент участки на ви-

у которых вычисленные относительные лучевые

димой орбите с наиболее быстрым относительным

скорости и динамические суммы масс лучше со-

движением.

гласуются с дополнительными данными, получают

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 11

2021

ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНЫХ ЗВЕЗД

791

преимущество по сравнению с другими орбитами.

10.

Герреро и др. (C.A. Guerrero, V.G. Orlov, M. Borges

В статье орбиты COU 66, 99, 610, 1346, 1531, 1845

Fernandes, and F. Angeles), MNRAS 475, 1725

определены с учетом фотометрических сумм масс.

(2018).

На примере COU 66 показано, что использование

11.

Докобо, Тамазян (J.A. Docobo and V. Tamazian), Inf.

Circ. 179, 1 (2013).

фотометрической суммы масс может быть полезно

даже при определении орбиты достаточно хорошо

12.

Жирарди и др. (L. Girardi, A. Bressan, G. Bertelli,

and C. Chiosi), Astron. Astrophys. Suppl. Ser. 141,

изученной визуально-двойной звезды.

371 (2000).

Представленный метод определения орбит поз-

13.

Измайлов И.С., Письма в Астрон. журн. 45, 35

воляет работать с неполными данными. Это акту-

(2019) [I.S. Izmailov, Astron. Lett. 45, 30 (2019)].

ально, если для некоторых эпох имеются наблю-

14.

Киселев А.А., Кияева О.В., Астрон. журн. 57, 1227

дения только позиционных углов, или обнаружено,

(1980) [A.A. Kiselev and O.V. Kiyaeva, Sov. Astron.

что невязки (o - c)_ρ всех разделений, измеренных

24, 708 (1980)].

визуально, оказываются положительными либо от-

15.

Киселев А.А., Теоретические основания фото-

рицательными. Последнее говорит о наличии си-

графической астрометрии (М: Наука, 1989).

стематических ошибок наблюдений (в статье по-

16.

Кияева О.В., Киселев А.А., Поляков Е.В., Рафаль-

добная особенность обнаружена у COU 66, 357,

ский В.Б., Письма в Астрон. журн. 27, 456 (2001)

610, 1752). В этом случае алгоритм метода незна-

[O.V. Kiyaeva et al., Astron. Lett. 27, 391 (2001)].

чительно преобразуется: элементы Тиле-Иннеса

17.

Кияева О.В., Романенко Л.Г., Калиниченко О.А.,

(A, B, F , G) определяются без учета визуальных

Изв. ГАО в Пулкове 225, 231 (2018).

наблюдений, позиционные углы, измеренные визу-

18.

Кияева О.В., Жучков Р.Я., Измайлов И.С., Аст-

ально, используются только при выборе решений в

рофиз. бюлл. 75, 478 (2020) [O.V. Kiyaeva, et al.,

новую популяцию.

Astrophys. Bull. 75, 425 (2020)].

Работа поддержана Министерством высшего

19.

Кияева О.В., Романенко Л.Г., Письма в Аст-

рон. журн.

46,

590

(2020)

[O.V. Kiyaeva and

образования и науки РФ, грант № 0707-2020-

L.G. Romanenko, Astron. Lett. 46, 555 (2020)].

0025. Авторы благодарят наблюдателей двойных

20.

Колавита и др. (M.M. Colavita, J.K. Wallace,

звезд, данные которых использовались в работе.

B.E. Hines, Y. Gursel, F. Malbet, D.L. Palmer,

Выбор звезд, наиболее удобных для исследования,

X.P. Pan, M. Shao, et al.), Astrophys. J. 510, 505

был осуществлен благодаря данным сайта обсер-

(1999).

ватории в Ницце. Авторы благодарят создателей

21.

Контэль и др. (D.Le Contel, J.-C. Valtier, and

этого сайта.

D. Bonneau), Astron. Astrophys. 377, 496 (2001),

https://sidonie.oca.eu/Sidonie/Default.htm.

СПИСОК ЛИТЕРАТУРЫ

22.

Куто П., Наблюдения визуально-двойных звезд

1. Байдин А.Э., Вестник ЮУрГУ. Сер. Математика.

(М.: Мир, 1981) [Couteau P., LТobservation des

Механика. Физика. 7 (1), 11 (2015).

etoiles doubles visuelles (Flammarion, Paris, 1978)].

2. Байдин А.Э., Перов Н.И., Романенко Л.Г., Вестник

23.

Куто и др. (P. Couteau, J.A. Docobo, and J. Ling),

СПбУ. Математика. Механика. Астрономия. 5 (1),

Astron. Astrophys. Suppl. Ser. 100, 305 (1993).

154 (2018).

24.

Куто (P. Couteau), Catalogue of

2700

double

3. Байдин А.Э., Дис. канд. физ.-мат. наук (ЯГПУ им.

stars (Observatoire de la C ˆote d’Azur, Nice,

К.Д. Ушинского, Ярославль, 2018).

1995), http://vizier.u-strasbg.fr/viz-bin/VizieR?-

4. Байдин А.Э., Кречет В.Г., Астрофиз. бюлл. 76, 100

source=I/209A.

(2021) [A.E. Baidin and V.G. Krechet, Astrophys.

25.

Куто (P. Couteau), Catalogue de

2700

Etoiles

Bull. 76, 84 (2021)].

Doubles COU (Observatoire de la C ˆote d’Azur, 3rd

5. Браун и др. (A.G.A. Brown, A. Vallenari, T. Prusti,

ed., Nice, 1999).

J.H.J. de Bruijne, C. Babusiaux, C.A.L. Bailer-Jones,

26.

Мэйсон и др. (B.D. Mason, G.L. Wycoff,

M. Biermann, D.W. Evans, et al.), Astron. Astrophys.

W.I. Hartkopf, G.G. Douglass, and Ch.E. Worley),

616, A1 (2018).

Astron. J. 122, 3466 (2001).

6. Браун и др. (A.G.A. Brown, A. Vallenari, T. Prusti,

27.

Риелло и др. (M. Riello, F. De Angeli, D.W. Evans,

J.H.J. de Bruijne, C. Babusiaux, M. Biermann,

P. Montegriffo, J.M. Carrasco, G. Busso,

O.L. Creevey, D.W. Evans, et al.), Astron. Astrophys.

L. Palaversa, P.W. Burgess, et al.), Astron. Astrophys.

649, A1 (2021).

649, A3 (2021).

7. Буссо и др. (G. Busso, C. Cacciari, J.M. Carrasco,

et al.), Gaia DR2 documentation release

1.2,

28.

Рика Ромеро (F.M. Rica Romero), Inf. Circ. 181, 1

Chapter 5: Photometry (ESA and DPAC, 2019).

(2013).

8. Быков О.П., Холшевников К.В., Прямые методы

29.

Серо (J. S ´erot), J. Double Star Observ. 13, 268

определения орбит небесных тел (СПб: Изд.

(2017).

Санкт-Петербургского университета, 2013).

30.

Скардия и др. (M. Scardia, J.-P. Rivet, J.-L. Prieur,

9. Ван Лейвен (F.Van Leeuwen), Astron. Astrophys.

L. Pansecchi, R.W. Argyle, J.F. Ling, E. Aristidi,

474, 653 (2007).

A. Zanutta, et al.), Astron. Nachr. 340, 771 (2019).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 11

2021

792

КИССЕР, КРЕЧЕТ

31. Токовинин А.А., Астрон. журн. 71, 293 (1994)

42. Харткопф, Мэйсон (W.I. Hartkopf and B.D. Mason),

[A.A. Tokovinin, Astron. Rep. 38, 258 (1994)].

Sixth Catalog of Orbits of Visual Binary Stars

32. Токовинин А.А., Письма в Астрон. журн. 24, 217

(US Naval Observatory, Washington,

2021),

(1998) [A.A. Tokovinin, Astron. Lett. 24, 178 (1998)].

http://www.astro.gsu.edu/wds/orb6.html.

33. Токовинин, Кияева (A.A. Tokovinin and

43. Хорч и др. (E.P. Horch, S.E. Robinson, R. Meyer,

O.V. Kiyaeva), MNRAS 456, 2070 (2016).

W.F. van Altena, Z. Ninkov, and A. Piterman), Astron.

34. Токовинин и др. (A.A. Tokovinin, B.D. Mason,

J. 123, 3442 (2002).

R.A. Mendez, E.P. Horch, and C. Briceno), Astron. J.

44. Хорч и др. (E.P. Horch, W.F. van Altena, W.M. Cyr,

158, 48 (2019).

Jr., L. Kinsman-Smith, A. Srivastava, and J. Zhou),

35. Токовинин (A.A. Tokovinin), MNRAS 496,

987

Astron. J. 136, 312 (2008).

(2020).

45. Хорч и др. (E.P. Horch, D. Falta, L.M. Anderson,

36. Фабрициус, Макаров (C. Fabricius and

M.D. DeSousa, C.M. Miniter, T. Ahmed, and

V.V. Makarov), Astron. Astrophys. 356, 141 (2000).

W.F. van Altena), Astron. J. 139, 205 (2010).

37. Фабрициус и др. (C. Fabricius,E. Hog, V.V. Makarov,

46. Хорч и др. (E.P. Horch, L.A.P. Bahi, J.R. Gaulin,

B.D. Mason, G.L. Wycoff, and S.E. Urban), Astron.

S.B. Howell, W.H. Sherry, R. Baena Galle, and

Astrophys. 384, 180 (2002).

W.F. van Altena), Astron. J. 143, 10 (2012).

38. Харшоу и др. (R. Harshaw, R. Genet, J. Hass, and

47. Хорч и др. (E.P. Horch, D.I. Casetti-Dinescu,

K. Phung), J. Double Star Observ. 12, 238 (2016).

M.A. Camarata, A. Bidarian, W.F. van Altena,

39. Харткопф и др. (W.I. Hartkopf, H.A. McAlister, and

W.H. Sherry, M.E. Everett, A.B. Howell, et al.),

O.G. Franz), Astron. J. 98, 1014 (1989).

Astron. J. 153, 212 (2017).

40. Харткопф и др. (W.I. Hartkopf, B.D. Mason,

48. Хорч и др. (E.P. Horch, G.T. van Belle,

G.L. Wykoff, and D. Kang), Catalog of Rectilinear

J.W. Davidson, Jr., D. Willmarth, F.C. Fekel,

Elements of Visual Double Stars (USNO Double

M. Muterspaugh, D.I. Casetti-Dinescu, F.W. Hahne,

Star CD 2006.5).

et al.), Astron. J. 159, 233 (2020).

41. Харткопф и др. (W.I. Hartkopf, B.D. Mason,

49. ESA, The Hipparcos and Tycho Catalogues.

G.L. Wycoff, and H.A. McAlister), Fourth Catalog

Astrometric and photometric star catalogues

of Interferometric Measurements of Binary

derived from the ESA Hipparcos Space Astrometry

Stars (US Naval Observatory, Washington, 2020),

Mission (ESA Publ. Division, Noordwijk,

1997)

http://www.astro.gsu.edu/wds/int4.html.

(ESA SP Ser., No. 1200).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 11

2021