ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2021, том 47, № 12, с. 900-908

КИНЕМАТИЧЕСКИЕ СВОЙСТВА КАТАЛОГА Gaia EDR3

¹Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

Поступила в редакцию 22.08.2021 г.

После доработки 16.11.2021 г.; принята к публикации 04.12.2021 г.

Проведено решение звездно-кинематических уравнений Огородникова-Милна на материале всего

звездного каталога Gaia EDR3, содержащего 1.8 млрд объектов. В силу недостаточной точности

индивидуальных тригонометрических параллаксов произведено аналогичное решение на подкаталоге

избранных 98 млн звезд, для которых параллакс известен с точностью лучше 10%. Проведен

подробный анализ результатов этих решений в зависимости от звездной величины и расстояний до

звезд.

Ключевые слова: Gaia, астрометрия, космическая астрометрия, звездная кинематика, структура

Галактики.

DOI: 10.31857/S0320010821120056

ВВЕДЕНИЕ

лов, объемом около 200 Мбайт каждый. При рас-

паковке объем файла возрастает примерно в два

Космический аппарат Gaia продолжает свою

раза и составляет 400-450 Мбайт. Таким обра-

работу на орбите, финальный каталог планируется

зом, полный объем скачиваемых данных состав-

к выпуску в первой половине

2022

г. (ESA,

ляет около 670 Гбайт, а распакованные данные

Gaia). Уже были выпущены предварительные

требуют хранилища объемом уже около 1.5 Тбайт.

каталоги Data Release: DR1 и DR2. 3 декабря

Формат файлов — CSV — текстовый, поля записи

2020 г. вышел в свет Gaia Early Data Release 3

каждой звезды разделены запятыми. Если какие-

(Gaia EDR3) — “ранний релиз финального ката-

либо данные отсутствуют (а это часто бывает),

лога” (Gaia, EDR3). Методика его построения и

две запятые идут подряд. Такой формат исходных

детали подробно изложены в (Gaia Collaboration,

данных легко поддерживается языком FORTRAN

2021). Этим данным посвящено такое количество

(Бартеньев, 2000).

работ, что даже кратко привести только их назва-

ния не представляется возможным.

Каждая строка содержит информацию о 99 по-

Качество

индивидуальных

параллаксов

лях для одной звезды. Подробное описание каж-

в Gaia EDR3 еще весьма далеко от прогнози-

дого поля приведено в (Gaia, Chapter 13). Поля

можно разделить по следующим категориям:

руемого (об этом ниже), поэтому мы провели

серию стандартных исследований, которые уже

применялись (Витязев и др., 2017) к массовым

• идентификаторы;

каталогам звезд, таким как NOMAD (Захариас

и др., 2004), содержащим

1.1

млрд. объектов,

• астрометрические параметры: координаты,

или PPMXL (Рёзер и др., 2010) — 910 млн звезд.

собственные движения, параллакс и их

Эти исследования включают в себя получение

ошибки;

различных статистических сведений, стандартный

звездно-кинематический анализ и анализ с по-

• корреляции между параметрами;

мощью сферических функций (Витязев, Цветков,

2014).

• число и качество астрометрических наблю-

дений (самая большая группа);

ОРГАНИЗАЦИЯ КАТАЛОГА

• фотометрия в трех полосах;

Исходные данные каталога EDR3 доступны на

официальном сайте Gaia в виде 3386 сжатых фай-

• лучевые скорости (из DR2);

^*Электронный адрес: a.s.tsvetkov@inbox.ru

• галактические и эклиптические координаты.

900

КИНЕМАТИЧЕСКИЕ СВОЙСТВА

901

ТОЧНОСТЬ ПАРАЛЛАКСОВ

ближнего ультрафиолета до красного цвета, “крас-

ная” G_RP — от красного до инфракрасного диа-

Самый важный планируемый результат Gaia —

пазона. От шкалы UBV эту систему отличают

высокоточные индивидуальные параллаксы звезд.

не только другие границы диапазонов полос, но и

В настоящее время заявленная точность (0.01 мсд)

их ширина. Связь фотометрической шкалы Gaia c

для большинства звезд еще не достигнута (Браун

другими фотометрическими системами будет уста-

и др., 2021). Данные о параллаксе в EDR3 имеют

новлена позднее (Риелло и др., 2021).

1 467744 818 звезд, в то время как 343 964 953 звезд

Звездная величина G имеется практически у

этих данных не имеют. Анализ параллаксов пока-

всех звезд (отсутствует только у 5 млн), в то время

зал, что существует большая доля звезд, у которых

как фотометрия G_BP и G_BP присутствует у чуть

ошибки составляют десятые доли мсд и выше. Точ-

более, чем 1.5 млрд звезд (отсутствует у 270 млн

ность лучше 0.2 мсд имеют только 500 млн звезд,

звезд).

т.е. примерно треть звезд, имеющих данные о па-

В каталоге приведены измеренные потоки фото-

раллаксах. Это приводит к тому, что лишь 520 млн

нов в трех полосах и их ошибки, а ошибок самих

имеют относительную погрешность параллакса

звездных величин нет, так как “звездные величины

лучше 50%, а лучше 10% — только 98 млн, 283 млн

связаны нелинейным образом с измеренным пото-

звезд имеют вообще отрицательный параллакс (что

ком” (Gaia, Chapter 13).

противоречит геометрическому смыслу параллак-

са). При этом, как показывает более детальный

анализ, совершенно необязательно, чтобы у этих

КИНЕМАТИЧЕСКИЙ АНАЛИЗ

параллаксов были большие среднеквадратичные

СОБСТВЕННЫХ ДВИЖЕНИЙ ЗВЕЗД

ошибки. Этот факт демонстрирует, что работа над

ПОЛНОГО КАТАЛОГА

параллаксами Gaia требует значительной работы и

БЕЗ ИСПОЛЬЗОВАНИЯ

установления точного нуль-пункта параллаксов.

ИНДИВИДУАЛЬНЫХ РАССТОЯНИЙ

Таким образом, индивидуальные параллаксы

В каталоге Gaia приводятся только экватори-

следует использовать с большой осторожностью,

альные собственные движения звезд μ_α cos δ и μ_δ.

хотя статистически для больших групп звезд усред-

Не составляет никакого труда перевести их в га-

ненные параллаксы дают довольно надежные ре-

лактические μ_l cos b и μ_b, которые будут использо-

зультаты.

ваться в наших исследованиях.

В качестве основной модели мы используем

широко известную модель Огородникова-Милна

ТОЧНОСТЬ СОБСТВЕННЫХ ДВИЖЕНИЙ

(Огородников, 1965), подробный вид уравнений

Данные о собственных движениях имеют все

этой модели изложен также в (дю Монт, 1977) и

без исключения 1 811 709 771 звезд. Приведенные

(Рыбка, 2004). В этой модели поле скоростей звезд

в каталоге точности в случайном отношении тоже

представляется линейным выражением

еще не достигли проектируемых. Лишь 213 млн

V = V₀ + Ω × r + M⁺ × r,

(1)

звезд имеют полную точность собственного дви-

жения лучше 0.1 мсд/год, а 406 млн — лучше

где V — скорость звезды, V₀ — влияние посту-

пательного движения Солнца, Ω — угловая ско-

0.2 мсд/год. Однако относительная точность соб-

рость твердотельного вращения звездной систе-

ственных движений значительно лучше, чем у па-

раллаксов, в силу того, что сами собственные дви-

мы, M⁺ — симметричный тензор деформации поля

скоростей.

жения больше параллактических смещений. Пол-

Модель содержит всего 12 параметров, однако

ное собственное движение 77% звезд заключено в

не все они могут быть независимо определены из

интервале от 2 до 8 мсд/год, а 93% — в интервале

собственных движений, и не все параметры входят

от 0 до 10 мсд/год. Таким образом, почти полови-

в уравнения для лучевых скоростей:

на звезд каталога имеет относительную точность

[U, V, W ] — компоненты вектора V₀ поступа-

собственных движений лучше 10%. Такая высо-

тельного движения Солнца среди звезд;

кая точность позволяет проводить любые звездно-

кинематические исследования, базирующиеся на

[ω₁, ω₂, ω₃] — компоненты вектора угловой ско-

анализе собственных движений звезд.

рости Ω;

[M⁺¹¹, M⁺²², M⁺³³] — параметры тензора дефор-

мации, описывающие сжатие-растяжение вдоль

ФОТОМЕТРИЧЕСКИЕ ДАННЫЕ

главных осей галактической системы координат;

Gaia использует свою собственную фотомет-

[M⁺¹², M⁺¹³, M⁺²³] — параметры тензора M⁺,

рическую систему (Монтегриффо и др.,

2020).

описывающие деформацию поля скоростей в

“Синяя” компонента G_BP охватывает область от

основной и двух перпендикулярных плоскостях.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 12

2021

902

ЦВЕТКОВ

Таблица 1. Значения компонент скорости движения Солнца и угловой скорости твердотельного вращения в

км/с/кпк, полученные из совместного решения для звезд различных величин G

U/〈r〉

V/〈r〉

W/〈r〉

ω₁

ω₂

ω₃

158.1 ± 44.5

294.2 ± 45.4

159.4 ± 42.5

45.6 ± 45.2

19.4 ± 45.7

-26.4 ± 42.3

184.9 ± 31.3

209.2 ± 32.0

128.1 ± 29.3

-59.5 ± 32.2

25.8 ± 32.6

3.6 ± 29.3

116.5 ± 10.6

181.0 ± 10.7

71.5 ± 9.9

-13.1 ± 10.8

13.2 ± 10.9

-21.1 ± 9.8

75.0 ± 4.9

132.3 ± 5.0

50.7 ± 4.5

6.1 ± 5.0

8.2 ± 5.1

-15.6 ± 4.5

59.6 ± 1.9

111.2 ± 1.9

38.4 ± 1.8

1.9 ± 1.9

-7.5 ± 2.0

-12.2 ± 1.8

44.8 ± 1.0

91.3 ± 1.0

30.4 ± 1.0

0.6 ± 1.0

-4.9 ± 1.0

-11.4 ± 1.0

35.0 ± 0.6

77.7 ± 0.6

25.2 ± 0.6

1.5 ± 0.6

-4.4 ± 0.6

-10.7 ± 0.6

30.1 ± 0.3

67.1 ± 0.3

19.5 ± 0.3

0.6 ± 0.3

-2.8 ± 0.3

-11.6 ± 0.3

24.9 ± 0.2

58.8 ± 0.2

15.9 ± 0.2

0.8 ± 0.2

-2.4 ± 0.2

-11.8 ± 0.2

20.6 ± 0.1

51.6 ± 0.1

13.1 ± 0.1

0.2 ± 0.1

-2.0 ± 0.1

-11.9 ± 0.1

17.3 ± 0.1

46.3 ± 0.1

10.7 ± 0.1

0.3 ± 0.1

-1.1 ± 0.1

-12.4 ± 0.1

14.9 ± 0.1

42.5 ± 0.1

8.8 ± 0.1

0.4 ± 0.1

-0.9 ± 0.1

-12.8 ± 0.1

12.7 ± 0.1

39.8 ± 0.1

7.3 ± 0.1

0.5 ± 0.1

-0.7 ± 0.1

-12.9 ± 0.1

10.9 ± 0.1

38.1 ± 0.1

6.3 ± 0.1

0.6 ± 0.1

-0.7 ± 0.1

-12.6 ± 0.1

9.63 ± 0.05

36.95 ± 0.05

5.51 ± 0.05

0.62 ± 0.05

-0.70 ± 0.05

-12.29 ± 0.05

8.37 ± 0.04

35.48 ± 0.04

4.92 ± 0.04

0.38 ± 0.04

-0.57 ± 0.04

-12.08 ± 0.04

7.15 ± 0.04

33.19 ± 0.04

4.36 ± 0.04

0.25 ± 0.04

-0.46 ± 0.04

-11.93 ± 0.04

6.48 ± 0.03

31.69 ± 0.03

4.15 ± 0.03

0.33 ± 0.03

-0.51 ± 0.03

-11.80 ± 0.03

Таблица 2. Значения компонент тензора деформации в км/с/кпк, полученные из совместного решения для звезд

различных величин G

M⁺¹²

M⁺¹³

M⁺²³

M∗11

-36.1 ± 55.2

18.3 ± 58.1

-126.9 ± 57.1

192.9 ± 110.8

1.1 ± 103.8

-1.8 ± 37.8

4.1 ± 41.5

28.3 ± 39.6

-127.3 ± 78.5

37.2 ± 74.8

15.1 ± 13.0

9.3 ± 13.7

2.1 ± 13.5

6.9 ± 25.9

-39.9 ± 25.1

25.2 ± 6.0

17.1 ± 6.4

-5.0 ± 6.3

1.3 ± 11.9

8.9 ± 11.6

14.6 ± 2.3

-3.3 ± 2.5

-3.4 ± 2.4

2.8 ± 4.6

-7.0 ± 4.4

15.2 ± 1.3

-2.3 ± 1.3

-2.9 ± 1.3

-3.0 ± 2.5

-2.1 ± 2.3

15.6 ± 0.8

-1.9 ± 0.8

-1.2 ± 1.6

1.6 ± 1.4

17.1 ± 0.4

-0.9 ± 0.4

-1.1 ± 0.4

-0.3 ± 0.9

-0.7 ± 0.7

15.9 ± 0.2

-0.5 ± 0.2

-1.3 ± 0.2

-1.3 ± 0.5

1.3 ± 0.4

15.2 ± 0.2

-0.5 ± 0.2

-0.4 ± 0.2

-1.2 ± 0.3

0.6 ± 0.3

14.3 ± 0.1

-0.1 ± 0.1

-1.4 ± 0.2

1.4 ± 0.2

13.3 ± 0.1

-0.3 ± 0.1

-1.1 ± 0.2

1.0 ± 0.1

12.7 ± 0.1

-0.4 ± 0.1

-0.9 ± 0.1

0.9 ± 0.1

12.1 ± 0.1

-0.3 ± 0.1

-0.5 ± 0.1

-0.3 ± 0.1

0.5 ± 0.1

11.4 ± 0.1

-0.1 ± 0.1

-0.4 ± 0.1

0.1 ± 0.1

0.3 ± 0.1

10.2 ± 0.1

0.1 ± 0.1

-0.1 ± 0.1

0.4 ± 0.1

9.12 ± 0.05

0.18 ± 0.05

-0.02 ± 0.05

0.5 ± 0.1

0.6 ± 0.1

8.64 ± 0.04

0.12 ± 0.04

-0.15 ± 0.04

0.4 ± 0.1

0.6 ± 0.1

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 12

2021

КИНЕМАТИЧЕСКИЕ СВОЙСТВА

903

Зависимость кинематических параметров U, V, W от звездной величины

140

120

100

G mag

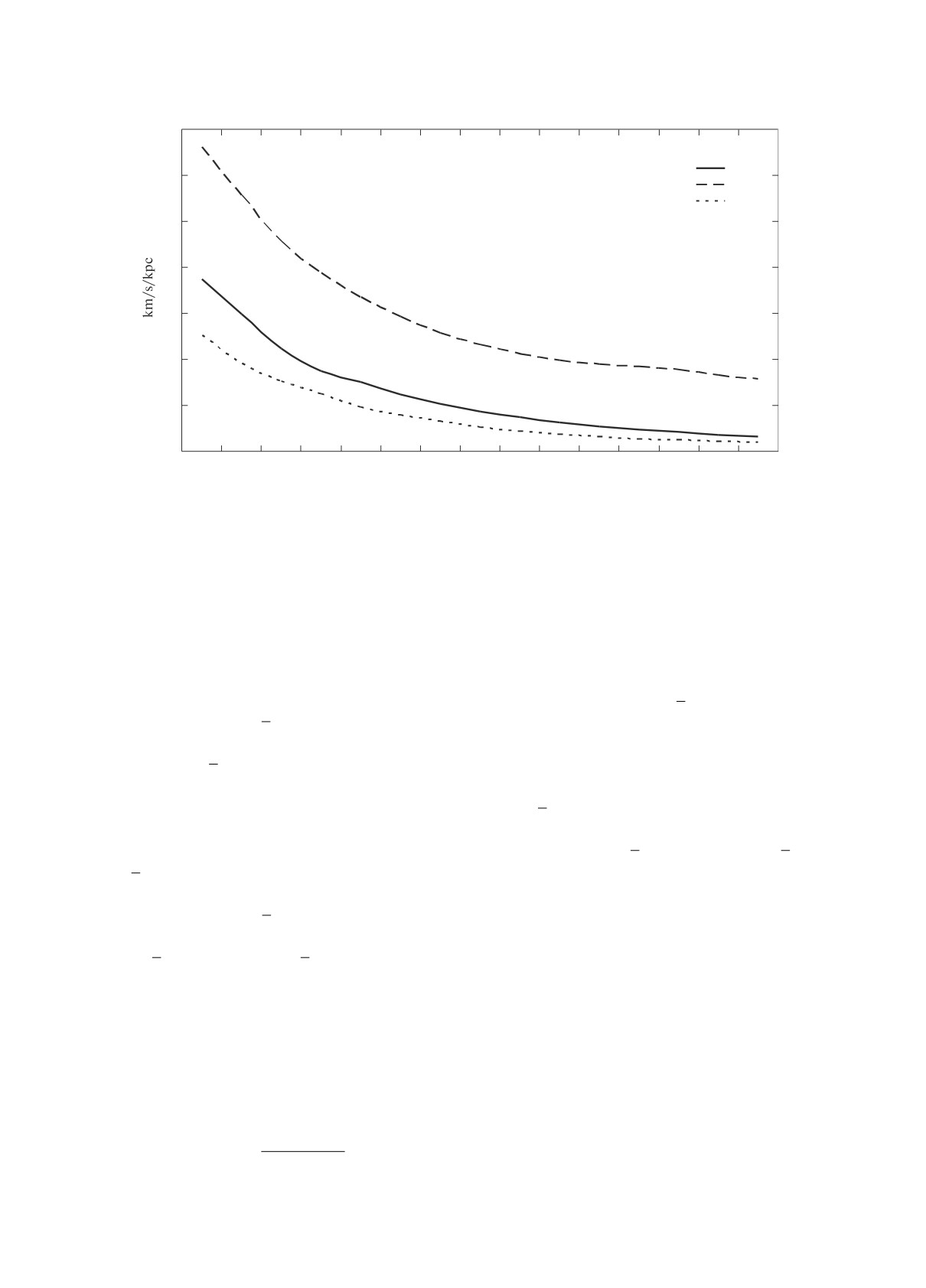
Рис. 1. Зависимость кинематических параметров движения Солнца U/〈r〉, V/〈r〉, W/〈r〉 от звездной величины

(км/с/кпк).

Спроецировав уравнение (1) на орты галакти-

В этом случае уравнения (2) и (3) переписыва-

ческой системы координат, имеем для собственных

ются в виде

движений:

kμ_l cosb = U/r sin l - V/r cos l -

(5)

kμ_l cosb = U/r sin l - V/r cos l -

(2)

− ω1 sinbcosl - ω2 sinbsinl + ω3 cosb +

+ M+12 cosbcos2l - M+13 sinbsinl +

+ M+23 sinbcosl -

M∗11 cosbsin 2l,

+ M+23 sinbcosl -

M⁺¹¹ cos bsin 2l +

kμ_b = U/r sinbcos l + V/r sinb sinl -

(6)

M⁺²² cos bsin2l,

- W/r cos b + ω₁ sinl - ω₂ cosl -

kμ_b = U/r sinbcos l + V/r sin b sinl -

(3)

sin 2b sin 2l + M⁺¹³ cos 2b cos l +

^-2

- W/r cos b + ω₁ sinl - ω₂ cosl -

+ M+23 cos2bsinl -

M∗11 sin 2bcos² l +

X sin 2b.

M⁺¹² sin 2bsin 2l + M⁺¹³ cos 2bcos l +

Уравнения (5)-(6) часто используют для сов-

+ M+23 cos2bsinl -

M⁺¹¹ sin2bcos² l -

местного решения по полным собственным дви-

жениям какого-либо каталога. При этом если не

известно расстояние до звезд или известно недо-

−

M⁺²² sin 2bsin² l +

M⁺³³ sin 2b.

статочно точно, то вместо величин U, V , W опре-

деляют U/〈r〉, V/〈r〉, W/〈r〉, где 〈r〉 — среднее рас-

В формулах (2) и (3) имеется линейная зависи-

стояние выборки звезд, для которой производят

мость между коэффициентами M⁺¹¹, M⁺²², M⁺³³, по-

решение.

этому авторы при анализе собственных движений

В табл. 1 и 2 приведено совместное решение

обычно вводят замены M∗11 = M⁺¹¹ - M⁺²² и M∗33 =

для звезд Gaia EDR3, а графики на рис. 1-3

иллюстрируют данные таблиц.

= M⁺³³ - M⁺²² (дю Монт, 1977) либо (Витязев и др.,

2018) вместо M∗33 вводят величину

Анализ этих результатов показывает, что сол-

нечные члены U/〈r〉, V/〈r〉, W/〈r〉, как и следо-

M⁺¹¹ + M⁺

вало ожидать, убывают с ростом звездной вели-

X =M⁺³³ -

(4)

чины, так как имеется полная корреляция между

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 12

2021

904

ЦВЕТКОВ

Зависимость компонент угловой скорости от звездной величины

10.0

5.0

10.0

15.0

G mag

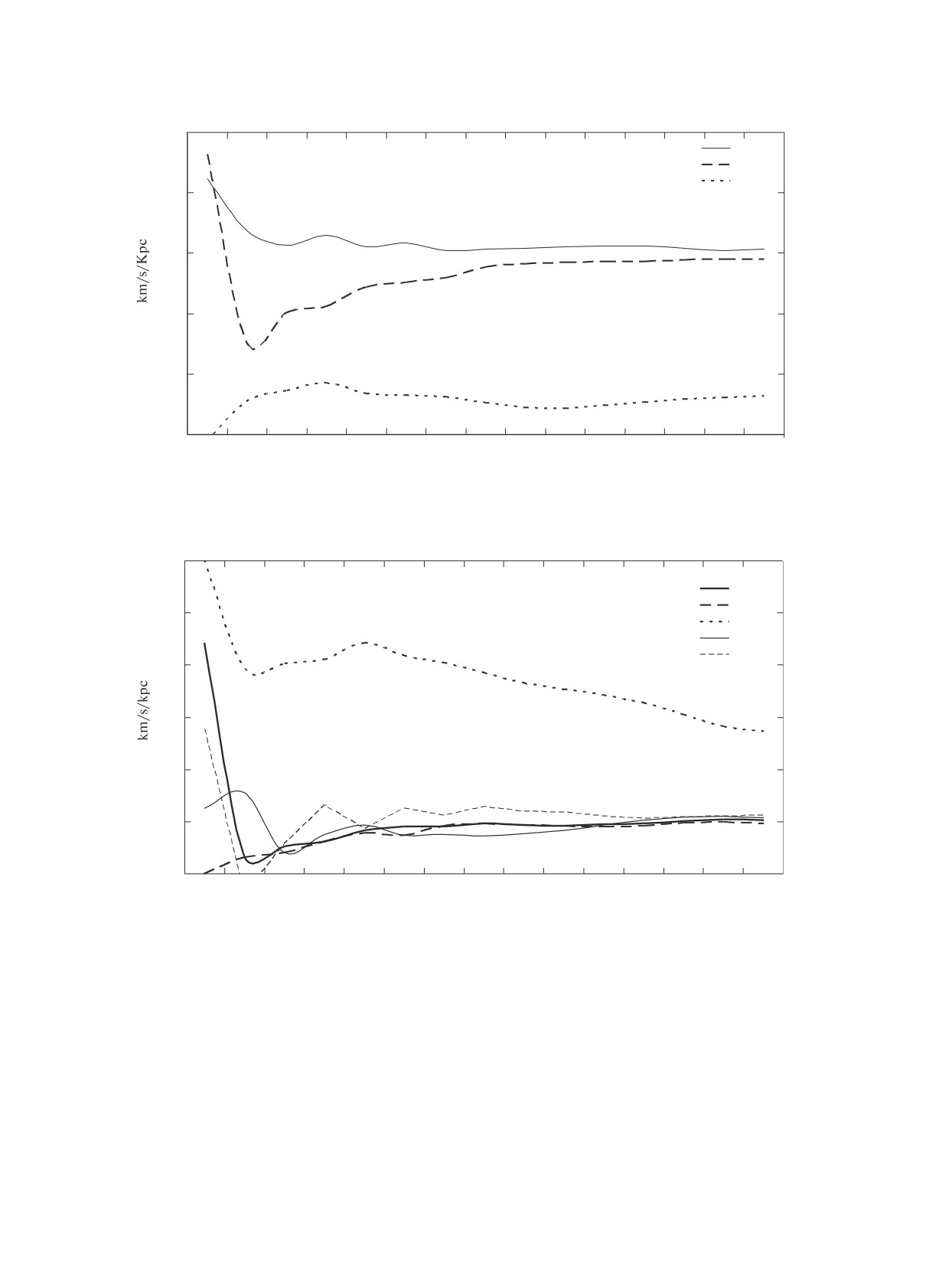
Рис. 2. Зависимость угловой скорости твердотельного вращения ω1, ω2, ω3 от звездной величины (км/с/кпк).

Зависимость компонент тензора деформации от звездной величины

25.0

M13

M23

20.0

M12

M11

15.0

10.0

5.0

G mag

Рис. 3. Зависимость компонент тензора деформации M⁺¹², M⁺¹³, M⁺²³, M⁺¹¹, X от звездной величины (км/с/кпк).

блеском звезды и расстоянием. Самая большая

обращали внимание исследователи еще с 1950-х

годов (Шацова, 1950).

компонента — по оси Y — V/〈r〉. Для ярких звезд

Рассматривая такой важный параметр, как уг-

3, 4, 5, 6 величин эти параметры определяются

ловая скорость твердотельного вращения системы

ненадежно, это справедливо и для всех остальных

ω₁, ω₂, ω₃, мы видим также, что для самых ярких

параметров. Причина этого не только небольшое

звезд параметры вектора угловой скорости вообще

не определяются, а начиная со звезд 7-й величины,

количество звезд в этом диапазоне (их, все-таки,

вектор определяется хорошо, но не перпендикуля-

не так мало для уравнений с 11-ю параметрами),

рен плоскости Галактики, это факт также известен

но и пекулярная кинематика близких звезд. На это (Цветков, Амосов, 2019). Интересны следующие

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 12

2021

КИНЕМАТИЧЕСКИЕ СВОЙСТВА

905

Таблица 3. Значения компонент скорости движения Солнца в км/с и угловой скорости твердотельного вращения в

км/с/кпк, полученные из совместного решения для звезд различных расстояний

ω₁

ω₂

ω₃

0-100

10.2 ± 0.1

22.0 ± 0.1

7.2 ± 0.1

-1.1 ± 1.4

-12.1 ± 1.4

-1.5 ± 1.4

100-200

9.7 ± 0.0

23.2 ± 0.0

7.3 ± 0.0

1.2 ± 0.2

-6.3 ± 0.2

-10.1 ± 0.2

200-300

9.9 ± 0.0

24.7 ± 0.0

7.7 ± 0.0

1.1 ± 0.1

-2.5 ± 0.1

-12.5 ± 0.1

300-400

10.3 ± 0.0

25.8 ± 0.0

7.8 ± 0.0

0.8 ± 0.1

-1.3 ± 0.1

-13.0 ± 0.1

500-600

10.8 ± 0.0

27.7 ± 0.0

7.8 ± 0.0

1.0 ± 0.0

-1.1 ± 0.0

-13.7 ± 0.0

700-800

11.5 ± 0.0

30.7 ± 0.0

7.8 ± 0.0

-0.1 ± 0.0

-0.4 ± 0.0

-13.7 ± 0.0

900-1 К

12.1 ± 0.0

34.6 ± 0.0

8.0 ± 0.0

0.1 ± 0.0

0.2 ± 0.0

-13.7 ± 0.0

1.2-1.3 К

2.9 ± 0.1

40.5 ± 0.1

8.0 ± 0.1

0.7 ± 0.0

0.5 ± 0.0

-13.8 ± 0.0

1.5-1.6 К

13.4 ± 0.1

46.5 ± 0.1

8.1 ± 0.1

1.2 ± 0.1

0.4 ± 0.1

-14.0 ± 0.1

1.8-1.9 К

13.4 ± 0.1

52.4 ± 0.1

8.0 ± 0.1

1.2 ± 0.1

0.4 ± 0.1

-14.2 ± 0.1

2.1-2.2

13.5 ± 0.2

58.2 ± 0.2

8.0 ± 0.2

1.2 ± 0.1

0.3 ± 0.1

-14.5 ± 0.1

2.4-2.5

13.9 ± 0.2

62.2 ± 0.2

7.8 ± 0.2

0.0 ± 0.1

-14.9 ± 0.1

Таблица 4. Значения компонент тензора деформации в км/с/кпк, полученные из совместного решения для звезд

различных расстояний, а также число звезд, участвовавших в решении

M⁺¹²

M⁺¹³

M⁺²³

M∗11

0-100

28.0 ± 1.8

4.2 ± 1.8

-2.4 ± 1.8

-1.7 ± 3.6

0.1 ± 3.6

372 226

100-200

19.4 ± 0.3

-1.3 ± 0.3

-1.2 ± 0.3

-2.3 ± 0.5

0.1 ± 0.5

1 862 090

200-300

15.7 ± 0.1

-0.7 ± 0.1

-0.8 ± 0.1

-5.1 ± 0.2

1.6 ± 0.2

3 515 477

300-400

14.7 ± 0.1

-0.5 ± 0.1

-0.3 ± 0.1

-5.9 ± 0.2

2.2 ± 0.1

4 696 935

500-600

14.5 ± 0.1

-1.1 ± 0.1

-0.6 ± 0.1

-6.5 ± 0.1

2.1 ± 0.1

5 245 459

700-800

14.1 ± 0.1

-0.4 ± 0.1

0.8 ± 0.1

-5.3 ± 0.1

2.1 ± 0.1

5 272 993

900-1 К

13.5 ± 0.1

-0.1 ± 0.1

0.3 ± 0.1

-4.1 ± 0.1

1.8 ± 0.1

5 235 217

1.2-1.3 К

12.8 ± 0.1

-0.1 ± 0.1

-0.6 ± 0.1

-3.4 ± 0.1

1.2 ± 0.1

4 741 504

1.5-1.6 К

12.4 ± 0.1

-0.2 ± 0.1

-1.1 ± 0.1

-3.0 ± 0.1

1.4 ± 0.1

3 871 940

1.8-1.9 К

11.8 ± 0.1

-0.3 ± 0.1

-1.2 ± 0.1

-2.8 ± 0.2

1.4 ± 0.1

2 839 861

2.1-2.2

11.1 ± 0.1

-0.4 ± 0.1

-1.2 ± 0.1

-2.5 ± 0.2

1.2 ± 0.1

1 655 812

2.4-2.5

10.3 ± 0.1

-0.7 ± 0.1

-0.5 ± 0.1

-2.4 ± 0.2

1.2 ± 0.2

1 041 495

обстоятельства. Во-первых, начиная со звезд 12-

исключение составляет параметр M∗11, ответствен-

й величины, ошибки определяемых параметров

ный за разность растяжений звездной системы по

становятся чрезвычайно малыми. Малость оши-

осям X и Y . Он довольно долго сохраняет нену-

бок означает, что звезды идеально подчиняются

левое значение, и заметно уменьшается лишь для

принятой модели и не содержат никаких других

звезд 16-17-й величины и слабее.

кинематических компонент, но мы увидим, что это

не совсем так. Во-вторых, компоненты вектора

вращения ω₁, ω₂ значимо отличаются от нуля даже

КИНЕМАТИКА ЗВЕЗД С ТОЧНОСТЬЮ

для слабых (и, по-видимому, далеких) звезд, что

ПАРАЛЛАКСОВ ЛУЧШЕ 10%

указывает на то, что вектор вращения не совсем

Анализ распределений звезд по параллаксам

перпендикулярен плоскости Галактики.

и их точностям показывает, что для звездно-

Анализ компонент тензора деформации показы-

кинематических исследований, которые нуждаются

вает, что практически все компоненты, за исклю-

в расстояниях, следует использовать звезды с

чением параметра M⁺¹² (а это параметр Оорта A),

высокой относительной точностью параллаксов.

быстро убывают к нулевым значениям. Небольшое

Для этого мы создали подкаталог, состоящий из

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 12

2021

906

ЦВЕТКОВ

Зависимость кинематических параметров U, V, W от расстояния до звезд

80.0

70.0

60.0

50.0

40.0

30.0

20.0

10.0

R (pc)

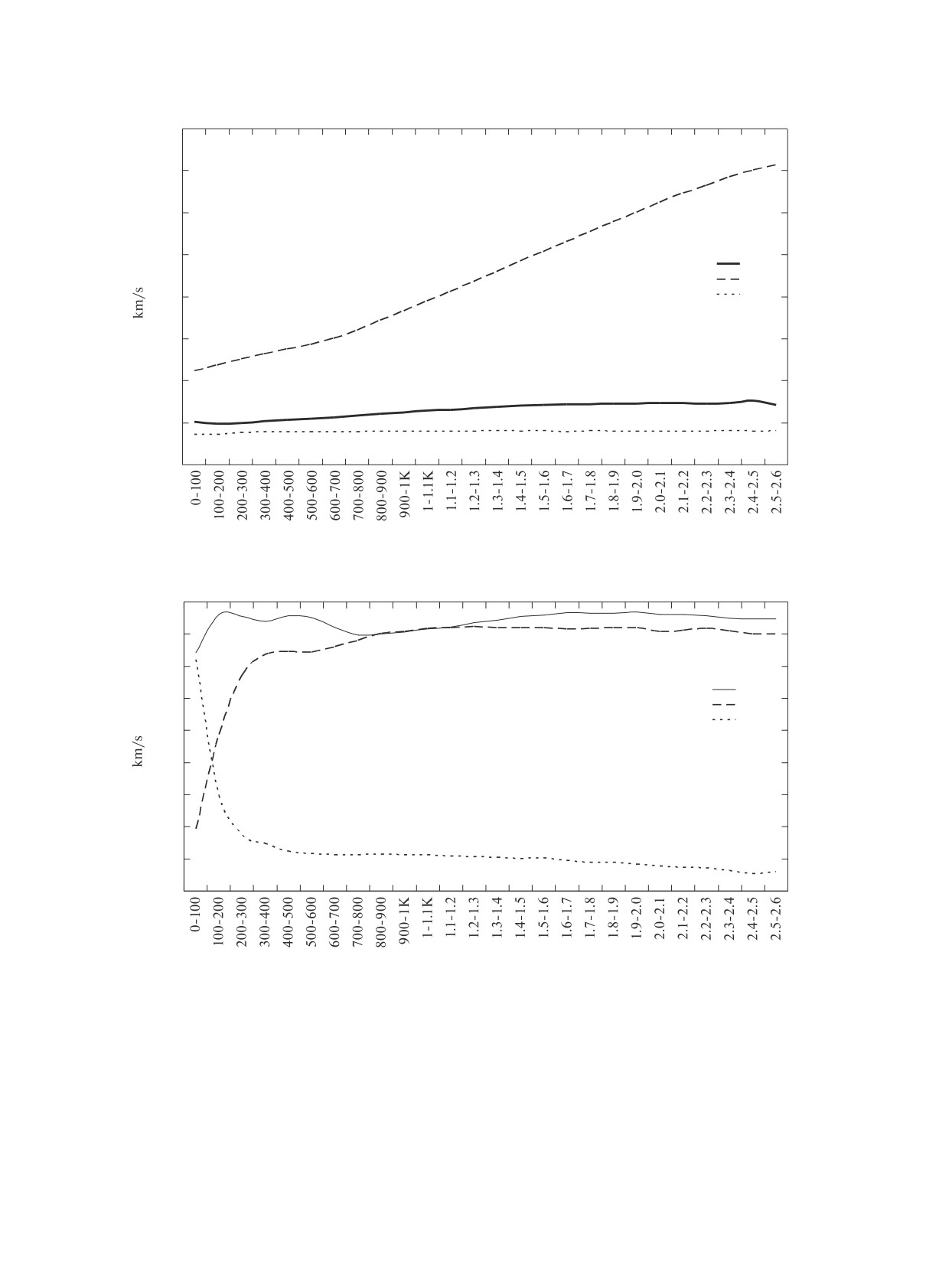
Рис. 4. Зависимость кинематических параметров движения Солнца U, V , W от расстояния до звезд (км/с).

Зависимость компонент угловой скорости от расстояния до звезд

2.0

4.0

6.0

8.0

10.0

12.0

14.0

16.0

R (pc)

Рис. 5. Зависимость угловой скорости твердотельного вращения ω1, ω2, ω3 от расстояния до звезд (км/с/кпк).

98506335 звезд, которые удовлетворяют этому

Милна и разложение собственных движений по

критерию. Так как пока даже формальная 10%-я

системе векторных сферических функций. Резуль-

точность параллакса не гарантирует надежного

таты приведены в табл. 3 и 4. Для компактности,

значения параллакса каждой звезды, мы поступили

начиная 400 пк, приведены не подряд, так как

стандартным образом, разбив звездный материал

значения изменяются довольно медленно. В табл. 4

на сферические слои, удаленные от Солнца на

дополнительно указано число звезд, использовав-

разные расстояния. Для этих групп звезд были ре-

шихся в решении. Само решение базировалась

шены уравнения в рамках модели Огородникова-

на усредненных данных собственных движений и

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 12

2021

КИНЕМАТИЧЕСКИЕ СВОЙСТВА

907

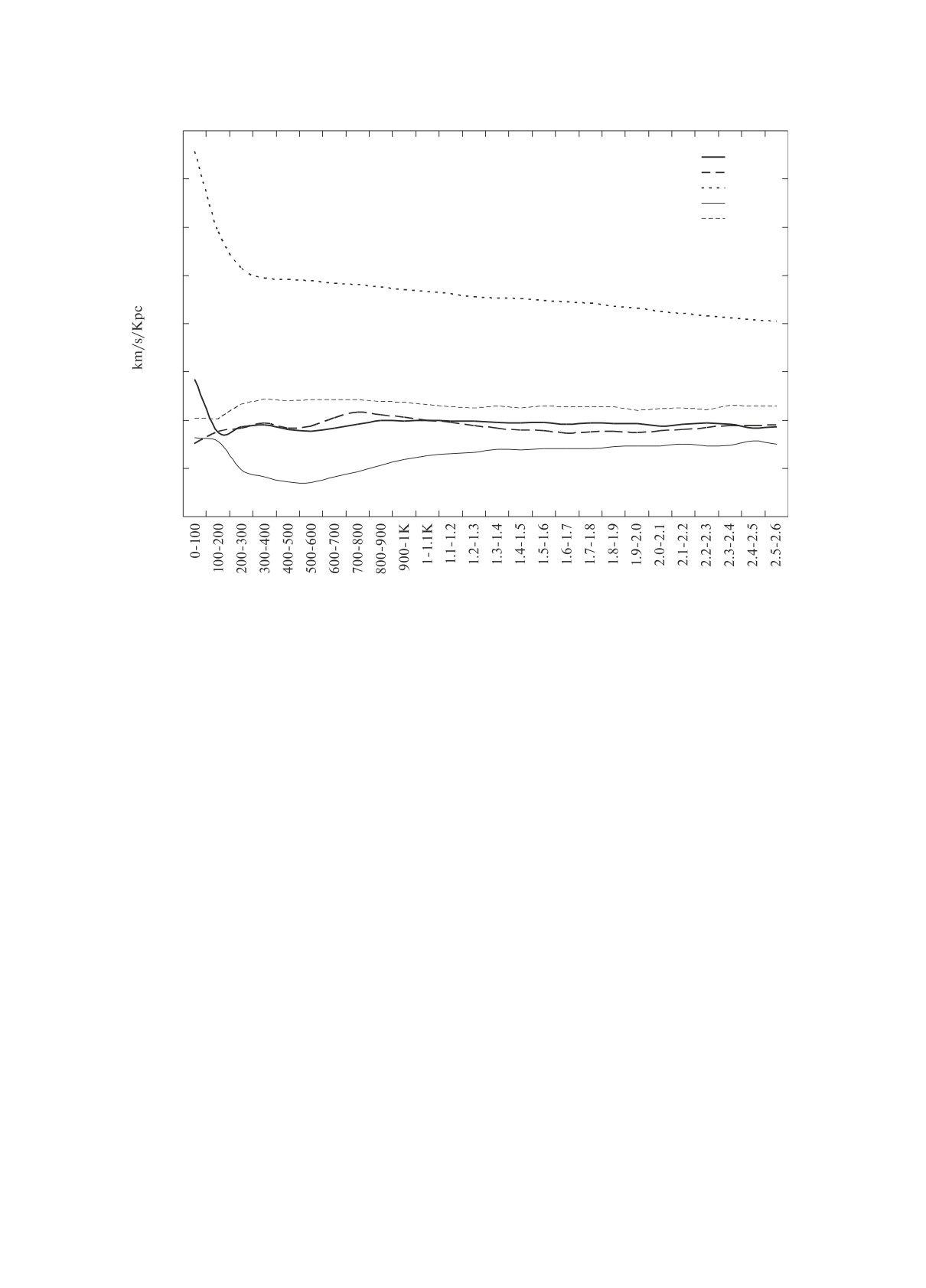
Зависимость компонент тензора деформации от расстояния до звезд

30.0

M13

25.0

M23

M12

M11

20.0

15.0

10.0

5.0

10.0

R (pc)

Рис. 6. Зависимость компонент тензора деформации M⁺¹², M⁺¹³, M⁺²³, M⁺¹¹, X от расстояния до звезд (км/с/кпк).

расстояний по 49 152 площадкам HealPix (N =

нулю значениям. Разве что только M∗11 показывает

= 64) с равными весами площадок. Рисунки 4-6

ненулевые значения (разность сжатия системы по

иллюстрируют содержание табл. 3 и 4.

оси X и Y ).

Анализ результатов показывает, что в пределах

1.5-2 Кпк трехмерная модель в состоянии удо-

Сильнее всего бросается в глаза ход параметра

влетворительно описывать кинематику звезд, хотя

V —скорости движения Солнца вдоль оси Y , т.е.

сами параметры претерпевают порой значитель-

вдоль оси, направленной по вращению Галактики.

ные изменения в зависимости от рассматриваемой

Объяснение, очевидно, может быть таким: ско-

группы звезд (особенно солнечный параметр V ).

рость движения Солнца оценивается относительно

По-прежнему самые близкие звезды составляют

групп звезд на разных расстояниях, а эти группы

проблемную область, в которой кинематика не под-

сами движутся относительно друг друга. В плос-

чиняется трехмерной модели. Однако с расстоя-

кости Галактики по направлению, перпендикуляр-

ния примерно 300 пк кинематические параметры

ному на центр Галактики, эти различия сильны и

принимают свои обычные значения. Звезды ближе

имеют большой систематический ход. Аналогичные

100 пк имеют большие пекулярные скорости, кото-

результаты были получены нами ранее по каталогу

рые с расстоянием просто перестают быть замет-

Gaia DR2 with RV (Цветков, Амосов, 2019), но

ными, поскольку нарастают глобальные эффекты

поведение параметра V было несколько иным. Его

вращения Галактики.

значение оставалось стабильным (около 22 км/с)

Вообще говоря, считается, что упрощенная

до расстояний 800 пк, далее начинался линейный

линейная модель Оорта-Линдблада или полная

рост. В нашем случае мы наблюдаем линейный рост

Огородникова-Милна может использоваться до

сразу же.

расстояний 1-1.5 кпк (Огородников, 1965). Но

мы видим, что параметры Оорта A = M⁺¹² и B =

Еще одна особенность параметров движения

= ω₃ хотя и меняются с расстоянием, но очень

Солнца — это их надежные и предсказуемые зна-

плавно, сохраняя свой общий характер. Прочие

чения даже для самых близких звезд, чего не

параметры (компоненты угловой скорости ω₁,

скажешь о параметрах вращения и деформации,

ω₂ и тензора деформации M∗11, M⁺¹³, M⁺²³, X) с

которые выходят на стабильные значения только с

увеличением расстояния стремятся к близким к

расстояний 400-500 пк.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 12

2021

908

ЦВЕТКОВ

ЗАКЛЮЧЕНИЕ

10.

Витязев В.В. и др., Письма в Астрон. журн. 44, 265

(2018) [V.V. Vityazev, et al., Astron. Lett. 44, 236

Полученные результаты находятся в хорошем

(2018)].

согласии с данными других исследователей на

11.

Витязев и др. (V.V. Vityazev, A.S. Tsvetkov,

материале каталогов Gaia предыдущих версий

V.V. Bobylev, and A.T. Bajkova), Astrophysics

(Й. Бови, 2017; Величко и др., 2020). Показана

60, 503 (2017).

относительная постоянность на расстояниях более

12.

Горски и др. (K.M. Gorski, E. Hivon, A.J. Banday,

500 пк параметров движения Солнца U и W ,

et al.), Astrophys. J. 622 (2005).

всех трех компонент угловой скорости, компо-

13.

Джонсон, Морган (H.L. Johnsonand W.W. Morgan),

нент тензора деформации M⁺¹³, M⁺²³, M∗11, X.

Astrophys. J. 117, 313 (1953).

Отчетливо наблюдается систематический ход с

14.

Дю Монт (B.A. du Mont), Astron. Astrophys. 61, 127

расстоянием компоненты V и параметра Оорта

(1977).

A = M⁺¹². Изменение этих параметров является

15.

Захариас и др. (N. Zacharias, D.G. Monet,

следствием нелинейности хода угловой скоро-

S.E. Levine, et al.), Bull. Am. Astron. Soc. 36,

сти вращения Галактики в направлении центр-

1418 (2004).

антицентр. Построению такой модели и детальному

16.

Касагранд, Ванденберг (L. Casagrande and

ее анализу будет посвящена следующая статья.

D. VandenBerg), MNRAS: Lett. 479, L102 (2018).

Кроме этого остается под вопросом полнота

17.

Кац и др. (D. Katz, et al.), Astron. Astrophys. 622,

модели Огородникова-Милна. Проведенные нами

A205 (2019).

ранее исследования на материале предыдущего

18.

Михалик и др. (D. Michalik, L. Lindegren, and

релиза Gaia DR2 (Цветков и др., 2020) показывают

D. Hobbs), Astron. Astrophys. 574, id.A115, 8 p.

наличие систематических компонент в собственных

(2015).

движениях, не описываемых этой моделью. Этот

19.

Монтегриффо и др. (P. Montegriffo, F. De Angeli,

вопрос также будет обсужден в следующей работе.

M. Bellazzini, et al.), Gaia EDR3 passbands,

https://www.cosmos.esa.int/web/gaia/edr3-

passbands (2020).

СПИСОК ЛИТЕРАТУРЫ

20.

Огородников К.Ф., Динамика звездных систем

1. ESA Gaia: https://sci.esa.int/web/gaia

(М.: Физматгиз, 1965).

2. Gaia, EDR3: https://www.cosmos.esa.int/web/gaia/

21.

Рыбка С.П., Кинемат. и физ. небесн. тел 20, 437

earlydr3

(2004).

3. Gaia, Chapter 13: https://gea.esac.esa.int/archive/

22.

Рёзер и др. (S. Roeser, M. Demleitner, and

documentation/GEDR3/Gaia_archive/chap_data-

E. Schilbach), Astron. J. 139, 2440 (2010).

model/

4. Gaia Colloboration, Astron. Astrophys. 649, A1

23.

Риелло и др. (M. Riello, F. De Angeli, D.W. Evans,

(2021).

et al.), Astron. Astrophys. 649, A3 (2021).

5. Бартеньев О.В., Современный Фортран. 3-е изд.,

24.

Цветков А.С., Руководство по практической

доп. и перераб. М.: ДИАЛОГМИФИ, 449 с. (2000).

работе с каталогом Hipparcos (СПб, 2005).

6. Бови (Jo Bovy), MNRAS: Lett. 468, Iss. 1, L63

25.

Цветков А.С., Амосов Ф.А., Письма в Астрон.

(2017).

журн. 45, 517 (2019) [A.S. Tsvetkov, F.A. Amosov,

7. Браун и др. (A. Brown, A. Vallenari, T. Prusti, et al.),

Astron. Lett. 45, 462 (2019)].

Astron. Astrophys. 649 (2021).

26.

Цветков А.С., Амосов Ф.А., Трофимов Д.А., Пет-

8. Величко и др. (A. Velichko, P. Fedorov, and

ров С.Д., Письма в Асторн. журн. 46, 61 (2020)

V. Akhmetov), MNRAS 494, 1430 (2020).

[A.S. Tsvetkov, et al., Astron. Lett. 46, 58 (2020)].

9. Витязев, Цветков (V.V. Vityazev and A.S. Tsvetkov),

MNRAS 442, 1249 (2014).

27.

Шацова, Р.Б., Ученые записки ЛГУ, № 136 (1950).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47

№ 12

2021