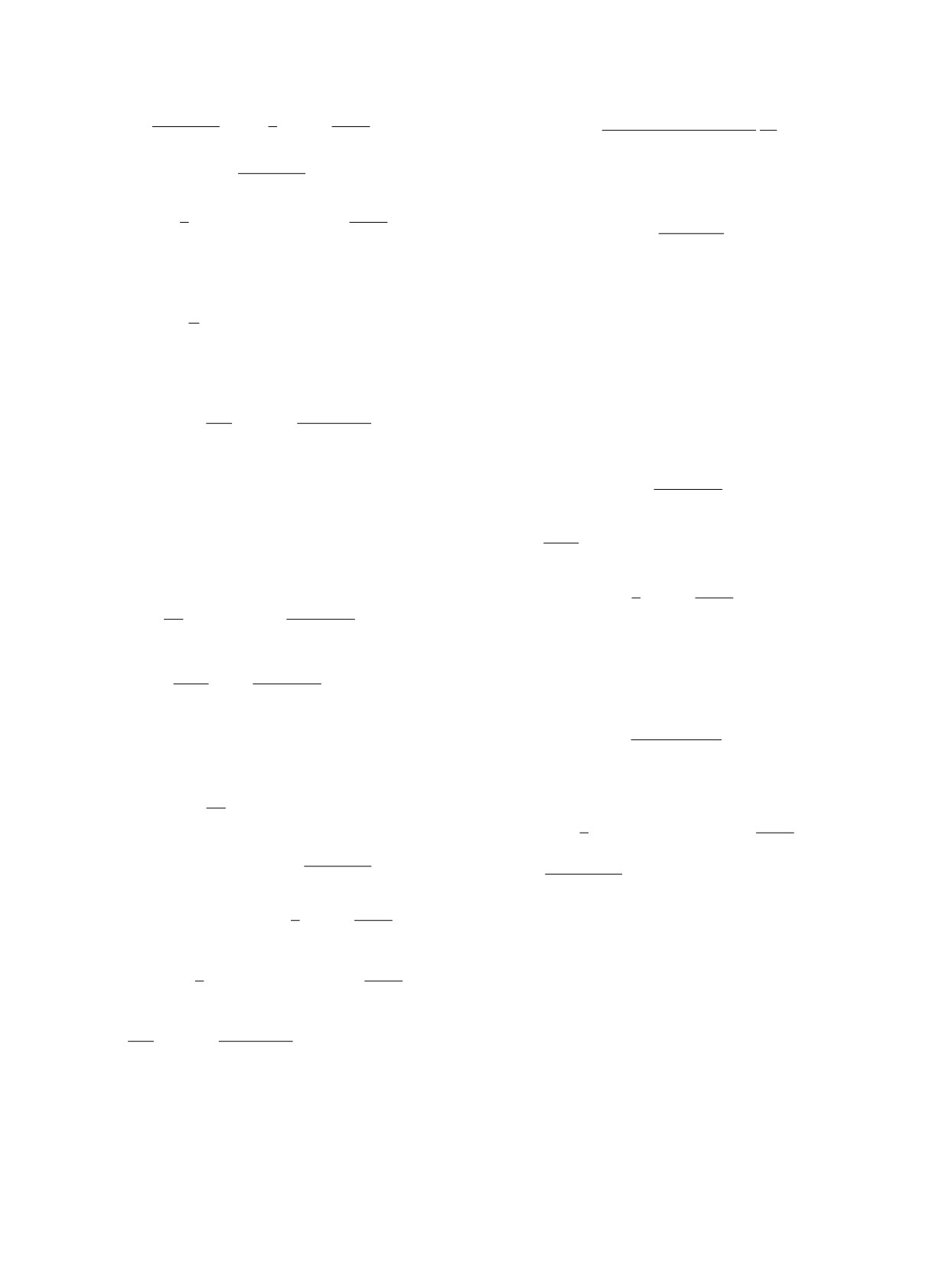ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2021, том 47, № 5, с. 369-380
ОБ ЭВОЛЮЦИИ ОРБИТ В ФОТОГРАВИТАЦИОННОЙ КРУГОВОЙ
ЗАДАЧЕ ТРЕХ ТЕЛ. ВНУТРЕННЯЯ ЗАДАЧА
© 2021 г. А. В. Доброславский1*, П. С. Красильников1
1Московский авиационный институт (национальный исследовательский университет), Москва, Россия
Поступила в редакцию 14.12.2020 г.
После доработки 30.01.2021 г.; принята к публикации 02.02.2021 г.
Рассмотрена пространственная ограниченная круговая задача трех тел в нерезонансном случае.
Предполагается, что пассивно гравитирующее тело (спутник) имеет большую парусность, поэтому
учитывается световое давление. Изучение эволюции орбиты спутника проводится на основе схемы
Гаусса: исследуются усредненные уравнения движений в кеплеровом фазовом пространстве, когда в
качестве невозмущенной орбиты берется кеплеровский эллипс с фокусом в основном теле (Солнце),
находящийся внутри сферы, радиус которой равен радиусу орбиты внешней планеты (внутренняя
задача). Известно, что исследование усредненной модели в классическом случае, когда световым
давлением пренебрегают, сталкивается с немалыми трудностями как при вычислении усредненной
силовой функции, так и при анализе эволюционирующих орбит. Впервые показано, что дважды усред-
ненная силовая функция допускает, на основе применения формулы Парсеваля, явное аналитическое
представление через гипергеометрические(обобщенные гипергеометрические)функции, допускающие
разложение в сходящиеся степенные ряды. Показано также, что усредненные уравнения движения,
учитывающие дополнительное влияние светового давления, интегрируются по Лиувиллю (имеем
три независимых первых интеграла в инволюции). Исследованы, при фиксированных значениях
интеграла Лидова-Козаи, стационарные режимы колебаний в случае малых значений большой
невозмущенной полуоси спутника (случай Хилла), их бифуркации в зависимости от коэффициента
светового давления δ. В плоскости кеплеровских элементов e, ω построены фазовые портреты
колебаний при разных значениях коэффициента светового давления. Описана перестройка портрета,
обусловленная как бифуркациями положений равновесия, так и расщеплением сепаратрис. Показано,
что расщепление сепаратрис приводит к изменению направления эволюции аргумента перицентра ω
на противоположное в случае ротационных движений.
Ключевые слова: световое давление, ограниченная пространственная задача трех тел, искусственный
спутник Солнца.
DOI: 10.31857/S0320010821040069
ВВЕДЕНИЕ
где было решено уравнение тени, работу Феррас-
Мелло (1964), в которой предложено учитывать
заход спутника в тень путем введения теневой
Световое давление имеет существенное значе-
функции, и работы Вашковьяк (1974, 1976), в
ние при расчете параметров движения небесных
которых было предложено теневую функцию рас-
объектов с большим отношением площади миде-
считывать в виде ряда по полиномам Лежандра
лева сечения к массе. Впервые с необходимостью
и выражать через элементы орбиты, в результате
учитывать этот эффект столкнулись в расчетах,
чего были получены вековые и долгопериодические
связанных со спутником Vanguard I в работе Мю-
возмущения элементов орбиты под влиянием све-
зена (1960) и Паркинсона и др. (1960), когда
тового давления. В монографии (Аксёнов, 1977)
для объяснения деградации орбиты потребовалось
исследовано влияние светового давления и земной
учесть и световое давление на спутник. Большую
тени на эволюцию кеплеровских элементов орбиты
роль световое давление сыграло при исследовании
в первом приближении метода малого параметра.
движения спутников-баллонов Echo 1, Echo 2 и
Исследование движения объектов большой па-
PAGEOS, чему посвящен целый ряд работ, среди
русности приобретает особое значение в связи с
которых следует упомянуть работу Козаи (1961),
космическим мусором, движущимся на высоких
орбитах. Так, в работе Кривова и др. (1995), на-
*Электронный адрес: a.dobroslavskiy@gmail.com
ряду с возмущениями от зональных гармоник, рас-
369
370
ДОБРОСЛАВСКИЙ, КРАСИЛЬНИКОВ
смотрены возмущения от сил светового давления.
движениях спутников на эволюционирующих ор-
Эта же задача, но дополненная возмущениями от
битах: усреднение используется в статьях Тихоно-
электромагнитных сил, рассматривается в работе
ва и др. (2017) и Александрова, Тихонова (2020)
Гамильтона, Кривова (1996).
при исследовании устойчивости программного вра-
щательного движения спутника вокруг его цен-
В августе 2018 г. стартовала миссия Parker Solar
тра масс на эволюционирующей орбите. Исполь-
Probe (Сабо, 2018) в задачи которой входит изуче-
зование метода функций Ляпунова в сочетании
ние солнечной короны. По своим параметрам зонд
с приемом усреднения уравнений вращательного
соответствует объектам с большим отношением
движения спутника эффективно применялось для
площади миделева сечения к массе.
обоснования асимптотической устойчивости ста-
Для исследования орбит вышеупомянутых объ-
билизируемого движения (Александров, Тихонов,
ектов на значительных временных промежутках
2020). В статье Амелькина (2019) методом усред-
применяется, в частности, метод усреднения,
нения определено среднее смещение перигелия
приложения которого к классической задаче трех
Меркурия в плоской планетной задаче.
тел были подробно разобраны в статье Моисеева
Авторами статьи ранее была исследована зада-
(1945). Брайант (1961), используя идеи метода
ча трех тел с учетом светового давления в плоской
усреднения, описал явное изменение большой
эллиптической задаче трех тел (Доброславский,
полуоси за период обращения спутника по орбите
Красильников, 2018). К сожалению, при записи
с учетом светового давления и эффекта тени.
силовой функции светового давления была допу-
Он показал также, что при отсутствии тени
большая полуось орбиты спутника сохраняет
щена ошибка1, как следствие, появились лишние
равновесия e = const, ω = π/2; остальные резуль-
свое невозмущенное значение. В работах Лидова
(1961, 1962) описана эволюция орбиты спутника
таты изменились мало. В следующей статье (Доб-
планеты в рамках эллиптической задачи трех
рославский, Красильников, 2020), посвященной
тел для случая Хилла (случай малого отношения
уже задаче четырех тел (Земля-Луна-Солнце-
большой невозмущенной полуоси орбиты спут-
спутник Земли), учитывающей световое давление,
ника к радиусу орбиты планеты); был описан
построены фазовые портреты колебаний в кепле-
ровских элементах орбиты, изучена перестройка
эффект падения спутника на центральное тело,
когда плоскость орбиты спутника перпендикулярна
фазовых портретов при разных значениях коэф-
плоскости орбиты возмущающего тела. В работе
фициента светового давления. В указанных рабо-
Козаи (1962) получено приближенное выражение
тах эффект захода в земную тень не учитывался
в силу того, что при значении большой полуоси
для дважды усредненной возмущающей силовой
эллиптической орбиты спутника, сравнимом с со-
функции в астероидной круговой задаче трех
тел, вычислены значения критических наклонений
ответствующим параметром Луны и превышающим
его, среднее время пребывания спутника в тени со-
орбит. В работе Сидоренко (2018) исследуется
ставляет порядка 0.62% за виток (Доброславский,
эксцентрический эффект Лидова-Козаи, который
может быть интерпретирован как резонансный
2020).
эффект. Аксёнов (1967) получил аналитическое
Цель данной работы — исследовать эволюцию
выражение для дважды усредненной возмущающей
пространственных орбит близкого спутника звезды
силовой функции в круговой задаче трех тел в виде
(солнечного зонда) с учетом возмущений от внеш-
ряда Фурье, коэффициенты которого выражаются
ней планеты (Юпитера) и от солнечного давления.
через специальные функции, записанные в виде
квадратур. В этой же работе дано обоснование
ПОСТАНОВКА ЗАДАЧИ
методу усреднения Гаусса, заменяющему проце-
дуру усреднения по средней аномалии движения
Рассмотрим круговую пространственную огра-
планеты равномерным размазыванием массы пла-
ниченную задачу трех тел с учетом сил светового
неты по ее орбите. В работах Аксёнова (1979a,б)
давления Fλ. Предположим, что пассивно гравити-
исследована плоская ограниченная эллиптическая
рующее тело (спутник) P , имея большое отношение
задача трех тел методом двойного усреднения,
площади поверхности к собственной массе, нахо-
изучена эволюция траекторий движения спутника,
дится в гравитационном поле двух массивных тел,
в частности, описаны траектории его падения на
движущихся друг относительно друга по круговой
центральное тело. Топология движений в усреднен-
орбите радиуса rJ ; центральное тело S (Солнце)
ной круговой задаче трех тел (внутренняя задача)
имеет массу mS и воздействует на спутник с силой
исследована численно в замечательной работе
FS, второе тело J (Юпитер) массы mJ оказывает
Вашковьяка (1981).
возмущающее действие с силой FJ . Считаем, что
Заметим также, что метод усреднения эффек-
тивно используется и в задачах о вращательных
1Проф. Н.И. Амелькин любезно указал на нее.
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
ОБ ЭВОЛЮЦИИ ОРБИТ В ФОТОГРАВИТАЦИОННОЙ КРУГОВОЙ ЗАДАЧЕ
371
z
P
F
F
S
FJ
S
i
J
J
N
x
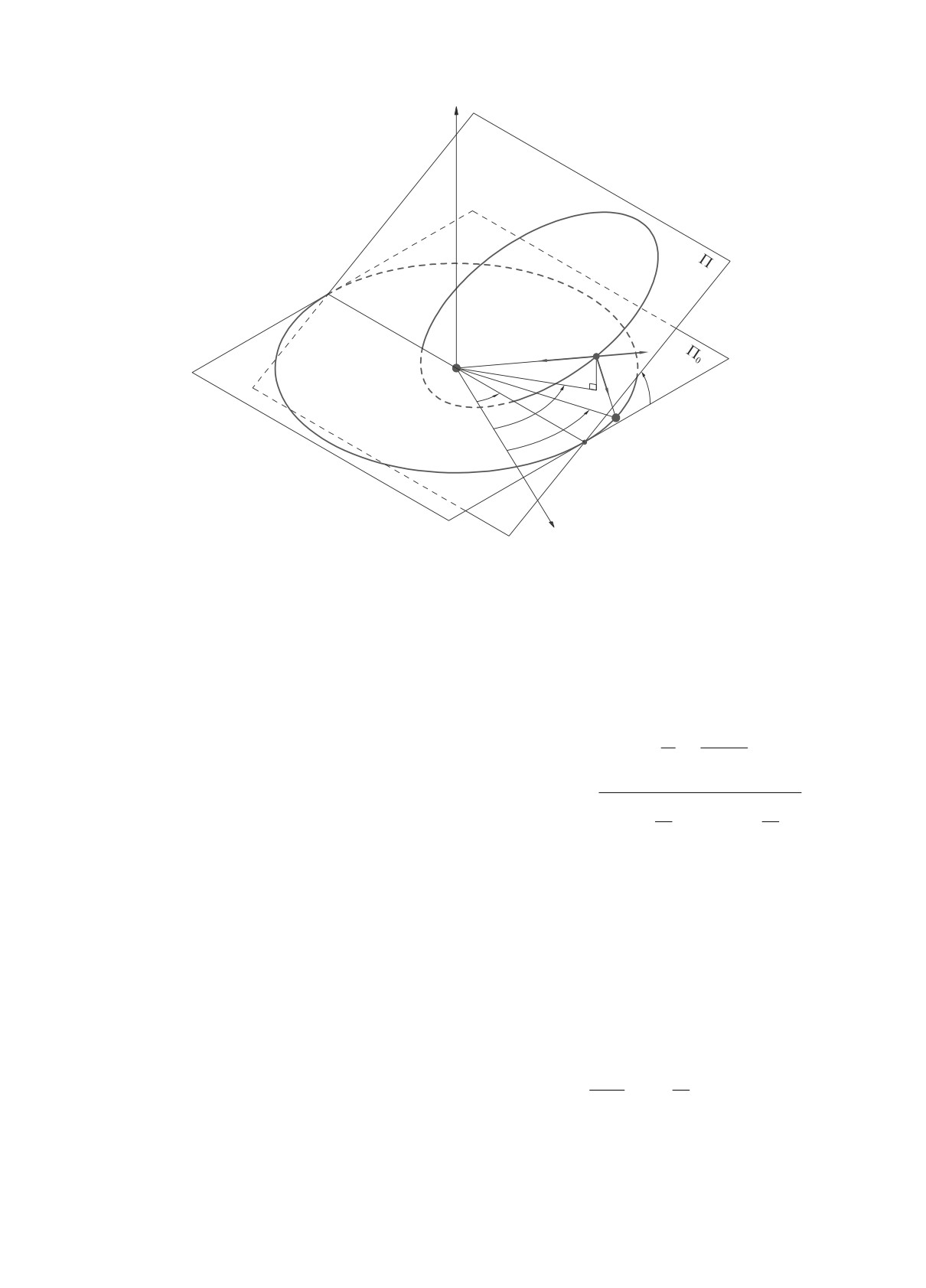
Рис. 1. Невозмущенные траектории небесных тел. Угловые переменные.
невозмущенная траектория спутника есть кепле-
Запишем выражение для возмущенной силовой
ровский эллипс с фокусом в S, плоскость которого
функции задачи:
Π образует с плоскостью движения Π0 притягива-
R=RJ +RS.
(1)
ющих тел угол i (рис. 1).
Здесь RJ — силовая функция гравитационного
Заметим, что в классическом случае, когда све-
воздействия со стороны тела J, имеющая вид
товое давление на спутник пренебрежимо мало,
)
задача подробно исследована в статье (Вашковьяк,
(1
(rJ , r)
RJ = fmJ
-
,
(2)
1981). Цель нашей статьи — описать новые эф-
Δ
r3
J
фекты в усредненном движении спутника, вызван-
ные световым давлением.
√
(
)
2
r
( r)
Введем гелиоцентрическую систему координат с
Δ=rJ
1-2
cos γ +
,
rJ
rJ
центром в S. Ось Sx направим в точку весеннего
равноденствия, SN — линия узлов орбиты спут-
где f — постоянная тяготения, γ — угол между rJ
ника, остальные оси, образующие правую систему
и r,
координат, на рис. 1 не указаны. Пусть r — радиус-
cos γ = cos (λJ - Ω) cos (ω + ν) +
(3)
вектор тела P , rJ — радиус-вектор тела J.
+ sin (λJ - Ω)sin (ω + ν)cos i,
Пусть Ω — долгота восходящего узла невоз-
мущенной орбиты спутника на плоскости Π0, e,
ν —истинная аномалия в движении спутника
ω — эксцентриситет и аргумент перицентра этой
вдоль невозмущенной орбиты.
орбиты, λJ — долгота тела J, а λ — долгота тела P
Функция (2) может быть разложена в ряд по
в плоскости Π0.
полиномам Лежандра с точностью до членов, не
Рассмотрим “внутренний” вариант задачи трех
зависящих от координат тела P :
тел, когда движение тела P происходит внутри
∑
сферы радиуса rJ :
RJ =
( r )n Pn(cosγ).
rJ
rJ
a(1 + e) < rJ .
n=2
Здесь a — большая полуось невозмущенной орби-
Силовая функция светового давления на сфери-
ты спутника.
ческий спутник, находящийся на круговой орбите,
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
372
ДОБРОСЛАВСКИЙ, КРАСИЛЬНИКОВ
может быть представлена в виде
Далее считаем, что частота
λJ не резонирует
с частотой n невозмущенного движения спутника.
δr20
RS = -
Проводя усреднение (5) по долготе λJ тела J,
r
получим, с учетом (3), (7) и равенства P2n+1(0) =
Здесь δ > 0 — коэффициент светового давления
= 0, однократно усредненную силовую функцию R∗
(Аксёнов, 1977)
задачи
κπρ2E0
1
δ=
,
(4)
R∗ =
×
(8)
mc
2π
2π
[
]
ρ— радиус поверхности спутника, m —его масса,
∫
∑(r)n
δr20
κ —коэффициент отражения поверхности спут-
×
-
+
Pn(cos γ) dλJ =
ника, равный 1 для полного поглощения или от-
r
rJ
rJ
n=2
0
ражения света, и 1.44 для диффузного рассеи-
∑
вания. E0 — солнечная постоянная, определенная
δr20
=-
+
( r)2n ×
как мощность светового потока на расстоянии r0
r
rJ
rJ
n=1
(1 а.е.) от Солнца (приблизительно 1367 Вт/м2),
c —скорость света в вакууме.
× P2n (0)P2n [sinisin(ν + ω)].
Тогда, с учетом выражений для RJ и RS , силовая
функция задачи принимает вид:
Выражение (8) совпадает с точностью до чле-
на, учитывающего световое давление, с силовой
∑
δr20
fmJ
функцией кольца Гаусса (Дубошин, 1961), что было
R=-
+
( r )n Pn(cosγ).
(5)
r
rJ
rJ
впервые установлено в работе Аксёнова (1967).
n=2
Усредним теперь полученное выражение (8) по
истинной аномалии ν тела P . Для этого необхо-
УСРЕДНЕНИЕ СИЛОВОЙ ФУНКЦИИ
димо записать выражение для r через истинную
Известно, что долгота λ тела P в плоскости эк-
аномалию ν, используя формулы невозмущенного
липтики описывается формулами (Аксёнов, 1967)
движения, и подставить в (8). Вычисления показы-
вают, что функция R∗ содержит под знаком суммы
cos (ν + ω)
cos λ =
√
,
произведение двух периодических по ν функций:
1 - sin2 isin2 (ν + ω)
(1 + ecos ν)-2n и P2n(sin icos θ), где θ = ν + ω -
sin (ν + ω) cos i
- π/2. Основная техническая проблема исследо-
sin λ =
√
1 - sin2 isin2 (ν + ω)
ваний — подсчитать среднее от этого произведе-
ния. Современные программные комплексы, такие
Тогда (3) можно переписать в виде
как Wolfram Mathematica и Maple, с этой задачей
cos γ = cos (λJ - Ω - λ) ×
(6)
не справляются. Для этого воспользуемся форму-
√
лой Парсеваля (Градштейн, 1963), описывающей
×
1 - sin2 isin2 (ν + ω).
главный (секулярный) член произведения двух ря-
дов Фурье:
Для преобразования выражения (5) к удобно-
му для усреднения виду воспользуемся теоремой
∫
2π
1
сложения для полиномов Лежандра. C учетом (6)
(1 + e cos ν)-2n ×
(9)
2π
будем иметь
0
Pn(cos γ) = Pn(0)Pn [sin isin(ν + ω)] +
(7)
× P2n (sinicosθ)dν =
∑
(n - k)!
∑
a0α
1
+2
P(k)n(0)P(k)n [sin isin(ν + ω)] ×
0
=
+
(amαm + bmβm).
(n + k)!
k=1
4
2
m=1
× cos k (λJ - Ω - λ).
Здесь
{a0, am, bm} — коэффициенты Фурье
Здесь
n
— присоединенные функции Ле-
функции (1 + e cos ν)-2n, {α0, αm, βm} — коэффи-
жандра, представимые в нуле следующим образом:
циенты Фурье функции P2n(sin i cos θ). Выражения
⎧
⎪
(n + k)!
для этих коэффициентов имеют вид
⎨(-1)(n-k)/2
(n-k)
(n+k) ,
2n
!
!
2π
2
2
∫
P(k)n(0) =
1
⎪n - k = 2m, m ∈ Z,
a0 =
(1 + e cos ν)-2ndν =
(10)
⎩
π
0, n - k = 2m + 1, m ∈ Z.
0
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
ОБ ЭВОЛЮЦИИ ОРБИТ В ФОТОГРАВИТАЦИОННОЙ КРУГОВОЙ ЗАДАЧЕ
373
)
2
(1
2e
∑
k
(α1)k (α2)k (α3)
z
=
F2,1
, 2n; 1;
,
k
=
,
(1 - e)2n
2
e-1
Γ(β1 + k)Γ(β2 + k) k!
k=0
2
am =
×
где Γ(a) — гамма-функция, (x)k — символ Похгам-
(1 - e)2n
)
мера:
(1
2e
×Freg
, 1, 2n; 1 - m, 1 + m;
,
Γ(x + k)
3,2
2
e-1
(x)k =
Γ(x)
bm = 0,
Достоверность формулы (13) была подтвер-
2π
ждена численно — результаты вычислений левой и
∫
1
правой частей формулы совпадают по всем знача-
α0 =
P2n(sin icos θ)dν =
(11)
π
щим цифрам для следующего декартового произве-
0
дения значений параметров: e от 0 до 1 с шагом 0.1,
= 2P2n(0)P2n(cos i),
ω от 0 до 2π с шагом π/6, i от -π/2 до π/2 с шагом
π/6 и n от 1 до 15 с шагом 1.
⎧
(mπ
) (2n - m)!
Выражение для усредненной силовой функции
⎪
2 cos
- mω
×
⎨
(12), (13) можно разложить в ряд Фурье по ω.
2
(2n + m)!
αm =
Вычисления показывают, что этот ряд имеет вид
⎪
× P(m)2n(0)P(m)2n(cos i), m ≤ 2n,
⎩
δr20
0, m > 2n,
R∗∗ = -
+
(14)
a(1 - e2)
βm = 0.
[
∑
fmJ
+
B2n(e)P2n(0)P2n(cos i) ×
В итоге дважды усредненная возмущенная си-
rJ
ловая функция принимает вид
n=1 (
)
1
2e
∫
2π
×F2,1
, 2n; 1;
+
1
δr20
2
e-1
R∗∗ =
R∗dν = -
+
(12)
(
)
]
2π
a(1 - e2)
∑
0
+ (-1)n
B2k(e)A(2k)2n(e,cos i) cos 2nω
∑
fmJ
k=n
+
[ a(1 - e2)]2n ×
rJ
rJ
n=1
Здесь
× P2n (0)I2n(i,e,ω).
a2k(1 + e)2k
B2k(e) =
P2k(0),
r2kJ
Здесь
∫
2π
1
A(2k)2n(e,cos i) =
I2n(i,e,ω) =
(1 + e cos ν)-2n ×
(13)
⎧
)
2π
reg
(1
2e
⎪
0
2F3
, 1, 2k; 1 - 2n, 1 + 2n;
×
⎪
,2
⎪
2
e-1
1
⎨
(2k - 2n)!
× P2n (sinicosθ)dν =
×
(1 - e)2n
×
P(2n)2k(0)P(2n)2k(cos i),
[
=⎪⎪
(2k + 2n)!
)
⎪
(1
2e
⎪
1≤n≤k,
× P2n(0)P2n(cos i)F2,1
, 2n; 1;
+
⎩
2
e-1
0, n > k.
)
∑
(1
2e
При выводе формулы (14) мы воспользовались
+2
Freg
, 1, 2n; 1 - m, 1 + m;
×
3,2
2
e-1
известным равенством P(2n+1)2k(0) = 0, обнуляю-
m=1
]
щим члены, содержащие sin 2nω.
(mπ
) (2n - m)!
Здесь следует отметить, что аналитическое
× cos
- mω
P(m)2n(0)P(m)2n(cos i) ,
2
(2n + m)!
представление дважды усредненной силовой функ-
ции задачи в виде ряда Фурье по ω впервые по-
F2,1 — гипергеометрическая функция, а Freg3,2 —
лучено в работе Аксёнова (1967). Коэффициенты
этого ряда автор статьи выразил через некоторые
обобщенная регуляризованная гипергеометриче-
неизвестные специальные функции, имеющие вид
ская функция, имеющая вид
квадратур. К сожалению, квадратуры не были
Freg3,2 (α1,α2,α3;β1,β2;z) =
разложены в сходящиеся ряды, автор ограничился
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
374
ДОБРОСЛАВСКИЙ, КРАСИЛЬНИКОВ
описанием рекуррентных соотношений для квад-
являются интегральными в редуцированной систе-
ратур. Поэтому использовать результаты статьи
ме уравнений (16). Действительно, производная от
Е.П. Аксёнова в аналитических исследованиях
R по ω имеет вид
крайне затруднительно.
ˆ
∑
∂
=-
(-1)n ×
∂ω
r
J n=1
УСРЕДНЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЙ
(
)
∑
(2k)
× 2n
B2k(e)A
(e, cos i) sin 2nω.
Усредненные уравнения в оскулирующих пере-
2n
менных (уравнения Лагранжа) имеют вид (Дубо-
k=n
шин, 1968)
Она обращается в ноль при e =
√1 - c1, так как
da
при этом cos i = ±1, а A(2k)2n(e,±1) = 0. Интеграль-
= 0,
(15)
dt
ность многообразия e = 0 следует из разложения
√
этой производной в ряд по e:
de
1-e2 ∂R∗∗
=-
,
dt
na2e
∂ω
ˆ
∑
∂
=-
(-1)n ×
di
ctg i
∂R∗∗
∂ω
rJ
=
√
,
n=1
dt
na2
1-e2
∂ω
{
∑
dΩ
cosec i
∂R∗∗
( a )2k (2k - 2n)!
× 4n
×
=
√
,
rJ
(2k + 2n)!
dt
na2
1-e2
∂i
k=n
√
dω
1-e2 ∂R∗∗
ctg i
∂R∗∗
× P2k(0)P(2n)2k(0)P(2n)2k(cos i) ×
=
-
√
[
(
dt
na2e
∂e
na2
1-e2
∂i
1
2k
×
+
-
Первые интегралы системы описываются равен-
Γ(1 - 2n)Γ(1 + 2n)
Γ(1 - 2n)Γ(1 + 2n)
ствами
)
]}
2k
a=c0,
(1 - e2) cos2 i = c1, R∗∗ = c2.
− Γ(2 - 2n)Γ(2 + 2n)e + O(e2)sin2nω.
Второй из этих интегралов принято называть инте-
гралом Лидова-Козаи. Заметим, что впервые ин-
Действительно, коэффициенты при e0, e1 обраща-
ются в ноль, так как целые числа m = 0, -1, -2, . . .
теграл был получен в работе фон Цейпеля (1910),
являются полюсами первого порядка гамма-
позже — в статье Моисеева (1945). С его помощью
исключаем угол i:
функции Γ(z). Как следствие, производная равна
(
√
)
нулю при e = 0.
c1
i = arccos
±
,
Отсюда получаем
1-e2
∂R
из усредненной силовой функции R∗∗ получаем ре-
∼ e2 sin2ω.
∂ω
дуцированную систему уравнений с одной степенью
свободы:
Отметим, что ранее это отношение было получено
√
√
в работе Зиглина (1976) с помощью специального
de
1-e2 ∂R
dω
1-e2 ∂R
преобразования усредненной силовой функции, не
=-
,
=
(16)
dt
na2e
∂ω
dt
na2e
∂e
имеющей явного описания в конечном виде, и пред-
ставленной в виде квадратуры по средней долготе
R= R(e,ω)—результатис-
Силовая функция
точки P .
ключения угла i. Очевидно, что интеграл энергии
Разложим редуцированную функциюR (e, ω) в
уравнений (16) имеет видR (e, ω) = const.
ряд по (a/rJ ) и удержим члены до второго порядка
Из интеграла Лидова-Козаи следует ограниче-
включительно:
ние на область изменения оскулирующего эксцен-
fmJa2
триситета орбиты: 0 ≤ e ≤
√1 - c1.
R(2) = -δr0
-
×
(17)
3
a (1 - e2)
8r
J
{[
]
1
(
)
×
√
6
1-e2
3/2 + 9e2 - 6 ×
КАЧЕСТВЕННЫЙ АНАЛИЗ
1-e2
(
)
}
c1 - 1
Для проведения качественного анализа отметим
×
+1
cos 2ω - 3c1 - e2 + 1
e2
прежде всего, что многообразия e = 0, e =
√1 - c1
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
ОБ ЭВОЛЮЦИИ ОРБИТ В ФОТОГРАВИТАЦИОННОЙ КРУГОВОЙ ЗАДАЧЕ
375
c1 = 0.3
1.00
A2
A4
A5
0.75
A3
= 0
0.50
= /2
A1
0.25
A6
0
2
109
4
109
6
109
Рис. 2. Диаграмма равновесий при c1 = 0.3.
Тогда уравнения стационарных точек, записан-
Удержание б ´oльшего количества членов по e в
ные с точностью до членов 5-го порядка малости
(18) мало меняет картину: было проведено чис-
по e, приводятся к виду
ленное сравнение полученных результатов с ре-
{
зультатами расчетов уравнений (18), содержащих
∂R(2)
2δ
члены до 7-го порядка малости по e включительно,
=
-
+
(18)
∂e
a
и показано, что кривые равновесий на рис. 2 незна-
[
]}
чительно смещались в сторону возрастания по оси
a2fmJ
9
+
-
(c1 - 1) cos 2ω + 3c1 + 1 e +
эксцентриситета e.
8r3J
2
Для стационарных значений e, ω долгота восхо-
{
4δ
a2fmJ
дящего угла Ω находится квадратурой из соответ-
+
-
-
[6(2c1 + 1) cos 2ω -
ствующего уравнения системы (16). Видно, что
a
16r3
J}
2√c1
- 9c1 - 1] e3 + · · · = 0,
Ω=Ω0 -
sign(cos i)
∂ R t.
na2
∂c
1
∂R(2)
3a2fmJ
Таким образом, стационарным решениям урав-
=
[3(c1 - 1)e2 +
∂ω
16r3
нений (16) отвечают эллиптические орбиты с фоку-
J
сом в основном притягивающем теле, имеющие по-
+ (2c1 + 1)e4 + . . . ] sin 2ω = 0.
стоянный угол наклона i по отношению к плоскости
движения основных тел, медленно и равномерно
Множество стационарных решений имеет вид
прецессирующие вокруг нормали к этой плоскости.
e = e(δ,ω,c1), ω = {0,π/2}. Следующие резуль-
При этом большая полуось орбиты совпадает с
таты имеют место для параметров a, e из диа-
линией узлов SN (случай ω = 0) во все время
пазона 0 ≤ a/rJ ≤ 0.5, 0 ≤ e < 1. Кривые рав-
движений либо перпендикулярна ей (случай ω =
новесий e(δ, ω, c1) построены при разных зна-
= π/2).
чениях ω и фиксированном c1 (рис. 2) для си-
Точке A5 отвечает бифуркация типа “седло-
стемы Солнце-Юпитер-спутник, когда a/rJ =
узел”, неустойчивые равновесия выделены пунк-
= 0.384, mJ = 0.00095, rJ = 5.204 a.e., c1 = 0.3,
тиром. В точках A2, A4, A6 исчезают реальные
0 ≤ e ≤ 1,
0 ≤ δ ≤ 6 × 10-9. На этом рисунке
равновесия, так как кривые равновесия уходят в
указаны некоторые реперные точки Aj с коор-
мнимые области e >
√1 - c1 либо e < 0 (на рис. 2
динатами (δj , ej ): A1 = (0, 0.3998), A2 = (0.054 ×
показана вся кривая равновесий при ω = π/2, со-
× 10-9, 0.83666), A3 = (1.15 × 10-9, 0.6432), A4 =
держащая куски, принадлежащие мнимой обла-
= (1.274 × 10-9, 0.83666),
A5 = (1.365 × 10-9,
сти e >
√1 - c1 возможных движений). Точке A3
0.7683), A6 = (5.102 × 10-9, 0).
отвечают сразу две одинаковые прецессирующие
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
376
ДОБРОСЛАВСКИЙ, КРАСИЛЬНИКОВ
0.8
0.6
0.4
0.2
B
A
0
0
3
4
2
4
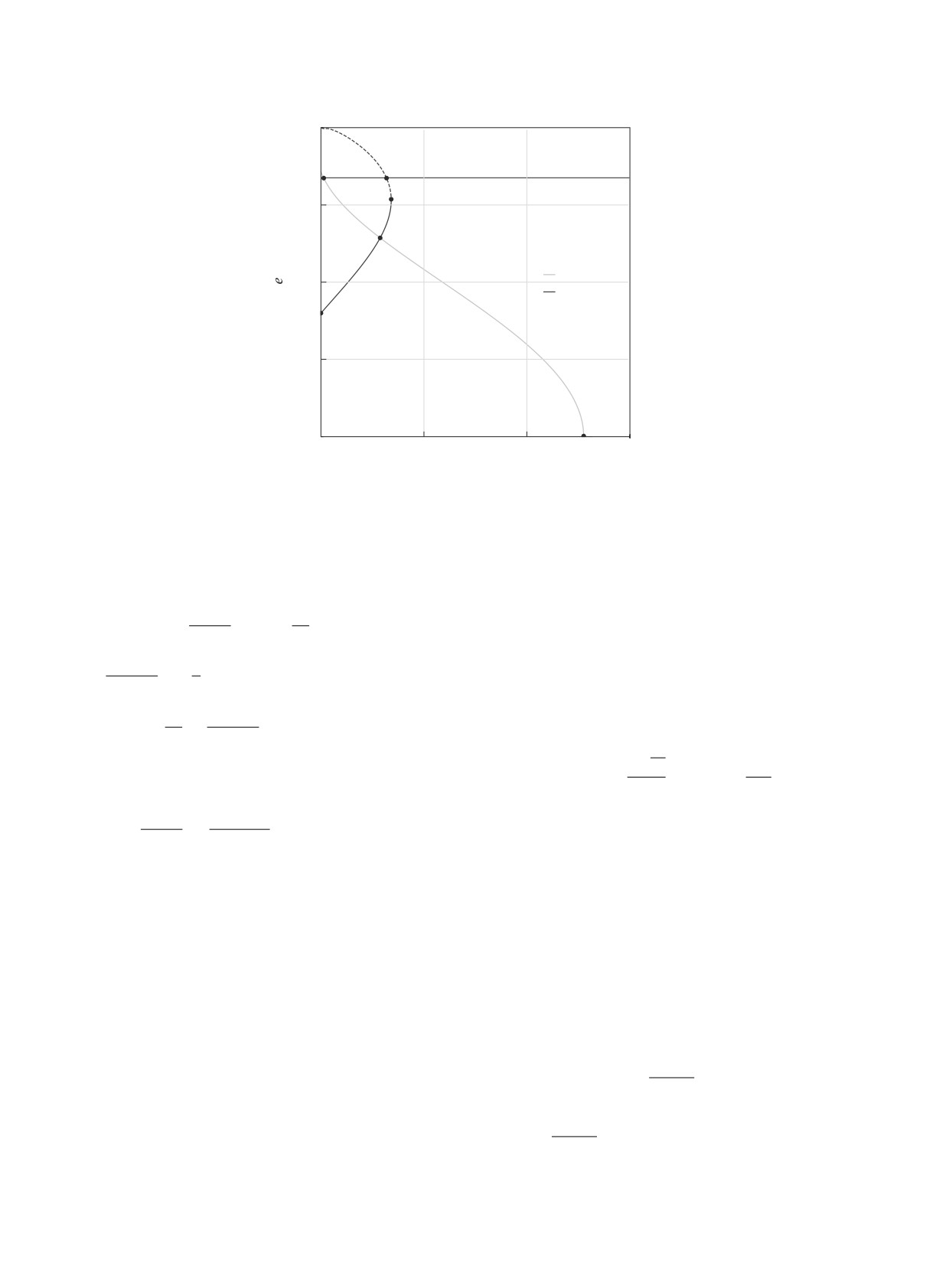
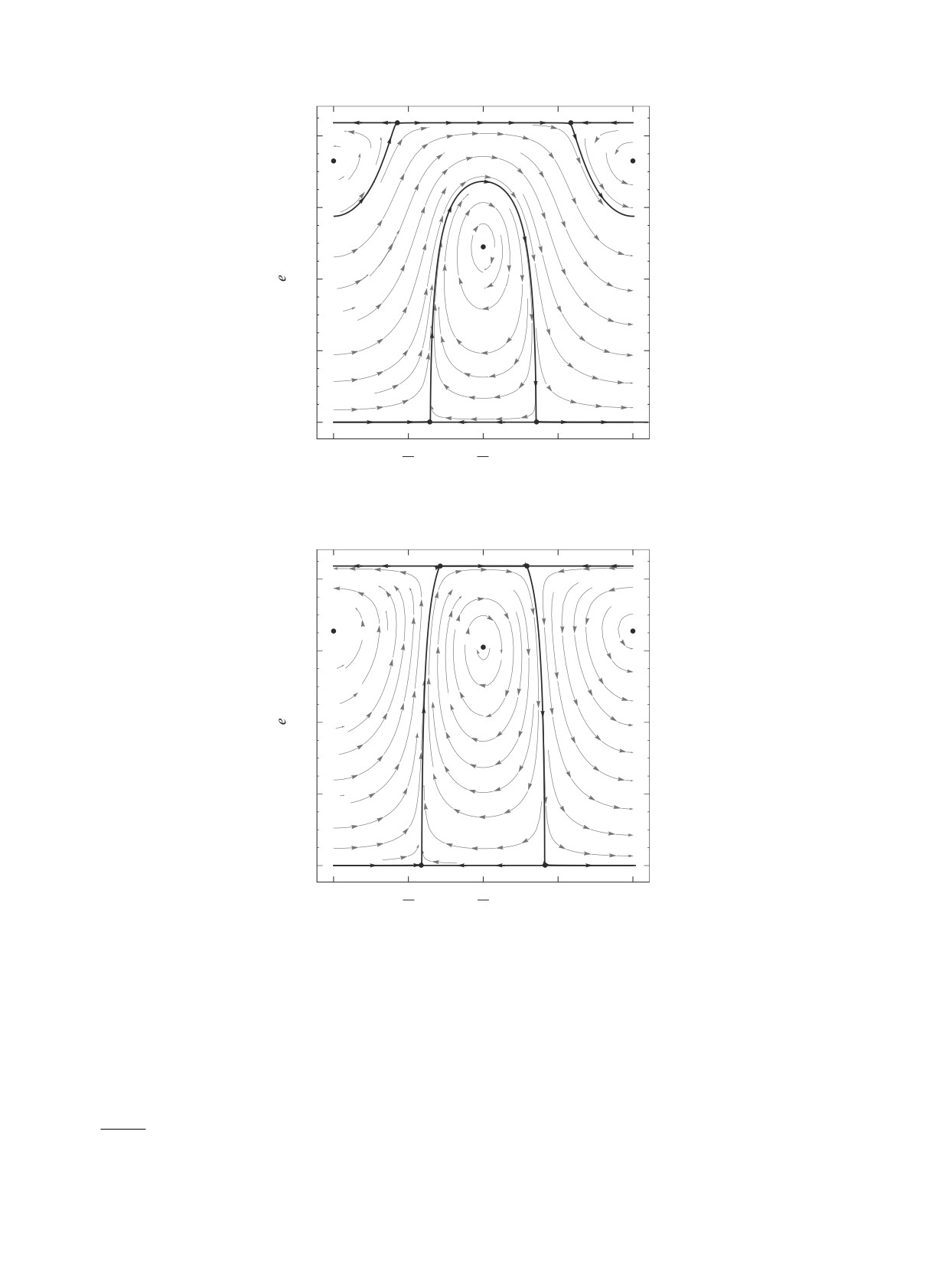
Рис. 3. Фазовый портрет при δ = 0.
эллиптические орбиты с фокусом в Солнце, но с
чественно сохраняется для любого δ из интервала
разными аргументами перицентра. Точке A1 со-
(δ1, δ2). Здесь можно видеть стационарную точку
ответствует равновесие классической задачи трех
типа центр с координатами e = 0.2472, ω = π/2.
тел, когда δ = 0.
В области A наблюдаем либрационные движения
Из рис. 2 следует, что на малом интервале
линии апсид, в то же время в области B линия
апсид совершает ротационное движение в сторо-
(δ1, δ2) = (0, 0.054 × 10-9) имеем одно устойчивое
ну увеличения аргумента перицентра. На фазовом
положение равновесия (случай ω = π/2). На ин-
портрете изображены два интегральных многооб-
тервале δ ∈ (δ2, δ4) = (0.054 × 10-9, 1.274 × 10-9)
разия e = 0 и e =
√1 - c1, ограничивающие собой
появляется второе устойчивое положение равнове-
область возможных движений. Эти интегральные
сия для значения параметра ω = 0. На интервале
многообразия указаны также и на других фазовых
δ ∈ (δ4,δ5) = (1.274 × 10-9,1.365 × 10-9) появля-
портретах.
ется еще одно неустойчивое равновесие на кривой
ω = π/2. В точке бифуркации A5 два равнове-
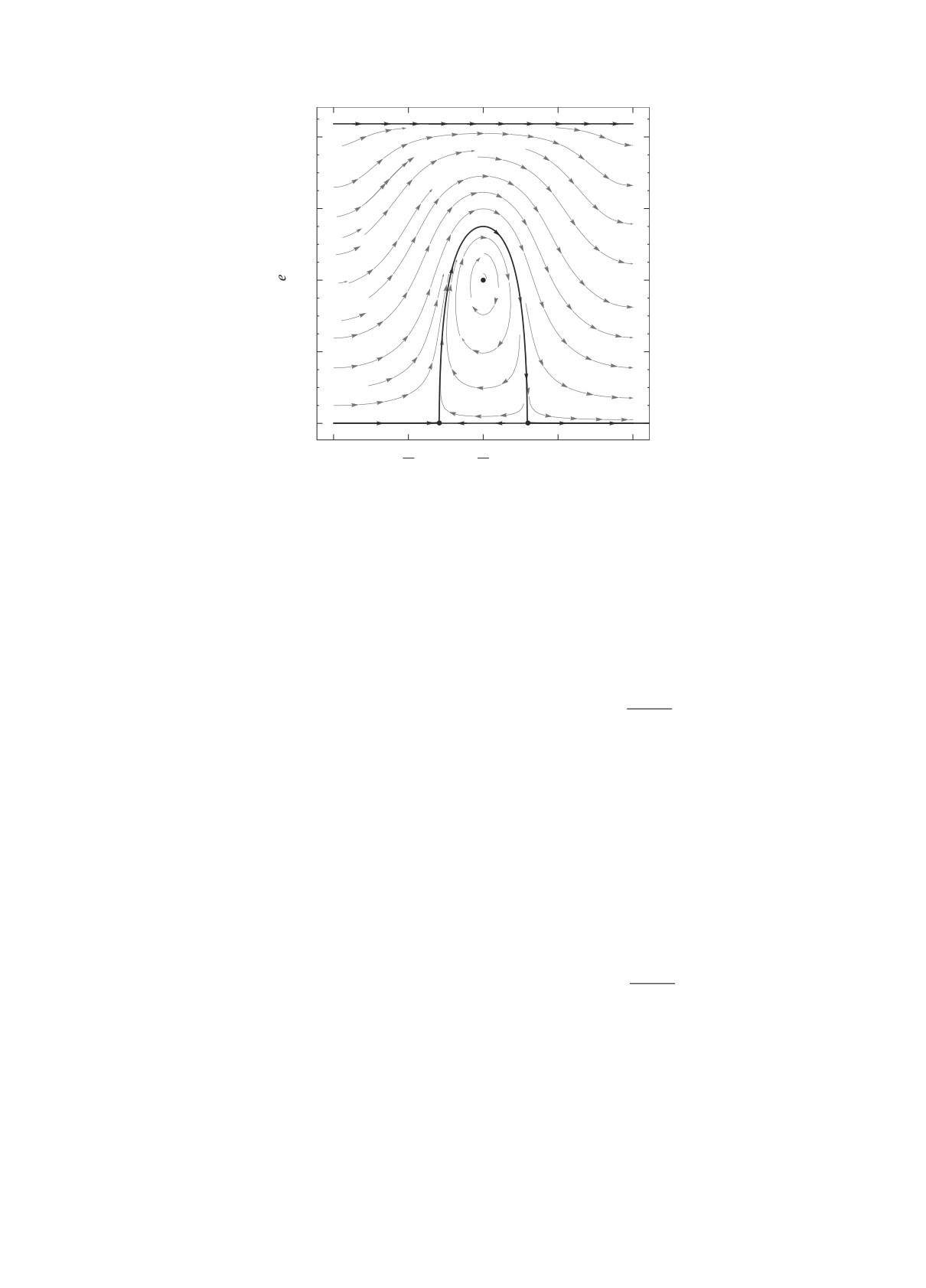
На фазовом портрете рис. 4, построенном для
сия на кривой ω = π/2 сливаются в одно и да-
значений параметров c1 = 0.3, a = 2 а.е., δ = 0.5 ×
лее пропадают. Так что на интервале δ ∈ (δ5, δ6) =
× 10-9 ∈ (δ2, δ4), присутствуют две стационарные
= (1.365 × 10-9, 5.102 × 10-9) остается единствен-
точки типа “центр” для значений ω = 0 и ω = π/2.
ное устойчивое равновесие, принадлежащее кри-
В окрестности стационарных точек имеем либра-
ционные движения, в области B — ротационные
вой ω = 0, а при δ ∈ (δ6, +∞) положения равнове-
сия исчезают полностью.
движения в сторону увеличения аргумента пери-
центра. При увеличении δ наблюдаем вытягивание
Для всех перечисленных интервалов по δ, путем
области A по вертикали вверх, до тех пор, пока
численного интегрирования уравнений (16), были
верхняя точка этой области не коснется верхнего
построены фазовые портреты колебаний, изобра-
многообразия e =
√1 - c1. Точка касания, являю-
женные на рис. 3-9. Результаты численного инте-
щаяся равновесием на этом многообразии, раздва-
грирования были подтверждены построением ли-
ивается при дальнейшем увеличении параметра δ,
ний уровня интегралаR(2). Поскольку ряд Фурье
появляются две сепаратрисы (гетероклинические
дляR содержит только четные гармоники cos 2nω,
траектории), соединяющие нижние равновесия с
то интегральные кривыеR = h симметричны отно-
верхними (рис. 5). Параметр δ = 1.0352 × 10-9 (см.
сительно ω = π/2. Фазовый портрет на рис. 3 по-
рис. 5) является бифуркационным, так как ведет
лучен для значений параметров c1 = 0.3, a = 2 а.е.,
к расщеплению сепаратрис. Каждая из двух се-
δ = 0 и качественно совпадает с фазовым портре-
паратрис расщепляется на пару кривых так, что
том в статье (Вашковьяк, 1981). Эта картинка ка-
две вновь появившиеся кривые из области A стре-
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
ОБ ЭВОЛЮЦИИ ОРБИТ В ФОТОГРАВИТАЦИОННОЙ КРУГОВОЙ ЗАДАЧЕ
377
0.8
C
C
0.6
0.4
B
0.2
A
0
0
3
4
2
4
Рис. 4. Фазовый портрет при δ = 0.5 × 10-9.
0.8
0.6
0.4
B
B
0.2
A
0
0
3
4
2
4
Рис. 5. Фазовый портрет при δ = 1.0352 × 10-9.
мятся асимптотически (при t → ±∞) к верхним
явлению сначала узкой, а потом расширяющейся
равновесиям, образуя единую кривую, ограничи-
области ротационных движений, когда аргумент
вающую новую либрационную область B (рис. 6).
перицентра ω монотонно убывает. Вдоль этих тра-
Пара крайних кривых, появившихся слева и справа
екторий движения орбита спутника медленно по-
от области A рис. 5, сохраняют асимптотическое
ворачивается в своей оскулирующей плоскости в
стремление к нижним равновесиям при t → ±∞,
направлении, противоположном случаю δ = 0.
асимптотически приближаясь к многообразию e =
На фазовом портрете рис. 7, отвечающем слу-
=
√1 - c1 (рис. 6).
чаю δ = 1.3 × 10-9 ∈ (δ4, δ5), появляется дополни-
Описанное расщепление сепаратрис ведет к по-
тельно неустойчивая стационарная точка D, распо-
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
378
ДОБРОСЛАВСКИЙ, КРАСИЛЬНИКОВ
0.8
0.6
C
C
0.4
B
0.2
A
0
0
3
4
2
4
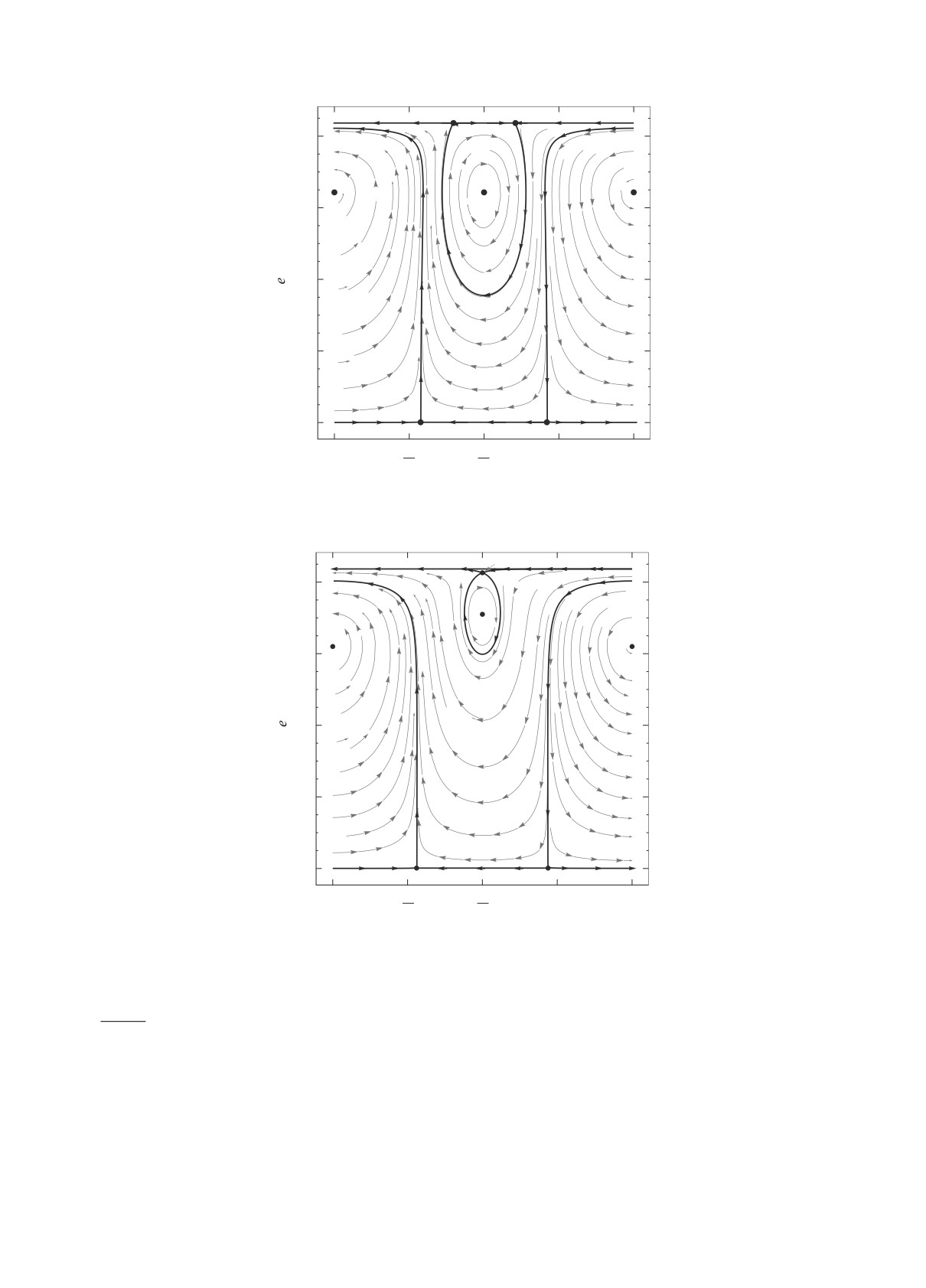
Рис. 6. Фазовый портрет при δ = 1.1497 × 10-9.
D
0.8
B
B
C
0.6
0.4
A
0.2
0
0
3
4
2
4
Рис. 7. Фазовый портрет при δ = 1.3 × 10-9.
ложенная вблизи интегрального многообразия e =
точек, имеем вековой уход линии апсид в сторону
уменьшения аргумента перицентра.
=
√1 - c1. Дальнейшее увеличение δ ведет к сли-
янию устойчивой и неустойчивой точек при δ =
Показано, что члены четвертого и шестого по-
= 1.365 × 10-9 и последующему их исчезновению
рядков малости по a/rJ в редуцированной силовой
при сохранении стационарной точки на второй вет-
функции
R практически не влияют на фазовый
ви равновесий ω = 0 (рис. 8, случай δ ∈ (δ5, δ6)).
портрет колебаний, незначительно смещая точки
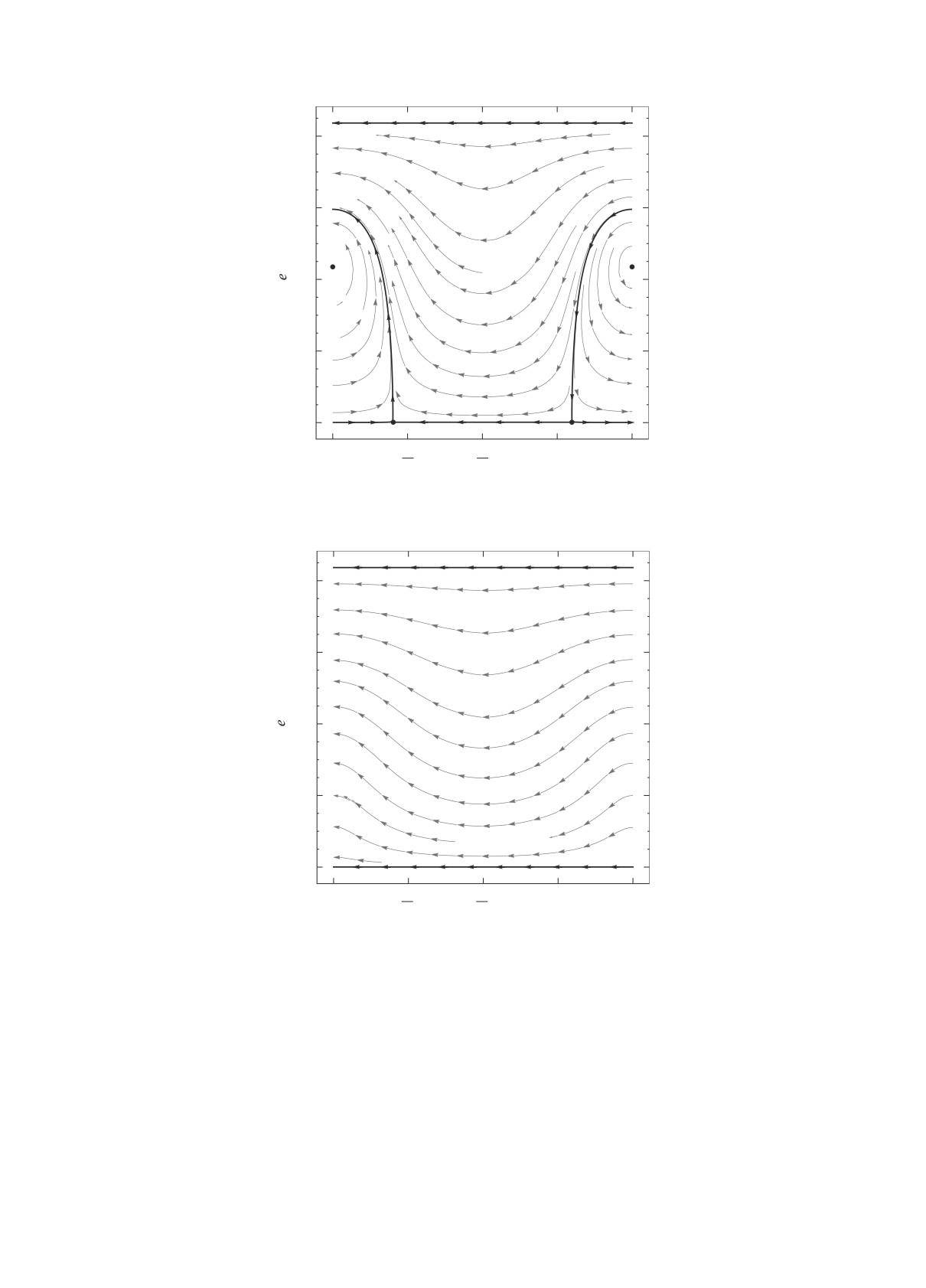
Для случая δ > δ6 фазовый портрет колебаний
равновесий по вертикальной прямой, мало меняя
изображен на рис. 9. Он не содержит стационарных бифуркационные значения δ.
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
ОБ ЭВОЛЮЦИИ ОРБИТ В ФОТОГРАВИТАЦИОННОЙ КРУГОВОЙ ЗАДАЧЕ
379
0.8
0.6
0.4
0.2
B
A
B
0
0
3
4
2
4
Рис. 8. Фазовый портрет при δ = 2.88 × 10-9.
0.8
0.6
0.4
0.2
0
0
3
4
2
4
Рис. 9. Фазовый портрет при δ = 5.5 × 10-9.
ЗАКЛЮЧЕНИЕ
и истинной аномалии невозмущенного движения
спутника. Впервые получено явное аналитическое
Мы рассмотрели оскулирующие эллиптические
выражение усредненной силовой функции в виде
движения астероида (солнечного зонда) бесконеч-
ряда Фурье, коэффициенты которого выражаются
но малой массы вокруг звезды (Солнца) под дей-
ствием двух возмущений: гравитационного притя-
через известные специальные функции. Аналити-
жения со стороны внешней планеты (Юпитера)
ческое выражение усредненной силовой функции
и солнечного светового давления. Использована
позволяет быстро и эффективно получить любое
схема Гаусса двукратного усреднения возмущен-
приближение функции по малому параметру a/rJ ,
ной силовой функции задачи по долготе планеты
просто доказать интегральность некоторых много-
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021
380
ДОБРОСЛАВСКИЙ, КРАСИЛЬНИКОВ
образий, в частности, интегральность многообра-
7.
Брайант (R.W. Bryant), Astron. J. 66, 430 (1961).
зия e =
√1 - c1 в редуцированной системе, что яв-
8.
Вашковьяк М.А., Космич. исслед. 19, 5 (1981).
ляется новым результатом и в классической задаче
9.
Вашковьяк С.Н., Вест. Моск. ун-та, Сер. 3. Физ.
трех тел.
Астрон. 5, 584 (1974).
10.
Вашковьяк С.Н., Астрон. журн. 53, 1085 (1976)
Анализ эволюционных движений показал, что
[S.N. Vashkov’yak, Sov. Astron. 20, 615 (1976)].
влияние солнечного давления весьма существенно
11.
Гамильтон, Кривов (D.P. Hamilton and A.V. Krivov),
уже при малых значениях коэффициента све-
Icarus 123, 503 (1996).
тового давления, когда δ ∼ 10-9: в диапазоне
12.
Градштейн И.С., Рыжик И.М., Таблицы интегра-
0 ≤ a/rJ ≤ 0.5,
0 ≤ e < 1 появляется дополни-
лов, сумм, рядов и произведений (М.: Физматгиз,
тельная ветвь семейства стационарных движений
1963), с. 1100.
e(δ) = const, ω = 0, наблюдается бифуркация рав-
13.
Доброславский А.В., Красильников П.С., Письма
новесий типа “седло-узел” на ветви традиционного
в Астрон. журн. 44, 618 (2018) [A.V. Dobroslavskiy
случая ω = π/2, исчезают реальные равновесия,
and P.S. Krasilnikov, Astron. Lett. 44, 567 (2018)].
когда семейство стационарных точек выходит за
14.
Доброславский А.В., Красильников П.С.,
границы области возможных движений.
Прикладная матем. и мех.
84,
26
(2020)
Существенно осложняется фазовый портрет ко-
[A.V. Dobroslavskiy and P.S. Krasilnikov, Mechanics
лебаний в сравнении с фазовым портретом оску-
of Solids 55, 999 (2020)].
лирующих движений в классической круговой за-
15.
Доброславский (A.V. Dobroslavskiy), Cosmic Res.
даче трех тел. К примеру, появляются седловые
58, 501 (2020).
точки вблизи многообразия e =
√1 - c1 в обла-
16.
Дубошин Г.Н., Теория притяжения (М.: Физмат-
сти (δ4, δ5), наблюдается расщепление сепаратрис
гиз, 1961), с. 288.
для значений параметра δ из интервала (δ2, δ4),
17.
Дубошин Г.Н., Небесная механика. Основные за-
что приводит к изменению направления эволюции
дачи и методы (М.: Наука, 1964), с. 800.
аргумента перицентра ω на противоположное в
18.
Зиглин С.Л., Исследование предельных случа-
случае ротационных движений.
ев осредненной задачи трех тел, (Диссер-
Указанные значения параметра δ по порядку
тация на соискание степени кандидата физико-
величины характерны для Parker Solar Probe. Та-
математических наук
01.02.01. Москва,
1976),
ким образом, полученные результаты могут быть
с. 122.
использованы при оценке параметров движения
19.
Козаи (Y. Kosai), Smithsonian Astrophys. Obs.
при учете светового давления на данный зонд.
Special Rept. 56, 25 (1961).
20.
Козаи (Y. Kozai), Astron. J. 67, 591 (1962).
Авторы признательны рецензенту за сделанные
замечания.
21.
Кривов и др. (A.V. Krivov, L.L. Sokolov, and
V.V. Dikarev), Celest. Mech. Dyn. Astron. 63, 313
Исследования выполнены в Московском авиа-
(1996).
ционном институте при поддержке Российского
22.
Лидов М.Л., Искусственные спутники Земли 8, 5
фонда фундаментальных исследований (грант
(1961).
№ 18-01-00820 А).
23.
Лидов (M.L. Lidov), Planet. Space Sci. 9, 719 (1962).
24.
Моисеев Н.Д., Тр. ГАИШ XV, 100 (1945).
СПИСОК ЛИТЕРАТУРЫ
25.
Мюзен (P. Musen), J. Geophys. Res. 65, 1391 (1960).
1. Аксенов Е.П., Тр. ун-та дружбы народов им. П. Лу-
26.
Паркинсон и др. (R.W. Parkinson, H.M. Jones, and
мумбы 21, 184 (1967).
I.I. Shapiro), Science 131, 920 (1960).
2. Аксенов Е.П., Теория движения искусственных
27.
Сабо (A. Szabo), Nat. Astron. 2, 829 (2018).
спутников Земли (М.: Наука, 1977), с. 360.
28.
Сидоренко (V.V. Sidorenko), Celest. Mech. Dyn.
3. Аксенов Е.П., Астрон. журн. 56,
419
(1979a)
Astron. 130, 2 (2018).
[E.P. Aksenov, Sov. Astron. 23, 236 (1979a)].
29.
Тихонов и др. (A.A. Tikhonov, K.A. Antipov,
4. Аксенов Е.П., Астрон. журн. 56,
623
(1979б)
D.G. Korytnikov, and D.Yu. Nikitin), Acta
[E.P. Aksenov, Sov. Astron. 23, 351 (1979b)].
Astronautica 141, 219 (2017).
5. Александров, Тихонов (A.Yu. Aleksandrov and
30.
Феррас-Мелло (S. Ferraz-Mello), Comptes rendus
A.A. Tikhonov), Aerospace Science and Technology
de l’Acad ´emie des Sciences. Paris. 258, 463 (1964).
104 (2020).
31.
фон Цейпель (H. von Zeipel), Astronomische
6. Амелькин Н.И., Докл. РАН
489,
570
(2019)
Nachrichten 183, 345 (1910).
[N.I. Amel’kin, Doklady Physics 489, 570 (2020)].
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 47
№5
2021