ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2022, том 48, № 7, с. 492-505
ПАРАМЕТРЫ ГАЛАКТИЧЕСКОЙ СПИРАЛЬНОЙ ВОЛНЫ
ПЛОТНОСТИ ПО МАЗЕРАМ С ОШИБКАМИ
ПАРАЛЛАКСОВ МЕНЕЕ 10%
© 2022 г. В. В. Бобылев1*, А. Т. Байкова1
1Главная (Пулковская) астрономическая обсерватория РАН, Санкт-Петербург, Россия
Поступила в редакцию 10.04.2022 г.
После доработки 26.05.2022 г.; принята к публикации 20.06.2022 г.
Изучена кинематика галактических мазерных источников и радиозвезд с измеренными методом
РСДБ тригонометрическими параллаксами и собственными движениями. Рассматривались мазеры
с относительными ошибками тригонометрических параллаксов менее 10%. По ним определены
параметры вращения Галактики. В частности, линейная скорость вращения Галактики на околосол-
нечном расстоянии R0 найдена равной 244.4 ± 4.3 км/с (для принятого значения R0 = 8.1 ± 0.1 кпк).
Выполнен совместный и раздельный спектральный анализ радиальных, остаточных тангенциальных
и вертикальных скоростей мазеров. Так, по вертикальным скоростям мазеров получена оценка
амплитуды скорости возмущения fW = 5.2 ± 1.5 км/с с длиной волны λW = 2.6 ± 0.7 кпк, что говорит
в пользу представления о влиянии спиральной волны плотности на вертикальные скорости звезд.
По 104 мазерам из околосолнечной окрестности радиусом 3 кпк в результате совместного решения
получены оценки скорости радиальных fR = 6.7 ± 1.1 км/с и тангенциальных fθ = 2.6 ± 1.2 км/с
возмущений, длины волны возмущений λ = 2.1 ± 0.3 кпк, а также фазы Солнца в спиральной
галактической волне плотности χ⊙ = -148 ± 15◦. Подтверждено наличие волны Рэдклиффа в про-
странственном распределении мазеров и радиозвезд, принадлежащих Местному рукаву.
Ключевые слова: мазеры, радиозвезды, кинематика, спиральная волна плотности, волна Рэдклиффа,
вращение Галактики.
DOI: 10.31857/S0320010822070014
ВВЕДЕНИЕ
составляют менее 0.020 миллисекунд дуги (мсд).
Например, известен результат практически прямо-
Известны несколько классов объектов, пред-
го определения этим методом измерения расстоя-
ставляющих важнейшее значение для изучения
ния от Солнца до центра Галактики, R0. Речь идет
структуры и кинематики Галактики благодаря воз-
об измерении параллакса радиоисточника Sgr B,
можности оценить расстояния до них с приемлемой
π = 0.129 ±0.012 мсд, чтодает оценку R0 = 7.9+0.8-0.7
точностью. К ним относятся, например, звездные
(Рид и др., 2009).
скопления, OB-звезды, или цефеиды. Применение
РСДБ-метода в задаче по измерению тригономет-
Выполнено достаточно много исследований, по-
рических параллаксов галактических мазеров сде-
священных изучению фундаментальных свойств
лало их первоклассными объектами для изучения
галактического диска с использованием мазеров.
Галактики. Причем в настоящей работе нас будут
Отметим работы Хонмы и др. (2012), Санны и др.
интересовать только мазеры, связанные с наиболее
(2017), Расторгуева и др. (2017), Сюя и др. (2018),
молодыми звездами и протозвездами, которые на-
Рида и др. (2019), Хироты и др. (2020), Бобылева
ходятся в областях активного звездообразования.
и др. (2020), где по различным выборкам мазе-
ров были получены оценки расстояния R0, скоро-
В настоящее время имеется около 200 триго-
сти вращения околосолнечной окрестности вокруг
нометрических параллаксов мазеров (Рид и др.,
центра Галактики V0, а также геометрические ха-
2019; Хирота и др., 2020), измеренных с высокой
рактеристики спирального узора или кинематиче-
астрометрической точностью. Случайные ошибки
ские параметры спиральной волны плотности.
РСДБ-измерений большинства из этих источников
К настоящему времени практически все опуб-
*Электронный адрес: vbobylev@gaoran.ru
ликованные результаты РСДБ-измерений триго-
492
ПАРАМЕТРЫ ГАЛАКТИЧЕСКОЙ СПИРАЛЬНОЙ ВОЛНЫ
493
нометрических параллаксов мазеров получены ин-
где скорость U направлена от Солнца параллельно
струментами, расположенными в северном полу-
направлению на центр Галактики, точнее, на ось
шарии Земли. Поэтому, хотя и распределены эти
галактического вращения, V - в направлении вра-
источники по огромному галактическому простран-
щения Галактики и W на северный галактический
ству, все же имеется пустая зона в четвертом галак-
полюс. Две скорости: VR, направленную радиаль-
тическом квадранте. Измерений, впрочем, уже до-
но от галактического центра, и ортогональную ей
статочно для успешной оценки по пространствен-
скорость Vcirc, направленную вдоль вращения Га-
ному распределению, например, углов закрутки
лактики, можем найти на основе следующих соот-
спиральных рукавов (Рид и др., 2019) или значения
ношений:
R0 (Никифоров, Веселова, 2018).
Vcirc = U sin θ + (V0 + V )cos θ,
(2)
Радиоастрономы, выполняющие РСДБ-наблю-
VR = -U cos θ + (V0 + V )sin θ,
дения мазеров, постоянно отмечают наличие от-
клонений от круговых движений этих объектов с
где позиционный угол θ удовлетворяет соотноше-
величиной 10-20 км/с (Ву и др., 2019; Иммер и др.,
нию tg θ = y/(R0 - x), x, y, z — прямоугольные
2019; Сакаи и др., 2019; Хирота и др., 2020; Сюй и
гелиоцентрические координаты звезды (вдоль со-
др., 2021). Как известно, многие мазерные источ-
ответствующих осей x, y, z направлены скорости
ники связаны с двойными звездными системами,
U, V , W), V0 —линейная скорость вращения Га-
с расширяющимися, зачастую несимметричными,
лактики на околосолнечном расстоянии R0.
оболочками вокруг звезд. Не исключена также
принадлежность их к убегающим звездам. Все это
Определение параметров вращения Галактики
ведет к увеличению дисперсии наблюдаемых ско-
ростей этих объектов. Однако наличие системати-
Для определения параметров кривой галакти-
ческих отклонений от круговых движений наиболее
ческого вращения используем уравнения, получен-
молодых звезд вообще и мазерных источников, в
ные из формул Боттлингера, в которых произведе-
частности, мы связываем (Бобылев, Байкова, 2010;
но разложение угловой скорости Ω в ряд до членов
Бобылев и др., 2020) с влиянием галактической
второго порядка малости r/R0 :
спиральной волны плотности.
Vr = -U⊙ cos bcos l - V⊙ cos bsin l -
(3)
Целью настоящей работы является переопреде-
− W⊙ sinb + R0(R - R0)sinlcosbΩ′0 +
ление параметров вращения Галактики и галакти-
ческой спиральной волны плотности с использо-
+ 0.5R0(R - R0)2 sin l cos bΩ′′0,
ванием новейших данных о мазерных источниках
и радиозвездах с тригонометрическими параллак-
Vl = U⊙ sinl - V⊙ cosl - rΩ0 cos b +
(4)
сами и собственными движениями, измеренными
+ (R - R0)(R0 cos l - r cos b)Ω′0 +
РСДБ-методом. Для достижения этой цели мы ис-
пользуем наиболее точные данные — мазеры с от-
+ 0.5(R - R0)2(R0 cos l - r cos b)Ω′′0,
носительными ошибками параллаксов менее 10%.
Vb = U⊙ cos l sin b + V⊙ sin l sin b -
(5)
- W⊙ cosb - R0(R - R0)sinlsinbΩ′0 -
МЕТОДЫ
- 0.5R0(R - R0)2 sin l sin bΩ′′0,
Из наблюдений для каждой звезды имеем лу-
чевую скорость Vr, направленную вдоль луча зре-
где R — расстояние от звезды до оси вращения Га-
ния, и две проекции тангенциальной скорости Vl =
лактики R2 = r2 cos2 b - 2R0r cos b cos l + R20. Ско-
= 4.74rμl cos b и Vb = 4.74rμb, направленные вдоль
рости (U, V, W )⊙ являются средней групповой ско-
галактических долготы l и широты b соответствен-
ростью выборки, они отражают пекулярное дви-
но,
4.74
является коэффициентом размерности.
жение Солнца, поэтому взяты с обратными зна-
Все три скорости выражены в км/с, а r — гелио-
ками. Ω0 является угловой скоростью вращения
центрическое расстояние звезды в кпк. Компонен-
Галактики на солнечном расстоянии R0, параметры
ты собственного движения μl cos b и μb выражены
Ω′0 и Ω′′0 — соответствующие производные угловой
в мсд/год (миллисекунды дуги в год). Через ком-
скорости вращения V0 = R0Ω0.
поненты Vr, Vl, Vb вычисляются скорости U, V , W ,
Мы принимаем R0 равным 8.1 ± 0.1 кпк. Это
направленные вдоль прямоугольных галактических
значение было выведено как средневзвешенное из
осей координат:
большого количества современных индивидуаль-
U = Vr coslcosb - Vl sinl - Vb coslsinb,
(1)
ных оценок в работе Бобылева, Байковой (2021).
Интересно отметить высокоточное современное
V = Vr sinlcosb + Vl cosl - Vb sinlsinb,
индивидуальное измерение R0, полученное Абуте-
W = Vr sinb + Vb cosb,
ром и др. (2019) из анализа шестнадцатилетнего
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
494
БОБЫЛЕВ, БАЙКОВА
ряда наблюдений движения звезды S2 вокруг
анализа является выделение периодичности из ря-
массивной черной дыры Sgr A∗ в центре Галакти-
да данных в соответствии с принятой моделью,
ки, R0 = 8.178 ± 0.013 (стат.) ± 0.022 (сист.) кпк.
описывающей спиральную волну плотности с па-
Правда, в последней публикации этого коллектива
раметрами f, λ (или i) и χ⊙.
(Абутер и др., 2021) показано наличие инстру-
В результате учета логарифмического характера
ментальных аберраций. Поэтому все предыдущие
спиральной волны, а также позиционных углов
оценки коллаборации, начиная с 2018 г., были
объектов θn, наш спектральный анализ рядов воз-
пересмотрены, и предложено уточненное значение
мущений скоростей сводится к вычислению квад-
R0 = 8.275 ± 0.009 ± 0.033 кпк.
рата амплитуды (спектра мощности) стандартного
Решение условных уравнений вида
(3)-(5)
преобразования Фурье (Байкова, Бобылев, 2012):
ищется методом наименьших квадратов (МНК).
(
)
∑
1
2πR′n
В итоге получаем оценку шести следующих неиз-
Vλk =
V ′n(R′n)exp -j
,
(9)
вестных: (U, V, W )⊙, Ω0, Ω′0 и Ω′′0. Отметим, что
N
λk
n=1
скорости U, V и W в уравнениях (2) освобождены
от пекулярной скорости Солнца U⊙, V⊙ и W⊙
гд
Vλk — k-я гармоника преобразования Фурье с
со значениями, найденными в результате МНК-
длиной волны λk = D/k, D — период анализируе-
решения кинематических уравнений вида (3)-(5).
мого ряда,
R′n = R0 ln(Rn/R0),
(10)
Определение параметров волны плотности
V ′n(R′n) = Vn(R′n)exp(jmθn).
Влияние спиральной волны плотности в ради-
Пиковому значению спектра мощности Speak соот-
альных VR и остаточных тангенциальных скоро-
ветствует искомая длина волны λ. Угол закрутки
стях ΔVcirc является периодическим с амплитудой
спиральной волны плотности находится из вы-
около 10-15 км/с. Впрочем, уточнение конкретных
ражения (8). Амплитуду и фазу возмущений мы
значений амплитуд возмущений является одной из
находим в результате подгонки гармоники с най-
задач настоящего исследования. Согласно линей-
денной длиной волны к измеренным данным. Для
ной теории волн плотности Линя и Шу (1964),
оценки амплитуды возмущений также может быть
скорости возмущений удовлетворяют следующим
использовано соотношение
√
соотношениям:
fR(fθ,fW ) = 2
Speak.
(11)
VR = -fR cos χ,
(6)
При спектральном анализе оценка ошибок иско-
ΔVcirc = fθ sin χ,
мых параметров была выполнена с применением
статистического моделирования методом Монте-
где
Карло на основе выполнения 100 циклов вычис-
χ = m[ctg(i)ln(R/R0) - θ] + χ⊙
(7)
лений. При этом числе циклов средние значения
решений практически совпадают с решениями, по-
фаза спиральной волны (m — количество спираль-
лученными по исходным данным без добавления
ных рукавов, i — угол закрутки спирального узора,
ошибок измерения. Ошибки измерения добавля-
i < 0 для закручивающейся спирали, χ⊙ — ради-
альная фаза Солнца в спиральной волне); fR и
лись в скорости VR, ΔVcirc и W , а также в ошибки
координат источников x, y, z.
fθ — амплитуды возмущений радиальных и танген-
циальных скоростей, которые считаются положи-
тельными.
ДАННЫЕ
Выявление периодичностей в скоростях VR и
ΔVcirc осуществляется нами на основе спектраль-
Источниками мазерного излучения являются
ного (периодограммного) анализа, который описан
звезды с протяженными газо-пылевыми оболоч-
в работе Байковой, Бобылева (2012). Длина волны
ками, в которых возникает эффект накачки. Эф-
λ (расстояние между соседними отрезками спи-
фектом мазерного излучения обладают как моло-
ральных рукавов, отсчитываемое вдоль радиально-
дые звезды и протозвезды различной массы, так
го направления) вычисляется на основе соотноше-
и старые звезды, например, мириды. В настоящей
ния
работе мы используем наблюдения только молодых
объектов, которые тесно связаны с областями ак-
2πR0/λ = m ctg(|i|).
(8)
тивного звездообразования.
Пусть имеется ряд измеренных скоростей VRn (это
Основными источниками данных в настоящей
могут быть радиальные VR, тангенциальные ΔVcirc
работе являются каталоги Рида и др. (2019) и Хи-
или вертикальные W скорости), n = 1, 2, . . . , N,
роты и др. (2020). В список Рида и др. (2019) вклю-
где N — число объектов. Задачей спектрального
чены данные о 199 мазерах. РСДБ-наблюдения
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
ПАРАМЕТРЫ ГАЛАКТИЧЕСКОЙ СПИРАЛЬНОЙ ВОЛНЫ
495
14
IV
12
10
III
8
6
II
4
2
I
0
6
4
2
0
2
4
6
8
10
Y, кпк
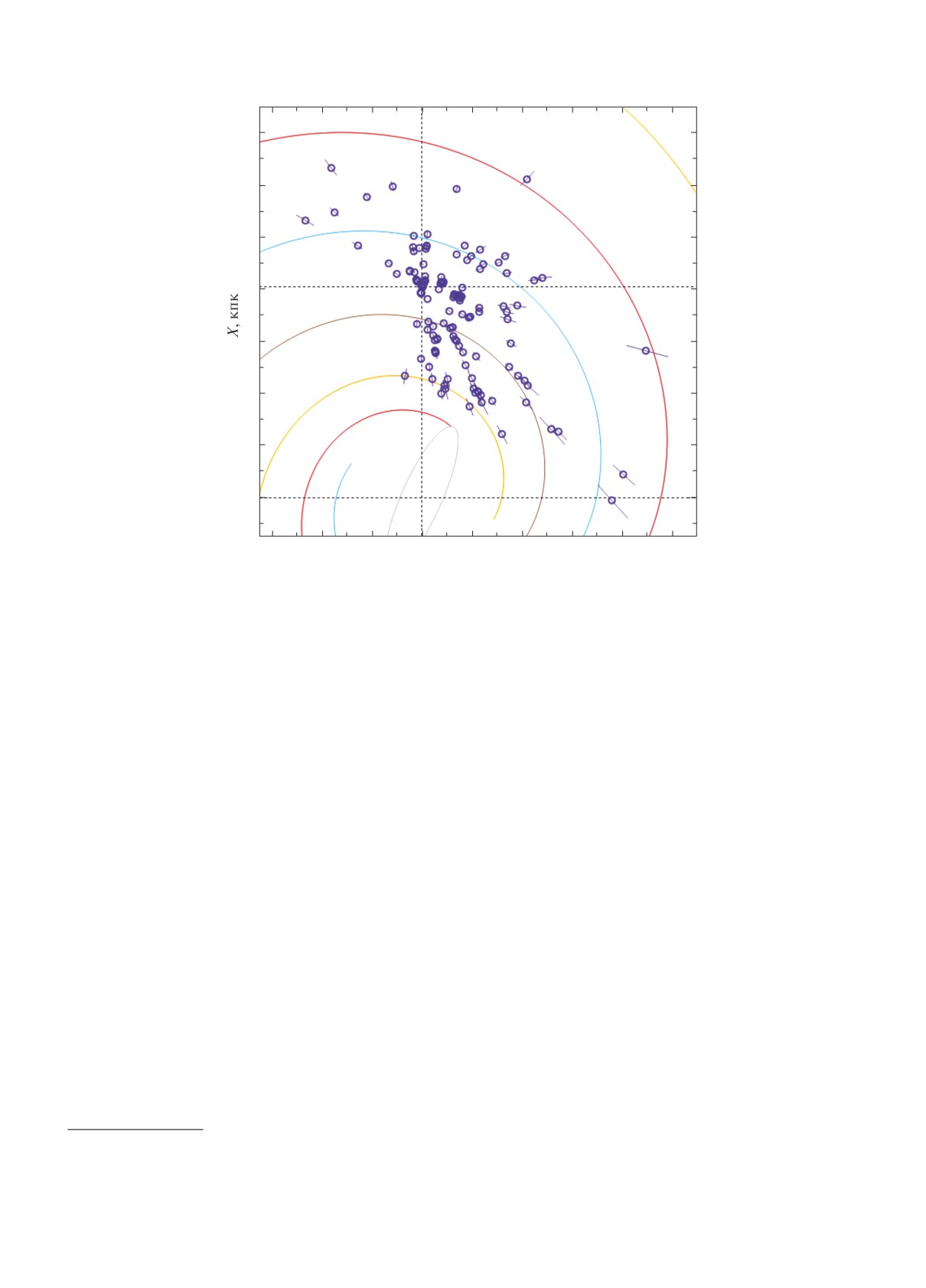
Рис. 1. Распределение 150 мазеров и радиозвезд с ошибками тригонометрических параллаксов менее 10% в проекции
на галактическую плоскость XY , показан четырехрукавный спиральный узор с углом закрутки i = -13◦, отмечен
центральный галактический бар.
проводились на нескольких радиочастотах в рам-
В настоящей работе используются источники
ках проекта BeSSeL (The Bar and Spiral Structure
с относительными ошибками параллаксов менее
Legacy Survey1). Хирота и др. (2020) представили
10%. Такой подход связан с тем, что при отно-
сительных ошибках измеренных параллаксов бо-
каталог из 99 источников мазерного излучения,
лее 10% необходимо учитывать, например, эффект
наблюдавшихся исключительно на частоте 22 ГГц
по программе VERA (VLBI Exploration of Radio
Лутца-Келкера (1973). Для применения этого эф-
фекта необходимо хорошо знать распределение
Astrometry2). Списки Рида и др. (2019) и Хироты и
вещества в Галактике. Реальное же распределение
др. (2020) имеют большой процент общих измере-
вещества на больших расстояниях от Солнца, где
ний, поэтому мы составили список данных без сов-
расположена б ´ольшая часть мазеров, в настоящее
падений. Кроме того, нами добавлены несколько
время не известно достаточно хорошо для решения
новых результатов определений параллаксов ряда
этой задачи. Поправки за этот эффект являются
мазерных источников, выполненных после 2020 г.
модельно зависимыми, поэтому необходимость в
(Сакаи и др., 2020; Ортиз-Леон и др., 2020; Сюй
них возникает лишь в крайних случаях. Как по-
и др., 2021; Сакаи и др., 2022; Биан и др., 2022).
казано в работе Степанищева, Бобылева (2013), в
Помимо мазерных источников в нашем списке име-
единичных случаях (при σπ/π ≫ 10%) для мазеров
ется некоторое количество радиозвезд, которые яв-
поправки могут быть значительными.
ляются очень молодыми звездами, расположенны-
ми в основном в области пояса Гулда. Наблюдения
Отбор источников выполнен при условии R >
этих звезд выполнены РСДБ-методом в контину-
> 4 кпк. Это связано с тем, что на кинематику
уме (Ортиз-Леон и др., 2018; Гайи и др., 2018).
звезд в области R < 4 кпк сильное гравитационное
На данный момент наш список содержит всего
влияние оказывает центральный бар, что приводит
к возникновению значительных отклонений от кру-
267 результатов определения РСДБ-параллаксов
говых орбит, к увеличению дисперсии наблюдае-
и собственных движений мазеров и радиозвезд.
мых пространственных скоростей звезд. Поэтому
при поиске параметров вращения Галактики обыч-
но (Рид и др., 2019) область R < 4 кпк исключается
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
496
БОБЫЛЕВ, БАЙКОВА
80
60
(а)
40
20
0
20
40
60
80
320
300
(б)
280
260
240
220
200
180
160
80
60
(в)
40
20
0
20
40
60
80
4
5
6
7
8
9
10
11
12
13
14
R, кпк
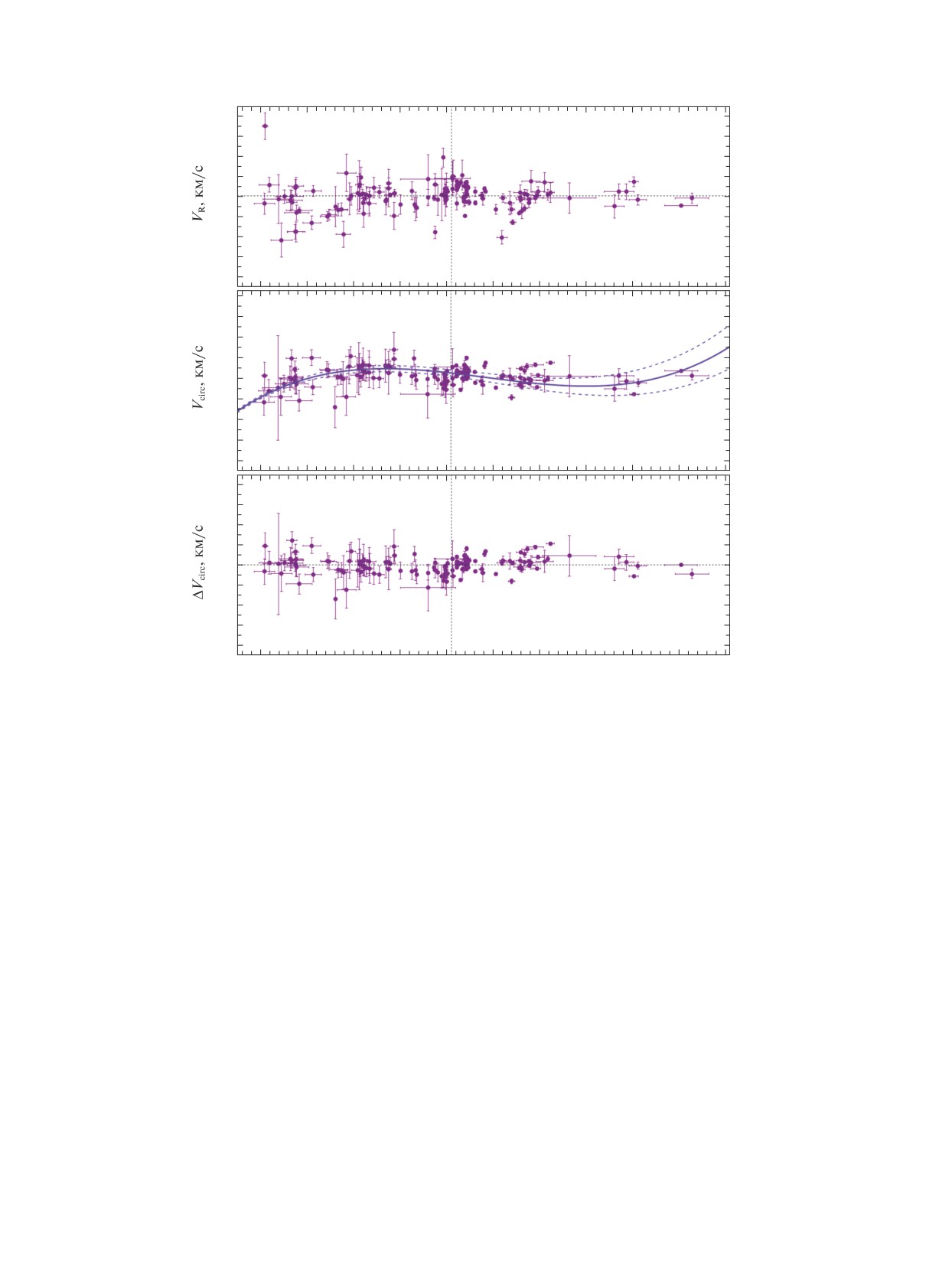
Рис. 2. Радиальные скорости VR (а), скорости вращения Vcirc (б) и остаточные скорости вращения ΔVcirc мазеров (в) в
зависимости от расстояния R. Дана найденная по этим источникам кривая вращения с указанием границ доверительных
областей, соответствующих уровню 1σ, вертикальной линией отмечено положение Солнца.
из рассмотрения. Более того, спиральный узор
же при поиске МНК-решения системы условных
начинается от концов центрального бара, поэтому
уравнений вида (3)-(5) используем критерий от-
и при поиске параметров спиральной волны плот-
брасывания 3σ.
ности в использовании объектов из области R <
< 4 кпк нет необходимости.
Чтобы избавиться от сильных отскоков, ис-
Распределение имеющихся мазерных источни-
пользуем следующие ограничения на простран-
ков с относительными ошибками параллаксов ме-
ственные скорости:
нее 10%, отобранных при условии R > 4 кпк, дано
|U| < 90 км/с,
(12)
на рис. 1. Количество таких объектов составляет
|V | < 90 км/с,
150. На этом рисунке использована система ко-
ординат, в которой ось X направлена от центра
|W | < 60 км/с,
Галактики на Солнце, направление оси Y совпадает
где скорости U, V и W являются остаточными, так
с направлением вращения Галактики. Четырехру-
как из них заранее вычтены пекулярная скорость
кавный спиральный узор с углом закрутки i = -13◦
Солнца и скорость вращения Галактики. В качестве
дан согласно работе Бобылева, Байковой (2014),
заранее известной используем кривую вращения
здесь он построен со значением R0 = 8.1 кпк,
Галактики, параметры которой найдены из анализа
мазеров в работе Бобылева и др. (2020). В ре-
римскими цифрами пронумерованы следующие че-
зультате применения критериев отбрасываются 5-
тыре спиральные рукава: I — Щита, II — Киля-
6 звезд с самыми большими отскоками. В целом
Стрельца, III — Персея и IV — Внешний рукав.
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
ПАРАМЕТРЫ ГАЛАКТИЧЕСКОЙ СПИРАЛЬНОЙ ВОЛНЫ
497
Таблица 1. Кинематические параметры, найденные по 150 мазерным источникам, расположенным в области
Галактики R > 4 кпк
Параметры
Vr + Vl + Vb
Vl + Vb
Vl
U⊙, км/с
9.15 ± 0.86
9.23 ± 1.46
8.89 ± 1.56
V⊙, км/с
12.81 ± 0.86
11.15 ± 1.01
11.22 ± 1.04
W⊙, км/с
8.93 ± 0.75
8.47 ± 0.67
-
Ω0, км/с/кпк
30.18 ± 0.38
29.46 ± 0.43
29.39 ± 0.45
Ω′0, км/с/кпк2
-4.368 ± 0.077
-3.914 ± 0.108
-3.906 ± 0.110
Ω′′0, км/с/кпк3
0.845 ± 0.037
0.652 ± 0.045
0.653 ± 0.046
σ0, км/с
8.9
8.1
8.5
V0, км/с
244.4 ± 4.3
238.6 ± 4.6
238.1 ± 4.7
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Кинематические параметры, найденные всеми
тремя способами по 150 мазерным источникам,
Параметры вращения Галактики
расположенным в области Галактики R > 4 кпк,
даны в табл. 1. На рис. 2 даны радиальные скорости
Для поиска МНК-решения системы условных
VR, скорости вращения Vcirc и остаточные скорости
уравнений вида (3)-(5) применялись три способа.
вращения ΔVcirc выборки из 150 мазеров.
В первом случае использовались все уравнения,
т.е. участвовали все три скорости — Vr, Vl и Vb.
На рис. 2 можно видеть, что радиальные и
тангенциальные скорости небольшой группировки
Во втором случае использовались два уравнения
вида (4) и (5) только с участием собственных дви-
звезд в области Пояса Гулда (r < 0.5 кпк) “стоят
жений мазеров. В третьем случае использовалось
торчком”. Для оценки влияния этой группировки
звезд на параметры общего решения нами было
только одно уравнение вида (4) с участием лишь
получено совместное (Vr + Vl + Vb) решение с ис-
одной компоненты скоростей Vl.
ключением области Пояса Гулда (r < 0.5 кпк). При
Применение трех подходов к использованию
таком подходе с использованием 119 мазерных
условных уравнений вида
(3)-(5) обусловлено
источников были найдены скорости (U, V, W )⊙ =
следующими соображениями. В первую очередь
= (5.02, 13.86, 8.77) ± (1.21, 1.22, 0.93) км/с, а так-
необходимо отметить, что РСДБ-наблюдения
же:
дают оригинальные значения тригонометрических
параллаксов и собственных движений мазеров или
Ω0 = 29.73 ± 0.48 км/с/кпк,
(13)
радиозвезд. Значения систематической лучевой
Ω′0 = -4.246 ± 0.089 км/с/кпк2,
скорости объектов берутся из других источников.
Поэтому интересно сравнить результаты, получен-
Ω′′0 = 0.826 ± 0.043 км/с/кпк3,
ные с участием и без участия лучевых скоростей.
где ошибка единицы веса составила σ0 = 9.9 км/с
Особенность в использовании компонент Vl и
и V0 = 240.8 ± 4.9 км/с (для принятого R0 = 8.1 ±
Vb заключается в том, что доминирующий вклад
в оценку почти всех искомых кинематических
± 0.1 кпк).
параметров вносят скорости Vl. Однако только при
В работе Расторгуева и др. (2017) была рас-
использовании компоненты Vl нельзя определить
смотрена выборка из 130 мазеров с измеренны-
значение скорости W⊙. Как можно видеть из
ми тригонометрическими параллаксами. Напри-
уравнения
(5), коэффициенты перед искомыми
мер, на основе модели чисто круговое вращение
параметрами (U, V )⊙, Ω0, Ω′0 и Ω′′0 содержат
диска (Модель A2 этих авторов) были найде-
очень близкий к нулю для далеких мазеров член
ны компоненты групповой скорости (U, V, W )⊙ =
sin b, и только при неизвестном W⊙ стоит cos b.
= (7.73, 17.69, 8.64) ± (1.52, 1.20, 0.91) км/с и сле-
Поэтому интересно сравнить решения, найденные с
дующие значения параметров кривой вращения Га-
участием и без участия скоростей Vb. Отметим, что
лактики:
наша выборка содержит значительное количество
Ω0 = 29.03 ± 0.52 км/с/кпк,
близких источников, с относительно большими
значениями углов b.
Ω10 = -3.94 ± 0.08 км/с/кпк2,
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
498
БОБЫЛЕВ, БАЙКОВА
Ω20 = 1.13 ± 0.07 км/с/кпк3,
Например, в работе Бобылева и др. (2020) была
проанализирована выборка мазеров из 239 источ-
Ω30 = 0.06 ± 0.11 км/с/кпк4,
ников (практически всех имеющихся на тот момент
измерений) без использования особых ограниче-
Ω40 = 0.30 ± 0.02 км/с/кпк5,
составила 12.8 км/с, что характерно,
ний, где σ0
Ω50 = -0.14 ± 0.02 км/с/кпк6,
скорее, для более старых звезд, например, для
классических цефеид.
где V0 = 241 ± 10 км/с для найденного значения
При этом были получены следующие оцен-
R0 = 8.31 ± 0.13 кпк. Можно отметить, что оценки
ки групповой скорости выборки мазеров U⊙ =
параметров, которые указаны в табл. 1, а также в
решении (13) получены с меньшими ошибками. Это
= 7.79+1.23-1.27 км/с, V⊙ = 15.04+1.24-1.25 км/с, W⊙ =
достигнуто нами путем использования большего
= 8.57+1.18-1.23 км/с и параметров кривой вращения
количества источников, применения ограничения
Галактики:
на величину относительной ошибка параллаксов
мазеров (менее 10%), а также критериев (12).
Ω0 = 29.01+0.33-0.34 км/с/кпк,
В работе Рида и др. (2019) был произведен
Ω′0 = -3.901+0.068-0.069 км/с/кпк2,
кинематический анализ выборки из 147 мазеров. В
отличие от нашего подхода, эти авторы применяли
Ω′′0 = 0.831+0.032-0.032 км/с/кпк3,
разложение в ряд линейной скорости вращения Га-
Ω′′′0 = -0.104+0.018-0.019 км/с/кпк4,
лактики. В итоге они получили оценки R0 = 8.15 ±
± 0.15 кпк и Ω⊙ = 30.32 ± 0.27 км/с/кпк, где Ω⊙ —
а также найдено R0 = 8.15+0.04-0.20 кпк. Можем и здесь
это угловая скорость вращения именно Солнца.
отметить, что в настоящей работе компоненты
Интересно также отметить результаты анали-
групповой скорости и параметры галактического
за собственных движений и тригонометрических
вращения оцениваются с меньшими ошибками.
параллаксов выборки из 9750 OB2-звезд, кото-
Далее была сформирована локальная выборка
рые были получены в работе Бобылева, Байковой
мазеров из
104
источников, отобранных при
(2022). Для поиска МНК-решения было использо-
ограничении на гелиоцентрическое расстояние
вано одно условное уравнение вида (4) с участием
r < 3 кпк. Кинематические параметры, найденные
лишь одной компоненты скоростей Vl. В итоге
по этой выборке, даны в табл. 2. Условные урав-
были найдены скорости (U, V )⊙ = (7.17, 7.37) ±
нения решались двумя способами. Здесь скорости
± (0.16, 0.24) км/с, а также:
Vb не исключались, так как звезды являются
близкими, поэтому имеют высоты b, достаточные
Ω0 = 29.700 ± 0.076 км/с/кпк,
для уверенного определения искомых неизвестных
Ω′0 = -4.008 ± 0.022 км/с/кпк2,
модели. Можем видеть возросшее значение Ω0
по сравнению с найденными выше по выборкам
Ω′′0 = 0.671 ± 0.011 км/с/кпк3,
более далеких мазеров. Этот эффект, скорее всего,
где V0 = 240.6 ± 3.0 км/с (для принятого значения
R0 = 8.1 ± 0.1 кпк).
Таблица 2. Кинематические параметры, найденные по
Имеется хорошее согласие перечисленных оце-
104 мазерным источникам, расположенным не далее
нок параметров вращения Галактики, полученных
3 кпк от Солнца
различными авторами, с результатами, указанными
в табл. 1 и в решении (13). В отношении же
Параметры
Vr + Vl + Vb
Vl + Vb
значений скоростей U⊙ и V⊙ полного согласия нет.
Ошибка единицы веса σ0, которую находим в
U⊙, км/с
11.90 ± 0.91
12.21 ± 1.85
результате поиска МНК-решения кинематических
V⊙, км/с
14.14 ± 0.93
12.49 ± 1.08
уравнений, вычисляется как средневзвешенное из
невязок. Таким образом, эта величина является
W⊙, км/с
9.29 ± 0.75
8.79 ± 0.72
средней по трем координатам дисперсией скоро-
стей звезд. Из табл. 1 и решения (13) можем видеть,
Ω0, км/с/кпк
33.5 ± 1.0
32.2 ± 1.4
что как при использовании только собственных
Ω′0, км/с/кпк2
-4.55 ± 0.16
-4.20 ± 0.24
движений мазеров, так и при использовании их
лучевых скоростей, значения σ0 сопоставимы, и не
Ω′′0, км/с/кпк3
1.20 ± 0.13
0.99 ± 0.14
превышают 10 км/с. Здесь свою роль выполняют
ограничения (12), но главным образом работают
σ0, км/с
7.6
6.9
ограничения на относительные ошибки параллак-
V0, км/с
271 ± 9
261 ± 12
сов.
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
ПАРАМЕТРЫ ГАЛАКТИЧЕСКОЙ СПИРАЛЬНОЙ ВОЛНЫ
499
60
20
50
(a)
(б)
40
30
15
20
10
0
10
10
20
30
5
40
50
60
60
12
50
(в)
(г)
40
10
30
20
8
10
0
6
10
20
4
30
40
2
50
60
40
8
30
(д)
7
(и)
20
6
10
5
0
4
10
3
20
2
30
1
40
0
4
5
6
7
8
9
10
11
12
1
2
3
4
5
R, кпк
, кпк
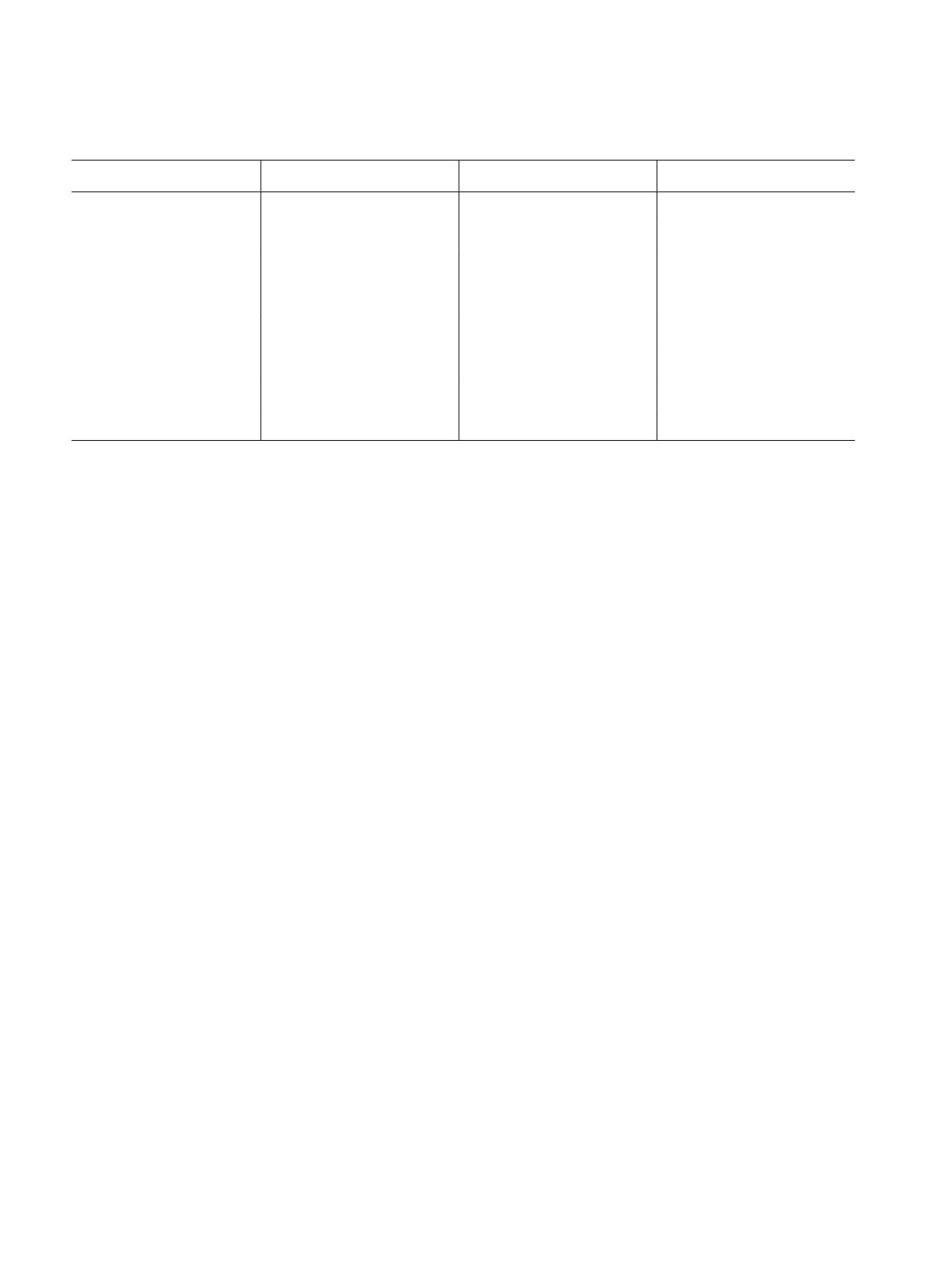
Рис. 3. Радиальные скорости VR в зависимости от расстояния R (а) и их спектр мощности (б), остаточные скорости
вращения ΔVcirc в зависимости от расстояния R (в) и их спектр мощности (г), вертикальные скорости W в зависимости
от расстояния R (д) и их спектр мощности (е) сплошные волнистые линии отражают результаты спектрального анализа.
Здесь использованы 134 мазерных источника с относительнымиошибками тригонометрическихпараллаксов менее 10%,
расположенных не далее 5 кпк от Солнца.
вызван влиянием мазеров и радиозвезд, принадле-
радиальных и тангенциальных возмущений не по-
жащих структуре Пояса Гулда. Главный результат,
стоянные. Действительно, спиральный узор вра-
полученный при этом подходе, заключается в
щается твердотельно, поэтому в области коротации
том, что найденное в последнем столбце табл. 2
разница линейных скоростей вращения Галактики
значение ошибки единицы веса σ0 = 6.9 км/с
и узора нулевая, а в области концов центрального
является очень маленькой величиной. Это говорит
бара она максимальная. Эффект повышенной дис-
о том, что мы имеем дело с популяцией очень
персии скоростей при R ∼ 4 кпк можно заметить
молодых объектов. При использовании все более
на рис. 2а и 2б, который особенно заметен в ра-
далеких выборок звезд значение этой величины
диальных скоростях. При анализе тангенциальных
возрастает, что объясняется совместным влиянием
скоростей полезно сократить радиус выборки —
ошибок тригонометрических параллаксов и оши-
лучше использовать такой интервал R, где кривая
бок собственных движений звезд.
галактического вращения наиболее близка к плос-
кой.
При раздельном спектральном анализе ради-
Спектральный анализ
альных VR, остаточных тангенциальных ΔVcirc и
вертикальных скоростей мазеров были получены
Раздельные решения. Для спектрального ана-
следующие оценки:
лиза были использованы данные о 134 мазерах
из околосолнечной окрестности радиусом 5 кпк.
fR = 8.1 ± 1.4 км/с,
Здесь мы немного сократили размер выборки по
fθ = 6.1 ± 1.7 км/с,
следующим соображениям. Согласно теории волн
плотности Линя, Шу (1984), амплитуды скоростей
fW = 5.2 ± 1.5 км/с,
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
500
БОБЫЛЕВ, БАЙКОВА
z, кпк
W, км/с
0.3
30
(a)
(б)
0.2
20
0.1
10
0
0
0.1
10
0.2
20
0.3
30
2
2
1
3
1
3
2
2
0
1
0
1
1
0
1
0
x, кпк
1
x, кпк
1
2
2
y, кпк
2
2
y, кпк
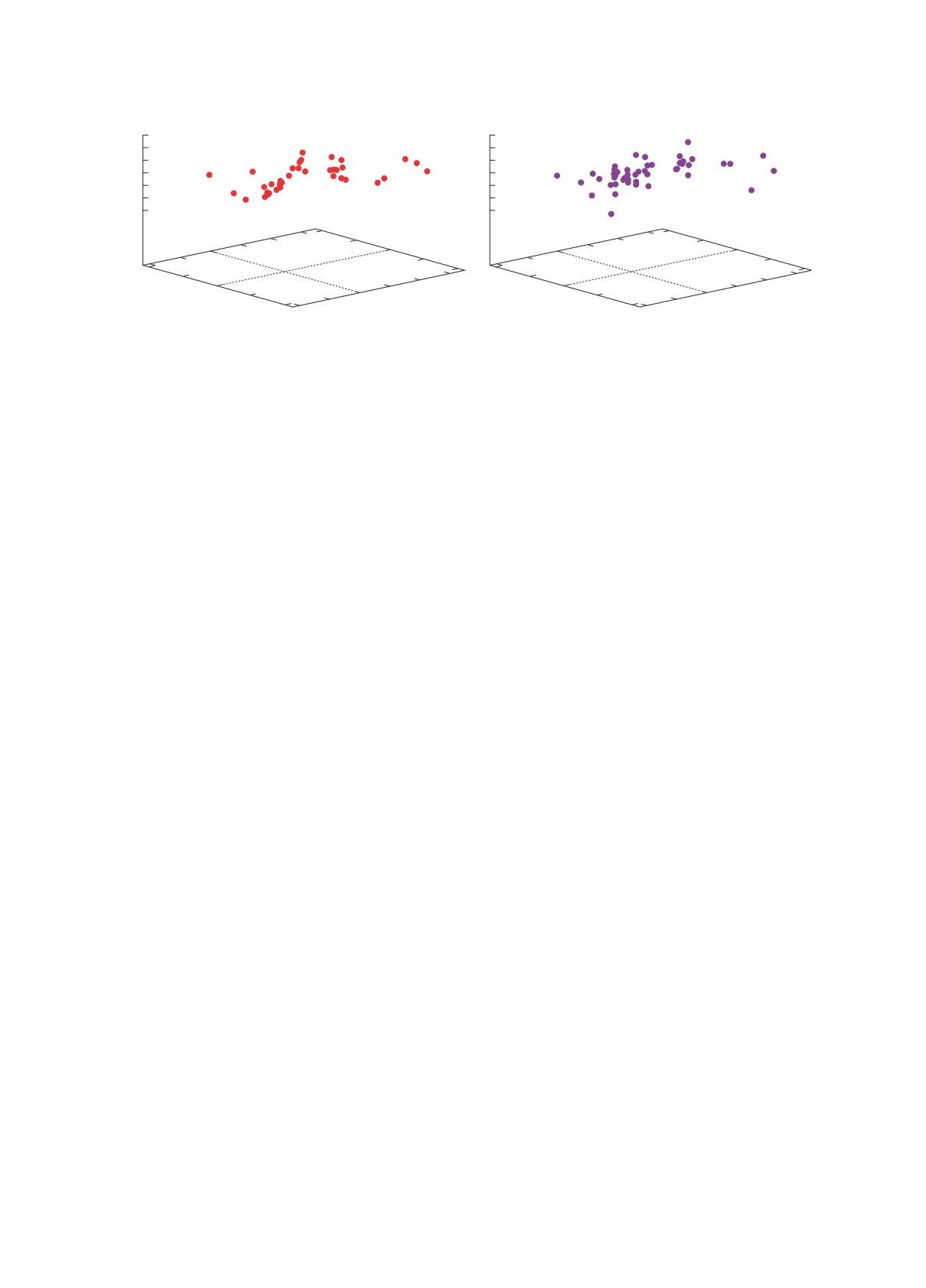
Рис. 4. Трехмерное распределение мазеров и радиозвезд, принадлежащих Местному рукаву (а), и их вертикальные
скорости (б).
λR = 2.1 ± 0.3 кпк,
собственными колебаниями диска или с влиянием
крупномасштабных магнитных полей и др.
λθ = 2.4 ± 0.8 кпк,
Отметим, что в локальной области из анализа
λW = 2.6 ± 0.7 кпк,
распределения молекулярных облаков недавно об-
(χ⊙)R = -158 ± 15◦,
наружена волна Рэдклиффа (Алвес и др., 2020),
распространяющаяся вдоль Местного рукава. По-
(χ⊙)θ = -140 ± 18◦,
мнению Алвеса и др. (2020), волна имеет длину
(χ⊙)W = -180 ± 18◦,
волны около 2 кпк с амплитудой около 160 пк
и является затухающей. Природа возникновения
Результаты такого анализа отражены на рис. 3.
этой волны пока не установлена.
Интересно отметить величину значимости (sig)
Мы отобрали мазеры и радиозвезды, принадле-
главного пика в каждом из отмеченных на рис. 3
жащие Местному рукаву. Эти источники отлично
случаях: sigR = 0.9997, sigθ = 0.9408 и sigW =
видны вблизи Солнца на рис. 1 в виде довольно
= 0.8386. Эти значения говорят о том, что наиболее
узкой цепочки. При отборе мы считали, что ис-
надежно определены параметры спиральной волны
точники Местного рукава расположены не далее
плотности по радиальным скоростям VR и наименее
3.5 кпк от Солнца, и ограничены двумя параллель-
надежно — по вертикальным скоростям W .
ными линиями: x = 0.286y - 0.8 и x = 0.286y + 0.3.
Всего в этой выборке оказалось 68 источников,
В то же время наличие периодичности в вер-
подавляющее большинство из которых являют-
тикальных скоростях мазеров является важным
ся маломассивными звездами типа Т Тельца. По
результатом настоящей работы. Дело в том, что
данным об отобранных звездах построен рис. 4.
в классической теории волн плотности Линя
В положениях звезд на рис. 4а отлично видна волна
и Шу (1964) вертикальные скорости звезд не
Рэдклиффа. Ярко выраженной волны в распреде-
рассматриваются. В работе Бобылева, Байко-
лении вертикальных скоростей отобранных звезд
вой
(2015) на основе спектрального анализа
(рис. 4б) не наблюдается.
впервые была обнаружена периодичность в верти-
В итоге мы склоняемся к тому, что вол-
кальных скоростях мазеров с длиной волны λW =
на в вертикальных скоростях мазеров, скорее,
= 3.4 ± 0.7 кпк и амплитудой fW = 4.3 ± 1.2 км/с.
связана с более крупномасштабным явлением,
В настоящее время известно наличие скоростей
например, с влиянием спиральной волны плот-
вертикальных возмущений различной природы в
ности (рис. 3д). Можно также отметить работу
диске Галактики (Лопес-Корредойра и др., 2014;
Мартинеса-Медины и др. (2022), где показано
Видроу и др., 2014; Антоха и др., 2018; Ванг и
наличие отличных от шумов крупномасштабных
др., 2020; Туласидхаран и др., 2021). Это могут
особенностей в распределении вертикальных ско-
быть крупномасштабные возмущения, связанные
ростей молодых звезд из каталога Gaia EDR3, свя-
с искривлением галактического диска, вызванные
занных с галактической спиральной структурой.
как гравитационным влиянием какого-либо внеш-
Причем наиболее заметная особенность отмечена
него фактора, так и негравитационным, например,
этими авторами при R ∼ 9.5 кпк, т.е. вытянутость в
падение на диск или близкий пролет карликовой
районе рукава Персея.
галактики-спутника Млечного Пути, либо сгустка
Совместное решение. При совместном спек-
темной материи большой массы. Могут быть и
тральном анализе радиальных VR и остаточных
возмущения вертикальных скоростей, связанные с
тангенциальных ΔVcirc скоростей предполагается,
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
2022
№7
ПАРАМЕТРЫ ГАЛАКТИЧЕСКОЙ СПИРАЛЬНОЙ ВОЛНЫ
501
60
50
(a)
40
30
25
20
(в)
10
0
20
-10
-20
-30
15
-40
-50
−60
10
40
(б)
30
5
20
10
0
0
-10
1
2
3
4
5
-20
λ, кпк
-30
-40
5
6
7
8
9
10
R, кпк
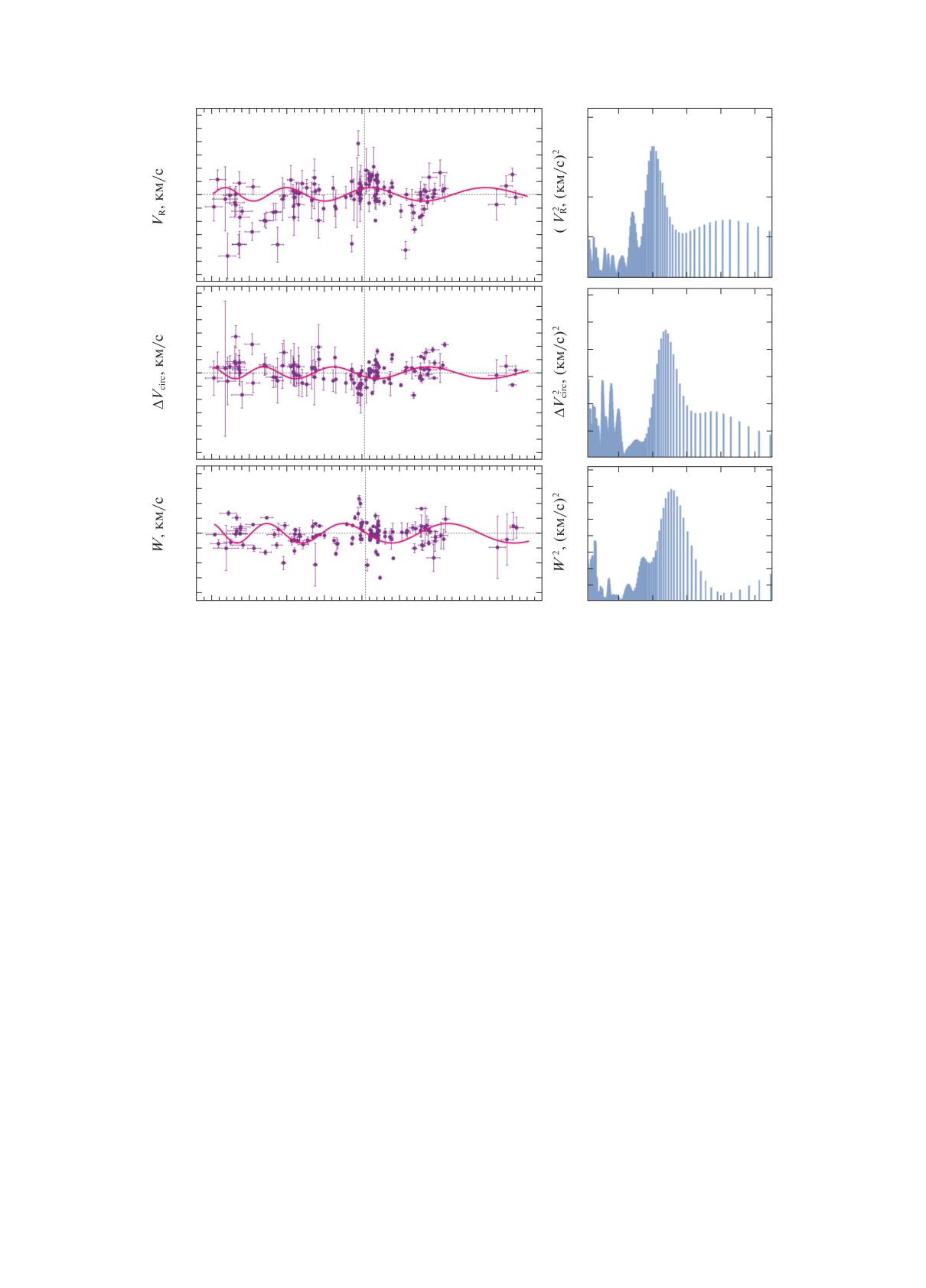
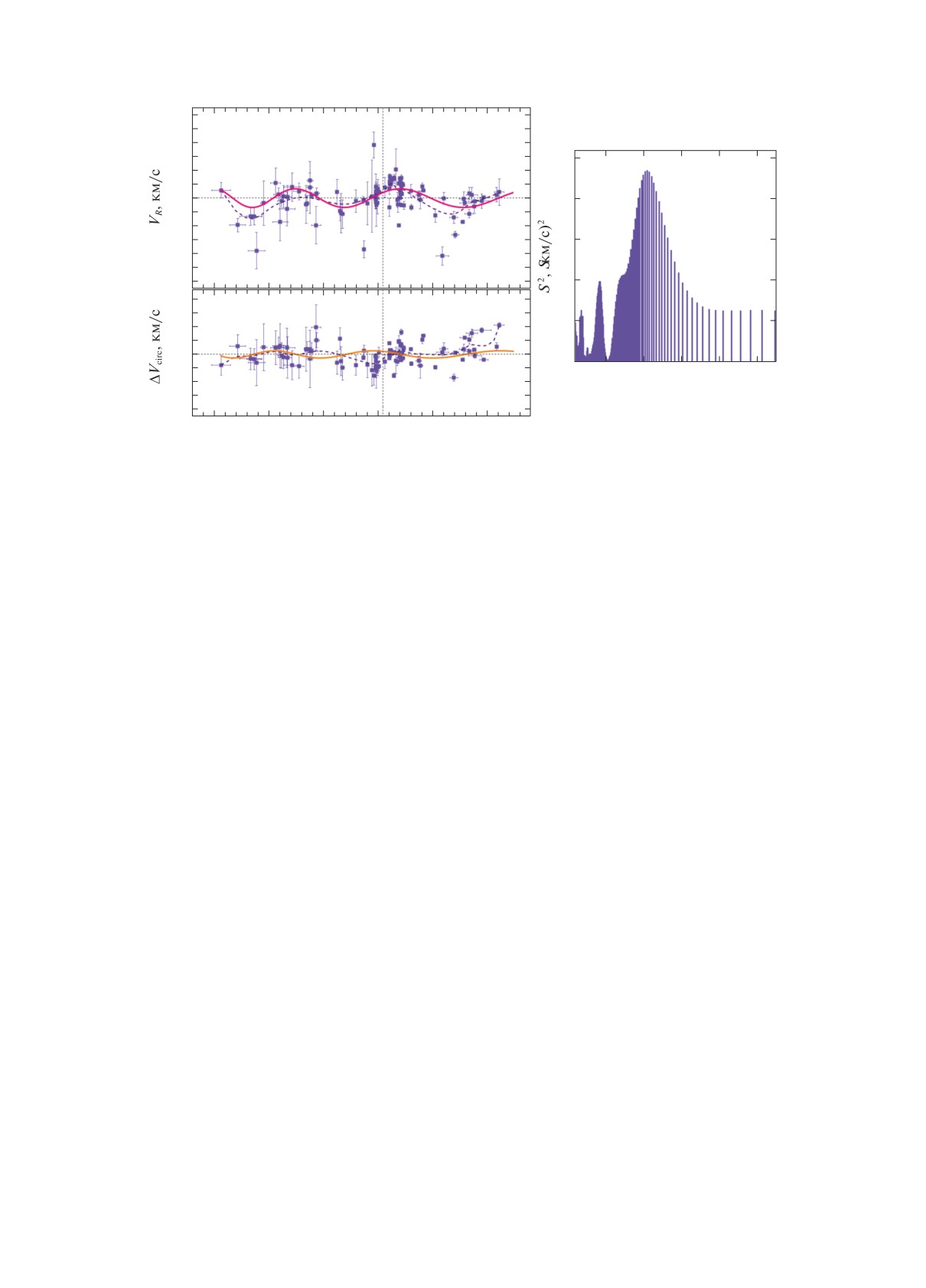
Рис. 5. Радиальные скорости VR (а) и остаточные скорости вращения ΔVcirc (б) в зависимости от расстояния R,
а также их спектр мощности (в), усреднение данных показано пунктирными линиями; сплошные волнистые линии
отражают результаты спектрального анализа. Здесь использованы104 мазерных источника с относительнымиошибками
тригонометрических параллаксов менее 10%, расположенных не далее 3 кпк от Солнца.
что имеется одно значение длины волны и фазы
fθ = 2.6 ± 1.2 км/с,
Солнца в волне плотности для обоих видов скоро-
λ = 2.1 ± 0.3 кпк,
стей.
χ⊙ = -148 ± 15◦.
По данным о 134 мазерах из околосолнечной
окрестности радиусом 5 кпк с относительными
Результаты этого спектрального анализа отражены
ошибками тригонометрических параллаксов менее
на рис. 5, где значимость главного пика на спектре
10% были получены следующие оценки: fR = 6.1 ±
мощности составляет sig = 0.99999. Здесь значе-
± 1.3 км/с, fθ = 3.2 ± 1.4 км/с и λ = 2.1 ± 0.3 кпк,
ние sig немного выше, чем в предыдущем случае,
χ⊙ = -141 ± 15◦. Значимость главного пика на
найденном при анализе более широкой околосол-
спектре мощности найдена равной sig = 0.99991.
нечной окрестности.
Отметим, что применяемый спектральный ана-
На рис. 5, помимо найденных периодичностей,
лиз учитывает как логарифмический характер спи-
отмеченных жирными линиями, пунктирными ли-
ральной волны плотности, так и распределение
ниями даны усредненные значения наблюдаемых
позиционных углов объектов. В логарифмической
скоростей мазеров. На больших расстояниях от
волне длина волны является переменной величи-
Солнца сравнение таких линий не имеет особого
ной — она возрастает с увеличением R. При этом
смысла из-за наличия больших значений пози-
оценка параметров λ, f{R,θ,W}, χ⊙ относится к ло-
ционных углов некоторых источников. Но в ло-
кальной области — к области вблизи Солнца. Как
кальной околосолнечной окрестности (охватываю-
видно из распределения мазеров в проекции на Га-
щей два ближайших к Солнцу отрезка спираль-
лактическую плоскость XY на рис. 1, практически
ных рукавов гранд-дизайна) такое сравнение имеет
в выборке представлены только два отрезка спи-
смысл. Как можно видеть из рис. 5а, имеется
ральных рукавов, Киля-Стрельца и Персея. По-
прекрасное согласие между жирной и пунктирной
этому мы решили провести спектральный анализ
линиями, что говорит о надежности найденных
и по локальной выборке, которая как раз и охва-
значений λ, fR, χ⊙. В тангенциальных скоростях
тывает этот район. При этом для формирования
имеем существенно худшее согласие между такими
остаточных скоростей вращения была использова-
линиями, но и амплитуда fθ здесь очень мала.
на кривая вращения Галактики, параметры которой
В табл. 3 представлены оценки параметров га-
были найдены по выборке из 150 мазеров (рис. 2б).
лактической спиральной волны плотности, полу-
В итоге по 104 мазерам были получены следующие
ченные по наиболее важным трассерам спиральной
оценки:
структуры. Как следует из этой сводки, значение fθ
fR = 6.7 ± 1.1 км/с,
(14)
обычно имеет меньшее значение по сравнению с fR.
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
502
БОБЫЛЕВ, БАЙКОВА
Таблица 3. Оценки параметров галактической спиральной волны плотности, найденные различными авторами
Выборка
Ref
fR, км/с
fθ, км/с
λ, кпк
|i|, град.
χ⊙, град.
m
OB-зв., цеф., РЗС
[1]
3.6 ± 0.4
4.7 ± 0.6
4.2 ± 0.2
-165 ± 1
2
Цефеиды
[2]
6.3 ± 2.4
4.4 ± 2.4
6.8 ± 0.7
-70 ± 16
2
Цефеиды
[3]
3.5 ± 1.7
7.5 ± 1.8
11.4
-20 ± 9
4
OB-ассоциации
[4]
6.6 ± 1.4
1.8 ± 1.4
2.0 ± 0.2
Цефеиды
[5]
6.7 ± 2.3
1.4 ± 1.6
6.0 ± 0.7
-85 ± 15
2
РЗС
[5]
5.5 ± 2.3
0.2 ± 1.6
12.2 ± 0.7
-88 ± 15
4
OB-звезды
[5]
6.6 ± 2.5
0.4 ± 2.3
6.6 ± 0.9
-97 ± 18
2
РЗС, HI, HII
[6]
5.9 ± 1.1
4.6 ± 0.5
2.1 ± 0.5
-119
Мазеры
[7]
7.7 ± 1.6
2.2 ± 0.3
5.0 ± 0.5
-147 ± 10
2
Мазеры
[8]
6.9 ± 1.4
2.8 ± 1.0
10.4 ± 0.3
-125 ± 10
4
OB-звезды
[9]
7.1 ± 0.3
6.5 ± 0.4
2.8 ± 0.2
-128 ± 6
4
РЗС
[10]
4.6 ± 0.7
1.1 ± 0.4
4
OB-звезды
[11]
4.8 ± 0.7
4.1 ± 0.9
2.1 ± 0.2
9.4 ± 0.9
-116 ± 12
4
Настоящая работа
6.7 ± 1.1
2.6 ± 1.2
2.1 ± 0.3
9.4 ± 1.0
-148 ± 15
4
Примечание. [1] — Бил, Овенден (1978); [2] — Мишуров и др. (1997); [3] — Мишуров, Зенина (1999); [4] — Мельник и др.
(2001); [5] — Заболотских и др. (2002); [6] — Бобылев и др. (2008); [7] — Байкова, Бобылев (2012); [8] — Расторгуев и др. (2017);
[9] — Бобылев, Байкова (2018); [10] — Локтин, Попова (2019); [11] — Бобылев, Байкова, (2022).
В первую очередь необходимо отметить ре-
звезд, поэтому и найденные по ним параметры
зультаты, полученные с использованием цефеид
должны быть более надежными (Мельник и др.,
(Мишуров и др., 1997; Мишуров, Зенина, 1999;
2001; Заболотских и др., 2002; Бобылев и др., 2008;
Заболотских и др., 2002). Они интересны тем, что
Локтин, Попова, 2019).
расстояния до этих звезд определяют независимую
Наконец, в таблице имеются и оценки, получен-
шкалу расстояний, так как они оцениваются на ос-
ные с использованием различных выборок мазеров
нове соотношения период-светимость. Случайные
с измеренными РСДБ-методом тригонометриче-
ошибки определения расстояний этим способом
скими параллаксами и собственными движениями
составляют 10-15% (Бердников и др., 2000). Са-
(Байкова, Бобылев, 2012; Расторгуев и др., 2017).
мые последние оценки расстояний до классических
цефеид с использованием фотометрических данных
и калибровок в ближнем инфракрасном диапазоне
ЗАКЛЮЧЕНИЕ
позволяют говорить о случайных ошибках около
Проведен кинематический анализ большой вы-
5% (Сковрон и др., 2019).
борки галактических мазерных источников и ра-
Несомненный интерес представляют и резуль-
диозвезд с измеренными методом РСДБ тригоно-
таты, полученные с использованием OB-звезд
метрическими параллаксами и собственными дви-
(Бил, Овенден, 1978; Заболотских и др., 2002;
жениями. Причем рассматривались только мазеры
Бобылев, Байкова, 2018). Важным фактором при
с относительными ошибками тригонометрических
оценке кинематических параметров является как
параллаксов менее 10%.
точность расстояний, так и точность собствен-
При оценке параметров вращения Галактики
ных движений. Некоторые современные оценки,
рассмотрены различные методы решения основных
указанные в таблице, получены с использованием
кинематических уравнений — с учетом и без учета
данных из каталога Gaia EDR3 (Браун и др., 2021).
лучевых скоростей, а также с использованием и без
Расстояния до OB-ассоциаций и РЗС более
использования мазеров из области Пояса Гулда.
точные по сравнению с расстояниями до одиночных Здесь мы ориентировались на значение ошибки
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
ПАРАМЕТРЫ ГАЛАКТИЧЕСКОЙ СПИРАЛЬНОЙ ВОЛНЫ
503
единицы веса σ0, которую можно рассматривать
По данным о 134 мазерах из околосолнечной
как среднюю по трем направлениям дисперсию
окрестности радиусом 5 кпк получены следующие
пространственных скоростей мазеров. При анализе
оценки:
выборки далеких мазеров показано, что как при
fR = 8.1 ± 1.4 км/с,
использовании только их собственных движений,
так и при добавлении лучевых скоростей значения
fθ = 6.1 ± 1.7 км/с,
σ0 близки между собой, их значения не превышают
fW = 5.2 ± 1.5 км/с,
10 км/с.
λR = 2.1 ± 0.3 кпк,
В результате совместного решения систе-
мы кинематических уравнений с использова-
λθ = 2.4 ± 0.8 кпк,
нием
150 мазеров из области Галактики R >
λW = 2.6 ± 0.7 кпк,
4 кпк найдены компоненты групповой скорости
(χ⊙)R = -158 ± 15◦,
(U, V, W )⊙ = (9.15, 12.81, 8.93) ± (0.86, 0.86, 0.75) км/с
и следующие параметры угловой скорости враще-
(χ⊙)θ = -140 ± 18◦,
ния Галактики:
(χ⊙)W = -180 ± 18◦.
Ω0 = 30.18 ± 0.38 км/с/кпк,
Мы рассматриваем логарифмическую волну,
Ω′0 = -4.368 ± 0.077 км/с/кпк2,
когда длина этой волны возрастает с увеличением
Ω′′0 = 0.845 ± 0.037 км/с/кпк3,
галактоцентрического расстояния R. Поэтому
полученные оценки λ относятся к околосолнечной
где ошибка единицы веса σ0 составила 8.9 км/с
окрестности, где λ является расстоянием между
и V0 = 244.4 ± 4.3 км/с для принятого значения
отрезками спиральных рукавов Киля-Стрельца и
R0 = 8.1 ± 0.1 кпк. С параметрами этой кривой
Персея.
вращения Галактики находим остаточные танген-
Важно отметить, что в вертикальных скоро-
циальные скорости.
стях мазеров подтверждено наличие периодиче-
Рассмотрена кинематика локальной выборки из
ских возмущений, впервые обнаруженных в работе
104 мазеров, расположенных в области радиусом
Бобылева, Байковой (2015). Найденные значения
3 кпк вокруг Солнца. Показано, что параметры
амплитуды возмущений fW и длины волны λW
галактического вращения по этой выборке опре-
близки к аналогичным значениям, полученным по
деляются с большими ошибками. Здесь имеет-
радиальным и остаточным тангенциальным ско-
ся сильное влияние объектов из Пояса Гулда.
ростям. Это говорит в пользу представления о
Это приводит к завышенной, по-нашему мнению,
влиянии спиральной волны плотности и на верти-
оценке угловой скорости вращения Ω0 = 33.5 ±
кальные скорости звезд.
± 1.0 км/с/кпк, следовательно, к завышенному
Согласно классической линейной теории га-
значению линейной скорости вращения V0 = 271 ±
лактической спиральной волны плотности Линя и
± 9 км/с. Положительным эффектом кинемати-
Шу (1964), можно ожидать наличие одного значе-
ческого анализа этой выборки мазеров является
ния длины волны λ (следовательно, и фазы Солнца
маленькое значение ошибки единицы веса σ0 =
в волне χ⊙) как для радиальных, так и для оста-
= 6.9 км/с. Это означает, что рассматриваемые в
точных тангенциальных скоростей. Вертикальные
настоящей работе мазеры и радиозвезды действи-
скорости в этой теории не рассматривались. Здесь
тельно являются представителями наиболее моло-
же мы видим лишь удовлетворительное согласие в
дой популяции звезд и протозвезд, принадлежащих
оценке λR,θ,W .
тонкому диску Галактики. Для более далеких ма-
зеров формальная оценка дисперсии их скоростей
Интересно отметить, что по локальной выборке
возрастает за счет влияния измерительных ошибок
из 104 мазеров неплохо определяются локаль-
тригонометрических параллаксов и ошибок их соб-
ные параметры спиральной волны плотности. Так,
ственных движений (случайные ошибки лучевых
в результате совместного спектрального анали-
скоростей звезд практически не зависят от рассто-
за радиальных VR и остаточных тангенциальных
яния).
ΔVcirc скоростей мазеров, были получены следую-
Для оценки параметров спиральной волны
щие оценки:
плотности применялся спектральный анализ ско-
fR = 6.7 ± 1.1 км/с,
ростей различных выборок мазеров. Для этого
использовались как раздельные, так и совместные
fθ = 2.6 ± 1.2 км/с,
решения. Раздельный спектральный анализ при-
λ = 2.1 ± 0.3 кпк,
менен к радиальным VR, остаточным тангенциаль-
χ⊙ = -148 ± 15◦.
ным ΔVcirc и вертикальным W скоростям мазеров.
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
504
БОБЫЛЕВ, БАЙКОВА
Рассмотрена выборка из 68 мазеров и радио-
18.
Ванг и др. (H.-F. Wang, M. L ´opez-Corredoira,
звезд, принадлежащих Местному рукаву. Подтвер-
Y. Huang, J. Chang, H.-W. Zhang, J. L. Carlin, et al.),
ждено наличие волны Рэдклиффа в пространствен-
Astrophys. J. 897, 119 (2020).
ном распределении этих источников.
19.
Видроу и др. (L.M. Widrow, J. Barber,
M.H. Chequers, and E. Cheng), Mon. Not. R.
Авторы благодарны Ю.Н. Мишурову за полез-
Astron. Soc. 440, 1971 (2014).
ное обсуждение результатов работы.
20.
Ву и др. (Y.W. Wu, M.J. Reid, N. Sakai, T.M. Dame,
K.M. Menten, A. Brunthaler, Y. Xu, J.J. Li, et al.),
Astrophys. J. 874, 13 (2019).
СПИСОК ЛИТЕРАТУРЫ
21.
Гайи и др. (P.A.B. Galli, L. Loinard, G.N. Ortiz-
1.
Абутер и др. (GRAVITY Collaboration, R. Abuter,
L ´eon, M. Kounkel, S.A. Dzib, A.J. Mioduszewski,
A. Amorim, N. Baub ¨ock, et al.), Astron. Astrophys.
L.F. Rodriguez, L. Hartmann, et al.), Astrophys. J.
625, L10 (2019).
859, 33 (2018).
2.
Абутер и др. (GRAVITY Collaboration, R. Abuter,
22.
Заболотских М.В., Расторгуев А.С., Дамбис А.К.,
A. Amorim, M. Baub ¨ock, et al.), Astron. Astrophys.
Письма в Астрон. журн.
28,
516
(2002)
647, A59 (2021).
[M.V. Zabolotskikh, et al., Astron. Lett. 28,
454
3.
Алвес и др. (J. Alves, C. Zucker, A.A. Goodman,
(2002)].
et al.), Nature 578, 237 (2020).
23.
Иммер и др. (K. Immer, J. Li, L.H. Quiroga Nu ˜nez,
4.
Антоха и др. (T. Antoja, A. Helmi, M. Romero-
M.J. Reid, B. Zhang, L. Moscadelli, and K.L.J. Rygl),
Gomez, et al.), Nature 561, 360 (2018).
Astron. Astrophys. 632, A123 (2019).
5.
Бердников и др. (L.N. Berdnikov, A.K. Dambis and
24.
Линь, Шу (C.C. Lin and F.H. Shu), Astrophys. J.
O.V. Vozyakova), Astron. Astrophys. Suppl. 143, 211
140, 646 (1964).
(2000).
25.
Локтин А.В., Попова М.Э., Астрофиз. Бюлл. 74,
6.
Байкова А.Т., Бобылев В.В., Письма в Астрон.
289 (2019) [A.V. Loktin, M.E. Popova, Astrophys.
журн. 38, 617 (2012) [A.T. Bajkova, V.V. Bobylev,
Bull. 74, 270 (2019)].
Astron. Lett. 38, 549 (2012)].
26.
Лопес-Корредойра и др. (M. L ´opez-Corredoira,
7.
Биан и др. (S.B. Bian, Y. Xu, J.J. Li, Y.W. Wu,
H. Abedi, F. Garz ´on, and F. Figueras), Astron.
B. Zhang, X. Chen, Y.J. Li, Z.H. Lin, et al.), Astron.
Astrophys. 572, A101 (2014).
J. 163, 54 (2022).
27.
Лутц, Келкер (T.E. Lutz and D.H. Kelker), Pub.
8.
Бил, Овенден (J. Byl and M.W. Ovenden),
Astron. Soc. Pacific 85, 573 (1973).
Astrophys. J. 225, 496 (1978).
9.
Бобылев В.В., Байкова А.Т., Степанищев А.С.,
28.
Мартинес-Медина и др. (L. Martinez-Medina,
Письма в Астрон. журн.
34,
570
(2008)
A. P ´erez-Villegas, and A. Peimbert), Mon. Not. R.
[V.V. Bobylev, et al., Astron. Lett. 34, 515 (2008)].
Astron. Soc. 512, 1574 (2022).
10.
Бобылев, Байкова (V.V. Bobylev and A.T. Bajkova),
29.
Мельник А.М., Дамбис А.К., Расторгуев А.С.,
Mon. Not. R. Astron. Soc. 408, 1788 (2010).
Письма в Астрон. журн.
27,
611
(2001)
[A.M. Mel’nik, et al., Astron. Lett. 27, 521 (2001)].
11.
Бобылев, Байкова (V.V. Bobylev and A.T. Bajkova),
Mon. Not. R. Astron. Soc. 437, 1549 (2014).
30.
Мишуров и др. (Yu.N. Mishurov, I.A. Zenina,
A.K. Dambis, A.M. Mel’nik, and A.S. Rastorguev),
12.
Бобылев, Байкова (V.V. Bobylev and A.T. Bajkova),
Mon. Not. R. Astron. Soc. 447, L50 (2015).
Astron. Astrophys. 323, 775 (1997).
13.
Бобылев В.В., Байкова А.Т., Письма в Астрон.
31.
Мишуров, Зенина (Yu.N. Mishurov and I.A. Zenina),
журн. 44, 739 (2018) [V.V. Bobylev, A.T. Bajkova,
Astron. Astrophys. 341, 81 (1999).
Lett. 44, 676 (2018)].
32.
Никифоров И.И., Веселова А.В., Письма в Астрон.
14.
Бобылев В.В., Крисанова О.И., Байкова А.Т.,
журн. 44, 102 (2018) [I.I Nikiforov, A.V. Veselova,
Письма в Астрон. журн. 46, 470 (2020) V.V. Bobylev,
Astron. Lett. 44, 81 (2018)].
O.I. Krisanova, A.T. Bajkova, Astron. Lett. 46, 439
33.
Ортиз-Леон и др. (G.N. Ortiz-Le ´on, L. Loi-
(2020)].
nard, S.A. Dzib, P.A.B. Galli, M. Kounkel,
15.
Бобылев В.В., Байкова А.Т., Астрон. журн. 98, 497
A.J. Mioduszewski, L.F. Rodriguez, R.M. Torres,
(2021) [V.V. Bobylev, A.T. Bajkova, Astron. Rep. 65,
et al.), Astrophys. J. 865, 73 (2018).
498 (2021)].
34.
Ортиз-Леон и др. (G.N. Ortiz-Le ´on, K.M. Menten,
16.
Бобылев В.В., Байкова А.Т., Письма в Астрон.
T. Kaminski, A. Brunthaler, M.J. Reid, and
журн. 48, 184 (2022) [V.V. Bobylev, A.T. Bajkova,
R. Tylenda), Astron. Astrophys. 638, 17 (2020).
Astron. Lett. 48, 169 (2022)].
35.
Расторгуев А.С., Заболотских М.В., Дамбис А.К.,
17.
Браун и др. (Gaia Collaboration, A.G.A. Brown,
Уткин Н.Д., Бобылев В.В., Байкова А.Т., Астрофиз.
A. Vallenari, T. Prusti, et al.), Astron. Astrophys. 649,
Бюллетень 72, 134 (2017) [A.S. Rastorguev, et al.,
1 (2021).
Astrophys. Bulletin 72, 122 (2017)].
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022
ПАРАМЕТРЫ ГАЛАКТИЧЕСКОЙ СПИРАЛЬНОЙ ВОЛНЫ
505
36. Рид и др. (M.J. Reid, K.M. Menten, X.W. Zheng,
43. Степанищев А.С., Бобылев В.В., Письма в Аст-
A. Brunthaler, and Y. Xu), Astrophys. J. 705, 1548
рон. журн. 39, 211 (2013) [Stepanishchev A.S., and
(2009).
Bobylev V.V., Astron. Lett. 39, 185 (2013)].
37. Рид и др. (M.J. Reid, N. Dame, K.M. Menten,
44. Сюй и др. (Y. Xu, S.B. Bian, M.J. Reid, J.J. Li,
A. Brunthaler, X.W. Zheng, Y. Xu, J. Li, N. Sakai,
B. Zhang, Q.Z. Yan, T.M. Dame, K.M. Menten,
et al.), Astrophys. J. 885, 131 (2019).
et al.), Astron. Astrophys. 616, L15 (2018).
38. Сакаи и др., (N. Sakai, M.J. Reid, K.M. Menten,
45. Сюй и др. (Y. Xu, S.B. Bian, M.J. Reid, J.J. Li,
A. Brunthaler, and T.M. Dame), Astrophys. J. 876, 30
K.M. Menten, T. M. Dame, B. Zhang, A. Brunthaler,
(2019).
et al.), Astrophys. J. Suppl. Ser. 253, 9 (2021).
39. Сакаи и др. (N. Sakai, T. Nagayama, H. Nakanishi,
N. Koide, T. Kurayama, N. Izumi, T. Hirota,
46. Туласидхаран и др. (L. Thulasidharan, E. D’Onghia,
T. Yoshida, et al.), PASJ 72, 53 (2020).
E. Poggio, et al.), arXiv: 2112.08390 (2021).
40. Сакаи и др. (N. Sakai, H. Nakanishi, K. Kurahara,
47. Хирота и др. (VERA collaboration, T. Hirota,
D. Sakai, K. Hachisuka, J.-S. Kim, and O. Kameya),
T. Nagayama, M. Honma, Y. Adachi, R.A. Burns,
PASJ 74, 209 (2022).
J.O. Chibueze, Y.K. Choi, K. Hachisuka, et al.), PASJ
41. Санна и др. (A. Sanna, M.J. Reid, T.M. Dame,
70, 51 (2020).
K.M. Menten, and A. Brunthaler), Science 358, 227
(2017).
48. Хонма и др. (M. Honma, T. Nagayama, K. Ando,
42. Сковрон и др. (D.M. Skowron, J. Skowron, P. Mr ´oz,
T. Bushimata, Y.K. Choi, T. Handa, T. Hirota, H. Imai,
et al.), Science 365, 478 (2019).
et al.), PASJ 64, 136 (2012).
ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 48
№7
2022