ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2023, том 49, № 12, с. 888-896

НЕЙТРИННОЕ ИЗЛУЧЕНИЕ ПРИ СВЕРХВСПЫШКАХ

НЕЙТРОННЫХ ЗВЕЗД

¹Физико-технический институт им. А.Ф. Иоффе РАН, Санкт-Петербург, Россия

Поступила в редакцию 17.09.2023 г.

После доработки 21.11.2023 г.; принята к публикации 21.11.2023 г.

Сверхвспышки нейтронных звезд — редкие, но мощные события, объясняемые взрывным горением

углерода в глубоких слоях внешней оболочки звезды. В данной работе выполнено моделирование

сверхвcпышек, предложен простой метод описания нейтринной стадии их охлаждения, а также метод

описания эволюции энергии взрыва на масштабах нескольких месяцев. Отмечено универсальное

соотношение для распределения температуры во вспыхнувшем слое на нейтринной стадии его

остывания, а также унификация болометрических кривых блеска и скорости нейтринного теплоотвода

для глубоких и мощных вспышек. Указано на возможность длительного удержания энергии вспышки

в оболочке звезды. Результаты могут быть полезны для интерпретации наблюдений сверхвспышек.

Ключевые слова: нейтронные звезды, рентгеновская астрономия.

DOI: 10.31857/S0320010823120033, EDN: RXKLDO

1. ВВЕДЕНИЕ

СВ происходят в глубоких слоях внешней

оболочки НЗ (например, Хенсель и др., 2007).

Нейтронные звезды (НЗ) проявляют взрывную

Оболочка простирается от поверхности НЗ до

активность различных типов. В частности, вспыш-

плотности нейтронизации вещества (ρ_drip ≈ 4.3 ×

ки аккрецирующих НЗ объясняются взрывным

× 10¹¹

г/см³). Толщина оболочки составляет

ядерным горением в их внешней оболочке. Сравне-

несколько сотен метров, а ее масса ∼10-5 M_⊙.

ние наблюдений с теоретическими моделями поз-

Ее вещество состоит, в основном, из электронов

воляет получать полезную информацию о физиче-

и ионов (частично или полностью ионизованных

ских условиях во взрывающихся слоях, о режимах

атомных ядер), причем ионы могут образовывать

аккреции, массах и радиусах НЗ, об уравнении

кристалл, жидкость или газ.

состояния сверхплотной материи в ядрах НЗ и о

В частности, нас будет интересовать нейтринное

многом другом (см., например, Занд, 2017; Гал-

охлаждение СВ. Ранее оно включалось в расчеты,

лоуэй, Кик, 2021).

но систематически не исследовалось. Кроме того,

Аккрецирующие НЗ в двойных системах де-

мы проанализируем динамику эволюции энергии

монстрируют рентгеновские вспышки, вызванные

СВ в течение нескольких месяцев и обратим вни-

взрывами аккрецированного водорода и гелия под

мание на возможность удержания энергии вспыш-

самой поверхностью звезды, а также значительно

ки в звезде длительное время.

более редкие, но сильные сверхвспышки (СВ),

инициированные взрывом углерода (¹²C) в более

глубоких слоях; см., например, обзор Занда (2017).

2. ЗАДАЧА И ЧИСЛЕННЫЙ КОД

В этой работе мы рассмотрим СВ. Их моде-

Хорошо известно (например, Кик, Хегер, 2011;

лирование активно ведется уже более двадцати

Альтамирано и др., 2012; Кик и др., 2012, 2015), что

лет с учетом динамики аккреции, цепочек ядерных

собственно вспышке предшествует стадия образо-

реакций, различных механизмов переноса тепла,

вания углерода (¹²C) за счет водородно-гелиевого

нейтринного охлаждения и др.; см., например, Кам-

горения в самых внешних слоях НЗ. Углеродсо-

минг, Макбет (2004); Камминг и др. (2006); Кик,

держащее вещество постепенно накапливается и

Хегер (2011); Альтамирано и др. (2012), Кик и др.

погружается в оболочку под весом вновь аккреци-

(2012, 2015).

рованного вещества и достигает условий взрывного

поджига на дне углеродного слоя с плотностью ρ_ign

^*Электронный адрес: kam@astro.ioffe.ru

и температурой T_ign (например, Кик, Хегер, 2011).

888

НЕЙТРИННОЕ ИЗЛУЧЕНИЕ ПРИ СВЕРХВСПЫШКАХ

889

Вслед за поджигом происходит быстрое (длящееся

выбранном слое энергия взрыва выделялась рав-

несколько минут) ядерное горение в широком угле-

номерно по времени в течение 100 с (в локаль-

родном слое, ρ_min ≤ ρ ≤ ρ_ign, где ρ_min — плотность

ной системе отсчета), после чего энерговыделение

на его наружной границе. Мощность взрыва опре-

прекращалось. Величина ρ_ign,9 варьировалась в

деляется параметром Q_b, задающим количество

пределах от 0.1 до 5.

выделенной энергии на один нуклон; Q_b может

Величины, введенные выше, определены в ло-

меняться в зависимости от условий задачи. Со-

кальной системе отсчета во внешней оболочке НЗ.

гласно расчетам, при взрыве углеродсодержащее

Величины в системе покоя удаленного наблюда-

вещество перегорает в элементы группы железа.

теля далее помечаются тильдой. Подчеркнем, что

По теории максимальная плотность поджига

всюду (на рисунках и в тексте), кроме раздела 3,

под временем t понимается координатное шварц-

ограничена величиной ρ_ign,9 = ρ_ign/(10⁹ г/см³) ≲ 5,

шильдово время. Однако в разделе 3 введено время

поскольку при более высоких ρ_ign ядра¹²C пере-

в системе отсчета, сопутствующей оболочке НЗ,

стают существовать из-за пикноядерных реакций

что учитывается при сравнении с результатами

и бета-захватов (например, Шапиро, Тьюколски,

остальных разделов.

1985).

После взрыва наступает тепловая релаксации

3. ЧИСТО НЕЙТРИННОЕ ОХЛАЖДЕНИЕ

нагретого слоя, наблюдаемая по кривым блеска на

протяжении нескольких часов или суток. Однако

Начальный период остывания нагретого слоя

внутренняя тепловая релаксация может длиться

после взрыва удобно описывать в простом при-

более года (например, Кик, Хегер, 2011). Она

ближении нейтринного охлаждения. Для этого до-

определяется диффузией выделившегося тепла к

статочно использовать хорошо известное прибли-

поверхности и внутрь НЗ, а также нейтринным

жение мгновенного взрыва (например, Альтами-

охлаждением нагретого вещества.

рано и др., 2012), в котором температура в слое

горения при каждой плотности ρ адиабатически

Для моделирования СВ мы использовали чис-

достигает максимального значения T_max(ρ). Затем

ленный код, разработанный для изучения остыва-

нейтринное излучение охлаждает каждый элемент

ния НЗ на различных пространственных и времен-

вещества независимо от других в соответствии с

ных масштабах и включающий современную мик-

уравнением

рофизику вещества НЗ (Потехин, Шабрие, 2018).

Особенностью этого кода, проявляющейся при мо-

∂T

= -Q_ν,

(1)

делировании распространения тепла во внешних

∂t

оболочках НЗ на сравнительно коротких временах,

где C — теплоемкость (при постоянном давле-

является аккуратный учет снятия электронного вы-

нии P ) единицы объема вещества, а Q_ν — ско-

рождения с уменьшением плотности или ростом

рость нейтринного энерговыделения в этом объе-

температуры. Рассчитывается тепловая эволюция

ме. Основными нейтринными процессами при СВ

всей звезды, хотя температура ее ядра почти не

являются излучение нейтрино при распаде ленг-

меняется за время наблюдений. Мы не претендуем

мюровских плазмонов и аннигиляция электронно-

на полное самосогласованное моделирование СВ,

позитронных пар в нейтринные пары. Решение

а сделаем несколько упрощений, допустимость ко-

уравнения (1),

торых обсуждается ниже.

∫

Мы не изучаем эволюцию аккрецированного

C(T^′)

dT^′,

(2)

вещества в оболочке НЗ перед взрывом, включая

Q_ν(T^′)

динамику поджига, образование и выход удар-

ной волны и сопутствующие явления (например,

зависит (параметрически) только от значений ρ

Кик, Хегер, 2011). Мы предполагаем, что взрыв

и Q_b в данном элементе вещества; поэтому T =

происходит в слое ρ_min ≤ ρ ≤ ρ_ign, в котором Q_b

= T(t,ρ,Q_b). Оно нечувствительно к модели НЗ

не зависит от плотности ρ. Величины ρ_min, ρ_ign,

(к массе, радиусу, уравнению состояния) и кар-

Q_b и T_ign считаются свободными параметрами.

динально упрощает изучение нейтринной стадии

Основная энергия СВ сосредоточена в окрест-

охлаждения СВ. Однако, когда становится важной

ности плотности поджига ρ_ign, поэтому результа-

диффузия тепла (см., например, Яковлев и др.,

ты нечувствительны к ρ_min, если ρ_min ≪ ρ_ign (для

2021), отмеченная универсальность нарушается.

определенности мы фиксировали ρ_min = 10⁷ г/см³).

Добавим, что при моделировании СВ вместо

Начальный профиль температуры соответствовал

плотности ρ часто используют колонковую плот-

тепловому квазиравновесию в остывающей НЗ при

ность (column depth) вещества y (г/см²), а вместо

T_ign ∼ (1-5) × 10⁸ К. При каждой плотности ρ в

Q_b — колонковую плотность энергии взрыва E_i

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 49

№ 12

2023

890

КАМИНКЕР и др.

(эрг/см²). Однако решение (2) нечувствительно к

(a)

M = 1.4 M₍ R = 12.8 км Q_b = 0.3 МэВ

модели НЗ именно при использовании величин

lgt [c] (код)

ρ и Q_b. Одно такое решение легко применимо

для любой модели. В этом смысле распределения

температуры на нейтринной стадии СВ для разных

моделей НЗ являются универсальными.

Это свойство полезно для тестирования расче-

(аппрокс.)

тов с помощью компьютерного кода. Кроме того,

решение (2) в принципе можно использовать и в

самом коде для ускорения вычислений на нейтрин-

ной стадии СВ.

4. РЕЗУЛЬТАТЫ

Приведем результаты моделирования СВ с по-

мощью численного кода и сравним их, где возмож-

Спокойная звезда

но, с приближением чисто нейтринного охлажде-

ния. На представленных рисунках (кроме рис. 6)

(б)

использована модель НЗ с массой 1.4 M_⊙, внут-

lgt [c] (код)

ренняя кора и ядро которой описываются урав-

нением состояния BSk24 (Пирсон и др., 2018), а

внешняя кора состоит из железа⁵⁶Fe (радиус такой

звезды составляет 12.8 км); мы рассматривали и

другие модели и получили похожие результаты.

(аппрокс.)

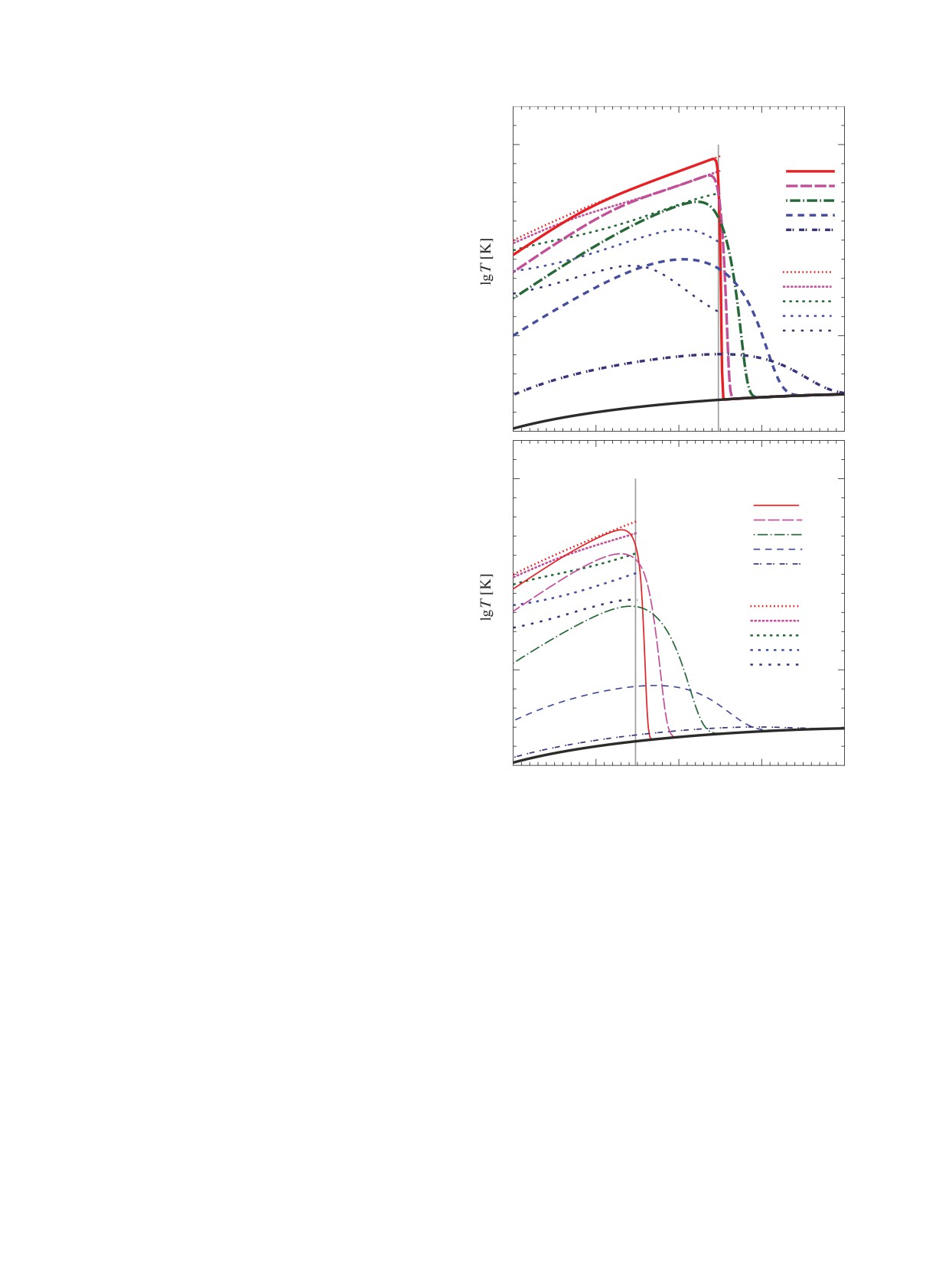
Рисунок 1 показывает профили T (ρ) во вспых-

нувшем слое и вблизи него для двух СВ в раз-

ные моменты времени t ≤ 10⁷ с в системе отсчета

внешней оболочки. Рисунок 1(а) отвечает ρ_ign,9 =

= 3, а 1(б) — ρ_ign,9 = 0.3; калорийность топли-

ва Q_b = 0.3 МэВ одинакова. Кривые помечены

значениями lg (t [с]). Верхние кривые (t = 1000 с,

почти сразу после СВ) близки к термодинамиче-

ской кривой T_max(ρ), единой при фиксированном

Спокойная звезда

Q_b. Отметим резкие изломы T_max(ρ) при ρ ≈ ρ_ign.

Растекание тепла из области взрыва постепенно

[г/см³]

превращает излом в размытый максимум, глубже

которого тепло диффундирует внутрь НЗ, а при

Рис. 1.

Зависимость внутренней температуры T от

плотности ρ в области вспышки в разные моменты

более низких ρ — наружу.

времени t при Q_b = 0.3 МэВ для двух глубин поджига,

Точечными линиями на рис. 1(а) и 1(б) пока-

(а) — ρign,9 = 3 (жирные кривые) и (б) — ρign,9 =

заны профили температуры при чисто нейтринном

= 0.3 (тонкие кривые). Точечные линии (аппрокс.) —

приближение нейтринного охлаждения; они обрезаны

охлаждении. При глубоком поджиге (ρ_ign,9 = 3) это

при ρ > ρign (при ρ < ρign точечные кривые одинаковы

приближение хорошо работает во всей энергоне-

в случаях (а) и (б)).

сущей области вспышки (ρ₉ ≳ 0.3) в течение t ≲

(1-3) × 10⁵ c. При чисто нейтринном охлаждении

профили температуры T (ρ, t) универсальны и мо-

гут быть легко получены без использования кода

При падении температуры T (ρ) приближение

остывания. При более мелком поджиге (ρ_ign,9 =

нейтринного охлаждения нарушается. Так, в слое

= 0.3) стадия нейтринного охлаждения оказывает-

с произвольной плотностью ρ нейтринное охла-

ся гораздо короче (t ≲ 10³ с) и практически незна-

ждение становится несущественным при достаточ-

чимой (см. ниже). Таким образом, приближенные

но низких Q_b, при которых T (ρ) ≲ T_ν , где T_ν ∼

решения совпадают с точными в тех случаях, когда

∼ (3-4) × 10⁹ К — характерная температура, зна-

охлаждение вещества определяется нейтринным

излучением, т.е. на достаточно малых временах при

чение которой слабо зависит от ρ. Это обстоятель-

большом вспышечном нагреве.

ство неоднократно отмечалось в литературе (см.,

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 49

№ 12

2023

НЕЙТРИННОЕ ИЗЛУЧЕНИЕ ПРИ СВЕРХВСПЫШКАХ

891

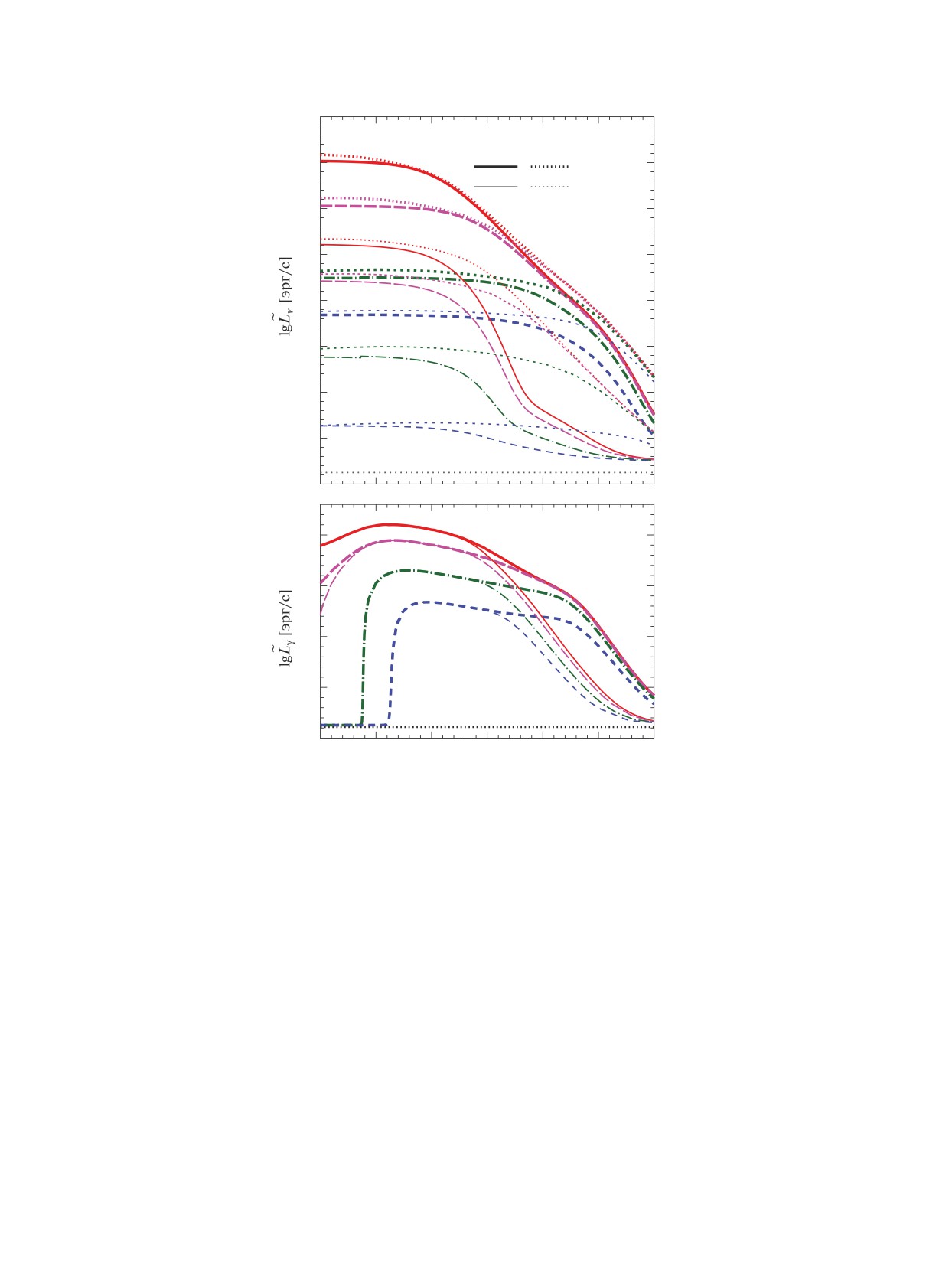
На рис. 3(а) и 3(б) представлены боломет-

Q_b [МэВ]

рические нейтринные и электромагнитные кривые

0.3

блеска,

L_ν(t) и

L_γ(t), для тех же моделей СВ,

0.2

что и на рис. 2. СравнениеLν (t) иLγ(t) показы-

0.1

вает, что в неглубокой вспышке (ρ_ign,9 = 0.3) при

0.05

всех выбранных значениях Q_b (за исключением

самых ранних моментов после ядерной вспышки)

доминирует фотонная светимостьLγ(t). В глубо-

кой вспышке (ρ_ign,9 = 3), особенно при высокой

калорийности топлива (Q_b = 0.3 и 0.2 МэВ), на-

оборот, нейтринный теплоотвод становится опре-

деляющим. Слияние кривыхLν (t) при Q_b = 0.3

= 3

и Qb = 0.2 подтверждает вывод об унификации

ign.9

остывания глубоких и мощных СВ при t ≳ 3 × 10⁴ с

ign.9

= 0.3

под действием мощного нейтринного излучения.

Точечные линии на рис. 3(а) показывают зави-

lgt [c]

симостиLν (t), вычисленные в приближении чисто

нейтринного охлаждения. Они получены интегри-

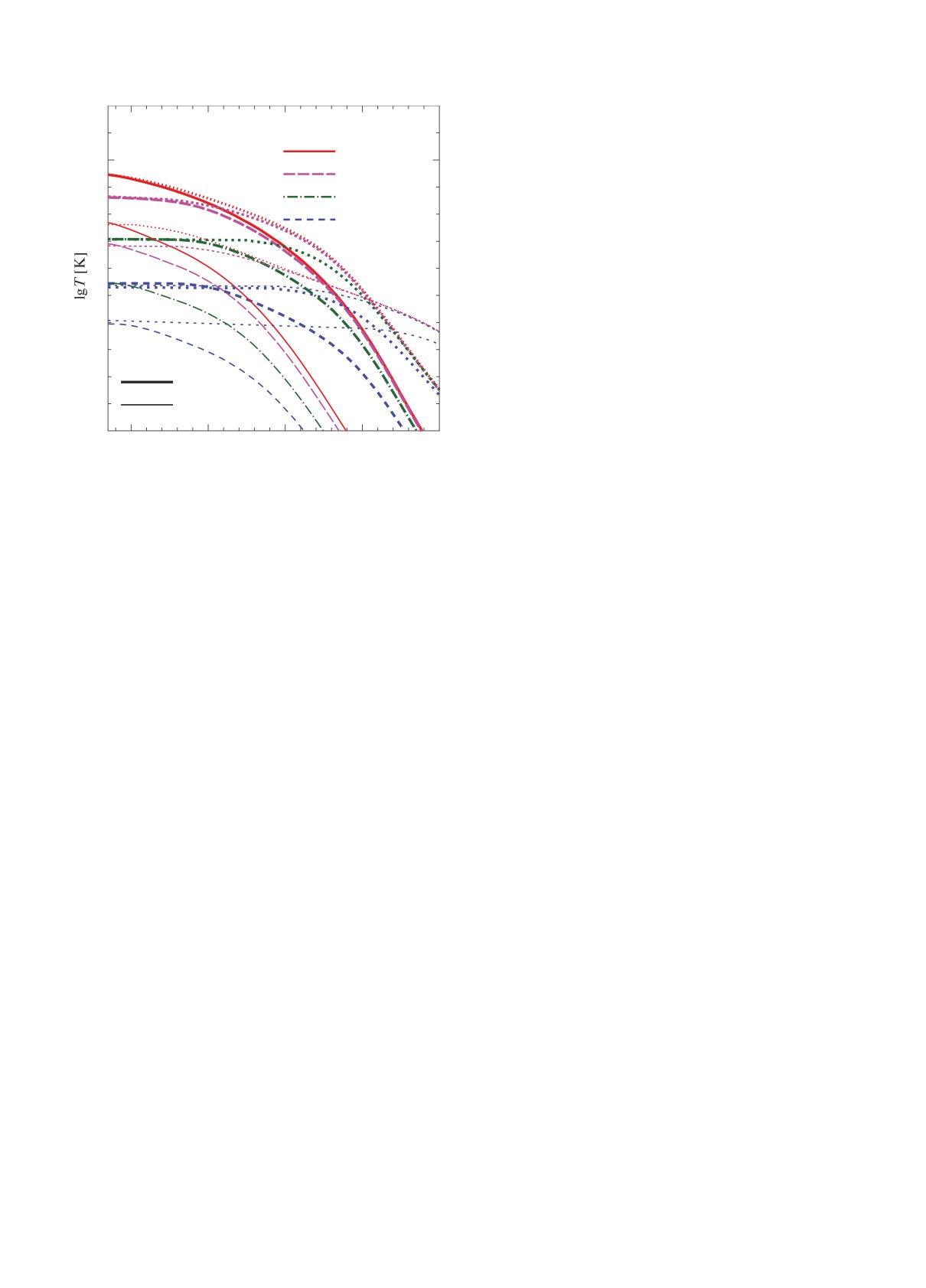
Рис. 2. Зависимость T(t) для двух моделей поджига

рованием нейтринных потерь энергии Q_ν (ρ, t) по

на рис. 1 в слоях с ρ = 0.8 ρign при Qb =0.3, 0.2, 0.1 и

0.05 МэВ. Сплошные, штриховые и штрихпунктирные

области вспыхнувшего слоя в оболочке НЗ. Срав-

линии — расчет, точечные — приближение нейтрин-

нение с результатами точных расчетов подтвержда-

ного охлаждения. Здесь и далее за начало отсчета t

ет выводы о длительности и эффективности стадии

принят момент окончания нагрева в слое (ρmin, ρign).

нейтринного охлаждения, сделанные при анализе

рис. 1 и 2.

например, Камминг, Макбет, 2004; Камминг и др.,

Участки электромагнитных кривых блеска, по-

2006).

казанные на рис. 3(б), формируются после выхода

на поверхность НЗ тепловой волны от вспыхнув-

На рис. 2 для примера изображена эволюция

шего слоя (например, Камминг, Макбет, 2004; Кик,

температуры T (t) в четырех СВ с разным тепло-

Хегер, 2011; Кик и др., 2012). Начальные участки

выделением (Q_b = 0.05-0.3) и с поджигом либо

определяются внешними частями этого слоя (ρ ∼

при ρ_ign,9 = 3 (жирные линии), либо при ρ_ign,9 =

∼ ρ_min), а более поздние — глубокими, энерго-

= 0.3 (тонкие линии). При каждом значении ρ_ign

несущими частями (ρ ∼ ρ_ign). Но на раннем эта-

профили T (t) изображены для слоя с плотностью

пе зависимости T (ρ) при одинаковых Q_b близки

ρ = 0.8ρ_ign.

между собой (рис. 1). Поэтому ранние участки (t ∼

Показательно, что кривые остывания T (t) для

∼ 10²-10⁴ с) кривых блеска Lγ(t) для СВ с такими

двух наиболее мощных СВ (ρ_ign,9 = 3, Q_b ≳ 0.2)

Q_b слабо отличаются друг от друга (рис. 3(б)).

при t ≳ 10⁴-10⁵ с сливаются в одну и ту же

Вспышки с ρ_ign,9 = 0.3 являются более короткими,

“универсальную” кривую. Такой эффект хорошо

чем глубокие вспышки с ρ_ign,9 = 3. Близость кри-

известен в теории нейтринного остывания НЗ (на-

выхLν (t), как и кривыхLγ (t), для глубоких СВ при

пример, Яковлев, Петик, 2004) как эффект “потери

Q_b =0.3 и 0.2 МэВ на поздних стадиях (t ≳ 10⁴ с)

памяти” о начальных условиях из-за сильной за-

объясняется тем же унифицирующим влиянием

висимости темпа нейтринного остывания от темпе-

мощного нейтринного теплоотвода в начале СВ.

ратуры: заметное превышение T над T_ν вызывает

быстрое нейтринное охлаждение до T ∼ T_ν , что и

На рис. 4 приведены кривые блескаLγ(t), рас-

“унифицирует” остывание. Если увеличивать Q_b

считанные для вспышек с Q_b =0.3 МэВ при шести

еще больше, то дополнительная энергия вспышки

глубинах поджига ρ_ign,9 от 0.1 до 5. При t ≲1000 с,

будет уноситься нейтрино, и зависимость T (t) при

все кривые почти совпадают, а далее различаются,

t ≳ 10⁵ с не изменится.

но обладают общими свойствами. Видно, что с ро-

Однако в других случаях, рассмотренных на

стом ρ_ign длительность послесвечения СВ растет,

рис. 2, нейтринное остывание (при lg t ≳ 4) оказы-

что связано с увеличением времени диффузии тепла

вается столь слабым, что фактически не влияет на

к поверхности НЗ из более глубоких слоев (см.,

T (t).

например, Яковлев и др., 2021).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 49

№ 12

2023

892

КАМИНКЕР и др.

(a)

Q_b = 0.3 МэВ

(код) (аппрокс.)

= 3

ign.9

0.2

ign.9

= 0.3

0.3

0.1

0.05

0.2

0.1

0.3

0.05

Спокойная звезда

= 0.3 МэВ

Q_b

(б)

0.2

0.1

0.05

0.3

Спокойная звезда

lgt [c]

Рис. 3. Нейтринные

L_ν(t) (а) и электромагнитные Lγ(t) (б) кривые блеска, рассчитанные для тех же моделей СВ, что и

на рис. 2. Светимости показаны с учетом гравитационного красного смещения.

Отметим, что наши расчеты позволяют изу-

сопутствующей системе отсчета, поскольку все

чать зависимость тепловой энергии СВ от време-

основные процессы тепловой эволюции происхо-

ни. Полная энергия СВ, E_tot, выделяется уже за

дят во внешней коре, достаточно тонкой, чтобы

пространство-время в ней было практически плос-

несколько минут после начала СВ в слое вспых-

ким, хотя и с иными временными и простран-

нувшего углерода. Зная из расчетов фотонную

ственными масштабами, чем в системе удаленного

L_γ(t) и нейтринную L_ν(t) светимости НЗ, а также

наблюдателя.

светимости Lγ0 и Lν0 в спокойной НЗ (до СВ),

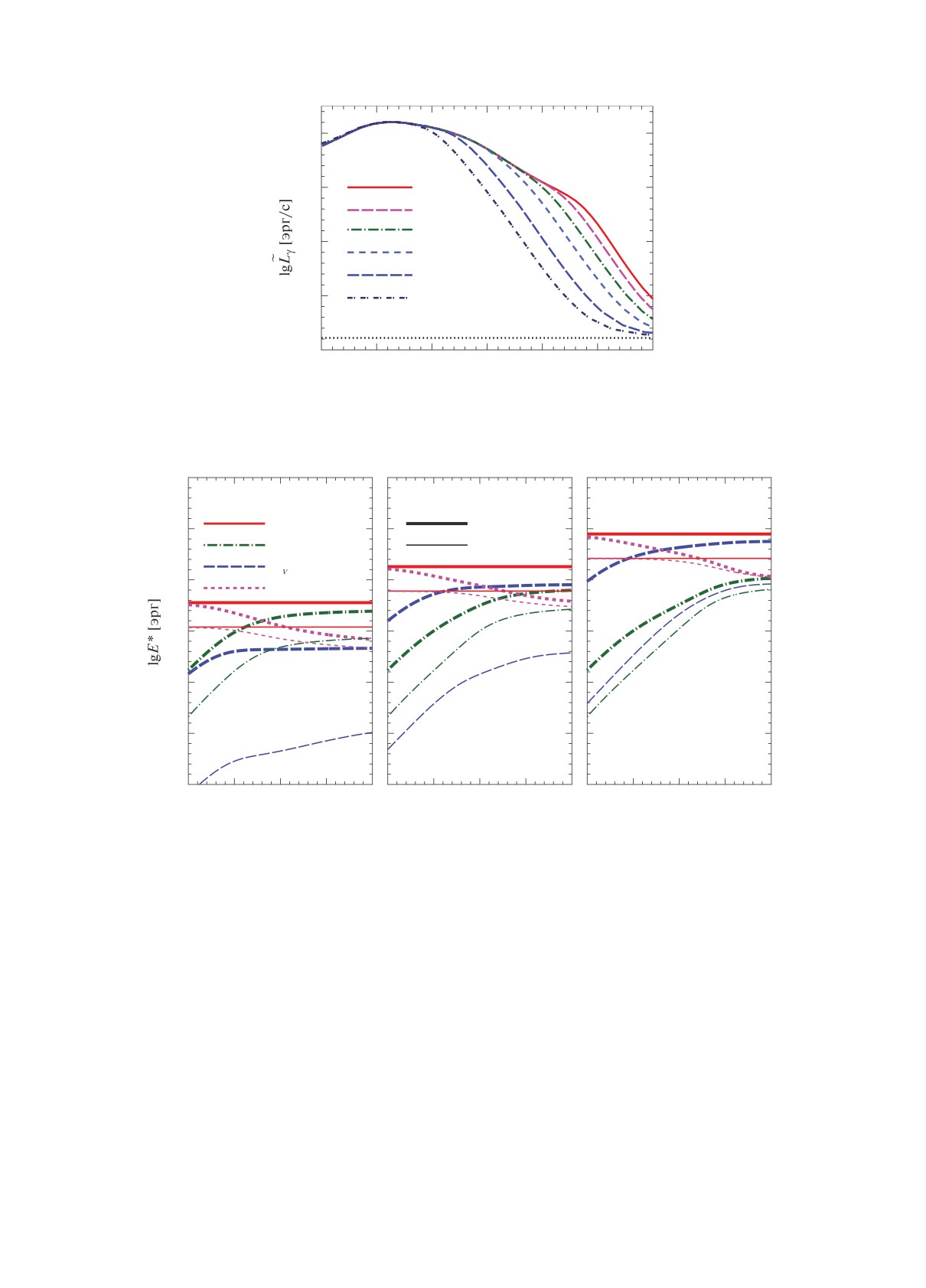
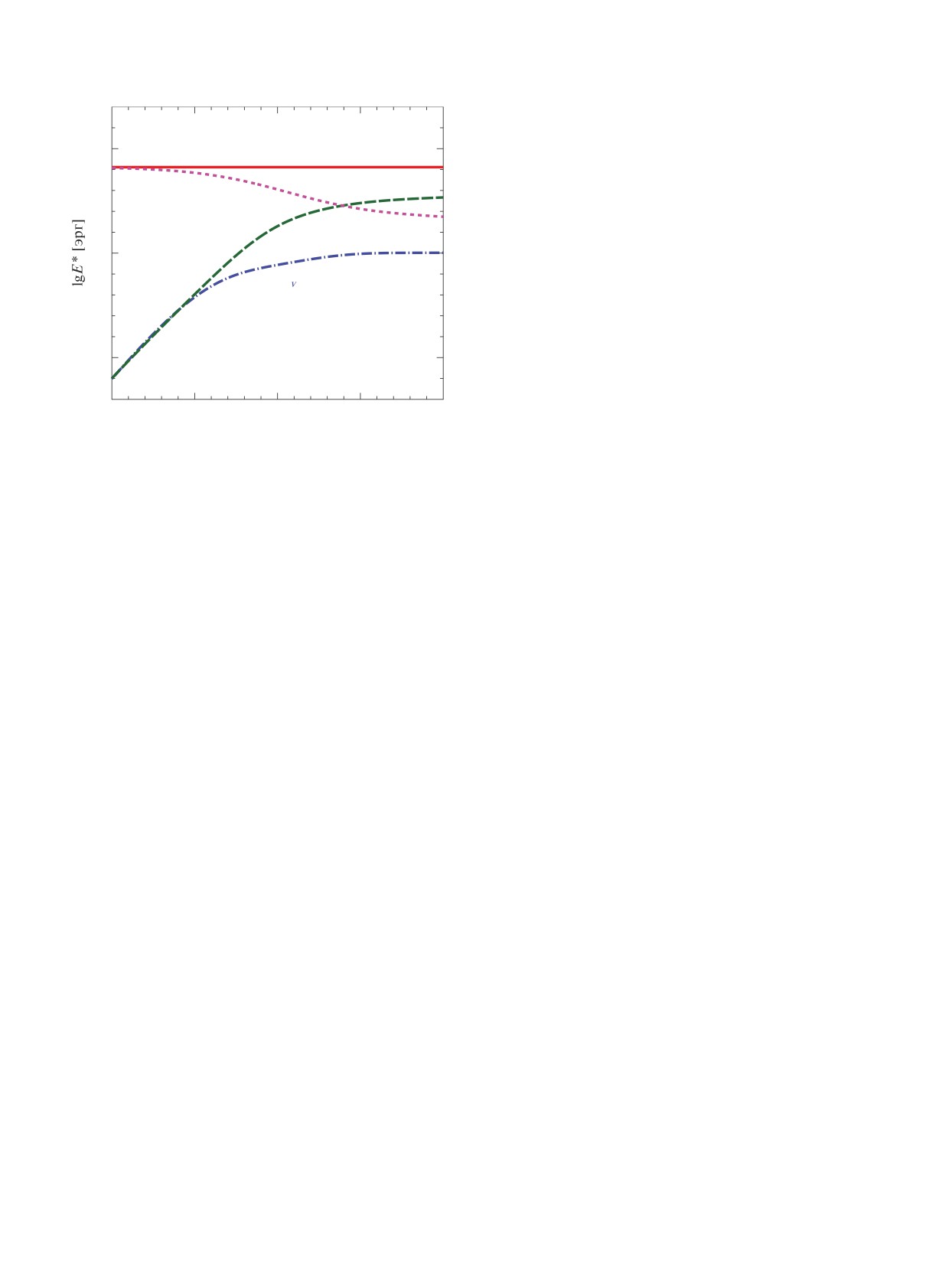
Рисунок 5 дает примеры зависимостей от вре-

находим светимости L^∗γ = L_γ - Lγ0 и L^∗ν = L_ν -

мени E^∗γ(t), E^∗ν(t) и E∗tot(t) для шести СВ при трех

- Lν0, обусловленные собственно СВ. Интегри-

значениях ρ_ign,9 = 0.3 (a), 1 (б) и 3 (в). Для каждой

руя их по времени от начала нагрева до текуще-

плотности поджига рассмотрено две вспышки, с

го момента t, получим фотонную и нейтринную

достаточно низкой (Q_b =0.1 МэВ) и высокой (Q_b =

энергии СВ, E^∗γ(t) и E^∗ν(t), унесенные из звезды к

= 0.3 МэВ) калорийностью топлива. Сплошные

моменту t. Величину E^∗T (t) = E_tot - E^∗γ(t) - E^∗ν(t)

горизонтальные линии показывают полные энергии

можно назвать остаточной тепловой энергией СВ

СВ. Активная фаза выноса энергии СВ из НЗ

в НЗ. Здесь энергии и светимости приведены в

продолжается тем дольше, чем выше ρ_ign.

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 49

№ 12

2023

НЕЙТРИННОЕ ИЗЛУЧЕНИЕ ПРИ СВЕРХВСПЫШКАХ

893

Q_b = 0.3 МэВ

ign.9

0.5

0.2

0.1

lgt [c]

Рис. 4. Фотонные кривые блеска

L_γ(t) сверхвспышек, рассчитанные при Q_b = 0.3 МэВ на разных глубинах поджига

ρ_ign,9, от 0.1 до 5.

(a) _ign = 3

10⁸ г/см³

(б) _ign = 10⁹ г/см³

(в) _ign = 3

10⁹ г/см³

E_tot

Q_b = 0.3

Q_b = 0.1

E *

393

7 3

lgt [c]

Рис. 5. Эволюциятепловой энергииСВ во времени, рассчитаннаяпри ρ_ign,9 = 0.3 (а), 1 (б) и 3 (в) в случаях Q_b = 0.3 МэВ

(жирные линии) и 0.1 МэВ (тонкие линии): E^∗γ — энергия СВ, излученная через поверхность звезды, E^∗ν — излученная

нейтринная энергия СВ, E^∗T — остаточная энергия СВ в НЗ. Сплошные горизонтальные линии показывают полную

энергию вспышки E_tot.

Рисунок 5а отвечает сравнительно неглубоким

Фотонное же охлаждение остается мощным, и за

вспышкам. Видно, что при слабой сверхвспышке

10⁷ с вычерпывает значительную долю E_tot.

(Q_b = 0.1 МэВ) энергия, уносимая нейтрино, пре-

Рисунок 5б соответствует двум СВ на умерен-

небрежимо мала. Основной механизм релаксации

ной глубине ρ_ign,9 = 1. Нейтринный теплоотвод бо-

такой СВ — излучение фотонов с поверхности.

лее слабой из них (Q_b = 0.1 МэВ) неэффективен,

Но даже через 10⁷ с, когда послесвечение с по-

так что основная энергия выносится излучением

верхности уже вряд ли наблюдаемо, в НЗ остается

через поверхность. К моменту t = 10⁷ с в НЗ все

более 10⁴¹ эрг энергии СВ. Более мощная вспышка

еще остается ∼10⁴² эрг энергии СВ. При более

(Q_b = 0.3 МэВ) на этой глубине сопровождается

сильной вспышке (Q_b = 0.3 МэВ), наоборот, избы-

заметно более сильным нейтринным охлаждением,

ток энергии уносится преимущественно нейтрино,

которое, однако, сравнимо по интенсивности с фо-

но остаточная энергия остается очень большой.

тонным охлаждением ∼1000 с, а затем ослабевает.

Рисунок 5в демонстрирует две СВ на глубине

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 49

№ 12

2023

894

КАМИНКЕР и др.

моделями дала (в наших обозначениях) ρ_ign,9 ≈ 1.3,

4U 1608 52

Q_b ≈ 0.17 МэВ.

tot

На рис. 6 представлены результаты наших рас-

четов для этой вспышки (с указанными параметра-

E *_T

E *

ми НЗ) в той же форме, что и на рис. 5. Нейтринное

излучение эффективно охлаждает СВ сравнитель-

но недолго. Несколько часов темп нейтринного

охлаждения (по случайным причинам) близок к

темпу излучения фотонов через поверхность НЗ.

E *

Далее доминирует фотонное охлаждение с поверх-

ности НЗ, но к моменту t = 10⁷ с (около 4 мес) и

оно становится слабым. За это время нейтринное

излучение уносит примерно четверть от полной

энергии вспышки, а фотонное — около 60%. Оста-

точная тепловая энергия составляет ≳10⁴² эрг.

Эти результаты, как и результаты, представ-

lgt [c]

ленные на рис. 5, свидетельствуют, что даже че-

рез несколько месяцев после СВ в звезде может

Рис. 6. Эволюция тепловой энергии мощной вспышки

оставаться значительная часть энергии взрыва.

НЗ в рентгеновском источнике 4U 1608-52, рассчи-

Расчеты показывают, что эта энергия (особенно

танная для параметров СВ, принятых из интерпрета-

ции ее наблюдений.

для глубоких СВ) в значительной мере стекает

в глубокие слои НЗ. Вопрос о дальнейшей ис-

тории этой энергии нетривиален. Например, при

горения¹²C, близкой к предельной. Более сла-

наличии регулярно повторяющихся вспышек тепло

бая из них отличается от слабых СВ на рис. 5а

от них постепенно прогревает всю звезду. Можно

и 5б: нейтринный теплоотвод теперь доминирует

подобрать частоту или интенсивность вспышек так,

над теплоотводом через поверхность, хотя разни-

чтобы в целом звезда оставалась в квазистацио-

ца между потерями тепла по этим двум каналам

нарном состоянии (например, Колпи и др., 2001;

невелика. При этом остаточная энергия к моменту

Кик, Хегер, 2011). Эволюция остаточного тепла

может определяться малыми и достаточно слож-

t = 10⁷ с всего в несколько раз меньше полной

ными градиентами температуры в оболочке НЗ,

энергии E_tot. Наши оценки показывают, что основ-

возникшими там по разным причинам. Этот вопрос

ная часть этой энергии в данном случае уносится

требует дальнейшего изучения.

внутрь звезды.

В дополнение к описанному выше, мы продела-

Наконец, более сильная вспышка (Q_b =

ли серию расчетов сверхвспышек НЗ с разными

= 0.3 МэВ) на рис. 5 сопровождается необык-

уравнениями состояния сверхплотного вещества,

новенно мощным нейтринным теплоотводом. Эта

варьируя массу (и радиус) НЗ, а также другие

вспышка принадлежит к особому классу угле-

параметры задачи, в том числе ρ_min и T_ign. Ис-

родных сверхвспышек, почти целиком управляе-

пользование разных уравнений состояния и пара-

мых нейтринными процессами. По расчетам ско-

метров НЗ не показало качественно новых эф-

рость переноса тепла внутрь звезды значительно

фектов. Уменьшение ρ_min ниже принятого значения

превосходит скорость вытекания энергии через

10⁷ г/см³ (что вполне допустимо; см., например,

поверхность. Возможность реализации подобных

Кик, Хегер, 2011; Кик и др., 2012; Альтамира-

вспышек в НЗ пока не ясна.

но и др., 2012) не может заметно изменить гло-

Для примера на рис. 6 мы изобразили тепловую

бальную эволюцию СВ. Оно может повлиять на

эволюцию СВ транзиентно аккрецирующей НЗ,

очень ранние участки фотонных кривых блеска,

входящей в состав маломассивной рентгеновской

моделирование которых мы все равно не проводим.

двойной системы 4U 1608-52. Вспышка наблю-

Вариации температуры поджига T_ign также слабо

далась 5 мая 2005 г. прибором “All-Sky Monitor”

сказываются на модели СВ до тех пор, пока эта

на борту космической рентгеновской обсерватории

температура заметно ниже, чем температура нагре-

им. Росси (Rossi X-ray Timing Explorer). Анализ

того вещества после взрыва. Температуру поджига

наблюдений (например, Кик и др., 2008; Занд,

можно определять самосогласованно для каждой

2017) показывает, что это была, по-видимому, одна

отдельной вспышки. Однако самосогласованный

из самых мощных и глубоких сверхвспышек. Для

расчет сложен и требует не всегда надежно из-

НЗ с M = 1.4 M_⊙ и R = 10 км подгонка наблюда-

вестной микрофизики (например, скоростей мно-

емой рентгеновской кривой блеска теоретическими

гих реакций, сопровождающих горение углерода).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 49

2023

№ 12

НЕЙТРИННОЕ ИЗЛУЧЕНИЕ ПРИ СВЕРХВСПЫШКАХ

895

Вывод о нечувствительности результатов нашего

Использованный код остывания позволяет лег-

упрощенного моделирования к точным значениям

ко моделировать эволюцию энергии вспышек со

T_ign подтверждает адекватность нашего подхода.

временем (рис. 5). Сравнение с наблюдениями мо-

жет помочь исследовать динамику энергии СВ для

По возможности мы старались сверять наши

конкретных событий (рис. 6).

результаты с результатами других авторов. В част-

ности, мы получили неплохое согласие с рис. 2

Еще раз подчеркнем, что моделирование СВ на

в работе Камминга и др. (2006), где сравнены

высоком уровне выполняется более 20 лет (см.,

мощности нейтринного и фотонного теплоотводов

например, Камминг, Макбет, 2004; Камминг и др.,

при СВ, и с рис. 5 в работе Кика и Хегера (2011),

2006; Кик, Хегер, 2011; Альтамирано и др., 2012;

где представлены зависимости L_γ (t) и L_ν (t) для

Кик и др., 2012, 2015; Занд, 2017; Галлоуэй, Кик,

одной из СВ.

2021, и ссылки там). Многие упомянутые резуль-

таты (например, возможность нейтринного отво-

5. ЗАКЛЮЧЕНИЕ

да основной части энергии СВ) были получены

ранее (см., например, Камминг и др., 2006; Кик,

Мы рассмотрели основные особенности редких

Хегер, 2011). Наше рассмотрение позволило сфор-

и очень энергичных событий

— сверхвспышек,

мулировать ряд общих свойств СВ. К ним отно-

происходящих в глубоких слоях внешних оболочек

сятся: упрощенное описание стадии нейтринного

аккрецирующих НЗ; они вызваны взрывным горе-

охлаждения внешней коры; возможность изуче-

нием накопленного углерода (¹²C) в глубоких слоях

ния эволюции тепловой энергии СВ на масштабах

внешней коры НЗ. Для их моделирования исполь-

нескольких месяцев и вывод о возможности удер-

зован численный код (Потехин, Шабрие, 2018),

жания энергии СВ внутри НЗ на таких временных

учитывающий современную микрофизику НЗ (раз-

масштабах.

дел 2), введено приближение чисто нейтринного

охлаждения (раздел 3), а также проанализирована

Рассмотренные максимальные глубины поджи-

динамика распространения тепла в период релак-

га ρ_ign,9 ∼ 5 являются, по-видимому, предельны-

сации вспышки (раздел 4).

ми для взрывного горения¹²C (см., например,

Предложен простой метод исследования стадии

Потехин, Шабрие, 2012). Однако не исключено,

нейтринного охлаждения внешней коры, который

что вспышки за счет горения вещества с другим

позволил сформулировать универсальное соотно-

составом возможны и в более глубоких слоях.

шение для распределения температуры T (t, ρ, Q_b)

Так, Паж и др. (2022) предположили, что мощная

во вспыхнувшем слое.

вспышечная активность источника MAXI J0556-

332 связана с гипервспышкой в НЗ при ρ_ign,9 ∼

Отмечено, что динамика СВ определяется двумя

основными параметрами: плотностью ρ_ign взрыв-

∼ 100 (у границы внешней оболочки и внутрен-

ного поджига углерода и калорийностью топлива

ней коры) под действием взрывного горения ряда

Q_b. При неглубоких СВ (ρ_ign,9 ≲ 0.3) нейтринное

нейтронно-избыточных изотопов. По теории такие

излучение оказывается несущественным для лю-

гипервспышки если и происходят, то очень редко.

бых рассмотренных Q_b; такие СВ можно назвать

Если все же происходят, то они представляют со-

“безнейтринными”. С ростом ρ_ign при достаточно

бой продолжение семейства обычных углеродных

высоких Q_b нейтринное излучение начинает играть

сверхвспышек, но в крайне необычном режиме.

важную роль. Длительность стадии нейтринного

Наши результаты могут быть полезны также для

охлаждения растет (от ∼10³ с при ρ_ign,9 ∼ 0.3 до

исследований обычных термоядерных вспышек в

≳ 10⁵ с при ρ_ign,9 ∼ 3). C ростом Q_b до значений

поверхностных слоях НЗ. Прежде всего, это так

∼0.3 МэВ нейтринная светимость L_ν (t), вызванная

называемые вспышки промежуточной длительно-

СВ, начинает превосходить фотонную светимость

сти (intermediate duration bursts), более короткие,

L_γ(t) с поверхности НЗ и определять остывание.

чем СВ. Они возникают в гелиевом слое на холод-

При особо глубоком поджиге ρ_ign,9 ≳ 3 и высокой

ной НЗ (см., например, Камминг и др., 2006; Занд,

калорийности Q_b ∼ 0.3 МэВ основная часть энер-

2017). Схожие проблемы переноса энергии возни-

гии СВ уносится нейтрино, а кривая блеска L_γ (t)

кают при СВ или обычных вспышках магнитаров

определяется лишь малой долей энергии СВ. Более

в их внутренней или внешней коре под действием

того, с ростом ρ_ign все больше энергии уносится

сверхсильных магнитных полей (например, Каспи,

теплопроводностью внутрь НЗ. В определенных

Белобородов, 2017).

случаях даже через несколько месяцев после СВ в

звезде может оставаться довольно большая энер-

Работа поддержана Российским научным фон-

гия вспышки.

дом (грант 19-12-00133-П).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 49

№ 12

2023

896

КАМИНКЕР и др.

СПИСОК ЛИТЕРАТУРЫ

10. Кик и др. (L. Keek, A. Cumming, Z. Wolf,

D.R. Ballantyne, V.F. Suleimanov, E. Kuulkers, and

1. Альтамирано и др. (D. Altamirano et al.), MNRAS

T.E. Strohmayer), MNRAS 454, 3559 (2015).

426, 927 (2012).

11. Колпи и др. (M. Colpi, U. Geppert, D. Page, and

2. Галлоуэй, Кик (G.K. Galloway and L. Keek),

A. Possenti), Astrophys. J. 548, L178 (2001).

Timing Neutron Stars: Pulsations, Oscillations

12. Паж и др. (D. Page, J. Homan, M. Nava-

and Explosions (Ed. T.M. Belloni, M. Mendez,

Callejas, Y. Cavecchi, M.V. Beznogov, N. Degenaar,

C. Zang), Astrophys. Space Sci. Library, Vol. 461

R. Wijnands, and A.S. Parikh), Astrophys. J. 933, 216

(Berlin, Heidelberg: Springer, 2021), p. 209.

(2022).

3. Занд(in ’t Zand), 7 years of MAXI: monitoring

X-ray transients (Ed. M. Serino, M. Shidatsu,

13. Пирсон и др. (J.M. Pearson, N. Chamel,

A.Y. Potekhin, A.F. Fantina, C. Ducoin, A.K. Dutta,

W. Iwakiri, T. Mihara; Saitama: RIKEN, 2017),

and S. Goriely), MNRAS 481, 2994 (2018).

p. 121.

14. Потехин, Шабрие (A.Y. Potekhin and G. Chabrier),

4. Камминг, Макбет (A. Cumming and J. Macbeth),

Astron. Astrophys. 538, A115 (2012).

Astrophys. J. 603, L37 (2004).

5. Камминг и др. (A. Cumming, J. Macbeth, J.J.M. in ’t

15. Потехин, Шабрие (A.Y. Potekhin and G. Chabrier),

Astron. Astrophys. 609, A74 (2018).

Zand, and D. Page), Astrophys. J. 646, 429 (2006).

6. Каспи,

Белобородов (V.M.

Kaspi

and

16. Хенсель и др. (P. Haensel, A.Y. Potekhin, and

A.M. Beloborodov), Ann. Rev. Astron. Astrophys. 55,

D.G. Yakovlev), Neutron Stars. 1. Equation of State

261 (2017).

and Structure. (New York: Springer, 2007).

7. Кик, Хегер (L. Keek and A. Heger), Astrophys. J.,

17. Шапиро С., Тьюколски С., Черные дыры, белые

743, 189 (2011).

карлики и нейтронные звезды (М.: Мир, 1985).

8. Кик и др. (L. Keek, J.J.M. in ’t Zand, E. Kuulkers,

18. Яковлев, Петик (D.G. Yakovlev and C.J. Pethick),

A. Cumming, E.F. Brown, and M. Suzuki), Astron.

Astron. Astrophys. 42, 169 (2004).

Astrophys. 479, 177 (2008).

19. Яковлев и др. (D.G. Yakovlev, A.D. Kaminker,

9. Кик и др. (L. Keek, A. Heger, and J.J.M. in ’t Zand),

A.Y. Potekhin, and P. Haensel), MNRAS 500, 4491

Astrophys. J. 752, 150 (2012).

(2021).

ПИСЬМА В АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 49

№ 12

2023