Широко известно, что так называемые структурные формулы теории механизмов не всегда дают верный результат. Это относится и к простейшей и исторически первой из них, формуле Чебышева, выражающей число степеней свободы (степень подвижности) плоского шарнирно-рычажного механизма через число его звеньев и число вращательных пар. Причиной этого является сложность геометрической природы механизмов. Степень подвижности определяется не только числом кинематических пар и звеньев, но и порядком их соединения, т.е. строением механизма. Подходящий язык для описания строения механизмов доставляет математическая теория графов. Она все больше начинает применяться при изучении структуры механизмов [1–3]. С ее использованием автор [4, 5] предложил формализацию основных понятий теории механизмов на основе кинематической модели плоских шарнирно-рычажных устройств. Эта формализация позволяет дать критерий применимости к типичным¹¹ устройствам данной структуры формул для числа степеней подвижности. В ней строение шарнирно-рычажного механизма задается графом G, вершины которого отвечают шарнирам, а ребра отвечают звеньям, в качестве которых выступают несущие на своих концах шарниры прямолинейные стержни.

В теории же механизмов [1, 2] в качестве структурного графа принято брать граф $\mathcal{G}$, вершины которого отвечают звеньям, а ребра – кинематическим парам. В статье будет выяснено, равносильны ли описания строения плоских шарнирно-рычажных устройств графами G и $\mathcal{G}$. А также приведен критерий применимости структурной формулы к типичным плоским шарнирно-рычажным устройствам, строение которых задано графом G.

Кинематическая модель шарнирно-рычажных механизмов и граф G. Мы рассматриваем плоские шарнирно-рычажные устройства, составленные из прямолинейных абсолютно твердых стержней (рычагов), соединенных на своих концах шарнирами. Каждый рычаг несет по шарниру на своих концах, внутри рычагов шарниров нет²². Если в шарнире соединены лишь два рычага, то этому шарниру отвечает обычная вращательная пара, допускающая произвольное проворачивание в плоскости одного из рычагов относительно другого. Мы называем такой шарнир 1-шарниром. Если в шарнире соединены k > 2 рычагов, то это так называемый совмещенный или сложный шарнир с одним общим центром вращения для всех k рычагов. Его мы называем (k – 1)-шарниром. В этом шарнире каждый из k рычагов допускает проворачивание, независимо от остальных рычагов. Если же конец рычага не соединен ни с каким другим рычагом, то в нем нет кинематической пары, но мы считаем его шарниром, и называем 0-шарниром. В теории механизмов принято рассматривать закрепленные в стойке конструкции. Мы будем проводить закрепление устройства в плоскости также допускающими полное проворачивание шарнирами, которые назовем закрепленными, и на рисунках будем обозначать крестиками в отличие от кружочков, отвечающих незакрепленным (свободным) шарнирам. В закрепленном шарнире имеется хотя бы одна кинематическая пара, и он не может быть 0-шарниром.

Нашему шарнирно-рычажному устройству естественно сопоставить граф³³ G, вершины которого отвечают шарнирам, а ребра, понимаемые как соединяющие пары вершин отрезки прямых, отвечают рычагам. Граф G мы считаем связным⁴⁴ без петель и кратных ребер. Более того, при наличии закрепленных шарниров, порожденный⁵⁵ свободными шарнирами подграф графа G также считаем связным. Это условие налагается, чтобы не считать одним механизмом кинематически не связанные между собой устройства. И, естественно, в G нет ребер, соединяющих вершины, отвечающие закрепленным шарнирам.

После задания в плоскости положений закрепленных шарниров исследование кинематики шарнирно-рычажных устройств с заданным графом G сводится к исследованию множества решений системы квадратичных уравнений. А именно, уравнений, накладывающих условия на расстояния между шарнирами

где $\left( {{{x}_{i}},~{{y}_{i}}} \right)$ – координаты i-го шарнира ${{p}_{i}}$; ${{d}_{{ij}}}$ – квадрат длины рычага, несущего на концах шарниры ${{p}_{i}}$ и ${{p}_{j}}$. Число уравнений равно числу рычагов в конструкции. Конфигурационное пространство механизма есть компонента связности положительной размерности множества решений этой системы. Компонентам связности нулевой размерности, т.е. состоящим из одной точки, отвечают шарнирные фермы.

В нашей идеализированной модели допускается пересечение различных рычагов и совпадение положений различных несмежных, т.е. не принадлежащих одному рычагу, шарниров.

Сравнение графов G и $\mathcal{G}$. Граф $\mathcal{G}$ для нашего шарнирно-рычажного устройства мы получим, сопоставив каждому рычагу и стойке по вершине, а каждому k-шарниру при $k > 0$ ребро, соединяющее вершины, отвечающие соединенным этим шарниром звеньям (либо двум рычагам, либо рычагу и стойке в случае закрепленного шарнира). 0-шарнирам ничего не сопоставляется.

Возникает вопрос: равносильно ли описание структуры шарнирно-рычажной конструкции с помощью графа $\mathcal{G}$ ее описанию графом G. На самом деле, нет, как показывает пример рис. 1. Для незакрепленных шарнирно-рычажных конструкций, для которых графом G являются полный⁶⁶ граф ${{G}_{1}} = {{K}_{3}}$ и полный двудольный⁷⁷ граф ${{G}_{2}} = {{K}_{{1,3}}}$, граф $\mathcal{G}$ один и тот же, а именно ${{K}_{3}}$. Эти конструкции существенно различны: одна из них ферма, а другая – механизм с двумя степенями подвижности⁸⁸. Итак, в этом случае по графу $\mathcal{G}$ строение конструкции однозначно не восстанавливается. Граф G несет все сведения о нем.

Однако если откинуть этот случай, то описания становятся равносильными.

Рассмотрим отвечающий незакрепленной шарнирно-рычажной конструкции граф G(V, E) = G. Для него граф $\mathcal{G}$ называют реберным⁹⁹ или смежностным по отношению к графу G. Известна следующая теорема [6].

Теорема. Пусть G и G₁– связные графы, у которых реберные графы изоморфны¹⁰¹⁰. Графы G и G₁ изоморфны всегда, кроме случая, когда один из них K₃, а другой K_1, 3.

Из этой теоремы непосредственно вытекают следующие утверждения.

Утверждение 1. Если в графе G связной незакрепленной шарнирно-рычажной конструкции более четырех вершин, то он восстанавливается по графу $\mathcal{G}$ с точностью до переобозначения вершин.

Утверждение 2. При отсутствии совмещенных шарниров описание структуры незакрепленной шарнирно-рычажной конструкции графом $\mathcal{G}$ равносильно ее описанию графом G.

Отметим, что в теории механизмов в случае наличия в устройстве совмещенных шарниров ему принято [1, 7] сопоставлять не граф $\mathcal{G}$, а модифицированный граф $\mathcal{G}$′. Граф $\mathcal{G}$′ получается из графа $\mathcal{G}$ удалением некоторых ребер. А именно, если $\mathcal{G}$ содержит s-шарнир ($s > 1$), то из полного подграфа ${{K}_{{s + 1}}}$, отвечающего в $\mathcal{G}$ этому шарниру, выкидывают часть ребер, чтобы получить включающее все вершины дерево¹¹¹¹. Это можно сделать многими способами. В случае 2-шарнира (рис. 1) из подграфа ${{K}_{3}}$ выкидывается одно из ребер. Однако такое действие ведет к потере информации о строении конструкции. Действительно, по полученному графу $\mathcal{G}$′ невозможно восстановить граф G нашей конструкции. Граф $\mathcal{G}$′ (рис. 1) является реберным для графа G′ неизоморфного ни графу G₁, ни графу G₂. Если взять в качестве G граф ${{K}_{{1,~4}}}$, то для него реберный граф $\mathcal{G}$ есть полный граф ${{K}_{4}}$, а в качестве графа $\mathcal{G}$′ можно выбрать, например, граф ${{K}_{{1,~3}}}$, который, как легко понять, не является реберным графом ни для какого графа. Итак, в приведенных примерах по графу $\mathcal{G}$′ граф G не восстанавливается. Из этого следует вывод о том, что граф $\mathcal{G}$ несет больше информации о строении шарнирно-рычажной конструкции, чем граф $\mathcal{G}$′.

О структурных формулах. Аналогом структурной формулы Чебышева для закрепленных устройств в нашей модели является формула

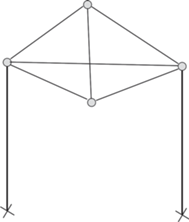
где W – число степеней свободы; m – число свободных шарниров; r – число рычагов. В ней учитываются все свободные шарниры, в том числе и 0-шарниры. Смысл ее прозрачен: из числа степеней свободы всех незакрепленных шарниров вычитается число условий на их положения, налагаемых рычагами. Эти условия считаются независимыми. В отличие от формулы Чебышева эта формула справедлива и при наличии совмещенных шарниров.

Возможно такое строение механизма, что эта формула будет нарушаться в типичном случае, как это имеет место для механизма на рис. 2.

Хотя наша структурная формула дает нулевое число степеней свободы, типичное устройство такого строения есть механизм – шарнирный четырехзвенник с избыточной связью в шатунном звене. В этом случае независимо от выбора длин рычагов, налагаемые ими условия зависимы.

В комбинаторной теории жесткости [8, 9] найдены условия, необходимые и достаточные для независимости накладываемых рычагами условий в плоском случае. Опишем их. Для произвольного подграфа графа G с m вершинами, отвечающими свободным шарнирам, n вершинами, отвечающими закрепленным шарнирам, и e ребрами (отвечающими рычагам конструкции) должны выполняться условия: 1) при n = 0, $e \leqslant 2m--3$; 2) при n = 1, $e \leqslant 2m--1$; 3) при $n \geqslant 2$, $e \leqslant 2m$. Эти условия необходимы и достаточны для справедливости подсчета числа степеней свободы типичных шарнирно-рычажных устройств по формуле (1). Отметим, что первое из них не выполняется для полного подграфа ${{K}_{4}}$, ребра которого нарисованы тонкими линиями на рис. 2.

Заключение. Строение механизмов может быть весьма сложным. Это сказывается уже при исследовании плоских механизмов с вращательными парами, структуре которых посвящены недавние работы [10, 11], выполненные в рамках традиционных понятий. Однако для анализа структуры даже шарнирно-рычажных устройств недостаточно оставаться в рамках традиционных понятий теории механизмов, таких как звенья, кинематические пары и кинематические цепи. Структуру механизмов естественно описывать графами. Одному механизму можно сопоставлять различные графы. Хотя описание графом $\mathcal{G}$ носит общий, не зависящий от типа кинематических пар, характер, но в случае плоских шарнирно-рычажных механизмов предпочтительнее использовать граф G. Особенно это заметно при изучении механизмов с совмещенными шарнирами. Использование графа G позволяет на современном уровне решить вопрос о применимости аналога структурной формулы Чебышева к типичным плоским шарнирно-рычажным механизмам.