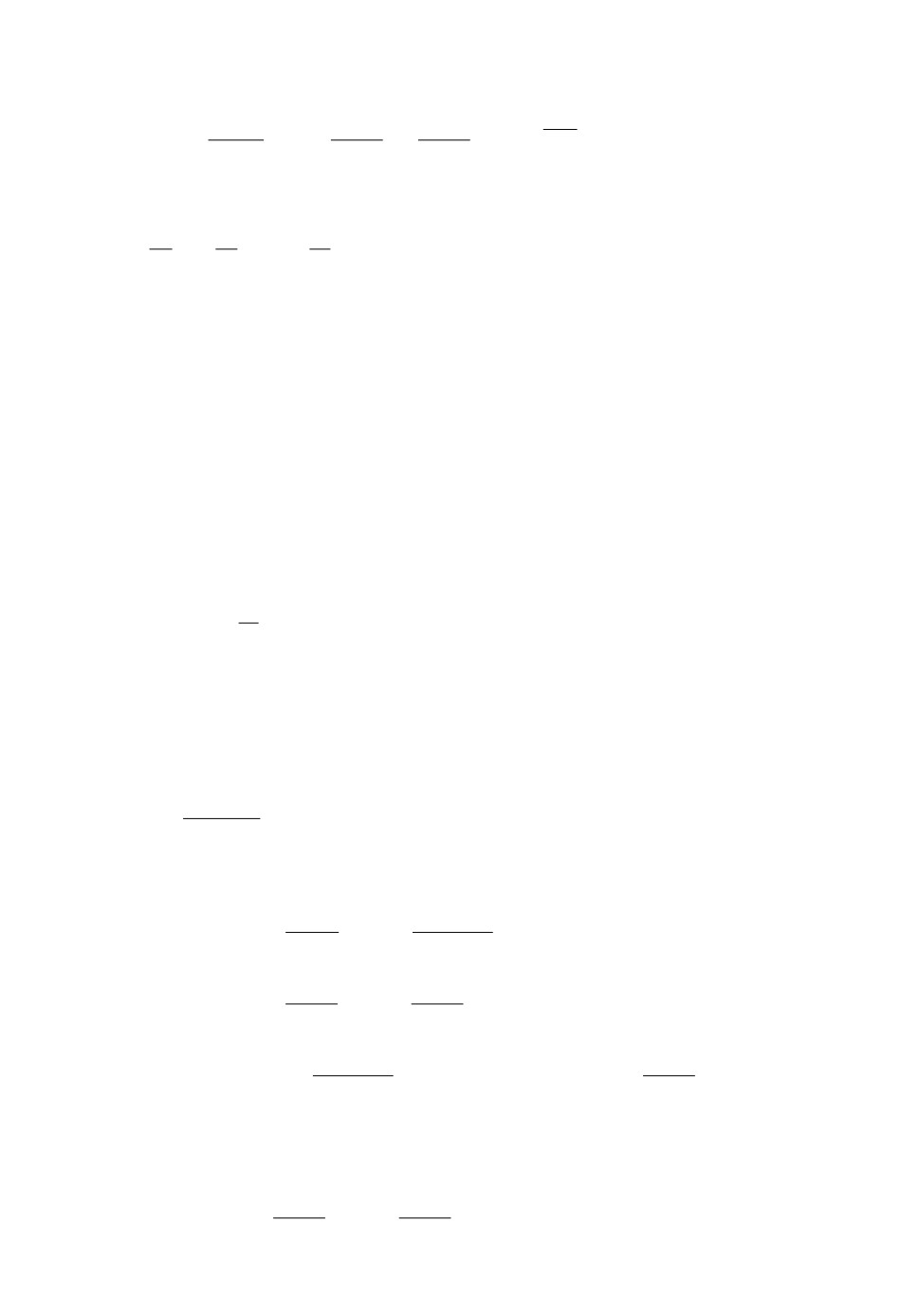ПРОБЛЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
Том 55
2019
Вып. 1
УДК 621.391.1 : 519.651 : 519.688
© 2019 г.
Е.А. Карацуба1, П. Моретти
ВЕРОЯТНОСТЬ ИНВЕРСИИ БОЛЬШОГО СПИНА В ВИДЕ
АСИМПТОТИЧЕСКОГО РАЗЛОЖЕНИЯ В РЯД ФУНКЦИЙ БЕССЕЛЯ
Точное выражение для вероятности инверсии большого спина устанавливает-
ся в виде асимптотического разложения в ряды функций Бесселя с порядками,
принадлежащими арифметической прогрессии. На основе нового асимптотиче-
ского разложения выведена формула для времени инверсии спина.
DOI: 10.1134/S0134347519010030
§ 1. Введение
Магнитные материалы снова вызывают большой интерес, что обусловлено недав-
ним синтезом молекул с большим магнитным моментом, так называемых магнит-
ных молекулярных кластеров. Когда они расположены в кристаллической решет-
ке, магнитные моменты взаимодействуют очень слабо, так как взаимное расстоя-
ние велико; однако может происходить магнитное упорядочение, поскольку высо-
кая магнитная анизотропия таких кластеров допускает параллельную ориентацию
осей анизотропии. Потенциальное применение магнитных кластеров в устройствах
с высокой плотностью хранения было основным стимулом исследований в этой об-
ласти [1]. Недостатком же такого применения является мобильность спинов - могут
возникнуть неконтролируемые спиновые инверсии, разрушающие любой магнитный
порядок. Поэтому необходимо понять микромеханизмы, на которых основаны такие
взаимодействия, чтобы их эффекты могли быть устранены или уменьшены; таким
образом, динамика спина играет очень важную роль в изучении молекулярных маг-
нитных кластеров. В частном случае кластеров железа, если используется мёссбауэ-
ровская спектроскопия, время инверсии спина является одним из наиболее важных
параметров в структуре экспериментальных данных [2].
В наглядном, интуитивном описании, когда общий электронный спин соседей из
ближайшего окружения переворачивается, магнитное поле на ядрах железа так-
же меняется. Тем самым, уровни ядерной энергии модифицируются, и проявляется
присутствие мёссбауэровского релаксационного спектра со структурой, зависящей
от частоты инверсии [3], а следовательно, можно получить информацию о структуре
спиновых состояний и спиновой динамике.
Динамика спина изучается на основе непосредственного применения уравнения
Шрёдингера. Рассматривается полный спин S под действием статического магнит-
ного поля. Кроме того, существует недиагональная часть взаимодействия, которая
вызывает переходы между соседними спиновыми состояниями. Это, очевидно, упро-
щенная ситуация, в некоторых случаях описывающая реальную физическую систе-
му, как показано в [4].
1 Работа выполнена при частичной финансовой поддержке грантов Российского фонда фунда-
ментальных исследований - Российских железных дорог (номер проекта 17-20-02222) и Российского
фонда фундаментальных исследований (номер проекта 19-07-00750).
59
В [4] коэффициент |bn(t)|2, который определяется как вероятность найти систе-
му в n-м спиновом состоянии, был вычислен и оказался некоторой сложной три-
гонометрической суммой. Примерное выражение для bn(t) через соответствующие
функции Бесселя было получено только при условии, что n ≪ N, αt ≪ N (N - об-
щее число спиновых состояний, α - размерный параметр недиагонального взаимо-
действия, который далее будет определен явно), поскольку только в этом случае
можно обоснованно заменить тригонометрическую сумму по всем спиновым состоя-
ниям соответствующим интегралом. Используя эвристические рассуждения, можно
предположить, что это соотношение справедливо также при n = N, что соответ-
ствует переходу от состояния “спин вверх” к состоянию “спин вниз”, и таким об-
разом можно вычислить время инверсии. Оно определяется первым максимумом
функции |bN(t)|2. Однако из-за важности установления момента времени инверсии,
связывающего теорию с экспериментальными данными, нужны были более точные
и обоснованные вычисления на основе строгого подхода, предложенного в [4]. Они
были проведены в [5].
Настоящая статья продолжает работу [5], где для амплитуды вероятности bN (t)
была выведена новая формула через функции Бесселя с большими индексами при
N ≥ 2 и для любого t.
Мы получим новые асимптотические разложения для функции bN (t), которые
позволят вычислить bN (t) с растущей точностью (см. рис. 2, 4, 5 в § 3).
Получено асимптотически точное выражение для времени инверсии спина. При-
менение этой полезной формулы показано на примере кластера Fe8.
§ 2. Постановка задачи
Гамильтониан нашей системы, который включает полный спин S, имеет вид
H = H0 + V , где H0 - статический гамильтониан (т.е. магнитное поле), а V - член,
отвечающий за переходы между спиновыми состояниями.
Начиная с дискретного набора N (N = 2S + 1) собственных состояний спина |n〉
при H0 с энергиями En, можно записать волновую функцию в виде
∑
ψ(t) =
an(t)|n〉exp(-iEnt/ℏ).
n=1
Из уравнения Шрёдингера получаем коэффициенты an(t):
∑
En - Eℓ
iℏan(t) =
aℓ(t)Vnℓ exp(iωnlt), ωnℓ =
ℏ
ℓ=1
Уместны некоторые упрощения. Во-первых, можно предположить, что V связы-
вает только соседние состояния и не имеет диагональных элементов; более того,
|ωn,n±1| = ω независимо от n, и V∗n,n+1 = Vn,n-1 = k.
Начальными условиями, представляющими интерес, являются следующие:
a1(0) = 1,
an(0) = 0, n = 2, 3, . . ., N,
что соответствует состоянию “спин вверх” (или “спин вниз”). Подстановка
bn(t) = an(t)e-inωt
приводит к системе уравнений, которая может быть решена преобразованием Ла-
пласа. Если рассмотреть n = N, т.е. именно амплитуду вероятности инверсии спина,
60
можно получить следующий результат (см. [4]):
N
∑
sπ
(-1)
sπ
Nsπ
bN (t) = -2
sin
sin
e2πiβcos
N +1 ,
(1)
N +1
N+1
N +1
s=1
где
kt
t
2k
β =
=α
,
α=
(2)
πℏ
2π
ℏ
Это уравнение получается в пределе ω → 0 и не зависит от ω. Может быть выполнен
подробный расчет до первого порядка по ω (см. [4]), и оказывается, что коэффици-
ент bN снова задается формулами (1), (2) в пределах фазового множителя. Таким
образом, если ω не слишком велико, значение bN почти не чувствительно к его ва-
рьированию.
§3. Асимптотическое разложение bN
Цель настоящей статьи - изучить функцию bN(t) при N ≥ 2.
В [5] доказана следующая
Теорема. Для bN(t) справедлива формула
∑
{
2
bN (t) = (-1)N
i(N+1)(2ν-1)
[(N + 1)(2ν - 1) - 1]J(N+1)(2ν-1)-1(αt) +
αt
ν=1
}
+ [(N + 1)(2ν - 1) + 1]J(N+1)(2ν-1)+1(αt) ,
N ≥ 2.
(3)
Доказательство теоремы основано на трех леммах.
Лемма 1. Для bN(t) справедливо следующее соотношение:
N
(-1)
bN (t) =
[S1 - S2 - (S3 - S4)] ,
2(N + 1)
где
N∑+1
[
)]
(2j - 1
(2j - 1)π
S1 =
exp 2πi
+ β cos
,
N+1
N +1
j=1
N∑+1
[
(
)]
2j
2jπ
S2 =
exp 2πi
+ β cos
,
N+1
N+1
j=1
N∑+1
[
]
N∑+1
(
)
(2j - 1)π
2jπ
S3 =
exp 2πiβ cos
,
S4 =
exp
2πiβ cos
N+1
N+1
j=1
j=1
Доказательство. Для доказательства леммы (подробнее см. в [5]) восполь-
зуемся тем, что
[
(
)]
s
sπ
(-1)s+1 exp 2πi
+ β cos
N+1
N +1
61
является функцией, периодической по s с периодом 2(N + 1):
[
(
)]
∑
s
sπ
(-1)s+1 exp 2πi
+ β cos
=
N+1
N+1
s=1
[
(
)]
∑
s
sπ
=
(-1)s+1 exp -2πi
- β cos
,
N+1
N+1
s=1
и следовательно,
{
[
(
)]
N
∑
(-1)
s
sπ
bN (t) =
(-1)s+1 exp 2πi
+ β cos
-
2(N + 1)
N+1
N+1
s=1
[
]}
sπ
- exp 2πiβ cos
(4)
N+1
Затем сумма в (4) представляется в виде суммы двух сумм, одна по нечетным s =
= 2j-1, j = 1, 2, 3, . . ., N +1, другая по четным s = 2j, j = 1, 2, 3, . . ., N +1, и отсюда
получаем утверждение леммы. ▴
Один из множителей в (1)
f (x) = e2πiβcos2πx
(5)
является периодической функцией с периодом 1. Представим f(x) в виде ряда Фурье
∑
f (x) =
c(k)e2πikx
(6)
k=-∞
с коэффициентами
1
∫1
∫2
c(k) = f(x)e-2πikx dx = 2 e2πiβcos2πx cos 2πkx dx.
(7)
0
0
Лемма 2. При |k| > 0 справедлива следующая оценка:
(2πβ)2 + 2π|β|
|c(k)| ≤
,
k2
и в частности, ряд Фурье (6) для функции f(x) сходится абсолютно.
Доказательство. Поскольку из (7) следует c(k) = c(-k), при k = 0 находим
∫1
∫
1
-2πikx
de
1
c(k) = f(x)
=
f′′(x)e-2πikx dx,
-2πik
(2πik)2
0
0
т.е.
∫1
1
1
|c(k)| ≤
|f′′(x)| dx ≤
max |f′′(x)|.
(2πk)2
(2πk)2
0≤x≤1
0
Оценивая на основе (5) вторую производную функции f(x) как |f′′(x)| ≤ (2π)4β2 +
+ (2π)3|β|, получаем отсюда утверждение леммы. ▴
62
Лемма 3. Предположим, что M и m - целые числа, M > 1, 0 ≤ m ≤ M,
а суммы A и B определяются равенствами
[
(
)]
(
)
(
)
∑
1
m
1
j-
2
A = exp 2πi
j-
+ β cos2π
,
M
2
M
j=1
[
)]
∑
(m
j
B = exp 2πi
j + β cos2π
M
M
j=1
Тогда справедливы соотношения
∑
A=M
(-1)rc(rM - m),
(8)
r=-∞
∑
B=M
c(rM - m),
(9)
r=-∞
где c(k) - коэффициенты Фурье функции f(x) = e2πiβcos2πx.
Доказательство. Представляя множитель e2πiβcos2πx каждого слагаемого
сумм A и B в виде ряда Фурье, находим
[
(
(
)
∑
)]+∞∑
m
1
j-1
2
A=
exp 2πi
j-
c(k) exp
2πi
k
=
M
2
M
j=1
k=-∞
[
(
)]
∑
∑
m+k
1
=
c(k)
exp 2πi
j-
,
(10)
M
2
k=-∞
j=1
(
)
∑
(
∑
m
j
B=
exp
2πi
j
c(k) exp
2πi
k
=
M
M
j=1
k=-∞
(
)
∑
∑
m+k
=
c(k)
exp
2πi
j
(11)
M
k=-∞
j=1
Поскольку
⎧
[
(
)]
∑
⎨(-1)rM, если m + k = rM, r целое,
m+k
1
exp 2πi
j-
-∞ < r < +∞,
M
2
=⎩
j=1
0,
если m + k не кратно M,
(
)
∑
m+k
{M, если m + k = rM, r целое, -∞ < r < +∞,
exp
2πi
j
=
M
0,
если m + k не кратно M,
j=1
то из (10) и (11) получаем, соответственно, формулы (8) и (9). ▴
Следствие. Из лемм 1 и 3 получаем
∑{
bN (t) = (-1)N+1
c[(N + 1)(2ν - 1) - 2] + c[(N + 1)(2ν - 1) + 2] -
ν=1 }
- 2c[(N + 1)(2ν - 1)]
(12)
63
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
10
20
30
40
50
60
70
80
90
100
t
Рис. 1. Два графика вместе: значение |bN (t)|2 (N = 10, α = 1), определяемое (1),
- линия из серых звездочек, а определяемое приближением (14) - непрерывная ли-
ния; k = 1
Доказательство теоремы. Сделав в (7) (подробнее см. в [5]) замену пере-
π
менной интегрирования y = 2πx, ϕ = y -
, получаем
2
∫
π
∫
1
ik
c(k) =
eiαtcosy cosky dy =
ei(kϕ-αtsinϕ) dϕ,
π
2π
0
0
α = 2πβ/t. Интеграл
∫
1
Jk(αt) =
ei(kϕ-αtsinϕ) dϕ
(13)
2π
0
представляет собой функцию Бесселя k-го порядка; пользуясь известными рекур-
рентными формулами [6], представим ряд (12) в виде (3). ▴
Замечание. Поскольку функция Jν(αt) убывает экспоненциально при возраста-
нии ν, а суммирование в (3) идет по ν, принадлежащим арифметической прогрессии
с разностью 2(N + 1), то уже первые слагаемые суммы (3) обеспечивают хорошее
приближение к bN (t).
Пусть k ≥ 1, и
∑
{
b(k)N(t) = (-1)N 2
i(N+1)(2ν-1)
[(N + 1)(2ν - 1) - 1] J(N+1)(2ν-1)-1(αt) +
αt
ν=1
}
+ [(N + 1)(2ν - 1) + 1] J(N+1)(2ν-1)+1(αt) ,
N ≥ 2.
(14)
Заметим сразу, что даже останавливаясь на k = 1, получаем весьма удовлетвори-
тельный до первого максимума результат, и выражение, используемое в [4], с одной
функцией Бесселя значительно улучшено. Это продемонстрировано на рис. 1-3 для
типичных значений N = 10, 15, 20 соответственно.
64
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
10
20
30
40
50
60
70
80
90
100
t
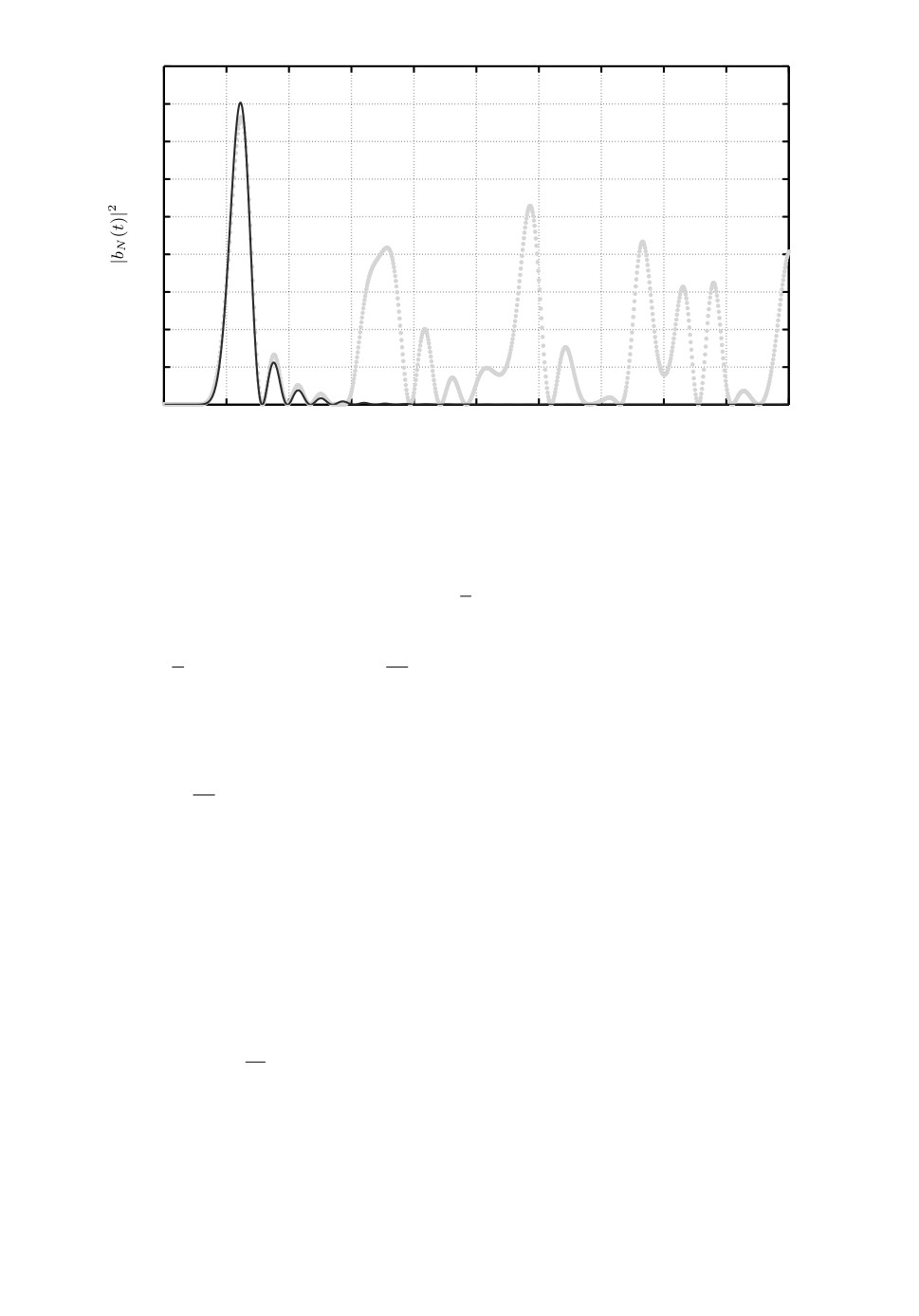
Рис. 2. Два графика вместе: значение |bN (t)|2 (N = 15, α = 1), определяемое (1),
- линия из серых звездочек, а определяемое приближением (14) - непрерывная ли-
ния; k = 1
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
10
20
30
40
50
60
70
80
90
100
t
Рис. 3. Два графика вместе: значение |bN (t)|2 (N = 20, α = 1), определяемое (1),
- линия из серых звездочек, а определяемое приближением (14) - непрерывная ли-
ния; k = 1
Новое асимптотическое выражение (3) дает возможность легко вычислить ам-
плитуду вероятности с использованием встроенных в компьютерные пакеты про-
грамм (Matlab) функций Бесселя (см. рис. 1-5). Однако чтобы увидеть, как ведет
себя функция bN (t) на разных временных интервалах, N ≥ 2, N → +∞, нам нужно
построить аппроксимации этой функции для разных t, используя соответствующие
приближения функций Бесселя.
65
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
10
20
30
40
50
60
70
80
90
100
t
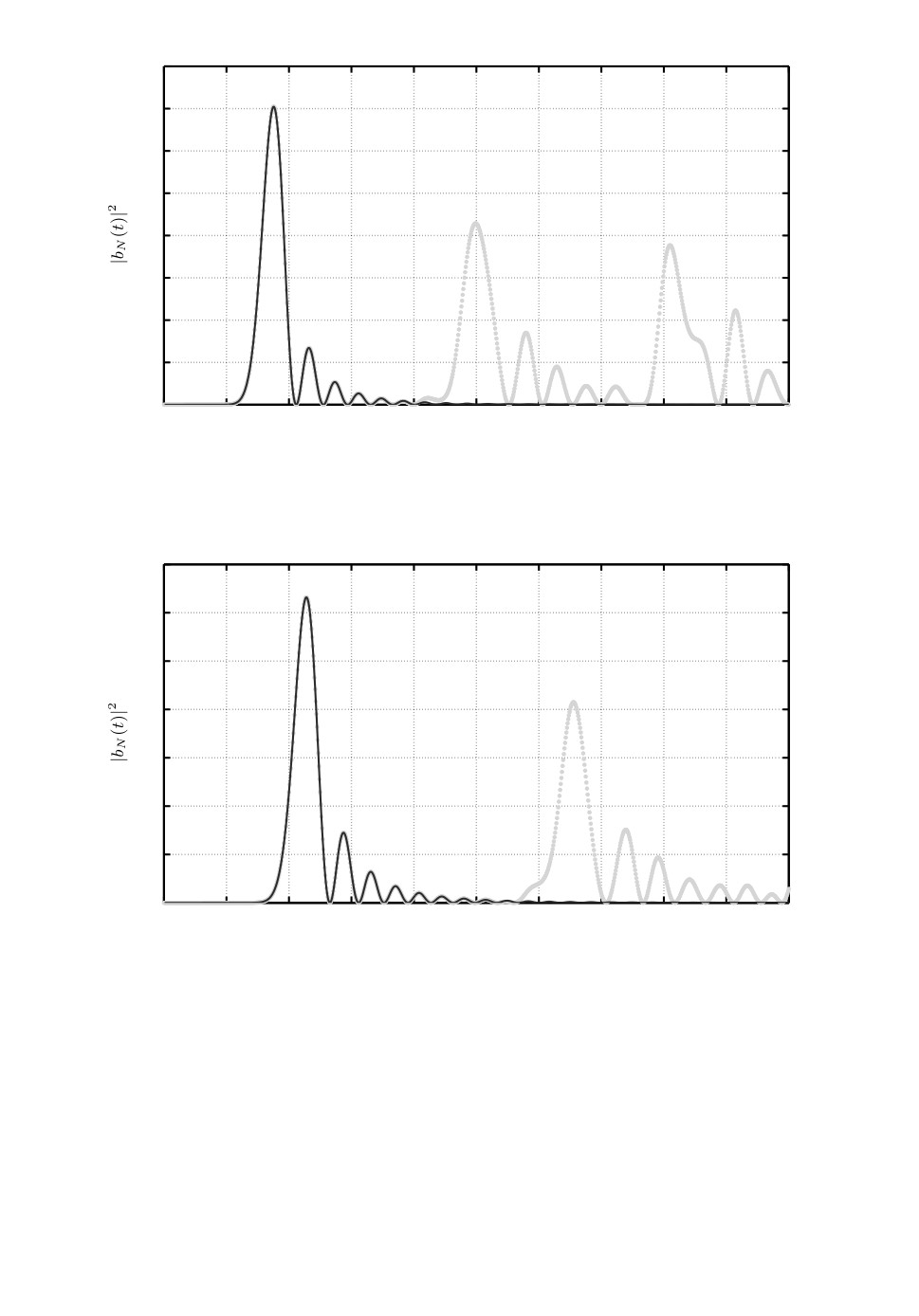
Рис. 4. Два графика вместе: значение |bN (t)|2 (N = 15, α = 1), определяемое (1),
- линия из серых звездочек, а определяемое приближением (14) - непрерывная ли-
ния; k = 2
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
10
20
30
40
50
60
70
80
90
100
t
Рис. 5. Два графика вместе: значение |bN (t)|2 (N = 15, α = 1), определяемое (1),
- линия из серых звездочек, а определяемое приближением (14) - непрерывная ли-
ния; k = 3
§4. Аппроксимация функции амплитуды вероятности
для фиксированного времени
Пусть αt = x. Без потери общности далее для простоты предполагаем, что
)2
(x
< 1.
(15)
2
66
Сначала оценим остаточные суммы (N ≥ 2):
∑
S(k)1(x) =
i(N+1)(2ν-1) [(N + 1)(2ν - 1) - 1]J(N+1)(2ν-1)-1(x) =
ν=k+1
∑
= i(N+1)(2ν+1) ((2ν + 1)N + 2ν)J(2ν+1)N+2ν(x),
(16)
ν=k
∑
S(k)2(x) =
i(N+1)(2ν-1) [(N + 1)(2ν - 1) + 1]J(N+1)(2ν-1)+1(αt) =
ν=k+1
∑
= i(N+1)(2ν+1) ((2ν + 1)N + 2ν + 2)J(2ν+1)N+2ν+2(x).
(17)
ν=k
(x)n 1
Учитывая (см. [6]), что Jn(x) = θ0
, |θ0| ≤ 1, из (16) имеем
2
n!
S(k)1(x) = i(N+1)(2k+1) ((2k + 1)N + 2k)J(2k+1)N+2k(x) ×
(
)4N+4
(x)2N+2 ((2k + 1)N + 2k - 1)!
(x
× 1+θ
1
+θ2
×
2
((2k + 3)N + 2k + 1)!
2
)
((2k + 1)N + 2k - 1)!
×
+...
= i(N+1)(2k+1) ((2k + 1)N + 2k) ×
((2k + 5)N + 2k + 3)!
(
)
(x)2N+2
∑
((2k + 1)N + 2k - 1)!
× J(2k+1)N+2k(x)
1+θ1
=
2
((2k + 2r + 1)N + 2k + 2r - 1)!
r=1
(
)2N+2
(x
= i(N+1)(2k+1) ((2k + 1)N + 2k)J(2k+1)N+2k(x) 1+
×
2
)
θ2
×
= i(N+1)(2k+1) ((2k + 1)N + 2k)J(2k+1)N+2k(x) +
((2k + 1)N + 2k)2N+1
θ3
+
,
|θ1| ≤ 1,
|θ2| ≤ 1,
|θ1| ≤ 1,
|θ2| ≤ 1,
|θ3| ≤ 1.
(18)
((2k + 1)N + 2k)2N
Аналогично
S(k)2(x) = i(N+1)(2k+1) ((2k + 1)N + 2k + 2)J(2k+1)N+2k+2(x) +
θ4
+
,
|θ4| ≤ 1.
(19)
((2k + 1)N + 2k + 2)2N
С другой стороны, можно вывести аппроксимационную формулу для функции Бес-
селя Jn(x) большого целого порядка n, n → +∞, для фиксированных значений
аргумента x. Имеем (см. [6])
(
)
(x)n 1
(x)2
1
(x)4
1
Jn(x) =
1-
+
-...
=
2
n!
2
1! (n + 1)
2
2! (n + 1)(n + 2)
(
)
(x)n 1
(x)2
1
(x)4
θ5
=
1-
+
,
|θ5| ≤ 1.
(20)
2
n!
2
1! (n + 1)
2
2! (n + 1)(n + 2)
Прологарифмируем (20):
x
(x)2
1
(x)4
θ6
ln Jn(x) = n ln
- ln n - ln Γ(n) -
+
,
|θ6| ≤ 1,5.
(21)
2
2
n+1
2
(n + 1)2
67
Воспользуемся следующим известным выражением для функции ln Γ(x) (см. [7, 8]):
(
)
1
√
ln Γ(x) = x -
ln x - x + ln
2π + I(x),
2
где
∞
∫
1
1
∑
I0(x, j)
cos2πju du
I(x) =
-
,
I0(x, j) =
,
12x
2π2
j2
(u + x)2
j=1
0
откуда
1
1
1
I(x) =
-
+ R(x),
0 < R(x) <
,
12x
360x3
1260x5
и
(
)
1
√
1
1
ln Γ(n) = n -
ln n - n + ln
2π +
-
+ R(n),
2
12n
360n3
(22)
1
0 < R(n) <
1260n5
Из (21), (22) находим
(
)
(
√
1
x)
1
ln Jn(x) = - n +
ln n +
1 + ln
n - ln
2π -
-
2
2
12n
(x)2
1
θ7
−
+
,
|θ7| ≤ 1,5.
2
n+1
n2
Отсюда получаем асимптотическое выражение (n → +∞)
)
(
1
1
) (ex
12+(2 )2-n
Jn(x) =
√
n-n+
2
)n e-n
,
|θ7| ≤ 1,5.
2π
2
Таким образом, имеем следующее приближение бесселевой функции Jn(x) большого
целого порядка n → +∞ и фиксированного аргумента x ≤ 2:
(
)
)
)n(
)2
1
(ex
1
1
(x
θ8
Jn(x) =
√
1-
+
+
,
|θ8| ≤ 2.
(23)
2πn
2n
n
12
2
n2
Для функции bN (t) при t < 2/α из (23), (15)-(19) и (14) находим
N +1
(
)
2i
bN (t) =
NJN(αt) + (N + 2)JN+2(αt) + S(0)1(αt) + S(0)2(αt)
=
αt
√
(
)
)N
2N
( e
θ0
=iN+1
(αt)N-1
1-
,
|θ0| ≤ 2, N ≥ 2.
(24)
π
2N
N2
§5. Приближение функции амплитуды вероятности для растущего времени
Перепишем интеграл (13) в виде
∫
1
Jk(αt) =
eiFk(ϕ) dϕ, Fk(ϕ) = kϕ - αt sinϕ.
(25)
2π
0
68
Отсюда
F′k(ϕ) = k - αt cos ϕ.
(26)
Пусть k > αt. Тогда F′k(ϕ) > 0. Из (25), (26) находим
∫
∫
1
dei(kϕ-αtsinϕ)
αt
sinϕdei(kϕ-αtsinϕ)
Jk(αt) =
=-
=
2π
i(k - αt cos ϕ)
2π
(k - αt cos ϕ)3
0
0
∫
(
)
αt
cosϕ
3αt sin2 ϕ
=
ei(kϕ-αtsinϕ)
-
dϕ.
2π
(k - αt cos ϕ)3
(k - αt cos ϕ)4
0
Так как модуль интеграла не превосходит интеграла от модуля подынтегрального
выражения, то из последнего выражения имеем
(
)
1
3αt
|Jk(αt)| ≤ αt
+
,
(k - αt)3
(k - αt)4
и для произведения kJk(αt) справедливо неравенство
2
αt
4(αt)
3(αt)3
|kJk(αt)| ≤
+
+
(27)
(k - αt)2
(k - αt)3
(k - αt)4
Выделяя первое слагаемое суммы (3), представим ее в виде
N +1
2i
bN (t) = (-1)N
(NJN (αt) + (N + 2) JN+2(αt) + S) ,
(28)
αt
где
∑
(
S = i2(N+1)(ν-1) ((N + 1)(2ν - 1) - 1)J(N+1)(2ν-1)-1(αt) +
ν=2
)
+ ((N + 1)(2ν - 1) + 1) J(N+1)(2ν-1)+1(αt) , N ≥ 2.
(29)
Если 0 < αt ≤ N, то из (29) и (27) получаем
(
∑
2αt
8(αt)2
|S| ≤
+
+
(2(N + 1))2(ν - 1)2
(2(N + 1))3(ν - 1)3
ν=2
)
3
6(αt)
αt
(αt)2
3(αt)3
+
≤
ζ(2) +
ζ(3) +
ζ(4),
(30)
(2(N + 1))4(ν - 1)4
2(N + 1)2
(N + 1)3
8(N + 1)4
где ζ(μ) - дзета-функция Римана (см., например, [9]), для значений которой спра-
2
π
π4
ведливы неравенства
= ζ(2) > ζ(3) > ζ(4) =
. Отсюда и из (30) имеем
6
90
(
)
2
5
αt
(αt)
(αt)3
S =
θ0
+
+
,
|θ0| ≤ 1.
(31)
4
(N + 1)2
(N + 1)3
(N + 1)4
69
Из (28)-(31) получаем следующее асимптотическое выражение (N ≥ 2, N → +∞):
N +1
2i
bN (t) = (-1)N
(NJN (αt) + (N + 2) JN+2(αt)) +
αt
(
)
2
5
1
αt
(αt)
+
θ0
+
+
,
|θ0| ≤ 1.
(32)
2
(N + 1)2
(N + 1)3
(N + 1)4
Соотношение (32) справедливо для любого t из интервала 0 < t ≤ N/α. Если
t < N/α строго, то для оценки первых двух слагаемых суммы (32) также можно
использовать оценку (27). Следовательно, для 0 < t < N/α имеем
(
)
1
4αt
3(αt)2
bN (t) = 4θ1
+
+
+
(N - αt)2
(N - αt)3
(N - αt)4
(
)
2
5
1
αt
(αt)
+
θ0
+
+
,
|θ0| ≤ 1,
|θ1| ≤ 1.
2
(N + 1)2
(N + 1)3
(N + 1)4
При t = N/α из уравнения (25) следует, что F′N (0) = 0. В этом случае, воспользовав-
шись известными (см. [6, 9]) рекуррентными соотношениями для функций Бесселя
2(N + 1)
JN+2(N) =
JN+1(N) - JN (N),
(33)
N
JN+1(N) = JN (N) - J′N (N),
(34)
из (32) находим
((
)
(
)(
)
2
2
1
2
bN (N/α) = (-1)N iN+14
1+
+
JN (N) -
1+
1+
×
N
N2
N
N
)
(
)
5
3
3
1
× J′N(N)
+
θ0
-
+
= (-1)N iN+1 ×
2
(N + 1)2
(N + 1)3
(N + 1)4
(
)
2
2
3
2
× 4 JN(N) - J′N(N) +
JN (N) +
JN (N) -
J′N (N) -
J′N (N)
+
N
N2
N
N2
θ1
15
+
,
|θ0| ≤ 1,
|θ1| ≤ 1.
(35)
2 N2
Чтобы получить асимптотику для bN (N/α), нужно подставить в (35) асимптотиче-
ские выражения для JN (N) и J′N (N) (см., например, [6]). Имеем (используя o-сим-
волику Ландау)
)
1
(2))
(
)
(24/3Γ(
25/331/6Γ
3
3
1
bN (N/α) = (-1)N iN+1
-
+o
(36)
31/6πN1/3
πN2/3
N2/3
Здесь Γ(x+1) = xΓ(x) - гамма-функция Эйлера (см., например, [8,9]), и кроме того,
)
(1
(2)
24/3Γ
25/331/6Γ
3
3
< 1,8;
< 1,6.
31/6π
π
Пусть теперь αt > N. Рассмотрим снова ряд (3) бесселевых функций (13), которые
можно записать для удобства в виде
∫π
∫
π
1
1
Jk(αt) =
Re ei(kϕ-αtsinϕ) dϕ =
Re eiFk(ϕ) dϕ,
π
π
(37)
0
0
k = (N + 1)(2ν - 1) ∓ 1, ν = 1,2,3,...
70
При αt > N уравнение
F′k(ϕ) = 0: k - αt cosϕ = 0
(38)
имеет решения. Если назвать интеграл Jk(αt), в который входит функция Fk(ϕ),
имеющая свойство (38), “специальным”, то в (3) эти “специальные” интегралы появ-
ляются в следующем порядке:
• при N ≤ αt < N + 2 “специальным” интегралом будет JN (αt);
• при N + 2 ≤ αt < 3(N + 1) - 1 “специальными” интегралами будут JN (αt),
JN+2(αt);
• при 3(N + 1) - 1 ≤ αt < 3(N + 1) + 1 “специальными” интегралами будут JN (αt),
JN+2(αt), J3(N+1)-1(αt);
• при (2ν - 1)(N + 1) - 1 ≤ αt < (2ν - 1)(N + 1) + 1 “специальными” интегралами
будут JN (αt), JN+2(αt), . . . , J(2ν-1)(N+1)-1(αt).
Каждый из “специальных” интегралов оценивается тем же способом, что JN (N).
“Близкий” интеграл, индекс которого отличается на 2 и который не является “спе-
циальным” интегралом, но “близок” к нему (как, скажем, JN+2(N) к JN (N)) лучше
оценивать аналогично “специальному” вместе с ним (как, например, мы делали, ко-
гда оценивали JN+2(N) через производную JN (N) - см. (33), (34)). Оценка остатка
ряда (3), не содержащего “специальных” интегралов, проводится так же, как и рань-
ше, для суммы S из (29). Пусть
]
[ αt + N + 2
ν1 =
,
2(N + 1)
где [μ] - целая часть числа μ, тогда из (37), (38) ряд, который не содержит “специ-
альных” интегралов (плюс, возможно, “близкого” к одному из “специальных” инте-
гралов), содержит члены k(ν)Jk(ν)(αt) с ν = ν1 + 1 + ν′, ν′ = 1, 2, 3, . . . , для которых
справедливы следующие условия:
F′k(ϕ) ≥ k - αt cos ϕ > 0, k = (2ν - 1)(N + 1) ∓ 1.
(39)
Отсюда F′k(ϕ) > (N+1)(2ν′+1), ν′ = 1, 2, 3, . . ., и сумма (29) оценивается следующим
образом:
(
∑
∑
αt
|S| ≤
|k(ν)Jk(ν)(αt)| ≤
+
((N + 1)(2ν′ + 1))2
ν=ν1+2
ν′=1
)
2
4(αt)
3(αt)3
αtζ(2)
4(αt)2ζ(3)
+
+
<
+
+
((N + 1)(2ν′ + 1))3
((N + 1)(2ν′ + 1))4
(2(N + 1))2
(2(N + 1))3
(
)
2
3(αt)3ζ(4)
3
αt
(αt)
(αt)3
θ
+
=
+
+
,
|θ| ≤ 1.
(40)
(2(N + 1))4
5
(N + 1)2
(N + 1)3
(N + 1)4
Первые слагаемые - функции Бесселя можно оценить на основе асимптотических
разложений функций Бесселя большого аргумента через суммы тригонометриче-
ских функций (см., например, [6, 9]).
§ 6. Вычисление времени инверсии
Поскольку сумма (14) в интересующей нас области воспроизводит поведение
функции bN (αt) хорошо даже при k = 1, воспользуемся этой аппроксимацией,
71
чтобы найти положение первого максимума квадрата модуля этой функции, ко-
торый дает время инверсии. Этот максимум соответствует первому нулю функции
(
)
d/dτ
b(1)N(αt)
и задается уравнением (τ = αt)
(
)
(
)
d
JN (τ)
JN+2(τ)
d
2N(N + 1)
0=
N
+ (N + 2)
=
JN+1(τ) + 2JN+2(τ)
,
dτ
τ
τ
dτ
τ
и поскольку (см., например, [6])
d
N+2
JN+2(τ) = JN+1(τ) -
JN+2(τ),
dτ
τ
d
N +1
JN+2(τ) = -
JN+1(τ) +
JN+1(τ),
dτ
τ
в итоге получаем
)
2
dJN+1(τ)
JN+1(τ)
(2N(N + 1) + (N + 3)(N + 1) - τ
0=
-
,
(41)
dτ
τ
N2 + 2N + 3
что легко проверяется. Разлагая d/dτ(JN+1) в окрестности первого нуля (см. [9]),
непосредственными вычислениями приходим к результату
(
)
τ = N + 1 + 0,8N1/3 - 1,16N-1/3 + O
N-2/3
(42)
§ 7. Заключение
Разница между выражением (42) и значением, найденным в [4] для типично-
го значения N ∼ 10-20, примечательна. Что касается кластера Fe8 [10], то значение
экспериментального параметра (k/D), где D является константой анизотропии, ока-
зывается равной 0,22, что меньше значения 0,25, указанного в [4], и следовательно,
ближе к найденному экспериментальному значению 0,16, подтверждая тем самым,
что точное определение времени инверсии имеет фундаментальное значение для
корреляции структуры мёссбауэровских спектров с параметрами спинового гамиль-
тониана.
Мы хотели бы подчеркнуть, что в этой системе инверсия происходит с помо-
щью прыжков между вырожденными низшими дублетами, и поэтому использование
формул (1) и (42) вполне оправдано. Точная асимптотическая формула (42) была
бы бесполезной при наличии неопределенной ошибки из-за большого значения ω.
Еще лучший результат расчета можно получить, заметив, что во многих случаях
спиновые состояния вырождаются по энергии только в первом приближении. Как
указано в [4], полное исследование с учетом разностей энергий приводит к преобра-
зованию Лапласа многочленов Ломмеля, и работа идет в этом направлении.
СПИСОК ЛИТЕРАТУРЫ
1. Gatteschi D., Sessoli R., Villain J. Molecular Nanomagnets. Oxford: Oxford Univ. Press,
2006.
2. Blume M., Tjon J.A. Mössbauer Spectra in a Fluctuating Environment // Phys. Rev. 1968.
V. 165. № 2. P. 446-456.
3. Cianchi L., Mancini M., Moretti P., Spina G. Mossbauer Spectra in Paramagnetic Relaxing
Systems // Rep. Prog. Phys. 1986. V. 49. № 11. P. 1243-1291.
4. Moretti P., Lantieri M., Cianchi L. Quantum Study of the Spin Inversion // J. Math. Phys.
2004. V. 45. № 1. P. 107-113.
5. Karatsuba E.A., Moretti P. Inversion Time of Large Spins // J. Math. Phys. 2005. V. 46.
№ 4. P. 042101 (7 pp.).
72
6. Ватсон Дж.Н. Теория бесселевых функций. М.: Изд-во иностр. лит., 1949.
7. Karatsuba E.A. On the Computation of the Euler Constant γ // Numer. Algorithms. 2000.
V. 24. № 1-2. P. 83-97.
8. Karatsuba E.A. On the Asymptotic Representation of the Euler Gamma Function by Ra-
manujan // J. Comput. Appl. Math. 2001. V. 135. № 2. P. 225-240.
9. Справочник по специальным функциям с формулами, графиками и математическими
таблицами / Под ред. М. Абрамовица и И. Стиган. М.: Наука, 1979.
10. Cianchi L., Del Giallo F., Spina G., Reiff W., Caneschi A. Spin Dynamics Study of Mag-
netic Molecular Clusters by Means of Mössbauer Spectroscopy // Phys. Rev. B. 2002. V. 65.
№ 6. P. 064415.
Карацуба Екатерина Анатольевна
Поступила в редакцию
Вычислительный центр им. А.А. Дородницына
26.10.2018
Федерального исследовательского центра
После доработки
“Информатика и управление” РАН
04.01.2019
karatsuba@mi.ras.ru, ekaratsuba@gmail.com
Принята к публикации
Моретти Паоло
09.01.2019
Национальный исследовательский совет Италии,
Институт сложных систем, отдел Флоренции,
Сесто-Фьорентино, Флоренция, Италия
pmoretti56@gmail.com
73