ПРОБЛЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ

Том 55

2019

Вып. 3

УДК 621.391.1 : 519.1

Л.А. Бассалыго

ЗАМЕЧАНИЕ К СТАТЬЕ Н. АЛОНА И М. КАПАЛЬБО

“НЕБОЛЬШИЕ ЯВНЫЕ СУПЕРКОНЦЕНТРАТОРЫ”¹

Слегка улучшается конструкция суперконцентратора Алона и Капальбо.

Ключевые слова: граф-расширитель, концентратор, суперконцентратор.

DOI: 10.1134/S0555292319030082

Авторы [1] предложили оригинальную конструкцию суперконцентратора. Так

как мы лишь весьма незначительно изменим их конструкцию, то заимствуем и ис-

пользуем обозначения и результаты из [1].

Суперконцентратор Γ_N - это ориентированный граф без циклов с N входами

(множество входов обозначим через X) и N выходами (множество выходов обозна-

чим через Y ), такой что для любого подмножества входов S ⊆ X и выходов T ⊆ Y ,

|S| = |T |, в графе Γ_N существует |S| непересекающихся по вершинам ориентирован-

ных путей из S в T . Задача, как обычно, состоит в построении суперконцентратора

с наименьшим числом ребер. Предложенная в [1] рекуррентная конструкция супер-

концентратора использует (как и все предыдущие конструкции) граф-расширитель.

Понятие двудольного графа-расширителя было введено Пинскером в [2] для постро-

ения концентратора с линейным (по числу входов) числом ребер, хотя в неявном

виде это понятие уже содержалось в [3]. Нам понадобится лишь частный случай

графа-расширителя, так что мы не даем его общего определения, которое, к тому

же, теперь широко известно. Пусть E(X, X^′) - двудольный граф-расширитель с N

входами X и N выходами X^′ (нумерация входов и выходов одинаковая; i-я вер-

шина входа обозначается через x_i, а выхода - через x^′i). Пусть S ⊆ X, |S| = αN.

Используемый в [1] граф-расширитель таков, что:

1. Если α ≤ 1/4, то |N(S)| ≥ 2|S|;

2. Если 1/4 ≤ α ≤ 1/2, то |N(S)| ≥ |S| + N/4;

3. Если 1/2 ≤ α, то |N(S)| ≥ |S| + (1 - α)N/2,

где N (S) обозначает множество вершин X^′, смежных с S. Расширитель E(Y, Y^′)

является копией расширителя E(X, X^′). Паросочетанием в двудольном графе на-

зывается набор непересекающихся по вершинам ребер. Для любого S ⊆ X обозна-

чим через M_S паросочетание в E(X, X^′), множество вершин которого в X совпада-

ет с S, а через M_S(X^′) - множество вершин паросочетания M_S в X^′. В расширителе

E(Y, Y^′) подмножество вершин в Y будем обозначать буквой T .

Далее, не оговаривая особо, мы будем полагать, что оба расширителя E(X, X^′)

и E(Y, Y^′) удовлетворяют условиям 1-3. Соединим теперь последовательно графы

E(X, X^′) и E(Y, Y^′), отождествив X^′ и Y^′ (для X^′ = Y^′ введем общее обозначение Z),

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных

исследований (номер проекта 19-01-00364).

106

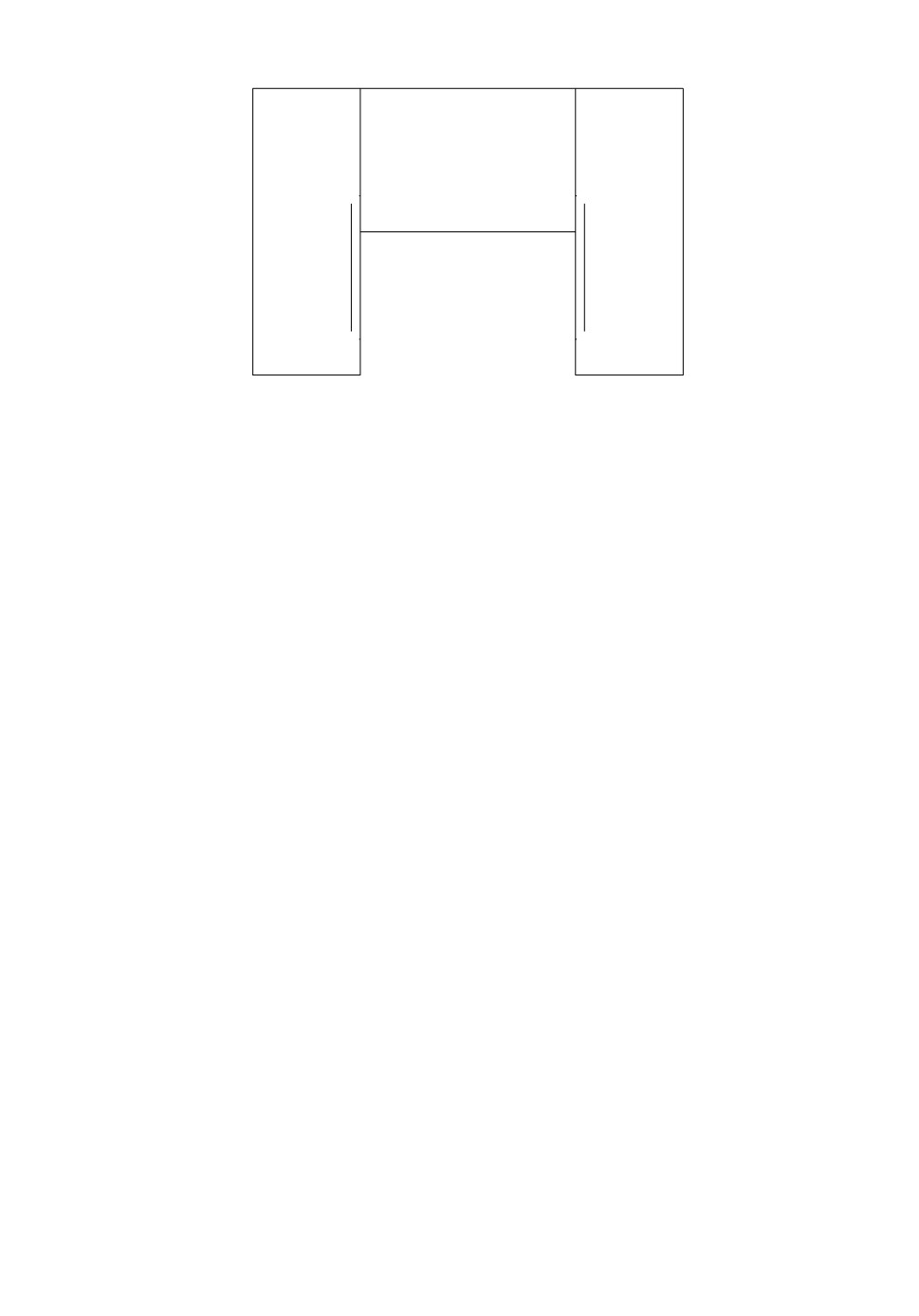
ΓN/2

x^′i

y^′i

ΓN =

E(X, X^′)

^E(Y, Y^′)

x′i+N/2

y^′

i+N/2

Рис. 1

и обозначим полученный граф через E(X, Z, Y ). Через I(S, T), I(S, T) ⊆ Z, обозна-

чим общие вершины в Z паросочетаний M_S в E(X, Z) и M_T в E(Y, Z): I(S, T ) =

= M_S(Z) ∩ M_T(Z). В [1] доказано следующее

Предложение. Пусть S ⊆ X, T ⊆ Y , |S| = |T| = αN. Тогда в графе E(X,Z,Y )

существуют паросочетания M_S в E(X, Z) и M_T в E(Y, Z), удовлетворяющие усло-

виям:

1^′. Если α ≤ 1/4, то |I(S, T)| ≥ 0;

2^′. Если 1/4 ≤ α ≤ 1/2, то |I(S, T)| ≥ (α - 1/4)N;

3^′. Если 1/2 ≤ α, то |I(S, T)| ≥ ((α - (1 - α)/2)N;

(B) Если z_i ∈ I(S, T ) и zi+N/2 ∈ I(S, T ), то {z_i, zi+N/2} ⊈ M_S (Z) и {z_i, zi+N/2} ⊈

⊈ M_T(Z).

Тривиальное уточнение этого предложения состоит в возможности замены усло-

вия (B) на условие

(B^′) Если z_i ∈ I(S, T ) и zi+N/2 ∈ I(S, T ), то zi+N/2 ∈ M_S (Z) и zi+N/2 ∈ M_T (Z).

Не повторяя доказательства условия (В) в [1], укажем единственное отличие

при доказательстве условия (B^′), а именно: из двух склеенных вершин {z_i, zi+N/2}

(см. доказательство в [1, с. 161]) в паросочетание всегда будем выбирать вершину z_i.

Несмотря на тривиальность такого уточнения, оно позволяет слегка изменить

конструкцию суперконцентратора, предложенную в [1], и даже уменьшить число ре-

бер в суперконцентраторе (правда, лишь весьма незначительно). Благодаря замене

условия (В) на (B^′) рекуррентная схема суперконцентратора, предложенная в [1]

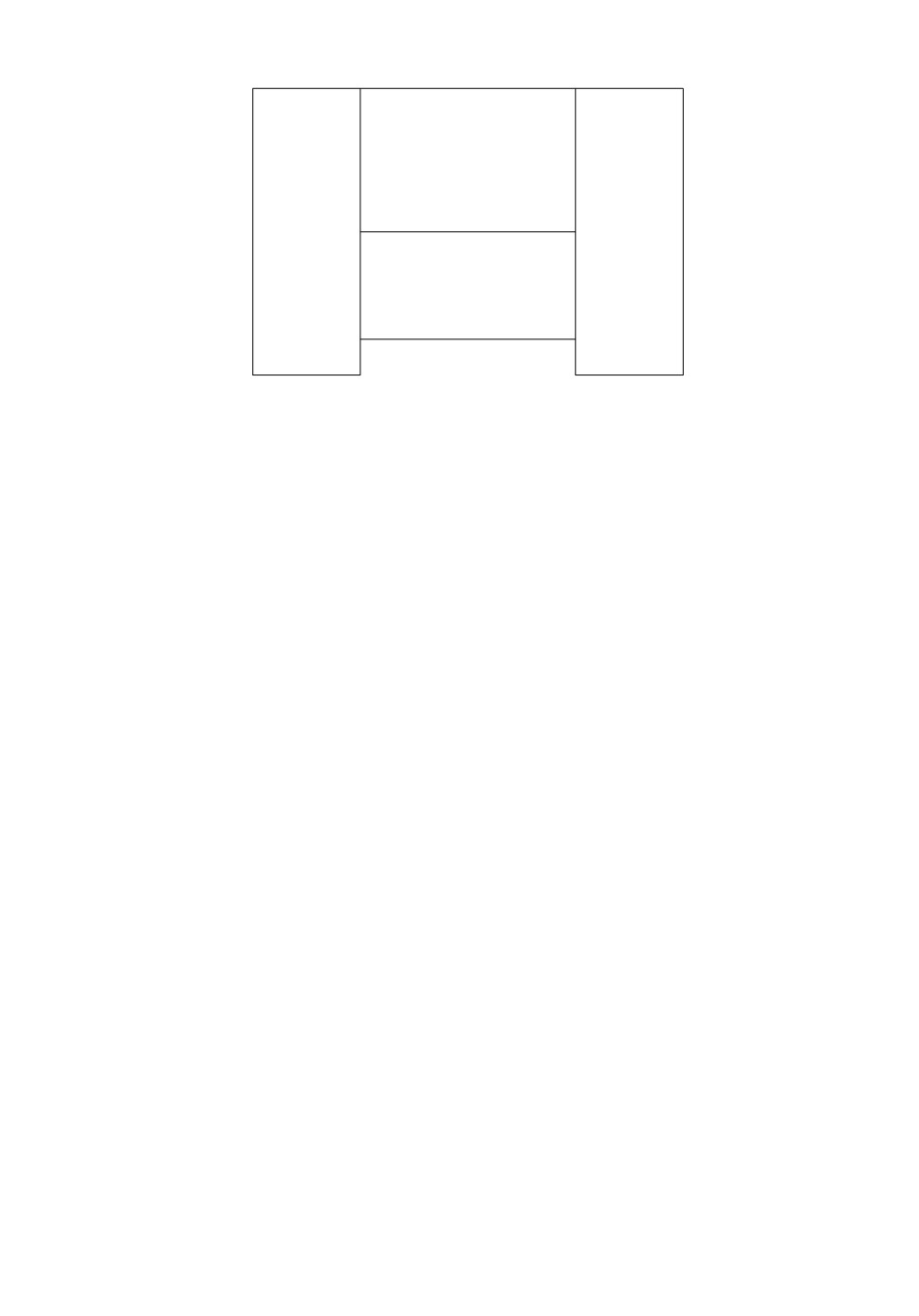
(см. рис. 1), заменяется на схему, изображенную на рис. 2, с сохранением свойств

суперконцентратора.

Действительно, для любого i, i = 1, 2, . . ., N, вершины x′i+N/2 и y′i+N/2 одновре-

менно принадлежат или не принадлежат I(S, T ). В первом случае они соединяются

непосредственно ребром (см. рис. 2). Второй случай рассмотрим подробнее. Пусть

x′i+N/2 ∈ M_S(X) \ I(S, T), а y′i+N/2 ∈ M_S(Y ). Тогда согласно условию (B^′) вершина

x^′i ∈ I(S, T), и следовательно, y^′i ∈ I(S, T) ⊆ M_S(Y ), так что достаточно соединить

ребром вершины x′i+N/2 и y^′i. Аналогично поступим, когда y′i+N/2 ∈ M_S(Y ) \ I(S, T ),

а x′i+N/2

∈ M_S(X), соединяя ребром вершину x′i ∈ MS(X) с вершиной y′i+N/2

(см. рис. 2).

Таким образом, вместо 2N ребер схемы рис. 1 мы проводим 3N/2 ребер. Так как

|Γ_N | = 2|E(X, X^′)| + |ΓN/2| + 3N/2 = 4|E(X, X^′)| + 3N + o(N),

107

ΓN/2

x^′i

y^′i

ΓN =

E(X, X^′)

^E(Y, Y^′)

x′i+N/2

y^′

i+N/2

Рис. 2

то окончательный результат зависит от числа ребер в расширителе, удовлетворя-

ющем условиям 1-3. Авторы [1] привели явную конструкцию расширителя с 10N

ребрами, а следовательно, и явную конструкцию суперконцентратора, изображенно-

го на рис. 1, с числом ребер, равным 44N + o(N). Параметры случайных достаточно

экономных расширителей давно известны [4] (см. также [5]), и в [6] было указано, что

существует расширитель с 6N ребрами, удовлетворяющий условиям 1-3, а следова-

тельно, существует суперконцентратор, изображенный на рис. 1, с числом ребер,

равным 28N + o(N). Переход к суперконцентратору, изображенному на рис. 2, поз-

воляет слегка понизить сложность суперконцентратора: до 43N + o(N) для явной

конструкции, и до 27N + o(N) для неявной.

Замечание. Небольшим преимуществом изображенного на рис. 2 суперконцен-

тратора, как нам представляется, является и отсутствие ребер, соединяющих выхо-

ды расширителей.

СПИСОК ЛИТЕРАТУРЫ

1. Alon N., Capalbo M. Smaller Explicit Superconcentrators // Internet Math. 2004. V. 1. № 2.

P. 151-163.

2. Pinsker M.S. On the Complexity of a Concentrator // Proc. 7th Int. Teletraffic Conf. (ITC 7).

Stockholm, Sweden. June 13-20, 1973. P. 318/1-318/4.

3. Колмогоров А.Н., Бардзинь Я.М. О реализации сетей в трехмерном пространстве //

Проблемы кибернетики. Вып. 19. М.: Физматлит, 1967. С. 261-268.

4. Бассалыго Л.А. Асимптотически оптимальные коммутационные схемы // Пробл. пере-

дачи инфор. 1981. Т. 17. № 3. С. 81-88.

5. Schöning U. Construction of Expanders and Superconcentrators Using Kolmogorov Com-

plexity // Random Structures Algorithms. 2000. V. 17. № 1. P. 64-77.

6. Schöning U. Smaller Superconcentrators of Density 28 // Inform. Process. Lett. 2006. V. 98.

№ 4. P. 127-129.

Бассалыго Леонид Александрович

Поступила в редакцию

Институт проблем передачи информации

14.12.2018

им. А.А. Харкевича РАН

После доработки

bass@iitp.ru

07.03.2019

Принята к публикации

21.05.2019

108