ПРОБЛЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
Том 56
2020
Вып. 2
УДК 621.391.15 : 519.725
© 2020 г.
А.В. Харин, К.Н. Заверткин, А.А. Овинников
ОБНАРУЖЕНИЕ ЦИКЛОВ ДЛИНЫ 8 В ГРАФЕ ТАННЕРА
КВАЗИЦИКЛИЧЕСКОГО МПП-КОДА ПО РЕЗУЛЬТАТАМ
АНАЛИЗА ПРОТОГРАФА1
Предложена процедура идентификации циклов длины 8 в графе Таннера,
основанная на анализе маршрутов в протографе. Сформулирован и доказан ряд
теорем, которые вводят правила идентификации циклов и ограничивают число
анализируемых подграфов. Для их различения предложен набор параметров,
однозначно определяющих группу анализируемых маршрутов в протографе.
Ключевые слова: граф Таннера, протограф, расширенный граф, объединение
циклов, базовое уравнение, метрика связанности цикла, МПП-код.
DOI: 10.31857/S0555292320020035
§ 1. Введение
В настоящее время широкое распространение в технике передачи и хранения
данных получили коды с малой плотностью проверок (МПП-коды). Среди них осо-
бое место занимает подкласс квазициклических (КЦ) МПП-кодов, которые были
предложены в работах [1-3]. Максимальную популярность в современных специ-
фикациях получили нерегулярные КЦ МПП-коды из-за их высокой энергетической
эффективности [4] и наличию относительно быстрых алгоритмов кодирования и де-
кодирования [5, 6]. Структура КЦ проверочных матриц обеспечивает компактность
хранения в памяти и упрощает процедуру кодирования МПП-кода. Однако с точки
зрения синтеза таких кодов еще остается ряд нерешенных задач. Первой из них явля-
ется оптимизация весовых распределений ненулевых элементов по строкам и столб-
цам проверочной матрицы в заданном канале связи с учетом ограниченной длины
кода и размера циркулянта. Вторая задача состоит в получении кодов с заданным
обхватом графа Таннера и распределением метрик связанности циклов (МСЦ) [7]
в нем. Представленное здесь исследование может выступать как теоретическая ос-
нова для решения последней задачи.
Величина обхвата графа Таннера считается [8] важной метрикой в оценке эффек-
тивности итеративного декодирования МПП-кодов. В работе [2] была предложена
формула, отражающая необходимое и достаточное условие существования цикла
в графе Таннера, определяемое по протографу. Там же было показано, что для
полносвязанных графов обхват ограничен значением g0 = 12. Впервые концепция
объединений циклов в протографе была введена в публикации [9]. Авторами [9] было
обнаружено, что процедура преобразования циклов в процессе расширения базово-
го графа КЦ МПП-кода является достаточно сложной и предложили необходимые
условия для получения g0 = 10. Однако ими была допущена ошибка при рассмот-
рении вариантов пар объединений циклов с длинами 4, один из них был пропущен,
1 Работа выполнена за счет гранта Российского научного фонда (проект № 17-79-20302).
82
о чем подробнее будет рассказано далее. Кроме того, ничего не сказано про необхо-
димые условия для достижения в графе Таннера обхвата, равного 12. Логическим
завершением работ [2,9] стал разработанный в [10] метод синтеза КЦ МПП-кодов,
основанный на двух теоремах, описывающих необходимые и достаточные условия
существования циклов в расширенных двудольных графах по обозначенным кон-
фигурациям объединенных циклов в протографе. Авторами [10] была выдвинута
гипотеза о существовании необнаруживаемого алгоритмом PEG [11] цикла в расши-
ренном графе, состоящая в том, что объединение циклов в базовом графе должно
содержать как минимум одно общее ребро. Полученные нами результаты, а также
исходное описание алгоритма PEG [11] говорят об ошибочности такого предположе-
ния. Однако даже в рамках рассматриваемых множеств объединений авторы [10]
упустили ряд важных конфигураций.
Первые предпосылки к полученным в настоящей статье результатам были обо-
значены в [12], где сформулированы и доказаны две теоремы о преобразовании оди-
ночного цикла протографа при его расширении в граф Таннера. Кроме того, в ра-
боте [12] введены необходимые понятия для описания параметров объединенных
циклов и получен первичный набор правил для их идентификации в базовом графе.
В то же время было упущено несколько важных исключений и дополнений, которые
не позволят достичь поставленной в работе [12] задачи для произвольных размеров
циркулянтов КЦ МПП-кодов. Таким образом, до настоящего времени не было по-
лучено исчерпывающего описания процесса топологического расширения базового
графа с точки зрения преобразования коротких циклов длины до 8 включительно.
Настоящая статья решает эту задачу как в части анализа соответствующих марш-
рутов в протографе, так и в рамках расчета МСЦ [7], чему посвящены последующие
параграфы.
§2. Общие теоретические сведения
Ненаправленный двудольный граф G = (V, C, E) определяется множествами ко-
довых V и проверочных C вершин, таких что V ∩ C = ∅, а также подмножеством
пар {(v, c), v ∈ V, c ∈ C}, соответствующих ребрам e = (v, c) ∈ E. Степени кодовых
и проверочных вершин обозначаются через dv, v ∈ V , и dc, c ∈ C. В силу того,
что в дальнейшем интерес будут представлять только значения dv, можно ввести
упрощенное обозначение вида dvi = di. Маршрут wg длины g в графе G представля-
ется последовательностью вершин вида v0, c0, v1, c1, . . . , vg-1, cg-1, vg. При этом если
v0 = vg, то маршрут называется замкнутым. Маршрут не содержит обратных прохо-
дов, если любая тройка вершин имеет вид vi, cj , vk или ci, vj , ck, i = k. В дальнейшем
будем рассматривать только замкнутые маршруты без обратных проходов и будем
называть их просто маршрутами. Циклом sg длины g называется такой маршрут,
в котором все промежуточные вершины за исключением v0 = vg отличаются друг
от друга. Обхватом графа G считается длина g0 кратчайшего цикла s0. В классе
двудольных графов g0 не может быть меньше gmin = 4. Общее количество кодовых
и проверочных вершин определяется формулами n = |V |, m = |C|. В статье рассмат-
риваются только такие двудольные графы, для которых отсутствуют кратные ребра.
Рассмотрим следующую конструкцию. Пусть Cq - циклическая подгруппа сим-
метричной группы Sq над множеством целых чисел Zq = {0, 1, . . . , q -1} мощности q
с единственной операцией - циклической перестановкой. Элементы Sq - это пере-
становки на множестве из q элементов. Рассмотрим циркулянт pa в Cq, который
соответствует циклическому сдвигу на a элементов вправо, где a - величина сдвига
циркулянта.
Пусть Gb и G - топологически связные двудольные графы, причем второй полу-
чается из первого следующим образом: копируем q раз каждую кодовую и провероч-
ную вершину в Gb, где vb ∈ Vb, cb ∈ Cb. Полученные q копий v = {v0b, v1b, . . . , vq-1b} ∈
83
q-1
∈ V и c = {c0,c1b, . . ., c
} ∈ C подвергаются циклической перестановке pa ∈ Cq
b
b
для каждой копии eb в e. Далее граф Gb будет называться базовым, или протогра-
фом, а G - расширенным графом. Число вершин в G определяется соотношениями
m=mbq иn=nbq.
Известно [2], что представленное топологическое преобразование графов при-
водит к тому, что интегральный сдвиг для маршрута в Gb определяется согласно
формуле
∑
Pgb =
(ai
(1)
k,jk -aik+1,jk)modq.
k=0
Для пояснения этого выражения рассмотрим базовую матрицу регулярного МПП-
кода, элементы которой соответствуют величинам сдвига циркулянтов pai,j . Любой
маршрут в связанном с ней протографе можно записать в виде последовательно-
сти элементов, например, a0,0, a0,1, a1,1, a1,0, a0,0. Согласно [2] сумма попарных раз-
ностей значений базовой матрицы, принадлежащих одному столбцу jk, позволяет
получить так называемый интегральный сдвиг, обладающий рядом чрезвычайно
важных свойств, которые рассмотрены далее,
⎡
⎤
a0,0
a0,1
a0,dc-1
⎢
a1,0
a1,1
a1,dc-1
⎥
Hb =
⎣
⎦.
(2)
adv-1,0
adv-1,1
. . . adv-1,dc-1
Формулу (1) и величину Pgb назовем базовым уравнением (БУ) и его решением
(РБУ) соответственно. Важно отметить, что изменение направления обхода марш-
рута на противоположный приводит к изменению знака РБУ с плюса на минус или
наоборот. Следующая теорема описывает необходимое и достаточное условие суще-
ствования циклов в расширенном графе [9].
Теорема 1. Маршрут wgb длины gb в базовом графе отображается в набор
циклов длины g = gb в расширенном графе тогда и только тогда, когда Pgb = 0
и wgb не содержит в себе маршрутов winc, для которых Pinc = 0. Здесь Pgb и Pinc
рассчитываются согласно (1), а индекс inc обозначает вложенность маршрута.
Данная теорема описывает возможные преобразования как одиночного цикла,
так и маршрута при расширении графа. Однако согласно [9, 10] объединения цик-
лов также могут быть подвержены изменениям. Циклы si и sj образуют объедине-
ние в протографе тогда и только тогда, когда они содержат хотя бы одну общую
вершину. Такая пара циклов в Gb описывается следующим набором параметров:
• gi и gj - длины пересекающихся циклов;
• ncv - число общих вершин между si и sj;
• nce - число общих ребер между si и sj;
• ncr - взаимное направление обхода, которое принимает значение, равное нулю,
при совпадении обходов циклов по общему ребру (общим ребрам), а в противном
случае ncr = 1.
В работе [7] рассмотрена мера, описывающая число ребер, связывающих кодовые
вершины цикла с внешними по отношению к нему проверочными вершинами. Для
определения числа таких связей используется формула (см. [7])
∑
γ =
(dk - 2).
(3)
k=0
Определим параметр γ как метрику связанности цикла (МСЦ) s с графом G.
84
в)
е)
а)
д)
г)
б)
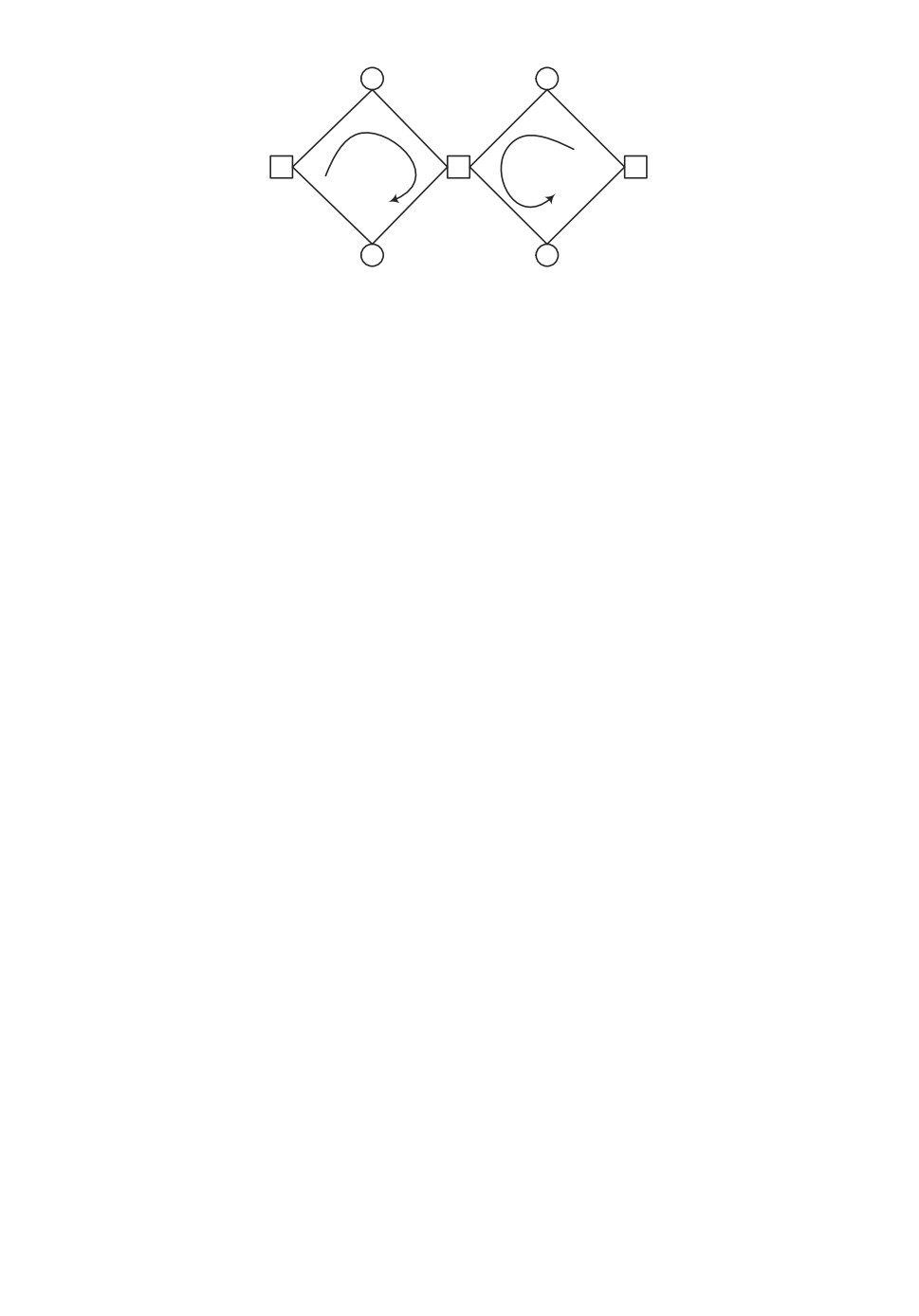
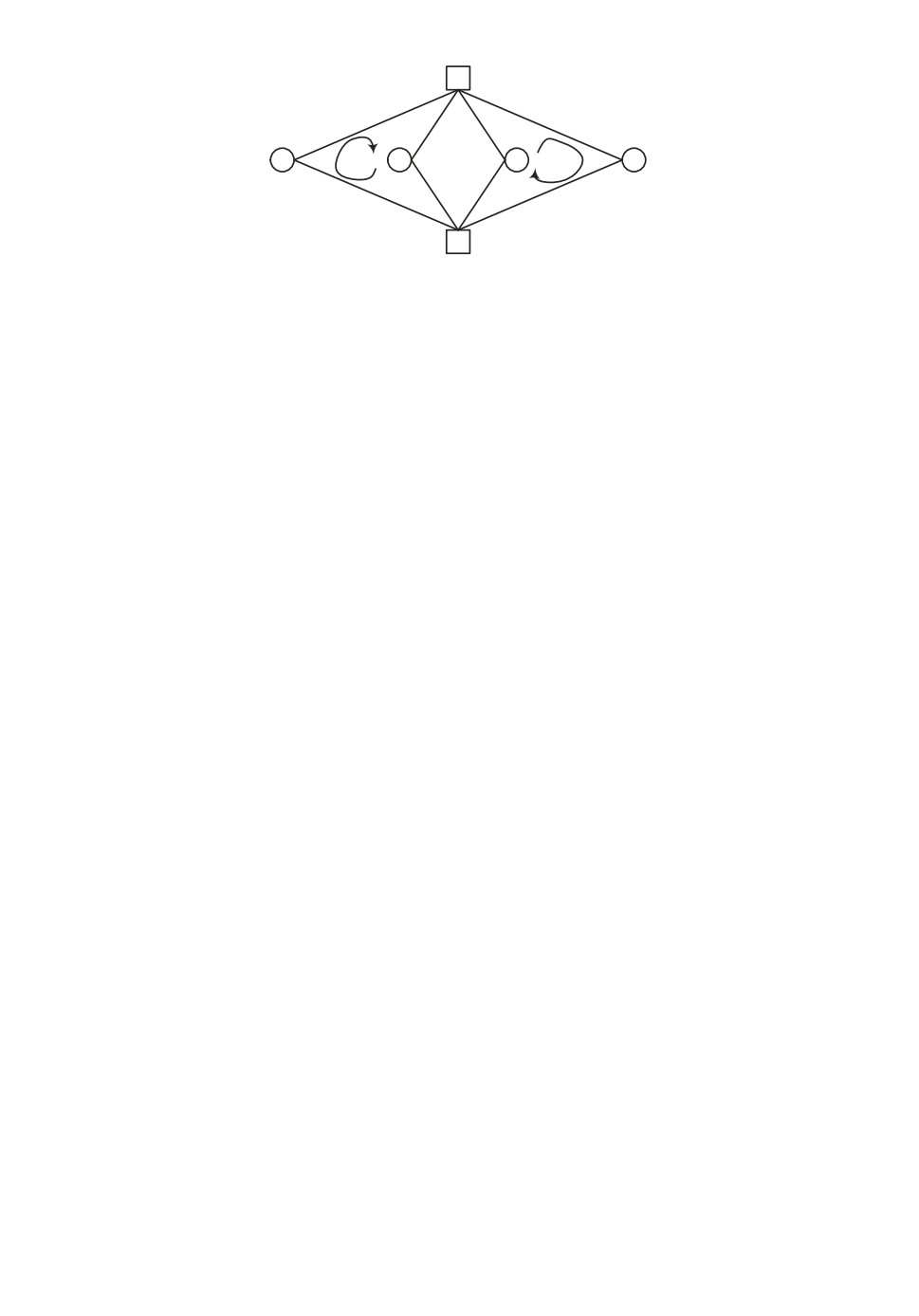
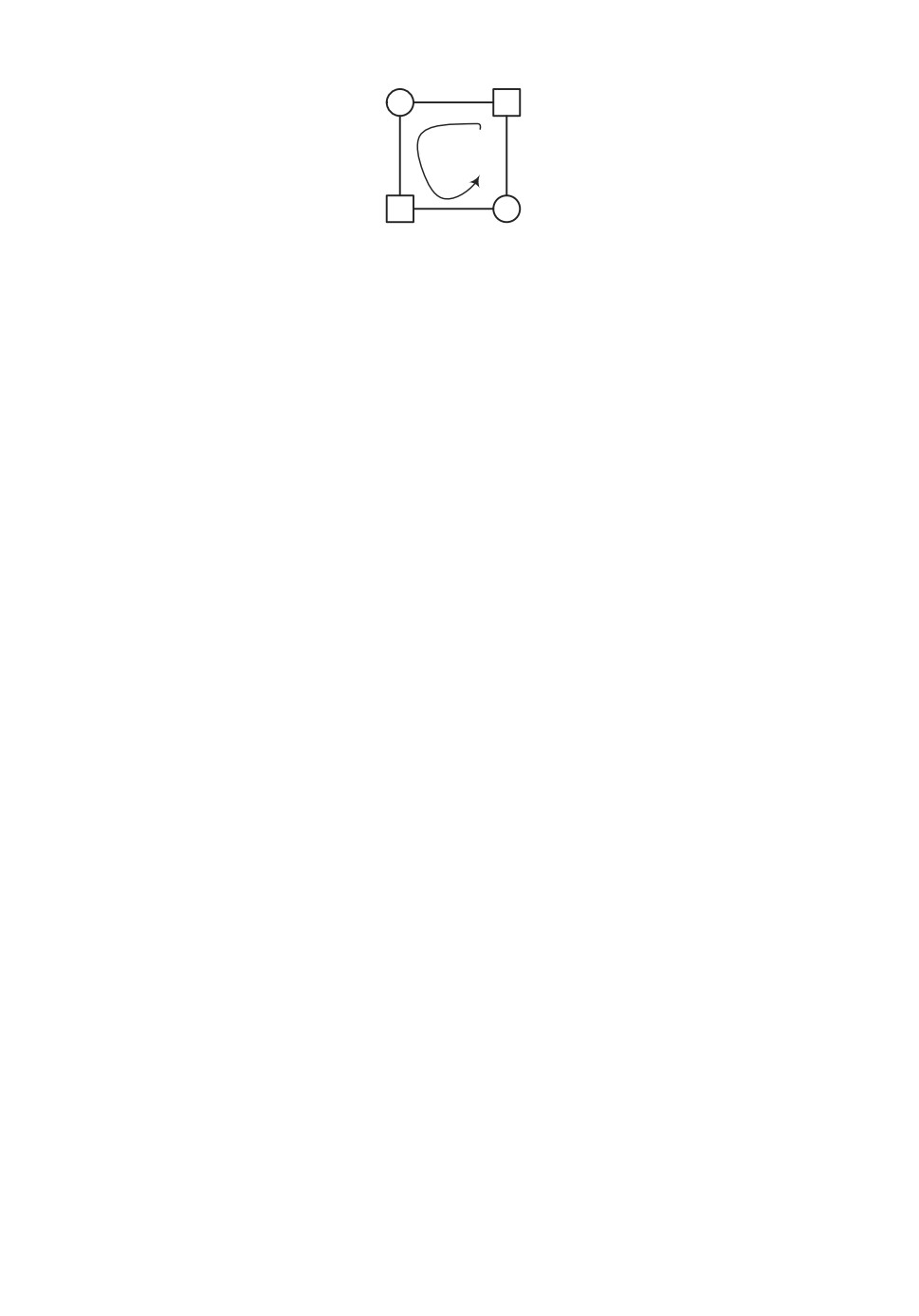
Рис. 1. Конфигурации подграфов, в которых возможно существование маршрутов
длины gx
В последующих параграфах рассмотрены маршруты целевой длины gx = 8 и об-
разующие их подграфы - элементы протографов, состоящие из объединений циклов
минимальной длины, а также аналитика изменения значений МСЦ при расширении
базового графа.
§3. Условия образования циклов
Теорема 2. Циклы sgx в расширенном графе G образуются из маршрутов wgx
в базовом графе Gb, таких что определяемые ими подграфы изоморфны одному из
шести графов, представленных на рис. 1.
Доказательство. Пусть цикл имеет вид sgx = (u1,u2,...,ugx,u1), где u ∈
∈ C ∪ V . Тогда маршрут в протографе, из которого образовался цикл, имеет вид
wgx = (f(u1), f(u2), . . . , f(ugx ), f(u1)), где f(vib) = vb, f(cjb) = cb для всех vb ∈ Vb,
cb ∈ Cb, i, j ∈ [0, q - 1].
Тогда маршрут wgx определяет в графе Gb подграф T с множеством вершин
{f(u1), f(u2), . . . , f(ugx )} и множеством ребер
{(f(u1), f(u2)), (f(u2), f(u3)), . . . , (f(ugx ), f(u1))}.
Теперь можно сформулировать следующие предложения.
Предложение 1. Подграф T изоморфен факторграфу графа S по разбиению P,
а именно T
= S/P, где S - цикл с вершинами {u1, u2, . . . , ugx} и ребрами {(u1, u2),
(u2, u3), . . . , (ugx , u1)}, а P = {i, j ∈ I | f(uj) = f(ui)}, I = {1, 2, . . . , gx}.
Предложение 2. Для всяких J ∈ P, ui,uj ∈ J разность i - j четна, но
отлична от двух.
Для gx = 8 из предложения 2 следует, что J либо одноэлементно, либо является
одной из пар (u1, u5), (u2, u6), (u3, u7), (u4, u8).
Пусть P - множество всех разбиений множества J, указанного в предложении 2.
Назовем P, Q ∈ P эквивалентными, P ∼ Q, если Q = {{a(uj) | uj ∈ J} | J ∈ P},
где a - автоморфизм цикла S. Тогда справедливо следующее
85
v1
v3
a13
a21
a11
a33
c2
c1
c3
a22
a12
a14
a34
v2
v4
Рис. 2. Графическое изображение подграфа а)
Предложение 3. Если P ∼ Q, P,Q ∈ P, то S/P
= S/Q. Если P эквивалент-
но Q, то факторграф графа S по разбиению P изоморфен факторграфу графа S по
разбиению Q.
Учитывая возможные значения J и предложение 3, существует шесть вариантов
для P :
{u1, u2, u3, u4, u5, u6, u7, u8},
{(u1, u5), u2, u3, u4, u6, u7, u8},
{(u1, u5), (u2, u6), u3, u4, u7, u8},
(4)
{(u1, u5), (u3, u7), u2, u4, u6, u8},
{(u1, u5), (u2, u6), (u3, u7), u4, u8},
{(u1, u5), (u2, u6), (u3, u7), (u4, u8)}.
Тогда S/P для этих вариантов P будет соответствовать подграфам е), а), в), б),
г) и д). ▴
В силу того, что подграф е) является одиночным циклом в базовом графе, его
учет является относительно тривиальной задачей и может быть выполнен на основе
любого алгоритма нумерации циклов.
Теорема 3. Базовое уравнение для любого маршрута wgx в протографе мо-
жет быть выражено через БУ пары циклов sgmin, покрывающих все вершины
маршрута wgx .
Доказательство. В соответствии с теоремой 2 маршруты длины gx могут
образовываться в одном из шести возможных подграфов, исключая из рассмотрения
случай е). Рассмотрим первый из них (рис. 2).
В данном подграфе возможно существование двух маршрутов длины gx:
wgx1 = v1, c1, v4, c3, v3, c1, v2, c2, v1,
wgx2 = v1, c1, v3, c3, v4, c1, v2, c2, v1.
Запишем БУ для этих маршрутов:
Pgx1 = (a3,4 - a1,4) + (a1,1 - a2,1) + (a2,2 - a1,2) + (a1,3 - a3,3),
(5)
Pgx2 = (a1,4 - a3,4) + (a3,3 - a1,3) + (a1,1 - a2,1) + (a2,2 - a1,2).
(6)
Уравнение для Pgx1 может быть представлено в виде следующих двух сумм:
= (a3,4 -a1,4)+(a1,3 -a3,3). При этом первая
Pgmin1 = (a1,1 -a2,1)+(a2,2 -a1,2) и
2
из них является записью БУ для цикла sgmin1 = v1, c1, v2, c2, v1, а вторая - для цикла
sgmin2 = v3, c1, v4, c3, v3. Таким образом, БУ для маршрута w1x может быть выражено
86
c1
a11
a14
a
12
a13
v1
v4
v2
v3
a22
a23
a21
a24
c2
Рис. 3. Графическое изображение подграфа б)
как сумма БУ циклов sgmin1 и s2min:
Pgx1 =
1
+ Pgmin2 .
(7)
=
Аналогично, уравнение для Pgx2 можно разбить на следующие две суммы:
1
= (a1,1 - a2,1) + (a2,2 - a1,2) и P′gmin2 = (a1,4 - a3,4) + (a3,3 - a1,3), где
2
= -Pgmin2.
Таким образом, БУ для маршрута wgx2 может быть выражено через БУ тех же
циклов, что и БУ для маршрута wgx1 :
Pgx2 =
1
- Pgmin2 .
(8)
В итоге БУ для обоих маршрутов длины gx, существующих в подграфе а), могут
быть выражены через БУ циклов длины gmin.
Далее рассмотрим второй из возможных подграфов (рис. 3). В нем возможно
существование шести маршрутов длины gx:
wgx1 = v1, c1, v2, c2, v3, c1, v4, c2, v1, w2x = v1, c1, v2, c2, v4, c1, v3, c2, v1,
wgx3 = v1, c1, v3, c2, v2, c1, v4, c2, v1, w4x = v1, c1, v3, c2, v4, c1, v2, c2, v1,
wgx5 = v1, c1, v4, c2, v2, c1, v3, c2, v1, w6x = v1, c1, v4, c2, v3, c1, v2, c2, v1.
Записав БУ для каждого из маршрутов, можно показать, что все они могут быть
выражены суммой или разностью БУ пары циклов длины gmin:
,
Pgxi =
i
+1
i = 1,3,5.
+1
=Pgmini -
i+1
,
Здесь Pgminj, j ∈ [1, 6], - БУ для циклов длины gmin: s1min = v1, c1, v2, c2, v1, s2min =
= v3, c1, v4, c2, v3, sgmin3 = v1, c1, v3, c2, v1, s4min = v2, c1, v4, c2, v2, s5min = v1, c1, v4, c2, v1
и sgmin6 = v2, c1, v3, c2, v2.
Таким образом, БУ для всех маршрутов длины gx, существующих в подграфе б),
могут быть выражены через БУ циклов длины gmin.
Далее рассмотрим третий из возможных подграфов (рис. 4). В нем возможно
существование одного маршрута длины gx:
wgx1 = v1, c1, v3, c2, v1, c1, v2, c3, v1.
Записав БУ для этого маршрута, можно показать, что оно может быть выражено
суммой БУ пары циклов длины gmin:
Pgx1 =
1
+ Pgmin2 ,
(9)
где Pgmin1 и
2
- БУ для циклов длины gmin: sgmin1 = v1, c1, v3, c2, v1 и s2min =
=v1, c1, v2, c3, v1.
87
c2
v1
c3
a
21
a31
a11
a23
a32
a13
a12
v3
c1
v2
Рис. 4. Графическое изображение подграфа в)
v1
a21
a31
a11
c2
c1
c3
a12
a22
a32
v2
Рис. 5. Графическое изображение подграфа г)
Таким образом, БУ для маршрута длины gx, существующего в подграфе в), мо-
жет быть выражено через БУ циклов длины gmin.
Далее рассмотрим четвертый из возможных подграфов (рис. 5). В нем возможно
существование одного маршрута длины gx:
wgx1 = v1, c1, v2, c2, v1, c1, v2, c3, v1.
Записав БУ для этого маршрута, можно показать, что оно может быть выражено
суммой БУ пары циклов длины gmin:
(10)
Pgx1 =
1
+ Pgmin2 ,
где Pgmin1 и
2
- БУ для циклов длины gmin: sgmin1 = v1, c1, v2, c2, v1 и s2min =
=v1, c1, v2, c3, v1.
Таким образом, БУ для маршрута длины gx, существующего в подграфе г), мо-
жет быть выражено через БУ циклов длины gmin.
Наконец, рассмотрим пятый из возможных подграфов (рис. 6). В нем возможно
существование одного маршрута длины gx:
wgx1 = v1, c1, v2, c2, v1, c1, v2, c2, v1.
Записав БУ для этого маршрута, можно показать, что оно может быть выражено
удвоенным БУ цикла длины gmin:
Pgx1 =
1
+ Pgmin1 ,
(11)
где Pgmin1 - БУ для цикла длины gmin: s1min = v1, c1, v2, c2, v1.
Таким образом, БУ для маршрута длины gx, существующего в подграфе д), мо-
жет быть выражено через БУ цикла длины gmin.
88
v1
c2
a
21
a11
a22
a12
c1
v2
Рис. 6. Графическое изображение подграфа д)
Из всего вышесказанного следует, что БУ любого маршрута длины gx может быть
выражено через БУ циклов длины gmin, которые существуют в подграфе, формиру-
емом маршрутом, и покрывают всего его вершины. ▴
Теорема 4. Условие образования цикла длины gx в расширенном графе из
маршрута в протографе может быть выражено через базовые уравнения циклов
длины gmin.
Доказательство. В соответствии с теоремой 1 маршрут в базовом графе бу-
дет преобразован в цикл в расширенном графе, если решение БУ для маршрута
равно нулю, а решения БУ для всех более коротких маршрутов, входящих в рас-
сматриваемый, будут отличны от нуля.
Рассмотрим пару маршрутов длины gx, образующихся в подграфе а). В соответ-
ствии с теоремой 3 БУ для каждого из них может быть выражено через БУ цик-
лов длины gmin. Также, обратившись к записи маршрутов, легко заметить, что они
содержат более короткие маршруты, являющиеся циклами длины gmin, через БУ
которых выражается БУ маршрутов. Далее такие короткие циклы будем называть
компонентными циклами.
Таким образом, преобразование маршрутов в протографе в цикл при расширении
графа происходит при выполнении системы условий вида
⎧
⎨(
1
± Pgmin2 ) mod q = 0,
gmin
P1
mod q = 0,
⎩
Pgmin2
mod q = 0.
Аналогичные системы условий можно составить для маршрутов, существующих
в подграфах в) и д):
⎧
⎨(
1
+ Pgmin2 ) mod q = 0,
gmin
P1
mod q = 0,
⎩
mod q = 0.
Pgmin2
Для подграфа г) количество дополнительных условий сводится к одному соглас-
но теореме 3, что позволяет составить следующую систему условий:
{(Pgmin1 +
1
) mod q = 0,
mod q = 0.
Pgmin1
Маршруты, образующиеся в подграфе б), отличаются от рассмотренных выше
тем, что каждый из них содержит по четыре дополнительных цикла. Используя
89
нумерацию циклов из описания подграфа б) в теореме 3, можно показать, что
wgx1 ⊃ s1min , s2min , s5min , s6min , w2x ⊃ s1min , s2min , s3min , s4min,
wgx3 ⊃ s3min , s4min , s5min , s6min , w4x ⊃ s3min , s4min , s1min , s2min,
wgx5 ⊃ s5min , s6min , s3min , s4min , w6x ⊃ s5min , s6min , s1min , s2min.
В таком случае происходит преобразование маршрута wgx в равновеликий цикл
при расширении протографа, если выполняется система условий
⎧
⎪
) mod q = 0,
(Pgmini +
i+1
⎪
⎨
Pgmini mod q = 0,
gmin
Pi
mod q = 0,
i = 1,3,5, k = 5,5,3, ℓ = 6,6,2,
+1
⎪
⎪
⎩Pgminkmodq=0,
Pgminℓmodq=0,
или
⎧
⎪
) mod q = 0,
(Pgmini -
i+1
⎪
⎨
Pgmini mod q = 0,
gmin
Pi
mod q = 0,
i = 1,3,5, k = 3,1,1.
+1
⎪
⎪
⎩Pgminkmodq=0,
mod q = 0,
+1
Таким образом, утверждение, указанное в формулировке теоремы, является вер-
ным для всех существующих маршрутов. ▴
Теорема 5. Значение МСЦ для циклов sgx в расширенном графе определяется
суммой метрик связанности циклов, через которые выражено БУ маршрута.
Доказательство. В соответствии с теоремой 3 БУ любого маршрута дли-
ны gx может быть описано суммой БУ циклов длины gmin.
В случае подграфа а) МСЦ циклов длины gx, образованных соответствующими
им маршрутами, равны и вычисляются согласно выражению
γgx = (d1 - 2) + (d2 - 2) + (d3 - 2) + (d4 - 2).
(12)
При этом МСЦ компонентных циклов длины gmin равны
γgmin1 = (d1 - 2) + (d2 - 2),
(13)
γgmin2 = (d3 - 2) + (d4 - 2).
Объединяя (12) и (13), получим
γgx = γgmin1 + γ2min .
Если в подграфе а) все кодовые вершины заменить проверочными и наоборот,
то выражения для вычисления МСЦ изменятся, однако соотношение между ними
сохранится:
γgx = 2(d1 - 2) + (d2 - 2) + (d3 - 2),
γgmin1 = (d1 - 2) + (d2 - 2),
γgmin2 = (d1 - 2) + (d3 - 2),
γgx = γgmin1 + γ2min .
90
В случае подграфа б) МСЦ для циклов длины gx, образующихся из всех шести
возможных маршрутов, одинакова:
γgx = (d1 - 2) + (d2 - 2) + (d3 - 2) + (d4 - 2),
а МСЦ компонентных циклов выражаются следующим образом:
γgmin1 = (d1 - 2) + (d2 - 2), γ2min = (d3 - 2) + (d4 - 2),
γgmin3 = (d1 - 2) + (d3 - 2), γ4min = (d2 - 2) + (d4 - 2),
γgmin5 = (d1 - 2) + (d4 - 2), γ6min = (d2 - 2) + (d3 - 2),
и тогда МСЦ для циклов длины gx может быть выражено одной из трех сумм:
(14)
γgx = γgmin1 + γ2min = γ3min + γ4min = γ5min + γ6min .
Если в подграфе б) все кодовые вершины заменить проверочными и наоборот, то
выражения для МСЦ циклов изменятся:
γgx = 2(d1 - 2) + 2(d2 - 2),
γgmin1 = γ2min = γ3min = γ4min = γ5min = γ6min = (d1 - 2) + (d2 - 2),
а формула (14) останется верной.
Запишем выражение для МСЦ циклов, образующихся из подграфа в):
γgx = 2(d1 - 2) + (d2 - 2) + (d3 - 2).
Эту же метрику для компонентных циклов выразим уравнениями
γgmin1 = (d1 - 2) + (d2 - 2),
γgmin2 = (d1 - 2) + (d3 - 2).
Объединяя приведенные выше выражения, получим
γgx = γgmin1 + γ2min .
Если в подграфе заменить типы вершин на противоположные, то выражения для
вычисления МСЦ не изменятся.
Формула для вычисления МСЦ циклов, образующихся из подграфа г), имеет вид
γgx = 2(d1 - 2) + 2(d2 - 2),
причем компонентные циклы характеризуются следующей метрикой связанности:
γgmin1 = (d1 - 2) + (d2 - 2),
γgmin2 = (d1 - 2) + (d2 - 2).
Объединяя приведенные выше выражения, получим
γgx = γgmin1 + γ2min .
Если в подграфе г) все кодовые вершины заменить проверочными и наоборот,
то выражения для вычисления МСЦ изменятся, однако соотношение между ними
91
Таблица 1
Параметры ncv и nce для подграфов
Подграф
а)
б)
в)
г)
д)
ncv
1
2
2
3
4
nce
0
0
1
2
4
сохранится:
γgx = 2(d1 - 2) + (d2 - 2) + (d3 - 2),
γgmin1 = (d1 - 2) + (d2 - 2),
γgmin2 = (d1 - 2) + (d3 - 2),
γgx = γgmin1 + γ2min .
И наконец, для подграфа д) МСЦ образующихся циклов вычисляется в соответ-
ствии со следующим выражением:
γgx = 2(d1 - 2) + 2(d2 - 2).
При этом МСЦ цикла длины gmin, БУ которого используется для выражения БУ
маршрута, равна
γgmin1 = (d1 - 2) + (d2 - 2).
В этом случае
γgx = γgmin1 + γ1min .
Замена типа вершин в подграфе на противоположные не изменяет выражений
для вычисления МСЦ.
Таким образом, утверждение, указанное в формулировке теоремы, является вер-
ным для всех типов подграфов при целевой длине цикла, равной gx. ▴
§ 4. Процедура определения наличия циклов длины gx в расширенном графе
путем анализа протографа
Полученные выше условия позволяют построить процедуру определения нали-
чия циклов длины gx в расширенном графе путем анализа циклов, существующих
в протографе.
Сравнение алгоритмов обнаружения коротких циклов с прямым поиском марш-
рутов по вычислительной сложности говорит не в пользу последнего. Поэтому целе-
сообразно взять за основу именно первый вариант. Любой из пяти возможных под-
графов, в котором существуют маршруты длины gx, может быть представлен как
объединение двух циклов длины gmin с некоторым количеством общих вершин ncv
и ребер nce. В табл. 1 приведено соответствие между подграфами, в которых су-
ществуют маршруты длины gx, и параметрами ncv и nce объединения двух циклов
длины gmin.
Таким образом, сравнив записи двух циклов длины gmin и определив наличие
общих вершин и ребер, мы можем однозначно определить наличие и тип подграфа
согласно теореме 2. Также можно заметить, что для описания протографа и вы-
ражения БУ маршрута используется одна и та же пара циклов. Все это позволяет
нам предложить процедуру определения наличия циклов длины gx в расширенном
графе, который включает в себя следующие шаги:
92
1. Выполнить поиск одиночных циклов длины gx и gmin;
2. Составить и решить БУ для одиночных циклов длины gx, найденных в п. 1. Если
хотя бы одно связанное с циклом РБУ равно нулю, то процедура завершается,
иначе переходим к следующему шагу;
3. Попарно сравнить все циклы длины gmin и обнаружить их объединения;
4. Определить тип подграфа по табл. 1 для каждого из обнаруженных объединений;
5. Составить и решить систему условий по всем объектам из п. 4;
6. Цикл длины gx считается обнаруженным, если хотя бы одна из систем условий
выполнена, иначе циклы целевой длины отсутствуют.
С помощью предложенной процедуры мы можем обнаружить циклы длины gx
без выполнения затратной процедуры расширения протографа.
§ 5. Заключение
В рамках проделанной работы предложена процедура определения наличия цик-
ла длины gx в графе Таннера КЦ МПП-кода путем анализа соответствующих марш-
рутов в протографе. Сформулирован и доказан набор теорем 2-5, которые лежат
в основе представленной процедуры. Они служат для определения множества под-
графов в базовом графе, образованных объединением одиночных циклов длины gmin
и позволяющих выявить факт существования циклов длины gx в расширенном гра-
фе с универсальной формулой расчета МСЦ. Таким образом, описан процесс топо-
логического расширения двудольного графа без параллельных ветвей в плоскости
изменения структуры циклов длины gx. В дальнейшем планируется продолжить ра-
боту в направлении увеличения длины анализируемого цикла в расширенном графе
без кратных ребер, а также разработать алгоритм, максимизирующий обхват графа
Таннера КЦ МПП-кода с g0 ≤ 12 на основе предлагаемого подхода.
Авторы выражают особую благодарность А.Н. Воропаеву за помощь в доказа-
тельстве теоремы 2, а также рецензенту за внимательное прочтение рукописи и
ценные замечания, позволившие улучшить качество итоговой работы.
СПИСОК ЛИТЕРАТУРЫ
1. Tanner R.M. On Quasi-cyclic Repeat-Accumulate Codes // Proc. 37th Allerton Conf.
on Communication, Control and Computing. Monticello, IL, USA. Sept. 22-24, 1999.
P. 249-259.
2. Fossorier M.P.C. Quasi-cyclic Low-Density Parity-Check Codes from Circulant Permutation
Matrices // IEEE Trans. Inform. Theory. 2004. V. 50. № 8. P. 1788-1793.
3. Fan J.L. Array Codes as Low-Density Parity-Check Codes // Proc. 2nd Int. Symp. on Turbo
Codes and Related Topics. Brest, France. Sept. 4-7, 2000. P. 543-546.
4. Richardson T.J., Shokrollahi M.A., Urbanke R.L. Design of Capacity-Approaching Irreg-
ular Low-Density Parity-Check Codes // IEEE Trans. Inform. Theory. 2001. V. 47. № 2.
P. 619-637.
5. Li Z., Chen L., Zeng L., Lin S., Fong W.H. Efficient Encoding of Quasi-cyclic Low-Density
Parity-Check Codes // IEEE Trans. Commun. 2006. V. 54. № 1. P. 71-81.
6. Kschischang F.R., Frey B.J., Loeliger H.-A. Factor Graphs and the Sum-Product Algo-
rithm // IEEE Trans. Inform. Theory. 2001. V. 47. № 2. P. 498-519.
7. Tian T., Jones C.R., Villasenor J.D., Wesel R.D. Selective Avoidance of Cycles in Irregular
LDPC Code Construction // IEEE Trans. Commun. 2004. V. 52. № 8. P. 1242-1247.
8. Mao Y., Banihashemi A.H. A Heuristic Search for Good Low-Density Parity-Check Codes
at Short Block Lengths // Proc. 2001 IEEE Int. Conf. on Communications (ICC’2001).
Helsinki, Finland. June 11-14, 2001. V. 1. P. 41-44.
9. Karimi M., Banihashemi A.H. On the Girth of Quasi Cyclic Protograph LDPC Codes //
IEEE Trans. Inform. Theory. 2013. V. 59. № 7. P. 4542-4552.
93
10. Diouf M., Declercq D., Fossorier M., Quya S., Vasić B. Improved PEG Construction of
Large Girth QC-LDPC Codes // Proc. 9th Int. Symp. on Turbo Codes & Iterative Infor-
mation Processing (ISTC’2016). Brest, France. Sept. 5-9, 2016. P. 146-150.
11. Hu X.-Y., Eleftheriou E., Arnold D.M. Regular and Irregular Progressive Edge-Growth
Tanner Graphs // IEEE Trans. Inform. Theory. 2005. V. 51. № 1. P. 386-398.
12. Овинников А.А. Способ идентификации циклов в графах Таннера LDPC кодов на осно-
ве пересечения коротких замкнутых структур в протографах // Цифровая обработка
сигналов. 2016. № 4. С. 26-30.
Харин Алексей Владимирович
Поступила в редакцию
Заверткин Константин Николаевич
05.07.2019
Овинников Алексей Анатольевич
После доработки
Рязанский государственный радиотехнический
08.05.2020
университет им. В.Ф. Уткина,
Принята к публикации
факультет радиотехники и телекоммуникаций,
12.05.2020
кафедра телекоммуникаций и основ радиотехники
kharin.a.v@tor.rsreu.ru
zavertkin.k.n@tor.rsreu.ru
ovinnikov.a.a@tor.rsreu.ru
94