О применении модели PC-SAFT для оценки скорости звука в синтетических и природных нефтегазовых смесях

231

Журнал прикладной химии. 2019. Т. 92. Вып. 2

УДК 534-13+536.71+54-135

О ПРИМЕНЕНИИ МОДЕЛИ PC-SAFT ДЛЯ ОЦЕНКИ СКОРОСТИ ЗВУКА

В СИНТЕТИЧЕСКИХ И ПРИРОДНЫХ НЕФТЕГАЗОВЫХ СМЕСЯХ

Санкт-Петербургский государственный университет, Институт химии

E-mail: i.prikhodko@spbu.ru

Поступила в Редакцию 31 июля 2018 г.

После доработки 25 октября 2018 г.

Принята к публикации 29 ноября 2018 г.

Рассмотрены возможности применения модели PC-SAFT (Perturbed Chain-Statistical Association Fluid

Theory) для оценки и расчета величин скорости звука в природном газе. Приведены примеры прогно-

зирования плотности и скорости звука для пяти многокомпонентных газовых смесей, содержащих

алканы, изоалканы, азот, диоксид углерода, в широком интервале температур и давлений (250-450 K и

0.5-60 МПа). Результаты расчетов сопоставлены с литературными экспериментальными данными.

Показано, что модель с высокой точностью воспроизводит экспериментальные значения плотности

и скорости звука.

Ключевые слова: термодинамические свойства, скорость звука, моделирование, уравнение состояния,

PC-SAFT, нефтегазовые смеси, природный газ.

DOI: 10.1134/S0044461819020142

Скорость звука — важная термофизическая вели-

чина, которая широко используется в практических

целях для характеристики гомогенных и гетероген-

ных смесей, для оценки плотности пластовых флю-

идов в скважинах в широком диапазоне внешних

где

— молекулярная масса системы

условий [1, 2]. Наряду с температурой и давлением

с учетом числа молей и молекулярных масс компо-

скорость звука — один из легко определяемых в экс-

нентов i.

перименте параметров, который можно применять

Среди современных уравнений состояния, кото-

для нахождения молекулярной массы и плотности

рые в последние 5-7 лет тестируются разными ис-

газовой смеси, а также оценки величины потребления

следователями на предмет улучшения количествен-

природного газа на газораспределительных станциях

ного описания скорости звука в чистых и смешанных

[3, 4]. Термодинамическая скорость звука представ-

флюидах различной природы, выделяются уравнения

ляет большой интерес для исследователей, прове-

семейства SAFT (Statistical Associating Fluid Theory)

ряющих возможности уравнений состояния для ее

[5-7]. Одно из таких уравнений состояния — урав-

точного описания (эта величина связана с адиабати-

нение состояния на основе статистической теории

ческой сжимаемостью вещества и выражается через

ассоциирующего флюида с возмущенной цепью

производную второго порядка энергии Гельмгольца

(Perturbed Chain-SAFT) — было предложено Гроссом

по объему). Расчет скорости звука u основан на зна-

и Садовски [8]. Оно представляет собой модифициро-

нии термодинамических величин, таких как общий

ванный вариант известной и популярной в последнее

объем V (или плотность), изобарная C_P и изохорная

время в инженерных расчетах молекулярно-стати-

теплоемкости C_V, а также производная давления по

стической модели SAFT и опирается на результа-

общему объему при заданных значениях температу-

ты теории возмущений и численного эксперимен-

ры и общего числа молей системы

согласно

та для флюида, образованного цепочками твердых

известной формуле

сфер. Молекулярная модель, заложенная в уравнение

232

Приходько И. В. и др.

PC-SAFT, учитывает эффекты образования цепо-

Гельмгольца для улучшения описания термодинами-

чек твердых сфер, дисперсионное взаимодействие,

ческих свойств чистых веществ и бинарных смесей

которое описывается с помощью теории возмуще-

в широком интервале условий, включая однофазные

ний Баркера-Хендерсона [9], а также ассоциацию;

и двухфазные состояния, околокритическую область.

предполагается наличие контактных участков на по-

В данной работе мы применили этот вариант мо-

верхности молекулы, способных к специфическим

дели PC-SAFT для оценки и прогнозирования ско-

взаимодействиям с контактными участками других

рости звука для ряда многокомпонентных систем,

молекул.

содержащих нефтегазовые флюиды. Проведенные

Отметим, что апробация модели PC-SAFT бы-

модельные расчеты дают хорошие результаты, до-

ла успешно проведена иранскими коллегами при

статочные для практических оценок и контроля ве-

расчетах термодинамических характеристик смесей

личин скорости звука (и плотностей) в рассматрива-

природного газа [10], которые являются объектом

емых флюидных смесях. Детальное описание модели

рассмотрения настоящей работы. Модель PC-SAFT

CP-PC-SAFT (Critical Point-based Perturbed Chain-

интенсивно развивается, и уже на ее основе создают-

Statistical Association Fluid Theory) и методика расчета

ся новые варианты уравнений состояния, направлен-

с помощью этого уравнения состояния приводятся

ные, в частности, на более точное описание скорости

в работах [15, 16], поэтому мы ограничимся лишь

звука [11-19], c сохранением при этом надежного

кратким рассмотрением.

описания P-V-T свойств изучаемых систем, в том

числе плотности жидкости и давления насыщенного

Моделирование

пара. В работе [12] предложен подход, улучшаю-

щий точность описания скорости звука с помощью

Согласно модели CP-PC-SAFT выражение для

уравнения состояния PC-SAFT на примере н-алка-

«остаточного» (обусловленного межмолекулярным

нов различной длины углеродной цепи; была сде-

взаимодействием) вклада в энергию Гельмгольца в

лана апробация двух приближений: использования

случае отсутствия в системе ассоциирующих и поляр-

величины скорости звука как исходного термоди-

ных компонентов может быть записано следующим

намического свойства для определения модельных

образом (аналогично модели PC-SAFT):

параметров чистых компонентов и ее использования

A_ост = A^hc + A^disp,

(1)

при получении универсальных констант при оценке

дисперсионной составляющей энергии Гельмгольца

где первое слагаемое относится к вкладу образования

и параметров модели. Авторами работы [13] детально

цепочек из твердых сфер, а второе — к дисперсион-

сопоставлялись возможности моделей SAFT и PC-

ной составляющей энергии Гельмгольца, которая от-

SAFT для предсказания термодинамических свойств

вечает за взаимодействия, связанные с притяжением.

неполярных и ассоциирующих веществ, однако, не-

Формулы для расчетов составляющих суммы (1)

смотря на приемлемое описание скорости звука, при

приведены в работах [8, 15, 16]; полезные выражения

прогнозировании изохорной теплоемкости наблюда-

для расчетов термодинамических величин, связанных

лись значительные расхождения с эксперименталь-

с производными первого и второго порядка энергии

ными данными. В работе [14] рассмотрен вариант

Гельмгольца по объему (плотности), можно найти

уравнения состояния PC-SAFT на основе метода

также в статье [10]. Выражение для уравнения со-

«групповых вкладов —group-contribution» для описа-

стояния, записанное через фактор сжимаемости или

ния термодинамических свойств чистых углеводоро-

давление, может быть легко получено из (1) с помо-

дов разных классов в широком интервале изменения

щью известных формул термодинамики. Применяя

температур и давлений. Апробация модификации

модель для смесей, используют комбинационные

уравнения состояния PC-SAFT, дающей более точ-

правила Лоренца-Бертло, причем вводится только

ную оценку скорости звука в различных системах,

один подгоночный параметр бинарного взаимодей-

проводилась в работах Полишука и др. [11, 15-19].

ствия k_ij, который подправляет дисперсионную со-

Авторами были преодолены некоторые недостатки

ставляющую взаимодействий в уравнении CP-PC-

оригинальной версии PC-SAFT (неточности пред-

SAFT:

сказания скорости звука в жидкой фазе, завышенные

значения критических констант чистых компонентов,

(2)

некорректное описание теплоемкостей при очень вы-

соких давлениях) и введены незначительные уточне-

(3)

ния для выражений вкладов в «остаточную» энергию

О применении модели PC-SAFT для оценки скорости звука в синтетических и природных нефтегазовых смесях

233

где индексы i и j относятся к различным сегментам

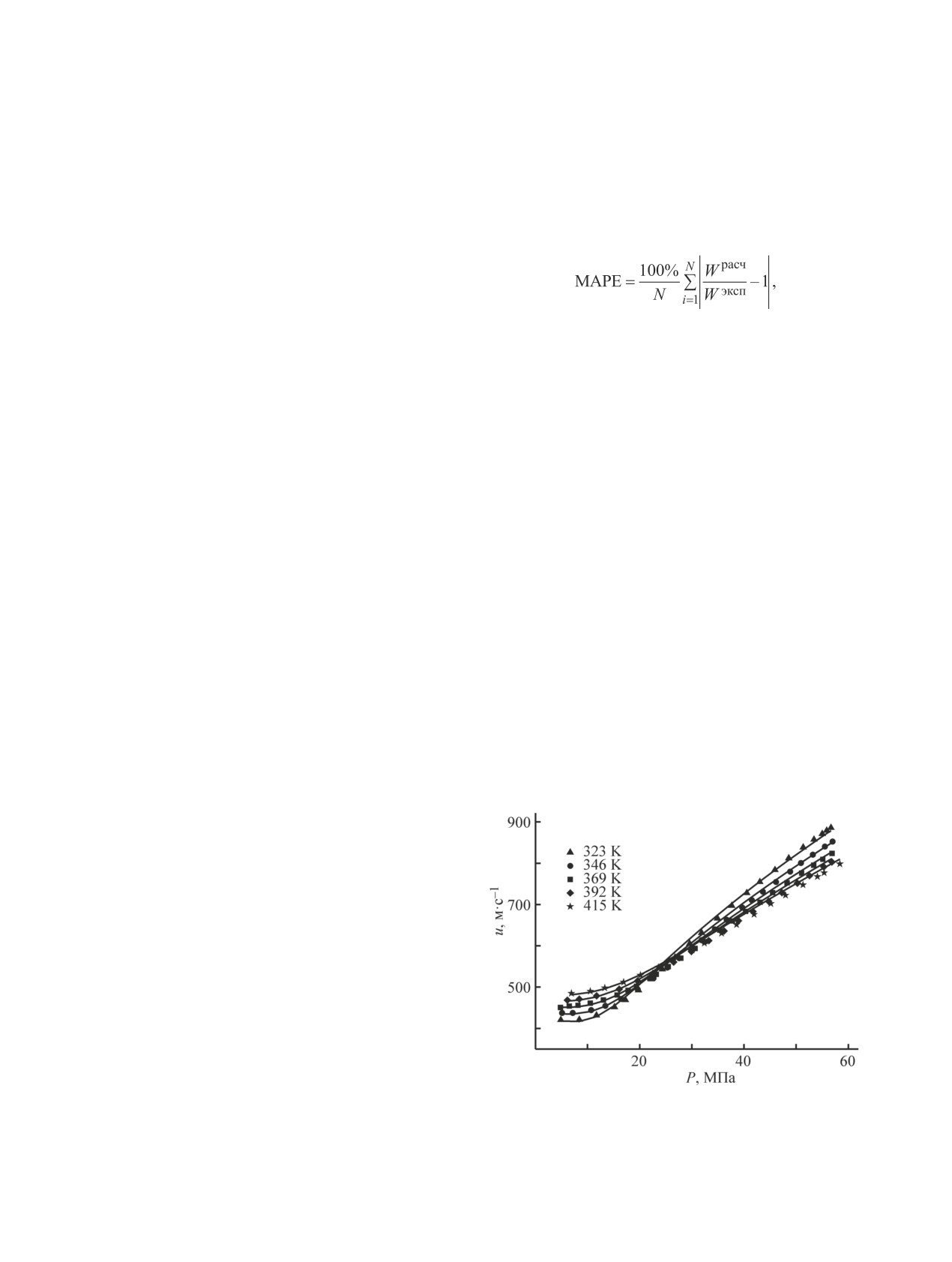
Сравнение результатов, даваемых моделью CP-

системы, σ_i — диаметр сегмента i, ε_i — энергия взаи-

PC-SAFT, и экспериментальных данных (см. рису-

модействия сегментов сорта i, k_ij — параметр бинар-

нок) оценивалось по значениям средней абсолют-

ного взаимодействия разноименных сегментов i и j

ной ошибки в процентах (MAPE — Mean Absolute

молекул-цепочек компонентов.

Percentage Error) и приведено в табл. 2:

Для описания чистого неполярного вещества в

рамках модели CP-PC-SAFT i требуется четыре па-

раметра: число сегментов m_i, образующих молеку-

лу-цепь, диаметр сегмента σ_i, энергия взаимодей-

ствия сегментов ε_i/k (k — постоянная Больцмана).

Дополнительно требуется знать параметр δν_c, отвеча-

где W — термодинамическое свойство, W^расч — рас-

ющий за смещение критического объема (отношение

считанные по уравнению состояния величины плот-

вычисленного по модели критического объема к его

ности газовой фазы или скорости звука, W^эксп — экс-

экспериментальному значению). Значения параме-

периментальные значения плотности или скорости

тров уравнения состояния CP-PC-SAFT для многих

звука, N — число экспериментальных точек.

нефтегазовых компонентов приведены в литературе

Как видно из данных табл. 2, средняя абсолютная

[15]; список параметров расширяется и включает

ошибка полученных значений скорости звука во всех

полярные и ассоциирующие компоненты [16-19].

рассматриваемых системах не превышает 2.0%, что

Дополнительно переоцениваются величины универ-

свидетельствует о высокой точности, характеризую-

сальных параметров (констант) оригинальной модели

щей свойства изученных газовых смесей. Согласно

PC-SAFT, требующихся для оценки дисперсионной

литературным данным [20] результаты предсказания

составляющей «остаточной» энергии Гельмгольца.

скорости звука и плотности для синтетической га-

Процедура расчета на основании численного решения

зовой смеси с помощью модели CP-PC-SAFT не-

для нахождения параметров уравнения состояния

сколько уступают в точности, даваемой многопара-

приводится в работе [15] и отлична от метода оценки

метрическим корреляционным уравнением состояния

(подгонки) параметров модели PC-SAFT. Идея ис-

GERG-2008 [22] (0.1%), которое рекомендовано и

пользуемого подхода состоит в том, что параметры

популярно в инженерных расчетах для нефтяной и

уравнения CP-PC-SAFT определяются в экспери-

газовой промышленности. Отметим, что уравнение

ментальных критических точках чистых компонентов

GERG-2008 имеет преимущественно эмпирическое

(для заданных значений критических констант) и

обоснование в отличие от уравнения состояния PC-

данных о плотности жидкости в тройной точке (из баз

SAFT и его аналогов (модифицированных вариантов).

термодинамических данных). Параметры бинарного

взаимодействия k_ij для описания бинарных и много-

компонентных систем приняты равными нулю, поэ-

тому представленные в настоящей работе результаты

расчетов скорости звука и плотности можно считать

предсказанием.

Обсуждение результатов

В работе проведена апробация уравнения состо-

яния CP-PC-SAFT и проверка работоспособности

предложенной методики Полишука и сотрудников

при оценке скорости звука для многокомпонентных

систем, содержащих компоненты природного газа

с различным содержанием метана (74-97 мол%).

Выбранные для расчетов синтетическая газовая смесь

и природные газовые смеси разных месторождений,

а также их составы представлены в табл. 1 (для этих

Зависимость скорости звука в природном газе от давле-

же составов известны экспериментальные значения

ния при различных температурах.

скорости звука в широком интервале давлений для

Символы — экспериментальные данные; линии — расчет

ряда температур) [20, 21].

по уравнению состояния CP-PC-SAFT.

234

Приходько И. В. и др.

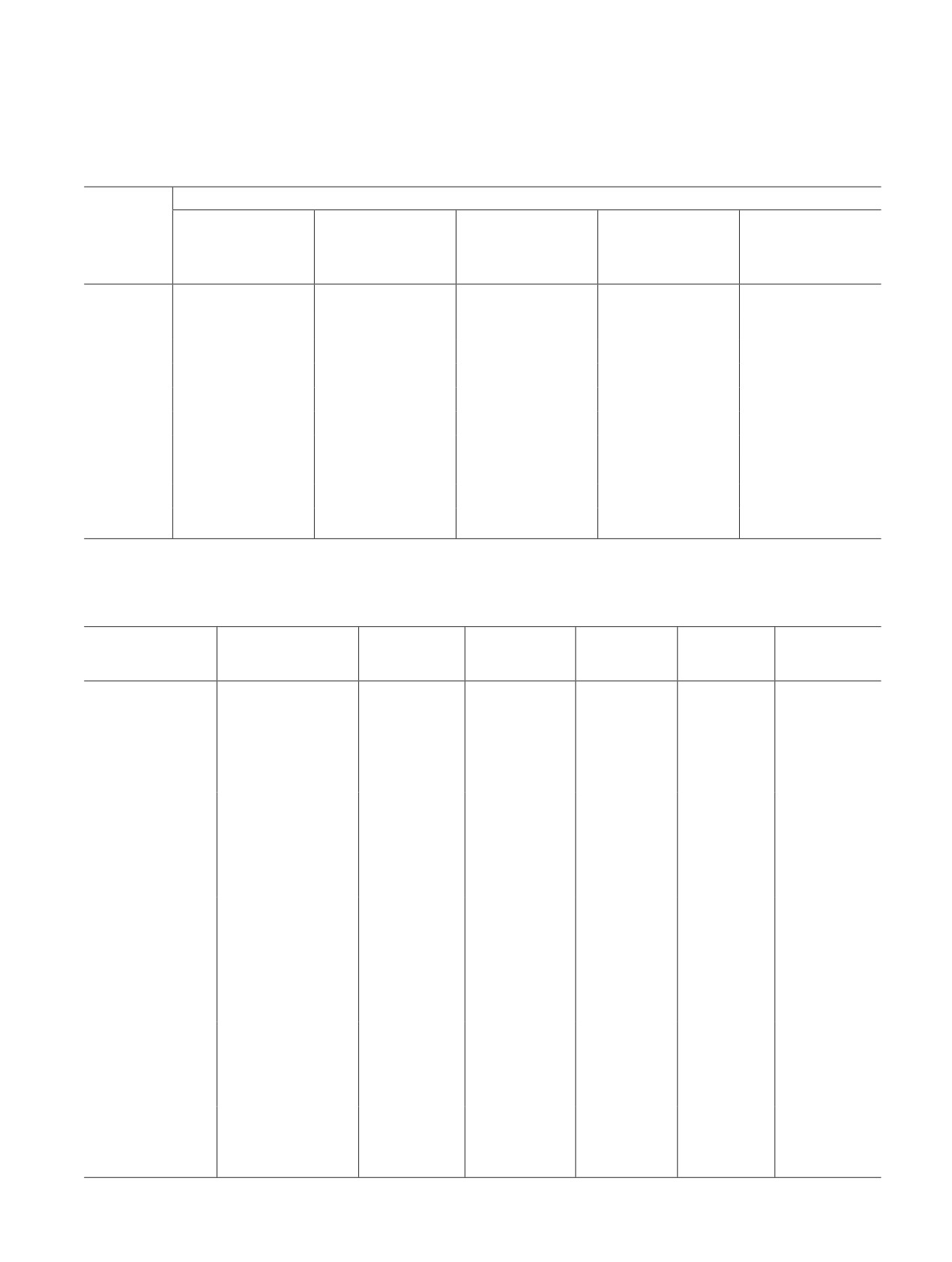
Таблица 1

Составы нефтегазовых смесей, используемые для расчетов плотности и скорости звука

Концентрация, мол. доля

природная

Компонент

природная

синтетическая

нефтегазовая смесь

газовая смесь [20]

(Statoil Statvordgass)

(Gulf Coast) [21]

(Amarillo) [21]

(Statoil Dry Gas) [21]

[21]

CH₄

0.879427

0.96561

0.90708

0.83980

0.74348

C₂H₆

0.060000

0.01829

0.04491

0.13475

0.12005

C₃H₈

0.020430

0.00410

0.00815

0.00943

0.08251

n-C₄H₁₀

0.002998

0.00098

0.00141

0.00067

0.03026

i-C₄H₁₀

0.001995

0.00098

0.00106

0.00040

n-C₅H₁₂

0.00032

0.00065

0.00008

0.00575

i-C₅H₁₂

0.00046

0.00027

0.00013

n-C₆H₁₄

0.00067

0.00034

0.002 30

N₂

0.015020

0.00262

0.03113

0.00718

0.00537

CO₂

0.020130

0.00597

0.00500

0.00756

0.01028

Таблица 2

Результаты расчетов плотности и скорости звука в рассматриваемых системах

Газовая смесь

Число

MAPE

Температура,

Интервал

MAPE для

Литературный

или

экспериментальных

для скорости

давлений, МПа

плотности, %

источник

месторождение

точек

звука, %

Синтетическая

323.31

4.86-56.69

1.30

1.14

[20]

газовая смесь

346.48

5.11-56.69

1.25

1.11

369.41

4.79-56.90

1.16

1.12

392.34

6.12-56.86

1.08

1.27

415.45

6.90-58.37

0.85

1.36

Gulf Coast

250.00

0.59-10.41

0.95

[21]

275.00

0.50-10.33

0.38

300.00

0.47-10.31

0.38

325.00

0.54-10.38

0.36

350.00

0.63-10.40

0.32

Amarillo

250.00

0.67-10.88

1.20

[21]

275.00

0.65-10.47

0.43

298.00

6.89-23.39

1.71

300.00

0.56-10.43

0.38

325.00

0.69-10.43

0.37

350.00

0.86-10.64

0.30

Statoil Dry Gas

250.00

0.80-10.34

2.51

[21]

275.00

0.52-10.42

0.65

300.00

0.53-10.30

0.41

325.00

0.47-10.40

0.42

Statoil Statvord-

300.00

1.86-10.38

1.37

[21]

gass

325.00

0.42-9.89

0.79

350.00

0.64-10.44

0.86

О применении модели PC-SAFT для оценки скорости звука в синтетических и природных нефтегазовых смесях

235

Выводы

[9] Barker J. A., Henderson D. // J. Chem. Phys. 1967.

V. 47. P. 2856-2861.

Установлено, что результаты расчетов скорости

[10] Фарзанех Горд М., Рузбахани М., Рахбари Х. Р.,

звука и плотности в системах, образованных нефте-

Хагхигхат Хоссейни С. Д. // ЖПХ. 2013. Т. 86.

газовыми компонентами, свидетельствуют о пер-

№ 6. С. 926-937 [Farzaneh Gord M., Roozbahani M.,

спективности дальнейшего использования модели

Rahbari H. R., Haghighat Hosseini S. J. // Russ. J.

PC-SAFT для оценки термодинамических и термофи-

Appl. Chem. 2013. V. 86. N 6. P. 867-878].

зических свойств природного газа для практических

[11] Polishuk I., Katz M., Levi Yu., Lubarsky H. // Fluid

целей.

Phase Equilib. 2012. V. 316. P. 66-73.

Авторы выражают благодарность проф. И. Поли-

[12] Liang X., Maribo-Mogensen B., Thomsen K., Yan W.,

Kontogeorgis G. M. // Ind. Eng. Chem. Res. 2012.

шуку (Ариэльский университет, Израиль) за предо-

V. 51. P. 14903-14914.

ставление программного кода модели CP-PC-SAFT

[13] de Villiers A. J., Schwarz C. E., Burger A. J., Konto-

и помощь в расчетах.

georgis G. M. // Fluid Phase Equilib. 2013. V. 338.

Работа выполнена при финансовой поддержке

P. 1-15.

РФФИ (грант РФФИ 17-58-560018).

[14] Burgess W. A., Tapriyal D., Gamwo I. K., Wu Y.,

McHugh M. A., Enick R. M. // Ind. Eng. Chem. Res.

2014. V. 53. P. 2520-2528.

[15] Polishuk I. // Ind. Eng. Chem. Res. 2014. V. 53.

Список литературы

P. 14127-14141.

[1] Meng G. T., Jaworski A. J., White N. M. // Chem. Eng.

[16] Lubarsky H., Polishuk I. // J. Supercritical Fluids.

Process. 2006. V. 45. P. 383-391.

2015. V. 97. P. 133-144.

[2] Machefer S., Schnitzlein K. // Chem. Eng. Technol.

[17] Polishuk I., Sidik Y., NguyenHuynh D. // Am. Inst.

2007. V. 30. N 10. P. 1381-1390.

Chem. Eng. J. 2017. V. 63. N 9. P. 4124-4135.

[3] Farzaneh-Gord M., Arabkoohsar A., Koury R. N. N. //

[18] Polishuk I., Lubarsky H., NguyenHuynh D. // Am. Inst.

J. Nat. Gas Sci. Eng. 2016. V. 30. P. 195-204.

Chem. Eng. J. 2017. V. 63. N 11. P. 5064-5075.

[4] Farzaneh-Gord M., Rahbari H. R. // J. Eng. Thermo-

[19] Melent′ev V. V., Postnikov E. B., Polishuk I. // Ind. Eng.

phys. 2012. V. 21. N 4. P. 213-234.

Chem. Res. 2018. V. 57. P. 5142-5150.

[5] Chapman W. G., Gubbins K. E., Jackson G., Radosz M.

[20] Ahmadi P., Chapoy A., Tohidi B. // J. Nat. Gas Sci.

// Ind. Eng. Chem. Res. 1990. V. 29. P. 1709-1721.

Eng. 2017. V. 40. P. 249-266.

[6] Huang S. H., Radosz M. // Ind. Eng. Chem. Res. 1990.

[21] Younglove B., Frederick N., McCarty R. Speed of

V. 29. P. 2284-2294.

sound data and related models for mixtures of natural

[7] Huang S. H., Radosz M. // Ind. Eng. Chem. Res. 1991.

gas constituents. NIST Monograph 178. Washington,

V. 30. P. 1994-2005.

U.S. Government Printing Office, 1993. P. 1-97.

[8] Gross J., Sadowski G. // Ind. Eng. Chem. Res. 2001.

[22] Kunz O., Wagner W. // J. Chem. Eng. Data. 2012.

V. 40. P. 1244-1260.

V. 57. P. 3032-3091.