Журнал прикладной химии. 2020. Т. 93. Вып. 10

ОСОБЫЕ ТЕХНОЛОГИЧЕСКИЕ РЕШЕНИЯ

УДК 636.085.62

ИСТИРАНИЕ ЧАСТИЦ В АППАРАТАХ ВЗВЕШЕННОГО СЛОЯ

Санкт-Петербургский государственный технологический институт (технический университет),

190013, г. Санкт-Петербург, Московский пр., д. 26

Е-mail: flissiyk@mail.ru

Поступила в Редакцию 15 ноября 2019 г.

После доработки 26 мая 2020 г.

Принята к публикации 3 июня 2020 г.

Исследован процесс истирания частиц в аппарате со взвешенным слоем материала. Предложена

математическая модель процесса истирания частиц, позволяющая определить плотность функции

распределения частиц по массе, а также степень истирания в зависимости от среднего времени

пребывания в слое. Проведено экспериментальное исследование процесса истирания частиц на при-

мере гранул сульфата аммония в аппарате с фонтанирующим слоем и подтверждена адекватность

предложенной модели реальному процессу.

Ключевые слова: кинетика истирания; математическая модель; функция распределения частиц по

массе

DOI: 10.31857/S0044461820100084

Многие процессы, такие как сушка, адсорбция,

существенно зависит от скорости соударения, размера

гранулирование, охлаждение, каталитический кре-

частиц и многих других факторов [8].

кинг, осуществляются в аппаратах со взвешенным

В литературе немного статей, посвященных из-

слоем дисперсных частиц [1-3]. В этих аппаратах

учению процесса истирания частиц в аппаратах со

обеспечивается высокая интенсивность тепломассо-

взвешенным слом. Как следствие, отсутствуют на-

обменных процессов за счет интенсивных гидродина-

дежные методики количественной оценки величины

мических режимов и развитой поверхности контакта

истирания, позволяющие учесть его влияние на ос-

фаз. Однако такой способ организации процесса име-

новной процесс.

ет и свой недостаток — это истирание частиц, кото-

Цель исследования — получение расчетных соот-

рое может приводить к целому ряду нежелательных

ношений для определения потери твердого материала

последствий: потере продукта, пылеуносу, загрязне-

за счет истирания в условиях работы аппарата со

нию газовых потоков и т. д. Кроме того, в таких про-

взвешенным слоем.

цессах с течением времени изменяется дисперсный

состав твердых частиц, что, несомненно, сказывается

Методология исследования

на протекании тепломассообмена. Аналогичная про-

блема возникает и при пневмотранспорте сыпучих

Теоретический анализ процесса. Существующие

материалов [4], перемешивании [5], при нанесении

модели истирания и измельчения частиц, сопрово-

покрытий на гранулы [6] и твердые лекарственные

ждающего технологические процессы во взвешенном

формы [7]. Как показали исследования, истирание

слое, исходят из стохастических представлений об

1468

Истирание частиц в аппаратах взвешенного слоя

1469

этом явлении, что позволяет использовать веро-

случаем большого класса процессов, в которых

ятностную теорию марковских процессов [9-13].

гранулометрический состав дисперсной фазы непо-

Общим недостатком таких моделей можно считать

стоянен. В общем случае, когда одновременно идут

формальный учет кинетики истирания, который

процессы коагуляции и дробления частиц, эволю-

оставляет без внимания физический механизм этого

ция дисперсного состава описывается уравнением

явления. Между тем истирание является частным

[14]

(1)

где f(m, z, t) — плотность распределения вероятно-

сти распределения частиц f(m, z, t) в данном сечении

сти частиц по их массе. Это значит, что величина

аппарата за счет среднего движения твердой фазы,

f(m, z, t)dm представляет собой число частиц с массой

за счет прилипания частиц с массой (m, m + dm) к

от m до m + dm в единице объема слоя в сечении ап-

другим частицам, за счет дробления частиц с массой

парата с координатой z в момент времени t. Функции

(m, m + dm), за счет коагуляции пары частиц с образо-

k(m, s) и g(m - s, s) характеризуют соответственно

ванием одной частицы с массой (m, m + dm) и за счет

вероятность коагуляции двух частиц с массами m и s

дробления более крупной частицы с образованием

в единицу времени и вероятность дробления частицы

осколка с массой (m, m + dm).

массой m в единицу времени на две частицы массами

Если во взвешенном слое коагуляция отсутствует,

m - s и s. Таким образом, уравнение (1) представляет

имеет место только процесс истирания частиц, то

собой символьную запись баланса частиц с массами в

для проточного аппарата с идеальным перемеши-

диапазоне (m, m + dm) в единице объема взвешенного

ванием твердой фазы уравнение (1) существенно

слоя. Оно учитывает изменение плотности вероятно-

упростится:

(2)

где τ — среднее время пребывания крупных частиц в

кратных актов дробления, в каждом из которых от

аппарате; f₀(m) — функция распределения частиц по

крупной частицы отделяется мельчайшая частич-

массе исходного материала, поступающего в рабочий

ка с минимально возможной массой. Обозначим

объем. Второе и третье слагаемые в левой части (2)

такую массу через х. Тогда вероятность дробления

отражают соответственно выход и поступление ча-

частиц симметрична относительно своих аргументов

стиц в слой в единицу времени. Для конкретизации

g(m - x, x) = g(x, m - x) и пропорциональна скорости

функции g(m - s, s) следует учесть, что истирание

истирания u, а уравнение (2) может быть записано в

частиц представляет собой частный случай много-

виде [15]

(3)

Решение этого уравнения для установившегося ре-

жима может быть представлено следующим образом:

(4)

Раскладывая логарифм в ряд и переходя к преде-

лу при х → 0, окончательно получим соотношение,

связывающее функцию распределения частиц по их

Функции f_k(m) имеют ясный физический смысл:

массе при известных среднем времени пребывания

каждая из них характеризует плотность распреде-

и скорости истирания с функцией распределения

ления частиц во всем аппарате, которые k раз (k = 0,

частиц, поступающих в аппарат:

1, 2,…) подвергались элементарному акту истира-

ния; u(m) — массовая скорость истирания частиц.

(5)

Выражение (4) может быть записано иначе:

1470

Флисюк О. М., Марцулевич Н. А.

Это соотношение принимает особенно простой

ный материал был рассеян на ситах и отобрана фрак-

вид в том случае, когда в аппарат подается материал

ция с размером гранул 3 мм, такой состав твердой фа-

монодисперсного состава. В этом случае исходное

зы с большой степенью точности можно было считать

распределение частиц описывается дельта-функцией

монодисперсным.

Дирака: f₀(m) = N₀δ(m₀ - m), где m₀ — масса частиц,

Перед началом эксперимента в аппарат загружали

поступающих в аппарат; N₀ — их число. Подставляя

слой гранул массой 2 кг. В ходе опыта в аппарат не-

указанное распределение в (5), получим

прерывно подавался и выгружался твердый материал

в таком количестве, чтобы масса слоя в аппарате была

постоянной. Этот параметр контролировали по вели-

(6)

чине гидравлического сопротивления слоя. Среднее

время пребывания гранул в аппарате оценивалось

где θ(m₀ - m) — функция Хевисайда.

как τ = М_сл/G, где М_сл — масса слоя, G — массовый

Для количественной оценки величины истирания

расход выгружаемых из аппарата гранул. При этом

частиц необходимо иметь явный вид зависимости

считали, что насыпная плотность подаваемых и вы-

u(m). Приведенные в работах [16, 17] результаты ис-

гружаемых гранул не изменяется.

следований показали, что преимущественным меха-

Загрузка и выгрузка гранул из аппарата в опытах

низмом истирания частиц является трение. Поэтому

осуществлялась таким образом, чтобы среднее время

скорость истирания отдельной частицы пропорцио-

пребывания гранул в аппарате составляло 5, 10, 15

нальна площади ее поверхности или квадрату ее ха-

и 20 мин. Скорость воздуха в опытах изменялась в

рактерного размера r: u ~ r². Поскольку масса части-

пределах от 1.5 до 3.0 м·с^-1. Масса отобранных проб

цы пропорциональна кубу ее характерного размера,

для анализа степени истирания частиц составляла

для скорости истирания имеем

около 150 г. Опытное определение степени истира-

ния частиц проводили на основе оценки изменения

u(m) = Am^2/3.

(7)

их размера с помощью ситового анализа. Ситовой

Значение константы А зависит от множества фак-

анализ проводился на ситах с размером ячеек 3, 2.8,

торов: механической прочности материала частиц, ве-

2.6, 2.4 и 2.2 мм.

личины сил адгезии, формы частиц и т. п. Оно может

Опытную проверку справедливости приведенных

быть найдено только опытным путем. Подстановка

модельных представлений, величины погрешности

зависимости (7) в выражение (6) приводит к следую-

полученных расчетных соотношений, а также опре-

щему виду нормированной функции распределения

деление зависимости величины истирания частиц от

частиц в зависимости от среднего времени пребы-

скорости газа проводили на установке, схема которой

вания:

представлена на рис. 1. Основной частью установ-

ки является аппарат с фонтанирующим слоем (С) с

(8)

тангенциальным подводом воздуха в слой. В этом

аппарате пседоожижающий агент поступает в камеру

Тогда степень истирания частиц при известном

через вертикально расположенную газораспреде-

среднем времени их пребывания в слое может быть

лительную решетку и с помощью направляющего

оценена величиной

элемента плавно изменяет свое направление вдоль

поверхности. При этом в центральной части аппарата

(9)

формируется интенсивное и устойчивое фонтани-

рование, что особенно важно для частиц, склонных

к слипанию при контакте друг с другом. Такая кон-

струкция аппарата обеспечивает гидродинамическую

Экспериментальная часть

стабильность работы слоя.

В качестве объектов исследования использова-

Исходные гранулы загружались в аппарат с помо-

ли гранулы сульфата аммония с влажностью 0.3%

щью шнекового питателя (Ш), а выгружались из ап-

и прочностью 1.2 МПа, а также гранулы двуокиси

парата через боковой штуцер с помощью секторного

марганца с влажностью 0.5% и прочностью 1.3 МПа,

затвора (СЗ).

полученные на опытно-промышленной установке со

Вытяжным вентилятором (В) в нижнюю каме-

взвешенным слоем научно-производственной компа-

ру аппарата подавался воздух. Регулировка расхода

нии ООО «ДИОМА». Для проведения эксперимента

воздуха осуществлялась вентиляционной заслонкой

по истиранию гранул во взвешенном слое получен-

(ВЗ). Мелкая фракция, образовавшаяся при истира-

Истирание частиц в аппаратах взвешенного слоя

1471

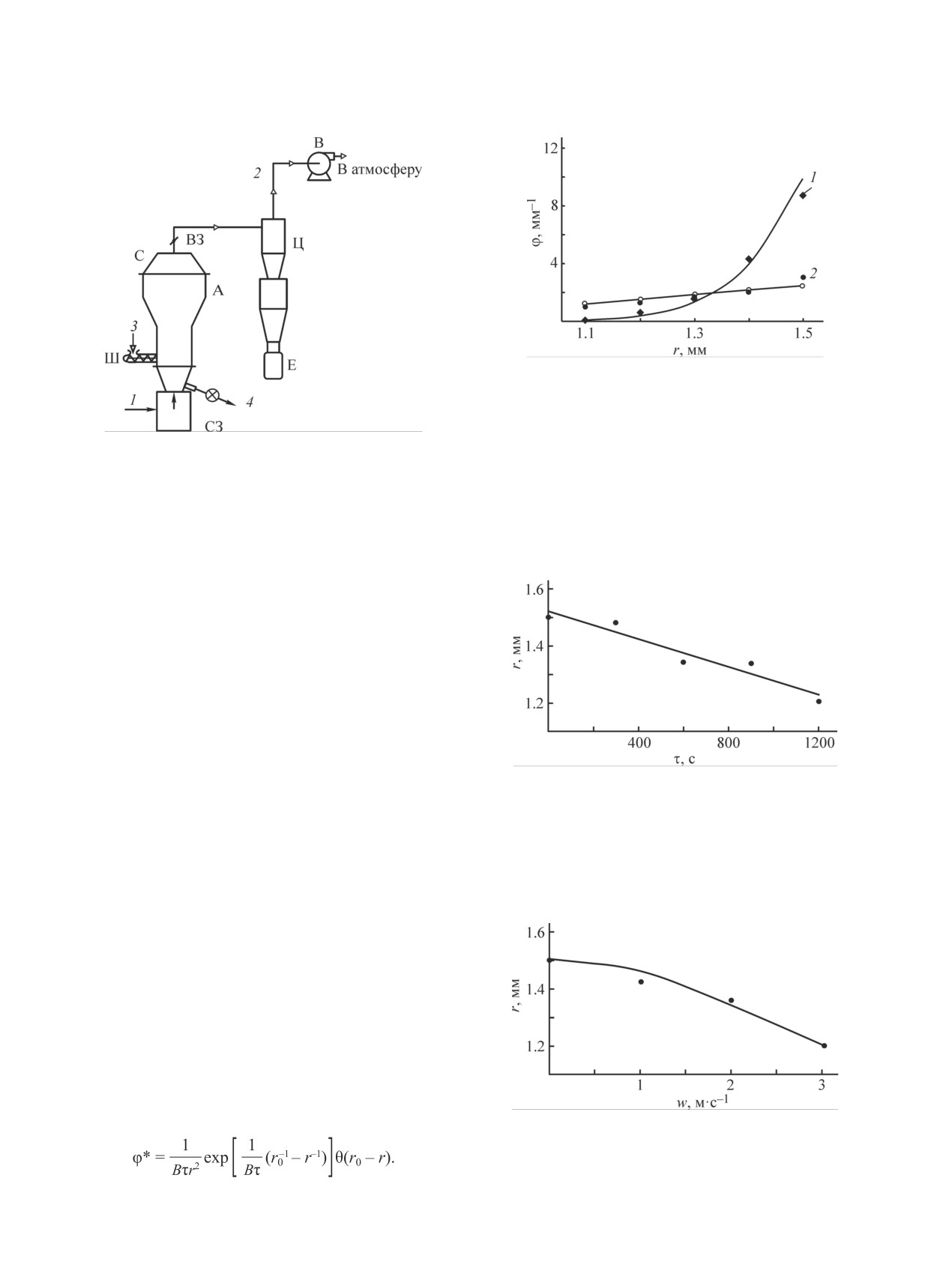
Рис. 2. Дифференциальная функция распределения гра-

нул по размерам.

Диаметр исходных гранул сульфата аммония 3 мм, влаж-

ность гранул 0.3%, прочность 1.2 МПа.

Рис. 1. Схема установки для экспериментального иссле-

τ (с): 1 — 300, 2 — 1200.

дования истирания в фонтанирующем слое.

Сплошная линия — расчетные значения, точки — экспе-

риментальные.

А — аппарат фонтанирующего слоя, Ц — циклон,

Значение константы В = 0.15 (м·с)^-1.

В — вытяжной вентилятор, Ш — шнековый питатель,

Е — емкость для пыли, ВЗ — вентиляционная заслонка,

СЗ — секторный затвор.

Потоки: 1 — атмосферный воздух, 2 — отработанный воз-

дух, 3 — загрузка исходных гранул, 4 — выгрузка твердой

фазы.

нии, выносилась из аппарата вместе с потоком возду-

ха в циклон (Ц), а затем выгружалась в емкость для

пыли (Е). Отработанный воздух, прошедший очистку

в циклоне, вытяжным вентилятором выбрасывался в

атмосферу.

Такие же опыты проводились и с гранулами дву-

окиси марганца, используемыми в качестве сорбента

для улавливания сернистых газов.

Рис. 3. Изменение среднего размера (радиуса) с изме-

нением среднего времени пребывания гранул в слое

при скорости газа w = 3 м·с^-1.

Обсуждение результатов

Диаметр исходных гранул сульфата аммония 3 мм, влаж-

ность гранул 0.3%, прочность 1.2 МПа.

С целью сопоставления экспериментальных дан-

ных и результатов расчета формула (8) была преоб-

разована к форме зависимости функции распреде-

ления от размера частиц. Поскольку уравнение (1)

инвариантно относительно замены массы частиц на

их радиус, все преобразования, приводящие к соотно-

шению (8), будут справедливы и для функции распре-

деления частиц по размеру φ(r). При этом скорость

истирания будет не массовой, а линейной: u = Br².

Константа В, так же как и константа А в (7), должна

определяться экспериментально. С учетом этого для

нормированной функции распределения частиц φ*(r)

получим

Рис. 4. Изменение среднего размера (радиуса) с измене-

нием скорости газа на зеркале слоя при τ = 1200 с.

(10)

Диаметр исходных гранул сульфата аммония 3 мм, влаж-

ность гранул 0.3%, прочность 1.2 МПа.

1472

Флисюк О. М., Марцулевич Н. А.

Для среднего радиуса частиц, покидающих рабо-

Марцулевич Николай Александрович, декан, зав.

чий объем, соответственно имеем

кафедрой механики СПбГТИ (ТУ), д.т.н., проф.,

ORCID: https://orcid.org/0000-0001-9206-5976

(11)

Список литературы

Результаты сравнения распределения гранул по

[1]

Романков П. Г., Фролов В. Ф., Флисюк О. М.

размерам, полученного из опытов и рассчитанного

Массообменные процессы химической техноло-

по формуле (10), приведены на рис. 2. Анализ полу-

гии. СПб:Химиздат, 2011. C. 407-437.

ченных результатов показал, что принятая гипотеза

[2]

Фролов В. Ф., Флисюк О. М. Гранулирование в

о кинетике истирания частиц соответствует действи-

псевдоожиженном слое. СПб: Химиздат, 2008.

тельности. Кроме того, хорошая сходимость расчет-

C. 5-45.

ных и экспериментальных значений свидетельствует

[3]

Jiménez-García G., Aguilar-López R., Maya-Yescas R.

об эффективности предлагаемого авторами подхода

The fluidized-bed catalytic cracking unit building its

к оценке изменения дисперсного состава частиц в

future environment // Fuel. 2011. V. 90. N 12. P. 3531-

аппаратах со взвешенным слоем твердой фазы.

3541. https://doi.org/10.1016/j.fuel.2011.03.045

Влияние среднего времени пребывания матери-

[4]

Uzi F., Kalman H., Levy A. A novel particle attrition

ала в слое на размер частиц иллюстрирует рис. 3.

model for conveying systems // Powder Technol. 2016.

V. 298. P. 30-41.

В интервале диаметров 2-3 мм зависимость близка

https://doi.org/10.1016/j.powtec.2016.05.014

к линейной. Значительно сильнее зависимость раз-

[5]

Tadamasa A., Takahashi K. Abrasion of particles by a

мера частиц от скорости газа (рис. 4), особенно при

small Impeller in an Agitated Vessel // J. Chem. Eng.

больших скоростях. С учетом того что масса частиц

Jpn. 2011. V. 44. P. 882-887.

пропорциональна кубу их радиуса, степень истирания

https://doi.org/10.1252/jcej.10we311

для некоторых материалов может оказаться недопу-

[6]

Laarhoven B., Wiers S. E., Schaafsma S. H.,

стимой.

Meesters G. M. Attrition strength of different coated

Аналогичные результаты были получены и при

agglomerates // Chem. Eng. Sci. 2008. V. 63. P.1361-

экспериментальном исследовании истирания гранул

1369. https://doi.org/10.1016/j.ces.2007.07.006

на основе двуокиси марганца.

[7]

Gamble J., Hoffmann M., Hughes H., Hutchins P.,

Tobyn M. Monitoring process induced attrition of drug

substance particles within formulated // Int. J. Pharm.

Выводы

2014. V. 470. P. 77-87.

Разработанная математическая модель позволяет

https://doi.org/10.1016/j.ijpharm.2014.04.028

[8]

Azimian M., Reiter A., Bart H. Computational

достаточно точно описать полученные эксперимен-

investigation of impact attrition of particles // Powder

тальные результаты по истиранию гранул сульфата

Technol. 2015. V. 289. P. 169-181.

аммония в фонтанирующем слое. Методика расчета,

https://doi.org/10.1016/j.powtec.2015.11.055

основанная на указанной модели, может быть исполь-

[9]

Огурцов А. В., Жуков В. П., Овчинников Л. Н.,

зована для оценки величины потерь дисперсного ма-

Zbronski D. Вероятностная модель истирания по-

териала за счет истирания, а также для определения

рошка в кипящем слое // Изв. вузов. Химия и хим.

дисперсного состава частиц на выходе из аппаратов

технология. 2003. Т. 46. Вып. 2. С. 108-111.

взвешенного или фонтанирующего слоя [соотноше-

[10]

Огурцов А. В., Жуков В. П., Мизонов В. Е.,

ния (10) и (11)].

Овчинников Л. Н. Моделирование истирания

частиц в кипящем слое на основе теории цепей

Маркова // Изв. вузов. Химия и хим. технология.

Конфликт интересов

2003. Т. 46. Вып. 7. С. 64-66.

[11]

Chakraborty J., Ramkrishna D. Identification of

Авторы заявляют об отсутствии конфликта инте-

Markov matrices of milling models // Ind. Eng. Chem.

ресов, требующего раскрытия в данной статье.

Res. 2009. V. 48. P. 9763-9771.

https://doi.org/10.1021/ie900456j

[12]

Berthiaux H., Mizonov V., Zhukov V. Application

Информация об авторах

of the theory of Markov chains to model different

Флисюк Олег Михайлович, зав. кафедрой процес-

processes in particle technology // Powder Technol.

сов и аппаратов СПбГТИ (ТУ), д.т.н., проф.,

2005. V. 157. P. 128-137.

ORCID: https://orcid.org/0000-0003-0527-8725

https://doi.org/10.1016/j.powtec.2005.05.019

Истирание частиц в аппаратах взвешенного слоя

1473

[13] Berthiaux H. Analysis of grinding processes by Markov

роста, истирания и дробления частиц в аппаратах

chains // Powder Technol. 2014. V. 253. P. 385-392.

периодического и непрерывного действия // ЖПХ.

https://doi.org//10.1016/S0009-2509(00)00086-5

1985. Т. 58. № 5. С. 1158-1160.

[14] Флисюк О. М., Марцулевич Н. А., Шининов Т. Н.

[16] Горлов А. С. Исследование процесса истирания

Гранулирование порошкообразных материалов

частиц твердой фазы в камере измельчения вибро-

в скоростном грануляторе // ЖПХ. 2016. Т. 89.

акустического диспергатора // Вестн. БГТУ им.

№ 4. С. 489-494 [Flisyuk O. M., Martsulevich N. A.,

В. Г. Шухова. 2015. № 5. С 179-183.

Shininov T. N. Granulation of powdered materials in

[17] Горлов А. С., Порхало В. А., Горлов К. А. Мате-

a high-speed granulator // Russ. J. Appl. Chem. 2016.

матическое моделирование процесса истира-

V. 89. N 4. P. 603-608.

ния частиц // Вестн. БГТУ им. В. Г. Шухова.

https://doi.org/10.1134/S1070427216040133 ].

2017. № 9. С. 183-187. https://doi.org/10.12737/

[15] Пеньков Н. В., Флисюк О. М., Быков В. А. Сто-

article_59a93b0f7260b4.49300932

хастические методы моделирования процессов