1474

Кольцов Н. И.

Журнал прикладной химии. 2020. Т. 93. Вып. 10

УДК 541.12

МЕТОД ОПРЕДЕЛЕНИЯ КОНСТАНТ СКОРОСТЕЙ

СТАДИЙ ХИМИЧЕСКИХ РЕАКЦИЙ

В ЗАКРЫТОМ БЕЗГРАДИЕНТНОМ РЕАКТОРЕ

Чувашский государственный университет им. И. Н. Ульянова,

428015, г. Чебоксары, Московский пр., д. 15

E-mail: koltsovni@mail.ru

Поступила в Редакцию 12 февраля 2020 г.

После доработки 6 апреля 2020 г.

Принята к публикации 27 июля 2020 г.

Описан метод определения констант скоростей стадий химических реакций, протекающих в за-

крытом изотермическом безградиентном реакторе, по нестационарным данным. Метод основан на

описании релаксационных особенностей различных участков нестационарных экспериментальных

зависимостей концентраций реагентов с помощью непрерывных и гладких во всех эксперименталь-

ных точках кривых (тайм-сплайнов). Такой подход позволяет вычислять концентрации реагентов и

мгновенные скорости их изменения в любые моменты времени с точностью, не превышающей ошибки

измерений концентраций реагентов. С помощью этого метода определены константы скоростей

стадий и интервалы их возможных изменений для реакции гидроалюминирования олефинов. Устой-

чивость метода проверена изменением ошибок измерений концентраций реагентов (шума).

Ключевые слова: нестационарная химическая кинетика; закрытый безградиентный реактор; кон-

станты скоростей стадий; релаксация; тайм-сплайны; гидроалюминирование олефинов; ошибки

измерений; шум

DOI: 10.31857/S0044461820100096

Одной из актуальных задач химической кинетики

нестационарные концентрации). В работах [9, 10]

является задача расчета кинетических констант (об-

по линейным и нелинейным временам релаксации

ратная задача) для сложных многостадийных реакций

определены константы скоростей стадий адсорбции--

по нестационарным экспериментальным данным.

десорбции диоксида углерода на хром- и галлий-

Основными трудностями при решении такой задачи

оксидных катализаторах в предположении протека-

являются неточности измерений концентраций реа-

ния процесса по трем альтернативным механизмам

гентов (шум), неоднозначность результатов решений

(линейному, диссоциативному и бимолекулярному),

(разные результаты решений могут одинаково хорошо

а также установлен наиболее вероятный диссоциа-

описывать экспериментальные данные) и проблема

тивный механизм адсорбции. Для упрощения метода

устойчивости метода расчета (малые возмущения не

оценки констант скоростей адсорбции-десорбции

должны вызывать резких отклонений решений). Для

диоксида углерода на хромоксидном нанесенном

преодоления этих трудностей, как правило, исполь-

катализаторе в работе [11] предложен подход к ре-

зуются сложные подходы и математические методы

шению обратной задачи, основанный на использова-

оптимизации [1-7]. В работе [8] изложен метод опре-

нии экспериментальных значений нестационарных

деления констант скоростей стадий и интервалов их

концентраций диоксида углерода без применения

изменений для некоторых классов каталитических

времен релаксаций. Однако это подход не учитывает

реакций без оптимизационных методов за счет ис-

особенности нестационарного поведения реакции

пользования различных релаксационных характери-

на различных временных этапах ее осуществления.

стик (линейные и нелинейные времена релаксации,

Поэтому представляет интерес разработать метод

Метод определения констант скоростей стадий химических реакций в закрытом безградиентном реакторе

1475

решения обратной задачи, учитывающий специфику

сохранения концентрации остальных реагентов, ис-

релаксационного поведения реакции в любые момен-

ключим их из (2) и получим систему K уравнений,

ты времени.

содержащих только независимые реагенты.

Цель работы — разработка и апробация метода

Метод определения констант скоростей ста-

решения обратной задачи без оптимизационных ме-

дий с помощью нелинейных тайм-сплайнов. Тайм-

тодов, учитывающего релаксационные особенности

сплайны представляют собой наборы кусочно-непре-

различных участков нестационарных эксперимен-

рывных нелинейных полиномов, образующих одну

тальных кинетических кривых, снятых в закрытом

непрерывную гладкую кривую, проходящую точно

изотермическом реакторе идеального смешения.

через все экспериментальные точки без изломов [14].

Выберем n = 1, …, N ≥ 5 (необходимое условие при-

менимости метода) экспериментальных значений

Экспериментальная часть

концентраций независимых реагентов A_kn, k = 1, …, K

Рассмотрим в общем виде механизм химической

в моменты времени t_n (узловые точки). Опишем для

реакции

каждого реагента эти значения кусочно-непрерывны-

ми полиномами, совпадающими с A_kn во всех узлах

a₊₁₁A₁ + … + a+1JA_J = a_-11A₁ + … + a-1JA_J,

(1)

(тайм-сплайном):

…

a+I1A₁ + … + a+IJA_J = a-I1A₁ + … + a-IJA_J,

S_kn(t) = a_kn(t - t_n)³ + b_kn(t - t_n)² + c_kn(t - t_n) + A_kn,

(5)

n = 1, 2, …, N - 1,

где a±ij ≥ 0 — стехиометрические коэффициенты ре-

агента A_j, j = 1, …, J в стадии i = 1, …, I. Динамика

где a_kn, b_kn, c_kn — коэффициенты n-ного полинома

такой реакции в закрытом изотермическом безгради-

для реагента A_k, которые определяются параметрами

ентном реакторе в рамках закона действующих масс

интерполяции

описывается системой J обыкновенных дифференци-

a_kn = (σk,n+1 - σ_kn)/h_kn, b_kn = 3σ_kn,

альных уравнений [12, 13]

(6)

c_kn = (Ak,n+1 - A_kn)/h_kn - h_kn(σk,n+1 + 2σk,n),

A_j′ = ∑(a-ij - a+ij)(r+i - r-i), j = 1, …, J,

(2)

где σ_N = α_N/β_N, σ_kn = (β_kn - h_knσk,n+1)/α_kn

где A = (a+ij - a-ij) — матрица стехиометрических

n = N - 1, …, N - 2, …, 1, h_kn — расстояние между

коэффициентов, r±i = k±i∏_jAka±ij — скорости стадий

соседними узлами для реагента A_k.

в прямом и обратном направлениях (с^-1), k±i — кон-

Для каждого реагента такая интерполяция опреде-

станты скоростей стадий (с^-1), A_j = A_j(t) — текущие

ляет непрерывную и гладкую кривую из N - 1 фраг-

значения концентраций реагентов (мол. доли), t —

ментов и позволяет рассчитать с хорошей точностью

время (с), A_j(t₀) = Aj0 — начальные условия, t₀ — на-

концентрации и скорости изменения всех реагентов

чальный момент времени.

в любые моменты времени t*:

В закрытых системах всегда выполняются линей-

ные стехиометрические законы сохранения вида

A_kn(t*) = S_kn(t*), n = 1, 2, …, N - 1,

(7)

∑γ_mjA_j = C_m, m = 0, 1, 2,…,

(3)

A_kn′(t*) = S_kn′(t*) = 3a_kn(t - t_n)² + 2b_kn(t - t_n) + c_kn,

n = 1, 2, …, N - 1.

(8)

где γ_mj и C_m — константы, зависящие от стехиомет-

рии стадий.

Разделим далее фрагменты сплайнов на участки

Метод вычисления этих констант приведен в ра-

быстрой, средней и медленной релаксации (типично

боте [2], где также показано, что точное число не-

для переходных процессов). Выберем для расчетов

зависимых линейных стехиометрических законов

N* ≤ N - 1 фрагментов с различным типом релакса-

сохранения (число зависимых реагентов) равно

ции (определяется визуально) и опорные точки на

N_s = J - K,

(4)

них t_n* в середине фрагментов (анализ показал, что

достаточно использовать первые два участка — бы-

где K = rank(A) — ранг матрицы A.

строй и средней релаксации). Рассчитаем значения

Выберем наблюдаемые экспериментально реа-

концентраций (7) и скорости изменения реагентов (8)

генты в качестве независимых, выразим через них

в выбранных опорных точках, подставим найденные

c помощью линейных стехиометрических законов

значения в (2) и получим систему K × N* линейных

1476

Кольцов Н. И.

уравнений для определения 2 × I констант скоростей

Обсуждение результатов

стадий k±i реакции (1):

Применим описанный подход к реакции гидро-

алюминирования олефинов для алюминийоргани-

∑(a-ik - a_ik)(k+i∏_kA_kna+ik - k-i∏_kAkn-ik) = A_kn′,

(9)

ческих соединений HAlBu_2i (диизобутилалюминий-

где k = 1, 2, …, K, n = 1, 2, …, N*.

гидрид), AlBu_3i (триизобутилалюминий), ClAlBu_2i

Эта система разрешима только тогда, когда

(диизобутилалюминийхлорид). Кинетика этой реак-

ции экспериментально изучалась при температуре

K × N* ≤ 2 × I.

(10)

-40°С в присутствии катализатора Cp₂ZrCl₂ (дихло-

рид дикоперниций-циркония). В работах [3, 4] бы-

При K × N* = 2 × I система (9) имеет единственное

ло установлено, что реакция гидроалюминирования

решение, и точечные значения констант скоростей

протекает по схеме

всех стадий определяются однозначно.

1) A

2B, 5) B + C

(16)

k±i = Δ±i/Δ, i = 1, …, s,

(11)

где Δ ≠ 0 и Δ±i — главный и вспомогательный опре-

где A ≡ A₁ = [Cp₂ZrH₂·ClAlBu_2i]₂, B ≡ A₂ =

делители системы (9).

= [Cp₂ZrH₂·ClAlBu_2i], C ≡ A₅ = HAlBu_2i, D ≡ A₈ =

Условия физичности констант имеют вид

= [Cp₂ZrH₂·HAlBu_2i·ClAlBu_2i]₂.

Запишем для этой схемы уравнения (2):

Δ+iΔ > 0, Δ-iΔ ≥ 0, i = 1, …, s.

(12)

A′ = -r₊₁ + r_-1, B′ = 2r₊₁ - 2r_-1 - r₊₅ + r_-5

Для оценки интервальных значений констант ско-

(17)

C′ = -r₊₅ + r_-5, D′ = r₊₅ - r_-5,

ростей стадий и устойчивости метода значения кон-

центраций реагентов будем искусственно искажать с

где r₊₁ = k₊₁A, r_-1 = k_-1B², r₊₅ = k₊₅BC, r_-5 = k_-5D.

помощью феноменологических соотношений, зада-

Согласно (3), (4), стехиометрическая матрица схе-

ющих ошибки измерений (шум):

мы (16) имеет вид A = (1 -2 0 0; 0 1 1 -1), ее ранг

A_ks = A_kSR_k(1 + S)sgn(S - 0.5),

(13)

K = 2 и число независимых линейных стехиометри-

= 2. Выберем в каче-

ческих законов сохранения N_s

где A_ks — «зашумленные» значения концентраций

стве независимых законов сохранения, например,

реагентов, S — максимальный уровень шума (доли),

следующие 2A + B + D = 2 и C + D = 1 (способ их

Rk — случайные числа в интервале (0,1) с равноверо-

получения подробно изложен в [2]). Выберем в ка-

ятным выбором знака, sgn — функция «знак».

честве независимых реагентов А и D, с помощью

Варьируя уровень шума, будем рассчитывать со-

этих законов сохранения определим концентрации

ответствующие значения констант скоростей стадий.

реагентов В и С через концентрации реагентов А и

Верхнюю и нижнюю положительные границы из-

D. Исключим концентрации реагентов В и С из (17)

менения значений констант будем использовать как

и получим систему уравнений, содержащих только

соответствующие границы их возможных физически

независимые реагенты А и D:

допустимых значений. Появление отрицательных

значений констант свидетельствует о потере устой-

A′ = -k₁A + k_-1(2 - 2A - D)²,

(18)

чивости метода. При K × N* > 2 × I система (9) имеет

D′ = k₊₅(2 - 2A - D)(1 - D) - k_-5D.

бесконечно много решений и константы скоростей

стадий определяются неоднозначно. Если условия

Согласно [3, 4], для схемы (16) примем значения

(10)-(12) не выполняются, то значения констант при

констант скоростей стадий равными: k₊₁* = 0.066,

выбранных параметрах интерполяции не опреде-

k_-1* = 0.0829, k₊₅* = 0.263, k_-5* = 0.0287 (с^-1).

ляются. Для оценки точности будем использовать

Зададим с учетом законов сохранения начальные

следующие соотношения:

условия: A⁰ = 1, B⁰ = D⁰ = 0, C⁰ = 1. Численно про-

интегрируем систему (18) с шагом h = 15 на интер-

R_Ak = 100∑[(A_k - A_k*)²]^0.5/N, k = 1, …, K,

(14)

вале t ∈ [0,100] и получим N = 7 точек: t_n = (0; 15;

E = 100∑[(k±i - k±i*)²]^0.5/(2I), k = 1, …, K,

(15)

30; 45; 60; 75; 90); A_n = (1.0; 0.4721; 0.3539; 0.3343;

0.3315; 0.3312; 0.3311), D_n = (0; 0.6267; 0.7957;

где R_Ak и E — среднеквадратические отклонения «ис-

0.8206; 0.8240; 0.8244; 0.8245). Разделим эти точки

тинных» значений от расчетных для концентраций

на N* = 2 фрагмента F₁ = {1-2} — точки быстрой ре-

реагентов и констант соответственно.

лаксации и F₂ = {2-7} — остальные точки. Выберем

Метод определения констант скоростей стадий химических реакций в закрытом безградиентном реакторе

1477

опорные точки t*₁ и t*₂ в середине этих фрагмен-

Запишем для этой схемы уравнения (2):

тов. Вычислим по каждому реагенту коэффициенты

A′ = -r₊₁ + r_-1,

сплайнов (5), (6), концентрации (7) (A₁, D₁), (A₂, D₂)

и скорости (8) A₁′, D₁′ и A₂′, D₂′ в этих двух точках.

B′ = 2r₊₁ - 2r_-1 - r₊₂ + r_-2 + r₊₃ - r_-3 - r₊₅ + r_-5,

Подставим эти значения в (18) и получим систему

F′ = r₊₂ - r_-2 - r₊₃ + r_-3, G′ = r₊₃ - r_-3,

(21)

из четырех линейных уравнений для определения

H′ = -r₊₂ + r_-2,

четырех констант скоростей стадий:

C′ = r₊₂ - r_-2 - r₊₅ + r_-5, D′ = r₊₅ - r_-5,

A₁′ = -k₁A₁ + k_-1(2 - 2A₁ - D₁)²,

где r₊₂ = k₊₂BH, r_-2 = k_-2CF, r₊₃ = k₊₃F, r_-3 = k_-3BG,

D₁′ = k₊₅(2 - 2A₁ - D₁)(1 - D₁) - k_-5D₁,

(19)

выражения для скоростей остальных (первой и пятой)

A₂′ = -k₁A₂ + k_-1(2 - 2A₂ - D₂)²,

стадий приведены в (17).

D₂′ = k₊₅(2 - 2A₂ - D₂)(1 - D₂) - k_-5D₂.

Согласно (3), (4), стехиометрическая матрица схе-

мы (20) имеет вид A = (1 -2 0 0 0 0 0; 0 1 -1 0 -1 0 1;

Результаты решения этой системы при разном

0 -1 0 0 1 -1 0; 0 1 1 -1 0 0 0), K = 4 и N_s = 3. Выберем

уровне шума и положении n₂ опорной точки t*₂ при-

три независимых линейных стехиометрических за-

ведены в табл. 1.

кона сохранения F + G + H = 1, C + D + H = 1 и

Решениями обратной задачи с учетом 20%-ного

2A + B + F + D = 2 и четыре независимых реагента А,

шума являются интервалы k₊₁ ∈ [0.0394, 0.0737],

D, F и G (наблюдаемые), выразим через них осталь-

k-1 ∈ [0.0497, 0.0942], k+5 ∈ [0.0205, 0.5136],

ные с помощью законов сохранения, исключим их из

k_-5 ∈ [0.0255, 0.0586] (табл. 1), которые близки

(21) и получим систему уравнений для независимых

к интервалам их изменений, найденным в [3, 4]:

реагентов

k₊₁ ∈ [0.0307,

0.0815], k_-1 ∈ [0.065,

0.187],

k₊₅ ∈ [0.0955, 0.4], k_-5 ∈ [0.0182, 0.0812]. Иллю-

A′ = -k₁A + k_-1B², D′ = k₊₅BC - k_-5D,

страция динамики концентраций ключевых реагентов

F′ = k₊₂BH - k_-2CF - k₊₃F + k_-3BG,

(22)

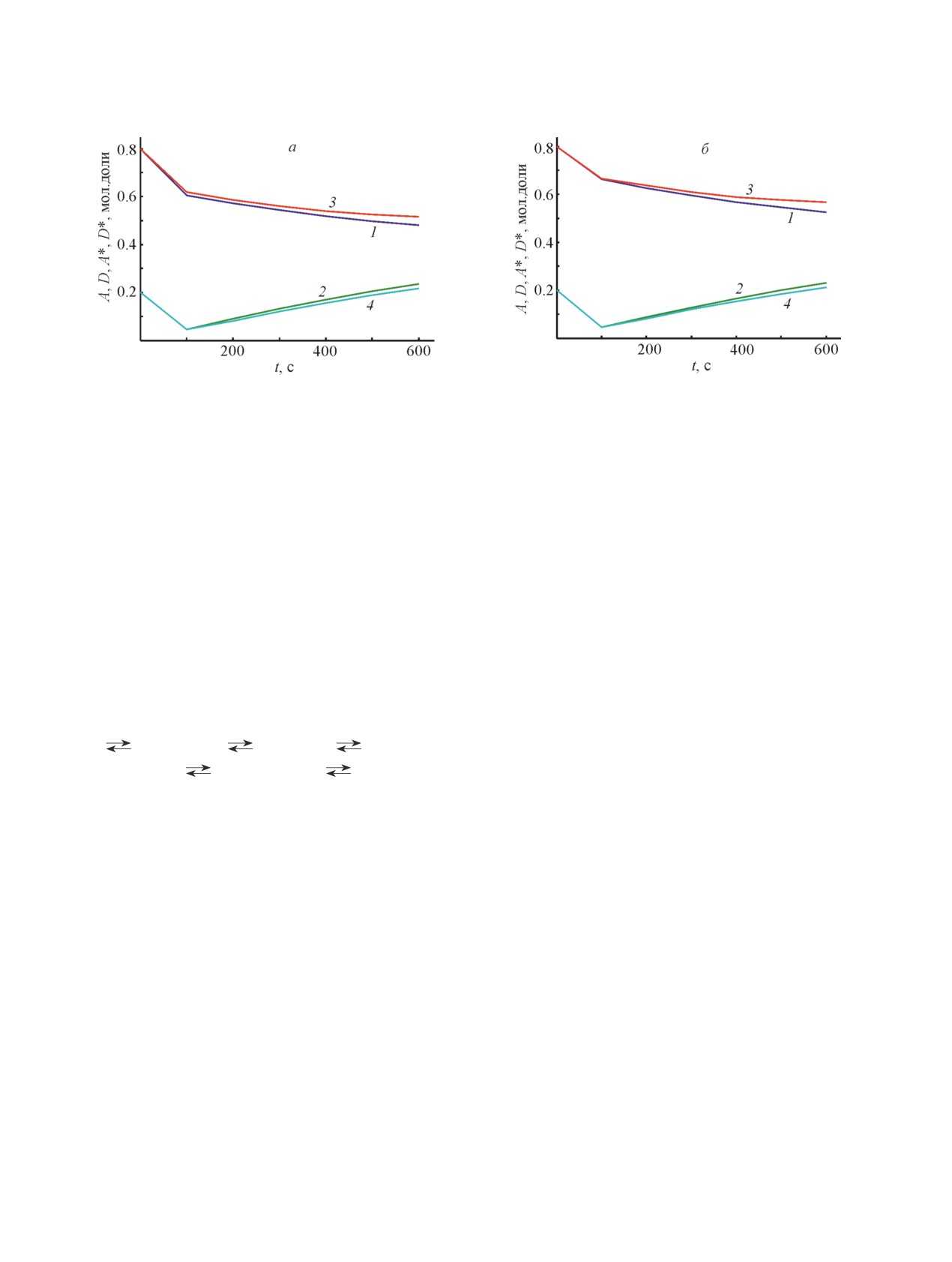
для опорной точки n₂ = 4 приведена на рис. 1.

G′ = k₊₃F - k_-3BG,

Реакция гидроалюминирования триизобутилалю-

миния протекает через стадии [3, 4]

где B = 2 - 2A - F - D, H = 1 - F - G, C = 1 - D - H.

Согласно [3, 4], примем k₊₁* = 0.066, k_-1* = 0.0829,

1) A

2B, 2) B + H

C + F,

(20)

k₊₂* = 0.0008, k_-2* = 0.0, k₊₃* = 0.0013, k_-3* = 0.0,

3) F

B + G, 5) B + C D,

k+5* = 0.263, k-5* = 0.0287 (с^-1) и начальные условия с

учетом линейных стехиометрических законов сохра-

где F ≡ A₁₂ = [Cp₂ZrHBu_2i·ClAlBu_2i], G ≡ A₁₃ = C₄H₈,

нения A⁰ = 0.8, D⁰ = 0.2, F⁰ = G⁰ = 0, H⁰ = 1 - F⁰ - G⁰,

H ≡ A₁₄ = AlBu_3i.

C⁰ = 1 - D⁰ - H⁰, B⁰ = 2 - 2A⁰ - F⁰ - D⁰. Численно

Таблица 1

Константы скоростей стадий реакции гидроалюминирования диизобутилалюминийгидрида с учетом шума

Константы скоростей стадий

Среднеквадратичные отклонения, %

Положение

Шум

опорной

по реагенту A

по реагенту D

конcтант скоростей

S, %

k₊₁

k_-1

k₊₅

k_-5

точки n₂

R_A

R_D

стадий E

0.0563

0.0497

0.0205

—

0.0593

0.0572

0.2405

0.0255

0.8856

0.5659

0.8743

0.0732

0.0931

0.2414

0.0257

0.1904

0.1127

0.6284

0.0737

0.0942

0.2372

0.0246

0.1873

0.1813

0.7376

0.0579

0.0572

0.2469

0.0263

0.8975

0.5752

0.7880

0.0566

0.0572

0.2536

0.0272

0.9093

0.5841

0.7247

0.0530

0.0574

0.2762

0.0300

0.9441

0.6081

0.7894

0.0478

0.0580

0.3254

0.0361

0.9984

0.6411

1.7507

0.0394

0.0607

0.5136

0.0586

1.0876

0.6872

6.3669

1478

Кольцов Н. И.

Рис. 1. Экспериментальные и расчетные зависимости концентраций исходного вещества (1, 3) и продукта (2, 4)

реакции гидроалюминирования диизобутилалюминийгидрида при уровне шума S = 0 (а), S = 20% (б).

проинтегрируем при этих параметрах систему (22)

A₁′ = -k₁A₁ + k_-1B₁₂, D₁′ = k₊₅B₁C₁ - k_-5D₁,

с шагом h = 100 на интервале t ∈ [0, 600] и получим

F₁′ = k₊₂B₁H₁ - k_-2C₁F₁ - k₊₃F₁ + k_-3B₁G₁,

N = 7 «экспериментальных» точек t_n = (0; 150; 300;

G₁′ = k₊₃F₁ - k_-3B₁G₁,

450; 600; 750; 900); A_n = (0.8; 0.6054; 0.5715; 0.5429;

(23)

0.5188; 0.4979; 0.4804), D_n = (0.2; 0.0458; 0.0905;

A₂′ = -k₁A₂ + k_-1B₂₂, D₂′ = k₊₅B₂C₂ - k_-5D₂,

0.1314; 0.1690; 0.2037; 0.2358). Разделим эти точки

F₂′ = k₊₂B₂H₂ - k_-2C₂F₂ - k₊₃F₂ + k_-3B₂G₂,

на N* = 2 фрагмента F₁ — точки быстрой релакса-

G₂′ = k₊₃F₂ - k_-3B₂G₂,

ции {1-2} и F₂ — остальные точки {2-7}. Выберем

опорные точки t₁*и t₂* в середине этих фрагмен-

тов. Вычислим по каждому реагенту коэффициенты

где B₁ = 2 - 2A₁ - F₁ - D₁, C₁ = 1 - D₁ - H₁, H₁ = 1 -

сплайнов (5), (6), концентрации (7) (A₁, D₁, F₁, G₁) и

- F₁ - G₁, B₂ = 2 - 2A₂ - F₂ - D₂, C₂ = 1 - D₂ - H₂,

(A₂, D₂, F₂, G₂) и скорости (8) A₁′, D₁′, F₁′, G₁′ и A₂′,

H₂ = 1 - F₂ - G₂.

D₂′, F₂′, G₂′ в этих двух точках. Подставим эти значе-

Результаты решения этой системы при разном

ния в (22) и получим линейную систему уравнений

уровне шума и положении n₂ опорной точки t ₂* при-

для определения констант скоростей стадий

ведены в табл. 2.

Таблица 2

Константы скоростей стадий реакции гидроалюминирования триизобутилалюминия с учетом шума

Среднеквадратичные

Константы скоростей стадий

Положение

отклонения, %

Шум

опорной

S, %

по реа-

конcтант

точки n₂

k₊₁

k_-1

k₊₂

k_-2

k₊₃

k_-3

k₊₅

k_-5

генту A

генту D

скоростей

R_A

R_D

стадий E

0.0107

0.0176

0.0010

0.0280

0.0013

—

0.0750

—

1.1451

3.9590

2.6497

0.0047

0.0042

0.0009

0.0364

0.0013

—

0.0313

0.0062

0.4259

1.1629

3.1986

0.0064

0.0080

0.0009

0.0398

0.0012

—

0.0417

0.0025

0.7814

0.4418

3.0729

0.0109

0.0219

0.0011

0.0233

0.0012

—

0.0790

—

0.8745

3.3044

2.5784

0.0047

0.0053

0.0010

0.0305

0.0012

—

0.0328

0.0068

0.4194

1.1032

3.1671

0.0065

0.0101

0.0010

0.0335

0.0012

—

0.0438

0.0032

0.8169

0.4341

3.0287

0.0111

0.0278

0.0012

0.0196

0.0012

—

0.0839

—

0.6804

2.8662

2.4943

0.0066

0.0129

0.0011

0.0285

0.0012

—

0.0463

0.0039

0.8460

0.4336

2.9800

Метод определения констант скоростей стадий химических реакций в закрытом безградиентном реакторе

1479

Рис. 2. Экспериментальные и расчетные зависимости концентраций исходного вещества (1, 3) и продукта (2, 4)

реакции гидроалюминирования триизобутилалюминия при уровне шума: S = 0 (а), S = 10% (б).

Решениями обратной задачи являются интер-

ных стехиометрических закона сохранения E + I +

валы k₊₁ ∈ [0.0047, 0.0111], k_-1 ∈ [0.0042, 0.0278],

+ 2J = 1, C + D + E + J = 1, F + G + I + E + J = 1 и 2A +

k₊₂ ∈ [0.0009, 0.0012], k_-2 ∈ [0.0196, 0.0398],

+ B + D + I + F = 3 и пять независимых реагентов А,

k₊₃ ∈ [0.0012, 0.0013], k_-3 ∈ [0, 0], k₊₅ ∈ [0.0313,

D, F, G и E, исключим с помощью линейных сте-

0.0839], k_-5 ∈ [0, 0.0068] (табл. 2), которые близки

хиометрических законов сохранения остальные и

к интервалам их изменений, приведенным в рабо-

получим систему уравнений для независимых реа-

тах [3, 4]: k₊₁ ∈ [0.0307, 0.0815], k_-1 ∈ [0.065, 0.187],

гентов

k₊₂ ∈ [0.0002, 0.0012], k_-2 ∈ [0, 0], k₊₃ ∈ [0, 0.053],

A′ = -k₁A + k_-1B₂, D′ = k₊₅BC - k_-5D,

k_-3 ∈ [0, 0], k₊₅ ∈ [0.0955, 0.4], k_-5 ∈ [0.0182, 0.0812].

Иллюстрация динамики концентраций ключевых ре-

F′ = -k₊₃F + k_-3BG + k₊₄EI - k_-4JF,

(26)

агентов для опорной точки n₂ = 5 приведена на рис. 2.

G′ = k₊₃F - k_-3BG,

Реакция гидроалюминирования диизобутилалю-

E′ = -k₊₂BE + k_-2CI - k₊₄EI + k_-4JF,

минийхлорида протекает по схеме [3, 4]

1) A

2B, 2) B + E

C + I, 3) F

B + G,

где J = F + G, C = 1 - D - E - J, I = 1 - E - 2J, B = 3 -

(24)

4) E + I

J + F, 5) B + C

- 2A - D - I - F.

Согласно [3, 4], для схемы (24) примем значения

где E ≡ A₉ = ClAlBu_2i, I ≡ A₁₀ = [Cp₂ZrHCl·ClAlBu_2i],

констант скоростей стадий равными: k₊₁* = 0.066,

J ≡ A₁₁ = Cl₂AlBuⁱ.

k_-1* = 0.0829, k₊₂* = 0.0023, k_-2* = 0.0, k₊₃* = 0.0013,

Для этой схемы уравнения (2) запишутся

k-3* = 0.0, k+4* = 0.0013, k-4* = 0.0, k+5* = 0.263, k-5* =

= 0.0287 (c^-1). Зададим с учетом законов сохране-

A′ = -r₊₁ + r_-1,

ния начальные условия: A⁰ = 0.72, D⁰ = 0.28, F⁰ =

B′ = 2r₊₁ - 2r_-1 - r₊₂ + r_-2 + r₊₃ - r_-3 - r₊₅ + r_-5,

= G⁰ = E⁰ = 0.1, J⁰ = 0.2, C⁰ = 0.42, I⁰ = 0.5, B⁰ =

= 0.68. Численно проинтегрируем при этих пара-

E′ = -r₊₂ + r_-2 - r₊₄ + r_-4,

(25)

метрах систему (26) с шагом h = 15 на интервале

I′ = r₊₂ - r_-2 - r₊₄ + r_-4, J′ = r₊₄ - r_-4,

t ∈ [0,100] и получим N = 7 «экспериментальных»

F′ = -r₊₃ + r_-3 + r₊₄ - r_-4, G′ = r₊₃ - r_-3,

точек t_n = (0; 150; 300; 450; 600; 750; 900); A_n = (0.72;

C′ = r₊₂ - r_-2 - r₊₅ + r_-5, D′ = r₊₅ - r_-5,

0.5576; 0.5542; 0.5525; 0.5523; 0.5528; 0.5536), D_n =

= (0.28; 0.6178; 0.6299; 0.6385; 0.6448; 0.6493; 0.6525).

где r₊₂ = k₊₂BE, r_-2 = k_-2CI, r₊₄ = k₊₄EI, r_-4 = k_-4JF,

Разделим эти точки на N* = 2 фрагмента — F₁ = точки

выражения для скоростей остальных стадий не из-

быстрой релаксации {1-2} и F₂ — остальные точки

менились и приведены в (17), (21). Согласно (3), (4),

{2-7}. Выберем опорные точки t ₁* и t ₂* в середине

стехиометрическая матрица схемы (24) имеет вид

этих фрагментов. Вычислим коэффициенты сплай-

A = (1 -2 0 0 0 0 0 0 0; 0 1 -1 0 1 -1 0 0 0; 0 -1 0

нов (5), (6) по каждому реагенту, концентрации (7)

0 0 0 0 1 -1; 0 0 0 0 1 1 -1 -1 0; 0 1 1 -1 0 0 0 0 0),

реагентов (A₁, D₁, F₁, G₁, E₁) и (A₂, D₂, F₂, G₂, E₁) и

K = 5 и N_s = 4. Выберем четыре независимых линей-

скорости (8) A₁′, D₁′, F₁′, G₁′, E₁ и A₂′, D₂′, F₂′, G₂′, E₂

1480

Кольцов Н. И.

в этих двух точках. Подставим эти значения в (26) и

Результаты решения этой системы при разном

получим линейную систему уравнений для определе-

уровне шума и положении n₂ = 3 опорной точки t₂*

ния констант скоростей стадий

приведены в табл. 3.

Решениями обратной задачи являются интерва-

A₁′ = -k₁A₁ + k_-1B₁₂, D₁′ = k₊₅B₁C₁ - k_-5D₁,

лы k₊₁ ∈ [0.0571, 0.2801], k_-1 ∈ [0.0746, 0.4178],

F₁′ = k₊₃F₁ + k_-3B₁G₁ + k₊₄E₁I₁ - k_-4J₁F₁,

k₊₂ ∈ [0.0015, 0.0016], k_-2 ∈ [0.0003, 0.0003],

G₁′ = k₊₃F₁ - k_-3B₁G₁,

k₊₃ ∈ [0.0013, 0.0017], k_-3 ∈ [0.0004, 0.0005],

k₊₄ ∈ [0.0042, 0.0042], k_-4 ∈ [0.0024, 0.0024],

E₁′ = -k₊₂B₁E₁ + k_-2C₁I₁ - k₊₄E₁I₁ + k_-4J₁F₁,

(27)

k₊₅ ∈ [0.0555, 0.0586], k_-5 ∈ [0.0100, 0.0105]

A₂′ = -k₁A₂ + k_-1B₂₂, D₂′ = k₊₅B₂C₂ - k_-5D₂,

(табл. 3), которые близки к интервалам их изменений

F₂′ = k₊₃F₂ + k_-3B₂G₂ + k₊₄E₂I₂ - k_-4J₂F₂,

[3, 4]: k₊₁ ∈ [0.0248, 0.0737], k_-1 ∈ [0.0735, 0.2537],

G₂′ = k₊₃F₂ - k_-3B₂G₂,

k₊₂ ∈ [0.0007, 0.0027], k_-2 ∈ [0, 0], k₊₃ ∈ [0, 0.0535],

E₂′ = -k₊₂B₂E₂ + k_-2C₂I₂ - k₊₄E₂I₂ + k_-4J₂F₂,

k-3 ∈ [0, 0], k+4 ∈ [0, 0.0357], k-4 ∈ [0, 0], k+5 ∈ [0.0720,

0.3130], k_-5 ∈ [0.0238, 0.1115]. Иллюстрация динами-

где J₁ = F₁ + G₁, C₁ = 1 - D₁ - E₁ - J₁, I₁ = 1 - E₁ - 2J₁,

ки концентраций ключевых реагентов для опорной

B₁ = 3 - 2A₁ - D₁ - I₁ - F₁, J₂ = F₂ + G₂, C₂ = 1 - D₂ -

точки n₂ = 3 приведена на рис. 3.

– E₂ - J₂, I₂ = 1 - E₂ - 2J₂, B₂ = 3 - 2A₂ - D₂ - I₂ - F₂.

Таблица 3

Константы скоростей стадий реакции гидроалюминирования диизобутилалюминийхлорида с учетом шума

Среднеквадратичные отклоне-

Константы скоростей стадий

ния, %

Шум

по

конcтант

S, %

k₊₁

k_-1

k₊₂

k_-2

k₊₃

k_-3

k₊₄

k_-4

k₊₅

k_-5

реагенту

скоростей

A R_A

D R_D

стадий E

0.0571

0.0746

0.0016

0.0003

0.0013

0.0004

0.0042

0.0024

0.0555

0.0100

1.53

2.50

2.08

0.0705

0.0951

0.0016

0.0003

0.0017

0.0004

0.0042

0.0024

0.0562

0.0101

1.51

2.50

2.08

0.0929

0.1297

0.0016

0.0003

0.0017

0.0004

0.0042

0.0024

0.0568

0.0102

1.50

2.49

2.14

0.1385

0.1997

0.0015

0.0003

0.0017

0.0005

0.0042

0.0024

0.0574

0.0103

1.47

2.49

2.48

0.2801

0.4178

0.0015

0.0003

0.0017

0.0005

0.0042

0.0024

0.0580

0.0104

1.45

2.49

4.47

—

0.0015

0.0003

0.0017

0.0005

0.0042

0.0024

0.0586

0.0105

—

Рис. 3. Экспериментальные и расчетные зависимости концентраций исходного вещества (1, 3) и продукта (2, 4)

реакции гидроалюминирования диизобутилалюминийхлорида при уровне шума S = 0 (а) S = 4% (б).

Метод определения констант скоростей стадий химических реакций в закрытом безградиентном реакторе

1481

Выводы

[5]

Aster R. C., Borchers B., Thurber C. H. Parameter

estimation and inverse problems. New York: Elsevier,

Результаты исследования показали, что приведен-

2013. P. 99-132.

ный в статье метод позволяет решать обратные задачи

[6]

Ягола A. Г., Янфей В., Степанова И. Э., Титарен-

химической кинетики для многостадийных реакций

ко В. Н. Обратные задачи и методы их решения.

в закрытом изотермическом реакторе идеального

М.: Бином. Лаборатория знаний, 2014. C. 113-141.

смешения без использования сложных оптимизаци-

[7]

Леонов А. С. Решение некорректно поставленных

онных методов. Получаемые с его помощью оценки

обратных задач: очерк теории, практические ме-

значений констант скоростей стадий характеризуются

тоды и демонстрации в МАТЛАБ. М.: Либроком,

хорошей точностью, а расчетные временные зависи-

2016. C. 148-163.

[8]

Федотов В. Х., Кольцов Н. И. Разработка метода

мости концентраций реагентов близки к эксперимен-

решения обратной задачи химической кинетики

тальным зависимостям, что подтверждено результа-

для каталитических реакций с участием основных

тами применения метода для реакций, исследованных

веществ в каждой стадии // Хим. физика. 2016.

в работах [3, 4]. Таким образом, метод может быть

Т. 35. № 10. С. 9-15.

использован как альтернативный подход к определе-

https://doi.org/10.7868/s0207401x1610006x

нию констант скоростей стадий химических реакций,

[Fedotov V. Kh., Koltsov N. I. Method of solving the

в особенности когда оптимизационные методы не

inverse problem of chemical kinetics for catalytic

позволяют найти приемлемых решений.

reactions in which each step involves main reactants //

Russ. J. Phys. Chem. B. 2016.V. 10. N 5. P. 753-759.

Благодарности

https://doi.org/10.1134/S1990793116050195 ].

[9]

Федотов В. Х., Кольцов Н. И., Гайдай Н. А., Ага-

Автор выражает благодарность за обсуждение

фонов Ю. А., Ботавина М. А., Лапидус А. Л.

результатов работы В. Х. Федотову.

Исследование адсорбции диоксида углерода на

хромоксидном катализаторе по линейному време-

Конфликт интересов

ни релаксации // ЖПХ. 2016. Т. 89. № 5. С. 582-

591 [Fedotov V. Kh., Kol′tsov N. I., Gaidai N. A.,

Автор заявляет об отсутствии конфликта интере-

Agafonov Yu. A., Botavina M. A., Lapidus A. L. Study

сов, требующего раскрытия в данной статье.

of carbon dioxide adsorption on chromium oxide and

gallium oxide catalysts on the basis of linear relaxation

Информация об авторах

times // Russ. J. Appl. Chem. 2016. V. 89. N 5. P. 719-

726. https://doi.org/10.1134/S1070427216050062 ].

Кольцов Николай Иванович, д.х.н., проф.,

[10]

Кольцов Н. И. Исследование адсорбции CO₂ на

ORCID: https://orcid.org/0000-0003-2264-1370

хромоксидном катализаторе по нелинейным вре-

менам релаксации // Изв. вузов. Химия и хим. тех-

Список литературы

нология. 2018. Т. 61. № 2. С. 46-52.

[1] Tarantola A. Inverse problem theory and methods for

https://doi.org/10.6060/tcct.20186102.5584

model parameter estimation. SIAM: Philadelphia, 2005.

[11]

Федотов В. Х., Кольцов Н. И. Исследование

P. 24-40.

адсорбции CO₂ на хромоксидном катализаторе

[2] Кольцов Н. И. Математическое моделирование ка-

по нестационарным концентрациям // Изв. вузов.

талитических реакций. Чебоксары: Изд-во Чуваш.

Химия и хим. технология. 2018. Т. 61. № 7. С. 37-

ун-та, 2007. C. 112-116.

43. https://doi.org/10.6060/ivkkt.20186107.5714

[3] Parfenova L. V., Vil′danova R. F., Pechatkina S. V.,

[12]

Бесков В. С. Общая химическая технология. М.:

Khalilov L. M., Dzhemilev U. M. Zr,Al-Complexes

Академкнига, 2005. C. 154-177.

as new reagents for olefin hydrometallation // J.

[13]

Быков В. И., Цыбенова С. Б. Нелинейные модели

Organomet. Chem. 2007. V. 692. N 16. P. 3424-3429.

химической кинетики. М.: URSS, 2011. C. 83-92.

https://doi.org/10.1016/j.jorganchem.2007.04.007

[14]

Вержбицкий В. М. Численные методы (математи-

[4] Исмагилова А. С., Спивак С. И. Обратные задачи

ческий анализ и обыкновенные дифференциаль-

химической кинетики. Saarbrucken: Lap Lambert

ные уравнения). М.: Изд. дом «ОНИКС 21 век»,

Acad. Publ., 2013. P. 91-110.

2005. С. 121-155.