Журнал прикладной химии. 2022. Т. 95. Вып. 2

ФИЗИКО-ХИМИЧЕСКИЕ ИССЛЕДОВАНИЯ СИСТЕМ И ПРОЦЕССОВ

УДК 621.928.37

МОДЕЛИРОВАНИЕ ДЕГАЗАЦИИ ВЯЗКОПЛАСТИЧЕСКИХ ЖИДКОСТЕЙ

В ЦИЛИНДРИЧЕСКОМ ГИДРОЦИКЛОНЕ*

Волгоградский государственный технический университет,

400005, г. Волгоград, пр. им. В. И. Ленина, д. 28

E-mail: everest58@mail.ru

Поступила в Редакцию 29 августа 2020 г.

После доработки 1 марта 2022 г.

Принята к публикации 13 марта 2022 г.

Разработана математическая модель дегазации вязкопластических жидкостей в цилиндрическом

гидроциклоне, учитывающая действие сил инерции, сил Кориолиса и присоединенную массу жидкости.

Система дифференциальных уравнений в частных производных, описывающая процесс дегазации,

сведена к системе обыкновенных дифференциальных уравнений и решена численным методом. На

основе разработанной математической модели проанализировано влияние числа пластичности при

различных значениях фактора разделения и показателя нелинейности кривой течения на степень

извлечения пузырьков газа. Приведено физическое обоснование полученных результатов, которые

могут быть использованы при разработке оборудования для очистки буровых растворов и дегазации

нефти при подготовке к транспортировке.

Ключевые слова: вязкопластическая жидкость; предел текучести; дегазация; цилиндрический гидро-

циклон; число пластичности; фактор разделения; показатель нелинейности; индекс консистентно-

сти; степень извлечения

DOI: 10.31857/S0044461822020050, EDN: DEETWB

Бурение скважин в нефтедобывающей промыш-

чем меньше содержится газа в жидкости, тем лучше

ленности сопровождается обогащением промывоч-

справляется сепаратор со своей задачей.

ной жидкости воздухом или газом, что приводит к

Применяемые в настоящее время гравитационные

резкому изменению ее плотности, реологических и

сепараторы** не обеспечивают высокой степени де-

структурно-механических свойств. При этом ухуд-

газации из-за низкой скорости движения газа, что в

шается работа насосов и уменьшается их подача,

сочетании с высокой металлоемкостью и потребно-

поэтому своевременная и эффективная дегазация

стью в значительных производственных площадях

промывочных жидкостей является важным условием

делает их применение во многих случаях нерацио-

обеспечения нормального процесса бурения.

нальным. Поэтому разработка новых конструкций

Основной показатель, на значения которого сле-

сепараторов и теоретическое изучение процесса

дует ориентироваться при выборе сепаратора для

дегазации с целью повышения его эффективности

промывочных жидкостей, — остаточный объем газа:

** Аксенова Н. А., Рожкова О. В. Буровые промывоч-

* Научное редактирование проведено научным редак- ные жидкости и промывка скважин. Учебное пособие.

тором журнала «Нефтехимия» к.х.н. Н. В. Шелеминой.

В 3 т. Т. 3. Тюмень: Изд-во ТИУ, 2016. 120 с.

246

Моделирование дегазации вязкопластических жидкостей в цилиндрическом гидроциклоне

247

является актуальной задачей, представляет научный

среды на эффективность процесса дегазации при раз-

интерес и направлена на решение важной практиче-

личных значениях числа Фруда (фактора разделения)

ской проблемы.

и различных реологических свойствах разделяемой

В работах [1, 2] на основе математической модели

среды.

численно исследован процесс дегазации в гидроци-

клоне. Показана возможность применения метода

Численное моделирование

гидроциклонирования для удаления воздушной фазы

из жидкости, однако полученные результаты при-

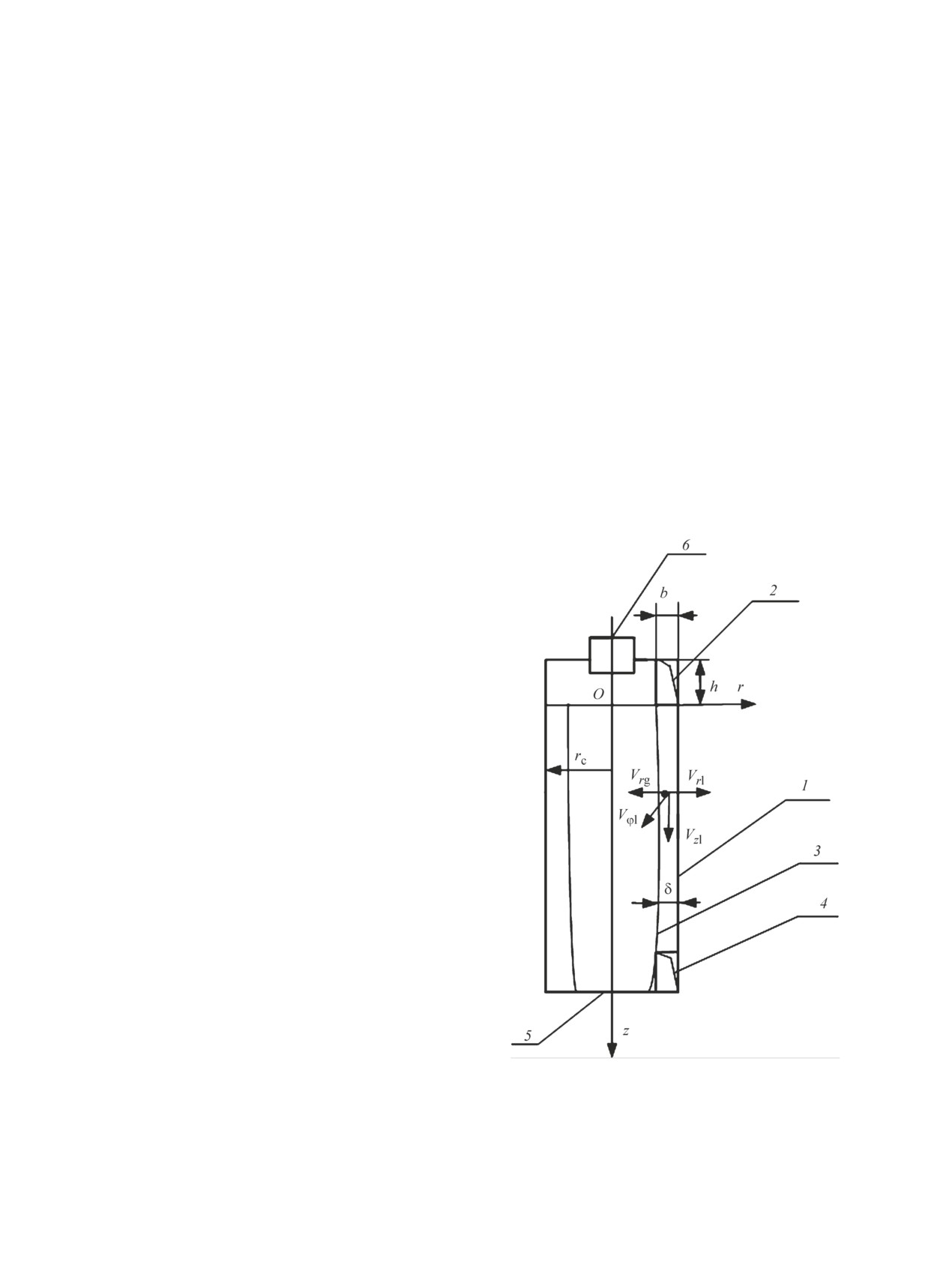
Гидроциклон (рис. 1) состоит из цилиндрическо-

менимы лишь для дегазации турбулентного потока

го корпуса 1, в который через входной патрубок 2,

ньютоновской жидкости в цилиндроконическом ги-

установленный в его верхней части, тангенциально

дроциклоне, имеющем невысокую эффективность в

подается исследуемая жидкость, содержащая вы-

процессах дегазации.

делившиеся из нее пузырьки газа. Поступившая в

В работе [3] рассмотрен процесс дегазации аэри-

корпус гидроциклона жидкость стекает, образуя вра-

рованной жидкости с неньютоновской дисперсион-

щающуюся пленку 3 толщиной δ, по его стенкам

ной средой и отмечается, что наиболее перспектив-

вниз, обладая радиальной V_r, окружной V_φ и осевой V_z

ным путем интенсификации процессов дегазации

составлющими скорости. Пузырьки газа извлекаются

аэрированных жидкостей является соединение двух

из жидкости под действием центростремительной

известных факторов — реализации процесса в тонкой

силы Архимеда на поверхность пленки. Очищенная

пленке и наложения центробежного поля. Разработка

методики моделирования и расчета аппаратов для

осуществления таких процессов представляет зна-

чительный теоретический и прикладной интерес,

что позволит расширить сферу их внедрения в про-

мышленность.

Как отмечается в [4], наиболее экономичными

методами дегазации являются механические. Один

из перспективных механических методов — дегаза-

ция в центробежном поле, а именно в центрифугах и

гидроциклонах.

В статье [5] выполнено численное моделирование

гидродинамики цилиндрического гидроциклона с

вязкопластической разделяемой средой. Полученные

результаты показали, что одним из аппаратов, позво-

ляющих интенсифицировать процесс дегазации за

счет использования центробежного поля в сочетании

с пленочным режимом течения, является цилиндри-

ческий гидроциклон, обеспечивающий минимальную

толщину пленки жидкости и имеющий сравнительно

небольшие габаритные размеры.

В связи с этим актуальной задачей является раз-

работка конструкции гидроциклонного сепаратора,

использующего интенсификацию процесса выделе-

ния пузырьков газа из жидкости в центробежном поле

и обеспечивающего пленочный режим течения. Для

эффективного использования цилиндрического ги-

дроциклона в процессе дегазации бурового раствора

необходимо определить его конструктивные параме-

Рис. 1. Схема дегазации жидкости в цилиндрическом

тры и оптимальные режимы работы при дегазации

гидроциклоне.

среды с различными реологическими свойствами.

1 — корпус гидроциклона, 2 — входной патрубок, 3 —

Цель работы — моделирование дегазации вязко-

вращающаяся пленка жидкости, 4 — патрубок для отвода

пластической жидкости в цилиндрическом гидроци-

жидкой фазы, 5 — днище гидроциклона, 6 — патрубок

клоне и выявление влияния пластических свойств

для отвода газа.

248

Яблонский В. О.

от пузырьков газа жидкость удаляется через нижний

деформаций, что оказывает влияние на гидродина-

слив гидроциклона 4, установленный на днище 5,

мику аппаратов.

а газ — через верхний отводящий патрубок 6.

В работе [6] сделано заключение, что к многофаз-

Эффективность дегазации в гидроциклоне опре-

ным гетерогенным системам применимо реологиче-

деляется гидродинамическими параметрами предва-

ское уравнение состояния неньютоновской жидкости,

рительно закрученной пленки жидкости, стекающей

которое для процессов очистки буровых растворов за-

по стенкам корпуса под действием силы тяжести и

писывают в виде закона Гершеля-Балкли. Полагаем,

давления, создаваемого центробежной силой.

что этим законом [7] описываются свойства нелиней-

Перерабатываемые в нефтедобывающей промыш-

но-вязкопластической жидкости.

ленности жидкости, в частности буровые растворы,

Реологическое уравнение состояния Гершеля-

во многих случаях обладают нелинейно-вязкопла-

Балкли для трехмерного течения с учетом условия

стическими свойствами. Такие жидкости имеют пре-

пластичности фон Мизеса, записанное через компо-

дел текучести, и их эффективная вязкость умень-

ненты тензора скоростей деформаций в цилиндриче-

шается с увеличением интенсивности скоростей

ской системе координат, имеет вид

τ_ij =

+ kAn-1 γ_ij,

(1)

A =

где τi,j — компоненты тензора напряжений (Па);

эффективной вязкостью, режим течения и режим

τ₀ — предельное напряжение сдвига (Па); γi,j — ком-

всплывания пузырьков газа ламинарный [8]; ростом

поненты тензора скоростей деформаций (с^-1); A —

пузырька газа за счет изменения давления в плен-

интенсивность скоростей деформаций (с^-1); n — по-

ке жидкости и массопередачи можно пренебречь.

казатель нелинейности кривой течения; k — индекс

Полагаем, что пузырьки являются монодисперсными,

консистентности (Па∙сⁿ); r, z — радиальная и осевая

что при моделировании процесса дегазации для пу-

координаты (м); φ — окружная координата (рад).

зырьков наиболее мелкой фракции позволит добиться

При n = 1 уравнение (1) переходит в уравнение

заданной степени их извлечения.

Шведова-Бингама для вязкопластической среды,

При разработке модели дегазации вязкопласти-

при τ₀ = 0 — в уравнение Оствальда-де Виля для

ческой жидкости в гидроциклоне необходимо учи-

псевдопластической жидкости, при n = 1 и τ₀ = 0 —

тывать силы инерции, действующие на пузырек газа

в уравнение Ньютона-Петрова для ньютоновской

и присоединенную массу жидкости в радиальном

жидкости.

направлении, которые являются существенными при

Математическая постановка задачи производится

высоких значениях числа Фруда. При условии дей-

при следующих допущениях: в корпус гидроциклона

ствия на пузырек газа и присоединенную массу жид-

подается вязкопластическая жидкость, насыщенная

кости центростремительной силы Архимеда, силы

равномерно распределенными в ней пузырьками вы-

сопротивления и кориолисовой силы с учетом того,

делившегося газа, объемная доля которых на входе

что масса газа в объеме пузырька пренебрежимо ма-

в гидроциклон равна c_g0; для пленочного течения

ла, уравнение движения пузырька газа в проекциях

вязкопластической жидкости, обладающей высокой

на оси r, φ имеет вид

(2)

где Vrg(r, z), Vzg(r, z), V_φg(r, z) — радиальная, осевая

новской жидкости в радиальном и окружном направ-

и окружная составляющие скорости пузырька газа

лениях, определяемые как для твердой сферы [9] при

(м·с^-1); Vrl(r, z) и V_φl(r, z) — радиальная и окружная

условии полной заторможенности адсорбционным

составляющие скорости жидкости (м·с^-1); d_g — ди-

слоем ПАВ поверхности пузырька [10] и всплывании

аметр пузырька газа (м); K_fr, Kfφ — коэффициенты

пузырька при малых значениях числа Рейнольдса

сопротивления движению пузырька газа в неньюто-

Reng < 1 по следующим зависимостям:

Моделирование дегазации вязкопластических жидкостей в цилиндрическом гидроциклоне

249

Поскольку скорость пузырьков газа отлична от

K_fr =

(3)

скорости неразрывного потока дисперсионной среды,

где

divV_g =

f₁(n) = 31.5(n-1)

;

уравнение (6) принимает вид

(7)

f₂(n) = 10.5n - 3.5; f₃(n) = 0.32n = 0.13;

Уравнение (7) решалось совместно с уравнени-

ями (2), описывающими движение пузырька газа.

Reng =

— локальное число Рей-

Дифференциальные уравнения в частных произво-

нольдса, характеризующее режим всплывания пу-

дных (2) и (7) сводятся в соответствии с методом

зырька газа; n — показатель нелинейности кривой

характеристик [12] к системе обыкновенных диффе-

течения; k — индекс консистентности (Па·сⁿ); ρ_l —

ренциальных уравнений, одно из которых описывает

плотность жидкости (кг·м^-3).

траекторию пузырька газа, а другое — изменение

Индекс консистентности k рассчитывался как эф-

объемной доли пузырьков газа на траектории. В ре-

фективная вязкость псевдопластической жидкости

зультате была получена система уравнений в безраз-

согласно реологическому уравнению (1) с учетом

мерном виде:

наличия у разделяемой среды предельного напряже-

ния сдвига τ₀.

Коэффициент сопротивления при окружном дви-

жении пузырька газа Kfφ вычисляли по аналогичным

зависимостям, но в качестве характерной разности

скоростей принимали соответствующую разность

(8)

скоростей пузырька газа и жидкости в окружном

направлении.

Ф — коэффициент, учитывающий стесненность

движения пузырьков газа, определяемый по формуле

Бреннера [10]:

где G_g(R, Z) =

, H_g(R, Z) =

, Θ_g(R, Z) =

Φ(с) =

(4)

— безразмерные радиальная, осевая и

где c_g — объемная доля пузырьков газа (м³·м^-3).

окружная составляющие скорости пузырьков газа;

Для математического моделирования поля концен-

G_l(R, Z) =

, H_l(R, Z) =

, Θ_l(R, Z) =

траций при дегазации вязкопластической жидкости

в цилиндрическом гидроциклоне использовалось

— безразмерные радиальная, осевая и

дифференциальное уравнение конвективной диф-

фузии в цилиндрических координатах [11], которое

окружная составляющие скорости жидкости; C_g =

при отсутствии молекулярной диффузии может быть

— безразмерная объемная доля пузырьков газа;

записано для объемной доли пузырьков газа следую-

щим образом:

D_g =

— безразмерный диаметр пузырька газа;

div(V_gc_g) = 0,

(5)

R =

; Z =

— безразмерные радиальная и осе-

где V_g — вектор скорости пузырьков газа, c_g — объ-

вая координаты; U₀ — средняя скорость жидкости

емная доля пузырьков газа (м³·м^-3).

во входном патрубке гидроциклона (м·с^-1); c_g0 —

Уравнение (5) может быть преобразовано к виду

объемная доля пузырьков газа во входном патрубке

гидроциклона (м³·м^-3); r_c — радиус корпуса гидро-

V_ggradc_g + c_gdivV_g = 0.

(6)

циклона (м).

250

Яблонский В. О.

Система обыкновенных дифференциальных урав-

ная степень извлечения пузырьков газа S [13], пред-

нений (8) решалась в проекциях на оси координат

ставляющая собой для процесса дегазации среднюю

методом Рунге-Кутта с фиксированным шагом по

безразмерную объемную долю пузырьков газа, извле-

программе, составленной на языке Compaq Vizual

ченных из жидкости в данном сечении пленки (при

Fortran, применительно к геометрии рабочего про-

Z = const), вычисляемая по формуле

странства цилиндрического гидроциклона при гра-

ничном условии

S = 1 -

(10)

Z = 0, R_c - B ≤ R ≤ R_c, C_g = C_g0,

(9)

где R_c — безразмерный радиус корпуса гидроцикло-

где С_g0 — безразмерная объемная доля пузырьков га-

на, B =

— безразмерная ширина входного патрубка,

за во входном патрубке гидроциклона, Δ(Z) =

—

b — ширина входного патрубка (м); C_g0 — безраз-

безразмерная толщина пленки жидкости, δ(z) — тол-

мерная объемная доля пузырьков газа во входном

щина пленки жидкости (м).

патрубке гидроциклона.

На основании результатов моделирования полей

составляющих скорости и давления при течении

Обсуждение результатов

нелинейно-вязкопластической жидкости в цилин-

Результаты численного моделирования приведены

дрическом гидроциклоне [5] и последующей ап-

на рис. 2, 3.

проксимации расчетных данных было выполнено

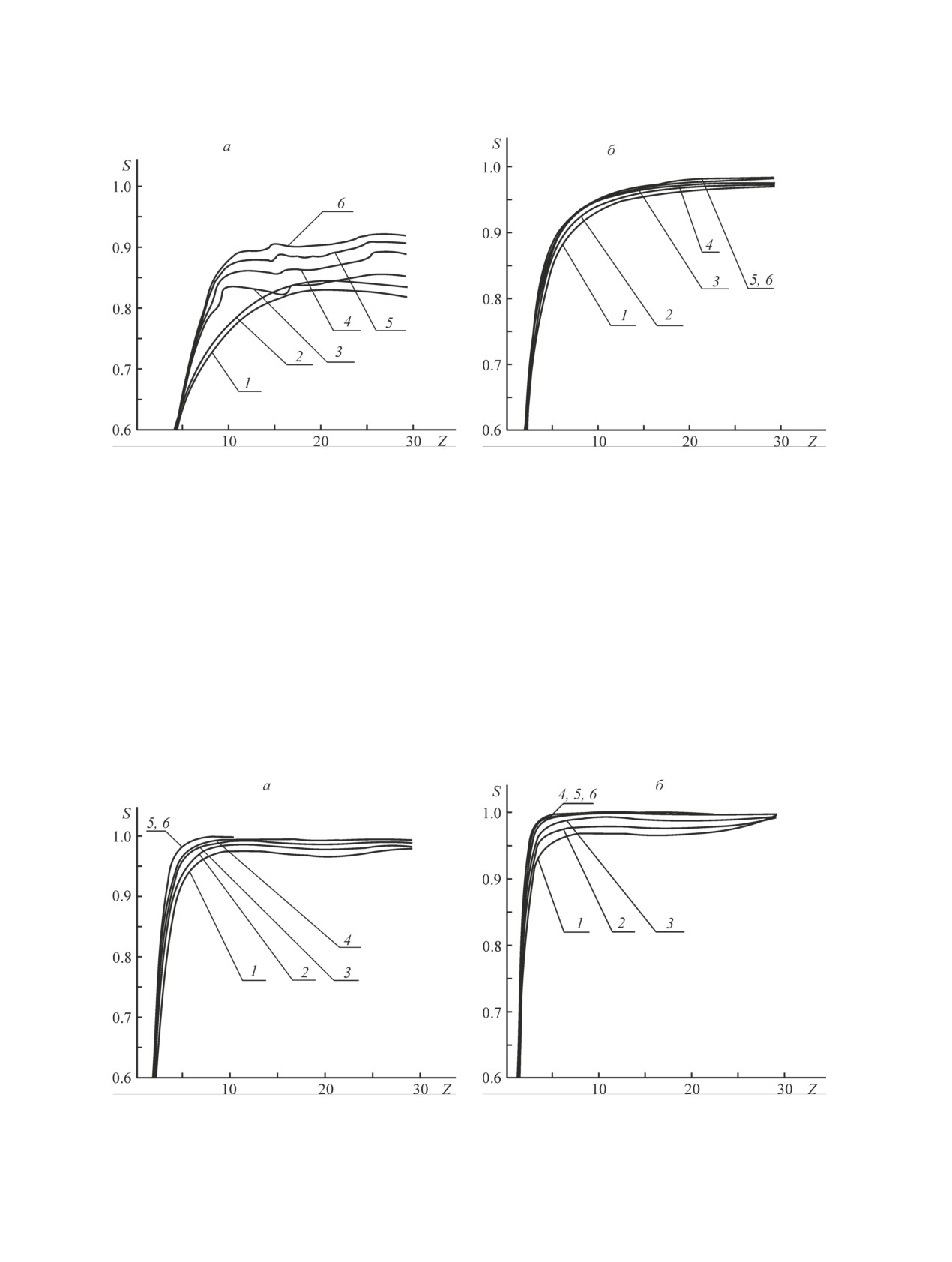
На рис. 2, а, б приведены зависимости степени

моделирование процесса дегазации нелинейно-вяз-

извлечения S пузырьков газа в цилиндрическом ги-

копластической жидкости в гидроциклоне, которое

дроциклоне от безразмерной осевой координаты

заключалось в численном решении полученной си-

Z при различных значениях числа Pl для значений

стемы дифференциальных уравнений при граничном

Fr = 20, k = 0.3132 Па·сⁿ (а) и Fr = 30, k = 0.3836 Па·сⁿ

условии (9) для различных значений определяющих

(б); Re_n = 4·10³; Q₀ = 2.0·10^-2; n = 1.0 (ньютонов-

чисел подобия и реологических констант диспер-

ская жидкость при Pl = 0 и вязкопластическая среда

сионной среды при изменении их в широком диапа-

Шведова-Бингама при Pl > 0). Из представленных

зоне.

зависимостей следует, что степень извлечения пу-

Течение нелинейно-вязкопластической жидкости

зырьков газа возрастает с увеличением осевой коор-

в цилиндрическом гидроциклоне характеризуется

динаты Z, что обусловлено выходом пузырьков газа

[5] числом пластичности Pl, характеризующим от-

на поверхность пленки жидкости. С увеличением

ношение сил пластичности к силам инерции, цен-

числа Pl (что соответствует повышению предельного

тробежным числом Фруда Fr (фактором разделения),

напряжения сдвига τ₀) степень извлечения пузырьков

модифицированным числом Рейнольдса Re_n и пара-

газа существенно увеличивается. Это объясняется

метром безразмерного расхода Q₀. Числа подобия

уменьшением толщины пленки жидкости, увеличени-

определялись следующим образом:

ем окружной составляющей скорости пузырьков газа

и, как следствие, возрастанием действующей на них

PL =

Fr =

Re_n =

Q₀ =

центростремительной силы Архимеда [5]. Сравнивая

рис. 2, а и рис. 2, б, можно установить, что увеличе-

где h — высота входного патрубка гидроциклона (м).

ние числа Fr также сопровождается ростом степени

Реологические свойства среды характеризуются

извлечения пузырьков газа S вследствие роста их

предельным напряжением сдвига τ₀ (которое входит

окружной составляющей скорости. Таким образом,

в число пластичности Pl), показателем нелинейности

наибольшая эффективность процесса дегазации на-

кривой течения n и индексом консистентности k.

блюдается для высоких значений чисел Pl и Fr.

Всплывание пузырька газа в поле центростремитель-

На рис. 3, а, б приведены те же зависимости, что

ной силы Архимеда в нелинейно-вязкопластической

и на рис. 2, для значений Fr = 20 и n = 0.6 (рис. 3, а)

дисперсионной среде характеризуется локальным

и Fr = 30 и n = 0.6 (рис. 3, б) (нелинейно-вязкопла-

числом Reng [13], изменяющимся вдоль траектории

стическая среда Гершеля-Балкли) для тех же зна-

пузырька.

чений определяющих параметров. Из представлен-

Показателем эффективности протекания процесса

ных зависимостей следует, что степень извлечения

дегазации в гидроциклоне является среднеинтеграль-

пузырьков газа S возрастает с увеличением осевой

Моделирование дегазации вязкопластических жидкостей в цилиндрическом гидроциклоне

251

Рис. 2. Зависимости степени извлечения S пузырьков газа в цилиндрическом гидроциклоне от осевой координаты

Z при различных значениях числа Pl.

а — Fr = 20, k = 0.3132 Па·сⁿ; б — Fr = 30, k = 0.3836 Па·сⁿ; Re_n = 4·10³; Q₀ = 2.0·10^-2; n = 1.0.

Pl: 1 — 0, 2 — 2.548·10^-3, 3 — 5.097·10^-3, 4 — 7.645·10^-3, 5 — 1.019·10^-2, 6 — 1.274·10^-2.

координаты Z при n = 0.6 более интенсивно, чем при

пузырьков газа S возрастает с увеличением числа пла-

n = 1.0, особенно при высоких значениях числа Pl,

стичности Pl вследствие уменьшения толщины пленки

когда толщина пленки жидкости минимальна [5]. С

жидкости [5], особенно при высоких значениях числа

ростом числа Pl степень извлечения пузырьков газа

Fr. Это является следствием возрастания степени вы-

возрастает до более высоких значений, чем для жидко-

раженности аномалии неньютоновских свойств разде-

сти Шведова-Бингама (рис. 2), и влияние числа Pl для

ляемой среды с увеличением числа пластичности Pl,

среды Гершеля-Балкли при меньшей толщине пленки

уменьшения толщины пленки жидкости и повышения

жидкости [5] сильнее. Из сравнения зависимостей на

степени наполненности радиального распределе-

рис. 3, а и рис. 3, б следует, что степень извлечения

ния окружной составляющей скорости V_φl(r, z) [5].

Рис. 3. Зависимости степени извлечения S пузырьков газа в цилиндрическом гидроциклоне от осевой координаты Z

при различных значениях числа Pl.

а — Fr = 20, k = 1.242 Па·сⁿ; б — Fr = 30, k = 1.650 Па·сⁿ; Re_n = 4·10³; Q₀ = 2.0·10^-2, n = 0.6.

Pl: 1 — 0, 2 — 2.548·10^-3, 3 — 5.097·10^-3, 4 — 7.645·10^-3, 5 — 1.019·10^-2, 6 — 1.274·10^-2.

252

Яблонский В. О.

С ростом числа Fr степень извлечения пузырь-

Список литературы

ков газа также возрастает вследствие увеличения

[1]

Варавва А. И., Вершинин В. Е., Трапезников Д. В.

действующей на них центростремительной силы

Численное моделирование процесса дегаза-

Архимеда [5]. Следовательно, при дегазации нели-

ции газожидкостной смеси в гидроциклоне

нейно-вязкопластических сред и высоких значениях

// Вестн. Тюмен. гос. ун-та. Физ.-мат. моде-

фактора разделения высота корпуса цилиндрического

лирование. Нефть, газ, энергетика. 2019. Т. 5.

гидроциклона может быть уменьшена.

№ 3. С. 213-229. https://elibrary.ru/download/

elibrary_41430031_62471749.pdf

[2]

Матвиенко О. В., Агафонцева М. В. Численное

Выводы

исследование процесса дегазации в гидроциклонах

// Вестн. Том. гос. ун-та. 2012. № 12. С.107-118.

1. С использованием разработанной математиче-

https://www.elibrary.ru/item.asp?id=18396385

ской модели дегазации вязкопластических жидко-

[3]

Щукина А. Г. Математическое моделирование про-

стей в цилиндрическом гидроциклоне установлено

цессов разделения неоднородных систем с ненью-

влияние числа пластичности, фактора разделения и

тоновской дисперсионной средой: Автореф. канд.

реологических свойств среды на процесс дегазации.

дис. Волгоград, 1996. 16 с.

2. Показано, что наибольшая эффективность про-

[4]

Терновский И. Г., Кутепов А. М. Гидроциклониро-

цесса дегазации наблюдается для нелинейно-вяз-

вание. М.: Наука, 1994. 350 с.

копластических жидкостей при высоких значениях

[5]

Яблонский В. О. Гидродинамика нелинейно-вязко-

чисел Pl и Fr. Эффективность процесса дегазации

пластической жидкости в цилиндрическом гидро-

циклоне // ЖПХ. 2013. Т. 86. № 8. С. 1236-1243.

возрастает с увеличением аномалии неньютоновских

https://www.elibrary.ru/item.asp?id=23200479

свойств среды, что соответствует уменьшению пока-

[Yablonskii V. O. Hydrodynamics of nonlinear

зателя нелинейности кривой течения n. Влияние чи-

viscoplastic fluid in cylindrical hydrocyclone // Russ.

сел Pl и Fr с увеличением аномалии неньютоновских

J. Appl. Chem. 2013. V. 86. N 8. P. 1212-1219.

свойств среды усиливается.

https://doi.org/ 10.1134/S1070427213080107 ].

3. Полученные результаты могут быть использо-

[6]

Вайнштейн И. А. Об уравнениях кинетики разделе-

ваны для разработки методики инженерного расчeта

ния суспензий // Инж.-физ. журн. 1983. Т. 45. № 4.

гидроциклонов для дегазации вязкопластических

С. 602-608.

сред, в частности, при разработке оборудования для

[7]

Левич В. Г. // Физико-химическая гидродинамика.

дегазации буровых растворов в нефтедобывающей

М.; Ижевск: Изд-во «ИКИ», 2016. C. 66-69.

промышленности.

[8]

Dyakowski T., Hornung G., Williams R. A. Simulation

of non-newtonian flow in a hydrocyclone // Chem.

Eng. Res. Des. A. 1994. V. 72. N 4. P. 513-520.

Благодарности

[9]

Acharya A., Mashelkar R. A., Ulbrecht J. Flow of

inelastic and viscoelastic fluids past a sphere // Rheol.

Автор выражает благодарность научному консуль-

Acta. 1976. V. 15. N 9. P. 454-463.

танту профессору Волгоградского государственного

[10]

Дерягин Б. В., Духин С. С., Рулев Н. Н. Микро-

технического университета д.т.н. Г. В. Рябчуку за по-

флотация: Водоочистка, обогащение. М.: Химия,

мощь в разработке теоретических аспектов процессов

1986. 112 с.

разделения и очистки неоднородных жидких систем

[11]

Берд Р. Б., Стьюарт В. Е., Лайтфут Е. Н. Явления

в центробежном поле и ценные советы.

переноса. М.: Химия, 1974. 687 с. [Bird R. B., Stewart

W. E., Lightfoot E. N. Transport Phenomena. Second

Rev. Ed. New York; London: J. Wiley, 1965. 920 p.].

Конфликт интересов

[12]

Матвеев Н. М. Дифференциальные уравнения. М.:

Автор заявляет об отсутствии конфликта интере-

Просвещение, 1988. 261 с.

сов, требующего раскрытия в данной статье.

[13]

Яблонский В. О. Влияние конструктивных параме-

тров гидроциклона на извлечение твердых частиц

суспензии напорной флотацией // Хим. и нефтегаз.

Информация об авторах

машиностроение. 2006. № 3. C. 3-7. URL: http://

www.library.ugatu.ac.ru/pdf/magazins/chma06_no3.

Яблонский Владимир Олегович, к.т.н., доцент кафе-

pdf [Yablonskii V. O. Effect of structural parameters

дры «Процессы и аппараты химических и пищевых

of hydrocyclones on the extraction of solid suspension

производств» Волгоградского государственного тех-

particles by pressurized flotation // Chem. Petrol. Eng.

нического университета,

2006. V. 42, P. 119-127.

ORCID: https://orcid.org/0000-0003-0893-1187

https://doi.org/ 10.1007/s10556-006-0064-7 ].