Журнал прикладной химии. 2022. Т. 95. Вып. 5

ФИЗИКО-ХИМИЧЕСКИЕ ИССЛЕДОВАНИЯ СИСТЕМ И ПРОЦЕССОВ

УДК 544.134

МОДЕЛЬ СТРУКТУРА-СВОЙСТВО

ДЛЯ ПРОГНОЗА ОКТАНОВЫХ ЧИСЕЛ ЦИКЛОАЛКАНОВ

ПО ТОПОЛОГИЧЕСКИМ ХАРАКТЕРИСТИКАМ МОЛЕКУЛ

М. Ф. Мухарметов¹, Р. В. Гарипов^1,*, М. Р. Валеев¹

¹ Уфимский государственный нефтяной технический университет,

450062, г. Уфа, ул. Космонавтов, д. 1

² Башкирский государственный университет,

450076, г. Уфа, ул. Заки Валиди, д. 32

* E-mail: g4ripov.robert@yandex.ru

Поступила в Редакцию 12 ноября 2021 г.

После доработки 13 июля 2022 г.

Принята к публикации 5 августа 2022 г.

Для прогноза октановых чисел алкилзамещенных изомерных углеводородов ряда циклоалканов — ком-

понентов бензинов, являющихся сырьем и продуктами процессов изомеризациии, каталитического

риформинга и каталитического крекинга, предложена нелинейная модель структура-свойство. Мо-

дель связывает октановые числа циклоакланов с топологическими индексами молекулярных графов:

индексом Винера, индексом Рандича и суммой квадратов собственных значений матрицы смежности.

Регрессионные многофакторные модели адекватно описывают октановое число циклоалканов. Сред-

няя относительная погрешность для октанового числа для ряда из 22 соединений составила 2.42 ед.

для исследовательского метода и 2.12 ед. для моторного метода. Предлагаемая модель может быть

использована для прогноза октановых чисел циклоалканов компонентов бензинов.

Ключевые слова: циклоалканы; октановое число; модель структура-свойство; индекс Винера; индекс

Рандича

DOI: 10.31857/S0044461822050139, EDN: DJOBIG

Циклоалканы являются компонентами фракций

является мерой устойчивости топлива к самовоспла-

с температурами кипения н. к.-125°C, которые ис-

менению (детонации). Моторные топлива c высоким

пользуются как сырье для процесса каталитического

ОЧ имеют низкий риск возникновения детонации

риформинга. Содержание циклоалканов в бензинах

двигателя, что позволяет достигать высокого сжатия

каталитического риформинга варьируется в пределах

и, следовательно, более высокой эффективности дви-

10-15%, и, по причине невысокого октанового числа

гателя [2].

циклоалканов, знание октановых чисел этого класса

Октановое число бензина, используемого в дви-

углеводородов необходимо для прогноза качества

гателе внутреннего сгорания, определяется путем

различных бензинов [1].

сравнения со смесью 2,2,4-триметилпентана и

Детонационная стойкость моторных топлив, тра-

н-гептана, которая характеризуется такой же дето-

диционно выражающаяся октановым числом (ОЧ), национной стойкостью, что и тестируемое моторное

666

Модель структура-свойство для прогноза октановых чисел циклоалканов по топологическим характеристикам молекул

667

топливо. Наиболее распространенными методами

Для характеристики разветвленности молекул ис-

измерения ОЧ являются моторный* и исследователь-

пользуется индекс Рандича, который характеризует

ский** [3].

разветвленность углеродного скелета и различается

Детонационная стойкость бензинов зависит от

для изомеров углеводородов (индекс молекулярной

их химического состава и структуры индивидуаль-

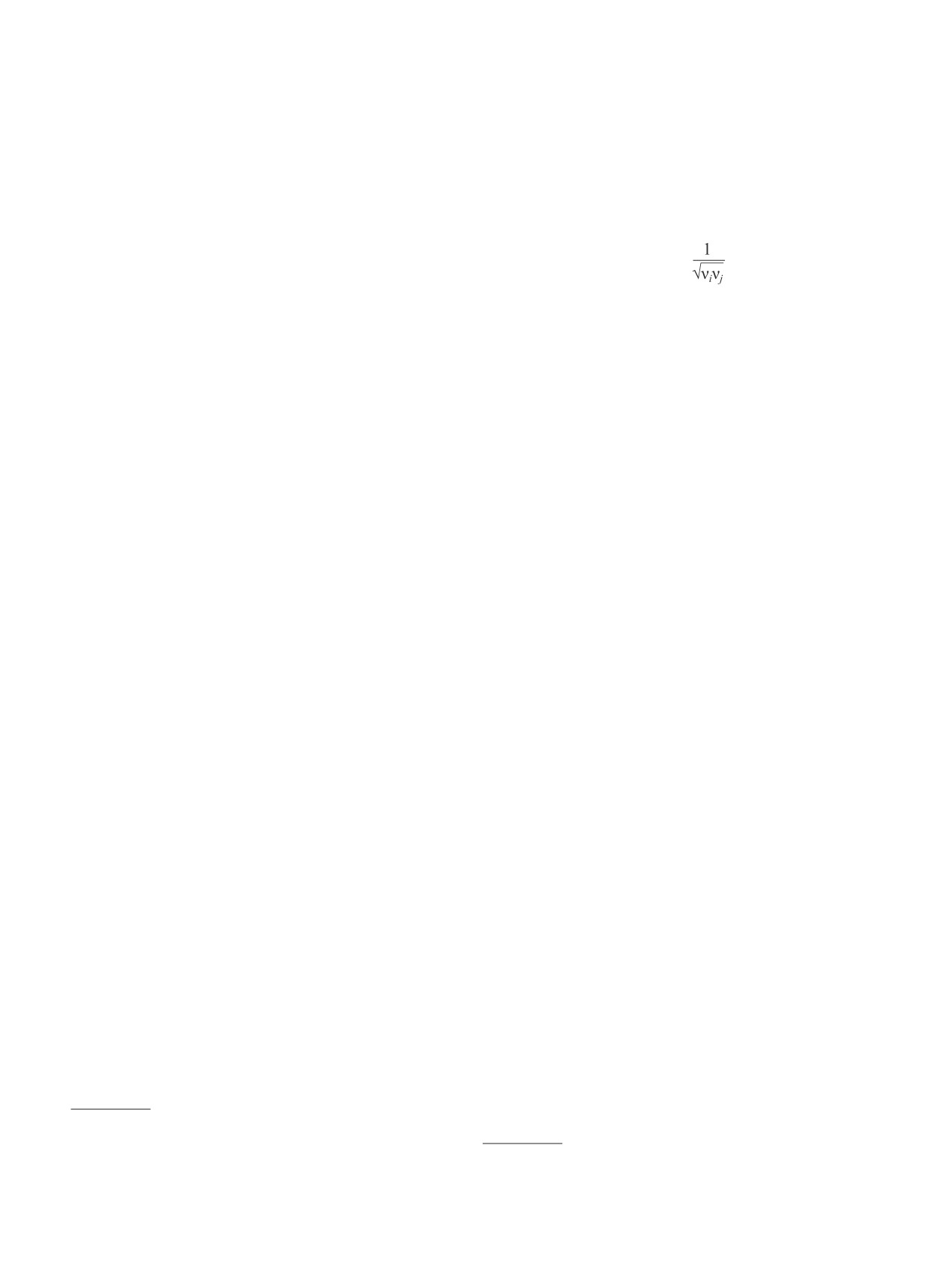
связности). Он вычисляется по формуле

ных молекул. Известно, что углеводороды, имею-

щие разветвленную и циклическую структуру, бо-

ρ =

∑

(3)

по всем

лее устойчивы к самовоспламенению по сравнению

ребрам

с углеводородами, имеющими линейную структу-

ру [4].

где ν_i — число ребер графа, отходящих от i-той вер-

Для выражения в математической форме хими-

шины; ν_j — число ребер графа, отходящих от j-той

ческой структуры вещества широко используются

вершины.

молекулярные дескрипторы (топологические ин-

Исходя из изложенного, рассмотрим полуэмпири-

дексы). Рассчитанные молекулярные дескрипторы

ческую модель в виде функции (4):

применяются в моделях структура-свойство и струк-

q = a₀ + a₁W + a₂L + a₃ρ + a₄WL + a₅Lρ + a₆Wρ,

(4)

тура-активность, которые позволяют эффективно

оценить свойства молекул без необходимости экс-

где q — ОЧ; а_n (n = 0, …, 6) — коэффициенты модели,

периментального определения. Разработаны группы

полученные методом наименьших квадратов.

моделей [5-8], использующие топологические индек-

В качестве объектов исследования рассмотрены

сы молекул для прогнозирования ОЧ углеводородов

22 углеводорода ряда циклоалканов, которые входят

ряда алканов, алкенов и циклоалканов. Несмотря на

в состав бензинов. Информация по ОЧ выбиралась

высокую эффективность таких моделей, в случае с

из базы данных.*** Отбор углеводородов в базо-

циклоалканами погрешности значительны.

вую и тестовую выборки проводился случайным об-

Цель исследования — разработка нелинейной

разом.

модели структура-свойство для прогноза ОЧ за-

Был проведен расчет индексов Винера, Рандича,

мещенных и изомерных углеводородов ряда цикло-

суммы квадратов собственных значений матрицы

алканов.

смежности для исследуемого ряда из 22 углеводоро-

дов (табл. 1).

Экспериментальная часть

После обработки данных табл. 1 методом наи-

меньших квадратов были получены соответствующие

В качестве характеристики протяженности угле-

значения коэффициентов модели (4) (табл. 2).

родного скелета молекулы, влияющей на ОЧ, исполь-

зовали индекс Винера (W):

n n

Обсуждение результатов

W = 0.5 ∑ ∑ d_ij,

(1)

i=1j=1

Чтобы определить, с какой степенью точности ре-

грессионное уравнение (4) аппроксимирует исходные

где n — число вершин в соответствующем молекуле

данные, был вычислен коэффициент детерминации

графе; d_ij — кратчайшее расстояние между верши-

(R²) для ОЧ, определенного исследовательским ме-

нами i и j.

тодом, R² = 0.906, для ОЧ, определенного моторным

В качестве энергетических характеристик молекул

методом, R² = 0.930. Для характеристики качества

использовали сумму квадратов собственных значений

модели структура-свойство был вычислен коэффи-

топологической матрицы:

циент множественной корреляции для октанового

числа, определенного исследовательским методом,

L = ∑ Ei2,

(2)

R = 0.952, для ОЧ, определенного моторным методом,

i=1

R = 0.964, что подтверждает сильную связь пред-

где E_i — собственное значение топологической ма-

ложенных топологических характеристик молекул

трицы.

углеводородов с их ОЧ. Для оценки статистической

* ГОСТ 511-2015. Моторный метод определения ок-

танового числа.

** ГОСТ 8226-2015. Исследовательский метод опреде-

*** Пат. РФ 201862459 (опубл. 2018). База данных

ления октанового числа.

физико-химических свойств органических соединений.

668

Коледин О. С. и др.

Таблица 1

Топологические индексы для циклоалканов

Сумма квадратов

Соединение

Индекс Винера

Индекс Рандича

собственных значений

1,3-Диметилциклогексан

15.999

3.787

1,цис-2-Диметилциклогексан

15.999

3.804

1,цис-3,транс-5-Триметилциклогексан

17.999

4.181

1,цис-3-Диметилциклогексан

15.999

3.787

1,цис-4-Диметилциклогексан

15.999

3.787

1,цис-2,транс-4-Триметилциклогексан

17.999

4.198

1,транс-2-Диметилциклогексан

15.999

3.804

1,транс-3-Диметилциклогексан

15.999

3.787

1,транс-4-диметилциклогексан

15.999

3.787

Изопропилциклогексан

17.999

4.304

Метилциклогексан

3.393

трет-Бутилциклогексан

114

19.999

4.605

Циклогексан

11.999

1,2-Диметилциклогексан

15.999

3.804

1,4-Диметилциклогексан

15.999

3.787

1,1,3-Триметилциклогексан

17.999

4.1

1,2,4-Триметилциклогексан

17.999

4.198

Изобутилциклогексан

126

19.999

4.787

Циклооктан

3-Метил-1-этилциклогексан

17.999

4.325

4-Метил-1-этилциклогексан

17.999

4.325

1-Метил-3-н-пропилциклогексан

124

19.999

4.825

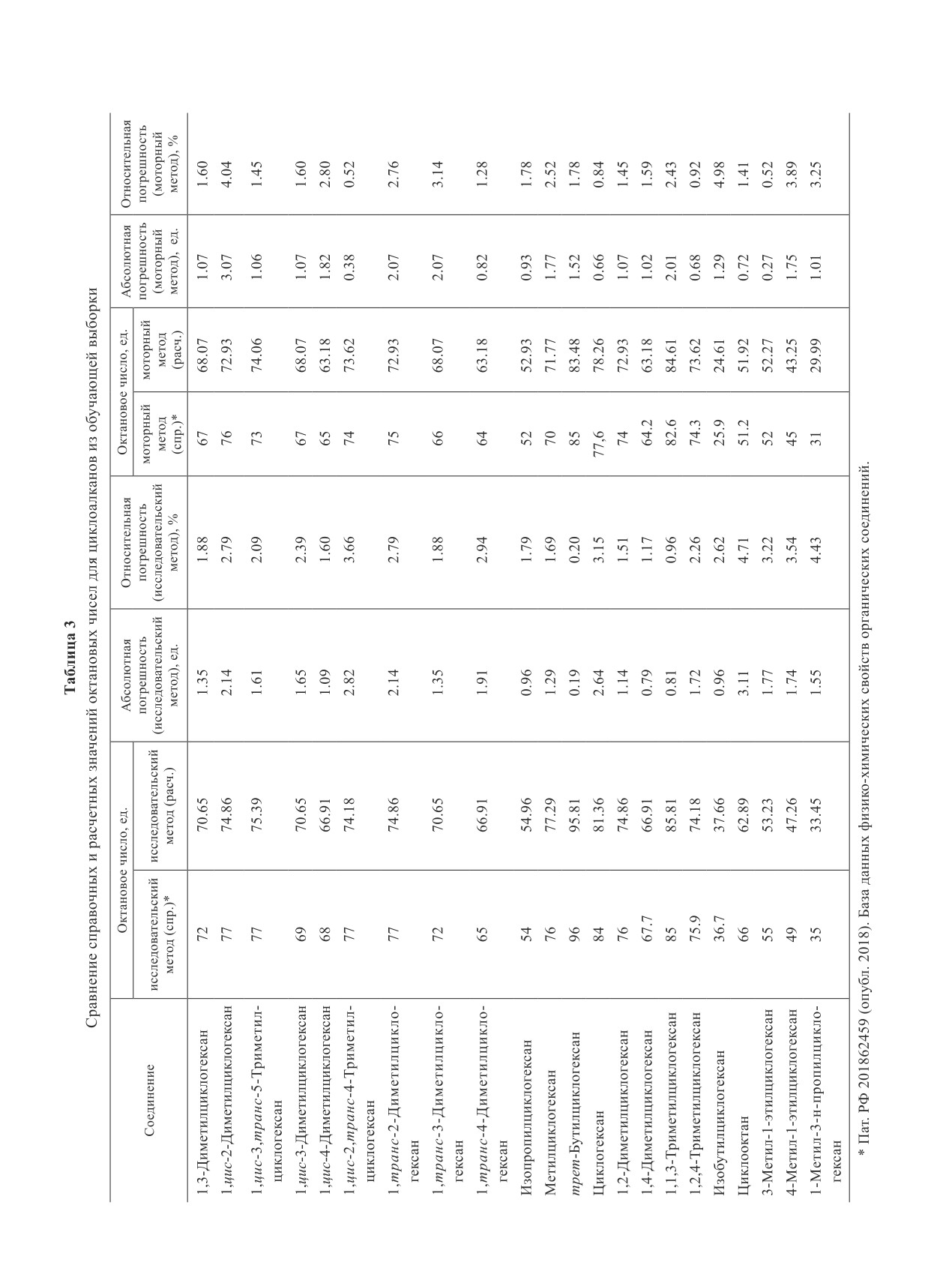
достоверности модели структура-свойство использо-

В нашем случае для ОЧ, определенного иссле-

вали корреляционную поправку S_R:

довательским методом, n = 22, R² = 0.906, получаем

S_R = 0.0686 и

= 13.88 ≥ 3; моторным

S_R =

(5)

S_R

методом — n = 22, R² = 0.930, получаем S_R = 0.0592

где R — коэффициент множественной корреляции,

= 16.28 ≥ 3, следовательно, связь ОЧ

n — число исследуемых соединений.

S_R

Таблица 2

Коэффициенты модели структура-свойство для прогноза октановых чисел циклоалканов

a_n

a₀

a₁

а₂

а₃

а₄

а₅

a₆

Октановое число, определенное по исследова-

-741.79

-11.29

17.29

434.99

1.16

-14.58

-2.90

тельскому методу, ед.

Октановое число, определенное по моторному

-18.50

-8.61

6.29

20.06

0.54

3.44

-1.29

методу, ед.

671

со структурными характеристиками молекул цикло-

модель структура-свойство. Данная модель позво-

алканов нельзя считать случайной, и график регрес-

ляет более адекватно по сравнению с аналогичными

сионного уравнения проходит через центр облака

моделями оценить ОЧ углеводородов ряда цикланов.

исходных точек.

В качестве топологических индексов используются

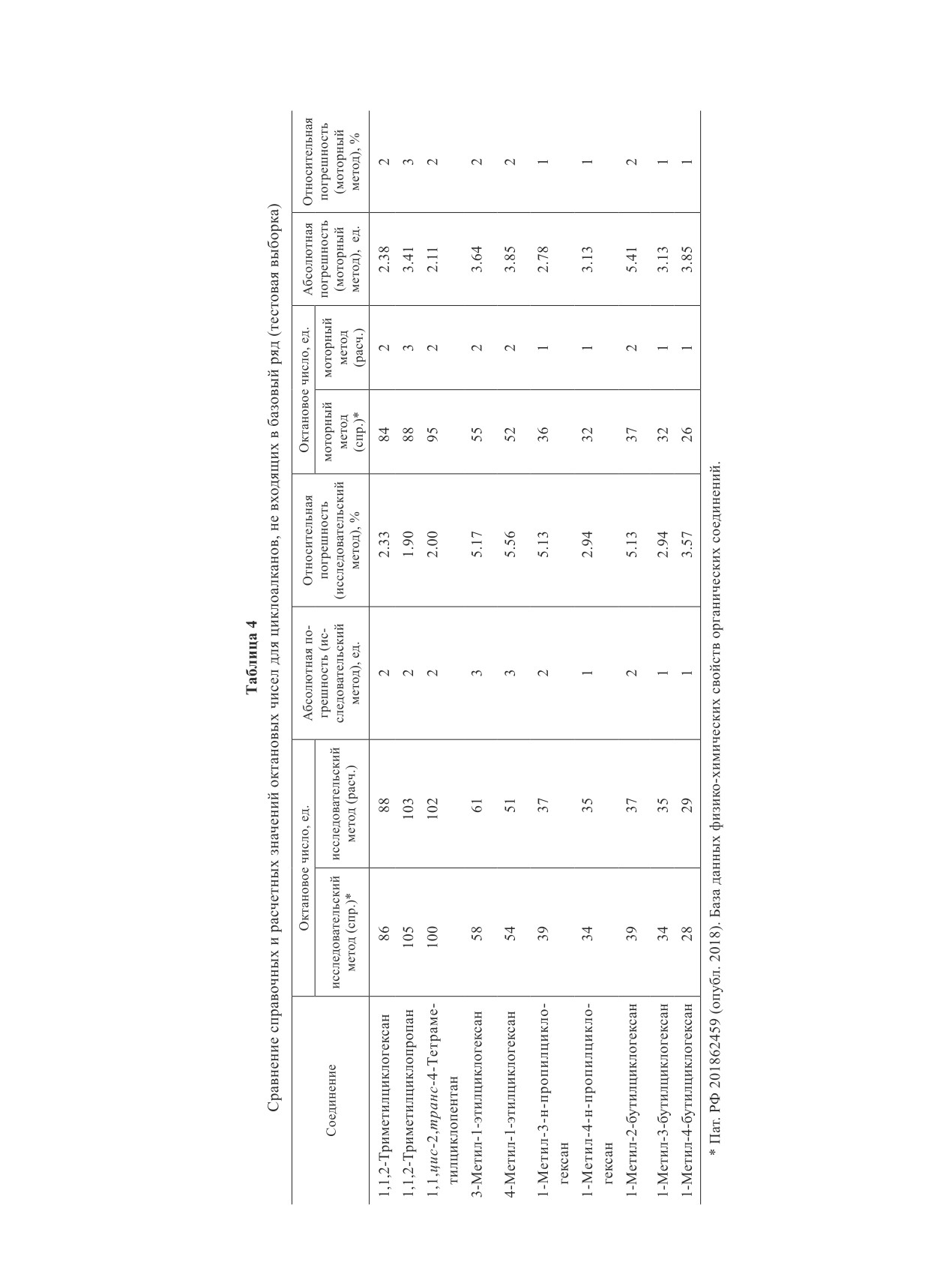
Для обоснования адекватности предложенной

индексы, характеризующие протяженность углерод-

модели для циклоалканов, входящих в обучающую

ного скелета, — индекс Винера, разветвленность

выборку, был осуществлен расчет октанового числа

углеродного скелета — индекс Рандича, а также сум-

(табл. 3).

ма квадратов собственных значений матрицы смеж-

Основными показателями адекватности получен-

ности. Коэффициент детерминации модели равен

ной модели служат абсолютная и относительная по-

0.906 для исследовательского метода, 0.930 для мо-

грешности. Абсолютные погрешности находятся в

торного метода. Разработанная модель может быть

интервале 0.19 ≤ Δ_абс ≤ 3.11, относительные — в ин-

использована при проведении инженерных и научных

тервале 0.2 ≤ Δ_отн ≤ 4.98. Это позволяет сделать вывод

расчетов ОЧ различных циклоалканов, являющихся

об адекватности построенной модели для обучающей

компонентами бензинов.

выборки циклоалканов.

Для дополнительной проверки адекватности мо-

Финансирование работы

дели рассмотрим стандартную ошибку регрессии

(S_regression), определяемую по формуле

Исследование выполнено при финансовой под-

держке Российского фонда фундаментальных иссле-

дований в рамках научного проекта № 20-38-90085

S_regression =

(6)

«Прогнозирование физико-химических свойств угле-

водородных и гетероатомных компонентов нефтяных

где q_ref — справочное значение ОЧ, q_calc — расчет-

систем и моторных топлив».

ное (полученное в результате прогноза) значение

переменной, m — число наблюдений (циклоалканов),

Конфликт интересов

k — число членов уравнения регрессии.

Авторы заявляют об отсутствии конфликта инте-

В нашем случае S_regression = 2.16 ед. для ОЧ, опре-

ресов, требующего раскрытия в данной статье.

деленного исследовательским методом, S_regression =

= 1.80 ед. — моторным методом.

Малая величина стандартной ошибки регрессии

Информация о вкладе авторов

по сравнению со значениями зависимой переменной

М. Ю. Доломатов, Р. Ш. Япаев и А. Т. Гильмут-

подтверждает адекватность предложенной модели

динов разработали концепцию работы и методику

(4).

расчета; Р. В. Гарипов и М. Р. Валеев произвели

Проверим полученную модель на тестовой выбор-

поиск исходных данных и рассчитали топологиче-

ке циклоалканов (табл. 4).

ские индексы требуемых молекул; О. С. Коледин и

Абсолютные погрешности для тестовой выборки

М. Ф. Мухарметов произвели обработку полученных

находятся в интервале 1 ≤ Δ_абс ≤ 3, относительные —

индексов с нахождением коэффициентов моделей

в интервале 1.9 ≤ Δ_отн ≤ 5.56, что в совокупности с

методом наименьших квадратов.

низкими значениями абсолютной и относительной

погрешностей для обучающей выборки и стандарт-

ной ошибкой регрессии, а также высокими значе-

Информация об авторах

ниями коэффициента корреляции и детерминации

означает, что модель (4) позволяет точно осущест-

Доломатов Михаил Юрьевич, д.х.н., проф.

влять прогноз ОЧ углеводородов ряда циклоалканов,

РИНЦ: SPIN-код: 8270-9944; Author ID: 129655

в том числе входящих в состав бензиновых фракций

Япаев Рустем Шамилевич, к.х.н., доцент

каталитического риформинга, крекинга и других про-

РИНЦ: SPIN-код :5253-0500; Author ID: 489730

цессов.

Гильмутдинов Амир Тимерьянович, д.х.н., проф.

РИНЦ: Author ID: 297336

Коледин Олег Сергеевич

Выводы

РИНЦ: SPIN-код: 8992-6231; Author ID: 1149962

Для определения ОЧ углеводородов ряда цикло-

Мухарметов Марсель Флоридович

акланов разработана трехфакторная регрессионная

ORCID: https://orcid.org/0000-0002-4033-0536

672

Коледин О. С. и др.

Гарипов Роберт Венерович

function method // Petrol. Chem. 2011. V. 51. N 5.

ORCID: https://orcid.org/0000-0002-7654-1781

P. 354-362.

Валеев Малик Рамилевич

https://doi.org/10.1134/S0965544111040074 ].

[6]

Смоленский Е. А., Рыжов А. Н., Милина М. И.,

ORCID: https://orcid.org/0000-0003-2699-2063

Лапидус А. Л. Моделирование октановых чи-

сел алкенов // ДАН. 2011. Т. 436. № 1. С. 58-

63 [Smolenskii E. A., Ryzhov A. N., Milina M. I.,

Список литературы

Lapidus A. L. Modeling the octane numbers of alkenes

[1] Rodriguez-Fernandez J., Ramos A., Barba J.,

// Doklady Chem. 2011. V. 436. N 1. P. 5-10.

Cardenas D., Delgado J. Improving fuel economy and

https://doi.org/10.1134/S0012500811010034 ].

engine performance through gasoline fuel octane rating

[7]

Лапидус А. Л., Смоленский Е. А., Бавыкин В. М.,

// Energies. 2020. V. 13. N 13. P. 1-14.

Мышенкова Т. Н., Кондратьев Л. Т. Модели для рас-

https://doi.org/10.3390/en13133499

чета и прогнозирования октановых и цетановых чи-

[2] Druzgalski C. L., Lapointe S., Whitesides R.,

сел индивидуальных углеводородов // Нефтехимия.

McNenly M. J. Predicting octane number from

2008. Т. 48. № 4. С. 277-285 [Lapidus A. L.,

microscale flame dynamics // Comb. Flame. 2019.

Smolenskii E. A., Bavykin V. M., Myshenkova T. N.

V. 208. N 5. P. 5-14.

Models for the calculation and prediction of the octane

https://doi.org/10.1016/j.combustflame.2019.06.019

and cetane numbers of individual hydrocarbons //

[3] Prakash A., Wang C., Janssen A., Aradi A. Impact of

Petrol. Chem. 2008. V. 48. N 4. P. 277-286.

fuel sensitivity (RON-MON) on engine efficiency //

https://doi.org/10.1134/S0965544108040051 ].

Shell Global Solutions. 2017. V. 10. N 1. P. 115-125.

[8]

Смоленский Е. А., Рыжов А. Н., Бавыкин В. М.,

https://doi.org/10.4271/2017-01-0799

Мышенкова Т. Н., Лапидус А. Л. Моделирование ок-

[4] Pasadakis N., Gaganis V., Foteinopoulos C. Octane

тановых чисел углеводородов с помощью оптималь-

number prediction for gasoline blends // Fuel Processing

ных топологических индексов для их топологиче-

Technol. 2006. V. 87. N 6. P. 505-509.

ских эквивалентов // Изв. АН. Сер. хим. 2007. Т. 56.

https://doi.org/10.1016/j.fuproc.2005.11.006

№ 9. C. 1619-1631 [Smolenskii E. A., Ryzhov A. N.,

[5] Рыжов А. Н., Стрижакова Ю. А., Смоленский Е. А.,

Bavykin V. M., Myshenkova T. N. Octane numbers

Лапидус А. Л. Моделирование октановых чисел ал-

(ONs) of hydrocarbons: A QSPR study using optimal

кенов методом обратных функций // Нефтехимия.

topological indices for the topological equivalents of the

2011. Т. 51. № 5. С. 360-368 [Ryzhov A. N.,

ONs // Russ. Сhem. Bull. 2007. V. 56. N 9. P. 1681-

Strizhakova Yu. A., Smolenskii E. A., Lapidus A. L.

1693. https://doi.org/10.1007/s11172-007-0262-2 ].

Modeling the octane numbers of alkenes by the Inverse