РАСПЛАВЫ
2 · 2019
УДК 538.913
СТЕКЛО КАК СРЕДА С ВЫСОКОЙ ПЛОТНОСТЬЮ
ТОПОЛОГИЧЕСКИХ ДЕФЕКТОВ
© 2019 г. Л. Д. Сонa, b, *
aУральский федеральный университет, ул. Мира, 19, Екатеринбург, 620002 Россия
bУральский государственный педагогический университет,
пр. Космонавтов, 26, Екатеринбург, 620017 Россия
*e"mail: ldson@yandex.ru
Поступила в редакцию 02.07.2018
После доработки 12.07.2018
Принята к публикации 19.07.2018
Для неупорядоченных систем, структура которых может быть описана как среда с
большой плотностью линейных топологических дефектов, предлагается механизм
появления сдвиговой жесткости. Он заключается в локализации перегибов на дис%
локационных линиях, что приводит к ограничению подвижности последних. Такой
подход позволяет определить температурную зависимость пластической деформа%
ции и связать ее с фрактальной размерностью системы дефектов, а также объяснить
зависимость температуры стеклования от скорости охлаждения.
Ключевые слова: стекло, дислокации, сдвиговая жесткость.
DOI: 10.1134/S0235010619010201
ВВЕДЕНИЕ
Структура неупорядоченного (жидкого или аморфного) конденсированного веще%
ства часто представляется в виде среды, в которой присутствует локальный порядок, а
дальний нарушен из за высокой плотности топологических дефектов.
В настоящее время такой подход широко распространен для двумерных систем, на%
чало чему было положено в знаменитых работах Березинского [1], Костерлица и Тау%
лесса [2], Нельсона и Хальперина [3]. В двух измерениях топологические дефекты яв%
ляются точечными, и их взаимодействие можно учесть в рамках теории БКТХНЯ (Бе%
резинского-Костерлица-Таулесса-Хальперина-Нельсона-Янга, см. обзор
[4]).
Плавление двумерного кристалла представляется при этом как появление в системе
асимптотически свободных топологических дефектов.
Для трехмерной системы статистика дефектов (теперь уже не точек, а линий) явля%
ется более громоздкой, но также вполне применимой для описания плавления, что
продемонстрировано в работе [8]. Для описания структуры стекол (особенно металли%
ческих) данный подход также применяется [9] - как альтернатива традиционному, ос%
нованному на формализме корреляционных функций.
Основы применения подхода к трехмерным системам сформулированы в работах
[5-7]. Благодаря локальному порядку, топологические дефекты имеют четко опреде%
ленные вектора Бюргерса (дислокации) или Франка (дисклинации). Линии дефектов
не могут оканчиваться внутри вещества - только друг на друге, или на внешней по%
верхности. Важным обстоятельством является то, что что бездефектная область веще%
ства с хорошо определенным локальным порядком является связной, что и создает
возможность такого описания [10, 11]. Отличие от одноименных кристаллических де%
фектов состоит в том, что эти вектора могут изменять свою ориентацию вдоль линии
дефекта, в соответствии с направлением осей локальной анизотропии, а также в том,
что локальный порядок может быть некристаллическим (т.е. не Федоровским).
Стекло как среда с высокой плотностью топологических дефектов
143
Несмотря на распространенность подхода, в его рамках недостаточно освещаются
вопросы, связанные с динамикой. Выше температуры стеклования такое рассмотре%
ние в литературе, хотя и скудное, все таки есть [12], однако основной смысл примене%
ния данного подхода - возможность описывать явления, происходящие ниже этой
температуры, например микроскопический механизм приобретения веществом сдви%
говой жесткости. Данная работа представляет собой шаг в устранении этого пробела.
Основная сфера применения - металлические системы. Именно для них применяют%
ся методы получения неравновесных состояний с помощью деформации [13], и для
них показано, что традиционные представления о структуре, основанные на форма%
лизме корреляционных функций [14, 15] не противоречат подходу, основанному на
топологических дефектах [16].
Естественно предположить, что в среде с хорошо определенным локальным поряд%
ком и топологическими дефектами релаксация сдвига происходит так же, как и в кри%
сталле - за счет движения (скольжения) дислокаций. Последнее происходит благода%
ря перемещению перегибов вдоль дислокации [17]. Разница состоит в том, что плос%
кость скольжения в неупорядоченной среде превращается в искривленную
поверхность, а само движение сопровождается взаимодействием с большим числом
других дефектов. В данной работе мы рассматриваем движение перегиба вдоль линии
дефекта в некотором эффективном самосогласованном потенциале.
ДВИЖЕНИЕ ПЕРЕГИБА
В среде существует два типа топологических дефектов - дислокации и дисклина%
ции. Следуя [10, 11] мы полагаем, что дисклинации могут быть представлены как со%
вокупность большого числа дислокаций, и на микроскопическом уровне как самосто%
ятельные дефекты не представлены.
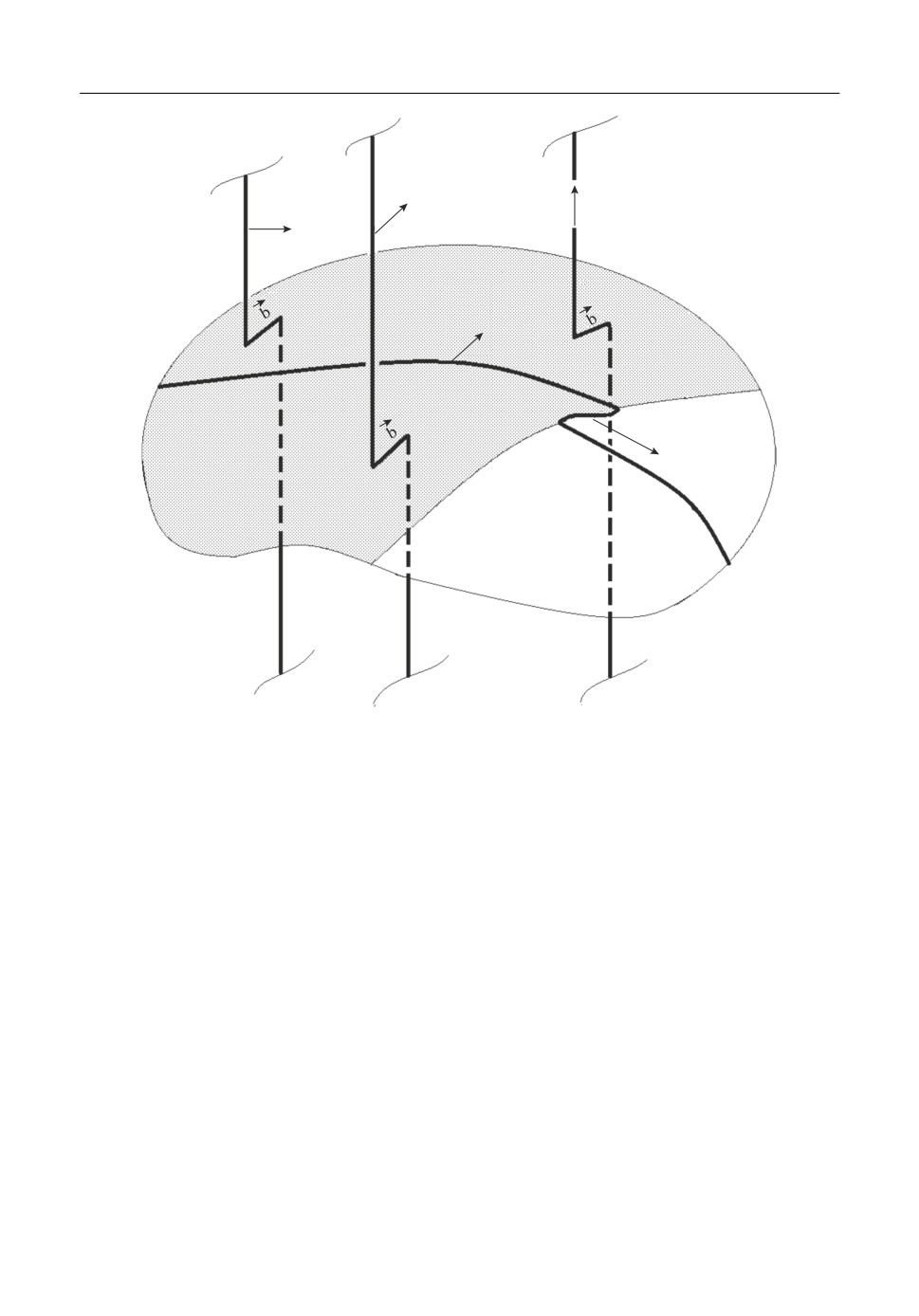
Схематически движение перегиба представлено на рис. 1.
Перегиб движется вдоль дефекта (дислокации) α в направлении, обозначенном
прозрачной стрелкой. Вектор Бюргерса дислокацииα обозначен на рисунке какb. Та%
ким образом, движение перегиба обеспечивает смещение дислокации по поверхности
скольженияΣ.Позади перегиба, вблизи линии дислокации
, среда “выше” и “ниже”
α
приобретает относительное смещение, равноеb (на рис. 1, поверхность сдвига зате%
Σ
нена). В результате все близлежащие дислокации, пересекающие поверхность сдвига,
приобретают изгибы, обладающие энергией. В зависимости от вектора Бюргерса (для
дислокаций
вектора Бюргерса изображены у их “верхних” концов) такие изгибы
β, γ, δ
могут представлять собой способные к скольжению перегибы (дислокация
), или
β
ступеньки (дислокации
), движение которых возможно за счет диффузии. Если пе%
γ, δ
региб вернется обратно за время, в течении которого такие изгибы остаются на месте,
они исчезнут, что приведет к обратному понижению энергии. Таким образом, если бы
возникающие изгибы были статичны, перегиб двигался бы в статическом потенциале
U(x) = u
0
x.
(1)
Здесь
- средняя энергия возникающих изгибов при смещении перегиба на еди%
0
u
ницу, а
- модуль координаты, отсчитываемой вдоль линии дефекта относительно
x
некоторого начального положения.
Возникающие изгибы, однако, не являются неподвижными - они могут покидать
место своего возникновения (путем скольжения или диффузии). По отношению к
движению рассматриваемого перегиба, все близлежащие дефекты, пересекающие по%
верхность скольжения, можно подразделить на “возмущенные” и “невозмущенные”.
Когда перегиб проходит мимо возмущенного дефекта, на нем исчезает избыточный
изгиб, и дефект становится невозмущенным. Наоборот, при прохождении вблизи не%
возмущенного дефекта, избыточный изгиб появляется на нем, и дефект становится
144
Л. Д. Сон
Рис. 1. Движение перегиба вдоль дислокацииα приводит к сдвигу на затененной поверхности, так что дис%
локации
β,γ,δ
приобретают изгиб с избыточной энергией.
возмущенным. Кроме того, наличие избыточных изгибов означает наличие избыточ%
ной энергии, так что плотность избыточных изгибов со временем релаксирует, т.е. воз%
мущенный дефект с течением времени может спонтанно превратится в невозмущен%
ный. Вероятность такого превращения за времяt мы обозначим как
mt).
Пусть в начальный момент времени координата перегиба равна нулю. Обозначим
вероятность для перегиба иметь координату меньше, чемx, как
По определе%
F(x,t).
нию это не что иное, как функция распределения перегиба по координате, а соответ%
ствующая плотность вероятности дается производной
Начальное усло%
f(x,t) = F '(x,t).
вие очевидно:
F(x,0) = θ(x), f (x,0) = δ(x).
(2)
Здесь
- функции Хевисайда и Дирака. В дальнейшем мы традиционно будем
( ), (x)
обозначат производную по x штрихом, а по времени - точкой. Потенциал
в ко%
U(x,t),
тором движется перегиб, зависит и от координаты, и от времени. Для него справедли%
во очевидное равенство
U'(x,t) = (1-
2F(x,t))u
0
(ω1-ω
0
),
(3)
где
- вероятности для близлежащего к точке x в момент t дефекта быть возму%
ω,ω10
щенным или невозмущенным соответственно.
Стекло как среда с высокой плотностью топологических дефектов
145
Составим уравнение на величины
ω1,0.
В течении малого времени
Δt,
вероятность
невозмущенного состояния в точке x изменяется:
ω
0
(x,t
+Δt)
=ω
1
(x,t)m(Δt) +ω
0
(x,t)(1-
f x,t)Δt).
(4)
Первый член соответствует переходу из возмущенного в невозмущенное состояние, а
второй - возможности остаться в невозмущенном состоянии. Очевидное условие
ω1+ω0=1
дает замкнутое уравнение
ω1+ω
(m
+
f x,t))
=
f x,t) ,
m
=
mt)|
,
(5)
1
0
0
t→0
которое легко решить:
t
−m
0
t-G
m
0
τ+G x
τ)
ω1 =
e
f x
τ)e
dτ
,
G x,t)
=
f x,t)dt
(6)
∫
∫
0
Плотность вероятности, в свою очередь,
f(x,t)
удовлетворяет уравнению Фоккера-
Планка [18]
T f
"
+
1(
U
'
f
)'
=
f
,
(7)
γ
γ
где
T
- температура (в энергетических единицах), а
γ
- эффективный коэффициент
трения. Равенства (3, 6, 7) вместе с условием
дают замкнутое уравнение на
ω +ω =101
функцию распределения
Начальное условие при
задается равенством (2).
F(x,t).
t = 0
Ниже рассматриваются его возможные стационарные решения.
СТАЦИОНАРНЫЕ РЕШЕНИЯ
Стационарные решения соответствуют состояниям, для которых плотность вероятности
имеет равновесный характер и не зависит от времени
Из (5) имеем:
f(x,t)=
f x),
ω =0.e
f x)
ω
e
=
(8)
0
m + f(x)
Уравнение (7) можно проинтегрировать по
x:
T
u
0
F
'
-
m
0
F
''
+
(1
−
2F)
F'
= 0.
(9)
γ
γ
F'+m
0
Поскольку полученное уравнение не содержит x, можно использовать подстановку
F'' = F'dF'/dF,
что приводит к уравнению
⎡
dF'
u
0
F
'
−
m
0
⎤
F
'
+
(1
−
2
F)
=
0.
(10)
⎢
⎥
⎣
dF T
F'+m
0
⎦
Оно имеет очевидное решение
F' = 0 = f(x),
которое соответствует однородному “раз%
мазыванию” перегиба вдоль по линии дефекта. Кроме того, имеет место нетривиаль%
ное решение
⎛
m
0
-
F'⎞
u
0
2
F
'
+
2m
ln
=
(
F
−
F).
(11)
0
⎜
⎟
⎝
m
0
⎠
T
Константа интегрирования выбрана исходя из условий
F'= 0
при
F = 0( x → -∞)
или
F =1(x → +∞).
При малых x,для решения (11) можно заменить функцию
F(x)
ее раз%
ложением. В силу четности ее производной
f(x),
в это разложение войдут только не%
четные степени:
1
3
F
=
+α
x
-β
x
+…
(12)
2
146
Л. Д. Сон
Сохраняя члены до третьего порядка включительно и используя (11), получаем урав%
нения на коэффициенты разложения
α,β:
2
u
0
⎛
α⎞
α
u
0
(m
0
−α)
α+
=
−2m
ln
1-
,
β
=
(13)
0
⎜
⎟
4T
⎝
m
0
⎠
3 (
0
+α)
При больших x можно воспользоваться тем, что плотность вероятности (производная
F')
мала. Тогда разложение логарифма в (11) дает
1
⎛u
0
⎞
F
=
+
1th⎜
x⎟
(14)
2
2
⎝2T
⎠
Нетривиальное решение существует не всегда - очевидным условием его возник%
новения является возможность гладкой сшивки функций (12) и (14) при некотором
промежуточном значенииx. Для (12) плотность вероятности
представляет
f(x) = F'(x)
собой параболический купол, ширину которого можно оценить как
2T(m
0
+α
Δx
1
≅
).
(15)
α
0
u (m
0
−α)
В случае (14), плотность вероятности описывается экспоненциальной “шапкой”
u
0
−
2
u
0
x
f x)
=
ch
,
(16)
4T
2
T
ширина которой
Δx
2
≅
4T u
0
(17)
Гладкая сшивка возможна, если
Δx
≥Δx
Уравнения (15), (17) определяют значения
1
2.
параметров, при которых появляется нетривиальное решение:
u
0
α
=
z
,
=
y
,
(18)
Tm
0
m
0
где
z,
y
есть решения алгебраической системы уравнений
⎧8
y
(1
−
y) (1+
y)
=
z
⎨
(19)
⎩
y
+
z
4
=-
2 ln(1-
y).
Отметим, что соотношение (18) не является точным, поскольку получено с использо%
ванием приближенных решений. Точное соотношение можно получить, решая систе%
му (3, 6, 7) с начальным условием (2) численно. В рамках данной работы в этом нет не%
обходимости - точное решение изменит численные значения
но качественной
z, y,
картины, которая обсуждается ниже, не затронет.
ОБСУЖДЕНИЕ
Стационарные решения дают понимание некоторых важных особенностей поведе%
ния стеклующейся системы. Превращение дефекта из возмущенного в невозмущен%
ный заключается в том, что избыточный изгиб покидает поверхность Σ (см. рис. 1).
Вероятность этого определяется пуассоновским процессом
-λt
mt)=
e
,
(20)
где
- пуассоновская частота смещения изгиба, совпадающая с m из (5). Для среды с
λ
0
простым кубическим локальным порядком
T
2
m
=λ=
+
D
,
(21)
0
3γ
3
Стекло как среда с высокой плотностью топологических дефектов
147
где
- коэффициент диффузии. Данная формула учитывает, что для кубического ло%
D
кального порядка две трети всех изгибов являются ступеньками, которые движутся за
счет диффузии, описываемой коэффициентомD, а оставшаяся треть - скользящие
перегибы с коэффициентом подвижности
Равенства (18) дают уравнение на тем%
T γ.
пературу появления нетривиального решенияT
:
c
3γ
u0
T
=
(22)
c
z(T
c
+2γD(T
c
))
Зависимость коэффициента диффузии от температуры в плотных средах (актива%
ционный механизм) выражается законом Аррениуса:
E
D
D(T)=D
exp
−
,
(23)
0
{
}
T
где
- энергия активации диффузии.
E
D
НижеT осуществляется нетривиальное решение - перегиб локализован в некото%
c
рой области, так что дислокации не могут самопроизвольно двигаться (стекло с ко%
нечной сдвиговой жесткостью). ВышеT перегиб свободно движется вдоль дислока%
c
ции, в результате чего сами дислокации становятся подвижными. При этом нетриви%
ального решения не существует, так что это температура абсолютной неустойчивости
стекла: выше нее дислокации могут быть либо неравновесными и вытесняться из объ%
ема - в этом случае система станет кристаллической, либо равновесными - в таком
случае мы получим жидкость.
Длина локализации, отсчитанная вдоль дислокационной линии, составляет
l
≈
4T u
0
В пространстве размер области локализации есть
1
1
d
d
rl
~l
~T
,
(24)
где
- фрактальная размерность дефектной линии. Чтобы создать в среде пластиче%
d
скую деформацию, нужно “выгнать” перегибы за область локализации, т.е. создать де%
формацию сдвига, пропорциональную размеру этой области
1
d
ε
~r
l
~T
(25)
Тогда, измеряя температурную зависимость предельной упругой деформации, можно
определить фрактальную размерность дефектов.
Величина u представляет собой плотность энергии избыточных изгибов, создавае%
0
мых на окружающих дефектах при скольжении перегиба вдоль дислокации. Чтобы ак%
тивировать движение дислокации, нужно затратить пропорциональную энергию, по%
этому в жидкости
u
0
~E
V
,
(26)
где
E
- энергия активации вязкого течения. При закалке плотность дефектов убыва%
V
ет, так что в стекле
⎧
c
⎫
u0 ~E
V
exp
⎨−
⎬,
(27)
⎩
υ
T
⎭
где
c
- некоторая постоянная,
- скорость охлаждения при закалке. Выражения
υT
(22, 27) предполагают зависимость температуры неустойчивости стекла от скорости
закалки, которая должна существовать, по крайней мере, для металлических стекол.
Кроме того, “коэффициент трения” при скольжении перегибаγ,входящий в (22), оче%
видно пропорционален вязкости в жидком состоянии.
148
Л. Д. Сон
Таким образом, при рассмотрении жидкостей и стекол как сред со связной обла%
стью локального порядка и высокой плотностью дислокаций, поведение системы
определяется величинами, легко измеримыми в эксперименте. В частности, темпера%
тура абсолютной неустойчивости стеклаT оказывается связанной с коэффициентом
c
диффузии, вязкостью, энергией активации вязкого течения и скоростью охлаждения
при закалке, а температурная зависимость предельной упругой деформации дает
фрактальную размерность линейных дефектов.
Работа поддержана РФФИ (проект 18%03%00433) и Правительством Российской фе%
дерации (постановление № 211, контракт № 02.A03.21.0006).
СПИСОК ЛИТЕРАТУРЫ
1. Б е р е з и н с к и й В . Л . Разрушение дальнего порядка в одномерных и двумерных си%
стемах с непрерывной группой симметрии. I. Классические системы // ЖЭТФ. 1970. 59. № 3.
С. 907-920.
2. K o s t e r l i t z J . M . , T h o u l e s s D . J . Ordering, metastability and phase transition in two%
dimensional systems // J. Phys. C. 1973. 6. № 7. P. 1181.
3. H a l p e r i n B . I . , N e l s o n D . R . Dislocation mediated melting in two dimensions //
Phys. Rev. B. 1979. 19. № 5. Р. 2457.
4. Р ы ж о в В . Н . , Та р е е в а Е . Е . , Ф о м и н Ю . Д . , Ц и о к Е . Н . Переход Бере%
зинского-Костерлица-Таулеса и двумерное плавление // УФН. 2017. 187. № 9. С. 921-951.
5. R i v i e r N . Disclination lines in glasses // Phil.Mag. 1979. A10. Р. 859
6. N e l s o n D . R . Order frustration and defects in liquids and glasses // Phys.Rev. 1983. B28.
№ 0-15. Р. 5515-5535.
7. N e l s o n D . R . , To n e r J . Continual theory of melting // Phys.Rev. 1981. B24. Р. 363-387.
8. О б у х о в С . П . Дислокационный механизм плавления кристаллов // ЖЭТФ. 1982. 83.
№ 11. С. 1978-1984.
9. Ш у д е г о в В . Е . Стеклообразование, стеклография, принципы организации и кон%
струирования некристаллических структур: автореф. дисс. д%ра физ.%мат.наук: 01.04.07.
Санкт%Петербург. 1993. 43 с.
10. П а т а ш и н с к и й А . З . , Ш у м и л о Б . И . Теория конденсированного вещества, ос%
нованная на гипотезе локального кристаллического порядка // ЖЭТФ. 1985. 89. № 1. С. 315.
11. П а т а ш и н с к и й А . З . , С о н Л . Д . Жесткость конденсированного вещества при
высоких температурах // ЖЭТФ. 1993. 103. № 3. С. 1087.
12. Va s i n M . G . Theoretical description of non%Debye relaxation, and Boson peak in terms of
gauge theory of glass transition // J. of Non%Crystalline Solids. 2014. 387. Р. 139-142.
13. Va l i e v R . Nanostructuring of Metallic Materials by SPD Processing for Advanced Proper%
ties // Int. J. Mat. Res. 2009. 100. Р. 757.
14. D u b i n i n N . E , Yu r y e v A . A , Va t o l i n N . A . Straightforward calculation of the
WCA entropy and internal energy for liquid metals // Thermochim. Acta. 2011. 518. P. 9-12.
15. D u b i n i n N . E . Thermodynamics of liquid Fe-Ni alloys: calculations at different tempera%
tures // J. Phys.: Conf. Series. 2009. 144. Р. 012115.
16. D o y a m a M . , C o t t e r i l l R . M . J . Atomic configurations of disclinations by computer
simulations // Phil. Mag. A. 1984. 50. № 4. P. L7.
17. N a b a r r o F. R . N . Theory of crystal dislocations. Oxford: Clarendon Press. 1979.
18. Б а з а р о в И . П , Ге в о р к я н Е . В . , Н и к о л а е в П . Н . Неравновесная термоди%
намика и физическая кинетика. Издательство МГУ. Москва. 1989.
Glass as a Media with High Density of Topological Defects
L. D. Son1, 2
1Ural Federal University, Mira st., 19, Yekaterinburg, 620002 Russia
2Ural State Pedagogical University, Cosmonavtov av., 26, Yekaterinburg, 620017 Russia
For disordered systems, structure of which may be presented as a media with high density
of linear topological defects, we offer a mechanism of shear rigidity. The last is localisation of
Стекло как среда с высокой плотностью топологических дефектов
149
kinks on the defect that results in limitation of its motion. The approach allows to predict the
plastic deformation threshold temperature dependence and to connect it with the fractal di%
mension of defects, and also to explain the dependence of glass temperature on cooling rate.
Keywords: glass, dislocations, shear rigidity
REFERENCES
1. Berezinsky V.L. The destruction of the long%range order in one%dimensional and two%dimen%
sional systems with a continuous symmetry group. I. Classical systems [Razrusheniye dal’nego poryad"
ka v odnomernykh i dvumernykh sistemakh s nepreryvnoy gruppoy simmetrii. I. Klassicheskiye sistemy] //
ZHETF.1970. 59. № 3. P. 907-920. [In Rus.].
2. Kosterlitz J.M., Thouless D.J. Ordering, metastability and phase transition in two - dimension%
al systems // J. Phys. C. 1973. 6. № 7. P. 1181.
3. Halperin B.I., Nelson D.R. Dislocation mediated melting in two dimensions // Phys. Rev. B.
1979. 19. № 5. Р. 2457.
4. Ryzhov V.N., Tareyeva Ye.Ye., Fomin YU.D., Tsiok Ye.N. Berezinsky-Kosterlitz-Taules transi%
tion and two%dimensional melting [Perekhod Berezinskogo-Kosterlitsa-Taulesa i dvumernoye plav"
leniye] // UFN. 2017. 187. № 9. P. 921-951. [In Rus.].
5. Rivier N. Disclination lines in glasses // Phil.Mag. 1979. A10. Р. 859
6. Nelson D.R. Order frustration and defects in liquids and glasses // Phys.Rev. 1983. B28. № 0-15.
Р. 5515-5535.
7. Nelson D.R., Toner J. Continual theory of melting // Phys.Rev. 1981. B24. Р. 363-387.
8. Obukhov S.P. Dislocation mechanism of crystal melting [Dislokatsionnyy mekhanizm plavleniya
kristallov] // ZHETF. 1982. 83. № 11. P. 1978-1984. [In Rus.].
9. Shudegov V.Ye. Glass formation, glass, principles of organization and design of non%crystalline
structures [Stekloobrazovaniye, steklografiya, printsipy organizatsii i konstruirovaniya nekristalli"
cheskikh struktur]. author. diss. Dr. Phys. - science: 01.04.07. St. Petersburg. 1993. 43 p. [In Rus.].
10. Patashinskiy A.Z., Shumilo B.I. Theory of Condensed Matter Based on the Local Crystalline
Order Hypothesis [Teoriya kondensirovannogo veshchestva, osnovannaya na gipoteze lokal’nogo kristal"
licheskogo poryadka] // ZHETF. 1985. 89. № 1. P. 315. [In Rus.].
11. Patashinskiy A.Z., Son L.D. Rigidity of a Condensed Matter at High Temperatures [Zhestkost’
kondensirovannogo veshchestva pri vysokikh temperaturakh] // ZHETF.1993. 103. № 3. P. 1087.
[In Rus.].
12. Vasin M.G. Theoretical description of non%Debye relaxation, and Boson peak in terms of
gauge theory of glass transition // Journal of Non%Crystalline Solids. 2014. 387. Р. 139-142.
13. Valiev R. Nanostructuring of Metallic Materials by SPD Processing for Advanced Properties //
Int. J. Mat. Res. 2009. 100. Р. 757.
14. Dubinin N.E, Yuryev A.A, Vatolin N.A., Straightforward calculation of the WCA entropy and
internal energy for liquid metals // Thermochim. Acta. 2011. 518. P. 9-12.
15. Dubinin N.E. Thsermodynamics of liquid Fe%Ni alloys: calculations at different temperatures //
J. Phys.: Conf. Series. 2009. 144. Р. 012115.
16. Doyama M., Cotterill R.M.J. Atomic configurations of disclinations by computer simulations //
Phil. Mag. A. 1984. 50. № 4. P. L7.
17. Nabarro F.R.N. Theory of crystal dislocations. Oxford: Clarendon Press. 1979.
18. Bazarov I.P, Gevorkyan Ye.V., Nikolayev P.N. Nonequilibrium thermodynamics and physical
kinetics [Neravnovesnaya termodinamika i fizicheskaya kinetika]. Publishing House of Moscow State
University. Moscow. 1989. [In Rus.].