Российская сельскохозяйственная наука, 2021, № 3

УДК 631.6.02

DOI: 10.31857/S2500262721030029

СТОХАСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВЛИЯНИЯ

ЗАЩИТНЫХ ЛЕСНЫХ НАСАЖДЕНИЙ. РАСПРЕДЕЛЕНИЕ КОШИ

А.Н. Салугин, доктор сельскохозяйственных наук,

А.В. Кулик, А.И. Узолин, кандидаты сельскохозяйственных наук

Федеральный научный центр агроэкологии, комплексных мелиораций и защитного лесоразведения РАН,

400062, г. Волгоград, Университетский просп., 97

E-mail: kulik-a@vfanc.ru

Исследование динамики природных объектов в пространстве и времени тесно связано с их стохастическим пове-

дением, обусловленным климатическими и антропогенными факторами. Случайные явления в агролесомелиорации

мало изучены. Теорию вероятности используют в этом разделе сельскохозяйственной науки в контексте формальной

статистической обработки данных и не более. Распределения вероятностей случайной переменной в пространстве и

времени принимают на веру без физического обоснования, используя методы правдоподобия или моментов. Вместе с

тем природа случайных явлений может быть математически сформулирована с соответствующей функцией распре-

деления: Пуассона - для вероятности осадков; Гаусса - при описании древостоя; Стьюдента - для малых выборок и

др. Распределение Коши, как и нормальное распределение, относится к классическим и имеет своеобразную геометри-

ческую интерпретацию, что весьма важно для практики агролесомелиорации. Оно описывает протяженное в про-

странстве поведение случайной величины с плотностью вероятности, зависящей от угла наблюдения за источником

ее появления. С учетом этого обстоятельства авторы попытались аппроксимировать воздействия лесозащитных на-

саждений на межполосное пространство. Удаленность от лесной полосы - основной фактор защиты от ветра, эро-

зии и др. При этом для описания стохастического ветрового воздействия следует принимать во внимание не только

удаленность, но и протяженность лесозащитных насаждений. В работе описана процедура регрессии на кривую рас-

пределения Коши данных снегопереноса в межполосном пространстве. Зависимость ветрового воздействия лесополос

отражена в кумулятивном распределении. Высокая аппроксимирующая способность этого распределения определяет

его неоспоримую ценность в практическом приложении.

STOCHASTIC MODELING OF THE INFLUENCE

OF PROTECTIVE FOREST BELTS. THE CAUCHY DISTRIBUTION

Salugin A.N., Kulik A.V., Uzolin A.I.

Federal Scientific Centre of Agroecology, Complex Melioration, and Protective Afforestation Russian Academy of Sciences,

400062, Volgograd, Universitetskii prosp., 97

E-mail: kulik-a@vfanc.ru

The studies of natural objects behavior dynamics in space and time are closely related to their stochastic behavior, due to climatic

and anthropogenic factors. Random phenomena in agroforestry have been studied insufficiently. Probability theory in this section

of agricultural science is used in the context of formal statistical data processing and no more. The probabilities distributions of a

random variable in space and time are taken to faith without physical explanation, using likelihood or moment methods. However, the

random phenomena nature can be mathematically formulated with the corresponding distribution function: Poisson distribution -

for the probability of precipitation; Gauss distribution - when describing a tree stand; Student - for small samples, etc. The Cauchy

distribution, as well as the normal one, belongs to the classical distribution and has a peculiar geometrical interpretation, which is

very important for the practice of agroforestry. This distribution describes the random variable behavior extended in space with a

probability density depending on the observation angle for its occurrence source. This circumstance forced the authors to attempt

the approximation of the forest protection plantations effects on the interband space by the Cauchy distribution. Distance from the

forest strip is the main factor of protection against wind, erosion, etc. At the same time for the stochastic wind impact describing, not

only the distance, but also the extent of forest protection plantations should be taken into account. The paper describes a regression

procedure on the Cauchy distribution curve of snow transport data in the interstrip space. The dependence of the wind impact of

forest belts is reflected in the cumulative distribution. The high approximation ability of this distribution determines its undeniable

value in practical applications.

Ключевые слова: защитные лесные полосы, стохастическое

Key words: protective forest shelter-belts, stochastic modeling,

моделирование, снегоотложение, снегозапасы, распределение

snow deposition, snow reserves, Cauchy distribution

Коши

В научных исследованиях по агролесомелиорации

ведения природных объектов используют нормальное

встречаются задачи по изучению пространственного

распределение случайных величин, хотя метод правдо-

влияния защитных лесных насаждений (ЗЛН) на био-

подобия может дать иные результаты [2, 3, 4]. К ориги-

тические факторы защищаемых территорий, к числу

нальным, на наш взгляд, можно отнести наблюдения

которых относятся плодородие почвы, влажность, во-

по определению влияния лесозащитных насаждений

дная эрозия, дефляция и др. [1]. Как правило, при оцен-

в зависимости от удаленности до точки наблюдения.

ке влияния ЗЛН учитывают их конструкцию, высоту

Одна из основных задач агролесомелиорации - изу-

и расстояние до точки наблюдения. Математическое

чение эффективности ЗЛН в связи с ее конструкцией,

аналитическое моделирование в этом случае затруд-

представляющей собой протяженную пространствен-

нено сложностью аэро- и гидродинамики процессов, а

ную линейную систему насаждений с заданными па-

также неоднородностью среды. В связи с этим может

раметрами строения, и выявление механизма влияния

оказаться весьма плодотворным использование стоха-

насаждения на межполосное пространство.

стических приемов. При изучении хаотического по-

Цель исследований

- стохастическое моделиро-

Российская сельскохозяйственная наука, 2021, № 3

вание процесса снегопереноса на межполосном про-

Из рисунка 1 видно, что влияние ЗЛН возрастет по

странстве защитных лесополос различных конструк-

мере удаления от нее. Это происходит из-за увеличе-

ций с использованием распределения Коши.

ния угла обзора (угла наблюдения, под которым вид-

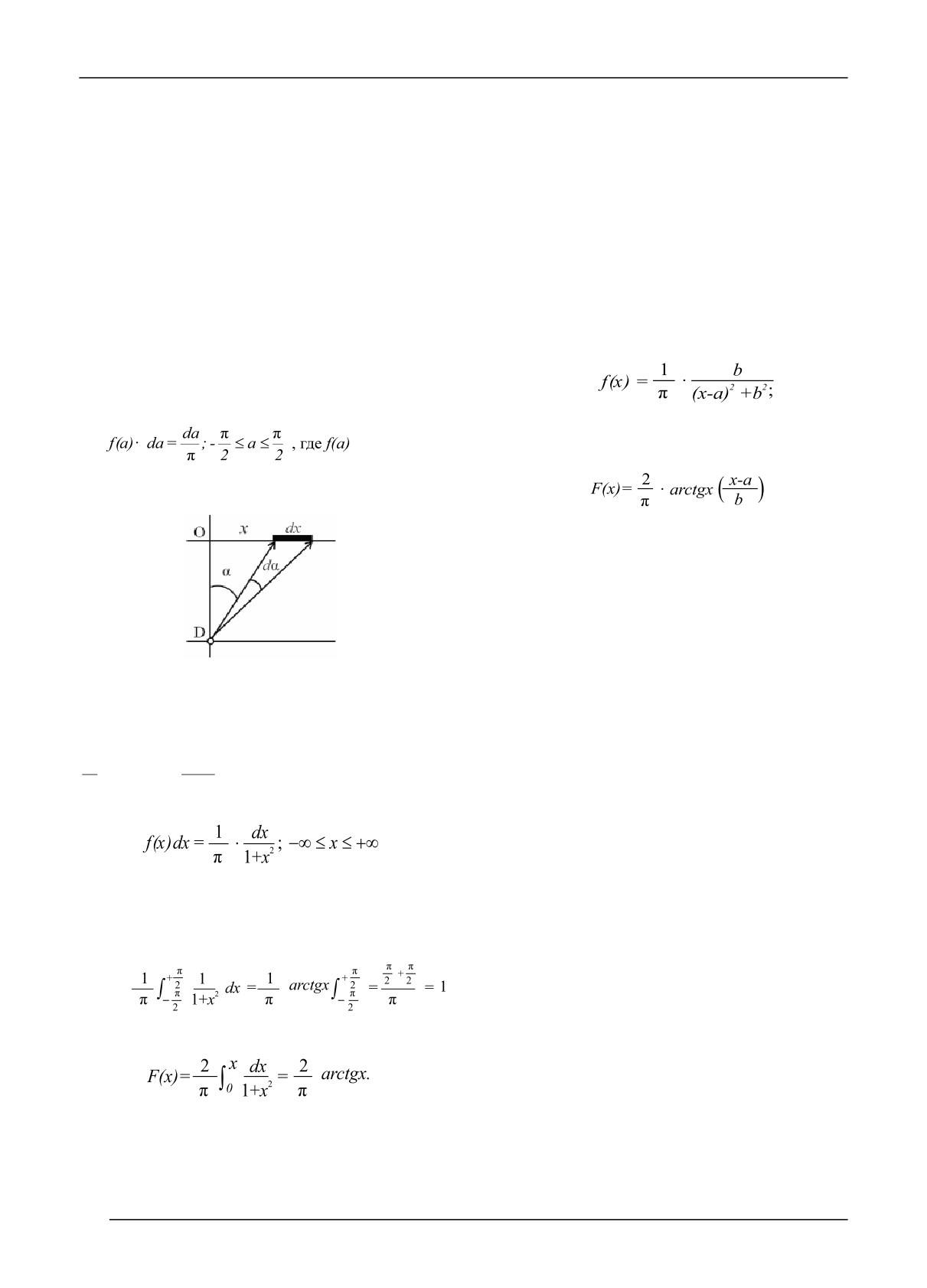
Методика. Наблюдатель, находящийся в межпо-

на полоса). Непосредственное (контактное) влияние

лосном пространстве ЗЛН, отмечает изменения ее вли-

полосы убывает по закону: 1/π 1/(1+x²). Полученное

яния по мере удаления от наблюдаемого элементарного

пространственное распределение относится к числу

участка dx (рис. 1), видимого под некоторым элемен-

классических [2], будучи частным случаем распреде-

тарным

углом dα. Поскольку мы рассматриваем про-

ления Стьюдента и близким по своим параметрам к

цессы, имеющие случайный характер, можно перейти

нормальному распределению. Однако практического

к поиску закономерностей проявления такой случайно-

применения оно не получило. Вместе с тем существу-

сти как функции расположения элемента dx. В нашем

ют более общие формы такого распределения, которые

случае это может быть, например, воздействие ветро-

включают в себя параметр медианы (аналог среднего

ломной полосы на дефляционные потери гумуса или

в нормальном распределении) и параметр размерности

интенсивность снегозадержания. Такое влияние выра-

(дисперсии). Рассмотрим это более подробно.

жается зависимостью элементарного угла dα, под кото-

Общий вид плотности распределения будет двухпа-

рым виден элемент dх. Будем считать, что для углов α

раметрическим:

нет выделенного направления (значения направлений

α равновероятны - изотропность пространства). Тог-

(3)

да для функции распределения по углам наблюдения

вдоль ЗЛН слева направо можно записать (см. рис. 1)

где a и b - параметры (а - медиана, b - аналог диспер-

сии).

[5]:

- вероятность

Интегральная (кумулятивная) кривая выражается

проявления действия элементарного участка dx, види-

формулой:

мого под углом dα.

(4)

Воздействие лесополосы на любой агрофизиче-

ский параметр объектов, расположенных в межполос-

ном пространстве, определяет так называемый геоме-

трический фактор стохастического происхождения. В

рассмотренном варианте расстояние до лесной полосы

было взято равным единице, и фактически рассматри-

вали одну точку, из которой осуществлялось наблюде-

ние. При изменении положения наблюдателя (прибли-

жение к ЗЛН или удаление) реализуется перемещение

Рис. 1. Пространственное распределение влияния ЗЛН.

по кумулятивной кривой Коши.

Определение параметров а и b в (3) на множестве

Чтобы перейти к межполосному пространству, рас-

наблюдений за случайной величиной Y=(y₁, y₂,..., y_п)

смотрим связь между элемента dx и углом α (расстоя-

представляет некоторые трудности. Это объясняется

ние до полосы OD примем равным единице). Элемент

тем, что стандартные методы здесь не применимы [6,

угла dα при этом связан с х равенством:

7]. А.Н. Колмогоров [8] отмечает важность применения

da d

такой характеристики, как медиана. По определению

= (arctgx)=

. Таким образом, плотность распре-

медиана т(Y) случайной величины Y есть такое число

dx dx

1+x

деления вероятности случайной величины как функции

т, когда вероятность p(Y<m)=p(Y≥m)=1/2. В работе [6]

от х равна:

показано, что если имеется распределение Коши с па-

раметрами a и b, то для Y медиана будет равна m(Y)=a,

(1)

а для распределения |Y-a|, m|Y-a|=b. Таким образом,

если экспериментальные данные значений какой-ли-

Формула (1) переводит равномерное распределение

бо случайной величины упорядочить по возрастанию:

по углам к нелинейному распределению с ярко выра-

y₁< y₂< y₃<… y_n, то медиана принимается равной y_k при

женным максимумом по координате х вдоль ЗЛН. Не-

n=2k-1 и (y_k+y_(k+1))/2, если n четно n=2k. Для двухпа-

трудно подсчитать, что полная вероятность при охвате

раметрического распределения Коши можно получить,

всех углов наблюдения равна единице, что соответ-

что выборочная медиана распределена нормально при

ствует адекватности полученной плотности распреде-

n→∞ с математическим ожиданием а и среднеквадра-

тичным отклонением σ=πb/(2√n) [2]. Таким образом,

ления:

параметры а и b двухпараметрического распределения

по данным наблюдений равны a=median(y₁, y₂, y₃,… y_n),

Зависимость кумулятивного влияния лесозащитных

b= a=median(|y₁-a|, |y₂-a|, |y₃-a|, … |y_n-a|) с дисперсией

насаждений от их протяженности можно представить

σ=πb/(2√n).

в виде:

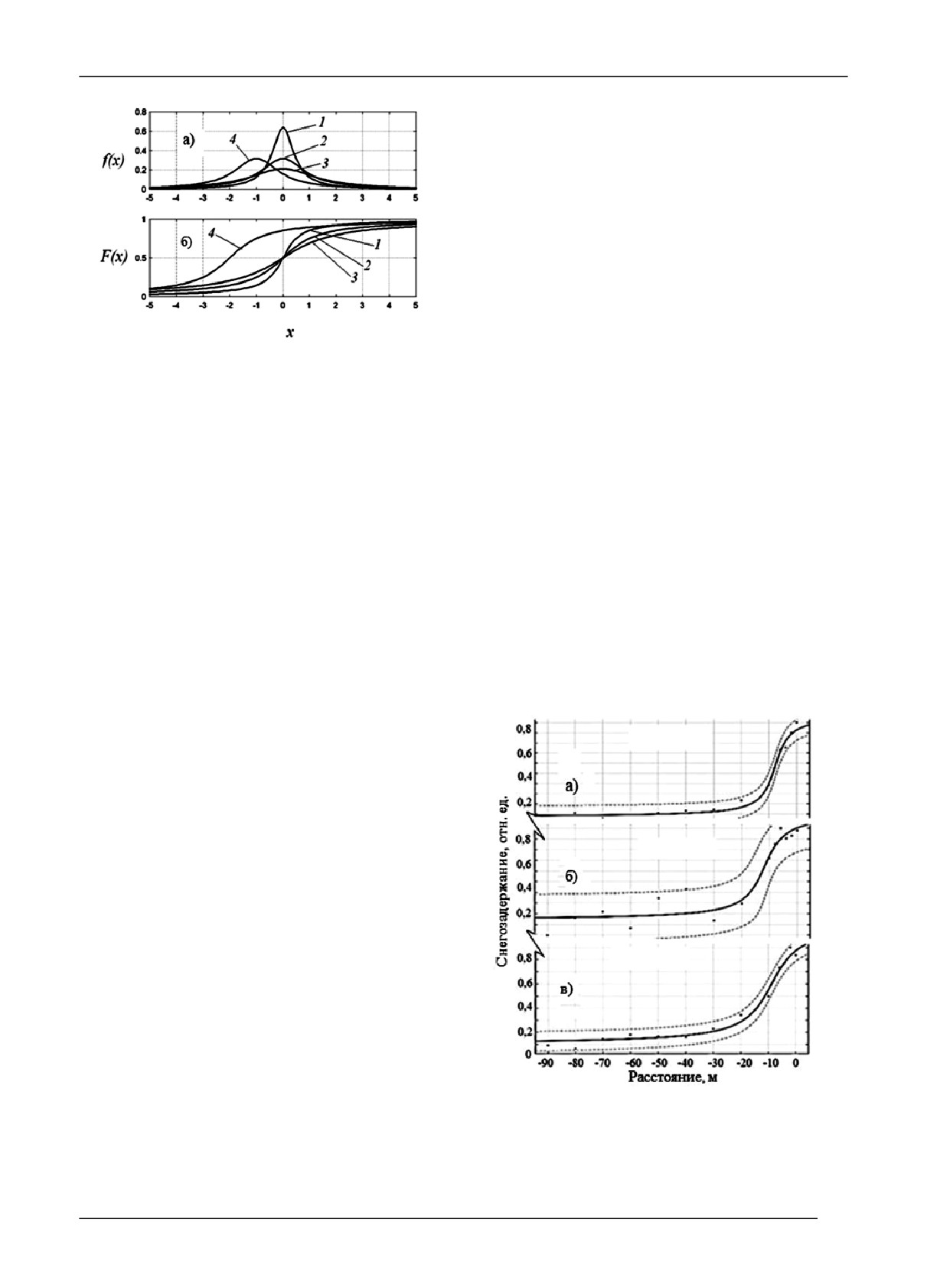
Результаты анализа двухпараметрических кривых

Коши с различными параметрами а и b свидетельству-

(2)

ют о качественном совпадении распределения Коши с

нормальным распределением (рис. 2). При этом боль-

Множитель 2 в этом выражении появился из-за чет-

шей чувствительностью для анализа данных обладает

ности подынтегральной функции. Это важно в практи-

плотность распределения f(x) (рис. 2 а). Положение

ческом приложении, так как исследователю предостав-

центра (максимума) распределения определяется как

ляется возможность изучать одну из симметричных

медиана, что соответствует математическому ожида-

ветвей дифференциального распределения f(x).

нию распределения Гаусса (нормальному распределе-

Российская сельскохозяйственная наука, 2021, № 3

воздействием метельных ветров. При этом учет на-

правления и скорости ветров описывается математи-

ческой динамико-стохастической моделью. Суть этой

модели состоит в том, что процесс переноса снега на-

чинается с некоторой критической скорости ветра, при

которой происходит его отрыв и перенос [10, 11]. Как

уже отмечалось, ветроломное влияние ЗЛН зависит

от угла между направлением ветра и лесной полосой.

С учетом случайных ветровых направлений эффект

от ЗЛН можно моделировать Коши-распределением,

имеющим такую же физическую интерпретацию [5].

Используя двухпараметрическое распределение с при-

влечением медианы и дисперсии (см. рис. 2), представ-

ляется возможным описание влияния ЗЛН на снегоза-

держание.

Рис. 2. Двухпараметрическое распределение Коши:

Математический пакет Matlab имеет приложение

а) дифференциальное, б) кумулятивное; 1 - a=0, b=0,5;

Curve Fitting Toolbox для подгонки теоретических

2 - a=0; b=1; 3 - a=0; b=1,5; 4 - a=-1; b=1.

кривых к экспериментальным данным [12]. Этот ин-

струментарий позволяет выполнять предварительный

нию). Дисперсию при переходе к нормальному распре-

анализ исходной информации и сравнивать результа-

делению можно вычислить по формуле: σ= πb/(2√n),

ты моделирования с использованием аппроксимаций.

где n - число наблюдений, b - параметр распределения

Программа позволяет проводить регрессионный ана-

Коши, определяемый при обработке эксперименталь-

лиз с применением линий нелинейного метода наи-

ных данных.

меньших квадратов с заданными пользователем анали-

Приведем некоторые данные, отражающие спра-

тическими функциями аппроксимации.

ведливость отмеченного утверждения на примере рас-

Результаты приближения распределения Коши к

пределения снегозапасов между лесными полосами.

данным наблюдений показали, что оно достаточно точ-

Объект исследования расположен на северо-восточном

но описывает пространственное накопление снега для

склоне с уклоном 2…3º и длиной 1,5 км восточнее ст.

трех изучееных типов конструкций ЗЛН (плотной, про-

Клетской Волгоградской области на 2,8 км. Лесные по-

дуваемой и комбинированной), обладающих различны-

лосы двух-трехрядные (плотной, продуваемой и ком-

ми аэродинамическими свойствами [13, 14]. Отмеча-

бинированной конструкций) состоят из робинии лжеа-

ется сходная для всех типов ЗЛН картина - снижение

кации (Robinia pseudoacacia), ясеня зеленого (Fraxinus

скорости ветра при приближении к лесной полосе, что

lanceolata), смородины золотистой (Ribes aureum).

способствует осаждению снежных частиц и формиро-

Конструкцию насаждений формировали путем прове-

ванию сугробов (рис. 3). При этом кривые распределе-

дения необходимых рубок [9].

ния Коши F(x)=atan((x-a)/b) на графиках достаточно

Снегомерные съемки проводили в 2014-2019 гг.

близко располагаются к данным по снегоотложению.

После снегопадов перпендикулярно защитным лесным

насаждениям прокладывали снегомерные профили. На

их протяжении определяли высоту снежного покрова

в трехкратной повторности снегомерной рейкой через

каждые 4 м в полевой части, через 2 м в шлейфовых

зонах и через 1 м внутри насаждения. В каждой зоне

в трехкратной повторности весовым снегомером ВС-

43М проводили замеры снегозапасов.

Результаты и обсуждение. При анализе метеодан-

ных было установлено, что на долю метельных ветров

(скорость ветра более 3 м/с) приходилось 58,6 %, то

есть снегоперенос был достаточно активным. Наи-

большие средние скорости характерны для метелей

южного (6,6 м/с), юго-юго-восточного (5,5 м/с) и се-

веро-северо-западного (5,1 м/с) направлений. Эффек-

тивность расположения лесной полосы по отношению

к розе ветров оценивается углом подхода потока к ле-

сонасаждению. Ветроломная эффективность при этом

зависит от отклонения направления от перпендикуляра

к направлению ветра. Дальность ветроломного влия-

ния лесополосы также зависит от угла между направ-

лением ветра и лесополосой. По результатам анализа

расположения лесополосы относительно основных

направлений снегопереноса установлено, что при от-

клонении на угол более 30° (при метелях восточного

направления - 50°, северо-северо-западного - 65°, юж-

Рис. 3 Кумулятивные кривые влияния лесных полос

ного - 40°) дальность ветроломного влияния уменьша-

на снегозадержание, полученные нелинейным методом

ется на 20…30 %, при 30° - на 13 % (западно-юго-за-

наименьших квадратов с использованием распределения

падные - 29°), при 20° - на 2…6 % (юго-западные - 6°).

Коши для трех типов ЗЛН: а) - плотная;

Установленные закономерности можно интерпре-

б) - продуваемая; в) - комбинированная; пунктиром на

тировать как процесс формирования снегозапаса под

графиках отражены 95 %-ные доверительные интервалы.

Российская сельскохозяйственная наука, 2021, № 3

Параметры Коши-распределения

использованы для измерения угловой корреляции меж-

и точность аппроксимации

ду преимущественным направлением ветра из «розы

Конструкции ЗЛН

Параметры распределения

RMSE*

R²

ветров», снегозадержанием и распределением Коши.

Для этого на кривой распределения Коши необходимо

перейти от координаты х к соответствующим углам

Плотная

-7,74 ± 1,2

3,8 ± 0,54

0,051

0,98

наблюдения α (х=tgα). Таким образом, стохастическая

Продуваемая

-11,77 ± 2,2

5,5 ± 1,8

0,115

0,92

природа снегопереноса и ее геометрический характер

адекватно моделируются распределением Коши, по-

Комбинированная

-8,81 ± 2,3

7,5 ± 2,1

0,042

0,98

зволяющем, как показано в статье, получать количе-

*среднеквадратичная ошибка метода наименьших квадратов.

ственные данные при расчетах снегонакопления. Ре-

зультаты, полученные по снегозадержанию - частный

Результаты анализа параметров Коши-распределения

случай использования распределения Коши, которое

и точности аппроксимации свидетельствуют, что значения

может найти применение для динамико-стохастиче-

медианы (а) для разных типов конструкций существенно

ского моделирования в агроэкологии.

различаются, отражая дальность влияния ЗЛН. Значения

дисперсий (b) изменяются от 3,8 до 7,5 (см. табл.).

Литература.

Визуальный анализ регрессии (см. рис. 3) указыва-

1. Кулик К.Н., Салугин А.Н. Математические модели

ет на различие форм кривых распределения. Наиболее

процессов деградации почвенно-растительных си-

точно аппроксимируются кривые (а) и (в). Для плотной

стем// Труды Института геологии Дагестанского

и комбинированной ЗЛН R² равен 0,98, в то время как

научного центра РАН. 2016. № 67. С. 261-264.

для продуваемой R²=0,92. Параметр а для продувае-

2. Ван дер Варден. Математическая статистика. М.:

мой конструкции принимает наибольшее значение, что

изд-во Иностранной литературы, 1960. 436 с.

свидетельствует о наибольшем отклонении распреде-

3. Анализ данных и математическое моделирование в эко-

ления от нулевого значения.

логии и природопользовании / И.С. Белюченко, А.В. Сма-

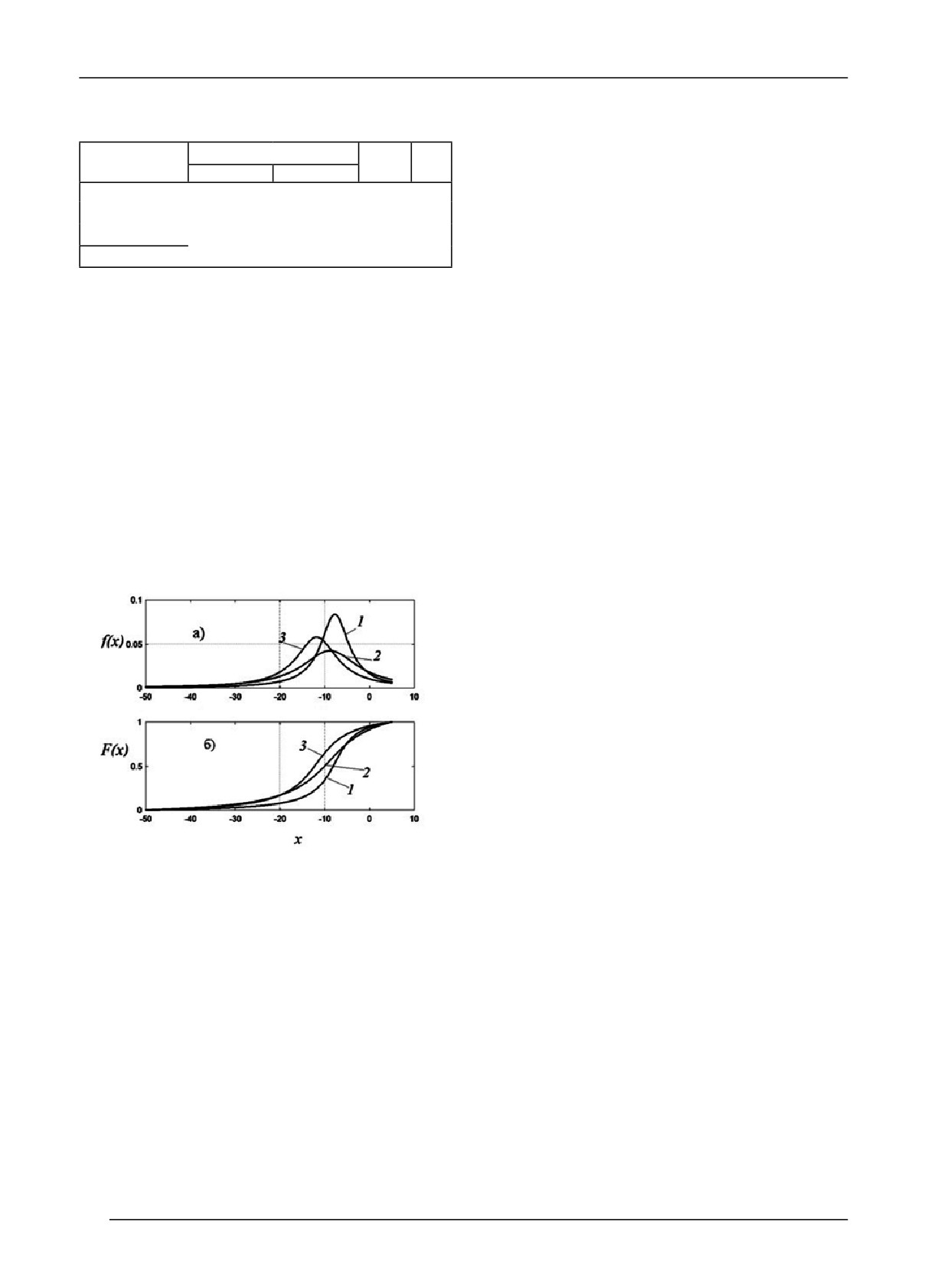
Более наглядно видны различия для плотностей

гин, Л.Б. Попок и др. Краснодар: КубГАУ, 2015. 313 с.

распределения при графическом отображении (рис. 4).

4. Шинкеев М.Л. Оценка параметров распределения

Для плотной ЗЛН f(x) смещена вправо, относительно

Коши // Научное обозрение. 2012. № 3. С. 77-80.

других конструкций, свидетельствуя о том, что ее вли-

5. Худсон Д. Статистика для физиков: лекции по тео-

яние на снегоотложение начинается раньше и захваты-

рии вероятностей и элементарной статистике. М.:

вает большее межполосное пространство.

Мир, 1970. 296 с.

6. Галкин В.М., Ерофеева Л.Н., Лещева С.В. Оценки па-

раметров распределения Коши // Труды Нижегород-

ского государственного технического университета

им. Р.Е. Алексеева. 2014. №2(104). С. 314-319.

7. Некоторые оценки параметров распределения Коши

/ Е.Д. Галкина, С.В. Лещева, Н.С. Лукичев и др. // Тру-

ды Нижегородского государственного техническо-

го университета им. Р.Е. Алексеева. 2015. № 3(110).

С. 322-325.

8. Колмогоров А.Н. Метод медианы в теории ошибок //

Матем. сб. 1931. Т. 38. №3-4. С. 47-50.

9. Узолин А.И., Кулик А.В. Эффективность защитных

лесных полос в формировании и перераспределении

снежного покрова на водосборах // Известия Ниж-

неволжского агроуниверситетского комплекса: На-

ука и высшее профессиональное образование. 2018.

№2 (50). С. 100-106.

10. Гельфан А.Н. Динамико-стохастическое моделирование

Рис. 4. Теоретические кривые распределений:

формирования талого стока. М.: Наука, 2007. 294 с.

а) плотности вероятностей и

11. Гельфан А.Н., Морейдо В.М. Динамико-стохастиче-

б) кумулятивные кривые; 1 - плотная, 2 - продуваемая,

ское моделирование формирования снежного покро-

3 - комбинированная конструкции ЗЛН.

ва на Европейской территории России // Лёд и cнег.

2014. Т. 54. №2. С.44-52. doi: 10.15356/2076-6734-

Таким образом, возможность использования рас-

2014-2-44-52.

пределения Коши при описании снегораспределения

12. Matlab // MathWorks от 02.12.2019. URL: https://www.

в межполосном пространстве обусловлено статисти-

mathworks.com/products/matlab.html.

ческим характером геометрического происхождения

13. Барабанов А.Т., Кулик А.В. Роль стокорегулирующих

этого процесса. Угловые распределения влияния ЗЛН,

лесополос в регулировании снегоотложения и про-

моделируемые кривой Коши, как и распределения ве-

мерзания почв в европейской части РФ // Известия

тровой направленности снегопереноса необходимо

Нижневолжского агроуниверситетского комплек-

учитывать одновременно. При выводе распределения

са: Наука и высшее профессиональное образование.

Коши предполагается, что приоритетных направле-

2017. №2 (46). С. 85-90.

ний не существует - изотропность пространства. Это

14. Иващенко Н.Н. Влияние лесных полос различных кон-

означает равновероятные угловые испытания. Вместе

струкций на ветро-вой поток и снегораспределение

с тем полученные при переходе к пространственному

// Известия Оренбургского государственного аграр-

распределению влияния ЗЛН результаты могут быть

ного университета. 2013. №3 (41). С. 16-19.

Поступила в редакцию 24.02.2021

После доработки 30.03.2021

Принята к публикации 12.05.2021