ЯДЕРНАЯ ФИЗИКА, 2019, том 82, № 1, с. 62-69

ЯДРА

ИОНИЗАЦИЯ L-ОБОЛОЧЕК ПРИ α-РАСПАДЕ

СВЕРХТЯЖЕЛЫХ ЯДЕР ИЗ ЦЕПОЧЕК РАСПАДА

ТЕННЕССИНА²⁹⁴¹¹⁷Ts И ПОЛОНИЯ²¹⁰⁸⁴Po

Поступила в редакцию 31.05.2018 г.; после доработки 31.05.2018 г.; принята к публикации 31.05.2018 г.

Выполнены вычисления и анализ вероятности ионизации L-оболочек дочерних атомов, сопровож-

дающей α-распад ядер сверхтяжелых элементов²⁹⁴¹¹⁷Ts,²⁸⁶¹¹³Nh,²⁷⁸¹⁰⁹Mt,²⁷⁰¹⁰⁵Db, которые входят в

распадную цепочку теннессина, открытого в ОИЯИ (Дубна), и изотопа²¹⁰⁸⁴Po. В основе расчетов

лежит квантово-механическая модель с учетом туннелирования α-частицы через кулоновский ба-

рьер атома. Использовались релятивистские электронные волновые функции, полученные методом

Дирака-Фока. Вычисленные значения вероятности ионизации L-оболочек для изотопа²¹⁰⁸⁴Po лучше

согласуются с экспериментом, чем предыдущие расчеты. В отличие от ионизации K-оболочки, где

основной вклад в вероятность вносят монопольные переходы, для L-оболочек существенный вклад

дают дипольные и квадрупольные переходы. Полученные данные важны для обработки спектров

сверхтяжелых элементов, исследуемых методами объединенной α-, γ- и электронно-конверсионной

спектроскопии.

DOI: 10.1134/S0044002719010094

1. ВВЕДЕНИЕ

которая для указанных элементов рассматрива-

лась в нашей работе [4].

Сверхтяжелый элемент теннессин Ts с заря-

Изучение вероятности ионизации внутренних

дом ядра Z = 117 (первоначальное название —

атомных оболочек, сопровождающей α-распад,

“ununseptium”) был впервые получен в ОИЯИ

имеет давнюю историю. Ионизация K- и L-

(Дубна) в 2009 г. [1]. Позднее были идентифици-

оболочек при α-распаде была предсказана в

рованы две цепочки распадов изотопов теннессина

294

1941 году Мигдалом [5]. В 1950-х годах этот

Ts и²⁹³¹¹⁷Ts, а также продуктов их деления, вклю-

117

процесс был подтвержден экспериментально для

чающих α-распад и спонтанное деление. Одной из

210

α-распада ядра

Po, причем было получено

этих цепочек является α-распадная ветвь, приво-

хорошее соответствие с теоретическими значени-

дящая к долгоживущему изотопу²⁷⁰¹⁰⁵Db, который

ями [5]. Однако позднее более точные расчеты

сам является α-излучателем и заселяет новый изо-

показали, что это согласие случайное, возникшее

топ²⁶⁶¹⁰³Lr [2]. История синтеза и изучения свойств

в результате того, что расчет [5] был выполнен в

теннессина приведена в обзоре [3].

дипольном приближении без учета более суще-

Целью работы является теоретическое изучение

ственных монопольных переходов. Детали этих

вероятности ионизации L_I (2s1/2)-, L_II (2p1/2)- и

исследований приведены в работах [6, 7]. Впер-

вые полное квантово-механическое рассмотрение

L_III (2p3/2)-оболочек дочерних атомов, участвую-

ионизации K-оболочки при α-распаде с учетом

щих в цепочке α-распадов:²⁹⁴¹¹⁷Ts,²⁸⁶¹¹³Nh,²⁷⁸¹⁰⁹Mt,

туннелирования α-частицы через кулоновский

270

Db. Для сравнения с имеющимися в литературе

105

барьер атома выполнено в работе [8].

теоретическими и экспериментальными значения-

В работах [4, 9] мы вычислили вероятности

ми мы вычислили также вероятность ионизации

ионизации K-оболочки дочерних атомов при α-

L_I-, L_II-, L_III-оболочек изотопа²¹⁰⁸⁴Po. В некоторых

распаде ряда изотопов сверхтяжелых элементов, а

случаях вероятность изучаемой здесь ионизации L-

также при распаде изотопов₈₄Po и изотопа²²²⁸⁶Rn.

оболочек сравнивается с ионизацией K-оболочки,

Расчеты были выполнены на основе квантово-

механической модели, предложенной в [8], в при-

¹⁾Физико-технический институт им. А.Ф. Иоффе, Санкт-

ближении внезапности. Учитывался эффект отдачи

Петербург, Россия.

²⁾НИЦ “Курчатовский институт”— Петербургский инсти-

ядра, а также эффект туннелирования α-частицы

тут ядерной физики, Гатчина, Россия.

через кулоновский барьер атома, для которого на-

^*E-mail: trzhask@thd.pnpi.spb.ru

ми получены уточненные формулы [9]. Использо-

ИОНИЗАЦИЯ L-ОБОЛОЧЕК ПРИ α-РАСПАДЕ

вались электронные волновые функции с учетом

процентов вносят даже октупольные переходы L =

экранирования и точного обменного взаимодей-

= 3.

ствия, вычисленные методом Дирака-Фока (ДФ),

В разд. 2 кратко описаны методы расчета и

вместо водородоподобных функций, обычно при-

приведены основные формулы. В разд. 3 обсуж-

меняемых в предыдущих работах.

даются результаты, полученные нами для распада

Сравнение показало, что наши значения веро-

изотопа полония²¹⁰⁸⁴Po и сверхтяжелых элементов.

ятности ионизации K-оболочки P_K (Q_α), где Q_α —

Результаты для полония сравниваются с экспери-

энергия α-частицы, полученные в [4, 9] для пяти

ментом [11] и с расчетами [12, 13]. Здесь же при-

изотопов полония и изотопа²²²⁸⁶Rn, лучше согласу-

водятся вычисленные впервые значения вероятно-

ются с экспериментом, чем расчеты [8]. Показано,

стей ионизации L_I-III-оболочек дочерних атомов

при распаде сверхтяжелых ядер, участвующих в

что вклад монопольных переходов (монопольный

цепочке α-распадов теннессина.

вклад) в величину вероятности P_K (Q_α) может быть

в несколько раз больше, чем вклад дипольных

переходов (дипольный вклад). В частности, моно-

2. МЕТОДЫ РАСЧЕТА И ОСНОВНЫЕ

польный вклад превышает дипольный в 4.5 раза

ФОРМУЛЫ

для²¹⁰⁸⁴Po, Q_α = 5305 кэВ и в 13 раз для²⁹⁴¹¹⁷Ts,

Q_α = 10 810 кэВ. В отличие от утверждения ра-

Согласно [8] полная амплитуда ионизации обо-

боты [8] получено, что учет туннелирования ока-

лочки при α-распаде представляется в виде суммы

зывается чрезвычайно существенным при расчете

стандартной полуклассической амплитуды процес-

вероятности ионизации K-оболочки.

са ионизации и квантовой амплитуды туннелиро-

вания α-частицы через кулоновский барьер ато-

Для более внешних L_I-III-оболочек было пред-

ма. Вылетающая α-частица представлена расхо-

сказано [10], что вероятность ионизации PLI-III (Q_α)

дящейся волной, которая сшивается с волновой

при α-распаде тяжелых ядер существенно увели-

функцией внутри ядра на расстоянии, равном ра-

чивается по сравнению с P_K (Q_α). Это подтвер-

диусу ядра R_nucl. Квантово-полуклассическая ам-

дил эксперимент [11], выполненный для²¹⁰⁸⁴Po при

плитуда вычислялась в приближении внезапности,

энергии Q_α = 5403 кэВ. Позднее появился расчет

при этом использовалась классическая траектория

вероятности PLI-III (Q_α) [12], выполненный с волно-

движения α-частицы от кулоновского барьера до

выми функциями с приближенным учетом экрани-

бесконечности.

рования, и расчет [13] с учетом экранирования.

В этой модели дифференциальная вероятность

В работе с использованием приближений и

ионизации i-й оболочки дочернего атома при α-

методов, подробно описанных в [4, 9], выполне-

распаде ядра с зарядом Z в приближении объеди-

ны расчеты вероятности ионизации L_I-III-оболочек

ненного атома [8] записывается в виде

210

Po при энергии Q_α = 5403 кэВ для сравнения

dP_i(E_f )

с имеющимися теоретическими и эксперименталь-

= (Z₁α)²(2j_i + 1)(2l_i + 1) ×

(1)

ными значениями. Впервые выполнены расчеты ве-

dE_f

роятности ионизации L_I-III-оболочек при распаде

∑

^∑ (2j_f + 1)(2l_f + 1)

сверхтяжелых ядер, участвующих в цепочке α-

(2L + 1)²

распадов²⁹⁴¹¹⁷Ts,²⁹⁶¹¹³Nh,²⁷⁸¹⁰⁹Mt и²⁷⁰¹⁰⁵Db. В вычис-

L κf

лениях использовались компьютерные программы,



(L)



входящие в наш комплекс RAINE [14].

× (CL0l

)²W²[l_ij_il_fj_f ;1/2L]H



².

i0lf 0

Расчеты показали, что ионизация L_I-III-обо-

Здесь Z₁ — заряд α-частицы, l и j — орбиталь-

лочек существенно отличается от случая K-

ный и полный моменты электрона, участвующе-

оболочки. Во-первых, вероятность ионизации

го в ионизации, L — мультипольность перехо-

L_I-III-оболочек приблизительно на два порядка

да, α = e²/ℏc — постоянная тонкой структуры,

величины больше, чем вероятность ионизации K-

оболочки. Во-вторых, для L_I-III-оболочек учет

κ = (l - j)(2j + 1) —релятивистское квантовое

туннелирования вносит очень небольшой вклад

число, CL0l

— коэффициент Клебша-Гордана,

i0lf 0

в вероятность. Этот вклад не превышает

W [l_ij_il_f j_f ; 1/2L] — коэффициент Рака. Индексы

для L_I-III-оболочек, в то время как вероятность

i и f относятся соответственно к начальному

ионизации K-оболочки изменяется за счет тун-

(связанному) состоянию и конечному (свободному)

нелирования на 60-70%. В-третьих, если для K-

состоянию, E_f — энергия вылетающего электрона.

и L_I-оболочек подавляющий вклад в вероятность

H(L)

Матричный элемент

= H(L)if/Z₁. Формулы

ионизации вносят монопольные переходы L = 0, то

для L_II- и L_III-оболочек дают вклады дипольные

записаны в релятивистской системе единиц, ℏ =

и квадрупольные переходы L = 1, 2. Несколько

= m₀ = c = 1.

ЯДЕРНАЯ ФИЗИКА том 82

№1

2019

НИКУЛИН, ТРЖАСКОВСКАЯ

∞

∫

[

]

Полная вероятность P_i(Q_α) ионизации i-й обо-

лочки атома при энергии α-частицы Q_α получается

+R^L

Gi(r)Gf (r) + Fi(r)Ff (r) dr.

rL+1

в результате интегрирования дифференциальной

вероятности dP_i(E_f )/dE_f по энергиям конечного

состояния электрона E_f . Матричный элемент H(L)if

Интегралы I(1)if и I(-1)if имеют следующий вид:

без учета туннелирования α-частицы через куло-

∞

∫

[

]

новский барьер имеет вид [4, 9]:

⎡

I(1)if = r Gi(r)Gf(r) + Fi(r)Ff(r) dr,

(7)

∫

∞

(L)

dΦ

(R)

H(L)if = Z₁ ⎣¹

sin(ωt)^R(t)

dt -

(2)

∫∞

]

1^[

⎤

I(-1)if =

Gi(r)Gf (r) + Fi(r)Ff (r) dr.

(8)

∫

∞

Z₂

-δL,1

I⁽¹⁾

cos(ωt)

dt^⎦ +

M₂

R²(t)

Функции G(r) = rg(r) и F (r) = rf(r) представля-

⎧

ют собой большую и малую компоненты реляти-

∫

dΦ(L)if(R)

вистской электронной волновой функции Дирака.

+ iZ₁

cos(ωt)^R(t)

dt +

Производная формфактора может быть представ-

⎩ ω

лена следующим образом:

∫

∞

(L)

dΦ

(R)

Z₂

+δL,1

I⁽¹⁾

sin(ωt)

dt +

(9)

M₂

R²(t)

⎧

⎫

⎨

[

]

⎬

LΦ(L)if(R) - (2L + 1)R-(L+1) ×

R⎩

Φ(L)if(R₀) - δL,0I(-1)

⎭

⎫

∫R

[

]

⎬

Здесь ω = E_f + ε_i — энергия электронного пере-

× r^L G_i(r)G_f(r) + F_i(r)F_f(r) dr

⎭

хода и ε_i — собственное значение энергии ионизу-

емой оболочки. Функция^R(t) следующим образом

связана с траекторией по времени R(t) движения

В расчетах используются электронные волно-

α-частицы от кулоновского барьера атома с ради-

вые функции начального и конечного состояний,

усом R₀ до бесконечности:

вычисленные методом ДФ с точным учетом обмен-

[

]1/2

ного взаимодействия как между связанными элек-

R₀

тронами, так и между связанными и свободными

^R(t) = v 1-

(3)

R(t)

электронами [14]. Волновая функция начального

состояния вычислялась в самосогласованном ме-

причем в начальный момент времени t = 0

тодом ДФ поле нейтрального атома, а волновая

R(0) = R₀ ;

^R(0) = 0.

(4)

функция конечного состояния — в ДФ-поле иона с

вакансией в i-оболочке. При вычислении волновых

Здесь R₀ = Z₁Z₂α/(Q_α - ω) и Z₂ = Z - Z₁. Ко-

функций учитывались конечные размеры ядра в

нечная скорость α-частицы v в формуле (3) опре-

предположении, что заряд равномерно распреде-

деляется следующим образом:

лен по сфере с радиусом R_nucl. В выражении (1)

[

∕

]1/2

сумма по мультипольностям L вычислялась с уче-

v = 2(Q_α - ω) μ

(5)

том всех членов, вносящих значимый вклад.

где μ — приведенная масса для массы α-частицы

M₁ и массы дочернего ядра M₂.

3. ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ

РЕЗУЛЬТАТОВ

Релятивистский формфактор Φ(L)if(R) в выра-

жении (2) записывается:

3.1. Вклад переходов различных мультипольностей

Φ(L)if(R) =

(6)

Как показано в [4, 9], основной вклад в вероят-

ность ионизации K-оболочки вносят монопольные

∫

[

]

переходы. Рассмотрим, какие мультипольности

r^L G_i(r)G_f (r) + F_i(r)F_f (r) dr +

важны при вычислении ионизации L_I-III-оболочек.

RL+1

На рис. 1 приведены вклады в дифференциальную

ЯДЕРНАЯ ФИЗИКА том 82

№1

2019

ИОНИЗАЦИЯ L-ОБОЛОЧЕК ПРИ α-РАСПАДЕ

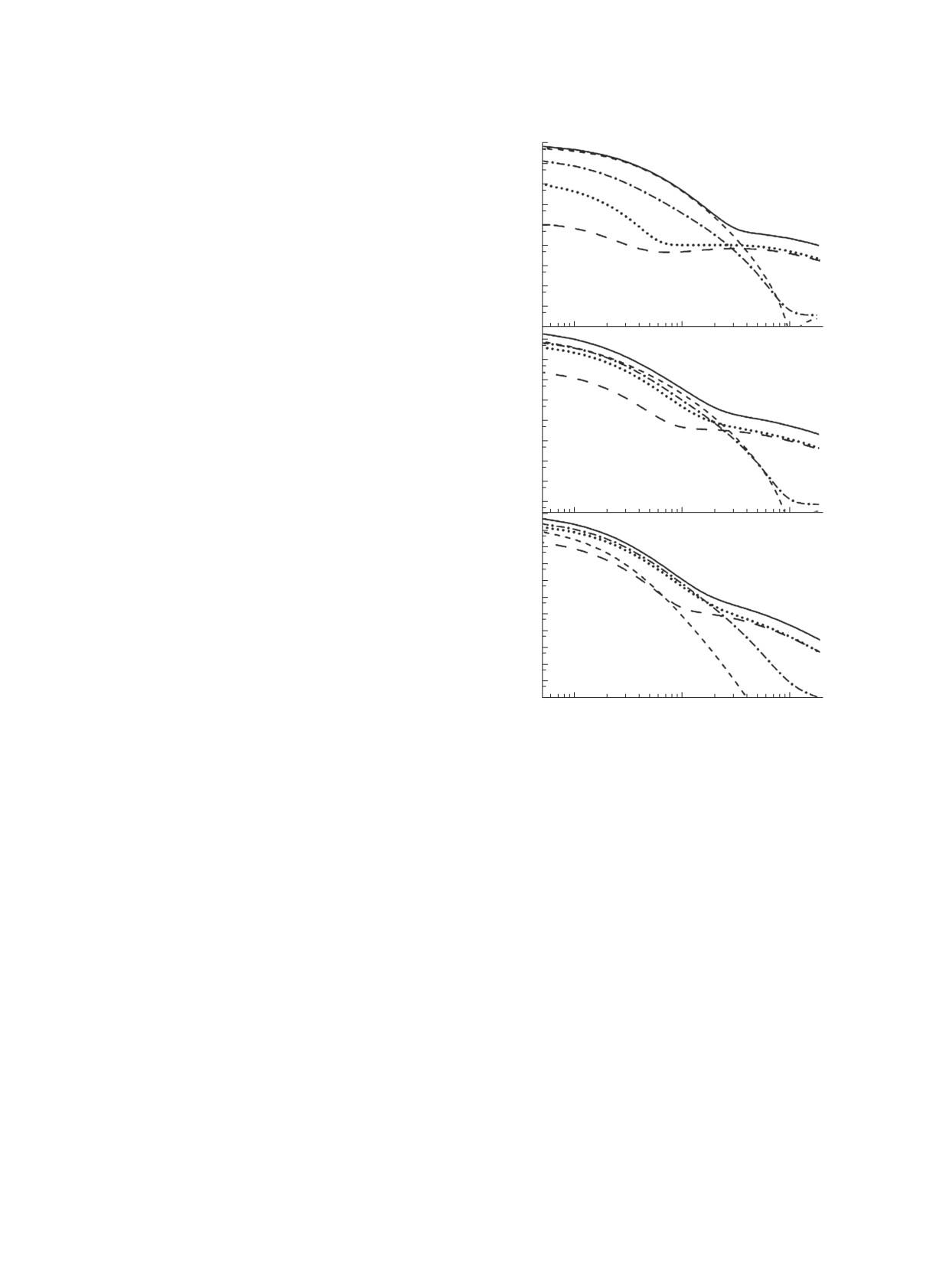
вероятность ионизации dPLI-III (E_f )/dE_f при α-

dP_L(E

)/dE_f, (мс²)^-1

распаде изотопа дубния²⁷⁰¹⁰⁵Db с энергией Q_α =

10^-2

= 8800 кэВ, соответствующие переходам муль-

типольности L = 0 (штриховые кривые), L = 1

10^-4

(штрихпунктирные), L = 2 (точечные) и L = 3

(штриховые с длинными штрихами). Сплошные

10^-6

кривые представляют собой сумму этих вкла-

дов. Рисунок 1а демонстрирует, что при низких

10^-8

энергиях E_f для L_I-оболочки основной вклад

дают монопольные переходы, дипольные вносят

10^-10

значительно меньший вклад, а квадрупольные —

малы. Для L_II-оболочки (рис. 1б) монопольный

и дипольный вклады приблизительно одинаковы,

10^-4

а квадрупольный — несколько меньше. Для L_III-

оболочки (рис. 1в) дипольный и квадрупольный

10^-6

вклады приблизительно одинаковы, а монополь-

ный — меньше и уменьшается с увеличением

10^-8

энергии E_f , оказываясь при E_f ≥ 80 кэВ даже

меньше октупольного вклада.

10^-10

Видно, что при увеличении энергии свободного

электрона (E_f ≥ 300 кэВ) вклады высоких мульти-

польностей L = 2, 3 падают медленнее, чем вклады

10^-4

L = 0,1, однако величина этих вкладов, как и сама

сумма, в этой области сильно уменьшаeтся по

10^-6

сравнению с областью низких энергий E_f и при

интегрировании вносит небольшой вклад в полную

10^-8

вероятность ионизации. Рисунок 1 показывает так-

же, что для разных L-подоболочек вклады, соот-

10^-10

ветствующие одинаковым мультипольностям, раз-

10^-12

личаются по величине и поведению. Это приводит

к тому, что в полной вероятности ионизации L_I-,

10¹

10²

10³

L_II- и L_III-оболочек доминируют вклады различных

E_f, кэВ

мультипольностей.

Рис.

Вклады

переходов

различных

Относительные вклады разных мультипольно-

мультипольностей в дифференциальную вероятность

стей в полную вероятность ионизации PLI-III (Q_α)

dPL_I-III (Ef )/dEf ионизации LI- (а), LII- (б) и (в)

представлены в табл. 1 для L_I-III-оболочек при α-

L_III-оболочек при α-распаде изотопа²⁷⁰¹⁰⁵Db с энергией

Qα = 8800 кэВ. Кривые: штриховая — монопольный

распаде²¹⁰⁸⁴Po с энергией Q_α = 5403 кэВ,²⁷⁰¹⁰⁵Db с

вклад (L = 0), штрихпунктирная — дипольный вклад

энергией Q_α = 8800 кэВ и²⁹⁴¹¹⁷Ts с энергией Q_α =

(L = 1); точечная — квадрупольный вклад (L = 2);

= 10 810 кэВ. Для сравнения даны также вклады

штриховая с длинными штрихами — октупольный

вклад (L = 3); сплошная — сумма всех этих вкладов.

для K-оболочки. Данные показывают, что вели-

чина вероятности ионизации L_I-оболочки, как и

K-оболочки, формируется в основном за счет мо-

уместно вспомнить, что в [5] при расчете иониза-

нопольных переходов. Значительно меньший, но

ции этих оболочек учитывался только дипольный

весьма заметный вклад вносят дипольные перехо-

вклад.

ды. Как отмечалось в [4, 9], вклад квадрупольных

переходов в вероятность ионизации K-оболочки

Для L_II-оболочки ситуация меняется. Для α-

незначителен. Как видно из таблицы, квадруполь-

распада²¹⁰⁸⁴Po основной вклад в полную вероят-

ный вклад для L_I-оболочки тоже небольшой —

ность ионизации (46%) вносят дипольные пере-

∼3% для полония и ∼1% для дубния и теннес-

ходы, и существенные вклады дают монопольные

сина. Сравнение данных для разных элементов

и квадрупольные переходы — 22% и 30% соот-

показывает, что с увеличением заряда ядра отно-

ветственно. Небольшой вклад вносят даже окту-

сительный вклад монопольного члена в вероят-

польные переходы. Однако с увеличением Z это

ность ионизации K- и L_I-оболочек увеличивает-

соотношение изменяется в сторону увеличения мо-

ся, а вклад дипольного члена уменьшается. Здесь

нопольного вклада. Расчеты показали, что вклад

ЯДЕРНАЯ ФИЗИКА том 82

№1

2019

НИКУЛИН, ТРЖАСКОВСКАЯ

Таблица 1. Относительные вклады (в %) переходов разных мультипольностей в полную вероятность ионизации

K- и L_I-III-оболочек при α-распаде изотопов 21084 Po с энергией α-частицы Q_α = 5403 кэВ, ²⁷⁰¹⁰⁵Db с энергией

Q_α = 8800 кэВ и²⁹⁴¹¹⁷Ts с энергией Q_α = 10 810 кэВ

210

270

294

Обо-

105

117

лочка

L=0

L=1

L=2

L=3

L=0

L=1

L=2

L=3

L=0

L=1

L=2

L=3

81.8

17.9

0.3

0.0

88.7

11.2

0.1

0.0

93.0

7.0

0.0

L_I

69.8

27.6

2.6

0.0

85.4

13.7

0.8

0.1

90.7

8.5

0.5

0.3

L_II

21.5

46.3

29.8

2.4

40.8

37.5

20.6

1.1

67.4

21.0

10.7

0.9

L_III

16.2

48.3

31.4

4.0

14.1

50.8

31.8

3.3

15.6

49.9

30.8

3.6

монопольных переходов составляет 41% для Db,

полученные в наших расчетах, с предыдущими

49% для Mt, 58% для Nh и 67% для Ts.

вычислениями [12, 13] и с экспериментальными

Для L_III-оболочки всех рассматриваемых эле-

значениями [11]. Сравнение показывает, что наши

ментов основной вклад вносят дипольные (∼50%)

значения вероятности PLI-III (Q_α), Q_α = 5403 кэВ

и квадрупольные (∼30%) переходы. Монополь-

отличаются от величин, полученных в работе [13],

ные переходы вносят меньший, но заметный вклад

и еще больше отличаются от значений [12]. Однако

∼15%. Несколько процентов, обычно ≤4% во всех

во всех трех расчетах L_I-оболочка имеет наиболь-

рассматриваемых случаях дает октупольный член.

шую вероятность ионизации, для L_II-оболочки эта

3.2. Влияние эффекта туннелирования

Таблица 2. Вероятности P_i(Q_α) × 10⁴ ионизации K-

на вероятность ионизации

и L_I-III-оболочек, сопровождающей α-распад изотопов

210

Другое отличие ионизации L_I-III-оболочек от

Po при энергии Q_α = 5403 кэВ и²⁸⁶¹¹³Nh при энергии

ионизации K-оболочки состоит в том, что эффект

Q_α = 9300 кэВ, вычисленные с учетом туннелирования

туннелирования α-частицы через кулоновский ба-

(TUN) и без учета туннелирования (NoTUN) α-частицы

рьер практически не вносит вклад в вероятность

через кулоновский барьер

PLI-III (Q_α). Для оценки вклада туннелирования мы

вычисляли вероятность ионизации L_I-III-оболочек

210

286

113

Оболочка

при α-распаде с учетом и без учета этого эффекта.

TUN NoTUN TUN NoTUN

Результаты этих расчетов для ядер полония²¹⁰⁸⁴Po

и нихония²⁸⁶¹¹³Nh представлены в табл. 2, где для

0.0318

0.0504

0.0539

0.0970

сравнения приведены также вычисления для K-

оболочки.

L_I

3.08

3.10

2.90

2.95

Данные табл. 2 демонстрируют, что, как отмеча-

L_II

0.875

0.879

5.47

лось в [4, 9], учет туннелирования уменьшает веро-

ятность ионизации K-оболочки на 58% для Z = 84

L_III

2.45

2.46

1.05

и на 80% для Z = 113. Однако эффект туннелиро-

вания очень мало влияет на вероятность ионизации

всех L_I-III-оболочек. Максимальное изменение ве-

Таблица 3. Сравнение вероятностей ионизации L_I-III-

роятности составляет 1.7% для L_I-оболочки при

оболочек PLI-III (Q_α) × 10⁴, сопровождающей α-распад

α-распаде ядра²⁸⁶¹¹³Nh. Из табл. 2 видно также,

ядра²¹⁰⁸⁴Po при энергии Q_α = 5403 кэВ, с расчетами [12,

что вероятность ионизации L_I-III-оболочек на два

13] и экспериментальными значениями [11]

порядка превышает вероятность ионизации K-

оболочки.

Обо- Расчет

Расчет

Наш Экспери-

лочка

[12]

[13]

pасчет мент [11]

3.3. Сравнение вероятности ионизации

L_I

1.73

2.43

3.08

3.05

L_I-III-оболочек с другими расчетами

и экспериментом

L_II

0.25

1.14

0.878

2.83

В табл. 3 мы сравниваем вероятности ионизации

L_III

0.76

1.90

2.46

3.20

L_I-III-оболочек, сопровождающей α-распад²¹⁰⁸⁴Po,

ЯДЕРНАЯ ФИЗИКА том 82

№1

2019

ИОНИЗАЦИЯ L-ОБОЛОЧЕК ПРИ α-РАСПАДЕ

P_L(Q_α) × 10⁴

5.0

5.2

5.4

5.6

10.4

10.8

11.2

11.6

Q_α, МэВ

Рис. 2. Зависимость полной вероятности PL_I-III (Qα) ионизации LI- (сплошная кривая), LII- (штриховая) и LIII-

(штрихпунктирная) оболочек от энергии α-частицы Qα для α-распада изотопов полония⁸⁴⁰Po (а) и теннессина¹¹⁷Ts (б).

вероятность сильно падает, а для L_III-оболочки

в широком интервале энергий α-частицы для ядер

снова возрастает примерно в 3 раза в данном рас-

210

Po и²⁹⁴¹¹⁷Ts. Как видно, зависимость PLI-III (Q_α)

чете и в [12], но только в 1.7 раза в расчете [13]. На-

во всех случаях представляет собой прямую линию

ши результаты очень хорошо совпадают с экспери-

с небольшим и приблизительно одинаковым углом

ментом [11] для L_I-оболочки и меньше отличаются

наклона по отношению к оси x, т.е. вероятность

от экспериментальных значений, чем вероятности

ионизации изменяется с энергией Q_α плавно и не

ионизации для L_III-оболочки из [12, 13].

очень значительно.

3.4. Вероятность ионизации L_I-III-оболочек

4. ЗАКЛЮЧЕНИЕ

при α-распаде сверхтяжелых ядер

Вычислена вероятность ионизации L_I-, L_II- и

Мы вычислили вероятности ионизации L_I-III-

L_III-оболочек дочерних атомов при α-распаде изо-

оболочек дочерних атомов при α-распаде изото-

топов сверхтяжелых ядер, которые в настоящее

пов, входящих в распадную цепочку теннессина, а

время синтезируются и активно изучаются экспе-

именно для изотопов²⁹⁴¹¹⁷Ts,²⁸⁶¹¹³Nh,²⁷⁸¹⁰⁹Mt и²⁷⁰¹⁰⁵Db.

риментально, а также изотопа²¹⁰⁸⁴Po, для которого

Эти данные важны при обработке спектров, по-

имеются полученные ранее теоретические и экспе-

лучаемых в объединенной α-, γ- и электронно-

риментальные результаты.

конверсионной спектроскопии. Вероятности иони-

Наши расчеты основаны на квантово-механи-

зации L_I-III-оболочек при α-распаде сверхтяже-

ческой модели [8]. Учитывалось туннелирование

лых ядер приведены в табл. 4. Расчеты выполнены

α-частицы через кулоновский барьер атома. Ис-

описанным выше методом с учетом туннелирования

пользовались релятивистские электронные волно-

α-частицы через кулоновский барьер и с электрон-

вые функции c точным учетом экранирования и

ными волновыми функциями, полученными мето-

обменного взаимодействия как между связанными

дом ДФ. В работах [2] и [3] приведены существенно

электронами, так и между связанными и свободны-

различные значения энергии α-распада сверхтя-

ми электронами, полученные методом ДФ.

желых ядер с зарядами 105 ≤ Z ≤ 117, поэтому в

Сравнение с имеющимися теоретическими и

табл. 4 представлены расчеты для двух наборов

экспериментальными значениями вероятности

энергий Q_α.

210

ионизации L_I-III-оболочек для α-распада

Как показывают данные табл. 4, вероятность

показывает, что полученные в работе значения

PLI-III (Q_α) слабо зависит от энергии α-частицы

PLI-III (Q_α) лучше согласуются с эксперимен-

в отличие от вероятности K-оболочки. Напри-

том [11], чем расчеты [12, 13].

мер, для изотопа дубния²⁷⁰¹⁰⁵Db отличие в энергии

Результаты показали, что вероятность иониза-

Q_α на 11% приводит к изменению вероятности

ции L_I-III-оболочек полония и сверхтяжелых эле-

P_K(Q_α) на 41%, тогда как в случае L-оболочек

ментов превышает вероятность ионизации наибо-

наибольшее различие в вероятностях составляет

лее внутренней K-оболочки в несколько десятков

21% для L_II-оболочки. Зависимость вероятности

раз. В отличие от K-ионизации учет туннелиро-

ионизации L_I-III-оболочек от Q_α демонстрируется

вания для L_I-III-оболочек оказывается несуще-

на рис. 2, где приведены значения PLI-III (Q_α) × 10⁴

ственным при вычислении вероятности PLI-III (Q_α).

ЯДЕРНАЯ ФИЗИКА том 82

№1

2019

НИКУЛИН, ТРЖАСКОВСКАЯ

Таблица 4. Вероятность ионизации L_I-III-оболочек P_L

(Q_α) × 10⁴ при α-распаде изотопов сверхтяжелых

I-III

элементов

Изотоп

Оболочка

Qα1), кэВ [2]

P_L(Qα1)) × 10⁴

Qα2), кэВ [3]

P_L(Qα2)) × 10⁴

294

117

L_I

10810

3.346

11070

3.411

L_II

0.719

0.746

L_III

1.109

1.151

286

L_I

9300

2.899

9630

2.988

113

L_II

0.547

0.579

L_III

1.046

1.105

278

L_I

9420

2.947

9550

2.979

109

L_II

0.581

0.595

L_III

1.298

1.326

270

105

L_I

7890

2.616

8800

2.862

L_II

0.477

0.578

L_II

1.208

1.438

Подавляющий вклад в вероятность ионизации L_I-

5. А. Б. Мигдал, ЖЭТФ 11, 207 (1941).

оболочки, как и в случае ионизации K-оболочки,

6. L. Kocbach, in Proceedings of the Nordic Spring

вносят монопольные переходы. Для L_II- и L_III-

Symposium on Atomic Inner Shell Phenomena,

оболочек основными являются дипольный и квад-

Ed. by J. M. Hansteen and R. Gundersen (University

рупольный вклады. Заметным может быть даже

of Bergen, Norway, 1978), Vol. 2, p. 65.

октупольный вклад.

7. M. Lund, J. U. Andersen, E. Lagsgaard, and

Впервые выполнены расчеты вероятностей

L. Kocbach, http://www.phys.au.dk/main/publica-

ионизации PLI-III (Q_α) при α-распаде сверхтяже-

tions/ PhD/Martin_Lund.pdf

лых ядер, входящих в одну из цепочек теннессина:

294

Ts,²⁸⁶¹¹³Nh,²⁷⁸¹⁰⁹Mt и²⁷⁰¹⁰⁵Db. Сверхтяжелые ядра

117

8. R. Anholt and P. A. Amundsen, Phys. Rev. A 25, 169

интенсивно изучаются в настоящее время [1-

(1982).

3], поэтому выполненные расчеты важны для

интерпретации спектров, получаемых при синтезе

9. M. B. Trzhaskovskaya and V. K. Nikulin, Phys. Rev.

сверхтяжелых элементов в объединенной α-, γ- и

C 93, 034312 (2016).

электронно-конверсионной спектроскопии.

10. J. S. Levinger, Phys. Rev. 90, 11 (1953).

СПИСОК ЛИТЕРАТУРЫ

11. H. J. Fischbeck and M. S. Freedman, Phys. Rev. Lett.

34, 173 (1975).

1. Yu. Ts. Oganessian, F. Sh. Abdullin, C. Alexander,

et al., Phys. Rev. C 87, 054621 (2013).

12. J. Law, Nucl. Phys. A 286, 339 (1977).

2. J. Khuyagbaatar, A. Yakushev, Ch. E. D ¨ullmann,

et al., Phys. Rev. Lett. 112, 172501 (2014).

13. S. R. McConnell, A. N. Artemyev, and A. Surzhykov,

J. Phys. B 44, 145204 (2011).

3. https://en.wikipedia.org/wiki/Tennessine

14. I. M. Band, M. B. Trzhaskovskaya, C. W. Nestor, Jr.,

4. В. К. Никулин, М. Б. Тржасковская, Изв.

РАН. Сер. физ. 81, 1343

(2017)

[Bull. Russ.

P. O. Tikkanen, and S. Raman, At. Data Nucl. Data

Acad. Sci. Phys. 81, 1207 (2017)].

Tables 81, 1 (2002).

ЯДЕРНАЯ ФИЗИКА том 82

№1

2019