ЯДЕРНАЯ ФИЗИКА, 2019, том 82, № 3, с. 267-276
ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ
СРАВНИТЕЛЬНЫЙ АНАЛИЗ CP -НАРУШЕНИЯ
В ЭКСПОНЕНЦИАЛЬНОЙ И СТАНДАРТНОЙ ПАРАМЕТРИЗАЦИИ
МАТРИЦЫ СМЕШИВАНИЯ НЕЙТРИНО
© 2019 г. А. А. Давыдова, К. В. Жуковский*
Московский государственный университет им. М. В. Ломоносова, физический факультет, Россия
Поступила в редакцию 20.11.2018 г.; после доработки 20.11.2018 г.; принята к публикации 20.11.2018 г.
Проводится сравнительный анализ смешивания нейтрино в стандартной, кобимаксимальной, триби-
максимальной и экспоненциальной параметризациях. В соответствии с последними эксперименталь-
ными данными о смешивании нейтрино находится логарифм матрицы смешивания и точные значения
каждого элемента экспоненциальной матрицы смешивания нейтрино, которая позволяет факторизо-
вать вклады чисто вращательных компонент матрицы смешивания и ее элементов, отвечающих за CP -
нарушение. Подтверждается гипотеза дополнительности смешивания кварков и нейтрино. С помощью
инварианта Ярлског исследуется зависимость CP-нарушения от параметров матрицы смешивания
в различных параметризациях, а также взаимосвязь между самими параметрами. С использованием
экспоненциальной параметризации матрицы смешивания исследуются представление последней в
качестве элемента группы SU(3) с параметрами ϕ и θ и их зависимости от степени CP -нарушения.
DOI: 10.1134/S0044002719020041
1. ВВЕДЕНИЕ
механизм возникновения малой массы наблюдае-
мых нейтрино называется качельным механизмом
Стандартная модель [1-3] успешно объясняет
[6, 7]. Массовое слагаемое для нейтрино после
многие явления физики элементарных частиц. В еe
исключения из него правых нейтрино с помощью
рамках изначально предполагалось, что нейтрино
уравнений движения будет содержать недиаго-
имеют нулевую массу и левую киральность. Однако
нальную комплексную массовую матрицу [7]:
открытие нейтринных осцилляций [4, 5] позволило
сделать вывод о том, что нейтрино не является
1
безмассовой частицей, при том, что ее масса ока-
Lmass(ν) = -
(νeLνμLντL) ×
(2)
зывается на много порядков меньше масс дру-
2
гих элементарных частиц. Наиболее естественным
× mνLL(νeeLνeμLνeτL) + H.c.,
способом введения в стандартную модель малой
(
)
массы нейтрино является добавление в лагранжиан
где mνLL = -ν2uYν diag
M-11,M-12,M-13
YTν и
модели правых (RH) или стерильных нейтрино:
diag (M1, M2, M3) = VνR M∗RRVT . Это обуславли-ν
R
Lmass = -eLvdY∗eeR - vLvuY∗vvR -
(1)
вает нарушение CP -инвариантности действия в
1
стандартной модели и нарушение закона сохра-
-
vTRM∗RRvR + H.c.,
2
нения лептонных чисел для каждого поколения.
где eL, eR, vL, vR — поля левых и правых за-
Наличие недиагональных компонент в массовой
матрице приводит к смешиванию нейтрино. Это
ряженных лептонов и нейтрино, Ye, Yv — матри-
цы из безразмерных констант юкавского взаимо-
означает, что существует такое унитарное преоб-
действия для заряженных лептонов и нейтрино,
разование нейтринных полей, после которого мас-
MRR — майорановская массовая матрица, H2u
=
совая матрица становится диагональной. Новые
поля будут собственными массовыми состояниями
=υu, H1d
= υd — вакуумные средние значения
нейтрино, т.е. имеющими определенную массу.
поля Хиггса. Правые нейтрино являются скаляра-
Наблюдаемые флейворные состояния нейтрино νe,
ми относительно группы SU(3) × SU(2) × U(1) и
νμ, ντ представляют собой линейную комбинацию
имеют массу порядка 1016 ГэВ, что не позволяет
массовых состояний нейтрино ν1, ν2, ν3, переход к
их наблюдать в современных экспериментах. Такой
которым описывается унитарной матрицей смеши-
*E-mail: zhukovsk@physics.msu.ru
вания U Понтекорво-Маки-Накагавы-Сакаты
267
268
ДАВЫДОВА, ЖУКОВСКИЙ
(PMNS) [8]:
пропорциональна |Uαi|2. Аналогичное смешивание
∑
присутствует и в кварковом секторе; оно несколько
|να〉 =
U∗αi|νi〉, Uαi ≡ 〈να|νi〉,
(3)
меньше и описывается матрицей V Кабиббо-
i=1,2,3
Кобаяши-Маскавы (CKM). Наиболее распро-
α = e,μ,τ, i = 1,2,3.
страненной формой матрицы смешивания является
Амплитуда вероятности перехода данного флей-
трехфлейворное стандартное смешивание по схеме
вора α в массовое собственное состояние i Chau-Keung (CK) [9]:
⎛
⎞⎛
⎞⎛
⎞⎛
⎞
1
0
0
c13
0 s13e-iδCP
c12
s12
0
1
⎜
⎟⎜
⎟⎜
⎟⎜
⎟
⎜
⎟⎜
⎟⎜
⎟⎜
⎟
U=
⎜
⎟⎜
⎟⎜
⎟⎜
iα
⎟
=
(4)
c23
s23
0
1
0
s12 c12
0
⎝0
⎠⎝
⎠⎝-
⎠⎝ e
⎠
0 -s23 c23
-s13e-iδCP
0
c13
0
0
1
eiβ
⎛
⎞⎛
⎞
c12c13
s12c13
s13e-iδCP
1
⎜
⎟⎜
⎟
⎜
⎟⎜
⎟
=
⎜
⎟⎜
iα
⎟
=U=UstPMjr,
s12c23 - c12s23s13eiδCP c12c23 - s12s23s13eiδCP
s23c13
⎝-
⎠⎝ e
⎠
s12s23 - c12c23s13eiδCP
-c12s23 - s12c23s13eiδCP c23c13
eiβ
√
где cij = cos θij , sij = sin θij, i = 1, 2, 3, θij — углы
sin2 θ23 = 1/2, sin θ12 = 1/
3:
смешивания (см. рис. 1), δCP — CP -нарушающая
⎛
⎞
1
1
√
√
0
фаза, PMjr = diag(1, eiα, eiβ ) — матрица фаз майо-
⎜
2
2
⎟
⎜
⎟
рановского нейтрино.
1
1
UBM =
⎜-1
√
⎟
,
(5)
⎝
2
2
2
⎠
Можно построить еще 11 матриц смешивания,
1
1
-12
√
2
2
похожих на (4) и различающихся только положе-
⎛
√
⎞
нием комплексной фазы и порядком сомножителей
2
1
√
0
3
3
(см. [9]). Также были предложены модели сме-
⎜
⎟
⎜
⎟
шивания, основанные на различных симметриях,
1
1
UTBM =
⎜
√
√
√
⎟
⎝
6
3
2
⎠
например, бимаксимальная (BM) матрица, связан-
1
1
ная с дискретной группой симметрий тетраэдра S4,
√
√
√
6
3
2
для которой sin θ13 = 0, sin2 θ12 = sin2 θ23 = 1/2, и
Трибимаксимальная матрица UTBM (5) (см. [10])
трибимаксимальная (ТВМ) матрица, основанная
согласуется с экспериментальными данными луч-
на группах симметрий A4 и S4 [10], где sin θ13 = 0,
ше, чем UBM, но она не вполне точно описывает
измеренные углы смешивания. В связи с этим
были введены малые поправки, описывающие от-
ν3
клонения от ТВМ матрицы [9]. Существует также
νμ
кобимаксимальная (CBM) форма записи матрицы
θ13
ν
τ
смешивания [11], в которой фиксируются два па-
θ
раметра: θ23 =π4 и δCP = ±π2 . Она получается из
θ
23
23
стандартной параметризации (4):
θ12
ν2
UCBM =
(6)
⎛
⎞
νε
c12c13
s12c13
∓is13
⎜
⎟
√
√
√
θ
θ13
⎜
⎟
ν1
12
2
2
2
=
⎜
-
(s12 ± ic12)
(c12 ∓ is12)
c13
⎟
⎝
2
2
2
⎠
√
√
√
2
2
2
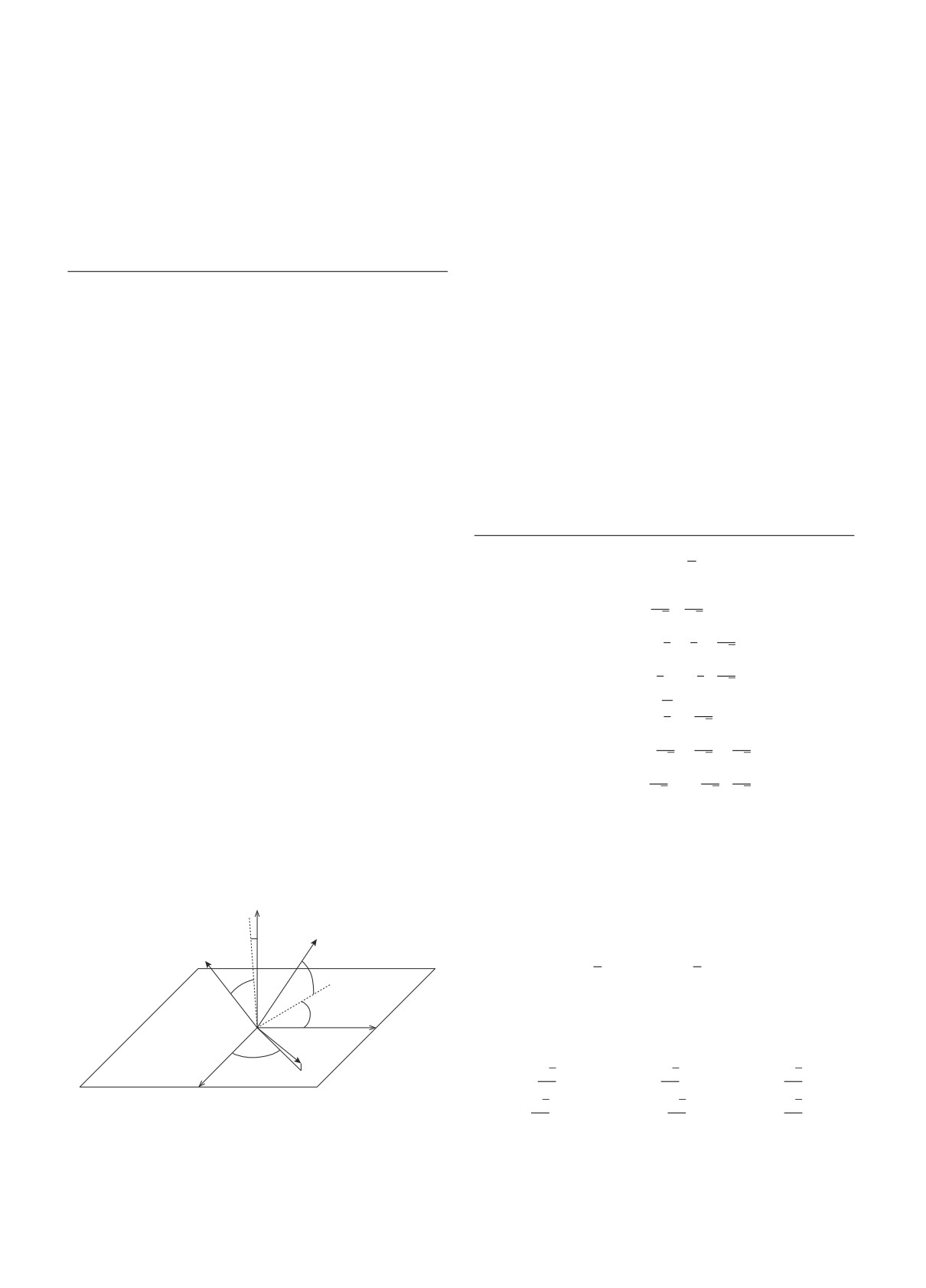
Рис.
1.
Углы смешивания нейтрино (без
(s12 ∓ ic12)
-
(c12 ± is12)
c13
2
2
2
CP-нарушения) могут быть представлены как
углы Эйлера, связывающие базис ν1, ν2, ν3 с базисом
Для кварков из-за малого смешивания и CP -
νe, νμ, ντ .
нарушения соответствующая матрица смешивания
ЯДЕРНАЯ ФИЗИКА том 82
№3
2019
СРАВНИТЕЛЬНЫЙ АНАЛИЗ CP -НАРУШЕНИЯ
269
V близка к единичной. Малые параметры отклоне-
проверяется кварк-лептонная комплементарность
ния от единичной матрицы λ, A, ρ, η были введены
с помощью параметризации матрицы смешивания
Вольфенштейном [12]. Для нейтрино был также
в виде матричной экспоненты [14-20]. Мы будем
предложен способ определения малых поправок,
рассматривать дираковские нейтрино, так что α =
выраженных через параметры Вольфенштей-
= β = 0. Таким образом, матрица смешивания U
на с использованием эмпирических соотноше-
полностью определяется четырьмя параметрами:
ний [13], — кварк-лептонная комплементарность
углами смешивания θ12, θ23, θ13 и фазой δCP ,
(Quark-lepton complementarity (QLC)) и лептонная
комплементарность (Self-lepton complementarity
соответствующей CP -нарушению. С эксперимен-
(SC)) — которые связывают углы смешивания
тальными данными [21] матрица смешивания имеет
для кварков и нейтрино. В настоящей работе
следующее численное значение:
⎛
⎞
0.823
0.548
-0.087 + 0.120i
⎜
⎟
⎜
⎟
Ubestfit =
⎜
0.323 + 0.073i
0.601 + 0.049i
0.726
⎟
(7)
⎝-
⎠
0.456 + 0.068i
-0.578 + 0.045i
0.672
Абсолютные значения ее элементов изменяются в следующих пределах:
⎛
⎞
0.799 → 0.844 0.516 → 0.582 0.141 → 0.156
⎜
⎟
⎜
⎟
|U|3σ =
⎜
.242 → 0.494 0.467 → 0.678 0.639 → 0.774⎟
(8)
⎝0
⎠
0.284 → 0.521 0.490 → 0.695 0.615 → 0.754
2. ИНВАРИАНТ ЯРЛСКОГ
где Uαi ≡ 〈να|νi〉, α = e, μ, τ, i = 1, 2, 3. Соотно-
В силу унитарности матрицы смешивания спра-
шения (9) можно представить как треугольники на
ведливы следующие соотношения:
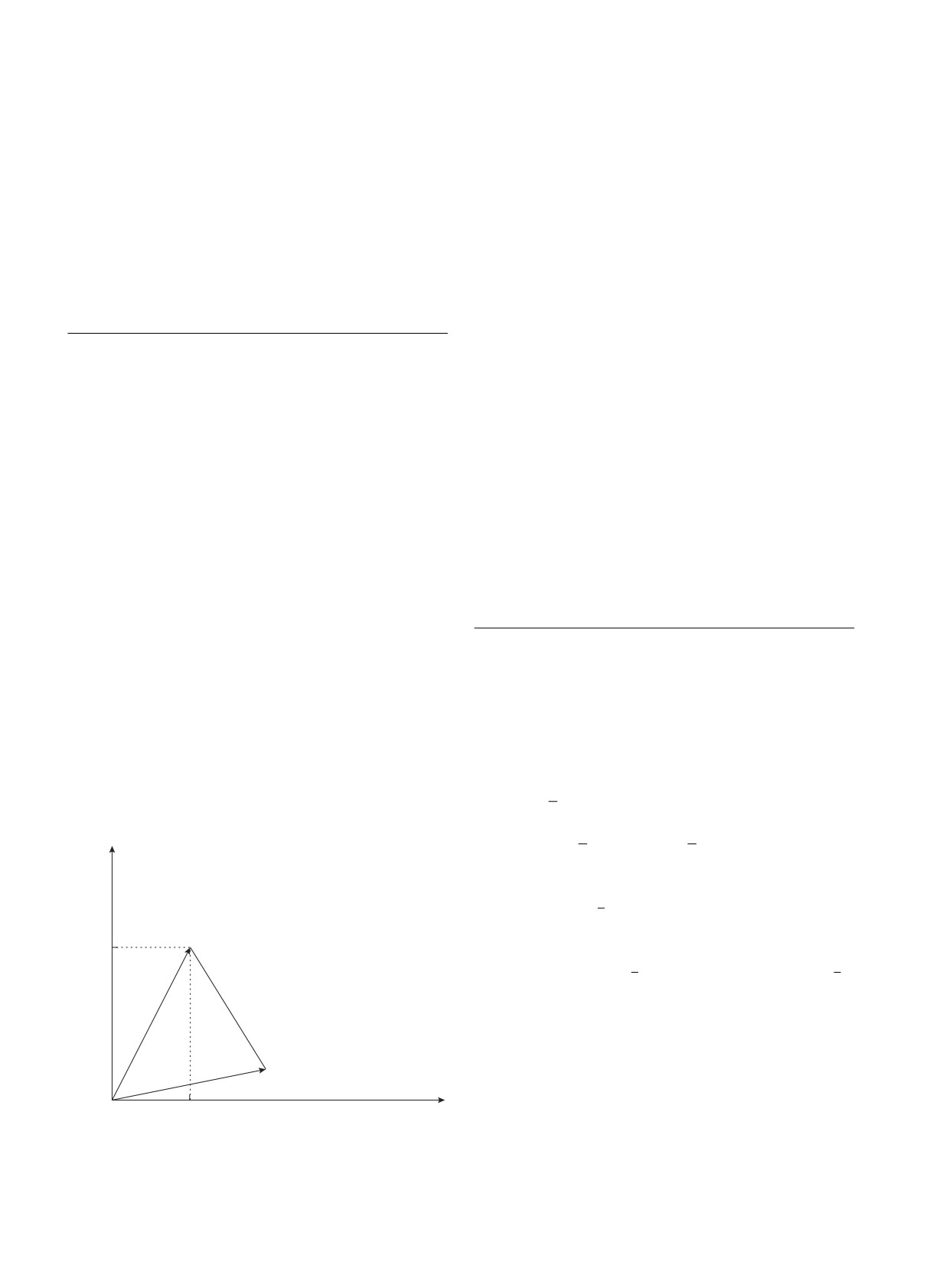
комплексной плоскости (см. рис. 2) в трехмерном
∑
пространстве. Площадь такого треугольника (см.
UiαU∗jα = δij,
(9)
рис. 2) равна половине модуля векторного произ-
i=1,2,3
ведения векторов {Rea, Ima, 0} и {Reb, Imb, 0}:
∑
UiαU∗iβ = δαβ,
1
i=e,μ,τ
S=
|(Rea) (Imb) - (Reb) (Ima)| =
(10)
2
1
1
y
|Im (a∗b)| .
= 2|Im(ab∗)|=
2
Взяв в качестве чисел a = Ue1U∗e3 и b = -Uμ1U∗μ3,
1
получаем S =
Im(Ue1U∗e3U∗μ1Uμ3)
. В силу
2
унитарности матрицы U справедливо равенство
U∗e3Ue3 = -U∗e1Uμ1 - U∗e2Uμ2, из которого следу-
1
= 1
ет, что площадь S =
Im(Ue1Uμ2U∗e2U∗μ1)
J.
2
2
a
Аналогичным образом можно вычислить площади
Im(a)
других треугольников и показать, что их площади
равны 1/2J, где J — инвариант Ярлског [22]. Для
матрицы U в виде (4) получим:
b
J = Im(Ue1Uμ2U∗e2U∗μ1) = cosθ12 sinθ12 ×
(11)
Re(a)
x
× cos2 θ13 sin θ13 cos θ23 sin θ23 sin δCP .
Рис. 2. Визуализация треугольника Ярлског на ком-
Поскольку J пропорционален sin δCP , то он отли-
плексной плоскости.
чен от 0 тогда и только тогда, если имеет место
ЯДЕРНАЯ ФИЗИКА том 82
№3
2019
270
ДАВЫДОВА, ЖУКОВСКИЙ
0.65
sinθ23
0.70
0.75
0.03
0.02
J
0.01
0
200
250
δCP
300
350
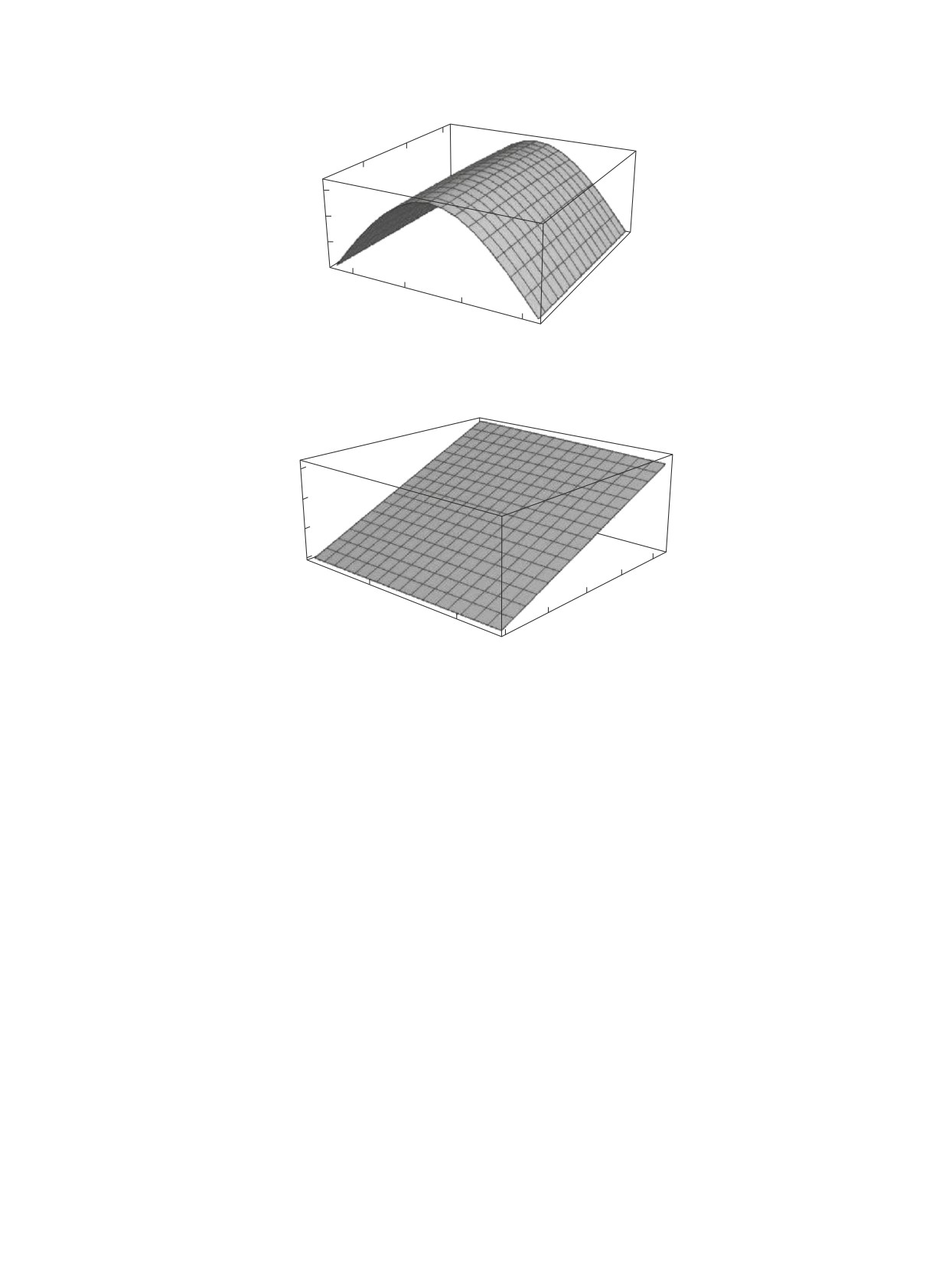
Рис. 3. Зависимость модуля J от sin θ23 и δCP для нейтрино. Значения остальных параметров фиксированы в
соответствии с экспериментальными данными [21].
J
0.00006
0.00004
0.00002
0
0.08
0.06
70
0.04
δCP
0.02
sinθ23
65
0
Рис. 4. Зависимость J от sin θ23 и δCP для кварков.
нарушение CP-инвариантности. Фактически инва-
(6) на рис. 5 исправляет ранее полученный в [11]
риант Ярлског представляет собой меру нарушения
результат.
CP-инвариантности, которая не зависит от кон-
кретного вида параметризации матрицы смешива-
3. ЭКСПОНЕНЦИАЛЬНАЯ
ния, и позволяет графически оценивать величину
ПАРАМЕТРИЗАЦИЯ
CP-нарушения; пример в стандартной параметри-
Матрицу смешивания можно записать в виде
зации на основе экспериментальных данных [21]
матричной экспоненты [14]:
приведен на рис. 3.
Uexp = exp A.
(12)
Выбор sin θ23 и δCP в качестве изменяющихся
Достоинство экспоненциальной параметризации
величин на рис. 3 связан с тем, что они определены
(12) заключается в том, что она позволяет факто-
с меньшей точностью, чем другие. Диапазон изме-
ризовать вклады вращения и CP -нарушения в виде
нения величин sin θ23 и δCP совпадает с реальным
новой унитарной параметризации:
разбросом их значений в пределах точности 3σ (см.
U=PRotPCPPMjr,
(13)
(8)). Вычисления J для реальных углов смешива-
ния дают абсолютное значение Jν = 0.027+0.0065-0.0270,
где вращению отвечает PRot = eARot , PMjr присут-
что примерно совпадает со значением из [21]. Для
ствует у майорановских нейтрино и нами не рас-
кварков масштаб CP-нарушения оказывается при-
сматривается, а за CP -нарушение отвечает экспо-
мерно на три порядка меньше (см. рис. 4). По
ненциальная матрица PCP = eACP ; ее показатель
данным PDG 2018 г. для кварков эксперименталь-
АCP — соответственно CP-нарушающие компо-
ное значение инварианта Ярлског составляет Jq =
ненты матрицы А. Зная экспериментальные зна-
= (3.18 ± 0.15) × 10-5 (см. рис. 4). Зависимость
чения для смешивания (7), можно получить мат-
инварианта Ярлског J от соответствующих пара-
рицу А в показателе экспоненты, вычислив лога-
метров sinθ12 и sin θ13 в CBM-параметризации
рифм матрицы смешивания. Существует несколько
ЯДЕРНАЯ ФИЗИКА том 82
№3
2019
СРАВНИТЕЛЬНЫЙ АНАЛИЗ CP -НАРУШЕНИЯ
271
методов вычисления матричных логарифмов (см.,
0.15◦
31◦
например, [22, 23]); программы аналитических вы-
числений, такие как Mathematica, также позволя-
ют это сделать. По данным на 2018 г. [21] углы
смешивания для нейтрино составляют:
Исходя из значений (14), получаем экспоненту
,
(14)
матрицы смешивания (12) в виде
0.76◦
3.9◦
⎛
⎞
-0.0195381i
0.515348 + 0.043224i
-0.321446 + 0.110995i
⎜
⎟
⎜
⎟
A=
⎜
0.515346 + 0.043224i
0.0387475i
0.771994 + 0.026604i
⎟
(15)
⎝-
⎠
0.321446 + 0.110995i
-0.771994 + 0.026604i
-0.0192094i
⎛
⎞
Таким образом, экспоненциальная параметризация
-0.0253631i
0
0
⎜
⎟
матрицы (3) с данными (8) есть формула (12) с А
⎜
⎟
=
⎜
⎟,
(15); она точно воспроизводит эксперименталь-
0
0.0502214i
0
⎝
⎠
ные данные (8). Диагональные элементы матрицы
0
0
-0.0248582i
А (15) малы, ее след точно равен нулю: trA = 0, и
она представима в виде следующей суммы:
AdiagIm2018 =
(22)
A=ARot +ACP_1 +AdiagIm,
(16)
⎛
⎞
ARot = Re[A] =
(17)
-0.0195381i
0
0
⎜
⎟
⎛
⎞
⎜
⎟
=
⎜
0
0.0387475i
0
⎟
0
0.515348
-0.321446
⎝
⎠
⎜
⎟
⎜
⎟
=
⎜
⎟,
0
0
-0.0192094i
-0.515348
0
0.771994
⎝
⎠
0.321446
-0.771994
0
По данным 2016 г. отклонение значений α1 и α3 от
/2 составляет 2.524 × 10-4 (≈1%), на
значения -α2
где (17) описывает действительное вращение, а
2018 г. оно стало меньше: 1.6435 × 10-4(≈0.8%).
CP-нарушение описывает матрица
Мнимая диагональ AdiagIm (19) дает комплексную
ACP_1 = iIm[A - AdiagIm] =
(18)
диагональную экспоненциальную матрицу
⎛
⎞
Pdiag Im =
(23)
0
0.0432243i
0.110995i
⎜
⎟
⎜
⎟
=
⎜
.0432243i
0
0.0266036i⎟
⎝0
⎠
0.6
sinθ12
0.110995i
0.0266036i
0
0.4
0.2
Мнимая диагональ матрицы А (15) в (16) представ-
0
лена матрицей
AdiagIm = idiag{α1,α2,α3},
(19)
0.08
0.06
в которой элементы 1 и 3 почти точно равны друг
J
0.04
другу и составляют практически точно половину
0.02
величины матричного элемента A22:
α1 = α3 = -α2/2, α2 = 0.0387475i.
(20)
00
0.2
0.4
Заметим, что соотношения (20) для матрич-
sinθ13
0.6
ных элементов с экспериментальными результата-
ми 2018 г. [21] выполняются точнее, чем с резуль-
татами 2016 г. [25]:
Рис. 5. Зависимость J от sin θ12 и sin θ13 в CBM-
параметризации (6).
AdiagIm2016 =
(21)
ЯДЕРНАЯ ФИЗИКА том 82
№3
2019
272
ДАВЫДОВА, ЖУКОВСКИЙ
{
}
= exp[AdiagIm] = diag
eiα1 ,eiα2 ,eiα3
вокруг выделенной оси в трехмерном пространстве
в следующем виде:
Матрица A = ARot + ACP1 (см. (16)) представляет
⎛
⎞
сумму слагаемого ARot (17), отвечающего за сме-
0
λ μ
⎜
⎟
шивание без CP -нарушения и соответствующее
⎜
⎟
⎜
⎟
⎜-λ
0
ν⎟
ему вращение вокруг действительной оси, и слага-
⎝
⎠
емого ACP1 (18), отвечающего за CP -нарушение и
-μ -ν 0
PRot
=eARot =e
=
(26)
соответствующее ему вращение вокруг мнимой оси.
⎛
⎞
Для δCP = 234◦ имеем:
0
-nz n
y
⎜
⎟
⎜
⎟
A1 = ARot + ACP1 =
(24)
⎜
⎟
Ф
⎜
nz
0
-nx⎟
⎛
⎞
⎝
⎠
0
0.517ei5◦
0.340ei161◦
-ny nx
0
⎜
⎟
=e
⎜
⎟
=
⎜
-0.517e-i5◦
0
0.772ei2◦
⎟
⎝
⎠
Легко посчитать координаты вектора n =
(
)
−0.340e-i161◦ -0.772e-i2◦
0
=
-νΦ,μΦ,-λΦ
, а также угол поворота Φ =
√
=±
λ2 + μ2 + ν2. Так для трибимаксимальной
Абсолютные значения элементов матрицы А1 (24) с
матрицы получаем
учетом экспериментального разброса 3σ (8) могут
меняться в следующих пределах:
nTBM = (0.7858,0.2235, 0.5777),
(27)
|A1|3σ =
(25)
ΦTBM = 56.6◦.
⎛
⎞
В зависимости от экспериментальных данных для
0
0.439 → 0.552 0.324 → 0.421
⎜
⎟
нейтрино угол Φ и ось поворота nν меняются. По
⎜
⎟
=⎜
.439 → 0.552
0
0.629 → 0.836⎟
данным PDG 2016 г. имеем (в диапазоне погреш-
⎝0
⎠
ности 3σ):
0.324 → 0.421 0.629 → 0.836
0
n2016ν
= (0.8094, 0.2417, 0.5353),
(28)
Экспоненциальная матрица смешивания является
;
антиэрмитовой, что обеспечивает унитарность мат-
9.67◦
рицы смешивания: U-1exp · Uexp = U+exp · Uexp = I.
по данным на 2018 г. получаем:
n2018ν
= (0.7859, 0.3272, 0.5246),
(29)
4. ДОПОЛНИТЕЛЬНОСТЬ СМЕШИВАНИЯ
НЕЙТРИНО И КВАРКОВ
6.48◦
Для кварков на основе данных PDG за 2017 г.
Для действительной матрицы ARot вращения
имеем:
PRot = eARot существует представление вращения
n2017q = (0.1810,0.0141,0.9834),
(30)
y
0.30
0.2
x
0.03◦
0.2
0.1
0.4
0
0.6
Сопоставление координат вектора и угла вращения
0.8
в (28), (29) друг с другом показывает, что они
1.0
довольно сильно различаются из года в год. Угол
поворота (27) для ТВМ-матрицы стал ближе по
1
значению к углу поворота (29), вычисленного с
новыми данными. Однако сравнение направления
вектора действительного вращения для нейтрино в
3
0.5z
отсутствие CP-нарушения с направлением анало-
гичного вектора вращения для кварков в рамках
2
той же экспоненциальной параметризации пока-
зывает, что угол между вектором для кварков nq
и вектором для нейтрино nν составлял 45.8◦ по
0
данным на май 2016 г., 48.5◦ на январь 2018 г. и
43.6◦ для ТВМ-матрицы. Таким образом, наблю-
дается постоянство величины угла между nq и nν
(см. рис. 6), с хорошей точностью равного 45◦ даже
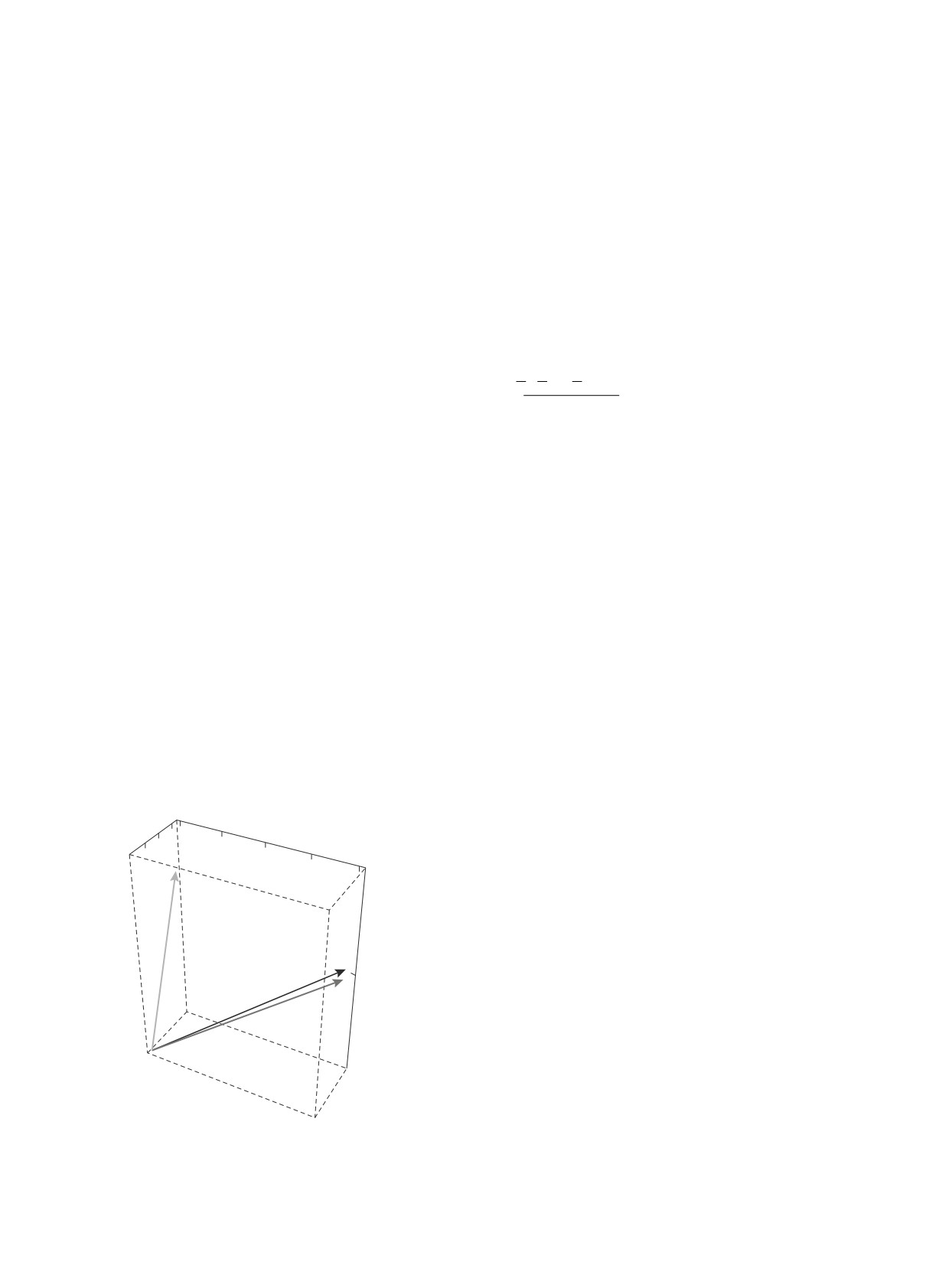
Рис. 6. Оси вращения в пространстве для смешивания
при сильном разбросе экспериментальных данных
кварков (1), нейтрино по данным на май 2016 г. (2) и
по смешиванию нейтрино из года в год.
январь 2018 г. (3).
ЯДЕРНАЯ ФИЗИКА том 82
№3
2019
СРАВНИТЕЛЬНЫЙ АНАЛИЗ CP -НАРУШЕНИЯ
273
φ, град
θ, град
60
6
а
б
5
59
4
58
3
2
57
1
56
200
250
300
350
200
250
300
350
δCP, град
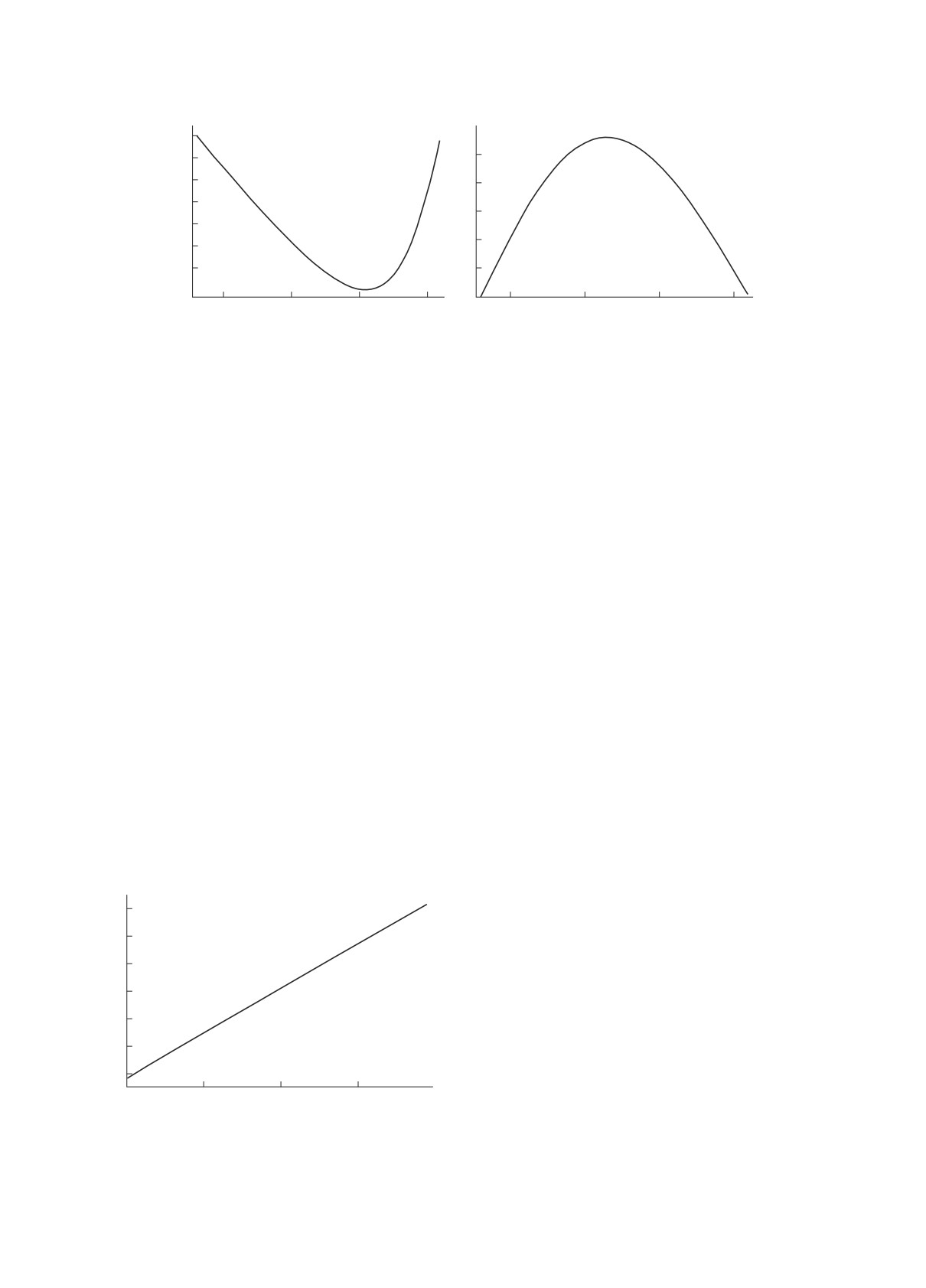
Рис. 7. a — Зависимость θ от CP-нарушающей фазы δCP . б — Та же зависимость для угла ϕ.
5. МАТРИЦА СМЕШИВАНИЯ
Выделим в экспоненциальной параметризации
КАК ЭЛЕМЕНТ ГРУППЫ SU(3)
матрицы смешивания Uexp = exp A множитель
iθ так, чтобы привести (12) в соответствие с
Матрица смешивания U, являясь элементом
выражением
(31). Тогда с учетом нормировки
группы SU(3), может быть выражена следующим
tr[H2] = 2 получаем для параметра θ следующее
образом:
выражение:
U = exp[iθH],
(31)
(
[
])1/2
θ=
-tr
A2/2
,
(34)
через параметр θ вращения группы и антиэрмито-
ву матрицу H, принадлежащую соответствующей
определяющее по существу угол поворота в груп-
алгебре группы с нормировкой tr[H2] = 2. С помо-
пе SU(3). Используя экспериментальные данные
щью вычислений в программе Mathematica полу-
2016 г., можно вычислить значения соответствую-
чаем в явном виде
щих углов для нейтрино [25]:
H=
(32)
,
(35)
8.06◦
6.05◦
⎛
⎞
-0.020
0.044 - 0.520i 0.112 + 0.325i
По новым данным для нейтрино на 2018 г. [21]
⎜
⎟
⎜
⎟
=
⎜0.044 + 0.520i
0.039
0.027 - 0.779i⎟
,
,
(36)
7.23◦
5.49◦
⎝
⎠
а для кварков получаем:
0.112 - 0.325i 0.027 + 0.779i
-0.019
◦
θq = 13.23◦+0.0◦-0.02
,
(37)
ϕq = -0.25−
0.01◦
Инвариант, det(H) = -0.109, может быть пере-
определен в терминах угла ϕ [26]:
Полученная нами зависимость параметров мат-
(
)
)
√
рицы смешивания нейтрино как элемента группы
1
(3
π
ϕ=
arccos
3det (H)
-
(33)
SU(3) от CP-нарушающей фазы δCP приведена на
3
2
2
рис. 7.
Также можно исследовать связь элементов дан-
φ, град
ной группы с параметрами экспоненциальной па-
15
раметризации, в частности, с углами, находящими-
ся в показателях экспонент матрицы (24). Устано-
10
вив в (31)-(34) соответствие матрицы смешивания
5
как элемента группы SU(3) (31) и ее экспонен-
циальной формы (12), мы продемонстрировали на
50
100
150
200
250
300
350
рис. 8 зависимость параметра ϕ (33) от определя-
-5
δ1, град
ющего CP -нарушение угла δ1 в элементах (1, 3) и
(3, 1) матрицы A1 (24).
-10
На основании экспериментальных данных с
-15
учетом вида (24) матрицы A1 имеем δ1 = 161◦,
δ2 = 5◦, δ3 = 2◦. Угол θ по построению (34) не
Рис. 8. Связь угла ϕ с фазой δ1 в экспоненциальной
зависит от недиагональных элементов матрицы
матрице (24).
A, следовательно, он не будет зависеть от δ1, δ2,
ЯДЕРНАЯ ФИЗИКА том 82
№3
2019
274
ДАВЫДОВА, ЖУКОВСКИЙ
δ1, град
δ2, град
180
а
б
175
5
170
4
165
3
160
2
155
150
1
200
250
300
350
200
250
300
350
δCP, град
Рис. 9. Зависимость δ1 (a) и δ2,3 (б) от δCP .
δ3. Так как реальные значения угла δ1 с учетом
Представляет интерес вклад мнимой диагональ-
разброса лежат в пределах [145.3◦-180◦], то видно,
ной матрицы AdiagIm = idiag {α1, α2, α3}, которая
что ϕ (33) не будет достигать своего максимального
внешне напоминает вклад для майорановских ча-
значения и будет почти равен 0 для δ1 = 180◦.
стиц в (4), но происходит от CP -нарушения. Как
Связь значений δ1,2 в матрице A1 (24) с CP -
было показано в (20), между элементами матрицы
нарушающей фазой δCP представлена на рис. 9.
AdiagIm с высокой точностью выполняется соотно-
Анализ зависимости δ1 (рис. 9a) и δ2,3 (рис. 9б)
шение α1 = α3 = -α2/2. Поэтому матрицу AdiagIm
от δCP показывает, что для δ1 минимальным
можно параметризовать следующим образом:
значением является 145.3◦, при этом δCP = 305.7◦,
а реальному значению δCP = 234◦ соответствует
AdiagIm = idiag {-α,2α,-α} .
(38)
величина δ1 = 160.6◦. Зависимости для δ2 и для δ3
от δCP получились практически одинаковыми.
Нами получена зависимость величины инварианта
Ярлског от параметра α в (38), представленная на
рис. 10, где величина α изменяется от 0 до значения
6. ИССЛЕДОВАНИЕ СВЯЗИ
α2 в (20).
CP-НАРУШЕНИЯ С ПАРАМЕТРАМИ
ЭКСПОНЕНЦИАЛЬНОЙ ФОРМЫ
Поведение J(α) показывает (см. рис. 10), что,
МАТРИЦЫ СМЕШИВАНИЯ
если положить элементы матрицы AdiagIm равными
нулю, то инвариант Ярлског уменьшится несильно:
Используя экспоненциальную параметризацию
он станет равным примерно |J| = 0.0264 (исходное
(12) матрицы U, можно исследовать зависимость
значение |J| = 0.027); таким образом, оставшаяся
инварианта Ярлског J как меры CP -нарушения
кроме AdiagIm мнимая часть матрицы A, т.е. мат-
от элементов матрицы A (15) экспоненты (12).
рица ACP_1 (18), в подавляющей степени отвечает
(17)
за CP-нарушение. С учетом экспоненты ARot
J
матрицы действительного вращения A1 = ARot +
0.0276
+ ACP_1 (см. (16)) CP-нарушение описывается в
0.0274
основном за счет δ1,2, в меньшей степени δ3, в
показателях экспонент в матрице (24). Построим
0.0272
зависимость J(δ1, δ2). Результат представлен на
0.0270
рис. 11.
0.0268
График на рис. 11 отражает разброс абсолют-
0.0266
ных значений инварианта Ярлског, который он
может принимать, когда углы смешивания и CP -
0.0264
нарушающая фаза определены в интервале по-
0.01
0.02
0.03
α
грешности 3σ. Диапазон углов смешивания рас-
считан в терминах δ1, δ2. Из рис. 11 очевидно, что
Рис. 10. Зависимость абсолютного значения инвари-
определяющей для инварианта Ярлског J является
анта Ярлског J от параметра мнимой диагонали α.
зависимость от δ1; влияние δ2,3 мало.
ЯДЕРНАЯ ФИЗИКА том 82
№3
2019
СРАВНИТЕЛЬНЫЙ АНАЛИЗ CP -НАРУШЕНИЯ
275
≈45◦, что подтверждает гипотезу кварк-лептонной
дополнительности [27, 28].
J
Матрица смешивания нейтрино рассмотрена
0.04
как элемент группы SU(3): получены значения
0.03
инварианта det(H) = -0.109, самой матрицы
0.02
H, соответствующего ей параметрического уг-
0.01
0
5.49◦
и значение угла θ2018ν =
150
вращения в группе SU(3). Разброс
7.23◦
2
160
полученных значений соответствует эксперимен-
δ2
4
тальному разбросу 3σ. Исследована связь SU(3)
170
δ1
параметров θ и φ с углом δCP CP -нарушения в
6
180
стандартной параметризации, а также связь φ с
CP-нарушающей фазой в экспоненциальной па-
Рис. 11. Зависимость модуля J (δ1, δ2); δ1 изменяется
раметризации (см. рис. 7-9). Угол θ по построению
в диапазоне 145◦-180◦, для δ2 от 0◦ до 6◦, δ3 = 2◦.
не зависит от значений δ1,2,3 в экспоненциальной
параметризации.
7. РЕЗУЛЬТАТЫ И ВЫВОДЫ
Установлено соответствие между эксперимен-
тально определенной CP -фазой δCP в стандарт-
С помощью экспоненциальной параметризации
ной параметризации с CP -нарушением в экспо-
матрицы смешивания нейтрино проанализированы
ненциальной параметризации, для которой получе-
данные о смешивании из Particle Data Group
на иерархия значений комплексных элементов (1,
2016 и 2018 гг. Экспонента матрицы смешивания
3), (2, 3), (3, 2) матричной экспоненты с фаза-
A содержит вещественную часть ARot, мнимую
ми δ1 = 161◦, δ2 = 5◦, δ3 = 2◦. Наибольшее CP -
недиагональную часть ACP_1 и чисто мнимую
нарушение приходится на смешивание электрон-
диагональную часть AdiagIm: A = ARot + ACP_1 +
ных и таонных нейтрино. Для наиболее вероятного
+ AdiagIm. Так как величины коммутаторов матриц
значения фазы δCP ≈ 234◦ величина δ1, определя-
ARot, ACP_1, AdiagIm малы, то можно фактори-
ющая главный вклад CP -нарушения в экспонен-
зовать в экспоненциальной матрице смешивания
циальной параметризации, соответствует середине
Uexp = exp A вклад CP-нарушения и враще-
допустимого диапазона значений. Углы δ2 и δ3
ния вокруг действительной оси: U = PRotPCP ,
зависят одинаково от δCP (см. рис. 9), что говорит о
PRot = eARot , PCP = eACP = eACP_1 . Экспонента
симметрии между процессами CP -нарушения при
ACP_1 матрицы CP-нарушения имеет нулевую
смешивании e- и μ-нейтрино и μ- и τ-нейтрино.
диагональ и мнимые составляющие; она хорошо
Проведен сравнительный анализ CP -нарушения
описывает CP -нарушение. Мнимая диагональ
в стандартной, трибимаксимальной, кобимакси-
матрицы A: AdiagIm = idiag {α1, α2, α3}, α1 =
мальной и экспоненциальной параметризациях с
= -0.0195381, α2 = 0.0387475, α3 = -0.0192094,
помощью инварианта Ярлског J. Исследована
напоминает вклад майорановских нейтрино, но
зависимость инварианта Ярлског J как меры
происходит из-за CP-нарушения. Ее угловые
нарушения CP -инвариантности от соответству-
элементы (1, 3) и (3, 1) примерно равны друг другу:
ющих фаз в стандартной и экспоненциальной
α1 = α3 = -α2/2, причем данное соотношение
формах матрицы смешивания (см. рис. 3-5 и
выполняется лучше, чем когда-либо ранее.
рис. 10, 11). Сделан вывод, что определяющей
Проведено сравнение векторов и углов пово-
для инварианта Ярлског является зависимость от
рота для трибимаксимальной параметризации и
sin δCP в стандартной параметризации и от δ1 в
для экспоненциальной параметризации по дан-
экспоненциальной параметризации.
ным PDG 2016-2018 гг.: nTBMν = (0.7858, 0.2235,
Экспоненциальное представление матрицы
0.5777), ΦTBMν = 56.6◦; n2016ν = (0.809, 0.2417,
смешивания и полученные на ее основе результаты
9.67◦
; n2018ν = (0.786,0.327,
и интерпретации могут быть полезны при анализе и
. Несмотря на значи-
обработке экспериментальных данных по осцилля-
6.48◦
циям нейтрино в экспериментах, проводимых как в
тельный разброс координат векторов nν в разные
настоящее время, так и планируемых в будущем.
года измерений (больше всего различаются ny ∈
∈ [0.22, 0.33]), взаимное расположение векторов nν
Авторы благодарят проф. А.В. Борисова за
для нейтрино и nq для кварков в экспоненциальной
ценные советы, полезные замечания и обсуждение
параметризации остается с высокой точностью
полученных результатов.
ЯДЕРНАЯ ФИЗИКА том 82
№3
2019
276
ДАВЫДОВА, ЖУКОВСКИЙ
СПИСОК ЛИТЕРАТУРЫ
15. G. Dattoli and K. Zhukovsky, Eur. Phys. J. C 52, 591
(2007).
1.
S. Weinberg, Phys. Rev. Lett. 19, 1264 (1967).
16. K. Zhukovsky and F. Melazzini, Eur. Phys. J. C 76,
2.
A. Salam, Elementary Particle Theory, Ed. by
462 (2016).
N. Svartholm (Almquist and Wiksell, Stockholm,
1968).
17. K. Zhukovsky and A. Borisov, Eur. Phys. J. C 76, 637
3.
S. L. Glashow, Nucl. Phys. 22, 579 (1961).
(2016).
4.
Б. Понтекорво, ЖЭТФ 33, 549 (1958) [Sov. Phys.
18. К. В. Жуковский, Вестн. МГУ. Сер. 3. Физика,
JETP 6, 429 (1958)].
Астрономия, № 5, 3 (2017) [Moscow Univ. Phys.
5.
Б. М. Понтекорво, УФН 95, 517 (1968) [Sov. Phys.
Bull. 72, 433 (2017)].
Usp. 11, 528 (1969)].
19. K. В. Жуковский, Ученые записки физического
6.
M. Gell-Mann, P. Ramond, and R. Slansky, in
факультета Моск. ун-та, вып. 4, 1740902 (2017).
Supergravity: Proceedings of the Supergravity
20. К. В. Жуковский, ЯФ 80, 379 (2017) [Phys. At. Nucl.
Workshop, Stony Brook, Ed. by D. Z. Freedman and
80, 690 (2017)].
P. van Nieuwenhuizen (North-Holland, Amsterdam,
21. I. Esteban, M. C. Gonzalez-Garcia, M. Maltoni,
1979), p. 315.
I. Martinez-Soler, and Th. Schwetz, NuFIT
3.2
7.
T. Fukuyama and H. Nishiura, hep-ph/9702253.
8.
Z. Maki, M. Nakagawa, and S. Sakata, Prog. Theor.
22. C. Jarlskog, Phys. Rev. Lett. 55, 1039 (1985).
Phys. 28, 870 (1962).
23. A. Wouk, J. Math. Anal. Appl. 11, 131 (1965).
9.
Y. Zhang, X. Zhang, and B.-Q. Ma, Phys. Rev. D 86,
24. T. A. Loring, Num. Linear Algebra Appl. 21, 744
093019 (2012); arXiv: 1211.3198 [hep-ph].
(2014).
10.
S. F. King, J. Phys. G 42, 123001 (2015); arXiv:
25. M. C. Gonzalez-Garsia, M. Maltoni, and
1510.02091.
11.
A. Damanik, J. Phys.: Conf. Ser. 909, 012024 (2017).
26. T. L. Curtright and C. K. Zachos, Rept. Math. Phys.
12.
L. Wolfenstein, Phys. Rev. Lett. 51, 1945 (1983).
76, 401 (2015).
13.
N. Li and B.-Q. Ma, Phys. Rev. D 71, 097301 (2005);
27. H. Minakata and A. Yu. Smirnov, Phys. Rev. D 70,
hep-ph/0501226.
073009 (2004).
14.
G. Dattoli and K. Zhukovsky, Eur. Phys. J. C 50, 817
28. M. Raidal, Phys. Rev. Lett. 93, 161801 (2004).
(2007).
COMPARATIVE ANALYSIS OF CP VIOLATION FOR NEUTRINO
IN THE EXPONENTIAL AND STANDARD PARAMETERIZATIONS
OF MIXING MATRIX
A. A. Davydova, K. V. Zhukovsky
Department of Theoretical Physics, Faculty of Physics,
M. V. Lomonosov Moscow State University, Russia
We perform the comparative analysis of neutrino mixing in standard, cobimaximal, tribimaximal, and
exponential parameterizations.Using the latest experimentaldata on neutrino mixing, we find the logarithm
of the mixing matrix and exact values for the entries of the exponential form of the PMNS matrix, which
allows factorization of the terms, responsible for pure rotation and CP violation. We confirm quark-neutrino
mixing complementarity. With Jarlskog invariant we study the dependence of the CP violation on mixing
parameters in the considered parameterizations of the PMNS matrix; we also reveal the underlying relations
between them. In the exponential parameterization we study the SU(3) group presentation for the PMNS
matrix, using the parameters θ and ϕ and their dependence on the CP violation.
ЯДЕРНАЯ ФИЗИКА том 82
№3
2019