ЯДЕРНАЯ ФИЗИКА, 2019, том 82, № 4, с. 339-348
ЯДРА
ЭКСТРАПОЛЯЦИЯ ЭНЕРГИИ СВЯЗАННОГО СОСТОЯНИЯ
В МЕТОДЕ SS-HORSE
© 2019 г. А. М. Широков1),2),3), В. А. Куликов1),2)*, А. И. Мазур2)
Поступила в редакцию 25.12.2018 г.; после доработки 25.12.2018 г.; принята к публикации 25.12.2018 г.
В работе предлагается новый метод экстраполяции энергии связанных состояний, полученных в
осцилляторном базисе, позволяющий также рассчитывать асимптотические нормировочные коэффи-
циенты. Приводится теоретическое обоснование метода и его апробация в модельной задаче.
DOI: 10.1134/S0044002719040172
1. ВВЕДЕНИЕ
Использование SS-HORSE позволяет предска-
зывать положение резонансов, а в настоящей рабо-
Для расчетов характеристик ядер активно ис-
те, опираясь на идеи теоретически обоснованного
пользуются подходы ab initio, в которых не делает-
метода SS-HORSE, мы предлагаем его расшире-
ся модельных предположений о структуре атомного
ние для экстраполяции результатов расчетов энер-
ядра. Большое количество расчетов ab initio раз-
гий связанных состояний в осцилляторном базисе,
личных ядер было проведено методом NCSM (No-
а также для расчета асимпотических нормиро-
Core Shell Model) [1, 2], в котором используется ос-
вочных коэффициентов (АНК), которые являются
цилляторный базис модели оболочек. Результаты
важными фундаментальными величинами [27].
таких расчетов ограничены мощностью современ-
В первой части статьи приводится теоретиче-
ных суперкомпьютеров и зависят от параметров
ское обоснование предложенного метода, далее
базиса — числа осцилляторных квантов возбужде-
следуют расчеты в модельной задаче и сравнение
ния Nmax, связанного с размерностью базиса, и
с методами экстраполяции, предложенными в [3],
частоты осциллятора ℏΩ.
а также в [4] (с учетом модификации, развитой в
[6, 7, 9]).
В методе NCFC (No-Core Full Configuration) [3]
зависимость получаемых в оболочечных расчетах
энергий от Nmax и ℏΩ используется для пред-
2. S-МАТРИЦА В МЕТОДЕ SS-HORSE
сказания энергии, соответствующей бесконечно-
му базису, и оценки погрешности предсказанного
В HORSE [25, 26] волновая функция Ψn,l с
значения. Такая экстраполяция позволяет улуч-
заданным орбитальным моментом l разлагается в
шить описание ядер и, в некоторой степени, обой-
ряд по базисным функциям,
ти ограничения, накладываемые характеристиками
∑
существующих суперкомпьютеров. Несколькими
Ψn,l =
AnlΦnl,
(1)
коллективами были предложены и другие методы
n=0
экстраполяции [4-16].
— собствен-
в качестве которых используются Φnl
Недавно был предложен метод Single-State
ные волновые функции гармонического осцилля-
Harmonic-Oscillator Representation of Scattering
тора с частотой ℏΩ, n — главное квантовое чис-
Equations (SS-HORSE) [17-21], в основе которо-
ло, l — орбитальный момент. При этом уравнение
го лежит J-матричный формализм теории рассе-
Шредингера переходит в систему линейных урав-
яния в осцилляторном базисе — HORSE [22-26].
нений для коэффициентов разложения Anl:
∑
1)НИИ ядерной физики им. Д.В. Скобельцына Московско-
(Hlnn′ - δnn′ E)An′l = 0, n = 0, 1,
(2)
го государственного университета им. М.В. Ломоносова,
Россия.
n′=0
2)Тихоокеанский государственный университет, Хабаровск,
Здесь Hlnn′ = Tlnn′ + Vlnn′ — матричные элементы
Россия.
3)Department of Physics and Astronomy, Iowa State
гамильтониана, кинетической энергии и потенциа-
University, USA.
ла в осцилляторном базисе соответственно. Мат-
*E-mail: kulikov@nucl-th.sinp.msu.ru
рица потенциала обрезается при некоем значении
339
340
ШИРОКОВ и др.
главного квантового числа n = N, то есть прини-
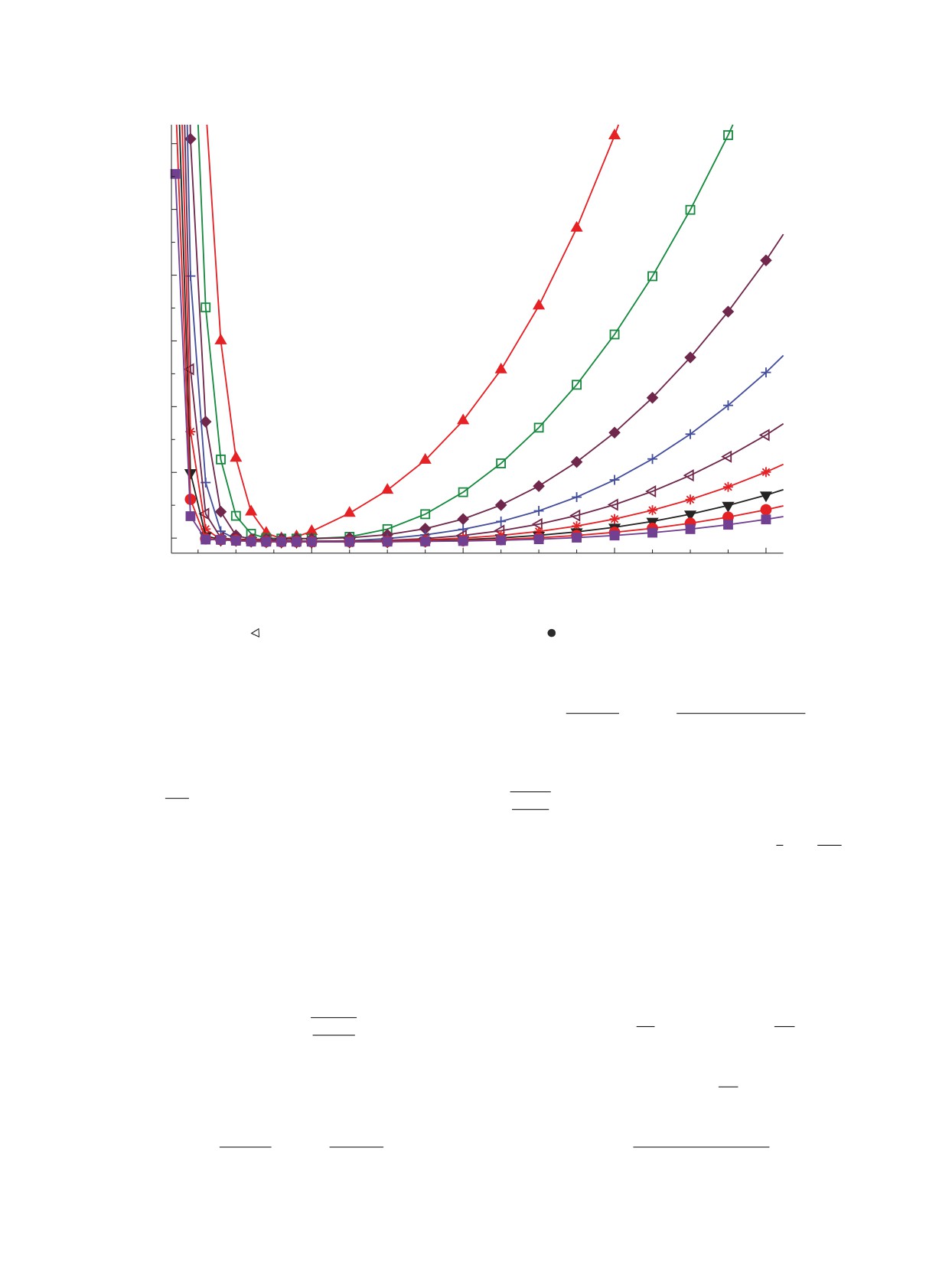
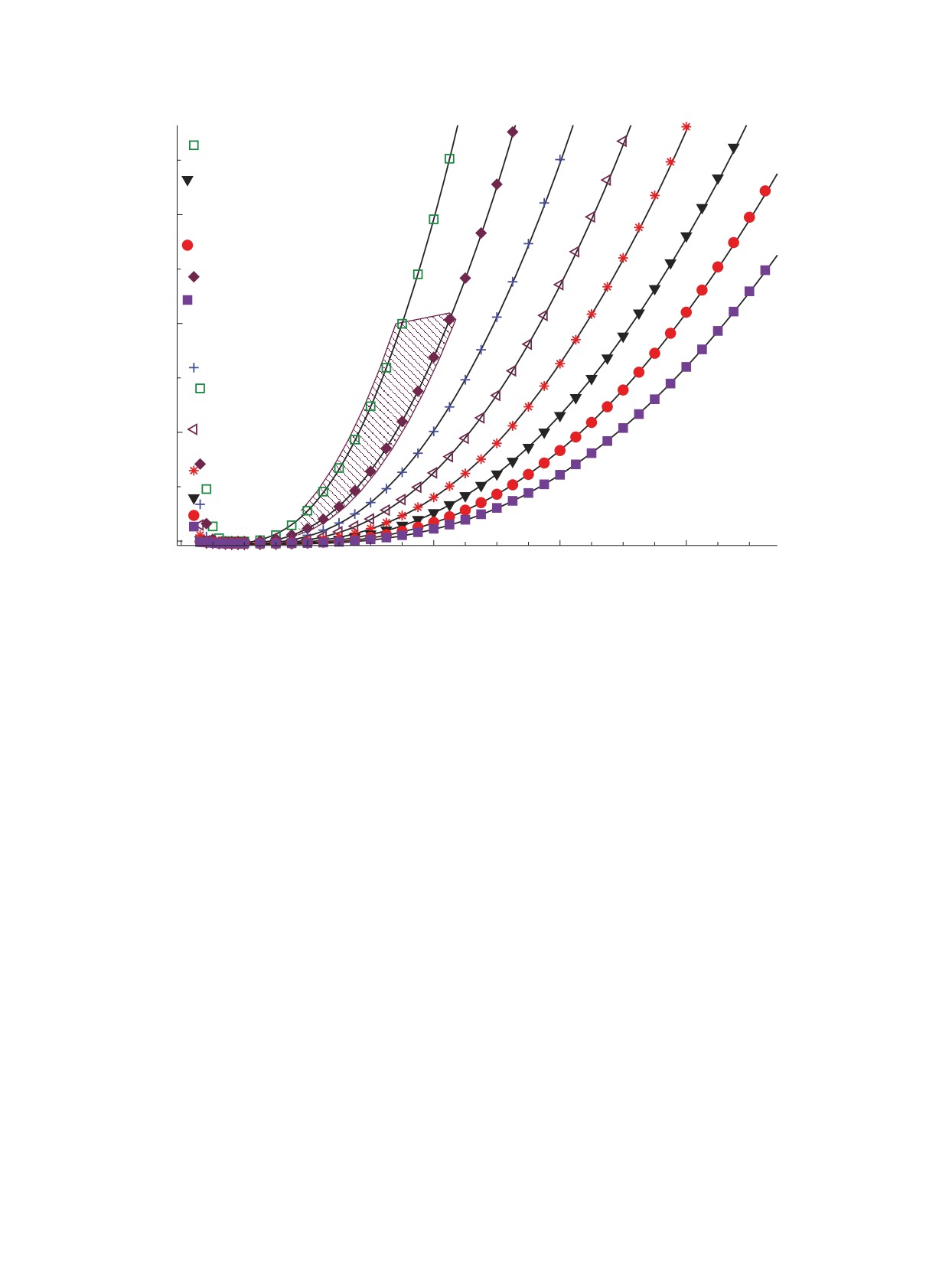
Обычно в расчетах получают зависимость энер-
мается условие
гии от ℏΩ для разного полного числа осциллятор-
{
ных квантов Ntot = 2N + l, типичный вид которой
приведен на рис. 1. Показанные на рисунке точки
V lnn′ =V nn′ приn ≤ Nиn′ ≤ N;
(3)
0
при n > N или n′ > N,
соответствуют собственным значениям гамильто-
и ℏΩ. Они были получены
ниана при известных Ntot
а матрица кинетической энергии не обрезается и
диагонализацией двухчастичного гамильтониана в
входит в теорию как бесконечная трехдиагональная
состоянии с l = 0 с потенциалом Вудса-Саксона
матрица. Такой подход оправдан ввиду того, что
VWS
при больших значениях n матричные элементы
V (r) =
(8)
потенциала малы по сравнению с матричными эле-
1 + exp(r-RWSD)
ментами кинетической энергии. В методе HORSE
Параметры потенциала: VWS = -22.0 МэВ, RWS =
вводятся функции C(-)nl(E/ℏΩ) и C(+)nl(E/ℏΩ), об-
= 3.080 Фм, D = 0.530 Фм. Использовалась при-
разующие фундаментальную систему решений для
веденная масса m = 751 МэВ. C этими параметра-
свободного гамильтониана (кинетической энергии)
ми потенциал приводит к появлению в системе од-
в осцилляторном представлении, аналитические
ного связанного состояния с энергией -7.011 МэВ.
выражения для которых, а также их асимптоти-
В работе [4] было показано, что в некотором
ческие свойства можно найти в [25]. Тогда S-
диапазоне значений ℏΩ и Ntot энергия будет за-
матрица в общем случае имеет следующий вид (см.
висеть только от скейлинговой переменной, явля-
[23, 25, 26]):
ющейся комбинацией этих параметров; в работах
S(E) =
(4)
[6, 7, 9] было уточнено значение этой перемен-
ной. Действительно, если рассмотреть поведение
(-)
CN
(E/ℏΩ) - GNN TlN,N+1C(-)N+1,l(E/ℏΩ)
l
функций C(-)N+1,l(E/ℏΩ) и C(+)N+1,l(E/ℏΩ) при N ≫
=
,
√
C(+)Nl(E/ℏΩ) - GNNTlN,N+1C(+)N+1,l(E/ℏΩ)
≫
2|E|/(ℏΩ) [25], то получим
где
C(-)N+1,l(E/ℏΩ)
∑
S=
≈
(9)
〈nl|λ〉〈λ|n′l〉
Gnn = -
,
(5)
C(+)N+1,l(E/ℏΩ)
Eλ - E
λ=0
(
√
√
)
(2)
E
H
2
Ntot +7
Eλ — собственные значения обрезанного при n =
l+1
2
ℏΩ
2
= N гамильтониана, а 〈nl|λ〉 — его собственные
≈-
(√
√
),
E
функции:
H(1)
2
Ntot +7
l+1
2
ℏΩ
2
∑
(Hlnn′ - δnn′ Eλ)〈λ|n′l〉 = 0,
(6)
где через H(1)
(x) и H(2)
(x) обозначены функции
l+1
l+1
2
2
n′=0
Ханкеля первого и второго рода соответственно.
n = 0,1,...,N.
Из (9) видно, что при достаточно большом Ntot S-
матрица зависит от комбинации
Выражение (4) справедливо для любой энергии
E, в частности для положительной, отрицательной
ℏΩ
s=
,
(10)
или комплексной. Для энергии связанного состоя-
Ntot +7
2
ния (отрицательной) выражение (4) должно иметь
полюс (нуль знаменателя). В бесконечном базисе
а не от ℏΩ и Ntot по отдельности. В дальнейшем s
собственным значением гамильтониана будет Eb,
будем называть скейлинговым параметром в соот-
соответствующее данному полюсу.
ветствии с работами [4, 6].
Выражение
(4) справедливо и при энергии
Отметим, что метод SS-HORSE работает толь-
E = Eλ какого-либо состояния, полученного в
> 0 [17], поэтому из рассмотрения надо
Ω
результате диагонализации гамильтониана при
исключить точки, лежащие левее минимума кривой
данном значении ℏΩ и с данным обрезанием при
для каждого значения Ntot на рис. 1.
n = N. Как было показано в работах [20, 22,
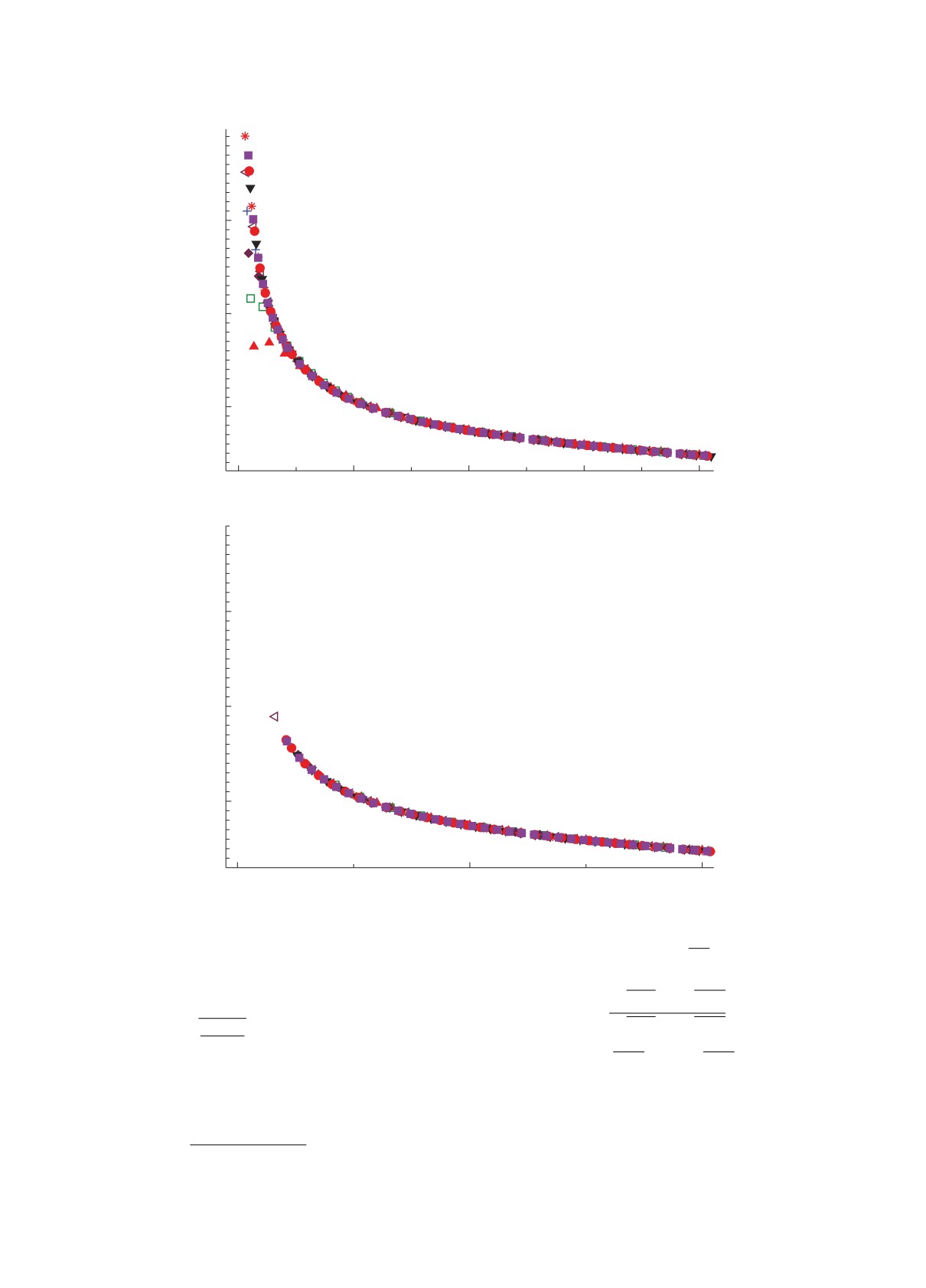
Для иллюстрации монотонной зависимости S-
28, 29], точность расчета S-матрицы при E = Eλ
матрицы от скейлинга и от энергии возьмем тот же
выше, чем в других точках. В этом случае (4)
потенциал (8), что использовался для построения
существенно упрощается и принимает вид
рис. 1. На рис. 2 показана зависимость логарифма
(-)
CN
(Eλ/ℏΩ)
S-матрицы при E = Eλ=0 от скейлингового па-
+1,l
S(Eλ) =
(7)
раметра s. Из рис. 2a видно, что б `ольшая часть
C(+)N+1,l(Eλ/ℏΩ)
точек, за исключением области малых значений
ЯДЕРНАЯ ФИЗИКА том 82
№4
2019
ЭКСТРАПОЛЯЦИЯ ЭНЕРГИИ СВЯЗАННОГО СОСТОЯНИЯ
341
E0, МэВ
-5.8
-6.0
-6.2
-6.4
-6.6
-6.8
-7.0
10
20
30
40
"Ω, МэВ
Рис. 1. Зависимость энергии нижайшего состояния E0 от ℏΩ для разных значений Ntot: ▴ — Ntot = 4, □ — Ntot = 6, ♦ —
Ntot = 8, × — Ntot = 10,
— Ntot = 12, ∗ — Ntot = 14, ▾ — Ntot = 16,
— Ntot = 18, ■ — Ntot = 20. На остальных
рисунках результаты диагонализации гамильтониана обозначены так же.
)
∏
∏
скейлингового параметра, которые соответствуют
( (κ - γi)2 + (kir)2
×
,
энергиям E0, лежащим левее минимума их зави-
κ+κiv
(κ + γi)2 + (kir)2
симости от ℏΩ, образуют общую кривую, как и
i=1
i=1
должно быть в соответствии с формулой (9) и
здесь для сохранения свойств симметрии S-
работами [4, 6]. Тогда, если оставить только точки,
матрицы ϕ(κ) — нечетная функция κ =√
> 0, то они будут лежать на общей
2m|E|
Ω
=
кривой, как показано на рис. 2б. В этом случае мы
ℏ2
(
)
можем параметризовать S-матрицу, чтобы в конеч-
1+z
Если учесть соотношение arth(z) =12 ln
,
1-z
ном итоге зафиксировать ее полюс и тем самым
найти энергию, соответствующую этому полюсу,
справедливое
при
|z| < 1,
то
при
уже не зависящую от параметров Ntot и ℏΩ.
κ2 ≤ κ2f и κ2 ≤ κ2v, т.е. когда энергия E ближе к
нулю, чем особенности типа ложного полюса или
3. ПАРАМЕТРИЗАЦИЯ S-МАТРИЦЫ
виртуального состояния, данную формулу можно
Рассмотрим теперь возможные способы пара-
переписать в виде
метризации S-матрицы на мнимой оси импуль-
S(E) = e-2ϕ(κ) ×
(12)
сов. Можно выписать выражение для S-матрицы,
(
учитывающее наличие nb связанных состояний с√
))
∑
) nf∑
(κ
(κ
2m|Eb|
× exp
2
arth
+2
arth
×
импульсом k = iκb, где κb =
, nf ложных
i
ℏ2
κi
κ
i=1
b
i=1
f
полюсов (k = iκf ), nv виртуальных состояний (k =
(
(
)
∑
= -iκv) и nr резонансов (k = kr + iγ) [30]:
κ
× exp
2
arth
-
-
κiv
S(E) =
(11)
i=1
(
)
(
))
∏
∏
∑
κ+κif
2κγi
=e-2ϕ(κ)
×
-2
arth
κi
-κ
κif
-κ
κ2 + (kir)2 + (γi)2
i=1
b
i=1
i=1
ЯДЕРНАЯ ФИЗИКА том 82
№4
2019
342
ШИРОКОВ и др.
ln(S(E0))
a
30
20
10
0
1
2
3
4
s, МэВ
ln(S(E0))
б
30
20
10
0
2
4
s, МэВ
Рис. 2. Зависимость логарифма S-матрицы от величины s: результаты диагонализации для различных модельных
пространств (а), отобранные точки для параметризации S-матрицы, удовлетворяющие условиюdE0
> 0 (б).
dℏΩ
(√
√
)
Разложив в ряд arth(z) и учитывая (7) и опре-
|Eb| +
|Eλ|
√
=
√
√
×
2m|Eλ|
|Eb| -
|Eλ|
деление κλ =
, для параметризации S-
ℏ2
(
)
√
√
матрицы получим
× exp R
|Eλ| + F (
|Eλ|)3 + · · ·
Если между интересующим нас связанным состоя-
C(-)N+1,l(Eλ/ℏΩ)
нием и нулем лежит еще одно связанное состояние,
=
(13)
то следует учитывать в явном виде как полюс, свя-
C(+)N+1,l(Eλ/ℏΩ)
занный с этим состоянием, так и расположенный
ЯДЕРНАЯ ФИЗИКА том 82
№4
2019
ЭКСТРАПОЛЯЦИЯ ЭНЕРГИИ СВЯЗАННОГО СОСТОЯНИЯ
343
между ними нуль S-матрицы, соответствующий
Нужно отметить, что знак подгоночного пара-
виртуальному состоянию; виртуальное состояние
метра Dl в общем случае определяется величиной
возникнет между ближайшим к нулю связанным
l, а с учетом ограничений на величину Al (см. [31])
состоянием и нулем также и в случае нечетно-
величина Dl также ограничена и связана с АНК Al
го значения l. При учете S(Eλ = 0) = 1 выраже-
следующей формулой:
ние (13) должно хорошо описывать S-матрицу при
√√
Eλ → 0. Ниже мы используем эту формулу с уче-
m
|Al| =
|Dl|.
(18)
том разного числа членов в показателе экспоненты.
ℏ
В приложениях может оказаться более удоб-
Cвязь между подходом, основанным на учете
ной другая формула, которая должна работать в
симметрии S-матрицы (формула (13)), и форму-
окрестности полюса, соответствующего подгоняе-
лой (17) станет видна, если экспоненту в выраже-
мому связанному состоянию. Так как S-матрица
нии (13) разложить в ряд в окрестности полюса
имеет полюс при импульсе k = iκb, то, в соответ-
по малому параметру (√Eb -√Eλ) и для простоты
ствии с [31] и определением k = iκ, имеем
принять F = 0:
Cl
S(E) =
(14)
iκ - iκb
C(-)N+1,l(Eλ/ℏΩ)
=
(19)
Здесь Cl — коэффициент, связанный с асимптоти-
C(+)N+1,l(Eλ/ℏΩ)
ческой нормировочной константой (АНК) Al [31],
√
√
√
которая является интересной наблюдаемой и кото-
|Eλ| +
|Eb|
|Eb|
= -eR
√
√
×
рую также желательно получить в расчете
|Eλ| -
|Eb|
[
√
√
Cl = (-1)l+1i|Al|2.
(15)
× α+β(
|Eλ| -
|Eb|) +
Отметим, что выражение (14) работает только
√
√
в непосредственной близости от полюса, а в более
+ γ(
|Eλ| -
|Eb|)2 +
общем случае надо записать сумму по всем полю-
√
√
]
сам:
+ δ(
|Eλ| -
|Eb|)3 + ... ,
⎛
1
D1l
где α, β, γ и δ — коэффициенты разложения, зави-
S(E) =
√
⎝
√
+
(16)
√
2
сящие, в том числе, от подгоночного параметра R.
|E| -
|E1b|
Таким образом, в нашем распоряжении есть
⎞
формула (17) и ее упрощенные варианты, в которых
D2l
+
√
+ ...⎠ ,
либо H = 0, либо и Q = 0, и H = 0. Также мы
√
|E| -
|E2b|
можем использовать формулу (13) с учетом одного
(R = 0, F = 0) или двух (R = 0, F = 0) параметров
в экспоненте.
где введено Djl = -iC
√m.Вэтомвыражениимы
учитывали только нерезонансные полюса. Если
можно предположить, что мы находимся достаточ-
4. ОТБОР ТОЧЕК И РАСЧЕТЫ ДЛЯ
но близко к первому полюсу, то основная зависи-
ОДНОГО СВЯЗАННОГО СОСТОЯНИЯ
мость от энергии определяется только первым чле-
Для апробации предложенных формул мы про-
ном в (16), а вклад всех остальных членов можно
извели подгонку по набору энергий, полученно-
учесть поправками, пропорциональными степеням
√
му диагонализацией гамильтониана с потенциалом
|Eλ|.
Вудса-Саксона (8), и сравнили полученные ре-
Тогда, учитывая (16) и (7), получим
зультаты с тем, что получается методами, предло-
женными в работах [4, 6] и NCFC [3], а также с
C(-)N+1,l(Eλ/ℏΩ)
=
(17)
решением данной модельной задачи стандартными
C(+)N+1,l(Eλ/ℏΩ)
численными методами.
(
)
При подгонке минимизировалось выражение
1
Dl
=
√
√
√
+
)2)
∑((
)2 (Ni
2
|Eλ| -
|Eb|
tot
E(1)iλ - E(2)i
(20)
√
λ
p
NM
+B+Q
|Eλ| + H|Eλ| +
i=1
Неизвестные здесь — Eb, Dl, B, Q и H, которые
Здесь p — число использованных для подгонки
надо определять подгонкой к имеющимся резуль-
значений энергии, добавлены множители, позво-
татам Eλ, полученным с теми или иными значения-
ляющие учесть с б ´ольшим весом значения, полу-
ми Ntot и ℏΩ.
ченные в б ´ольших модельных пространствах, NM
ЯДЕРНАЯ ФИЗИКА том 82
№4
2019
344
ШИРОКОВ и др.
Таблица 1. Подгоночные параметры для подгонки с 4 ≤ Ntot ≤ 20 c отбором точек по ℏΩ как показано на рис. 4 (для
метода NCFC в скобках указана погрешность экстраполяции)
Eb,
Ξ,
Al,
R,
F,
Dl,
Q,
H,
B
МэВ
кэВ Фм-1/2 МэВ-1/2 МэВ-3/2 МэВ1/2
МэВ-1/2
МэВ-1
Точное значение
-7.011
-
2.89
-
-
-
-
-
-
(13)
-7.011
1
2.9
0.65
0.02
-
-
-
-
(17)
-7.011
1
2.9
-
-
-59.93
-7.57
-4.2
-4.6
[9]
-7.011
2
-
-
-
-
-
-
-
NCFC
-7.008(2)
-
-
-
-
-
-
-
-
бралось равным наибольшему значению Nitot из
числом квантов Ntot. Эти соображения наклады-
вают другое условие снизу на допустимые значе-
подгоняемого набора. E(1)iλ — значения энергии,
ния ℏΩ при заданном значении Ntot, которое можно
полученные решением соответствующего уравне-
оценить как
ния (формулы (13) или (17)), параметризующего
2
(2Ntot + 3)ℏ
S-матрицу, E(2)iλ — собственные значения модель-
ℏΩ ≥ ℏΩmin =
,
(23)
mN2totR2
ного гамильтониана, полученные при тех же ℏΩ и
0
Ntot, что и E(1)iλ. В табл. 1 приводятся значения Ξ —
где R0 = RWS + D.
среднеквадратичного отклонения:
Здесь необходимо отметить, что метод, приве-
денный в работе [4], также предполагает отбор то-
∑(
)2
чек, связанный с ограничением значений ℏΩ снизу,
Ξ=√1
E(1)iλ - E(2)iλ
(21)
а именно допустимые значения ℏΩ должны удовле-
p
i=1
творять условию
√
m(Ntot + 3/2)ℏΩ ≥ Λ0,
(24)
Перед проведением подгонки нам надо опре-
делиться, какие результаты диагонализации мы
где величина Λ0 выбирается на основе поведения
можем использовать для анализа методом SS-
в импульсном пространстве взаимодействия (вооб-
HORSE, а какие — нет. Выше уже отмечалось,
ще говоря, нуклон-нуклонного, а не используемого
что метод SS-HORSE не работает для собствен-
в данной задаче потенциала Вудса-Саксона, кото-
ных состояний гамильтониана Eλ, полученных
рый играет роль среднего поля в ядре). Отметим
< 0,
впрочем, что условие (22) накладывает, как пра-
Ω
т.е. лежащих перед минимумом зависимости Eλ
вило, более сильные ограничения на допустимые
от ℏΩ [17]. Таким образом, мы будем использовать
значения ℏΩ, чем условия (23) и (24), так что в
далее только энергии Eλ, полученные с
дальнейшем можно ограничиться условием (23) на
значения ℏΩ снизу.
ℏΩ > ℏΩdEλ ,
(22)
dℏΩ
Кроме того, надо учесть, что при увеличении n
осцилляторные функции “сжимаются” и охваты-
где ℏΩdEλ обеспечивает минимум зависимости Eλ
dℏΩ
вают все меньшую область расстояний. Логичным
от ℏΩ при заданном значении Ntot.
будет потребовать, чтобы базис охватывал всю об-
ласть ядра и не учитывать результаты из модельных
Далее, используемый при диагонализации обре-
пространств, у которых классическая точка пово-
занного гамильтониана осцилляторный базис дол-
рота последней базисной осцилляторной волновой
жен обеспечивать адекватное описание волновой
функции лежит уже внутри потенциальной ямы, т.е.
функции внутри ядра или, в нашей модельной
оставить только результаты с
задаче, в области действия потенциала Вудса-
Саксона. В частности, хотя бы один узел одной
(2Ntot + 3)ℏ2
ℏΩ ≤ ℏΩmax =
(25)
из базисных функций должен попадать в область
mR2
0
действия потенциала. Поскольку плотность узлов
осцилляторных функций растет с ростом n, то
Чтобы убедиться в адекватности условия (25),
необходимо, чтобы в область действия потенциала
на рис. 3 мы представили результаты диагона-
попал хотя бы один узел последней из исполь-
лизации гамильтониана — нижайшие собственные
зуемых в базисе осцилляторных функций, соот-
энергии E0 как функции корня из скейлингового
ветствующей осцилляторному состоянию с полным
параметра
√s, полученные в различных модельных
ЯДЕРНАЯ ФИЗИКА том 82
№4
2019
ЭКСТРАПОЛЯЦИЯ ЭНЕРГИИ СВЯЗАННОГО СОСТОЯНИЯ
345
E0, МэВ
-1
3
-2
-3
2
1
-4
-5
-6
-7
1.0
1.5
2.0
2.5
√s, МэВ1/2
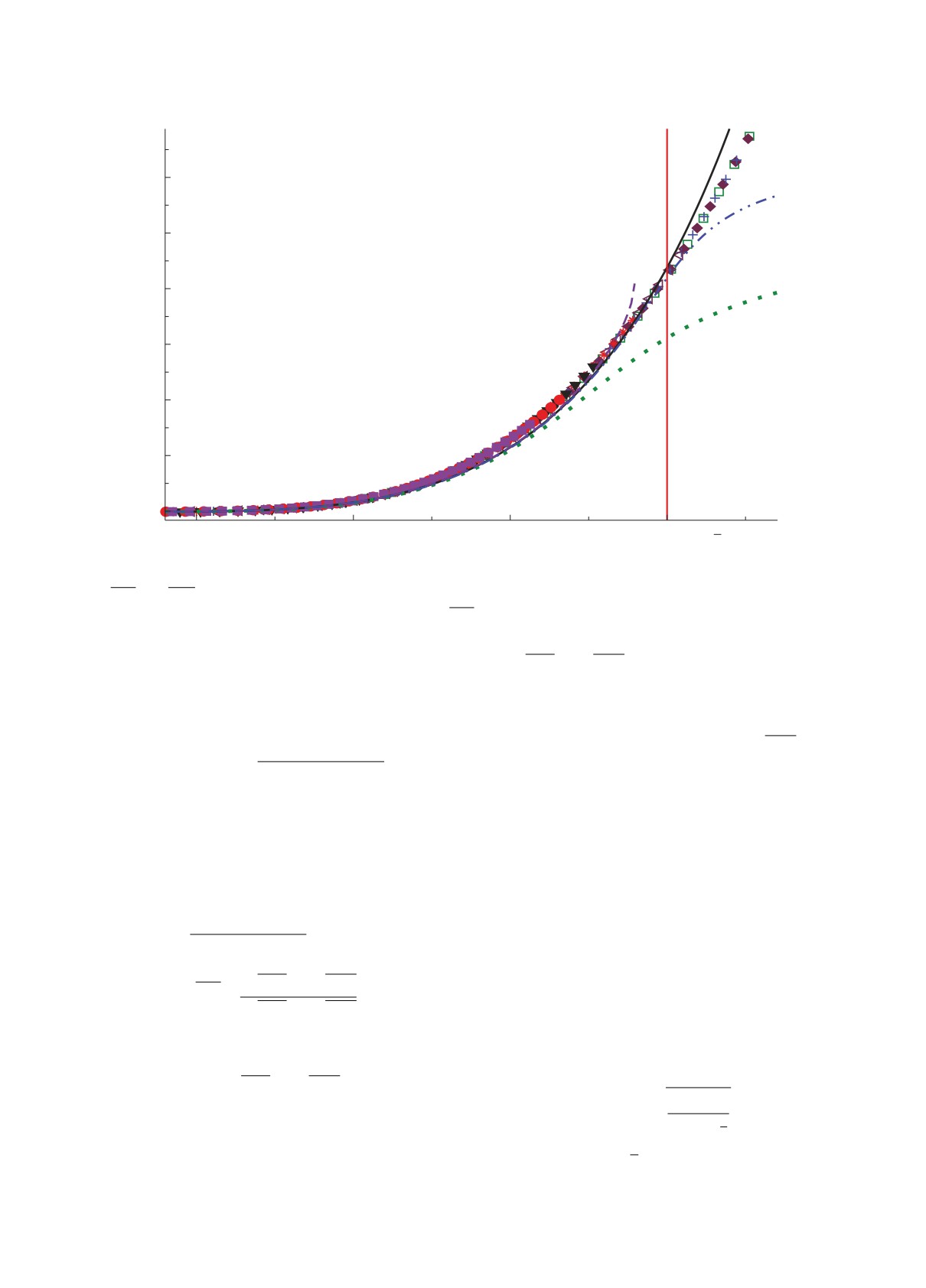
Рис. 3. Подгонка по формуле (27) в окрестности полюса (сплошная кривая) и ее разложения (19) в ряд по степеням
√
√
(
|Eb| -
|Eλ|). Цифрами 1, 2 и 3 обозначены кривые сообразно старшей степени, учтенной в разложении (19).
Вертикальная сплошная линия соответствует значению
√smax в условии (26) для Ntot = 6.
√
√
пространствах и удовлетворяющие условию (22),
по (
|Eb| -
|Eλ|) члены. Таким образом, при
но без учета ограничения (25). Условие (25) можно
использовании в подгонке выражения (17), кото-
переписать в виде ограничения на скейлинговый
рое фактически соответствует разложению (19),
параметр:
необходимо учитывать в нем хотя бы несколько
√
| или же
членов в разложении по степеням
|Eλ
2ℏ2(Ntot + 3/2)
s ≤ smax(Ntot) =
(26)
ограничиваться наборами собственных энергий,
mR20(Ntot + 7/2)
полученных с меньшими значениями ℏΩ, чем
Вертикальная линия на рис. 3 соответствует значе-
задаются условием (25).
нию smax для Ntot = 6.
Мы сопоставляем результаты экстраполяции на
На этом же рисунке мы приводим результаты
бесконечное базисное пространство, основанное
подгонки по простейшему варианту формулы (13)
на описанных выше подгонках, с экстраполяцией B
с двумя подгоночными параметрами R и Eb:
метода NCFC [3], которая основана на феномено-
логическом предположении об экспоненциальной
C(-)N+1,l(Eλ/ℏΩ)
сходимости энергий при увеличении Ntot, а также
=
(27)
с экстраполяцией, предложенной в работе [4]. В
C(+)N+1,l(Eλ/ℏΩ)
(√
)
последнем подходе подгонка осуществляется по
√
√
|Eb| +
|Eλ|
формуле
|Eλ|
=eR
√
√
|Eb| -
|Eλ|
Eλ = Eb + Ae-b/λsc ,
(28)
Также приведены линии, соответствующие раз-
где скейлинговый параметр λsc с учетом поправки,
ложению (19) экспоненты в выражении (13) в
предложенной в работе [9], задается формулой
√
√
ряд по степеням (
|Eb| -
|Eλ|). Видно, что
√
mc2ℏΩ
формула (27) описывает практически все точки
λsc) =
,
(29)
вплоть до ограничения (26). Однако разложение
Ntot +7
2
в ряд (19) перестает работать уже при меньших
значениях s, если в нем не учитывать кубические и пропорционален
√s.
ЯДЕРНАЯ ФИЗИКА том 82
№4
2019
346
ШИРОКОВ и др.
E0, МэВ
-5.8
-6.0
-6.2
-6.4
-6.6
-6.8
-7.0
20
40
60
80
"Ω, МэВ
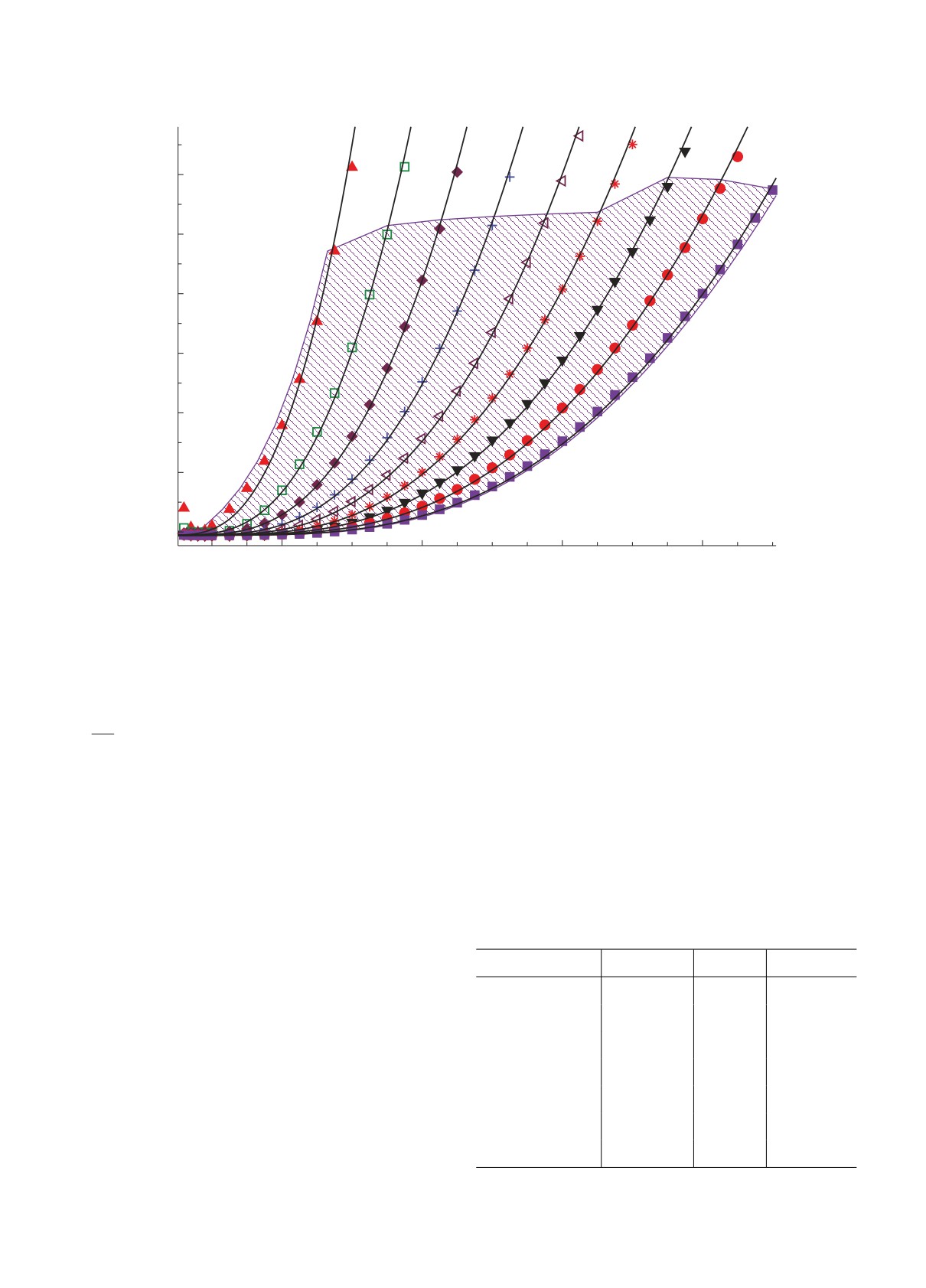
Рис. 4. Зависимость энергии нижайшего состояния E0 от ℏΩ для разных значений Ntot. Сплошные кривые — результат
подгонки по формуле (27). Отобранные для подгонки точки лежат в заштрихованной части рисунка.
На рис. 4 показаны наборы точек, по кото-
Важнейшим достоинством нашего подхода по
рым проводилась экстраполяция, отобранные в
сравнению с другими является возможность по-
соответствии с приведенными выше критериями
лучить также АНК. Рассчитанные значения АНК
ℏΩdEλ < ℏΩ ≤ ℏΩmax, и дополнительно отброшена
близки к теоретическому как в случае использова-
dℏΩ
ния формулы (13), так и при подгонке по форму-
часть точек для обеспечения подгонки по форму-
ле (17).
ле (17), а также зависимости E0 от ℏΩ для разных
С точки зрения приложений данного подхода к
Ntot, рассчитанные с параметрами, полученными в
исследованию конкретных ядер на основе расчетов
подгонке по формуле (27).
в NCSM следует отметить, что в многочастичных
задачах приходится довольствоваться результата-
До сих пор мы брали простейший вариант фор-
ми, полученными с существенным обрезанием ба-
мулы (13), полученной из свойств симметрии S-
матрицы — формулу (27). Однако проведенные на-
ми расчеты показали, что наилучшие результаты
Таблица 2. Сходимость результатов расчетов с ро-
получаются, если использовать полный вариант
стом Ntot
формулы (13), используя не только R, но и F
как подгоночный параметр. При использовании
Nmintot-Nmaxtot Eb, МэВ Al, Фм-1/2
формулы (17), как уже отмечалось, необходим учет
всех слагаемых, т.е. надо использовать пять подго-
Точное значение
-
-7.011
2.89
ночных параметров. Результаты проведенных нами
(13)
4-8
-7.015
2.92
подгонок представлены в табл. 1. Из этой табли-
(13)
4-10
-7.012
2.90
цы видно, что все методы позволяют предсказать
значение энергии связанного состояния Eb c высо-
(13)
4-20
-7.011
2.90
кой точностью. Интересно при этом отметить, что
(17)
4-8
-7.015
2.93
экстраполяция по методу NCFC дает несколько
меньшее значение энергии связи по сравнению с
(17)
4-10
-7.011
2.89
численным решением и другими методами экстра-
(17)
4-20
-7.011
2.89
поляции.
ЯДЕРНАЯ ФИЗИКА том 82
№4
2019
ЭКСТРАПОЛЯЦИЯ ЭНЕРГИИ СВЯЗАННОГО СОСТОЯНИЯ
347
E0, МэВ
-5.5
-6.0
-6.5
-7.0
0
20
40
60
80
"Ω, МэВ
Рис. 5. Предсказание собственных энергий при более высоких значениях Ntot, основываясь на результатах, полученных
c 6 ≤ Ntot ≤ 8, лежащих в заштрихованной области.
зиса, т.е. со сравнительно небольшими значения-
что данный метод позволяет предсказать положе-
ми Ntot, когда не удается достичь хорошей сходи-
ние полюсов S-матрицы, отвечающих связанным
мости полученных энергий. В связи с этим необ-
состояниям, и величину вычета в этих полюсах.
ходимо исследовать, позволяет ли данный метод
Проведенное сравнение с методами экстраполя-
предсказать значения энергий в б ´ольших модель-
ции, предложенными ранее в работах [3] и [4, 9],
ных пространствах, основываясь на результатах
показало, что данный подход позволяет предска-
подгонки точек, полученных с малыми значениями
зывать энергии связи не хуже других методов,
Ntot.
но основное его достоинство в том, что он поз-
воляет рассчитать АНК — важные наблюдаемые
На рис. 5 показаны результаты предсказания
в ядерных системах. В наших расчетах значение
энергий в б ´ольших модельных пространствах с
АНК получилось близким к точному решению, как
использованием экстраполяции по меньшим мо-
при экстраполяции по формулам (13), так и при
дельным пространствам (6 ≤ Ntot ≤ 8) на основе
расчетах по формулам (17).
формулы (17). Из табл. 2 можно увидеть, что
предлагаемый метод позволяет предсказывать ре-
Работа выполнена при поддержке Российского
зультаты в больших модельных пространствах при
научного фонда (проект № 16-12-10048).
подгонке по меньшим модельным пространствам,
т.е. обладает приемлемой сходимостью. Отметим,
что формулы (13) и (17) дают значение АНК,
СПИСОК ЛИТЕРАТУРЫ
близкое к точному.
1. B. R. Barrett, P. Navr ´atil, and J. P. Vary, Prog. Part.
Nucl. Phys. 69, 131 (2013).
2. J. P. Vary, P. Maris, H. Potter, M. A. Caprio, R. Smith,
5. ЗАКЛЮЧЕНИЕ
S. Binder, A. Calci, S. Fischer, J. Langhammer,
R. Roth, H. M. Aktulga, E. Ng, C. Yang,
Предложен метод экстраполяции результатов
D. Oryspayev, M. Sosonkina, and E. Saule, in
расчетов в осцилляторном базисе связанных со-
Proceedings of the International Conference
стояний квантовых систем на случай бесконеч-
“Nuclear Theory in the Supercomputing
ного базиса, являющийся развитием метода SS-
Era-2014” (NTSE-2014), Khabarovsk, Russia,
HORSE. На примере модельной задачи показано,
June 23-27, 2014, Ed. by A. M. Shirokov and
ЯДЕРНАЯ ФИЗИКА том 82
№4
2019
348
ШИРОКОВ и др.
A. I. Mazur (Pacific National University, Khabarovsk,
G. A. Negoita, J. P. Vary, G. R. Luecke, P. Maris,
Russia, 2015), p. 154.
A. M. Shirokov, I. J. Shin, Y. Kim, E. G. Ng, C. Yang,
3.
P. Maris, J. P. Vary, and A. M. Shirokov, Phys. Rev. C
M. Lockner, and G. M. Prabhu, arXiv:1810.04009
79, 014308 (2009).
[nucl-th] (Принято в печати в Phys. Rev. C).
4.
S. A. Coon, M. I. Avetian, M. K. G. Kruse,
17.
A. M. Shirokov, A. I. Mazur, I. A. Mazur, and
U. van Kolck, P. Maris, and J. P. Vary, Phys. Rev. C
J. P. Vary, Phys. Rev. C 94, 064320 (2016).
86, 054002 (2012).
18.
I. A. Mazur, A. M. Shirokov, A. I. Mazur, and
5.
S. A. Coon, in Proceedings of the International
J. P. Vary, Phys. Part. Nucl. 48, 84 (2017).
Conference
“Nuclear Theory in the Super-
19.
Л. Д. Блохинцев, А. И. Мазур, И. А. Мазур,
computing Era-2012” (NTSE-2012), Khabarovsk,
Д. А. Савин, А. М. Широков, ЯФ 80, 102 (2017)
Russia, June 18-22, 2012, Ed. by A. M. Shirokov
[Phys. At. Nucl. 80, 226 (2017)].
and A. I. Mazur (Pacific National University,
20.
Л. Д. Блохинцев, А. И. Мазур, И. А. Мазур,
Khabarovsk, Russia, 2013), p. 171.
Д. А. Савин, А. М. Широков, ЯФ 80, 619 (2017)
6.
R. J. Furnstahl, G. Hagen, and T. Papenbrock, Phys.
[Phys. At. Nucl. 80, 1093 (2017)].
Rev. C 86, 031301(R) (2012).
21.
A. M. Shirokov, A. I. Mazur, I. A. Mazur,
7.
S. N. More, A. Ekstr ¨om, R. J. Furnstahl, G. Hagen,
E. A. Mazur, I. J. Shin, Y. Kim, L. D. Blokhintsev,
and T. Papenbrock, Phys. Rev. C 87, 044326 (2013).
and J. P. Vary, Phys. Rev. C 98, 044624 (2018).
8.
M. K. G. Kruse, E. D. Jurgenson, P. Navr ´atil,
22.
E. J. Heller and H. A. Yamani, Phys. Rev. A 9, 1201
B. R. Barrett, and W. E. Ormand, Phys. Rev. C 87,
(1974).
044301 (2013).
23.
H. A. Yamani and L. J. Fishman, J. Math. Phys. 16,
9.
R. J. Furnstahl, S. N. More, and T. Papenbrock, Phys.
410 (1975).
Rev. C 89, 044301 (2014).
24.
Yu. F. Smirnov and Yu. I. Nechaev, Kinam 4, 445
10.
D. S ¨a ¨af and C. Forss ´en, Phys. Rev. C 89, 011303(R)
(1982); Ю. И. Нечаев, Ю. Ф. Смирнов, ЯФ 35, 1385
(2014).
(1982) [Sov. J. Nucl. Phys. 35, 808 (1982)].
11.
S. K ¨onig, S. K. Bogner, R. J. Furnstahl, S. N. More,
25.
С. А. Зайцев, Ю. Ф. Смирнов, А. М. Широков,
and T. Papenbrock, Phys. Rev. C 90, 064007 (2014).
ТМФ 117, 227 (1998) [Theor. Math. Phys. 117, 1291
12.
R. J. Furnstahl, G. Hagen, T. Papenbrock, and
(1998)].
K. A. Wendt, J. Phys. G 42, 034032 (2015).
26.
J. M. Bang, A. I. Mazur, A. M. Shirokov,
13.
K. A. Wendt, C. Forss ´en, T. Papenbrock, and D. S ¨a ¨af,
Yu. F. Smirnov, and S. A. Zaytsev, Ann. Phys.
Phys. Rev. C 91, 061301(R) (2015).
(N.Y.) 280, 299 (2000).
14.
S. A. Coon and M. K. G. Kruse, Int. J. Mod. Phys. E
27.
Л. Д. Блохинцев, И. Борбей, Э. И. Долинский,
25, 1641011 (2016).
ЭЧАЯ 8, 1189 (1977)
[Sov. J. Part. Nucl. 8, 485
15.
I. J. Shin, Y. Kim, P. Maris, J. P. Vary, C. Forss ´en,
(1977)].
J. Rotureau, and N. Michel, J. Phys. G 44, 075103
28.
H. A. Yamani and M. S. Abdelmonem, J. Phys. A 26,
(2017).
L1183 (1993).
16.
A. Negoita, G. R. Luecke, J. P. Vary, P. Maris,
29.
H. A. Yamani, Eur. J. Phys. 34, 1025 (2013).
A. M. Shirokov, I. J. Shin, Y. Kim, E. G. Ng,
30.
R. G. Newton, Scattering Theory of Waves and
and C. Yang, in Proceedings of the Ninth
Particles, 2nd ed. (Springer-Verlag, New York,
International Conference on Computational
1982).
Logics, Algebras, Programming, Tools, and
Benchmarking (COMPUTATION TOOLS 2018),
31.
А. И. Базь, Я. Б. Зельдович, А. М. Переломов, Рас-
February 18-22, 2018, Barcelona, Spain (IARIA,
сеяние, реакции и распады в нерелятивистской
2018), p. 20; arXiv:1803.03215 [physics.comp-ph];
квантовой механике (Наука, Москва, 1971).
SS-HORSE EXTRAPOLATION OF BOUND-STATE ENERGY
A. M. Shirokov1),2),3), V. A. Kulikov1),2), A. I. Mazur2)
1)Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
2)Department of Physics, Pacific National University, Khabarovsk, Russia
3)Department of Physics and Astronomy, Iowa State University, Ames, Iowa, USA
We propose a new approach to the extrapolation of bound-state energies obtained using the oscillator basis.
This approach makes it possible to calculate also the asymptotic normalization constants. We present the
derivation of this extrapolation technique and verify it by applying to a model problem.
ЯДЕРНАЯ ФИЗИКА том 82
№4
2019