ЯДЕРНАЯ ФИЗИКА, 2019, том 82, № 5, с. 382-387
ЯДРА
ПРИВЕДЕННЫЕ ВЕРОЯТНОСТИ E1- И E2-ПЕРЕХОДОВ В СПЕКТРЕ
ПЕРЕМЕННОЙ ЧЕТНОСТИ ТЯЖЕЛЫХ ЧЕТНО-ЧЕТНЫХ ЯДЕР
© 2019 г. М. С. Надирбеков1)*, С. Н. Кудиратов1), Ф. Н. Темиров2)
Поступила в редакцию 22.12.2018 г.; после доработки 19.02.2019 г.; принята к публикации 08.01.2019 г.
Изучены внутри/междуполосные приведенные вероятности E1- и E2-переходов в коллективные
состояния yrast- и первой nonyrast-полос переменной четности ядер в области лантанидов150Nd,
154Sm,154,160Gd,162,164Er и актинидов232Th,236,238U. Вычислены значения величин B(E1) и B(E2),
а также проведены их сравнения с доступными экспериментальными данными. Учтены изменения
поверхностной деформации ядра при коллективном возбуждении.
DOI: 10.1134/S0044002719040147
1. ВВЕДЕНИЕ
вырождены и связаны наличием туннельного пе-
рехода между формами ядер с положительной и
Спектр коллективных состояний ядер с квад-
отрицательной компонентами октупольной дефор-
рупольной и октупольной деформациями харак-
мации [13] и всегда [13, 20]
теризуется вращательной полосой переменной
ϵ′+ν < ϵ′-ν.
(1)
четности
[1-13]. Хорошее совпадение между
экспериментальными и теоретическими данными
Вычисления приведенных вероятностей E1- и
для энергетических уровней различных полос
E2-переходов выполнены в работах [21, 22]. В
позволяет использовать неадиабатическую модель
работе [21] был использован потенциал Дэвидсона
аксиально-симметричных ядер для исследования
для поверхностных деформаций, в [22] использован
внутри/междуполосных приведенных вероятно-
потенциал гармонического осциллятора в модели
стей EL-переходов (L = 1, 2, 3) как необходимый
CQOM (Coherent Quadrupole-Octupole Motion).
тест на надежность полученных результатов в
Но в этих работах изменения поверхностных ко-
модели. Отметим, что существует альтернативное
лебаний ядра при коллективном возбуждении не
описание коллективных полос переменной четно-
учитываются.
сти в рамках кластерного подхода [14-16].
Целью представленной работы является опи-
В представленной модели [17, 18] используется
сание внутри/междуполосных приведенных веро-
соответствующий потенциал, позволяющий разде-
ятностей E1- и E2-переходов. Вычислены вероят-
лять переменные в полярных координатах. В ана-
ности E1- и E2-переходов, и проведено сравнение
литическом виде получены энергетический спектр
с доступными экспериментальными данными. Как
и волновые функции возбужденных состояний по-
будет показано ниже, анализ позволит сделать
лос переменной четности четно-четных ядер ме-
вывод о применимости модельного формализма.
тодом Давыдова-Чабана [19]. Использованы по-
В разд. 2 представлены волновые функции, по-
тенциалы Гаусса и гармонического осциллятора
лученные путем решения уравнения Шредингера
для поверхностных колебаний. Учтены изменения
для потенциалов поверхностных колебаний Гаус-
поверхностных колебаний ядра в его коллективном
са и гармонического осциллятора. В разд. 3 и 4
возбуждении. В работах [17, 18] энергетические
представлены приведенные вероятности E2- и E1-
уровни выражаются параметрами: ℏω — энергети-
переходов соответственно. В разд. 5 представлены
ческий множитель (в кэВ), ϵ′±ν — параметр рас-
результаты вычислений и сравнения с эксперимен-
щепления (в кэВ) и μ — безразмерный параметр
тальными данными. В разд. 6 приведены заключи-
неадиабатичности. Величины ϵ′+ν и ϵ′-ν двукратно
тельные выводы.
1)Институт ядерной физики, АН Республики Узбекистан,
Улугбек, Ташкент.
2. ВОЛНОВЫЕ ФУНКЦИИ
2)Самаркандский государственный медицинский институт,
Узбекистан.
Волновые функции Φ±I(σ, ε), полученные при
*E-mail: mnadirbekov@yandex.ru
решении уравнения Шредингера в полярных коор-
382
ПРИВЕДЕННЫЕ ВЕРОЯТНОСТИ E1- И E2-ПЕРЕХОДОВ
383
динатах (σ, ε), имеют следующий вид [17, 18]:
q± является корнем трансцендентного уравне-
ния [19]:
Φ±Iν(σ,ε) = F±I(σ)χν(ξ±),
(2)
(
)
p±Iν
где
H±
-
= 0.
(12)
[
]
qν
μ±
(ξ±)2
Iν
χν(ξ±) = NνHν(ξ±)exp -
,
(3)
2
с
√
Bωε(ε ∓ ε0)
√
3. ПРИВЕДЕННЫЕ ВЕРОЯТНОСТИ
ξ± =
,
ωε =
Cε/B,
(4)
E2-ПЕРЕХОДОВ
2
где Nν — коэффициент нормировки, Hν (ξ±) — по-
Электрический квадрупольный переход между
лином Эрмита, B — массовый параметр, ωε и Cε
энергетическими уровнями коллективных состоя-
являются частотой и параметром жесткости для ε
ний выражается [13]
колебаний соответственно.
B(E2, q±νIi → q±ν
If ) =
(13)
i
f
Теперь определим F±I(σ) [17, 18]:
±
{
}
= Ba(E2,Ii → If )S2
±
(E2)G2(ε0),
Nq±
H
(ξ)
qνq
i
νf
ν
qν
ξ2
F±
(σ) =
√
exp
-
,
(5)
Iqν
2σ
2
здесь [13]
здесь Nq±
— коэффициент нормировки, H±
(ξ) —
3
ν
qν
Ba(E2,Ii → If ) =
Q20(Ii200|If 0)2,
(14)
16π
функция Эрмита, которая имеет вид
[
]-1
приведенные вероятности E2-переходов жестко-
H±
(ξ) =
2Γ(-q±ν)
×
(6)
qν
го аксиально-симметричного ротатора, Q0 — внут-
)
ренний квадрупольный момент ядра [11]. Функ-
∑
±
(-1)k
(k-q
ν
×
(2ξ)k · Γ
,
ция G2(ε0) учитывает вклад угловой части волно-
k!
2
k=0
вой функции (2) на приведенные вероятности E2-
переходов:
где
p±Iν(σ - σ0)
p±Iν
∫
ξ=
,
-
≤ ξ < ∞.
(7)
cos ε
μ±IνσIν
μ±
G2(ε0) =
χν(ξ±)
χν′(ξ±)sin εdε.
(15)
Iν
cos ε0
-π/2
Для потенциала гармонического осциллятора
величина p±Iν удовлетворяет следующему равен-
Вводим новый безразмерный параметр
ству:
√
]
[I(I + 1)
1
5
(p±Iν )3(p±Iν - 1) = μ4
∓ϵ′±ν ,
(8)
Ω2 =
(16)
3
4
√2gπQ0G2(ε0).
и
Таким образом,
{
}1
μ
[
]
μ±Iν = μ
1+
I(I + 1) ∓ 2ϵ′±ν
4 .
(9)
B(E2, q±ννiIi → q±ν
νfIf) =
(17)
i
f
p±
Iν
= Ω22(Ii200|If 0)2S2
(E2).
qν
qν
Такие же величины для потенциала Гаусса:
i
f
(p±Iν )3(p±Iν - 1) exp[-(p±Iν - 1)2] =
(10)
Множитель Sq±
]
νi qνf (E2)определяетсявыраже-
[I(I + 1)
нием:
=μ4
∓ϵ′∓ν
3
Nq±
Nq±
νi
νf
и
Sq±
×
(18)
{
νi qνf(E2)=
2σ
0
[
]
∞
√
√
∫
μ±Iν = μ
1 - 2(p±Iν - 1)2
×
(11)
1
1
×
×
[
]
μ±Iν
ξ+1
μ± ξ + 1Iν
±
i
f
× exp
-(p±Iν - 1)2
+
p
-
Iν
}-1
μ±
(
Iν
4
μ
)4 [
]
+
I(I + 1) ∓ 3ϵ′∓ν
,
×H±
(ξ)H±
(ξ)e-ξ2 dξ.
qν
qν
p±Iν
i
f
ЯДЕРНАЯ ФИЗИКА том 82
№5
2019
384
НАДИРБЕКОВ и др.
Таблица 1. Значения подгоночных параметров для рассматриваемых ядер
Параметры
150Nd
154Gd
154Sm
160Gd
164Er
232Th
236U
238U
Потенциал гармонического осциллятора
ℏω
682.03
929.3
970.144
803.426
945.576
786.733
887.721
894.952
ϵ′+0
0.061
0.274
5.145
8.848
2.622
0.549
0.594
0.19
ϵ′-0
7.73
9.79
6.172
9.14
12.9
12.456
13.879
12.316
ϵ′+1
0.35
3.145
2.6009
1.223
0.17
2.622
0.28
0.271
ϵ′-1
4.39
3.231
2.7047
6.592
7.63
3.464
0.343
0.415
μ
0.4127
0.342
0.2701
0.2926
0.3
0.2473
0.222
0.2207
Потенциал Гаусса
ℏω
791.83
1100.564
1119.526
982.27
862.892
864.251
966.45
994.323
ϵ′+0
0.06
0.147
0.166
9.196
6.37
3.867
0.34
0.824
ϵ′-0
15.68
22.289
22.05
22.48
25.246
22.056
29.697
25.512
ϵ′+1
1.592
4.85
1.83
0.42
0.155
0.9209
0.2277
3.345
ϵ′-1
6.828
4.87
5.69
14.379
14.147
1.271
0.242
3.42
μ
0.3751
0.3058
0.2632
0.2652
0.3069
0.2316
0.2112
0.206
Внутри [Iyr → (I - 2)yr или Ifir → (I - 2)fir] /между
Множитель S2
(E1) определяется выраже-
qνqν
i
f
[Iyr → (I - 2)fir или Ifir → (I - 2)yr]-полосные при-
нием
веденные вероятности E2-переходов (13) выража-
Sq±
(23)
ются параметрами: ϵ′+ν, ϵ′-ν, Ω2 и μ3).
νi qνf(E1)=NqνiNqνf ×
∫
∞
±
p
√
Iνi
×
×
4. ПРИВЕДЕННЫЕ ВЕРОЯТНОСТИ
2μ±Iν
σIνiξ + 2σ0p±
i
Iνi
E1-ПЕРЕХОДОВ
p±
-
Iν
±
μIν
Приведенные вероятности E1-переходов удобно
выражать через приведенные вероятности E1-
p±Iν
f
переходов аксиально-симметричного ротатора
×√
×
2μ±Iν
σIνf ξ + 2σ0p±
Ba(E1,Ii → If):
f
Iνf
B(E1, Ii + If ) =
(19)
×H±
(ξ)H±
(ξ)e-ξdξ.
qν
qν
i
f
= Ba(E1,Ii → If )S2
(E1)G1(ε0),
qνqν
i
f
Внутри
[Iyr → (I - 1)yr или Ifir → (I - 1)fir] /
между [Iyr → (I - 1)fir или Ifir → (I - 1)yr]-полосные
3
Ba(E1,Ii → If ) =
D20(Ii100|If 0)2.
(20)
приведенные вероятности E1-переходов (19) выра-
4π
и μ.
жаются параметрами: ϵ′+ν, ϵ′-ν, Ω1
G1(ε0) учитывает вклад угловой части волновой
функции
(2) на приведенные вероятности E1-
переходов:
5. СРАВНЕНИЕ С
ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ
∫
sin 2ε
Вычисления матричных элементов выраже-
G1(ε0) =
χν(ξ±)
χν′ (ξ±)sin εdε.
(21)
sin 2ε0
ний (18) и (23) являются громоздкими. Следо-
-π/2
вательно, матричные элементы этих выражений
вычисляются численно с учетом значения величин
Вводим новый безразмерный параметр
q±ν в (12) и p±ν для формул (8), (10), которые были
√
получены при расчете энергетических уровней
1
3
коллективных состояний
[17,
18]. Матричные
Ω1 =
(22)
2
√2gπD0G1(ε0).
элементы (18) и (23) для случая, когда q±ν яв-
ляются целыми, были вычислены в работе [19].
3)Индексы означают: yr — yrast-полоса и fir — первая
Но в действительности значения квантовых чисел
nonyrast-полоса.
q±
должны быть не целыми, т.е. они являются
ν
ЯДЕРНАЯ ФИЗИКА том 82
№5
2019
ПРИВЕДЕННЫЕ ВЕРОЯТНОСТИ E1- И E2-ПЕРЕХОДОВ
385
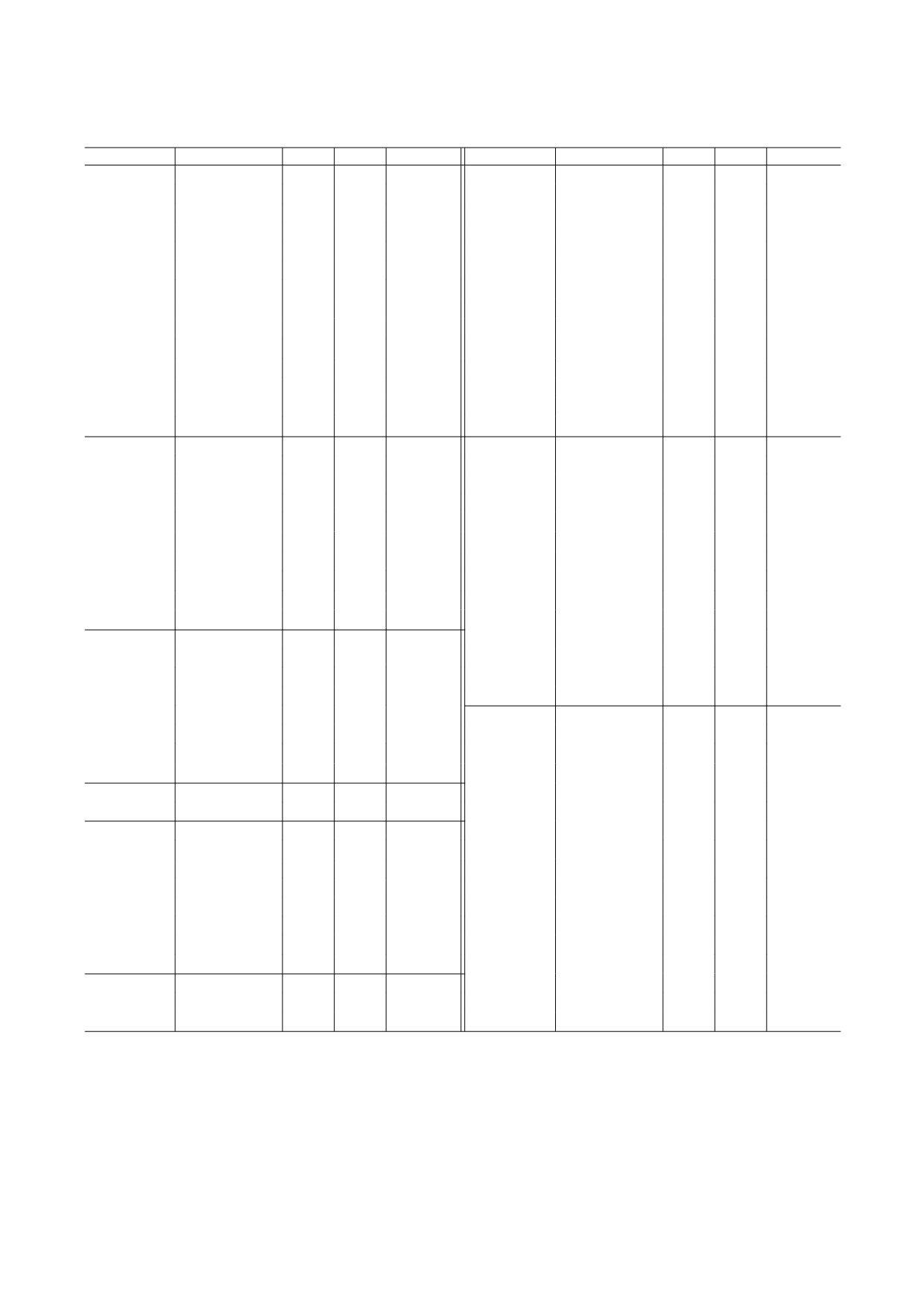
Таблица 2. Сравнения внутри/междуполосных приведенных вероятностей E2-переходов (в единицах Вайскопфа
(W. u.)) в энергетических уровнях yrast- и первой nonyrast-полос с экспериментальными данными [23]
Ядро
E2-переходы
[17]
[18]
Exp. [23]
Ядро
E2-переходы
[17]
[18]
Exp. [23]
150Nd
2+yr → 0+yr
121.8
122
116.3
8+yr → 6+yr
327.2
327.2
344
Ω2 = 1.7
4+yr → 2+yr
173.1
174.3
180.7
10+yr → 8+yr
336
336
363
6+yr → 4+yr
192.8
192.5
206.9
12+yr → 10+yr
342
342
370
8+yr → 6+yr
205.3
200.4
216.23
14+yr → 12+yr
346.3
346.3
390
10+yr → 8+yr
209
207
201
16+yr → 14+yr
349.5
349.5
390
12+yr → 10+yr
212.2
211.7
173
18+yr → 16+yr
352
352
450
2+fir → 0+yr
12.2
9.9
0.75
20+yr → 18+yr
354
354
360
2+fir → 2+yr
18.8
14.8
10.3
22+yr → 20+yr
355.7
355.7
420
4+fir → 2+yr
18.6
13.4
0.015
24+yr → 22+yr
357.1
357.1
240
0+fir → 2+yr
64.8
49.9
43.1
26+yr → 24+yr
358.2
358.2
350
2+fir → 4+yr
38.3
24.9
19.7
28+yr → 26+yr
359.2
359.2
700
4+fir → 6+yr
35.2
21.2
9.2
2+fir → 0+yr
6.5
5.7
2.8
2+fir → 0+fir
118.3
117.8
160.13
2+fir → 2+yr
9.3
8.2
0.52
4+fir → 2+fir
166.3
172.7
23.8
2+fir → 4+yr
17.4
16.2
3.3
154Gd
2+yr → 0+yr
156.7
156.7
157
236U
2+yr → 0+yr
243.8
244.7
250
Ω2 = 1.96
4+yr → 2+yr
223.8
223.8
245
Ω2 = 3.256
4+yr → 2+yr
348.4
349.6
357
6+yr → 4+yr
246.9
246.5
285
6+yr → 4+yr
383.7
385.1
385
8+yr → 6+yr
258.6
258.1
312
8+yr → 6+yr
401.6
403.1
390
10+yr → 8+yr
265.4
265.1
360
10+yr → 8+yr
412.5
414.1
360
2+fir → 0+yr
10.7
8.2
0.86
12+yr → 10+yr
419.8
421.4
410
2+fir → 2+yr
15.3
11.7
6
14+yr → 12+yr
425.1
426.7
450
0+fir → 2+yr
53.7
40.5
52
16+yr → 14+yr
429.1
430.6
380
2+fir → 4+yr
28.9
20.4
19
18+yr → 16+yr
432.2
433.7
490
2+fir → 0+fir
160.6
155.1
97
20+yr → 18+yr
434.6
436.2
510
154Sm
2+yr → 0+yr
170.1
170.1
176
22+yr → 20+yr
436.7
438.3
520
Ω2 = 2.042
4+yr → 2+yr
243
243
245
24+yr → 22+yr
438.4
440
670
6+yr → 4+yr
267.6
267.6
289
26+yr → 24+yr
439.8
441.4
670
8+yr → 6+yr
280.1
280.1
319
28+yr → 26+yr
441
442.7
1100
10+yr → 8+yr
287.7
287.7
314
238U
2+yr → 0+yr
267
267
281
12+yr → 10+yr
292.8
292.8
282
Ω2 = 3.42
4+yr → 2+yr
381.4
381.4
2+fir → 0+yr
7.1
6.4
0.58
6+yr → 4+yr
420.1
420.1
2+fir → 4+yr
18.2
16.4
<2.4
8+yr → 6+yr
439.8
439.8
410
160Gd
2+yr → 0+yr
201.5
201.5
201.2
10+yr → 8+yr
451.7
451.7
480
Ω2 = 2.28
4+yr → 2+yr
287.8
287.9
12+yr → 10+yr
459.7
459.7
500
164Er
2+yr → 0+yr
181.5
181.5
206
14+yr → 12+yr
465.5
465.5
491
Ω2 = 2.2
4+yr → 2+yr
259.3
259.3
260
16+ → 14+yr
469.8
469.8
490
6+yr → 4+yr
285.6
285.6
18+yr → 16+yr
473.2
473.2
480
8+yr → 6+yr
299
299
343
20+yr → 18+yr
475.9
475.9
460
10+yr → 8+yr
307.1
307.2
353
22+yr → 20+yr
478.1
478.1
490
12+yr → 10+yr
312.6
312.6
294
24+yr → 22+yr
480
480
530
14+yr → 12+yr
316.5
316.5
<526
26+yr → 24+yr
481.6
481.6
585
2+fir → 0+yr
9.4
10.5
0.23
28+yr → 26+yr
482.9
482.9
540
232Th
2+yr → 0+yr
198.6
198.6
198
30+yr → 28+yr
484.1
484.1
184
Ω2 = 2.9
4+yr → 2+yr
283.8
283.8
286
2+fir → 0+yr
6.9
5.9
0.38
6+yr → 4+yr
312.5
312.5
326
решениями трансцендентного уравнения (12). В
В табл. 2 представлены внутри/междуполосные
приведенные вероятности E2-переходов (в еди-
табл. 1 даны значения подгоночных параметров для
рассматриваемых ядер.
ницах Вайскопфа (W.u.)) в yrast- и первой
ЯДЕРНАЯ ФИЗИКА том 82
№5
2019
386
НАДИРБЕКОВ и др.
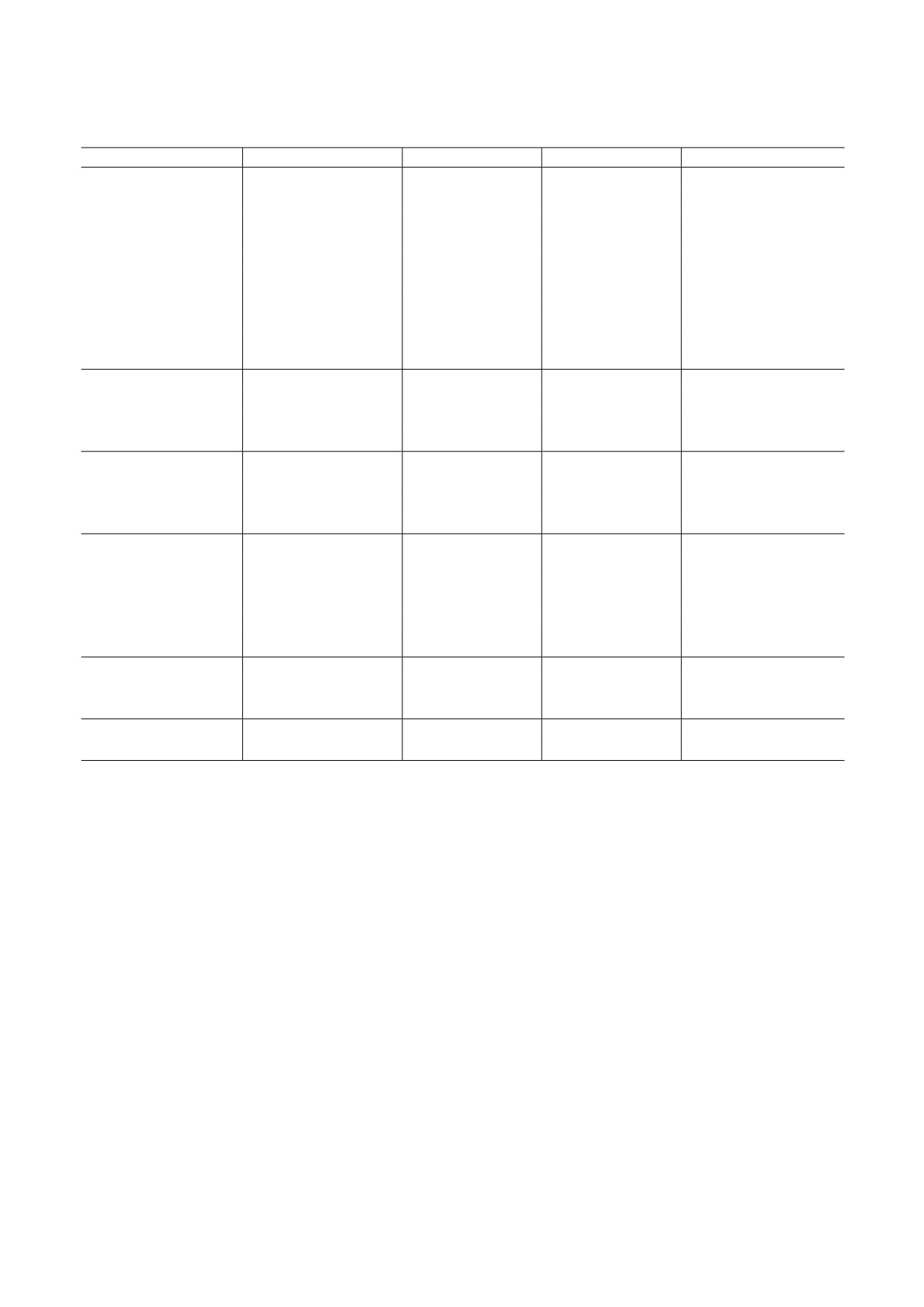
Таблица 3. Сравнения внутри/междуполосных приведенных вероятностей E1-переходов (в единицах Вайскопфа
(W. u.)) в энергетических уровнях yrast- и первой nonyrast-полос с экспериментальными данными [23]
Ядро
E1-переходы
[17]
[18]
Exp. [23]
150Nd
1-yr → 2+yr
0.0074
0.0074
0.0074
Ω1 = 0.0142
3-yr → 4+yr
0.0037
0.0064
0.0045
5-yr → 6+yr
0.0064
0.0061
0.007
1-yr → 0+yr
0.0049
0.0036
0.0039
3-yr → 2+yr
0.0068
0.0047
0.0042
5-yr → 4+yr
0.0063
0.0050
0.007
3-fir → 4+fir
8.0 × 10-4
1.1 × 10-5
3.7 × 10-4
3-fir → 2+fir
6.0 × 10-4
1.0 × 10-5
8.1 × 10-5
3-fir → 4+yr
7.1 × 10-6
3.6 × 10-4
1.7 × 10-4
3-fir → 2+yr
9.1 × 10-6
4.8 × 10-4
8.0 × 10-5
154Gd
1-yr → 0+yr
0.0436
0.0449
0.0436
Ω1 = 0.05
1-yr → 2+yr
0.0871
0.09
0.0485
1-yr → 0+fir
0.0029
0.0022
0.0057
1-yr → 2+fir
0.0037
0.0027
0.0064
154Sm
1-yr → 0+yr
0.0058
0.0058
0.0058
Ω1 = 0.018
1-yr → 2+yr
0.0116
0.0116
0.0113
3-yr → 2+yr
0.0074
0.0075
0.008
3-yr → 4+yr
0.0099
0.01
0.0092
160Gd
1-yr → 2+yr
0.0065
0.0065
0.006
Ω1 = 0.0136
1-yr → 0+yr
0.0032
0.0032
0.0032
3-yr → 4+yr
0.0055
0.0056
0.0013
3-yr → 2+yr
0.0042
0.0041
0.0016
1-fir → 2+yr
0.00035
0.00027
0.001
1-fir → 0+yr
0.00017
0.00011
0.00062
162Er
1-yr → 0+yr
1.2 × 10-7
1.2 × 10-7
-
ΩG1 = 0.0008
3-fir → 2+yr
1.5 × 10-7
1.5 × 10-7
<1.4 × 10-7
ΩO1 = 0.00008
3-fir → 4+yr
1.9 × 10-7
2.1 × 10-7
<1.1 × 10-7
238U
2+fir → 1-yr
1.3 × 10-4
1.2 × 10-4
1.1 × 10-4
Ω1 = 0.018
2+fir → 3-yr
2.0 × 10-4
1.7 × 10-4
3.5 × 10-4
nonyrast-полосах для деформируемых аксиально-
симметричных четно-четных ядер:150Nd,154Sm,
симметричных четно-четных ядер:150Nd,154Sm,
154,160Gd,
162Er и 238U с квадрупольной и ок-
154,160Gd,164Er,232Th и236,238U с квадрупольной
тупольной деформациями. Из табл. 3 ясно, что
и октупольной деформациями. Для всех рассмат-
представленная модель хорошо описывает приве-
денные вероятности E1-переходов в yrast-полосе
риваемых ядер внутриполосные приведенные веро-
рассматриваемых ядер.
ятности E2-переходов в yrast-полосе описываются
Отметим, что значения параметров Ω1 и Ω2
хорошо. Это показывает, что в yrast-полосе вра-
принимают одинаковые значения для обоих по-
щательное движение играет доминирующую роль.
Но междуполосные вероятности E2-переходов,
тенциалов, за исключением ядра164Er в случае
E1-переходов. По нашим расчетам Ω1 < Ω2, это
например 2+fir → 0+yr; 4+fir → 2+yr и 4+fir → 2+fir всех рас-
приводит и, как следствие, к основному вкладу
сматриваемых ядер, описываются плохо. Кажется,
квадрупольных колебаний поверхности тяжелых
что здесь необходимо учесть более сложный вид
ядер.
вращательно-колебательного движения.
6. ЗАКЛЮЧЕНИЕ
В табл. 3 представлены внутри/междуполосные
приведенные вероятности E1-переходов (в еди-
Представленная работа обеспечивает модель-
ницах Вайскопфа (W.u.)) в yrast- и первой
ное описание внутри/междуполосных приведен-
nonyrast-полосах для деформируемых аксиально-
ных вероятностей E1- и E2-переходов в тяжелых
ЯДЕРНАЯ ФИЗИКА том 82
№5
2019
ПРИВЕДЕННЫЕ ВЕРОЯТНОСТИ E1- И E2-ПЕРЕХОДОВ
387
четно-четных ядрах на основе неадиабатической
R. S. Simon, R. T ¨olle, and P. Zeyen, Phys. Lett. B
коллективной модели [19]. Полученный модель-
232, 447 (1989).
ный формализм обеспечивает приемлемое описа-
5.
S.
Aberg, H. Flocard, and W. Nazarewicz, Annu. Rev.
ние энергетического спектра переменной четности
Nucl. Part. Sci. 40, 439 (1990).
внутри высокой nonyrast-области коллективного
6.
G. A. Leander, W. Nazarewicz, G. F. Bertsch, and
возбуждения. На основе этой модели можно пред-
J. Dudek, Nucl. Phys. A 453, 58 (1986).
сказать возможные внутри/междуполосные при-
7.
P. A. Butler and W. Nazarewicz, Nucl. Phys. A 533,
249 (1991).
веденные вероятности E1- и E2-переходов меж-
8.
В. М. Струтинский, Ат. энергия 4, 150 (1956).
ду одинаковыми и противоположными четностями,
9.
В. Ю. Денисов, ЯФ 49, 399 (1989).
включая состояния с большими спинами. Показана
доминирующая роль вращательного движения в
10.
А. Я. Дзюблик, В. Ю. Денисов, Укр. физ. журн. 37,
рассматриваемых коллективных возбуждениях.
1770 (1992).
11.
А. Я. Дзюблик, В. Ю. Денисов, ЯФ 56(3), 30 (1993)
Отметим, что для описания приведенных ве-
[Phys. At. Nucl. 56, 303 (1993)]; Phys. At. Nucl. 57,
роятностей E1- и E2-переходов используются
1275 (Erratum) (1994).
подгоночные параметры, полученные при описании
12.
А. Я. Дзюблик, В. Ю. Денисов, ЯФ 56(3), 96 (1993)
энергетических уровней yrast-, первой nonyrast-
[Phys. At. Nucl. 56, 477 (1993)]; Phys. At. Nucl. 57,
и второй nonyrast-полос переменной четности
1275 (Erratum) (1994).
[17, 18].
13.
V. Yu. Denisov and A. Ya. Dzyublik, Nucl. Phys. A
Авторы выражают благодарность А.В. Хугаеву
589, 17 (1995).
за проявленный интерес к данной работе и крити-
14.
A. Arima and F. Iachello, Ann. Phys. 99, 253 (1976).
ческие замечания.
15.
T. Thomas, C. Bernadrs, J.-M. Regis, M. Albers,
Работа выполнена при поддержке гранта №
C. Fransen, J. Jolie, S. Heinze, D. Radeck, N. Warr,
OT-F2-14 Академии наук Республики Узбекистан.
and K.-O. Zell, Nucl. Phys. A 922, 200 (2014).
16.
Mushtaq A. Al-Jubbori, Huda H. Kassim, Fadhill
I. Sharrad, Amin Attarzadeh, and I. Hossain, Nucl.
СПИСОК ЛИТЕРАТУРЫ
Phys. A 970, 438 (2018).
1. A. Celler, Ch. Brian ¸con, J. S. Dionisio, A. Lefebvre,
17.
Ш. Шарипов, М. С. Надырбеков, Г. А. Юлдашева,
Ch. Vieu, J. Zylicz, R. Kulessa, C. Mittag,
Укр. физ. журн. 53, 11 (2008).
J. Fernandez-Niello, Ch. Lauterbach, H. Puchta, and
18.
М. С. Надырбеков, Г. А. Юлдашева, В. Ю. Денисов,
F. Riess, Nucl. Phys. A 432, 421 (1985).
ЯФ 78, 240 (2015) [Phys. At. Nucl. 78, 215 (2015)].
2. P. Sch ¨uler, Ch. Lauterbach, Y. K. Agarwal, J. De Boer,
19.
А. С. Давыдов, Возбужденные состояния атом-
K. P. Blume, P. A. Butler, K. Euler, Ch. Fleischmann,
ных ядер (Атомиздат, Москва, 1967).
C. G ¨uther, E. Hauber, H. J. Maier, M. Marten-Tolle,
20.
Л. Д. Ландау, Е. М. Лифщиц, Квантовая механи-
Ch. Schandera, R. S. Simon, R. T ¨olle, and P. Zeyen,
ка, нерелятивистская теория (Наука, Москва,
Phys. Lett. B 174, 241 (1986).
1974).
3. J. Fernandez-Niello, H. Puchta, F. Riess, and
21.
M. S. Nadirbekov and N. Minkov, Int. J. Mod. Phys.
W. Trautmann, Nucl. Phys. A 391, 221 (1982).
27, 1850069 (2018).
4. R. J. Poynter, Ch. Lauterbach, Y. K. Agarwal,
22.
N. Minkov, S. Drenska, M. Strecker, W. Scheid, and
J. De Boer, K. P. Blume, P. A. Butler, K. Euler,
H. Lenske, Phys. Rev. C 85, 034306 (2012).
Ch. Fleischmann, C. G ¨unther, E. Hauber,
H. J. Maier, M. Marten-T ¨olle, Ch. Schandera,
23.
REDUCED E1- AND E2-TRANSITION PROBABILITIES
IN THE ALTERNATING-PARITY SPECTRA
OF HEAVY EVEN-EVEN NUCLEI
M. S. Nadirbekov1), S. N. Kudiratov1), F. N. Temirov2)
1)Institute of Nuclear Physics, Uzbekistan Academy of Sciences, Tashkent
2)Samarkand State Medical Institute, Uzbekistan
Intra/interband reduced E1- and E2-transition probabilities in collective states of the yrast and first
nonyrast bands with the alternating parity of lanthanide150Nd,154Sm,154,160Gd,162,164Er and actinide
232Th,236,238U nuclei are studied. The B(E1), B(E2) values are calculated and compared with the available
experimental data. A variation surface deformations of nucleus at collective excitation were taken into
account.
ЯДЕРНАЯ ФИЗИКА том 82
№5
2019