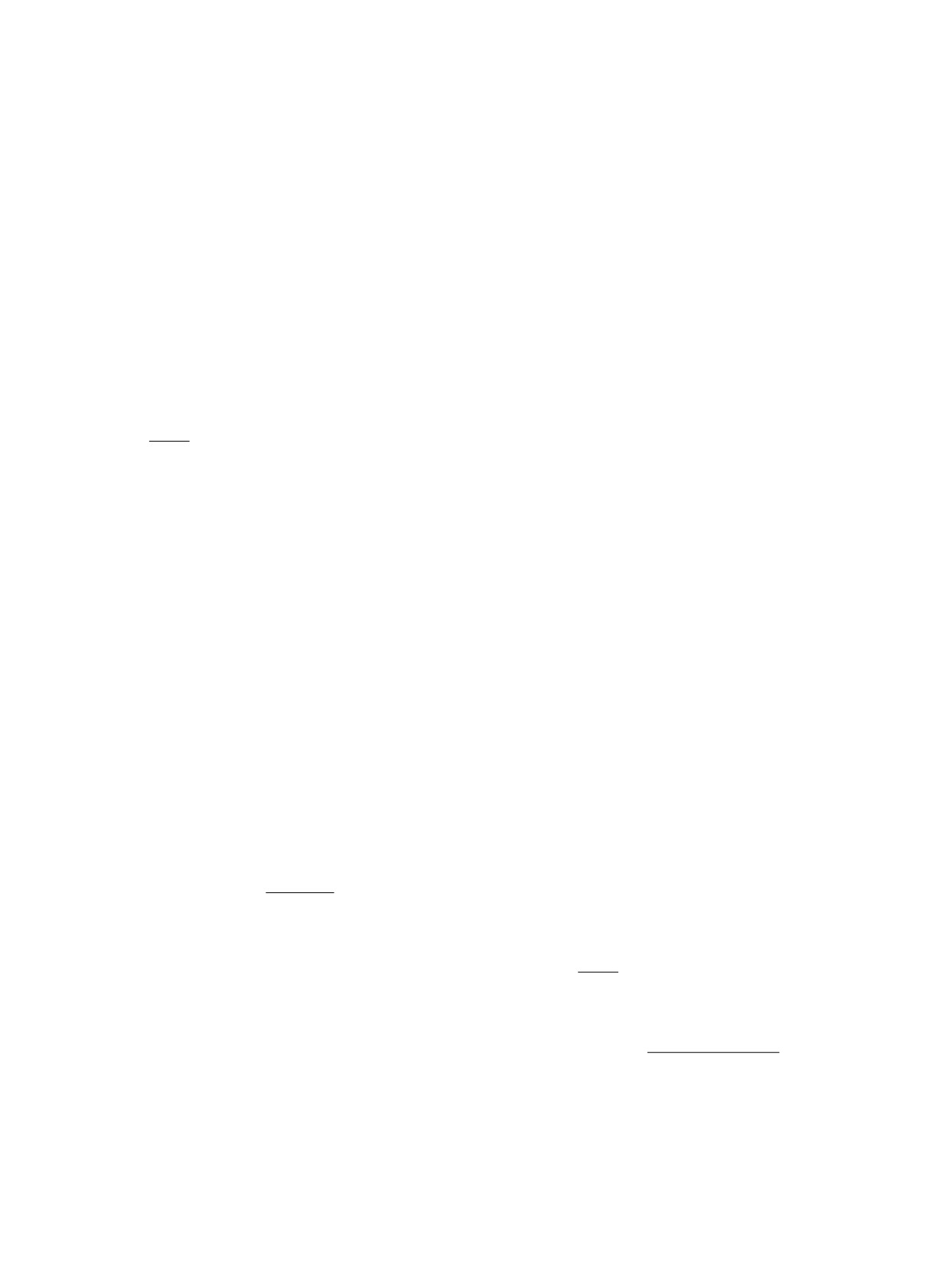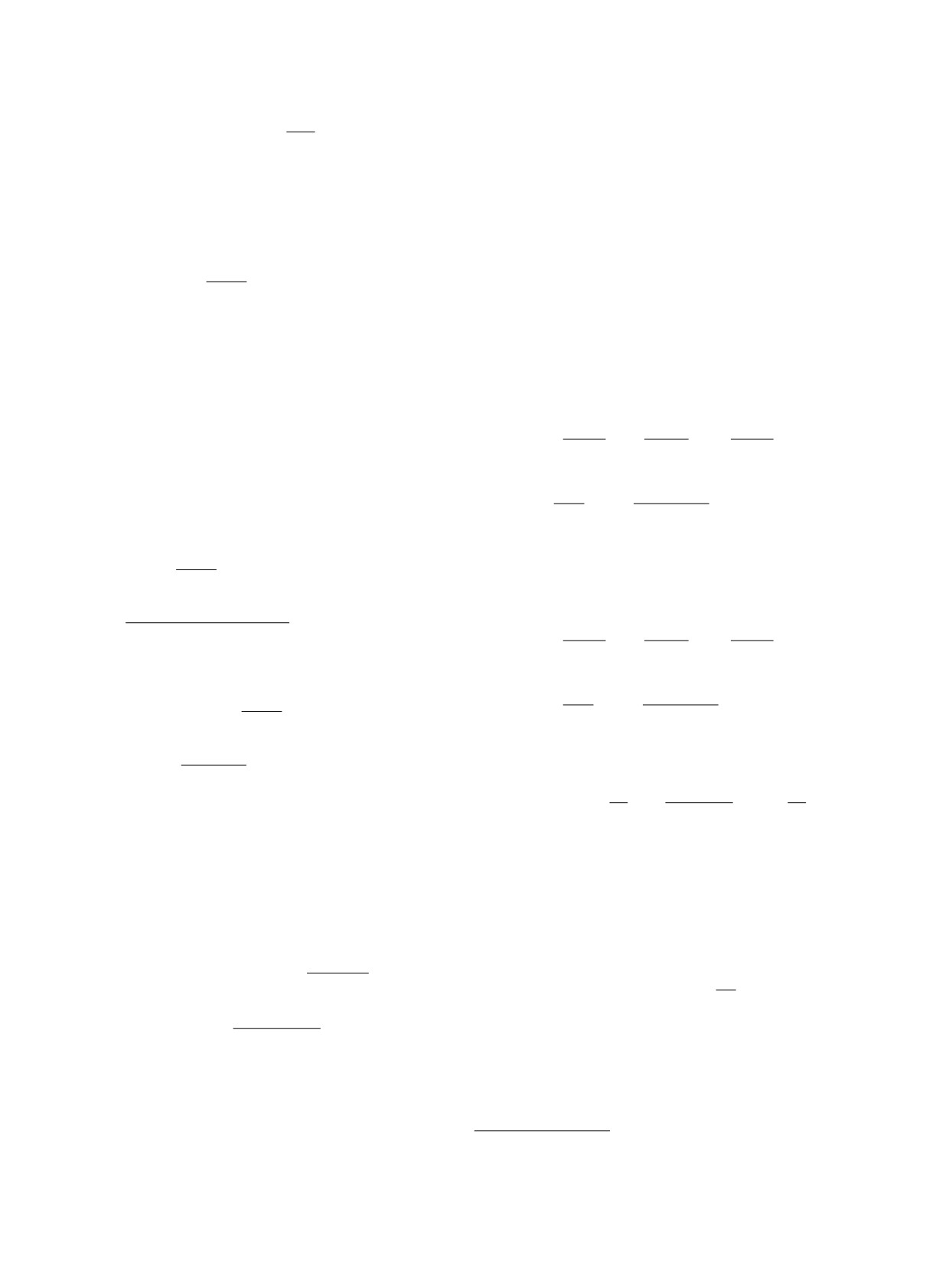ЯДЕРНАЯ ФИЗИКА, 2021, том 84, № 3, с. 262-276

ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ

ВОЛНОВЫЕ ФУНКЦИИ И S-ФАКТОР СОСТАВНОЙ СИСТЕМЫ ДВУХ

РЕЛЯТИВИСТСКИХ СПИНОВЫХ КВАРКОВ ПРОИЗВОЛЬНЫХ МАСС

Поступила в редакцию 9.06.2020 г.; после доработки 9.07.2020 г.; принята к публикации 9.07.2020 г.

Найдены точные решения релятивистских квазипотенциальных уравнений в конфигурационном

представлении для волновой функции s-состояния составной системы двух релятивистских спи-

новых кварков произвольных масс, взаимодействующих посредством кулоновоподобного хромоди-

намического потенциала. Рассмотрены составные системы, спиновая структура которых отвечает

случаю псевдоскаляра, псевдовектора и вектора. Определены условия квантования энергетических

уровней s-состояния мезонов в псевдоскалярном, псевдовекторном и векторном случаях. Для этих

спиновых структур мезонов получены выражения для релятивистского порогового ресуммирующего

S-фактора, отвечающего кулоновоподобному хромодинамическому потенциалу, и исследованы его

свойства. Установлены новые закономерности в поведении порогового S-фактора. Рассмотрение

проведено в рамках релятивистского квазипотенциального подхода, основанного на ковариантной

гамильтоновой формулировке квантовой теории поля, путем перехода от импульсной формулировки в

пространстве Лобачевского к трехмерному релятивистскому конфигурационному представлению для

случая составной системы двух релятивистских спиновых частиц произвольных масс.

DOI: 10.31857/S0044002721020057

1. ВВЕДЕНИЕ

системы двух релятивистских спиновых кварков

равных масс с хромодинамическим потенциалом

Релятивистский квазипотенциальный (РКП)

α_s

V (r) = -

α_s > 0,

(1)

подход Логунова-Тавхелидзе

[1], построенный

на основе ковариантной одновременной форму-

было получено в работе [11]²⁾. Найденное в [11]

лировки проблемы двух тел в квантовой теории

решение для радиальной волновой РКП-функции

поля, и ковариантный РКП-подход

[2,

3], не

составной системы в s-состоянии с хромодинами-

связанный с формализмом Бете-Солпитера и

ческим потенциалом (1) позволило получить вы-

ковариантным формализмом Фейнмана-Дайсона,

ражение релятивистского порогового ресуммирую-

а использующий гамильтонову формулировку

щого S-фактора составной системы двух спиновых

квантовой теории поля [4], являются одними из

кварков равных масс m [13]³⁾:

эффективных ковариантных методов описания

связанной системы двух релятивистских частиц

X_RQP,S(χ)

S_RQP,S(χ) =

[

] ×

(2)

и они нашли широкое применение для описания

1 - exp

-X_RQP,S(χ)

свойств атомов, адронов и ядер как связанных



состояний (см., например, работы [5-9]). При

×e^-πρΓ(2 + iρ)F (1 + iB, -iρ; 2; 1 - e-2χ)2 ,

этом РКП-подход, разработанный в [2, 3], поз-

где

воляет перейти от импульсной формулировки в

пространстве Лобачевского к трехмерному реля-

πα_s(ach2 χ + b)

X_RQP,S(χ) =

тивистскому конфигурационному представлению

2sh χ

(r-представление), введенному в [10] для случая

χ— быстрота, которая связана с полной энергией

взаимодействия двух релятивистских частиц рав-

частиц в с.ц.и.

√s соотношением

ных масс. В рамках РКП-подхода [2, 3] точное

решение РКП-уравнения в r-представлении [10]

√s = 2mch χ,

(3)

для радиальной волновой функции составной

²⁾Аналогичное решение для случая двух спиновых кварков

¹⁾Гомельский государственный технический университет

равных масс было получено в [12] при ином определении

имени П.О. Сухого; Международный центр перспектив-

волновой функции и квазипотенциала.

ных исследований, Гомель, Беларусь.

³⁾Здесь и всюду мы используем систему единиц, в которой

^*E-mail: chyud@mail.ru;chern@gstu.by

положено: ℏ = c = 1.

262

ВОЛНОВЫЕ ФУНКЦИИ И S-ФАКТОР

263

параметры ρ, B и α_s даются выражениями

Оно имеет такую же форму, как и в (6), и может

быть представлено в виде

α_sach χ

α_s(ach² χ + b)

ρ=

(4)

X_uneq(u)

4sh χ

S_uneq(u) =

[

(7)

1 - exp

-X_uneq(u)

α_s = α_sm,

√

πα_s

1-u

а значения спиновых параметров a,b зависят от

X_uneq(u) =

выбора матриц

Ô и определяются следующими

где скорость u определяется выражением

выражениями⁴⁾:

√

⎧

4m′2

⎪1

при

Ô₌ γ₅ (псевдоскаляр);

m^′ =

√m₁m₂.

(8)

⎨

s - (m₁ - m₂)²

при

Ô₌ γ_μ (вектор);

(5)

a=⎪2

⎪

Напомним о роли, которую играют релятивист-

⎩-1

при

Ô₌ γ₅γ_μ (псевдовектор);

ские ресуммирующие пороговые факторы при опи-

⎧

сании квантовых систем в околопороговой области,

⎪

при

Ô₌ γ₅ (псевдоскаляр);

например, кварк-антикварковых систем. Это свя-

⎪

⎨1

зано с тем, что при описании кварк-антикварковых

при

Ô₌ γ_μ (вектор);

систем вблизи их порога рождения ограничить-

b=⎪⎪

⎪3

ся конечным порядком теории возмущений нельзя

⎩

при

Ô₌ γ₅γ_μ ( псевдовектор).

даже в том случае, когда КХД-константа связи

α_s мала [22, 23]. Причина состоит в том, что

Выражения релятивистских волновых функций в

реальным параметром пертурбативного ряда из

r-представлении для составной системы двух бес-

фейнмановских диаграмм в околопороговой обла-

спиновых частиц равных масс, взаимодействую-

сти является сингулярная величина α_s/v, где v =

√

щих также посредством потенциала (1), были най-

1 - 4m²/s —скорость, а полная энергия вза-

дены ранее в работах [14-18]. В частности, най-

имодействующих частиц в с.ц.и.

√s была опреде-

денное в [18] решение для радиальной волновой

лена через быстроту χ в (3). Эта проблема хорошо

РКП-функции составной системы в s-состоянии

известна из квантовой электродинамики [24]. Такие

с хромодинамическим потенциалом (1), позволи-

пороговые сингулярности вида (α_s/v)ⁿ должны

ло авторам этой работы получить выражение для

быть просуммированы. Это ресуммирование вы-

релятивистского порогового ресуммирующего S-

полняют пороговые факторы. Поэтому их приме-

фактора составной системы двух бесспиновых ча-

нение к суммированию пороговых сингулярностей

стиц равных масс:

позволит учесть эффекты, обусловленные спина-

X(χ)

πα_s

ми частиц, составляющих связанную систему. В

S(χ) =

X(χ) =

(6)

нерелятивистском случае для кулоновского вза-

1 - exp[-X(χ)]

shχ

имодействия (1) такое пересуммирование выпол-

Развитый в [18] метод основан на РКП-подходе [1]

няет известный S-фактор Гамова-Зоммерфельда-

в форме, предложенной в [2, 3], путем перехода

Сахарова [25-27]

от импульсной формулировки в пространстве Ло-

X_nr

πα_s

бачевского к трехмерному релятивистскому кон-

S_nr =

X_nr =

(9)

1 - exp(-X_nr)

v_nr

фигурационному представлению, введенному в [10]

для случая взаимодействия двух релятивистских

который связан с волновой функцией непрерывно-

частиц равных масс.

го спектра в нуле через |ψ(0)|². Здесь 2v_nr — отно-

сительная скорость двух нерелятивистских частиц.

Обобщение релятивистского S-фактора (6) на

случай двух бесспиновых частиц произвольных

Релятивистская модификация выражения (9) в

масс m₁, m₂ было выполнено в работах [19-21].

КХД для описания эффектов вблизи порога рожде-

ния пар в процессах e⁺e^- → tt и e⁺e^- → W⁺W^-

⁴⁾Напомним, что для простоты рассмотрения, как и в рабо-

была выполнена в работах [28, 29] и заключалась

тах [11, 12], полагалось, что квазипотенциал имеет биспи-

в замене v_nr → v. Точно такой же вид S-фактора,

норную структуру вида I ⊗ I, а вершинная функция также

как и в работах [28, 29], был позднее предложен

имеет заданную спинорную структуру, пропорциональную

в [30]. В РКП-подходе [2, 3] нерелятивистское

матрице

Ô, не зависящую от импульсных переменных,

выражение (9) для случая двух бесспиновых ча-

причем в качестве

Ô выбиралась одна из матриц Дирака

стиц равных масс впервые было модифицировано

γ5, γμ, γ5γμ (μ = 0, 1, 2, 3). Такой выбор матрицы

Ô поз-

волил авторам работ [11, 12] найти точные решения РКП-

в работе [18] и дается выражением (6). Еще одно

уравнений.

релятивистское обобщение S-фактора и также для

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

264

ЧЕРНИЧЕНКО

случая двух бесспиновых частиц равных масс было

ведет себя как [(Q/M)2 ln(Q/M)2]-1, что вос-

получено в [31]. Релятивистский S-фактор для слу-

производит главное поведение потенциала в КХД,

чая двух частиц произвольных масс m₁ = m₂ был

который в лидирующем порядке пропорционален

предложен в работе [32]. Этот фактор был получен

α_s(Q²)/Q², где α_s(Q²) — инвариантный заряд. Та-

в рамках релятивистской квантовой механики на

кое КХД-подобное поведение потенциала (1) в

основе уравнения Шредингера. Однако, как было

РКП-подходе, учитывающее существенную осо-

показано в работе [19], релятивистские пределы

бенность КХД — свойство асимптотической сво-

S-факторов в [30-32] существенно отличаются от

боды и закон эволюции инвариантного заряда,

релятивистского предела (v → 1) S-фактора (6),

впервые было отмечено в работе [35]. Применение

равного единице.

релятивистского S-фактора (6) для описания ряда

Также напомним, что в двухчастичном при-

характеристик адронных процессов можно найти

ближении амплитуда Бете-Солпитера χ_BS(x = 0)

в [36-39], причем при его применении к задачам

связана с волновыми РКП-функциями в простран-

КХД требуется замена: α_s → 4α_s/3.

стве импульсов и в конфигурационном представле-

Настоящая работа является продолжением

нии (см. [18-21, 33, 34]) соотношением

работ автора [11, 13] и посвящена нахождению

χ_BS(x = 0) =

(10)

точных выражений волновых РКП-функций в

∫



r-представлении для составной системы двух



dΩ_pΨ_q(p) = ψ_q(r)

спиновых кварков произвольных масс, взаимо-

(2π)³

r=iλ

действующих посредством кулоновоподобного

а S-фактор в РКП-подходе [2, 3] определяется че-

хромодинамического потенциала (1). Рассмотрены

составные системы, спиновая структура которых

рез волновую РКП-функцию непрерывного спек-

отвечает случаю псевдоскаляра, псевдовектора и

тра ψ_q(r) выражением (подробности см. в [18-21,

вектора. Также будут определены условия кванто-

33])

вания энергетических уровней для этих спиновых

S_RQP(χ) = lim

|ψ_q(r)|² .

(11)

структур. Для этих же спиновых структур будут

r→iλ

получены новые выражения для релятивистского

Здесь dΩ_p = mdp/E_p — релятивистский трехмер-

порогового ресуммирующего S-фактора, отвеча-

ный элемент объема в пространстве Лобачевского,

ющего кулоновоподобному хромодинамическому

которое реализуется на верхней пол ´е массового ги-

потенциалу, и исследованы его свойства. Рассмот-

перболоида E2p - p² = E2q - q² = m², λ = 1/m —

рение проводится в рамках РКП-подхода [2, 3]

комптоновская длина волны, а модуль радиуса-

путем перехода от импульсной формулировки в

вектора r (r = rn, |n| = 1) является релятивист-

пространстве Лобачевского к r-представлению,

ским инвариантом.

введенному в [10] для случая составной системы

Подчеркнем, что S-фактор (6) был получен для

двух релятивистских спиновых частиц произволь-

потенциала (1), зависящего в конфигурационном

ных масс m₁, m₂ [40, 41].

представлении от модуля инвариантной реляти-

вистской относительной координаты r = |r| и име-

2. УРАВНЕНИЕ ДЛЯ ВЕРШИННОЙ

ющий форму кулоновского потенциала. В импульс-

ФУНКЦИИ

ном пространстве потенциал (1) воспроизводит по-

С помощью правил шпурионной диаграммной

тенциал взаимодействия между кварками, который

техники [2, 4, 41] уравнение для вершинной функ-

дается выражением

ции составной системы двух релятивистских спи-

α_s

V (χ_Δ) ∼ -

новых кварков произвольных масс m₁, m₂ запи-

χ_Δ sh χ_Δ

шется в виде

где относительная быстрота χ_Δ соответствует век-

Γ^αβQ (p₁,p₂;λ_Qτ_Q) =

(12)

тору передачи импульса в пространстве Лобачев-

∫

ского Δ = p(-)k и связана с квадратом пере-

dτ_Kd⁽⁴⁾k₁d⁽⁴⁾k₂ ×

данного 4-импульса Q² = -(p - k)² соотношением

(2π)³

Q² = 2M²(ch χ_Δ - 1), M² = (p + k)². Таким об-

× V ^αγ,δβ (p₁,p₂;λ_Qτ_Q|k₁,k₂;λ_Qτ_K) ×

разом, мы считаем, что внутри адрона взаимо-

Γ^κθQ (k₁,k₂;λ_Qτ_K)

действие между кварками осуществляется путем

× S(+)γκ (k₁,m₁)

обмена безмассовым скалярным глюоном, пропа-

τ_K - iε

гатору которого в РКП-подходе в r-представлении

× S(+)θδ(k₂,-m₂)δ⁽⁴⁾(-Q + k₁ + k₂ - λ_Qτ_K),

отвечает потенциал (1). В импульсном простран-

стве при больших значениях квадрата переданно-

где

S⁽⁺⁾(k_i,m_i) = θ(ki0)(ki + m_i)δ(k2i - m2i) —

го 4-импульса Q² относительная быстрота χ_Δ ≈

положительно-частотные части спинорных функ-

≈ ln(Q²/M²) и, следовательно, потенциа

V (χ_Δ)

ций Грина, а α, β, ..., θ — спинорные индексы;

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

ВОЛНОВЫЕ ФУНКЦИИ И S-ФАКТОР

265

p₁, m₁

будем выбирать одну из матриц γ₅, γ_μ, γ₅γ_μ. Такой

выбор матрицы^Ô позволит найти точные решения

уравнения (12).

p₁, m₁

В данном подходе скалярная часть вершин-

k₁

ной функции Γ_Q (p₁, p₂; λ_Qτ_Q) представляет собой

λ τ

четырехвостку, у которой два внешних импульса

коллинеарны в силу выбора вектора 4-скорости

составной частицы λ_Q = Q/M_Q. Значит, как и в

бесспиновом случае, для составной системы двух

k₂

спиновых частиц, которые находятся в состоя-

p₂, m₂

нии движения с относительным орбитальным мо-

ментом J, скалярная часть вершинной функции

p₂, m₂

Γ_Q (p₁,p₂;λ_Qτ_Q) будет зависеть только от одно-

го скалярного лоренц-инвариантного параметра, в

качестве которого выберем Qp₂ и введем следую-

Рис. 1. Графическое уравнение для вершинной функ-

щие обозначения (подробности см. в работе [42]):

ции составной системы двух релятивистских спиновых

частиц произвольных масс, соответствующее прави-

Γ_Q(p₁,p₂;λ_Qτ_Q) = ΓMQ(Qp₂),

лам шпурионной диаграммной техники.

V (p₁, p₂; λ_Qτ_Q|k₁, k₂; λ_Qτ_K) = V (Qp₂, Qk₂; M_Q).

Тогда, выполнив в (12) интегрирования по ki0 (i =

ki = kⁱγμ, γμ — матрицы Дирака (μ = 0, 1, 2, 3),

= 1, 2) и учитывая выбор вектора 4-скорости λ_Q,

m_i — масса i-й составляющей, которая переносит

получим уравнение

4-импульс k_i, i = 1, 2 (или p_i, q_i), причем все 4-

импульсы принадлежат верхним пол ´ам массовых

[SpÔ+ Ô]-1

ΓMQ(Qp₂) =

(14)

гиперболоидов:

(2π)³

∫

k2i = k2i0 - k2i = m2i, i = 1,2.

(13)

dk₁

dk₂

× dτ_K

√

Уравнению (12) отвечает его графический аналог

m²¹ + k²

m²² + k²²

на рис. 1. Сплошные линии соответствуют ее

V (Qp₂, Qk₂; M_Q)

составляющим, которые переносят

4-импульсы

O⁺(k1 + m₁) ×

τ_K - iε

p_i,k_i,i = 1,2; штриховые линии — квазичастицам-

шпурионам, а блок диаграмм, обозначенный на

× Ô(k2 - m₂)]Γ_M

(Qk₂) ×

рис.

трапецией, а в уравнении

(12) через

× δ(4) (-Q + k₁ + k₂ - λ_Qτ_K).

V^αγ,δβ (p₁,p₂;λ_Qτ_Q|k₁,k₂;λ_Qτ_K), рассматривает-

ся как квазипотенциал, которому соответствует

Теперь в уравнении (14) выполним интегрирования

сумма неприводимых в смысле одношпурион-

по k₁, τ_K. Для этого в интегралах по k_i (i =

ных и двухчастичных рассечений диаграмм. В

= 1, 2), как и в бесспиновом случае (подробности

качестве вектора 4-скорости составной части-

см. в работе [42]), выполним чистое преобразо-

цы для удобства рассмотрения выбран вектор

√

вание Лоренца (“буст”) Λ-1 , соответствующее 4-_λ

λ_Q = (λ0Q;λ_Q) = Q/

Q²,Q² = (q₁ + q₂)² = Q²⁰ -

скорости составной частицы λ_Q, и воспользуемся

−Q² =s_q =M2Q.

инвариантностью δ⁽⁴⁾-функции в (14) относитель-

Для простоты дальнейшего рассмотрения (как и

но чистого преобразования Лоренца. В результате

в работах [11, 12]) будем считать, что квазипотен-

уравнение (14) преобразуется к виду

циал в (12) имеет биспинорную структуру вида I ⊗

[SpÔ+ Ô]-1

⊗ I и решения этого уравнения также имеют опре-

ΓMQ(Δp2,m₂λ_Q) = -

(15)

деленную спинорную структуру, т.е. квазипотенци-

(2π)³

∫

ал V^αγ,δβ (p₁, p₂; λ_Qτ_Q|k₁, k₂; λ_Qτ_K) и вершинную

dΔk2,m₂λ

V (Δp2,m₂λ_Q , Δk₂,m₂λ_Q ; MQ) ×

функцию Γ^αβQ (p₁, p₂; λ_Qτ_Q) представим в виде

Δ⁰

k₂,m₂λ

V^αγ,δβ (p₁,p₂;λ_Qτ_Q|k₁,k₂;λ_Qτ_K) =

ΓMQ(Δk2,m₂λ_Q )

(

) ×

= Ô^αγ(Ô+)^δβV (p₁,p₂;λ_Qτ_Q|k₁,k₂;λ_Qτ_K),

M_Q -

^√s

+ iε

4Δ0k1,m₁λ_Q

^k2^,m2λQ

Γ^αβQ(p₁,p₂;λ_Qτ_Q) =ÔαβΓ_Q(p₁,p₂;λ_Qτ_Q),

× Sp[ Ô+(Δk1,m₁λ_Q + m1) ^Ô( Δk₂,m₂λ_Q - m2)],

где матрица^Ô не зависит от импульсных перемен-

где были введены обозначения

ных, причем шпур Sp[Ô+ Ô] = 0, а в качестве

ΓMQ(Qp₂) = ΓMQ(Δp2,m₂λ_Q ),

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

266

ЧЕРНИЧЕНКО

V (Qp₂, Qk₂; M_Q) =

(Λ-1λki)0 = Δ0k

=ki0λ0Q - k_i · λ_Q =

i,miλQ

√

= V (Δp2,m₂λ_Q, Δk₂,m₂λ_Q; MQ),

= m2i +Δ²

i = 1,2,

k_i,m_iλ_Q

Δk1,m₁λ_Q = -Δk₂,m₂λ_Q,

√

Δ0k

= m²¹ +Δ²

и было учтено, что Qp₂ — лоренцевый скаляр

1,m1λQ

k₂,m₂λ_Q

√

(Qp₂ = Λ-1λ(Qp2) = MQΔ0

), а полная энер-

p₂,m₂λ_Q

Δ0k

= m²² +Δ²

2,m2λQ

k₂,m₂λ_Q

гия двух свободных релятивистских частиц

√s_k =

√

(k₁ + k₂)² является инвариантом при преоб-

причем Δki,m_iλ_Q и Δ^k

(i = 1, 2) — про-

i,miλQ

разованиях Лоренца (16):

странственная и временная компоненты 4-вектора

Λ-1λki = Δki,miλQ из пространства Лобачевского,

√s_k = Λ-1λ√sk =√s

(17)

Δk2,m2λQ

моделями которого служат поверхности массовых

√

гиперболоидов (13), а группа Лоренца является его

+ m²² +Δ²

группой движения на гиперболоидах, т.е.

= m²¹ + Δ2k2,m₂λ_Q

k₂,m₂λ_Q

Λ-1λ

k_i = Δki,m_iλ_Q = ki(-)miλQ =

(16)

(

)

Вычисление шпуров для матриц

Ô₌ γ₅,γ_μ,γ₅γ_μ

k_i · λ_Q

дает

=k_i -λ_Q ki0 -

1+λ⁰

Sp[Ô+(Δk1,m₁λ_Q + m1)^Ô(Δk₂,m₂λ_Q - m2)] =

(18)

⎧

⎪-2[sΔk

- (m₁ - m₂)²]

при

Ô=γ5;

⎨

2^,m2λQ

при

Ô₌ γ₅;

−4[sΔk

- (m₁ - m₂)² + 2m₁m₂] при

Ô₌ γ_μ;

Sp[Ô+ Ô] =

при

Ô₌ γ_μ;

⁼⎪⎪

2^,m2λQ

⎩

4[sΔk

- (m₁ - m₂)² - 6m₁m₂] при

Ô₌ γ₅γ_μ;

при

Ô₌ γ₅γ_μ,

2^,m2λQ

пропорциональную энергии Δ0k′,m′λ_Q однойэффек-

которые при m₁ = m₂ = m совпадают с аналогич-

тивной релятивистской частицы массы m^′:

ными выражениями для шпуров в работе [11].

√s_k =^√(k₁ + k₂)2 =m′

Δ0k′,m′λ_Q ,

(19)

√

3. УРАВНЕНИЕ ДЛЯ ВОЛНОВОЙ

= m′2 +Δ²

ФУНКЦИИ

Δ0k′,m′λ_Q

k^′,m^′λ_Q

Напомним, что рассматриваемый здесь РКП-

где μ = m₁m₂/(m₁ + m₂) — обычная приведенная

подход для случая взаимодействия двух реляти-

масса двух частиц произвольных масс.

вистских спиновых частиц произвольных масс m₁ и

m₂ позволяет ввести концепцию эффективной ре-

Таким образом, двухчастичная задача сводит-

лятивистской частицы [40, 41], которая выступает

ся к одночастичной, описание которой ведется на

в качестве двухчастичной связанной системы, име-

языке эффективной релятивистской частицы. Для

ет массу m^′ =

√m₁m₂, относительный 3-импульс

перехода от двухчастичной задачи к одночастичной

Δ_k′,m′λ_Q и несет полную энергию двух свободных

в уравнении (15) выполним замену переменных

релятивистских частиц произвольных масс

√s_k, вида (подробности см. в работах [42, 43])

⎡

√

⎛

⎞2^⎤1/2

m₁

m²² + Δ2k2,m₂λ_Q -m2m1 +Δk2,m₂λ_Q

Δk2,m₂λ_Q

⎢

⎝

⎠ ⎦

(20)

Δ_k′,m′λ_Q =

⎣Δk2,m₂λ_Q

|Δk2,m₂λ_Q |

m₁ + m₂

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

ВОЛНОВЫЕ ФУНКЦИИ И S-ФАКТОР

267

а преобразование, обратное (20), дается выраже-

РКП-функции ΨMQ(Δ_p′_,m′λQ ):

нием

(Δ0q′_,m′_λ

- Δ0p′_,m′_λ

)ΨMQ(Δ_p′_,m′λQ ) =

(26)

m^′

m^′ √4μ2 +Δk′,m^′λQ

∫

Δk2,m₂λ_Q = Δk′,m′λ_Q

(21)

2μ m′2 + Δ²

k^′,m^′λ_Q

dΩ_Δ

(2π)³

k′,m′λQ

(

)

Тогда для квадрата трехмерного относительного

V Δ_p′_,m′λQ, Δ_k′_,m′λQ ; Δ⁰

импульса Δ_k′_,m′λQ эффективной релятивистской

q^′,m^′λ_Q

(

)

частицы, имеющей массу m^′, получаем выражение

k^′,m^′λ_Q

m₁m₂

[

]

×Aˆ

ΨMQ(Δ_k′_,m′λQ ).

s_k - (m₁ + m₂)²

m^′

Δ2k′,m′λ_Q =

(m₁ + m₂)²

Здесь введены следующие обозначения:

откуда и следует формула (19), а из выражений (17)

(

)

и (19) следуют соотношения

V Δ_p′_,m′λQ , Δ_k′_,m′λQ; Δ⁰

q^′,m^′λ_Q

√

m^′

(

)

f-1+(Δ_k′_,m′_λ

(22)

m²¹ + Δ2k2,m₂λ_Q =

2μ

= f(Δ_p′_,m′λQ)V Δ_p′_,m′λQ, Δ_k′_,m′λQ; Δ⁰

q^′,m^′λ_Q

√

m^′

f-1-(Δ_k′_,m′_λ

⎡

⎤

m²² + Δ2k2,m₂λ_Q =

(

)

(

)

2μ

Δ0k′,m′λ_Q

при m₁ > m₂;

⎣a′

+ b^′⎦ , (27)

m^′

√

m^′

f-1-(Δ_k′_,m′_λ

m²¹ + Δ2k2,m₂λ_Q =

2μ

где

√

⎧

m^′

f-1+(Δ_k′_,m′_λ

⎪g′2

при

Ô₌ γ₅ (псевдоскаляр);

m²² + Δ2k2,m₂λ_Q =

2μ

⎪

g′2

при

Ô=γμ (вектор);

при m₁ < m₂,

a^′ =

⎪2

где

^⎩-¹g′2

при

Ô₌ γ₅γ_μ (псевдовектор);

f_±(Δ_k′_,m′λQ) =

(23)

(28)

√

⎧

⎪1-g′2

при

Ô₌ γ₅ (псевдоскаляр);

m′2 + Δ2k′,m′λ_Q

⎪

√

⎨3

m′2 + Δ²

±m^′

m′2 - 4μ²

g′2

при

Ô₌ γ_μ (вектор);

k^′,m^′λ_Q

b^′ =

⎪

⎪1

При этом релятивистский трехмерный элемент

⎩

g′2

при

Ô₌ γ₅γ_μ (псевдовектор),

объема в пространстве Лобачевского в соот-

ветствии с (20)-(23) будет преобразовываться

а фактор g^′ определяется выражением

следующим образом:

m^′

m₁ + m₂

dΔk2,m₂λ_Q

g^′ =

√

(29)

√

(24)

2μ

m₁m₂

m²¹ + Δ²

m²² + Δ2k2,m₂λ_Q

k₂,m₂λ_Q

и его смысл будет раскрыт позже, причем значения

′

dΔ_k′,m′λ_Q

√

f (Δ_k′_,m′λQ ),

параметров a^′, b^′ в (28) при m₁ = m₂ = m совпада-

2μ

m′2 + Δ²

ют с соответствующими выражениями для a, b в (5),

k^′,m^′λ_Q

которые были получены в [11].

где

√

Волновая РКП-функция в пространстве им-

4μ² + Δ2k′,m′λ_Q

пульсов для случая взаимодействия двух реляти-

f (Δ_k′_,m′λQ ) =

(25)

вистских спиновых частиц произвольных масс m₁,

m′2 + Δ²

k^′,m^′λ_Q

m₂ в уравнении (26) определена, как и в бесспино-

вом случае [42, 43], выражением

Итак, выполнив в уравнении (15), как и в

ΨMQ(Δ_p′_,m′λQ ) =

работах [42, 43], замену переменных вида (20),

(21) и учитывая соотношения (18), (19), (24) и

f (Δ_p′_,m′λQ )ΓMQ (Δ_p′_,m′λQ )

√

(

(25), приходим к полностью ковариантному РКП-

23/2

m^′

уравнению в пространстве импульсов для волновой

2Δ0q′,m′λ_Q -2Δp

^′,m^′λ_Q

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

268

ЧЕРНИЧЕНКО

а dΩΔk′,m′λ

= m^′dΔ_k′_,m′λQ/Δ⁰

— реляти-

Переход в релятивистское конфигурационное

k^′,m^′λ_Q

представление осуществляется с помощью преоб-

вистский трехмерный элемент объема в про-

разований Шапиро

странстве Лобачевского, причем теперь все 4-

∫

импульсы принадлежат верхней пол ´е массового

ψMQ(r) =

dΩ_Δ

(34)

гиперболоида

p′,m′λQ

(2π)³

=m′2,

× ξ(Δ_p′_,m′λQ, r)ΨMQ(Δ_p′_,m′λQ),

^′,m^′λ_Q -Δk

^′,m^′λ_Q

∫

которая погружена в 4-мерное импульсное про-

ΨMQ(Δ_p′_,m′λQ ) = drξ^∗(Δ_p′_,m′_λ

, r)ψMQ (r).

странство и служит моделью этого релятивистско-

го неевклидова пространства импульсов, а группа

Для случая локального квазипотенциала

Лоренца на этой поверхности является его группой

движений, осуществляющей трансляцию в этом

V (Δ_p′_,m′λQ , Δ_k′_,m′λQ ; Δ⁰

)≡

(35)

q^′,m^′λ_Q

(

)

пространстве импульсов. Роль плоских волн, со-

ответствующих этим трансляциям в пространстве

≡

V (Δ_p′_,m′λQ (-)Δ_k′_,m′λQ )²; Δ⁰

q^′,m^′λ_Q

Лобачевского, выполняют функции Шапиро [44]

квадрат вектора передачи импульса в пространстве

ξ(Δ_p′_,m′λQ , r) =

(30)

Лобачевского Δ_p′_,k′ = p^′(-)k^′ является лоренце-

(

)-1-ir/λ′

вым инвариантом, что согласно (16) позволяет

Δ⁰

- Δ_p′,m′λ_Q · n

представить его в виде

= p^′,m′λ^Q

(

)

m^′

² -m′2 =

Δ2p′,k′ = (p^′(-)k^′)² =

Δ0p′,k′

(

)₂

где λ^′ = 1/m^′ — комптоновская длина волны эф-

⁽p^′k^′ )²

Λ-1λ

p^′Λ-1k^′λ

фективной релятивистской частицы массы m^′, а

-m′2 =

m^′

модуль радиуса-вектора r (r = rn, |n| = 1) явля-

ется релятивистским инвариантом. Эти функции

⁽Δ_p′,m′λ_Q Δk′,m′λ_Q )²

соответствуют главной серии унитарных неприво-

-m′2 =

m^′

димых представлений группы Лоренца и в нере-

лятивистском пределе (|Δ_p′_,m′λQ | ≪ 1/λ^′, r ≫ λ^′)

((

Δ_p′,m′λ_Q (-)Δk′,m′λ_Q

)₀)2 - m′2 =

ξ(Δ_p′_,m′λQ , r) → exp(iΔ_p′_,m′λQ · r). Кроме того,

(

)₂

функции (30) удовлетворяют условиям полноты и

Δ_p′,m′λ_Q (-)Δk′,m′λ_Q

=Δ^2Δ

p′,m′λQ,^Δk′,m′λQ

ортогональности

∫

Следовательно, квазипотенциал (35) в простран-

dΩ_Δ

(31)

стве Лобачевского зависит от квадрата разности

p′,m′λQ

(2π)³

двух ковариантно определенных векторов импуль-

× ξ(Δ_p′_,m′λQ,r)ξ^∗(Δ_p′_,m′_λ

,r^′) = δ(r^′ - r),

са частиц. С таким квазипотенциалом правая часть

∫

уравнения (26) представляет собой свертку в про-

drξ(Δ_q′_,m′λQ , r)ξ^∗(Δ_p′_,m′_λ

, r) =

странстве Лобачевского, что позволяет применить

(2π)³

преобразования (34). Тогда применение преобра-

Δ0q′,m′λ_Q

зований (34) к уравнению (26) и использование

δ(Δ_p′_,m′λQ - Δ_q′_,m′λQ ),

уравнения (32), условия полноты в (31), а также

m^′

теоремы сложения для релятивистских плоских

и уравнению в терминах конечных разностей

волн (30),

(

)

∫

(

)

Ĥ₀ - 2Δ0p′_,m′_λ

ξ(Δ_p′_,m′λQ , r) = 0.

(32)

dω_nξ

(36)

Δ_p′,m′λ_Q(-)Δk′,m′λ_Q , r

∫

Здесь

(

)

[

(

)

= dω_nξ(Δ_p′_,m′λQ , r)ξ^∗

Δ_k′,m′λ_Q , r

∂

Ĥ₀

= 2m^′ ch iλ^′

(33)

∂r

и эрмитовости оператора свободного гамильто-

]

ниана

(33), позволяет нам получить конечно-

(

)

(

)

′

iλ

∂

λ′2

∂

разностную форму релятивистского уравнения

sh iλ^′

Δ_θ,ϕ exp iλ^′

∂r

2r²

∂r

Шредингера в конфигурационном представлении

для волновой РКП-функции составной системы

- оператор свободного гамильтониана, являющий-

двух релятивистских спиновых кварков произволь-

ся конечно-разностным оператором, построенным

ных масс:

из операторов сдвига exp (±iλ^′∂/∂r), в то время

(2Δ0q′_,m′_λ

- H₀)ψ_M

(r) =

(37)

как Δ_θ,ϕ — его угловая часть.

2m^′

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

ВОЛНОВЫЕ ФУНКЦИИ И S-ФАКТОР

269

(

)

и интегральную формы релятивистского уравнения

= V (r;Δ0q′_,m′_λ

ψMQ(r).

Шредингера в конфигурационном представлении

2m^′

для радиальной волновой РКП-функции составной

системы двух релятивистских спиновых кварков

Здесь оператор

A иH0 определены в (27) и (33),

произвольных масс с относительным орбитальным

а потенциал V (r; Δ⁰

), являясь локальным в

q^′,m^′λ_Q

моментом ℓ в виде⁵⁾

смысле геометрии Лобачевского, дается в терми-

(

)

нах тех же релятивистских плоских волн:

Hrad

∫

- ch χ^′ ϕ_ℓ(ρ, χ^′) =

(39)

0,ℓ

(

)

V (r; Δ0q′_,m′_λ

dΩΔΔ

(2π)³

p′,m′λQ,Δk′,m′λQ

Hrad

= -V (ρ,χ^′

0,ℓ

ϕℓ(ρ, χ^′),

× ξ(ΔΔp′,m′λ

,Δ

, r) ×

k′,m′λQ

(

)

∫

∞

(ΔΔp′,m′λ

,Δk′,m′λQ )²; Δ^q

^′,m^′λ_Q

(

)

dχ(sh χ)2ℓ+2

ch χ^′ - ch χ

(40)

При том же условии локальности квазипотенциала

применение преобразований (34) к уравнению (26)

[(

)_ℓ (

)] (

)_ℓ

и использование теоремы сложения (36) для ре-

sin ρχ

лятивистских плоских волн (30) приводит к инте-

d ch χ

shχ

d ch χ

гральной форме релятивистского уравнения Шре-

дингера в конфигурационном представлении для

∫

∞

ρ^′ sin(ρ^′χ)

волновой РКП-функции составной системы двух

dρ^′

ϕℓ(ρ^′, χ^′) =

релятивистских спиновых кварков произвольных

sh χ

(-ρ^′)(ℓ+1)

масс:

∫

∞

∫

dΩ_Δ

(38)

= V (ρ;χ^′) dχ(shχ)2ℓ+2Aˆ(chχ) ×

p′,m′λQ

(2π)³

)

(Δ0q′,m′λ_Q -Δp

^′,m^′λ_Q

[(

)_ℓ (

)] (

)_ℓ

ξ(Δ_p′_,m′λQ , r) ×

sin ρχ

m^′

∫

d ch χ

shχ

d ch χ

× dr^′ξ^∗(Δ_p′_,m′_λ

,r^′)ψ_M

(r^′) =

∫

∞

∫

ρ^′ sin(ρ^′χ)

dρ^′

ϕℓ(ρ^′, χ^′),

= V (r;Δ0q′_,m′_λ

)

dΩ_Δ

k′,m′λQ

sh χ

(-ρ^′)(ℓ+1)

(2π)³

(

)

Δ⁰

где

×Aˆk′,m′λ^Q

ξ(Δ_k′_,m′λQ , r) ×

m^′

(

)

(

)

∫

ℓ(ℓ + 1)

Hrad

= ch i

exp i

0,ℓ

× dr^′ξ^∗(Δ_k′_,m′_λ

,r^′)ψ_M

(r^′).

dρ

2ρ(ρ + i)

dρ

– радиальная часть оператора свободного гамиль-

Считая потенциал сферически симметричным и

используя разложение волновой РКП-функции

тониана (33), а оператор

A по-прежнему опреде-

ψMQ(r) по функциям Лежандра первого рода

ляется выражением (27), ρ = r/λ^′, χ^′ — быстрота,

которая параметризирует импульс и энергию:

P^νμ(z),

Δ_q′,m′λ_Q = m^′ shχ^′nΔ

(41)

∑

q′,m′λQ

ϕℓ(r, χ^′)

ψMQ(r) =

(2ℓ + 1)i^ℓ

m^′

|nΔq′,m′λ

| = 1, M_Q =

Δ⁰

q^′,m^′λ_Q

ℓ=0(

)

Δ_q′,m′λ_Q · r

×P_ℓ

Δ⁰

= m′ chχ^′,

q^′,m^′λ_Q

|Δ_q′,m′λ_Q |r

выполняя в (37) и (38) выкладки в полной аналогии

а функция (-ρ)(ℓ) = i^ℓΓ(ℓ + iρ)/Γ(iρ) называет-

с выводом в [19-21, 33] конечно-разностной и ин-

ся обобщенной степенью [10], где Γ(z) — гамма-

тегральной форм уравнения для радиальной волно-

функция.

вой РКП-функции с относительным орбитальным

моментом ℓ для случая двух бесспиновых кварков

⁵⁾Аналогичные формы уравнения для случая двух спиновых

произвольных масс, получим конечно-разностную

кварков равных масс были получены в [11].

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

270

ЧЕРНИЧЕНКО

-χ + 4πi

χ + 4πi

шения

∫

∞

dρ^′ sin(ρ^′χ)eiρ′ζ =

Imζ > 0,

−χ + 2πi

χ + 2πi

iπ

iπ χ² - ζ²

α₊

приходим к уравнению

-χ

∫

α_-

(

)

dζe^iρζ

ch χ^′ - ch ζ

R₀(ζ,χ^′) =

-χ - 2πi

χ - 2πi

α_-

∫

α^′s

-χ - 4πi

χ - 4πi

dζe^iρζ Aˆ(ch ζ)R₀(ζ, χ^′),

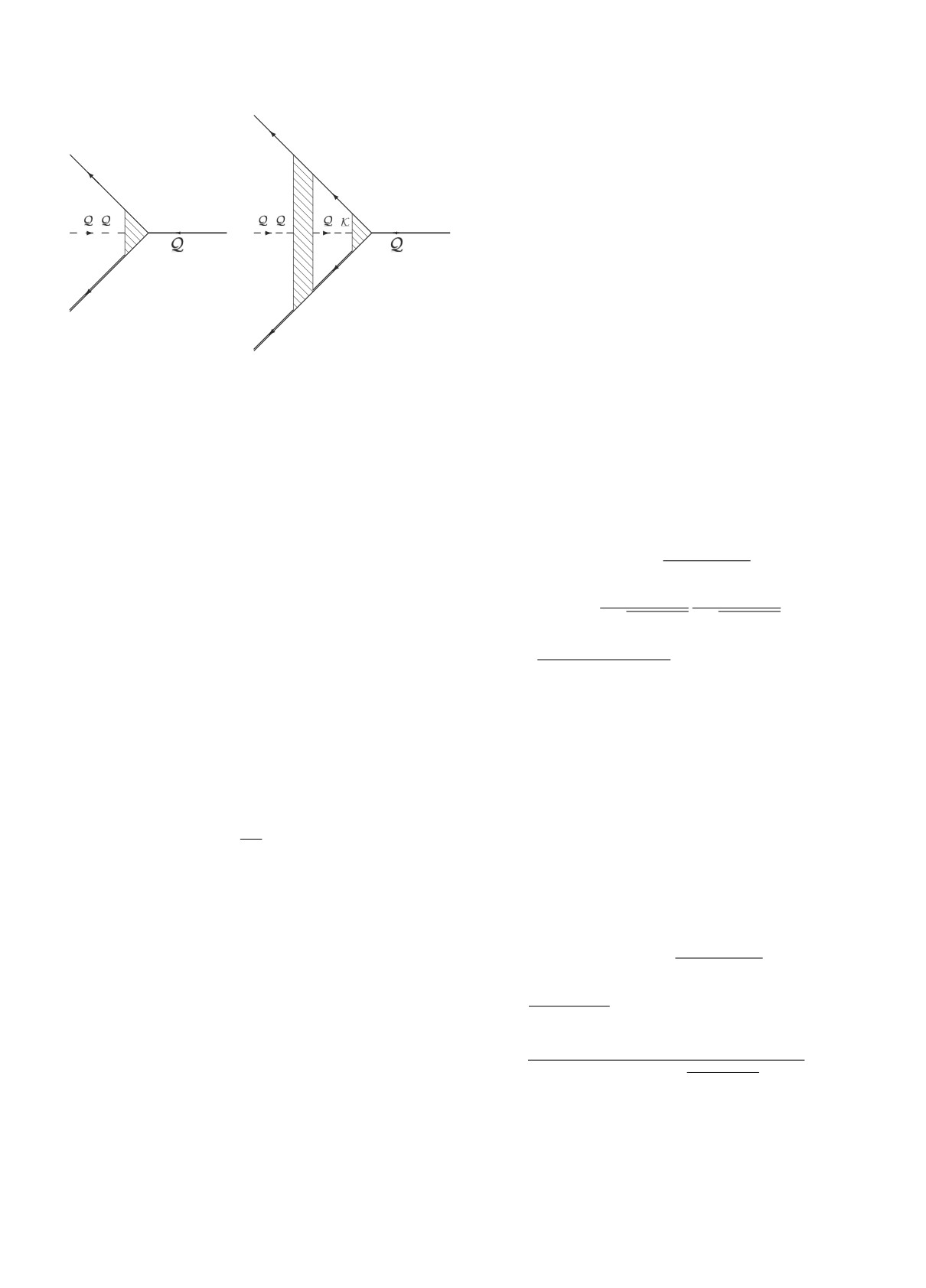
Рис. 2. Контур интегрирования в представлении (43)

α_-

и сингулярности решения (46) в комплексной ζ-

из которого после интегрирования по частям полу-

плоскости.

чаем для функции R₀(ζ, χ^′) уравнение

4. КУЛОНОВСКАЯ РАДИАЛЬНАЯ

[(ch ζ - ch χ^′)R₀(ζ, χ^′)] =

(44)

ВОЛНОВАЯ РКП-ФУНКЦИЯ

dζ

Радиальная волновая РКП-функция с отно-

= -iα^′sAˆ(ch ζ)R₀(ζ,χ^′)

сительным орбитальным моментом ℓ = 0 для со-

с граничным условием

ставной системы двух релятивистских спиновых

α+

кварков произвольных масс, взаимодействующих



e^iρζ(ch ζ - ch χ^′)R₀(ζ,χ^′)

= 0.

(45)

посредством кулоновоподобного хромодинамиче-

α_-

ского потенциала (1), которая не содержит i-

Решение уравнения (44) с граничным условием (45)

периодических констант, может быть найдена как

дается выражением

решение интегрального уравнения (40), которое

R₀(ζ,χ^′) = C₀(χ^′) ×

(46)

при относительном орбитальном моменте ℓ = 0 и с

[

]

потенциалом (1) принимает вид

iα^′sa^′

(

)

exp -

sh ζ +

1-iρ^′

ζ + iB^′χ^′

∞

∫

(

)

dχ

ch χ^′ - ch χ

sin ρχ ×

(42)

(e^ζ - eχ′ )²

[

]-1+iB′

e^ζ - e-χ′

∫∞

e^ζ - eχ′

× dρ^′ sin(ρ^′χ)ϕ₀(ρ^′, χ^′) =

где C₀(χ^′) — произвольная функция от быстроты

∞

∫

χ^′, которая параметризирует импульс и энергию

α^′s

A(ch χ) sin ρχ ×

в (41), значения параметров ρ^′ и B^′ определяются

выражениями

∫∞

α^′sa^′ ch χ^′

α^′s(a^′ ch² χ^′ + b^′)

ρ′ =

B^′ =

(47)

× dρ^′ sin(ρ^′χ)ϕ₀(ρ^′, χ^′),

α^′s = α_sm^′.

4sh χ^′

т.е. как и в (4), но в которых χ = χ^′, а входящие в

Решение уравнения (42) будем искать в виде кон-

них спиновые параметры a, b и параметр α_s теперь

турного интеграла

заменяются на их выражения в (28) и (42).

Напомним, что значения ζ = ±χ^′ + 2πni (n =

∫

= 0, ±1, ±2, ...) являются точками ветвления функ-

ϕ₀(ρ,χ^′) = dζe^iρζR₀(ζ,χ^′),

(43)

ции (46) (см. рис. 2). Контур интегрирования в

α_-

представлении (43) не должен пересекать разре-

зы, которые проводятся от -∞ + 2πni до ±χ^′ +

где интегрирование выполняется в комплексной

+ 2πni, n = 0, ±1, ±2,

В случае, когда взаи-

ζ-плоскости вдоль контура с концевыми точками

модействие выключено, α_s → 0, решение ϕ₀(ρ, χ^′)

α_± = -R ± iε, R → +∞, ε → +0 (см. рис. 2), т.е.

должно воспроизводить известную свободную вол-

подобно тому, как это делалось в работах [11, 18-

новую функцию

21, 33].

Подставляя представление (43) в уравнение (42)

sin(ρχ^′)

lim

ϕ₀(ρ,χ^′) ---→

(48)

и выполняя интегрирование с помощью соотно-

αs→0

ρ→∞ sh χ^′

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

ВОЛНОВЫЕ ФУНКЦИИ И S-ФАКТОР

271

поэтому выбираем α_± = -R ± iε при R → +∞,

× sin{(ρ - ρ^′)χ^′ + B^′ ln[2(ρ - ρ^′) sh χ^′] +

ε → +0. Вертикальную и горизонтальную части

+ arg Γ(1 - iB^′)},

контура интегрирования в правой его части нам

где Γ(z) — гамма-функция.

удобно выбрать в виде Reζ = +R и Imζ = ±π (см.

рис. 2), т.е. как и в работах [11, 18-21, 33].

Отметим, что при χ^′ = iκ (0 < κ < π/2) гипер-

Наконец, после подстановки решения (46) в

геометрическая функция в решении (50) становит-

представление (43) и последующего ζ-интегриро-

ся многочленом степени n, что приводит к точному

вания в комплексной плоскости вдоль контура с

условию квантования энергетических уровней для

концевыми точками α_±, т.е. также, как это дела-

s-состояния составной системы двух релятивист-

лось в работах [11, 18-21, 33], выражение для

ских спиновых кварков произвольных масс, вза-

имодействующих посредством кулоновоподобного

радиальной волновой РКП-функции ϕ₀(ρ, χ^′), не

содержащее i-периодических констант, принимает

хромодинамического потенциала (1),

вид

α^′s(a^′ cos² κ + b^′)

[

(

)]

= n, n = 1,2,

(52)

ϕ₀(ρ,χ^′) = 2C₀(χ^′)eiB′χ^′ sh

ρ-ρ^′

(49)

4sin κ

]

′

(

)

^[iα^′sa

Условие квантования энергетических уровней (52)

∫∞

exp

sh x +

1 + i(ρ - ρ^′)

также может быть получено и при решении спек-

× dx

тральной задачи для РКП-уравнения (39) с ку-

(e^x + eχ′ )²

-∞

лоновским потенциалом (1) при ℓ = 0 (подобно

[

]-1+iB′

тому, как это делалось в работе [11]). Решение

-χ^′

e^x + e

спектральной задачи для парциальной волновой

e^x + eχ′

РКП-функции ϕ₀(ρ, κ) имеет вид

∫

Нормировочный множитель C₀(χ^′) является дей-

C₀(κ)

ствительным, а решение (49) отличается от ре-

ϕ₀(ρ,κ) = -

dt ×

(53)

шения в бесспиновом случае (см. работы [19-

21, 33]) только наличием осциллирующего фактора

[

]

α^′sa^′

cos κ

exp[iα^′sa^′ sh(x)/4] и при a^′ = 0, b^′ = 2/g^′ — перехо-

× exp -ρt +

sin t +

дит в решение для бесспинового случая, где фак-

[

тор g^′ определяется выражением (29). Более того,

⁽t+κ)]iB′-¹[

⁽t-κ)]-iB′-¹

решение (49) по форме совпадает с решением для

× sin

sin

случая двух спиновых кварков равных масс [11].

Поэтому, как и в работе [11], вклад в интеграл от

где быстрота χ^′ = iκ параметризирует энергию

осциллирующего фактора exp[iα^′sa^′ sh(x)/4] мож-

M_Q = (m′2/μ)cos κ, 0 < κ < π/2, а интегрирова-

но положить равным единице. Очевидно, что такая

ние выполняется в комплексной плоскости пере-

аппроксимация не только не нарушает свойств

менной t вдоль контура Γ с концевыми точками

симметрии решения (49), но и позволяет пред-

a_± = +∞ ± iε, ε → +0, который лежит в полу-

ставить выражение радиальной волновой РКП-

плоскости Ret ≥ -π/2 и содержит внутри себя

функции для s-состояния через гипергеометриче-

особые точки t = κ + 2πk (k = 0, 1, ...) подынте-

скую функцию, т.е. подобно тому, как это делалось

гральной функции в решении (53).

в бесспиновом случае [19-21, 33],

Отметим, что решение спектральной задачи с

ϕ₀(ρ,χ^′) = C₀(χ^′)eiB′χ^′-χ′+i(ρ-ρ′)χ′ (ρ - ρ^′) ×

кулоновским потенциалом (1) на основе интеграль-

(50)

ного уравнения (40), взятого при относительном

(

)

орбитальном моменте ℓ = 0, также приводит к ре-

×F

1 - iB^′,1 - i(ρ - ρ^′);2;1 - e-2χ′ ,

шению (53).

где действительный нормировочный множитель

Поскольку в силу условия квантования энер-

2πC₀(χ^′) дается выражением

гетических уровней (52) точки t = κ + 2πk (k =

= 0, 1, ...) являются полюсами (n + 1)-го порядка

|2πC₀(χ^′)|² = eπB′ |Γ(1 - iB^′)|²

(51)

подынтегральной функции в решении (53), то кон-

и находится из граничного условия (48) и асимпто-

турный интеграл может быть легко вычислен с по-

тики

мощью теории вычетов. В частности, для основного

-πB^′/2

уровня (n = 1) волновая РКП-функция ϕ₀(ρ, κ)

2πC₀(χ^′)e

ϕ₀(ρ,χ^′)|ρ≫1 ≈

имеет вид

shχ^′|Γ(1 - iB^′)|

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

272

ЧЕРНИЧЕНКО

⎧

(

)

⎪

(ρ - ρ′κ1 )θ

ρ-ρ^′

κ₁

⎨C0(κ1)

exp[-(ρ - ρ^′κ

)κ₁];

1 - exp[-2π(ρ - ρ′κ1/2)]

ϕ₀(ρ,κ₁) =

(

)

(54)

⎪C0(κ1)(ρ - ρ′κ1)θ

-ρ + ρ′κ1 /2

exp[-(ρ - ρ′κ1 )κ₁],

⎩

ρ′κ1

= α^′sa′ cos(κ₁)/2,

причем ρ′κ1 > 0 для

Ô₌ γ₅ и γ_μ, но ρ^′

< 0 для

к бесспиновому случаю при a^′ = 0 и b^′ = 2/g^′. Та-

κ₁

ким образом, в рассматриваемом спиновом случае

Ô₌ γ₅γ_μ.

функция

Таким образом, волновая РКП-функция основ-

ного состояния имеет нуль на конечном расстоя-

ψ₀(ρ,χ^′) = e-πρ′/²Γ(1 + iρ^′)ϕ₀(ρ,χ^′)

нии при положительных значениях параметра a^′,

представляет собой физическую волновую функ-

когда^Ô = γ₅ или γ_μ, и не имеет нуля при отрица-

цию s-состояния составной системы двух реля-

тельном значении параметра a^′, когда^Ô = γ₅γμ6).

тивистских спиновых кварков произвольных масс,

взаимодействующих посредством кулоновоподоб-

Более того, из выражения (54) следует, что при

ного хромодинамического потенциала (1).

a^′ > 0 происходит фрагментация кварк-глюонной

материи основного состояния связанной системы

Тогда, используя соотношения (50), (51) и (55),

получаем следующее выражение для порогового

с энергией M_Q = (m′2/μ)cos κ₁ на две фракции:

ресуммирующего S-фактора составной системы

одна из фракций распределена внутри сферы (ядро)

двух релятивистских спиновых кварков произволь-

радиуса ρ = ρ′κ1 /2, а другая — в сферическом слое

ных масс:

(мантия) ρ′κ1 /2 < ρ < ρ′κ1 . При этом значение па-

X_uneq,s(χ^′)

раметра ρ′κ1 = α^′sa^′ cos(κ₁)/2 при a^′ > 0 определяет

S_uneq,s(χ^′) =

[

]×

(56)

1 - exp

-X_uneq,s(χ^′)

“размер” основного состояния связанной системы



с энергией M_Q = (m′2/μ)cos κ₁ и является точкой



×e-πρ′

Γ(2 + iρ^′)F (1 + iB^′, -iρ^′; 2; 1 - e-2χ′

)

²,

разрыва эффективного потенциала (рис. 3)

′

где

α^′sa

V_eff(ρ) = -

(

)

πα^′s(a′ ch2 χ^′ + b^′)

ρ-ρ^′

X_uneq,s(χ^′) = 2πB^′ =

(57)

κ₁

2sh χ^′

с предельной точкой ρ′0 = α^′sa^′/2 (κ₁ = 0), разде-

ляющей область конфаймента (область связанных

V_eff(ρ)

состояний) и область континуума (область рассея-

ния).

5. ПОРОГОВЫЙ РЕСУММИРУЮЩИЙ

S-ФАКТОР

Принимая во внимание соотношения (10) и (11),

пороговый ресуммирующий S-фактор составной

m'²

системы двух релятивистских спиновых кварков

2μM

произвольных масс, как и в случае спиновых квар-

ков равных масс [13], определим выражением

ρ_κ

S_uneq,s(χ^′) =

(55)



²



= lim

−πρ^′/2Γ(1 + iρ^′)ϕ0(ρ,χ′)

^e



ρ→i

где дополнительный фактор exp(-π ρ^′/2)Γ(1 + iρ^′)

обеспечивает не только правильный релятивист-

ский предел при χ^′ → +∞, равный 1, но и переход

Рис. 3. Поведение эффективного взаимодействия в

случае кулоновоподобного потенциала (1) при поло-

жительных значениях параметра a^′ с сингулярностью

⁶⁾Аналогичныйрезультат дляслучая двух спиновыхкварков

на конечном расстоянии.

равных масс был получен в [11, 12].

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

ВОЛНОВЫЕ ФУНКЦИИ И S-ФАКТОР

273

Пороговый S-фактор (56) может быть выражен в

Отметим, что пороговый S-фактор (56) имеет

терминах скорости u в (8) и относительной ско-

явно выраженный релятивистский характер, по-

рости u′rel эффективной релятивистской частицы

скольку как аргумент r (модуль радиуса-вектора r)

массы m^′, выступающей в качестве двухчастичной

в кулоновском потенциале (1), так и релятивист-

связанной системы, которая определяется выра-

ская относительная скорость v взаимодействую-

щих частиц являются релятивистскими инвариан-

жением [19-21]

тами [41], а, значит, в силу соотношения |v| =

u′rel =

√

(58)

= 2u/(1 + u²), скорость u в (8) и относительная

1-u²

скорость u′rel эффективной релятивистской части-

В частности, величина (57) в терминах скорости u

цы в (58) также обладают этим свойством [19-

и относительной скорости u′rel принимает вид

21]. При этом роль параметра скорости в S-

факторе (56) теперь играет не релятивистская от-

X_uneq,s(u) =

носительная скорость v взаимодействующих ча-

√

[

]

πα^′s

1-u

(

)

a^′u²

стиц, а скорость (58) эффективной релятивистской

g′2

a^′ + b^′

частицы, выступающей в качестве двухчастичной

2g^′u

1-u²

[

]

системы.

πα^′s

(

)

a^′

g′2

a^′ + b^′

u′2

rel

Новый релятивистский пороговый ресуммиру-

g^′u′rel

ющий S-фактор (56) для составной системы двух

Здесь кинематический фактор g^′ определяется вы-

релятивистских спиновых кварков произвольных

ражением (29) и устанавливает связь между пол-

масс имеет следующие важные свойства:

ной энергией

√s_k составной системы двух реля-

1) при m₁ = m₂ = m S-фактор (56) совпадает

тивистских спиновых кварков произвольных масс

со спиновым S-фактором (2), который при a = 0 и

и полной энергией 2Δ⁰

эффективной реляти-

k^′,m^′λ_Q

b = 2 переходит в бесспиновый S-фактор (6), вос-

вистской частицы массы m^′ с импульсом Δ_k′_,m′λQ

производящий в нерелятивистском пределе (v → 0)

(см. (19)), что отражает ассиметрию между этими

известный нерелятивистский результат [19-21];

двумя системами. Кроме того, фактор (29) пред-

ставляет собой отношение среднего арифметиче-

2) при m₁ = m₂ и a^′ = 0, b^′ = 2/g^′ S-фактор (56)

ского масс кварков к их среднему геометрическо-

совпадает с бесспиновым S-фактором (7);

му, а, значит, он описывает ассиметрию составной

системы двух релятивистских спиновых кварков

3) в нерелятивистском пределе χ^′ → +0 (u → 0)

его поведение дается выражением

произвольных масс, причем g^′ ≥ 1 ∀m₁, m₂, а ра-



венство имеет место (ассиметрии нет) только при



S_uneq,s(χ^′)

≈

m₁ = m₂ = m. С другой стороны, кинематический

χ^′→+0

фактор g^′ можно рассматривать и как отношение

πα^′s(a^′ + b^′)/2sh χ^′

≈

гиромагнитного отношения орбитального момента

1 - exp[-πα^′s(a^′ + b^′)/2shχ^′]

составной системы (мезона) с приведенной мас-

(

)

πα^′sa^′/2

(α^′sa^′)²

сой μ и зарядом e, равного g_L = e/2μc, где c —

скорость света, к гиромагнитному отношению для

exp(π α^′sa^′/2) - 1

спинового момента эффективной релятивистской

×|Φ(-iα^′sa^′/4; 2; iα^′s(a^′ + b^′)/2)|²,

частицы массы m^′ и с таким же зарядом e, равному

g_s = e/m^′c. Также фактор g^′, и это важно, устанав-

которое при m₁ = m₂ = m, a^′ = a = 0 и b^′ = b =

ливает явную зависимость спиновых параметров

= 2, как было отмечено выше, воспроизводит

a^′,b^′ в (28) от масс m₁, m₂ релятивистских спи-

известный нерелятивистский результат [19-21], где

новых кварков, образующих составную систему,

Φ(α; β; z)

- вырожденная гипергеометрическая

причем при m₁ = m₂ = m фактор g^′ = 1 и, следо-

функция;

вательно, в этом случае значения параметров a^′, b^′,

как это видно из (5) и (28), определяются только

4) в релятивистском пределе χ^′ → +∞ (u → 1)

собственными спинами кварков.

его поведение имеет асимптотику



2π(B^′ - ρ^′)



πα^′s



S_uneq,s(χ^′)

≈

≈1+

(a^′ + 2b^′)e-χ′ -----→

(59)

χ^′≫1

1 - exp[-2π(B^′ - ρ^′)]

χ^′→+∞

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

274

ЧЕРНИЧЕНКО

⎧

√

⎪1+0

при

Ô₌ γ₅ (псевдоскаляр) и 1 ≤ g^′ ≤

√

⎪

⎪1-0

при

Ô₌ γ₅ (псевдоскаляр) и g^′ >

⎨

√

1+0

при

Ô₌ γ_μ (вектор) и 1 ≤ g^′ ≤

-----→

√

χ^′→+∞ ⎪

1-0

при

Ô₌ γ_μ (вектор) и g^′ >

⎪

^⎩1 + 0 при

Ô₌ γ₅γ_μ (псевдовектор) и g^′ ≥ 1,

которая отвечает соответствующим значениям

при которых S-фактор (56), отвечающий случаю

спиновых параметров a^′ и b^′ в (28), являющихся

псевдоскаляра и вектора, будет обращаться в

функциями параметра g^′, а, значит, масс кварков;

единицу, приближаясь в пределе при χ^′ → +∞ к

единице снизу. Тем самым, для псевдоскалярного и

5) случай, когда одна из частиц покоится, озна-

векторного мезонов мы обнаружили новые законо-

чает, что m₁ → +∞, а другая частица имеет массу

m₂ и импульс k, что дает предельное значение для

мерности и эффекты, обусловленные их спиновыми

скорости u:

параметрами a^′, b^′, зависящими от фактора g^′.

|k|

u ------→

√

;

m₁→+∞

6. ЗАКЛЮЧЕНИЕ

m²² + k² + m₂

В настоящей работе найдены точные решения

6) в ультрарелятивистском пределе, как это бы-

задачи рассеяния и спектральной задачи для s-

ло доказано [45, 46], спектр связанных состояний

состояния составной системы двух релятивист-

исчезает, когда масса m^′ → 0, так как масса части-

ских спиновых кварков произвольных масс, вза-

цы является единственным размерным парамет-

имодействующих посредством кулоновоподобного

ром. Эта особенность отражает существенное раз-

хромодинамического потенциала (1). Рассмотре-

личие между потенциальными моделями и кванто-

ны случаи, когда квазипотенциал имеет биспинор-

вой теорией поля, где появляется дополнительный

ную структуру вида I ⊗ I, а спинорная структу-

размерный параметр. Кроме того, мы можем также

ра вершинной функции пропорциональна матри-

заключить, что S-фактор (56), который соответ-

це

^Ô, не зависящей от импульсных переменных,

ствует непрерывному спектру, будет стремиться к

1 при m^′ → 0.

где в качестве

Ô выбирались матрицы Дирака

γ₅,γ_μ и γ₅γ_μ (μ = 0,1,2,3). Такой выбор матри-

Таким образом, установлена зависимость ре-

лятивистского порогового ресуммирующего S-

цы

Ô для рассматриваемых спиновых структур

фактора (56) как от скорости u в (8) или относи-

мезонов позволил найти точные решения РКП-

тельной скорости u′rel эффективной релятивистской

уравнения в конфигурационном представлении для

частицы в (58), так и от спиновых параметров a^′ и

волновой функции s-состояния мезонов, как со-

ставной системы двух релятивистских спиновых

b^′, а, значит, и от различия масс кварков составной

кварков произвольных масс, взаимодействующих

системы (фактор g^′). Выполненный анализ поведе-

посредством кулоновоподобного хромодинамиче-

ния S-фактора (56) в нерелятивистском (u → 0),

ского потенциала (1), и определить для них усло-

релятивистском (u → 1) и в ультрарелятивистском

вия квантования энергетических уровней. Для этих

(m^′ → 0) пределах показал, что он воспроизводит

спиновых структур мезонов получены выражения

как известный нерелятивистский предел в бес-

для релятивистского порогового ресуммирующего

спиновом случае, когда m₁ = m₂ = m, a^′ = a = 0

S-фактора, отвечающего кулоновоподобному хро-

и b^′ = b = 2, так и ожидаемые релятивистский

модинамическому потенциалу, и исследованы его

и ультрарелятивистский пределы для всех трех

свойства. Рассмотрение было выполнено в рам-

случаев спиновых структур мезонов: псевдоска-

ках релятивистского квазипотенциального подхо-

ляра, вектора и псевдовектора. Более того, из

да, основанного на ковариантной гамильтоновой

асимптотики (59) следует, что новый пороговый

формулировке квантовой теории поля, путем пе-

S-фактор (56) в релятивистском пределе (u →

рехода к трехмерному релятивистскому конфигу-

→ 1) стремится к единице снизу для псевдоскаляра

√

рационному представлению [40, 41] для случая

(^Ô = γ₅) при g^′ >

2, а для вектора (^Ô = γ_μ) —

составной системы двух релятивистских спиновых

√

при g^′ >

3. Это означает, что для этих значений

частиц произвольных масс.

фактора g^′ (а, следовательно, масс кварков) суще-

Показано, что при положительных значениях

ствуют такие “критические” значения быстроты χ^′,

параметра a^′ волновая РКП-функция основного

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

ВОЛНОВЫЕ ФУНКЦИИ И S-ФАКТОР

275

состояния имеет нуль на конечном расстоянии ρ =

g^′, а, следовательно, масс кварков, существуют

= α^′sa′ cos(κ₁)/2, когда ^Ô = γ5 и γ_μ, и не имеет нуля

“критические” значения быстроты χ^′, при которых

S-фактор (56), отвечающий случаю псевдоскаляра

при отрицательном значении параметра a^′, когда

и вектора, обращается в единицу, приближаясь

Ô₌ γ₅γ_μ. Установлено, что при a^′ > 0 происходит

в пределе при χ^′ → +∞ к единице снизу. Такая

фрагментация кварк-глюонной материи основного

особенность поведения S-фактора (56) для псев-

состояния связанной системы с энергией M_Q =

доскалярного и векторного мезонов указывает на

= (m′2/μ) cos κ₁ на две фракции: одна из фракций

новые закономерности и эффекты, обусловленные

распределена внутри сферы (ядро) радиуса ρ =

различием масс кварков (фактор g^′).

= ρ′κ1/2, а другая —в сферическом слое (мантия)

Поскольку новый S-фактор (56) получен нами в

ρ′κ1 /2 < ρ < ρ^′

. При этом значение параметра

κ₁

рамках полностью ковариантного метода, то можно

ρ′κ1 = α^′sa^′ cos(κ₁)/2 при a^′ > 0 определяет “раз-

ожидать, что он более полно учитывает как реляти-

мер” основного состояния связанной системы с

вистский характер кварков составной системы, так

и эффекты, обусловленные их спинами и различием

энергией M_Q = (m′2/μ) cos κ₁ и является точкой

их масс.

разрыва эффективного потенциала с предельной

Автору приятно выразить искреннюю благодар-

точкой ρ′0 = α^′sa^′/2, разделяющей область конфай-

ность О.П. Соловцовой за поддержку и интерес к

мента (область связанных состояний) и область

этой работе, полезные обсуждения, стимулирую-

континуума (область рассеяния).

щие дискуссии и ценные замечания.

Установлена зависимость нового релятивист-

ского порогового ресуммирующего S-фактора (56)

СПИСОК ЛИТЕРАТУРЫ

от спиновых параметров a^′ и b^′, содержащих кине-

A. A. Logunov and A. N. Tavkhelidze, Nuovo Cimento

матический фактор g^′, который указывает на связь

29, 380 (1963).

между спинами и массами кварков, образующих

V. G. Kadyshevsky, Nucl. Phys. B 6, 125 (1968).

составную систему. Показано, что фактор g^′ уста-

V. G. Kadyshevsky and M. D. Mateev, Nuovo

навливает связь между полной энергией эффектив-

Cimento A 55, 275 (1967).

ной релятивистской частицы массы m^′ и полной

В. Г. Кадышевский, ЖЭТФ 46, 654, 872 (1964)

энергией составной системы двух релятивистских

[Sov. Phys. JETP 19, 443, 597 (1964)]; Докл. АН

спиновых кварков произвольных масс, и он отра-

СССР 160, 573 (1965)

[Sov. Phys. Dokl. 10, 46

жает как ассиметрию их масс, так и ассиметрию их

(1965)].

гиромагнитных отношений.

Н. Б. Скачков, И. Л. Соловцов, ЯФ 31, 1332 (1980)

[Sov. J. Nucl. Phys. 31, 686 (1980)].

Показано, что новый пороговый S-фактор (56)

Н. Б. Скачков, И. Л. Соловцов, ТМФ43, 330 (1980)

имеет явно выраженный релятивистский характер,

[Theor. Math. Phys. 43, 494 (1980)].

причем роль параметра скорости в нем теперь

А. Д. Линкевич, В. И. Саврин, Н. Б. Скачков, ТМФ

играет не релятивистская относительная скорость

53, 20 (1982) [Theor. Math. Phys. 53, 955 (1982)].

v взаимодействующих частиц, а скорость (58) эф-

В. А. Матвеев, В. И. Саврин, А. Н. Сисакян,

фективной релятивистской частицы, выступающей

А. Н. Тавхелидзе, ТМФ 132, 267 (2002)

[Theor.

в качестве двухчастичной системы.

Math. Phys. 132, 1119 (2002)].

Установлена связь нового S-фактора (56) с

D. Ebert, R. N. Faustov, and V. O. Galkin, Phys. Lett.

ранее найденными S-факторами как для случая

B 635, 93 (2006); ЭЧАЯ 41, 1579 (2010).

10.

V. G. Kadyshevsky, R. M. Mir-Kasimov, and

спиновых кварков равных масс, так и для бес-

N. B. Skachkov, Nuovo Cimento A 55, 233 (1968).

спиновых кварков произвольных и равных масс.

11.

Ю. Д. Черниченко, ЯФ 80, 396 (2017)

[Phys. At.

Выполнен анализ его поведения в нерелятивист-

Nucl. 80, 707 (2017)].

ском (u → 0), релятивистском (u → 1) и в ультра-

12.

N. B. Skachkov and I. L. Solovtsov, Preprint No.

релятивистском (m^′ → 0) пределах. Показано, что

E2-81-760, JINR (Dubna, 1981); Н. Б. Скачков,

он воспроизводит не только известный нереляти-

И. Л. Соловцов, ТМФ 54, 183 (1983) [Theor. Math.

вистский предел в бесспиновом случае, когда m₁ =

Phys. 54, 116 (1983)].

= m₂ = m,a^′ = a = 0 и b^′ = b = 2, но и ожидаемые

13.

Ю. Д. Черниченко, ЯФ 82, 172 (2019)

[Phys. At.

релятивистский и ультрарелятивистский пределы

Nucl. 82, 158 (2019)].

для всех трех случаев спиновых структур мезонов:

14.

M. Freeman, M. D. Mateev, and R. M. Mir-Kasimov,

псевдоскаляра, вектора и псевдовектора.

Nucl. Phys. B 12, 197 (1969).

15.

В. Г. Кадышевский, Р. М. Мир-Касимов, М. Фри-

Детальный анализ поведения нового S-фактора

ман, ЯФ 9, 646 (1969).

(56) в релятивистском пределе (u → 1) показал,

16.

N. B. Skachkov and I. L. Solovtsov, Preprint No.

что он стремится к единице снизу для псевдоска-

√

E2-11727, JINR (Dubna, 1978); Н. Б. Скачков, И.

ляра (^Ô = γ₅) при g^′ >

2, а для вектора (^Ô =

√

Л. Соловцов, ЯФ 30, 1079 (1979)

[Sov. J. Nucl.

= γ_μ) — при g^′ >

3. Для этих значений фактора

Phys. 30, 562 (1979)].

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021

276

ЧЕРНИЧЕНКО

17.

N. B. Skachkov and I. L. Solovtsov, Preprint No.

янв. 2008, Препринт Д4-2008-65, ОИЯИ (Дубна,

E2-11678, JINR (Dubna, 1978); Н. Б. Скачков, И.

2008), с. 73.

Л. Соловцов, ТМФ 41, 205 (1979)

[Theor. Math.

34.

R. Barbieri, P. Christillin, and E. Remiddi, Phys. Rev.

Phys. 41, 977 (1979)].

A 8, 2266 (1973).

18.

K. A. Milton and I. L. Solovtsov, Mod. Phys. Lett. A

35.

V. I. Savrin and N. B. Skachkov, Lett. Nuovo Cimento

16, 2213 (2001).

29, 363 (1980).

19.

О. П. Соловцова, Ю. Д. Черниченко, ЯФ 73,

1658 (2010)

[Phys. At. Nucl. 73, 1612 (2010)];

36.

K. A. Milton, I. L. Solovtsov, and O. P. Solovtsova,

Phys. Rev. D 64, 016005 (2001).

arXiv:0904.0754v1.

20.

О. П. Соловцова, Ю. Д. Черниченко, ТМФ 166, 225

37.

I. L. Solovtsov and O. P. Solovtsova, Nonlin. Phenom.

(2011) [Theor. Math. Phys. 166, 194 (2011)].

Complex Syst. 5, 51 (2002).

21.

Ю. Д. Черниченко, Релятивистский квазипо-

38.

K. A. Milton, I. L. Solovtsov, and O. P. Solovtsova,

тенциальный подход в задачах рассеяния (Изд.

Mod. Phys. Lett. A 21, 1355 (2006).

центр УО ГГТУ им. П. О. Сухого, Гомель, 2011).

39.

K. A. Milton, in Proceedings of the International

22.

T. Appelquist and H. D. Politzer, Phys. Rev. Lett. 34,

Seminar Denoted to the Memory of

43 (1975); Phys. Rev. D 12, 1404 (1975).

I. L. Solovtsov, Dubna, 15-18 Jan. 2008, Preprint

23.

E. C. Poggio, H. R. Quinn, and S. Weinberg, Phys.

No. D4-2008-65, JINR (Dubna, 2008), p. 82.

Rev. D 13, 1958 (1976).

24.

J. Schwinger, Particles, Sources, and Fields

40.

В. Г. Кадышевский, М. Д. Матеев, Р. М. Мир-

(Addison-Wesley, New York, 1973), Vol. II.

Касимов, ЯФ 11, 692 (1970) [Sov. J. Nucl. Phys. 11,

25.

G. Gamov, Z. Phys. 51, 204 (1928).

388 (1970)].

26.

A. Sommerfeld, Atombau und Spektrallinien

41.

В. Г. Кадышевский, Р. М. Мир-Касимов, Н.

(Vieweg, Braunschweig, 1939), Vol. II.

Б. Скачков, ЭЧАЯ 2, 635 (1972) [Sov. J. Part. Nucl.

27.

A. D. Sakharov, ЖЭТФ 18, 631 (1948).

2, 69 (1972)].

28.

В. С. Фадин, В. А. Хозе, ЯФ 48, 487 (1988);

42.

Ю. Д. Черниченко, ЯФ 77, 251 (2014)

[Phys. At.

V. S. Fadin, V. A. Khoze, and T. Sjostrand, Z. Phys.

Nucl. 77, 229 (2014)].

C 48, 613 (1990).

43.

Ю. Д. Черниченко, ЯФ 78, 226 (2015)

[Phys. At.

29.

V. S. Fadin, V. A. Khoze, A. D. Martin, and

A. Chapovsky, Phys. Rev. D 52, 1377 (1995).

Nucl. 78, 201 (2015)].

30.

A. H. Hoang, Phys. Rev. D 56, 7276 (1997).

44.

И. С. Шапиро, Докл. АН СССР 106, 647 (1956)

31.

J.-H. Yoon and C.-Y. Wong, Phys. Rev. C 61, 044905

[Sov. Phys. Dokl. 1, 91 (1956)]; ЖЭТФ 43, 1727

(2000); J. Phys. G 31, 149 (2005).

(1962) [Sov. Phys. JETP 16, 1219 (1963)].

32.

A. B. Arbuzov, Nuovo Cimento A 107, 1263 (1994).

45.

W. Lucha and F. F. Sch ¨oberl, Phys. Rev. Lett. 64, 2733

33.

И. Л. Соловцов, Ю. Д. Черниченко, в сб.: Труды

(1990).

международного семинара по современным во-

просам физики элементарных частиц, посвя-

46.

W. Lucha and F. F. Sch ¨oberl, Phys. Lett. B 387, 573

щенный памяти И. Л. Соловцова, Дубна, 15-18

(1996).

WAVE FUNCTIONS AND S FACTOR FOR A SYSTEM

OF TWO RELATIVISTIC SPINOR QUARKS WITH ARBITRARY MASSES

Yu. D. Chernichenko

P. Sukhoi Gomel State Technical University, Belarus;

International Center for Advanced Studies, Gomel, Belarus

In the framework of the Hamiltonian formulation of quasipotential approach in quantum field theory by

transition to the three-dimensional relativistic configurational representation the exact solutions of the

covariant two-particle equations, mass spectrum, and S factor are obtained for a system of two relativistic

spin-1/2 quarks with arbitrary masses interacting via a Coulomb-like chromodynamical potential. The

cases of the pseudoscalar, vector, and pseudovector are considered. The new regularities has been installed

in behavior of threshold resummation S-factor.

ЯДЕРНАЯ ФИЗИКА том 84

№3

2021