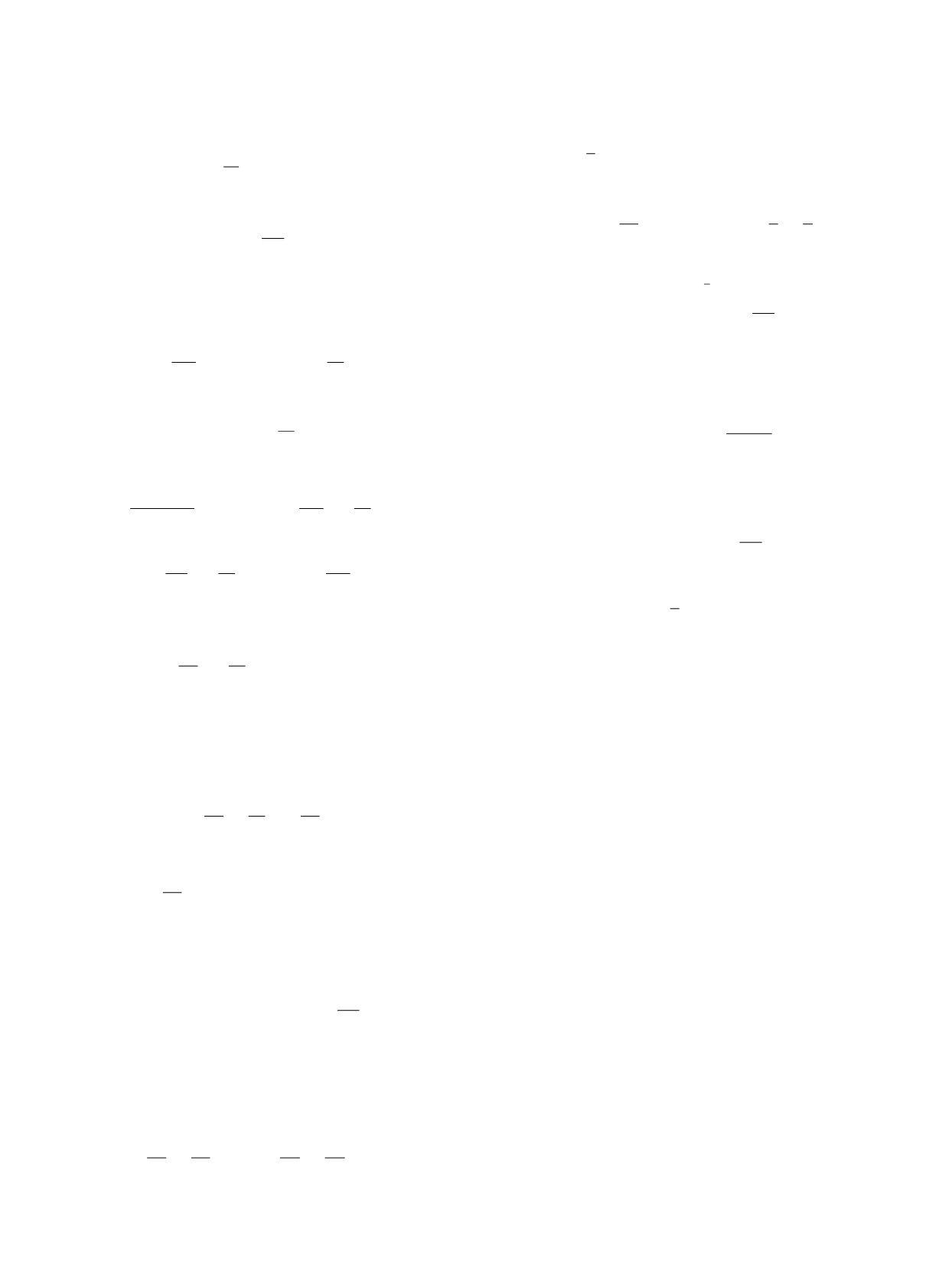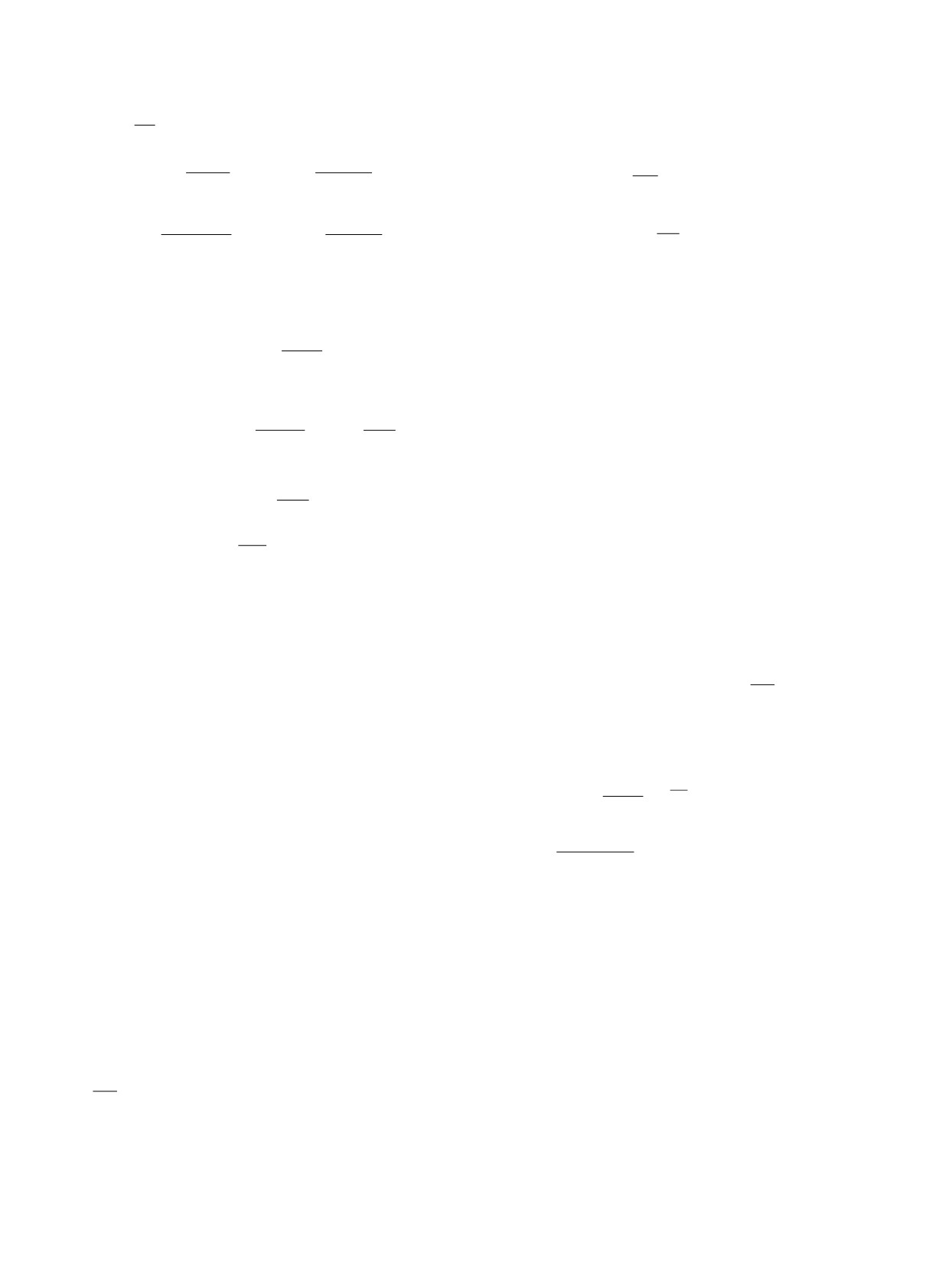ЯДЕРНАЯ ФИЗИКА, 2022, том 85, № 6, с. 419-424
ЯДРА
ПРОХОЖДЕНИЕ НЕЙТРОНОВ ЧЕРЕЗ ОСЦИЛЛИРУЮЩИЙ
ВДОЛЬ ПУЧКА ОБРАЗЕЦ
© 2022 г. Ф. С. Джепаров1),2)*, Д. В. Львов1),2), А. И. Франк3)
Поступила в редакцию 15.06.2022 г.; после доработки 15.06.2022 г.; принята к публикации 04.07.2022 г.
Рассмотрено прохождение тепловых нейтронов через плоскопараллельную пластину, совершающую
периодические колебания вдоль пучка нейтронов. Для анализа процесса построено нестационарное
приближение эйконала. Проведено сравнение эйконального результата с борновским приближением.
Получено аналитическое выражение для потока прошедших нейтронов.
DOI: 10.31857/S004400272206006X
1. ВВЕДЕНИЕ
тод анализа, позволивший получить аналитические
формулы для данного круга задач. Он основыва-
Исследования специфики взаимодействия ней-
ется на нестационарном обобщении эйконального
тронных волн с ускоренным веществом имеют
приближения, хорошо известного в стационарной
немалую историю, и в настоящее время можно
теории рассеяния, см., например, [8, 9].
считать твердо установленным наличие влияния
продольного ускорения нейтронно-оптически од-
нородной мишени на прошедший сквозь нее поток
2. НЕСТАЦИОНАРНЫЙ ВАРИАНТ
[1, 2]. Данное явление получило название эффекта
МЕТОДА ЭЙКОНАЛА
ускоряющегося вещества (ЭУВ), в его результате
частота волны, прошедшей через образец, движу-
Стационарный метод эйконала (также назы-
щийся с ускорением, отлична от частоты пада-
ваемый приближением высоких энергий) изложен
ющей волны. Планируются новые эксперименты
во многих учебниках по квантовой механике (см.,
для изучения ЭУВ в более сложных условиях и
например, [8]). В данном методе рассматривается
для поисков его приложений. Впервые вопрос о
решение задачи о рассеянии частицы с массой m и
прохождении нейтрона сквозь слой вещества, дви-
начальным импульсом k = kn = mv = (0, 0, k) для
жущийся с линейным ускорением, был рассмотрен
E ≫ U, где E —кинетическая энергия частицы,
в работе [3]. С тех пор проведенные исследования,
а U(r) —потенциальная энергия. Здесь и далее
по существу, основывались на чисто классическом
полагаем постоянную Планка ℏ = 1. Решение ста-
анализе [4, 1, 2] и численных методах [5], поскольку
ционарного уравнения Шредингера
аналитическое решение (в электродинамике) было
(
)
получено только для простейшего случая, когда
p2
k2
равноускоренно движущаяся мишень выбрана в
+ U(r) ψ =
ψ,
(1)
2m
2m
форме плоскопараллельной диэлектрической пла-
стины [6]. Аналогичное полуклассическое объяс-
где p = -i∇, ищется в форме ψ = eikzF (r). Функ-
нение получило явление ускорения нейтрона вбли-
ция F (r) медленно меняется по сравнению с мно-
зи брэгговского резонанса при прохождении ней-
жителем eikz, при U = 0 имеем F = 1. Для расчета
троном совершенного кристалла, движущегося с
F (r) удерживаются главные члены по 1/k, т.е. в
переменной скоростью [7]. В данной работе впер-
точном уравнении
вые сформулирован квантово-механический ме-
(
)
2
pk
p
1)Курчатовскийкомплекс теоретическойи эксперименталь-
+U F =-
F
(2)
ной физики НИЦ “Курчатовский институт”,Москва, Рос-
m
2m
сия.
пренебрегаем второй производной F в правой ча-
2)Национальный исследовательский ядерный университет
“МИФИ”, Москва, Россия.
сти (2). В результате получаем уравнение первого
3)Лаборатория нейтронной физики им. И. М. Франка,
порядка
Объединенный институт ядерных исследований, Дубна,
∂F
mU
Россия.
npF = -i
=-
F,
(3)
*E-mail: dzheparov@itep.ru
∂z
k
419
420
ДЖЕПАРОВ и др.
решение которого имеет вид
откуда находим связь переменных (ξ, τ) и (z, t)
⎛
⎞
∫
z
1
ξ = ξ(z,t) =
(z + vt) , τ = τ(z, t) = t - z/v.
F (r) = exp⎝-im
dz′U(r⊥, z′)⎠ =
(4)
2
k
Решая данную систему относительно (z, t), имеем
−∞
⎛
⎞
∫
z
vτ
ξ
τ
z = f(ξ,τ) = ξ -
,
t = u(ξ,τ) =
+
(14)
= exp⎝-idz′U (r⊥, z′)⎠ ,
2
v
2
v
Подстановка этих соотношений в (12) дает
-∞
1
где r⊥ — компонента вектора r, ортогональная
(
2
(z+vt)∫
оси z. Рассмотрим аналогичное приближение для
dξ′
F (r⊥, z, t) = exp
-i
×
(15)
нестационарного уравнения Шредингера
v
(
)
−∞
p2
∂
)
+ U(r,t) ψ = i
ψ.
(5)
(
)
2m
∂t
×U
r⊥,f(ξ′,t - z/v),u(ξ′,t - z/v)
Ищем решение в виде
2
vt - z
ψ(r, t) = eikz-
2m
tF(r,t).
(6)
Отсюда после замены ξ′ = z′ +
и элемен-
2
тарных упрощений окончательно получаем неста-
Подставляя (6) в (5), получаем
(
)
ционарное приближение эйконала для волновой
(
)
(p + k)2
k2
∂
функции
+U F =
+i
F,
(7)
( ∫z
2m
2m
∂t
dz′
F (r⊥, z, t) = exp
-i
×
(16)
(
)
v
pk
∂
p2
−∞
-i
+U F =
F.
(8)
m
∂t
2m
(
))
1
(
)
×U r⊥,z′,t-
z-z′
=
Как и в стационарном варианте, заменяем правую
v
часть на 0. Остается
(
)
= exp (-iΦ(r⊥, z, t)) .
∂
∂
-iv
-i
+ U(r,t) F = 0.
(9)
∂z
∂t
Легко видеть, что волновая функция непосред-
ственно зависит от значения потенциала в момент
Вводим вместо (z, t) новые переменные (ξ(z, t),
прохождения частицы через него.
τ (z, t)), т.е.
Очевидно, что в стационарном случае, т.е. при
z = z(ξ,τ) = f(ξ,τ), t = t(ξ,τ) = u(ξ,τ),
(10)
U (r⊥,z,t) = U(r⊥,z), из (16) получается стан-
дартная формула (4).
так, чтобы выполнялось равенство
∂
∂
∂
v
+
=v
(11)
3. ОСЦИЛЛИРУЮЩАЯ ПОТЕНЦИАЛЬНАЯ
∂z
∂t
∂ξ
СТЕНКА
Тогда вместо (9) получаем
В экспериментах, описанных в [1] и [2], образец,
(
)
представляющий собой плоскопараллельную пла-
∂
-iv
+ U(r⊥,f(ξ,τ),u(ξ,τ))
×
стинку толщины d, осциллирует с частотой ω в на-
∂ξ
правлении нейтронного пучка, которое ортогональ-
× F(r⊥,f(ξ,τ),u(ξ,τ)) = 0.
но плоскости пластинки. Потенциальная энергия
взаимодействия нейтрона с такой прямоугольной
Решение этого уравнения
стенкой определяется нейтронно-оптическим по-
тенциалом и равна:
∫
dξ′
U (r⊥,z,t) = V (z - s(t)) ,
(17)
F (r⊥, z, t) = exp
-i
×
(12)
v
V (z) = V0ϑ (0 < z < d),
−∞
)
s(t) = s0 sin ωt,
(
)
×U
r⊥,f(ξ′,τ(z,t)),u(ξ′,τ(z,t))
где ϑ(y) — функция Хэвисайда. Величину потен-
циала V0 мы считаем вещественной, т.е. поглоще-
Из (11) следует, что
ние нейтронов в образце не рассматривается. Из
(16) имеем
∂ξ
∂ξ
∂τ
∂τ
v
+
= v, v
+
= 0,
(13)
Φ (r⊥, z, t) =
(18)
∂z
∂t
∂z
∂t
ЯДЕРНАЯ ФИЗИКА том 85
№6
2022
ПРОХОЖДЕНИЕ НЕЙТРОНОВ
421
∫z
(
)
s′(h0)
dz′
1
(
)
=v
,
=
U r⊥,z′,t -
z-z′
=
v - s′(h0)
v
v
−∞
z
где h0 определяет нули δ-функции: h0 = t -
+
∫z
(
(
)
)
v
z-z′
=V0
dz′ϑ
0<z′ -s t-
<d
=
s(h0)
+
. В первом приближении
v
v
−∞
z
s0
= Φ(z,t).
h0 = t -
+
sin ω(t - z/v).
v
v
Далее удобно использовать поток импульса
Тогда
нейтронов, равный стандартному потоку, умножен-
(
)
z
s0
ному на массу нейтрона. В точке r он имеет только
s′(h0) = s0ω cos ω t -
+
sin ω(t - z/v)
≈
z-компоненту, равную
v
v
[
(
(
z)
s0ω
z)]
i
≈ s0ω cos ω t -
-
sin2 ω t -
j=
|∇zψ∗(r, t)ψ(r, t) - ψ∗(r, t)∇z ψ(r, t)| =
v
v
v
2
Подставляя данное выражение в (20), имеем
d
=k-
Φ (z, t) =
(
(
z)
s0ω
z)
dz
cos ω t -
-
sin2 ω t -
1
v
v
v
I =vs0ω
(
≈
=k-
V0ϑ (0 < z - s(t) < d) -
z)
v
v - s0ω cosω t -
z
(
(
)
)
v
∫
(
(
1
z-z′
z)
s0ω
−
V0
dz′∇zϑ
0<z′ -s t-
<d
≈ s0ω cos ω t -
+
×
v
v
v
v
[
(
(
−∞
z)
z)])
× cos2 ω t -
- sin2 ω t -
Поток на детекторе, расположенном в z > d + s0
v
v
∫
z
Вычисляя аналогично второй интеграл в (19), по-
1
лучаем
j =k+
V0
dz′∇t ×
(19)
v2
(
(
V0
z)
-∞
(
(
)
)
j=k-
s0ω cos ω t -
-
v2
v
z-z′
×ϑ
0<z′ -s t-
<d
=
(
))
v
z-d
V0
− cos ω t -
+
s20ω2 ×
∫
z
[ (
(
))
v
v3
V0
z-z′
(
(
)
(
=k-
dz′ δ z′ - s t -
-
z)
z-d
v2
v
× cos2 ω t -
- cos2 ω t -
+
−∞
v
v
(
)
(
(
))]
(
)
(
z-d
z))
z-z′
z-z′
+ sin2 ω t -
- sin2 ω t -
−δ z′ -d-s t-
∇ts t -
v
v
v
v
Из соотношений
(6) и
(16) следует, что
В эксперименте [1, 2] максимальная скорость
движения образца много меньше скорости ней-
|ψ(r, t)|2 = 1. Поэтому изменение потока Δj =
трона, т.е. ωs0/v ≪ 1. Вычислим интегралы в (19)
= j - k в (19) равно изменению Δk среднего
в главных порядках по этому малому параметру.
по ансамблю импульса нейтрона в точке z, а
Обозначим
соответствующее изменение его энергии может
∫z
(
(
))
быть оценено как
z-z′
I = dz′δ z′ - s t -
×
ΔE = vΔk = ΔE1 + ΔE2 =
(21)
v
(
)
−∞
2V0s0ω
ωd
z - d/2
(
)
=-
sin
sin ω t -
-
d
z-z′
v
2v
v
×
s t-
(
)
dt
v
2V0
ωd
z - d/2
-
s20ω2 sin
sin 2ω t -
′
ν2
2ν
ν
z-z
Сделаем замену переменной h = t -
. То-
v
Для определения же реального распределения
гда
по энергии в потоке прошедших частиц должна
∫t
d
использоваться волновая функция (6) с учетом (16)
I =
vdhδ (vh - vt + z - s(h))
s(h) =
(20)
и теория того прибора, который применяется для
dh
-∞
данного измерения.
ЯДЕРНАЯ ФИЗИКА том 85
№6
2022
422
ДЖЕПАРОВ и др.
ωd
В стационарной теории для амплитуды рассея-
Если
≪ 1, то из (21) следует
2v
ния в методе эйконала [8] получено:
(
)
∫
s0ω2d
z - d/2
k
ΔE1 = -V0
sin ω t -
,
(22)
f (q) =
d2ρeiqρ ×
(26)
v2
v
2πi
⎛
⎛
⎞
⎞
(
)
∫
∞
2V0s20ω3
d
z - d/2
ΔE2 = -
sin 2ω t -
(23)
×⎝exp ⎝-idz′U (ρ, z′)⎠ - 1⎠ .
v3
v
v
-∞
В работе [2] для этих же условий, но в рамках
классического приближения для изменения энер-
При этом правильная формула для амплитуды
рассеяния (т.е. в зоне Фраунгофера) в борновском
гии было получено выражение
приближении получается простым разложением
1-n
ΔEF = -ms0ω2d
sin ωt,
f (q) в ряд по U, а вопрос о совпадении эйкональ-
n
ного приближения ψe с борновским в окрестности
где n — показатель преломления. Учитывая, что
мишени (т.е. в зоне Френеля) не ставится. Для
(
)1/2
нас он важен как проверочный для новых фор-
V0
V
0
мул нестационарного эйконального приближения.
1-n=1-
1-
≈
,
mv2/2
mv2
Решить его на основе уравнения (25) нельзя, по-
скольку в борновском приближении оно очевидно
имеем
).
правильно и ничего не говорит о ψe(t′
V0
ΔEF = -ms0ω2d
sin ωt =
(24)
В борновском приближении из (25) следует:
mv2
ω2d
∫t
= -s0
V0 sin ωt,
v2
ψ = e-iH0(t-t0)ψ0 - i dt′e-iH0(t-t′) ×
(27)
что совпадает с (22) с точностью до фазы. При
t0
выводе величины эффекта в [2] фаза не отслежи-
× U(t′)e-iH0(t′-t0)ψ0 + O(U2).
валась, а необходимость измерения фазы осцил-
ляции в экспериментах [1, 2] была обусловлена
Выберем начальное условие в виде
поглощением в образце, которое в нашем выводе
игнорировалось. Выражение (23) дает поправку к
k2
ψ0(r) = exp(ikz), E0 =
(28)
данному результату следующего порядка малости
2m
по ωs0/v ≪ 1.
Пропагатор свободного движения
G0(r - r′,t) = r
e-iH0t
r′ =
(29)
4. СРАВНЕНИЕ ЭЙКОНАЛЬНОГО
∫
РЕЗУЛЬТАТА С БОРНОВСКИМ
d3p
=
e-i2mt +ip(r-r′) =
ПРИБЛИЖЕНИЕМ
(2π)3
Формула (16) работает в области мишени и
(
)3/2
m
около нее. Для продолжения результата на любые
=
e-m(r-r′)2/(2(ε+it)),
расстояния можно поступить аналогично тому, что
2π (ε + it)
делают в стационарном варианте: подставить в
где ε → +0. Подставляя (29) в (27), в координат-
правую часть точного соотношения
ном представлении имеем:
∫
ψ=e-iH0(t-t0)ψ0 -
(25)
ψ (r) = e-iE0(t-t0)+ikz - i d3r′ ×
(30)
∫t
- i dt′e-iH0(t-t′)U(t′)ψ(t′)
t
∫
t0
× dt′G0(r - r′, t - t′)U(r′, t′)e-iE0(t′-t0)+ikz′ =
(
t0
эйкональное приближение ψe(r, t′) = exp ikz -
[
∫
)
2
=e-iE0(t-t0)+ikz
1-i d3r′ ×
k
-i
t′ - iΦ(r⊥,z,t′) вместо ψ(t′).
2m
∫t
Однако интересен следующий вопрос: воспро-
изводят ли формулы (6), (16) борновское прибли-
× dt′G0(r - r′, t - t′) ×
жение в общей области применимости?
t0
ЯДЕРНАЯ ФИЗИКА том 85
№6
2022
ПРОХОЖДЕНИЕ НЕЙТРОНОВ
423
]
Выполнив еще одну замену переменной r′ =
√
× U(r′, t′)eiE0(t-t′)+ik(z′-z)
=
=
ka(r′′⊥, z′′ - τ), получим
∫
2
a5/2v1/2m3/2
=eikz-
2m
(t-t0)FB(r, t).
ΦB(r,t) =
d3r′ ×
(35)
(ka)3/2
Таким образом, в борновском приближении при
∫
∞
(
)3/2
(
)
t0 → -∞ получаем:
1
ir′2
× dτ
exp
×
∞
2π (ε + iτ)
2(τ - iε)
∫
∫
(r, t) = 1 - i d3r′ dsG0(r′, s) ×
(31)
0(
)
FB
r⊥
r′⊥
z
z′
aτ
0
×U1
-
,
-
- τ,t -
a
a
v
(ka)1/2
(ka)1/2
× U(r - r′,t - s)eiE0s-ikz′ = 1 - iΦB(r,t).
Раскладывая потенциал по малому параметру
Эта формула верна на любых расстояниях, то-
(ka)-1/2, получаем
гда как (16) работает только при r ≪ ka2, где a —
a
размер мишени. Для выяснения вопроса о том,
ΦB(r,t) =
×
(36)
v
совпадают ли формулы (16) и (31) в общей области
⎛
⎞
∫
∞
применимости, учтем, что
(r⊥
z
aτ)
(
)
-1
×⎝ dτU1
,
- τ,t -
+O
(ka)
⎠=
(
)3/2
a
a
v
m
0
G0(r′,s)eiE0s-ikz′ =
×
(32)
2π (ε + is)
z
∫
(
⎛
(
)⎞
dz′
z-z′)(
(
))
=
U r⊥,z′,t -
1+O
(ka)-1
im r′2⊥
+ (z′ - vs)2
v
v
× exp⎝
⎠=
−∞
2s
Подставляя полученное выражение в (31), в
= G0(r′⊥,z′ - vs,s).
главном порядке по малому параметру (ka)-1/2
имеем
Теперь с учетом (31) и (32) получаем, что
∫
z
(
)
∞
dz′
z-z′
∫
∫
(
)3/2
m
FB(r, t) = 1 - i
U r⊥,z′,t -
(37)
ΦB(r, t) = d3r′ ds
×
(33)
v
v
2π (ε + is)
-∞
0
⎛
(
)⎞
Это выражение в главном порядке по U совпа-
im r′2⊥
+ (z′ - ks/m)2
дает с (16).
× exp⎝
⎠U(r - r′, t - s).
Проведем аналогичные выкладки в стационар-
2(s - iε)
ном случае. Эйкональное решение в области мише-
ни
Выделим главный порядок по (ka)-1 = (mva)-1.
ψ (r) = eikzF (r, k),
(38)
Пусть
⎛
⎞
∫
z
(
)
(
)
r
r⊥
z
U (r, t) = U1
,t
=U1
,
,t
(34)
F (r, k) = exp⎝-idz′U (r⊥, z′)⎠ .
a
a
a
v
-∞
Подставляя (34) в (33) и выполняя замену пе-
В борновском приближении
aτ
∫
ременных r′ = ar′′ и s =
, с учетом v = k/m,
v
m
eik|r-r′|
получаем
ψB (r) = eikz -
d3r′
U (r′)eikz′ =
2π
|r - r′|
∞
(
)3/2
∫
∫
(39)
dτ
vm
[
]
ΦB(r, t) = a4 d3r′′
×
∫
v
2π (ε + iaτ )
m
eikr′
=eikz
1-
d3r′
U (r - r′)e-ikz′
0
(
)
2π
r′
⎛
⎞
ima2
r′′2⊥
+ (z′′ - τ)2
× exp⎝
⎠×
Экспоненты выделяют область размером k-1
2av (τ - iε)
вблизи r′ = z′ и r′⊥
= 0, определяющую значение
интеграла. Поэтому для r вблизи мишени имеем
(r⊥
z
aτ)
×U1
-r′′⊥,
-z′′,t -
a
a
v
ψB (r) ≈ eikz ×
(40)
ЯДЕРНАЯ ФИЗИКА том 85
№6
2022
424
ДЖЕПАРОВ и др.
[
]
∫
∫
ikr′
позволяет лучше понять природу явления. Данный
m
e
× 1-
dz′U(r⊥
,z - z′)e-ikz′
d2r′
подход может быть использован для анализа более
2π
⊥ r′
сложных экспериментов, например, для предска-
зания влияния поперечных пучку ускорений, когда
Используя выражение для пропагатора в импульс-
образцом служит не плоскопараллельная пласти-
ном представлении, получаем
на, а специально профилированная мишень.
∫
∫
eikr′
dp
eipz
i
d2r′
= 4π
= 4π
eik|z|.
⊥ r′
2π p2 - k2 - iε
2k
СПИСОК ЛИТЕРАТУРЫ
Подставляя данное выражение в (40), имеем
1. А. И. Франк, П. Гелтенборт, М. Жентшель,
ψB (r) = eikz ×
(41)
Д. В. Кустов, Г. В. Кулин, В. Г. Носов, А. Н. Стре-
[
∫
]
петов, ЯФ 71, 1686 (2008) [Phys. At. Nucl. 71, 1656
i
(2008)].
× 1 - 2m dz′
eik|z′|-ikz′U(r⊥,z - z′) =
2k
2. А. И. Франк, ЭЧАЯ 47, 1192 (2016) [Phys. Part.
⎡
⎤
z
Nucl. 47, 647 (2016)].
∫
(
)
dz′
3. F. V. Kowalski, Phys. Lett. А 182, 335 (1993).
= eikz ⎣1 - i
U (r⊥, z′) + O (ka)-1
⎦,
4. В. Г. Носов, А. И. Франк, ЯФ 61, 686 (1998) [Phys.
v
−∞
At. Nucl. 61, 613 (1998)].
5. M. A. Zakharov, G. V. Kulin, and A. I. Frank, Eur.
что соответствует (38).
Phys. J. D 75, 47 (2021).
6. K. Tanaka, Phys. Rev. А 25, 385 (1982).
7. Ю. П. Брагинец, Я. А. Бердников, В. В. Федоров,
5. ЗАКЛЮЧЕНИЕ
И. А. Кузнецов, М. В. Ласица, С. Ю. Семенихин,
Хотя наличие эффекта ускоряющегося веще-
Е. О. Вежлев, В. В. Воронин, ЯФ 80, 39 (2017)
ства на данный момент не вызывает сомнений,
[Phys. At. Nucl. 80, 38 (2017)].
изучение его природы продолжается, планируются
8. Л. Д. Ландау, Е. М. Лифшиц, Квантовая механи-
новые эксперименты. В работе [10] на основе прин-
ка (Физматлит, Москва, 2019).
ципа эквивалентности сформулирована гипотеза о
9. Ф. С. Джепаров, Д. В. Львов, Письма в ЖЭТФ 72,
более общем характере эффекта. Полученные в
518 (2000) [JETP Lett. 72, 360 (2020)].
данной работе решения дают первое аналитическое
10. А. И. Франк, УФН 190, 539 (2020) [Phys. Usp.
описание ЭУВ на основе квантовой механики, что
63, 500 (2020)].
PASSAGE OF NEUTRONS THROUGH A SAMPLE OSCILLATING
ALONG THE BEAM
F. S. Dzheparov1),2), D. V. Lvov1),2), A. I. Frank3)
1) Kurchatov Complex for Theoretical and Experimental Physics NRC “Kurchatov Institute”,
Moscow, Russia
2)National Research Nuclear University MEPhI, Moscow, Russia
3)Frank Laboratory of Neutron Physics, Joint Institute for Nuclear Research, Dubna, Russia
The passage of thermal neutrons through a plane-parallel plate performing periodic oscillations along the
neutron beam is considered. To analyze the process, a nonstationary eikonal approximation is constructed.
The eikonal result is compared with the Born approximation. An analytical expression for the flux of
transmitted neutrons is obtained.
ЯДЕРНАЯ ФИЗИКА том 85
№6
2022