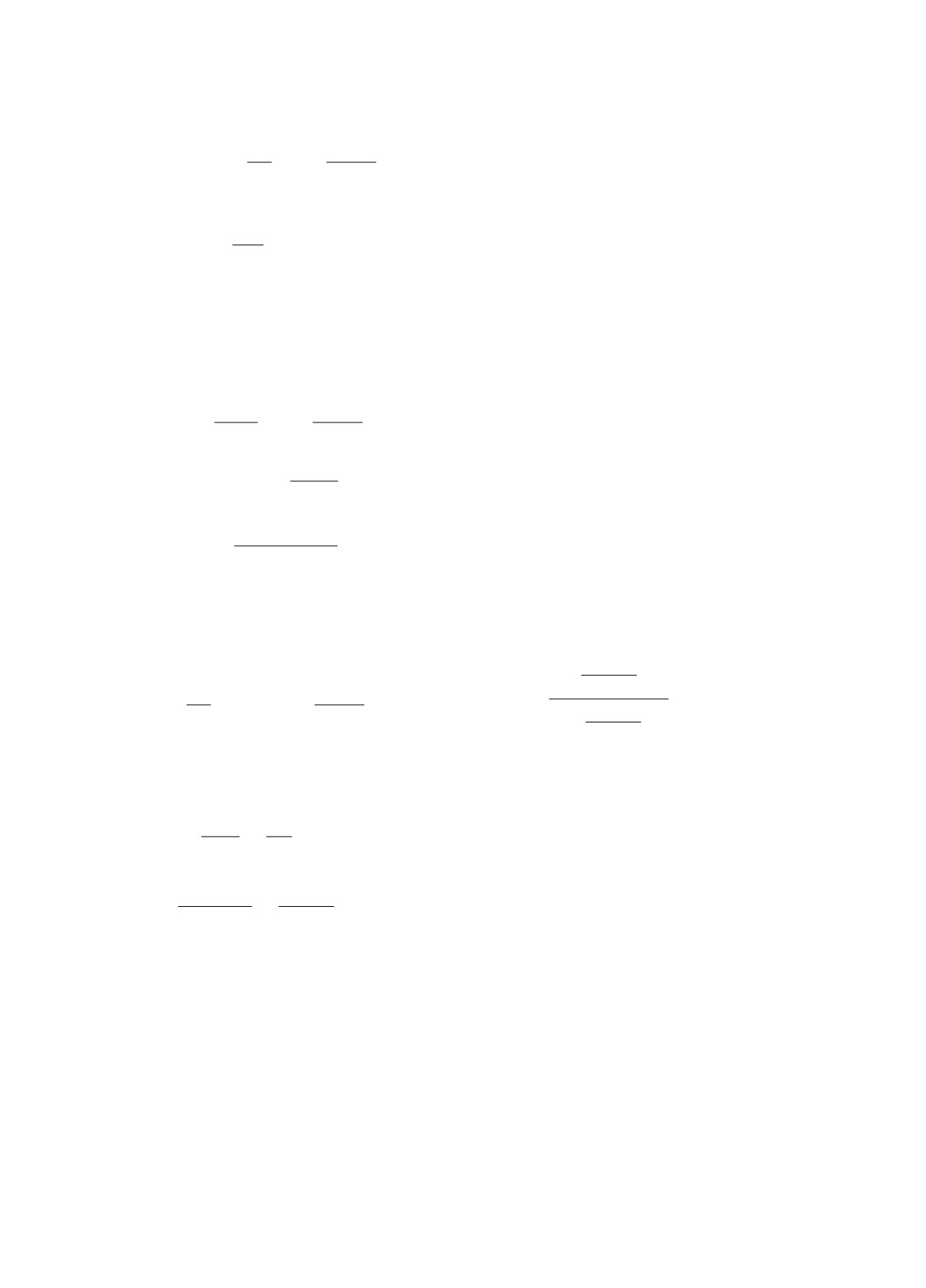ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 1, с. 13-23

ЯДРА

РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОНОВ ПО ЭНЕРГИЯМ

В МОДЕЛИ МИГДАЛА ИОНИЗАЦИИ АТОМОВ

Поступила в редакцию 16.08.2022 г.; после доработки 16.08.2022 г.; принята к публикации 26.08.2022 г.

Рассмотрен процесс ионизации по модели Мигдала, происходящий при упругом рассеянии тяжелой

нейтральной частицы, в том числе WIMP, на атоме благородного газа в случае малых энергий

его отдачи. Проведена оценка среднего числа первичных и вторичных электронов, испущенных в

отдельном акте такой ионизации, а также получены распределения по энергиям первичных электронов.

Расчеты выполнены для атомов различных благородных газов с учетом экспериментальных данных по

их ионизации фотонами.

DOI: 10.31857/S004400272301035X, EDN: RFMBSE

1. ВВЕДЕНИЕ

отличается от ударной ионизации атомов бесструк-

турными зарядами (электрон, протон, α-частица,

Изучение процессов столкновений слабовзаи-

...).

модействующих частиц с ядрами и электронами

При малых энергиях атома отдачи E_R ≲ E_min

атомов благородных газов составляет одну из при-

(∼1 кэВ для аргона) эффективен механизм МИ:

оритетных задач в общей картине научных ис-

при практически мгновенном ударе налетающей

следований по поиску гипотетических частиц тем-

частицы по его ядру электронная оболочка атома

ной материи. Этот интерес обусловлен необходи-

“встряхивается” и в результате происходит воз-

мостью существенного повышения эффективности

буждение и/или ионизация атома. Оценка веро-

регистрации событий, протекающих при движении

ятности этого процесса приведена в [9], а в на-

частицы темной материи в детектирующей среде.

шей работе [8] полученные соотношения на основе

Одним из таких событий рассматривается обра-

экспериментальных данных для сечений ионизации

атомов фотонами и электронами позволяют вычис-

зование свободных электронов, возникающих при

отдаче ядра атома вещества детектора в результате

лить вероятность осуществления МИ с достаточ-

его взаимодействия с частицей темной материи.

ной степенью надежности.

Именно это явление предлагается использовать в

В области энергий E_min ≲ E_R ≲ E_max, харак-

детекторах на сжиженных благородных газах [1, 2]

терных для имеющихся в литературе моделей, опи-

в качестве перспективного рабочего вещества.

сывающих столкновение атома с частицей темной

материи WIMP, основную роль в возбуждении и

Процессы образования таких электронов мо-

ионизации как самого атома, так и атомов сре-

гут иметь различную природу и объясняться ме-

ды при его торможении играет ПИ. Этот меха-

ханизмами линхардовской (МЛ) [3], паулиевской

низм свойственен только многоэлектронным ато-

(ПИ) [4, 5], а также мигдаловской (МИ) [6-8]

мам: при столкновении двух таких атомов занятые

ионизации атомов отдачи. Вероятность осуществ-

фермиевскими частицами - электронами, оболоч-

ления процесса ионизации по тому или иному ме-

ки начинают перекрываться, что, согласно прин-

ханизму, как отмечено в работе [5], зависит от

ципу Паули, вызывает их сильную деформацию,

величины энергии отдачи E_R этого атома.

ведущую к выбросу значительного числа первич-

ных электронов. В результате столкновения атома

Так, действие механизма Линхарда преоблада-

отдачи в этой области энергий могут привести к об-

ет в области высоких энергий отдачи E_R ≳ E_max

разованию свободных электронов, число которых

(∼4 МэВ, например, для аргона) и по своей сути не

примерно в 20 раз выше [5], чем появившихся по

механизму МИ.

¹⁾Национальный исследовательский центр “Курчатовский

институт”, Москва, Россия.

Тем не менее неопределенности, вызванные

^*E-mail: mleonid1954@mail.ru

недостаточностью знаний значений основных

^**E-mail: menshikov2005@mail.ru

величин для анализа данных экспериментов по

^***E-mail: Fayfman_MP@nrcki.ru

выяснению природы темной материи, а также

МЕНЬШИКОВ и др.

исследование столкновений нейтральных частиц

энергия атома. Основной вклад в эту энергию дают

(нейтронов, нейтрино) с атомами благородных

внутренние оболочки атома, а вклад от внешних

газов, требуют детальной оценки роли не только

оболочек сравнительно мал. В результате точность

процессов ПИ, но и дальнейшего изучения других

рассчитанных волновых функций электронов на

механизмов, в частности, МИ.

внешних оболочках оказывается невысокой и, что

В настоящей работе на основе подхода, сфор-

еще хуже, неизвестной.

мулированного в нашей работе [8], проведен расчет

По этой причине важно воспользоваться бо-

среднего числа свободных электронов, возникаю-

лее надежным способом нахождения вероятности

щих в одном отдельном акте процесса Мигдала,

ионизации атомов отдачи, что и было осуществлено

и получены функции распределения электронов по

в работе [8], где предложено применить данные из-

энергиям.

мерений сечений фотоионизации атомов благород-

ных газов [10-12], погрешность которых известна

и составляет ∼20%.

2. ФОРМУЛИРОВКА МЕТОДА

Приведем краткое изложение вывода формулы

Согласно модели Мигдала при взаимодействии

для вероятности ионизации [8] по модели Мигдала

частицы с ядром атома, достаточно коротком по

в форме, необходимой для расчетов различных

сравнению с временами, характерными для пери-

характеристик такого процесса, полученных в на-

одов электронов в атомной оболочке, этот атом мо-

стоящей работе.

жет ионизоваться с заметной вероятностью [6-9]

∑

При малых энергиях отдачи (в области которых

W_M =

|Q|².

(1)

наиболее эффективен механизм МИ)

E_R ≪ 30A (кэВ), A — атомный вес ядра,

(5)

Здесь

и показатель трансляционной экспоненты T в (3)

Q = 〈f |T|i〉,

(2)

мал, поэтому в разложении T в ряд Тейлора доста-

точно учесть лишь первое слагаемое, дающее нену-

|f〉 — конечные состояния электронной оболочки

левой вклад в матричный элемент (2). Поскольку

ионизированного атома и покинувших этот атом

в этом приближении возможна только одноэлек-

одного или нескольких электронов, по которым

тронная ионизация атома отдачи [8], то удобно

в (1) производится суммирование, |i〉 = |0〉 — ос-

использовать обозначение |f〉 = |p, a〉, где p —

новное состояние электронной оболочки атома.

импульс испущенного электрона, который далее

Трансляционная экспонента T в (2) определена

будем называть первичным, a = 1, 2, ..., n — номер

выражением [6-9]

(

)

атомной оболочки, от которой он оторвался. В

результате такого процесса ионизации образуется

T = exp

(3)

однократный ион с вакансией на a-ой оболочке.

Пусть E_a — энергия связи электрона на a-ой

где введены обозначения k = m_eV/ℏ, V — ско-

√

оболочке. Будем считать, что внешняя оболочка

рость атома отдачи, равная V =

2E_R/M, e —

имеет номер a = 1, тогда E₁ ≡ I, где I — потенциал

элементарный заряд, m_e — масса электрона, M —

ионизации атома, а K-оболочке будет соответ-

масса атома,

ствать a = n.

∑

Если вакансия образуется на внешней обо-

d = -e r_a

(4)

лочке, то состояние иона является стационарным,

устойчивым. Если же на внутренней, что соот-

a=1

ветствует a = 2, ..., n, то это состояние является

- оператор электрического дипольного момента

квазистационарным и распадается в результате ра-

атома с атомным номером Z и радиус-вектором

диационных переходов и оже-процессов. Типичные

a-го электрона r_a.

времена этих процессов [13, 14] составляют вели-

Выражения (1)-(4) определяют модель описа-

чины τ_rad ∼ 10-8 с и τ_Auger ∼ 10-14 с соответствен-

ния процесса МИ атома. В работе [9] матричный

но, что значительно больше характерных периодов

элемент (1) был рассчитан в приближении Хартри-

обращения электронов на внутренних оболочках

Фока. Такой подход требует громоздких числен-

ных расчетов и надежность его в применении к

≲10-17 с. Следовательно, с достаточной точностью

рассматриваемой задаче сомнительна по нижесле-

все состояния |p, a〉 можно считать стационар-

дующей причине. Наиболее вероятна ионизация

ными.

электронов с внешней оболочки атомов (как на-

Именно переход |0〉 → |p, a〉, для определенно-

ходящихся в наименее связанном энергетическом

сти, и будем называть процессом МИ, осуществля-

состоянии). В методе Хартри-Фока используют-

ющимся на атомной оболочке “a”. Его полная ве-

ся пробные функции, по которым минимизируется

роятность W_M при энергиях отдачи (5) составляет

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023

РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОНОВ ПО ЭНЕРГИЯМ

величину [8]

опытах [10-12] измерение сечения фотоиониза-

∫

ции атомов благородных газов производилось по

∑

d³p

поглощению излучения с использованием зако-

W_M =

|Q|² ≈k2

d2ap,

(6)

3e²

(2πℏ)³

на Бугера-Ламберта-Бера. За характерное для

a=1

оже-процессов время ∼10-14 с фотон, произво-

где

дящий вакансию в процессе фотоионизации, про-

∫

dΩ_p

ходит расстояние ∼3 мкм. Он имеет, как пра-

d2ap =

|〈p, a|d|0〉|²

(7)

вило, энергию ≳100 эВ, что соответствует длине

4π

волны ≲0.01 мкм. При взаимодействии с атомом

– квадрат матричного элемента дипольного мо-

фотон локализуется в области с размером порядка

мента, усредненный по направлениям вылета элек-

длины волны. Отсюда видно, что с достаточной

трона.

строгостью можно утверждать, что оже-процессы

Воспользуемся известным выражением для ве-

происходят значительно позже выбивания пер-

личины сечения фотоионизации в нерелятивист-

вичного электрона из внутренней оболочки атома.

ском приближении (см., например, [13]):

Добавим к этому, что при оже-процессах полная

∫

энергия электронов не меняется. По этим причинам

∑

4π²ε_γ

d³p

оже-процессы не влияют на измеряемую величи-

σ_ph(ε_γ) =

(8)

3ℏc

(2πℏ)³

ну поглощения. Следовательно, в опытах [10-12]

a=1

измерялось сечение фотообразования первичного

∑

2ε_γ m_e

электрона, то есть именно то сечение, которое

× δ(ε_γ - E_a - ε_e)d2ap =

p_ad2ap,

3cℏ⁴

использовалось для установления связи (11) с ве-

a=1

роятностью ионизации по модели Мигдала.

где обозначено:

√

p_a =

2m_e(ε_γ - E_a),

(9)

3. РАЗВИТИЕ МЕТОДА И РЕЗУЛЬТАТЫ

3.1. Количество свободных электронов

ε_e = p²/(2m_e) - энергия электрона,

по модели Мигдала

ε_γ - энергия фотона.

Рассмотрим функцию f(ε_γ ) от параметра ε_γ :

Переписывая (6) в виде

σ_ph(ε_γ)

∞

∫

∞

∫

∑

ε_γ

d³p

f (ε_γ ) =

∫

f (ε_γ )dε_γ = 1, (12)

W_M =

dε_γ

(10)

∞

σ_ph(ε_γ)

3e²

(2πℏ)³

a=1

dε

× δ(ε_γ - E_a - ε_e)d2ap,

определенную подынтегральным выражением (11).

Пример такой функции f(ε_γ) в случае ксенона

из (8) и (10), получаем

приведен на рис. 1.

∞

∫

dε_γ

В процессе Мигдала с наибольшей вероятно-

W_M =

σ_ph(ε_γ) =

(11)

стью первичный электрон стряхивается с внешней

4π²α

ε_γ

оболочки [8, 9]. Ей на рис. 1 соответствует основ-

∫

∞

ной максимум — “горб”, расположенный в области

m2eE_R

σ_ph(ε_γ)

энергий фотона ε_γ ≲ 60 эВ. “Горб”, расположен-

dε_γ ,

2π²Mℏ²α

ε_γ

ный при энергиях фотона ∼100 эВ, соответствует

выбиванию электрона из подоболочек N₄ и N₅

атома ксенона и образованию вакансии на этих

где α = e²/(ℏc) ≈ 1/137 — постоянная тонкой

подоболочках (см. символьные обозначения элек-

структуры и I — потенциал ионизации атома.

тронных подоболочек в монографии [15]).

Ценность формулы (11) состоит в том, что при

Уместно также добавить следующее пояснение

ее использовании удается избежать прямого вы-

относительно формы “горбов” представленной на

числения величин (7) d2ap и вместо этого воспользо-

рис. 1 измеренной зависимости f(εγ ). В слож-

ваться известными опытными данными для сечений

ных атомах уровни энергии электронов, вследствие

фотоионизации атомов благородных газов [10-12].

спин-орбитального взаимодействия и снятия куло-

Здесь необходимо добавить следующее заме-

новского вырождения, группируются в отдельные

чание. В квантовой механике нельзя с опреде-

сгустки, структуру которых невозможно различить

ленностью сказать, что оже-процессы происходят

при имеющих место в опытах [10-12] значениях

после вылета из атома первичного электрона. В

δε_γ — разброса фотонов по энергиям ε_γ. Если бы

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023

МЕНЬШИКОВ и др.

f(ε_γ)

0.12

0.10

0.08

0.06

0.04

0.02

120

160

ε_γ, эВ

Рис. 1. График функции f(εγ) для ксенона, полученный на основе экспериментальных данных по фотоионизации

согласно определению (12).

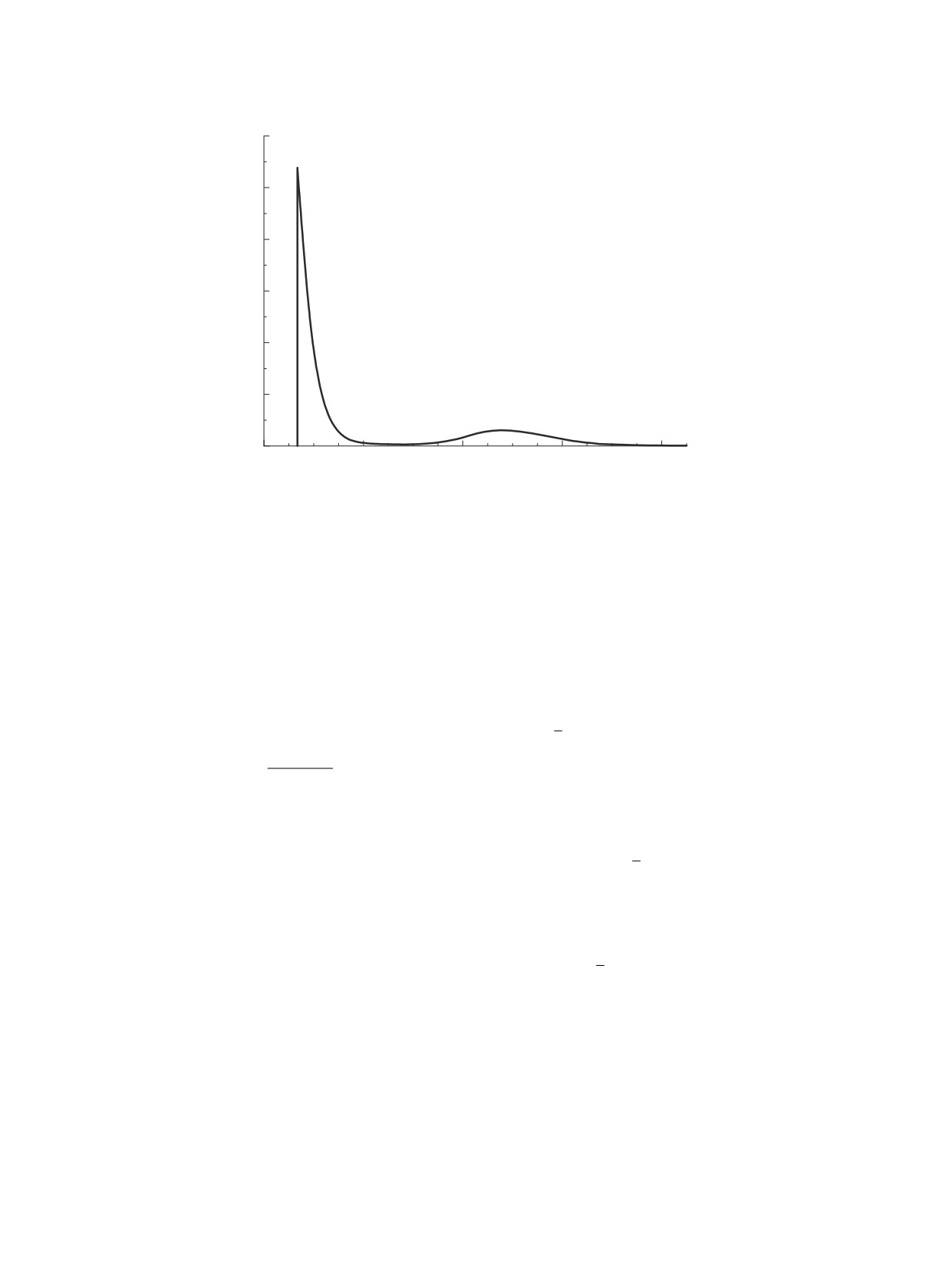
энергии подоболочек были отделены друг от друга

электронов, испущенных при торможении это-

на величину, превышающую разброс δε_γ , то изме-

го первичного электрона в веществе, N_Auger и

ренная зависимость f(ε_γ ), носила бы пороговый

N(2)S — числа, соответственно, вылетающих из

характер и качественно выглядела как на рис. 2.

атома оже-электронов и вторичных электронов,

В удобной для практических расчетов единицах

созданных этими тормозящимися в веществе оже-

и достаточной для оценок точностью формулу (11)

электронами. Ниже приводятся детали их расчета.

представим в виде

N(1)S = ε_e/ω, где ω — средняя энергия, необ-

E_R(кэВ)

ходимая для образования одной пары: атом, ли-

W_M = 0.0047

(13)

шенный одного электрона, и сам этот электрон.

Экспериментальные значения ω, взятые из [16-19]

Выражение (13) применимо при энергиях отда-

для разных веществ, приведены в табл. 2. Из этой

чи из интервала (5). Его погрешность составляет

таблицы видно, что для благородных газов, как и

∼20% [8] и определяется погрешностью данных

для всех веществ, характерна типичная величина

для сечений фотоионизации, которые содержатся в

ω ≈ 30 эВ. Величина ε_e —средняя энергия первич-

параметре B. Значения констант B для атомов раз-

ного электрона, которая рассчитана в настоящей

личных благородных газов определены в работе [8]

работе (табл. 1) с использованием функции рас-

и приведены в табл. 1.

пределения g(ε_e):

В табл. 1 также представлены необходимые

∫∞

для анализа работы детекторов частиц значения

ε_e = ε_eg(ε_e)dε_e,

(15)

среднего числа свободных электронов N_e, возни-

кающих при каждом акте процесса Мигдала. Эти

рассчитанные в настоящей работе величины для

нормированной на 1:

различного типа атомов определены следующей

∞

∫

суммой:

g(ε_e)dε_e = 1.

(16)

N_e ≈ 1 + N(1)S + N_Auger + N(2)S.

(14)

Здесь единица соответствует первичному элек-

Величина g(ε_e)dε_e определяет вероятность вы-

трону, образовавшемуся в результате стряхивания

битому из атома первичному электрону иметь энер-

с атомной оболочки, N(1)S — число вторичных гию ε_e в интервале (ε_e, ε_e + dε_e).

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023

РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОНОВ ПО ЭНЕРГИЯМ

f(ε_γ)

0.12

0.10

0.08

0.06

0.04

0.02

120

160

ε_γ, эВ

Рис. 2. Качественный вид графика функции (12) f(εγ) при фотоионизации с малыми значениями разброса фотонов по

энергиям εγ по сравнению с энергиями, отделяющими электронные подоболочки атома друг от друга.

Таблица 1. Значения параметра B и ионизационные характеристики для различных типов атомов благородных

газов

Атом

Заряд ядра, Z

Атомный вес, A (a.m.u.)

4.0

20.2

40.0

83.8

131.3

Параметр B, определенный из опытов по фотоионизации [10-12]

3.9

Средняя энергия первичного электрона, ε_e (эВ)

Число свободных электронов N_e, возникающих при отдельном

1.6

2.7

2.6

акте процесса Мигдала (см. (14))

Таблица 2. Средняя энергия ω (эВ) [16, 19] для атомов различных веществ, затрачиваемая первичным электроном

на образование одной пары (ион + электрон)

Вещество

Воздух

H₂

N₂

O₂

Энергия ионизации, I (эВ)

15.4

24.6

15.5

12.2

21.6

15.8

14.0

12.1

Средняя энергия, ω (эВ)

35.0

38.0

32.5

35.8

32.2

36.0

27.0

24.0

22.0

3.2. Распределение первичных электронов по

испущенного с оболочки под номером a, формулой

энергиям

ε_e = ε_γ - E_a.

(17)

Функция (12) задает распределение вероятно-

Величины E_a и n для подооболочек атомов имеют-

стей процесса Мигдала по энергиям ε_γ , которые

ся, например, в справочнике [15]. Для ксенона n =

в нашем подходе играют вспомогательную роль

= 16. Однако не все они видны на графике функции

и связаны согласно соотношениям (9)-(11) с ин-

f (ε_γ ) (см. рис. 1), полученном нами на основе

тересующей нас энергией первичного электрона,

данных [10-12], согласно которым n = 7.

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023

МЕНЬШИКОВ и др.

По этой причине при расчете функции распре-

Тогда соотношение (20) с учетом определения (12)

деления электронов g(ε_e) мы руководствовались

примет вид

данными экспериментов. В качестве энергий связи

k²

внутренних оболочек E_a для каждого атома есте-

W_M ≈

(22)

4π²α

ственно выбрать каждую последующую точку на

∫

∞

оси ε_γ , в которой начинается рост функции f(ε_γ).

∑

σ_ph(ε_γ)

Например, для ксенона (рис. 1) E₂ = 56.3 эВ, а

f (ε_e + E_a) dε_e

dε_γ .

ε_γ

согласно [15] в этом районе расположены подобо-

a=1

лочки N₄ и N₅ c E₂ ∼ 68 эВ. Далее, разобьем ось

Из сравнения соотношения (22) с формулой (11)

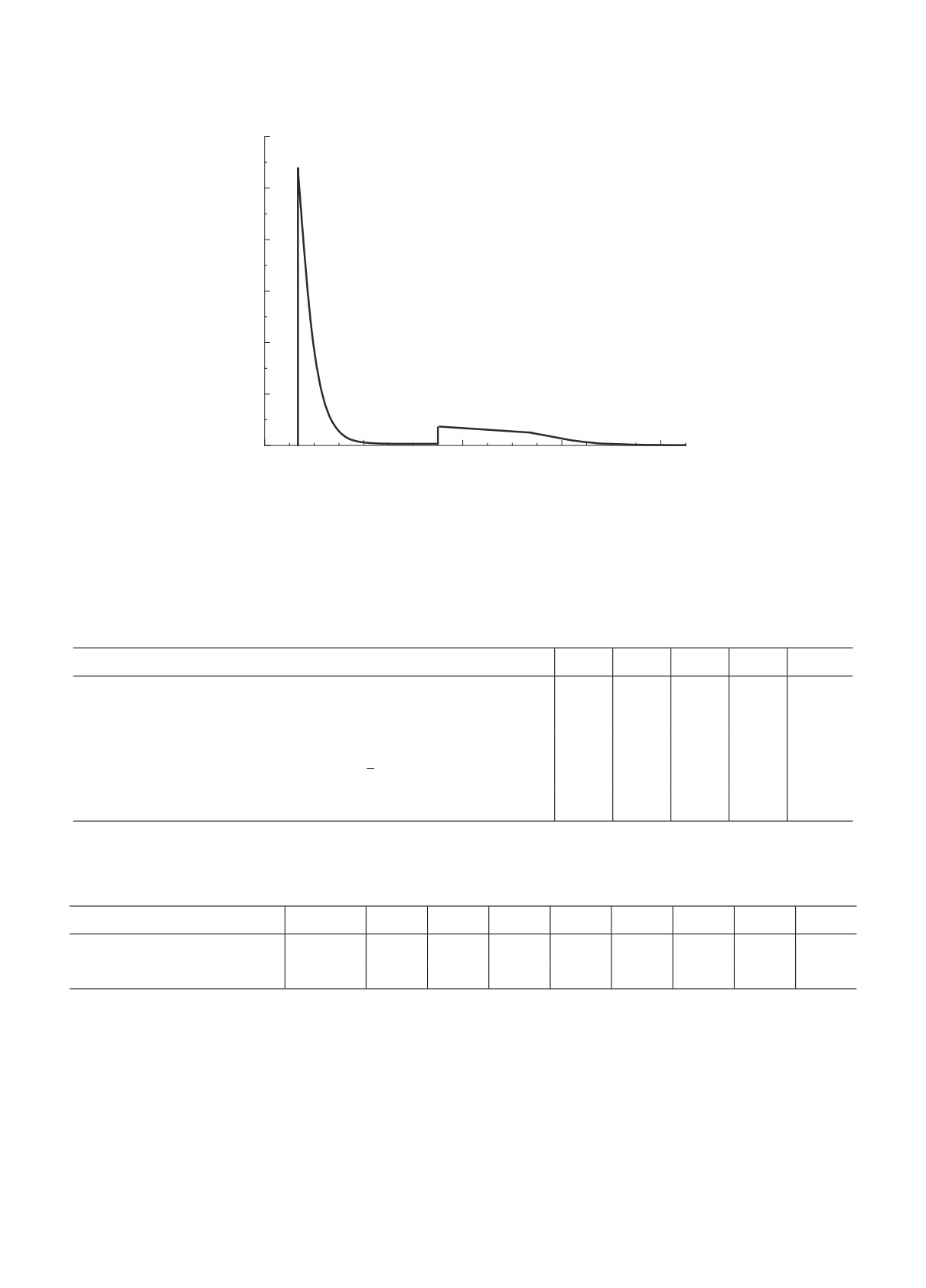
энергий фотона ε_γ на рис. 1 на n + 1 отрезков таким

следует, что

образом, чтобы, как показано на рис. 3, отрезку

с номером a соответствовали энергии E_a < ε_γ <

∫

∑

Ea+1, причем En+1 = +∞. Формулу (10), которая

dε_e f(ε_e + E_a) =

(23)

преобразуется в сумму интегралов по этим отрез-

a=1

кам, перепишем в виде

∞

∫

∑

∑∑

= dε_e s_a(ε_e) ≈ 1,

W_M =

J_ab,

(18)

3e²

a=1

a=1 b=1

b≥a

где введено обозначение

где

s_a(ε_e) = f(ε_e + E_a)θ(Ea+1 - E_a - ε_e).

(24)

Тогда функция

∫

∑

d³p

J_ab =

dε_γ

(19)

g(ε_e) =

s_a(ε_e),

(25)

(2πℏ)³

a=1

E_b

удовлетворяющая условию (16), т.е. нормирован-

∫

m_e

ная на единицу согласно (23), и будет искомым рас-

× δ(ε_γ - E_a - ε_e)d2ap =

dε_γ p_ad2ap.

пределением по энергиям первичных электронов,

2π²ℏ³

испущенных атомами.

E_b

Из изложенного ясно, что для построения функ-

Из рис. 1 видно, что для ксенона, вследствие

ции g(ε_e) следует ось ε_γ на рис. 1 разбить на n + 1

быстрого спадания величины σ_ph(ε_γ )/ε_γ с ростом

отрезков, как показано на рис. 3. После этого каж-

энергии фотона, J₁₂ ≪ J₂₂. Аналогичное свойство

дый отрезок на оси энергии, скажем, отрезок E_a <

J_ab ≪ J_bb при b = a выполняется для всех оболочек

< ε_γ < Ea+1, следует перенести как целое влево

всех атомов. По этой причине далее пренебрегаем

так, чтобы его левый конец совместился с левой

слагаемыми J_ab c b = a, что дает:

точкой E₁ первого отрезка. При этом значения

функции f, которые она принимала на отрезке

∑

E_a < ε_γ < Ea+1, прибавляются к соответствую-

W_M =

J_aa =

(20)

3e²

щим значениям на первом отрезке.

a=1

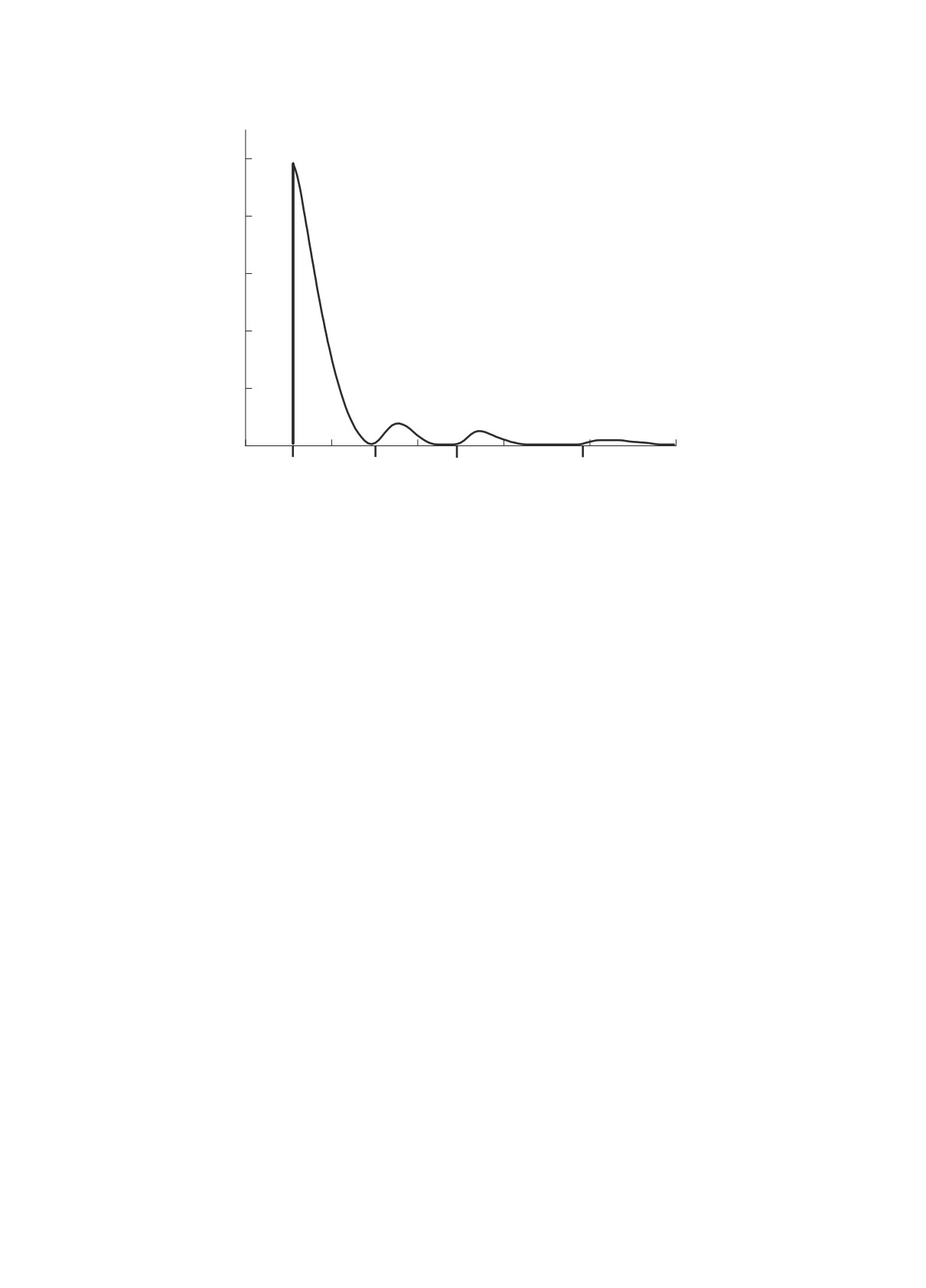
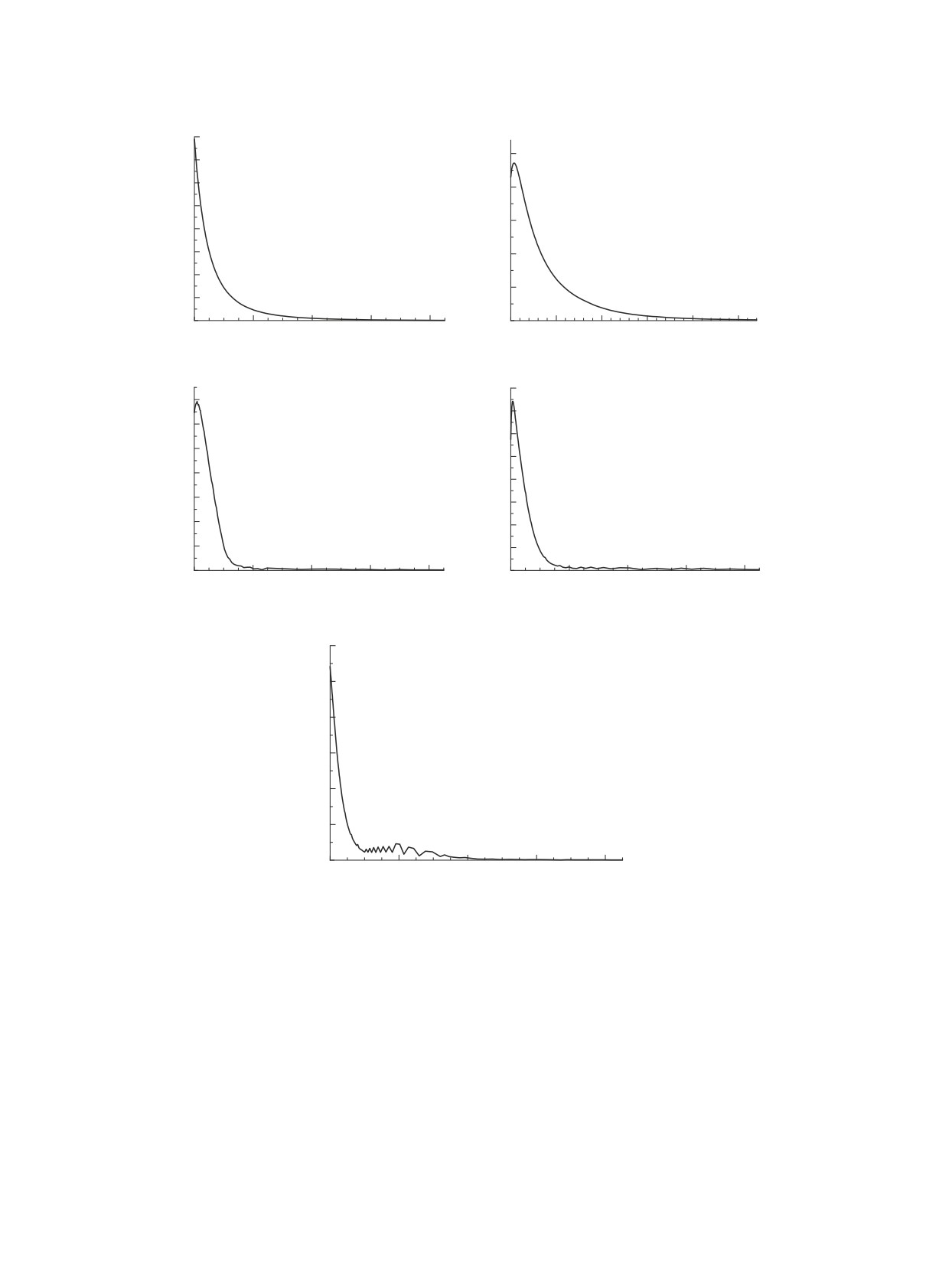
На рис. 4 представлены распределения g(ε_e)

∫

∑

для различных благородных газов. Кроме того, на

m_ek

dε_γ p_ad2ap.

рис. 5 представлены вероятности p(ε_e) для пер-

6π²ℏ³e²

вичного электрона иметь энергию выше заданного

a=1 Ea

значения ε_e:

Из выражений (17) и (9) следует, что на a-ом

∞

∫

отрезке

√

p(ε_e)=

g(ε_e)dε_e.

(26)

dε_γ = dε_e, p_a =

2m_eε_e ≡ p.

εe

Кроме того, на этом отрезке, по его определению,

Такие графики позволяют непосредственно нахо-

в сечении фотоионизации преобладает вклад от a-й

дить долю первичных электронов, испускаемых

орбитали, поэтому, согласно (8), здесь

в конкретном интервале энергий. Отдельно, для

сравнения, на рис. 6 приведены зависимости p(ε_e)

3cℏ

σ_ph(ε_γ)

p_ad2ap ≈

(21)

для областей малых и больших энергий электрона

2m_e ε_γ

ε_e.

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023

РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОНОВ ПО ЭНЕРГИЯМ

f(ε_γ)

E₁

E₂

E₃

E₄

ε_γ, эВ

Рис. 3. Пояснение формулы (25) (см. в тексте).

3.3. Среднее число свободных электронов с учетом

следует, что возникновение вакансии на внутрен-

испущенных при заполнении вакансий на

них подоболочках N₄ и N₅ атома ксенона при-

внутренних оболочках атомов отдачи

водит в среднем к образованию ∼(1 + 1/3) ≈ 1.3

свободных электронов, что согласуется с выводами

Схему расчета полного числа испущенных элек-

работы [20].

тронов в каждом отдельном акте МИ проследим

Согласно формулам (6), (11) и (12) при одном

на примере атома ксенона, учитывая образование

акте эффекта Мигдала, т.е. при испускании одного

вакансий на его внутренних оболочках при испус-

первичного электрона, вакансия на подоболочках

кании первичного электрона.

N₄ и N₅ появляется с вероятностью P_V ∼ 0.25.

Как отмечено в разд. 3.2, образованию ва-

Это значение есть не что иное, как доля площади

кансии на подоболочках N₄ и N₅ атома ксенона

под “горбом” в области энергий ∼100 эВ от пол-

соответствует на рис. 1 “горб” в области энер-

ной площади под кривой f(ε_γ), представленной на

гий ∼100 эВ. На выбивание электрона из такой

рис. 1 (отметим, что согласно (12) полная площадь

оболочки требуется затратить энергию E ≳ E₂ =

под этой кривой равна единице). Следовательно, с

= 68 эВ [15]. Эти вакансии заполняются электро-

вылетом из оболочки N4,5 первичного электрона,

нами с внешней оболочки, на которой их энергия

появляются еще N(N4,5) ∼ 0.25 × 1.3 ∼ 0.3 допол-

связи E₁ равна примерно потенциалу ионизации

нительных свободных электронов.

атома E₁ ≈ I = 12 эВ. Избыток энергии, примерно

равный ΔE = E₂ - E₁ ≈ 56 эВ, по механизму оже

Учтем теперь другие внутренние оболочки атома

передается электрону на внешней оболочке. По-

ксенона. Следующий “горб” функции f(ε_γ) имеет-

сле вылета первичного электрона атом становится

ся вблизи области энергий E₃ ∼ 650 эВ и, соглас-

ионом, поэтому энергия связи электрона на внеш-

но [15], соответствует подоболочкам M₄ и M₅ (на

ней оболочке увеличивается до ≈21 эВ — значе-

рис. 1 этот и последующие по энергии максимумы

ния потенциала ионизации I_Xe+ однократного иона

не представлены). В этом случае соответствующая

вероятность P_V ∼ 0.03, а суммарная энергия, уно-

ксенона. Поэтому этот электрон покидает ион Xe⁺

симая оже-электронами, близка к энергии связи

уже с энергией ε_S ≈ ΔE - I_Xe+ ≈ 35 эВ. В первом

столкновении с одним из соседних атомов элек-

и составляет ε_S ∼ E₃ ∼ 650 эВ. Торможение этих

трон возбуждает или ионизует его с вероятностями

электронов приводит к возникновению примерно

ε_S/ω ∼ 20 вторичных электронов (здесь исполь-

∼2/3 и ∼1/3 соответственно [20]. После этого

он начинает медленно термализоваться в упругих

зовано значение ω ≈ 30 эВ, характерное для бла-

столкновениях с атомами, поскольку его энергии

городных газов согласно табл. 2). Следовательно,

уже недостаточно для осуществления неупругих

в каждом процессе Мигдала среднее число вто-

процессов. Из приведенных рассуждений и оценок

ричных электронов, появившихся благодаря ранее

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023

МЕНЬШИКОВ и др.

g(ε_e)

0.08

0.025

0.07

0.06

0.020

0.05

0.015

0.04

0.03

0.010

0.02

0.005

0.01

120

160

100

150

200

250

ε_e, эВ

g(ε_e)

0.08

0.07

0.06

0.05

0.04

0.03

0.02

0.01

120

160

120

160

ε_e, эВ

g(ε_e)

0.12

0.10

0.08

0.06

0.04

0.02

120

160

ε_e, эВ

Рис. 4. Графики функции g(εe) для благородных газов, определенной формулами (15) и (25).

образованным вакансиям на оболочках M4,5, со-

0.38 и 0.2, соответственно. Следовательно,

ставит N(2)S ∼ P_V × ε_S /ω ∼ 0.6.

N_Auger ≈ P_V ×(0.42 × 3 + 0.38 × 4 + 0.2 × 5) ≈ 0.1.

(27)

Оценим теперь число оже-электронов N_Auger,

Таким образом, суммарно подоболочки M4,5 “по-

возникающих в процессе Мигдала, сопровожда-

ставляют”

ющимся образованием вакансии на подоболочках

N_M = N(2)S + N_Auger ∼ 0.7

M₄ и M₅ атома ксенона. Согласно измерениям [20],

в случае таких имеющихся вакансий, ион ксенона

свободных электронов на один акт процесса Ми-

испускает 3, 4 и 5 электронов с вероятностями 0.42,

гдала.

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023

РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОНОВ ПО ЭНЕРГИЯМ

p(ε_e)

1.0

0.8

0.6

0.4

0.2

120

160

200

100

200

300

400

500

ε_e, эВ

p(ε_e)

1.0

0.8

0.6

0.4

0.2

100

200

300

400

500

200

400

600

800

1000

1200

ε_e, эВ

p(ε_e)

1.0

0.8

0.6

0.4

0.2

500

1000

1500

2000

2500

3000

ε_e, эВ

Рис. 5. Графики функции p(εe) для благородных газов, определенной формулой (26).

Значения аналогичных величин для L-оболочки

оценок для ксенона получаем суммарную величину

ксенона составляют N(2)S ∼ 0.2, N_Auger ∼ 0.01 и то-

N_Auger + N(2)S ≈ N_M + N_N + N_L ≈ 1.2.

гда соответственно N_L = N_Auger + N(2)S ∼ 0.2. Об-

Окончательно вместе с другими слагаемыми выра-

разование вакансии на K-оболочке дает пренебре-

жение (14), где для ксенона (согласно табл. 1 и 2)

жимо малый вклад в N_e. К тому же, согласно [14],

N(1)S = ε_e/ω ≈ 2.1, приводит к результату N_e ≈ 4.

вакансия на этой оболочке заполняется главным

образом в результате радиационных переходов, при

Аналогичным образом рассчитаны значения N_e,

которых не возникает оже-электронов. Из этих

представленные в табл. 1, и для других атомов.

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023

МЕНЬШИКОВ и др.

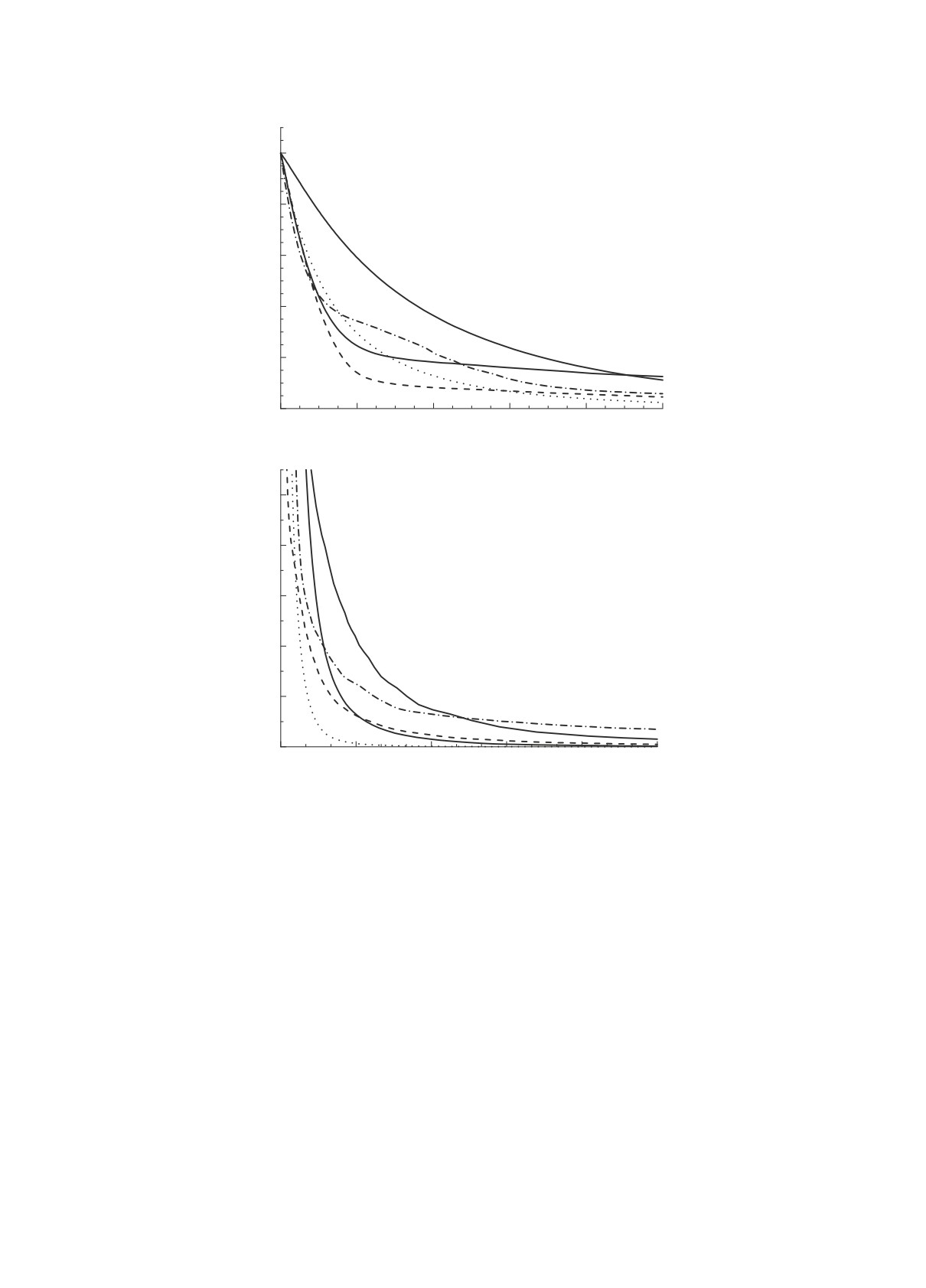
p(ε_e)

1.0

0.8

0.6

0.4

0.2

100

ε_e, эВ

p(ε_e)

0.10

0.08

0.06

0.04

0.02

300

600

900

1200

1500

ε_e, эВ

Рис. 6. Графики функции p(εe) в областях малых (а) и больших (б) энергий εe.

4. ЗАКЛЮЧЕНИЕ

получило отдачу в результате взаимодей-

ствия с известными или гипотетическими

нейтральными частицами;

На основе модели Мигдала в настоящей работе

развита схема расчета характеристик, необходи-

б) количество свободных электронов, возника-

мых для интерпретации отклика детекторов ча-

ющих в благородном газе мишени при еди-

стиц, в которых используется благородный газ в

ничном акте процесса Мигдала.

качестве рабочего тела. С учетом связи [8] между

вероятностью стряхивания первичного электрона

из атома при низкоэнергетическом столкновении

В полное число таких электронов входят:

нейтральной частицы с его ядром и эксперимен-

тальными сечениями фотоионизации такого атома

1) сам по себе первичный электрон, образо-

получены:

вавший вакансию на оболочке испытавшего

отдачу атома;

а) энергетические распределения первичных

2) вторичные электроны, выбитые из соседних

электронов, испущенных в процессе Ми-

атомов рабочего газа при торможении в нем

гдала, т.е. ионизации атома, ядро которого

первичного электрона;

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023

РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОНОВ ПО ЭНЕРГИЯМ

3) оже-электроны, образующиеся при запол-

А. Мигдал, ЖЭТФ 9, 1163 (1939).

нении вакансии на внутренней оболочке пер-

Л. Д. Ландау, Е. М. Лифшиц, Квантовая механи-

воначального атома отдачи;

ка (Наука, Москва, 1974).

Л. И. Меньшиков, П. Л. Меньшиков, М. П. Файф-

4) вторичные электроны, выбитые из соседних

ман, Письма в ЭЧАЯ 18, 181 (2021) [Phys. Part.

атомов рабочего газа при торможении в нем

Nucl. Lett. 18, 173 (2021)].

оже-электронов.

M. Ibe, W. Nakano, Y. Shoji, and K. Suzuki, J. High

Полученные в представленной работе характе-

Energ. Phys. 194, 35 (2018).

ристики электронов, возникающих в одном отдель-

10.

G. V. Marr and J. B. West, At. Data Nucl. Data Tables

ном акте процесса Мигдала, справедливы только

18, 497 (1976).

при низких энергиях атома отдачи E_R ≲ E_min (для

11.

J. B. West and G. V. Marr, Proc. R. Soc. Lond. A 349,

аргона E_min ∼ 1 кэВ), а в других областях энергий

397 (1976).

отдачи основной вклад дают другие механизмы (см.

12.

J. B. West and J. Morton, At. Data Nucl. Data Tables

разд. “Введение” и работу [5]) ионизации атомов

22, 103 (1978).

отдачи благородного газа.

13.

В. Б. Берестецкий, Е. М. Лифшиц, Л. П. Пи-

Вычисленные в настоящей работе распределе-

таевский, Релятивистская квантовая теория

ния по энергиям первичных электронов, а также

(Наука, Москва, 1968), ч. 1.

определение среднего числа электронов, испущен-

ных в отдельном акте ионизации по модели Ми-

14.

Э. С. Парилис, Эффект Оже (ФАН, Ташкент,

гдала, открывают новые возможности для анализа

1969).

экспериментальных данных, полученных при рабо-

15.

А. А. Радциг, Б. М. Смирнов, Параметры атомов

те детектора на основе выбранного благородного

и атомных ионов. Справочник (Энергоатомиз-

газа.

дат, Москва, 1986).

Авторы выражают искреннюю признательность

16.

В. И. Калашникова, М. С. Козодаев, Детекторы

М.Д. Скорохватову и И.Н. Мачулину за внимание

элементарных частиц (Наука, Москва, 1966).

к данной проблеме и полезные обсуждения.

17.

А. К. Пикаев, Дозиметрия в радиационной хи-

мии (Наука, Москва, 1975).

СПИСОК ЛИТЕРАТУРЫ

18.

Л. А. Аликбаева, М. А. Афонин, А. П. Ермолаева-

Маковская и др., Новый справочник хими-

1. G. Bertone, D. Hooper, and J. Silk, Phys. Rept. 405,

279 (2005).

ка и технолога. Радиоактивные вещества.

2. V. Chepel and H. Ara ´ujo, JINST 8, R04001 (2013).

Вредные вещества. Гигиенические нормативы

3. J. Lindhard, M. Scharff, and H. E. Schiott, Mat. Fys.

(АНО НПО “Профессионал”, Санкт-Петербург,

Medd. Dan. Vid. Selsk. 33, 14 (1963).

2004).

4. W. Brandt and R. Laubert, Phys. Rev. Lett. 24(19),

19.

К. Групен, Детекторы элементарных частиц

1037 (1970).

(Сибирский хронограф, Новосибирск, 1999).

5. Л. И. Меньшиков, П. Л. Меньшиков, М. П. Файф-

20.

T. A. Carlson, W. E. Hunt, and M. O. Krause, Phys.

ман, Письма в ЭЧАЯ 18, 560 (2021) [Phys. Part.

Rev. 151, 41 (1966).

Nucl. Lett. 18, 665 (2021)].

ELECTRON ENERGY DISTRIBUTIONS IN THE MIGDAL MODEL

OF ATOMIC IONIZATION

L. I. Men’shikov¹⁾, P. L. Men’shikov¹⁾, M. P. Faifman¹⁾

¹⁾National Research Center “Kurchatov Institute”, Moscow, Russia

The process of ionization that is due to the Migdal effect and which occurs in the elastic scattering of a

heavy neutral particle, including a weakly interacting massive particle (WIMP), on a noble-gas atom in the

case of its small recoil energy, is considered. The mean number of primary and secondary electrons emitted

in an individual event of such ionization is estimated, and the energy distributions of primary electrons are

obtained. The calculations were performed for various noble-gas atoms with allowance for experimental

data on their ionization by photons.

ЯДЕРНАЯ ФИЗИКА том 86

№1

2023