ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 2, с. 320-336

ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ

СТРУКТУРЫ МАТРИЦ СЛАБОГО СМЕШИВАНИЯ КАК СЛЕДСТВИЕ

НАРУШЕННОЙ ЗЕРКАЛЬНОЙ СИММЕТРИИ

Поступила в редакцию 04.10.2022 г.; после доработки 07.11.2022 г.; принята к публикации 09.11.2022 г.

Представлена модель нарушения симметрии системы, которая может спонтанно выбирать левый

или правый характер слабого тока. При иерархической структуре спектра масс фермионов такая

зеркально-симметричная система позволяет воспроизвести все качественные свойства матриц слабо-

го смешивания и кварков (матрица CKM), и лептонов (матрица PMNS), причем без дополнительного

численного подбора параметров модели. Иерархия матричных элементов CKM прямо связывается с

иерархическим спектром масс поколений кварков. Качественные свойства матрицы PMNS возникают

при инверсном характере спектра (m₃ — наименьшая масса) и дираковской природе нейтрино СМ.

Сравнительная малость угла смешивания нейтрино θ₁₃ обусловлена здесь малостью m₃ и малостью

отношений масс заряженных лептонов m_e/m_μ.

DOI: 10.31857/S004400272302006X, EDN: RIRHON

1. ВВЕДЕНИЕ

4]) и продолжаются до настоящего времени [5, 6].

Значительное число работ, разнообразие подходов

В течение многих лет считалось невозможным

к проблеме указывают на неудовлетворенность

физическими методами фиксировать, в какой си-

ситуацией с прямым несохранением четности,

стеме координат (левой (L) или правой (R)) рас-

несмотря на успешность и согласованность СМ,

сматривается то или иное явление. Несохранение

где это несохранение прямо включено в ее струк-

пространственной четности предоставило такую

туру.

возможность. Сказать, что большее число элек-

Основная задача существующих работ по моде-

тронов при распаде радиоактивных ядер летит по

лям зеркальных частиц — экспериментальные воз-

направлению магнитного поля, значит определить

можности их обнаружения и влияния на эффек-

направление аксиального вектора напряженности

ты СМ [7, 8]. Практически нет работ, которые

этого поля и тем самым характер системы коорди-

бы объясняли наблюдаемые свойства частиц СМ

нат, в которой явление рассматривается.

участием зеркального мира. В настоящей работе

В отличие от выбора точки начала координат

представлена попытка показать, что качественная

и направления осей в пространстве выбор L- или

структура матриц слабого смешивания (МСС) и

R-характера системы координат можно однознач-

кварков, и лептонов может объясняться именно су-

но закрепить физическим основанием благода-

ществованием очень тяжелых зеркальных частиц.

ря несохранению четности. Такая ситуация каза-

Причем качественные свойства МСС основывают-

лась неприемлемой уже первооткрывателям — Ли

ся исключительно на качественных же свойствах

и Янгу [1]. Они сразу же [2] предложили модель

системы частиц СМ — иерархическом характере

системы, устраняющей парадокс, дополнив наблю-

спектра масс фермионов и нарушенной группы

даемую систему частиц (на современном языке —

слабой симметрии SU(2), положенной в основу

систему Стандартной модели (СМ)) тождествен-

слабых взаимодействий в СМ.

ной системой тяжелых (поэтому еще не открытых)

Иерархии фермионных масс поколений имеют

аналогов с противоположными слабыми свойства-

важнейшее значение. Они задают иерархическую

ми (L ↔ R). Позднее такие объекты получили на-

структуру недиагональных элементов МСС квар-

звание “зеркальные частицы”.

ков и способны обеспечить возникновение отлич-

ной формы МСС лептонов. И все это без до-

Экспериментальные попытки их обнаружить

полнительного подбора величин констант модели.

и теоретические предложения разных вариантов

Точное качественное соответствие с формой МСС

идеи Ли и Янга не прерывались (см. обзоры [3,

не зависит от числа используемых параметров, их

величин и комплексностей.

¹⁾НИЦ “Курчатовский институт”— ПИЯФ, Гатчина, Рос-

сия.

Во многих работах пытались связать иерар-

^*E-mail: dyatlov@thd.pnpi.spb.ru

хический характер спектра с МСС кварков [9] и

320

СТРУКТУРЫ МАТРИЦ СЛАБОГО СМЕШИВАНИЯ

321

изобрести динамику его возникновения (см. [10] и

литературу к этим обзорам). В настоящей рабо-

1/μ

B⁺

те, приняв существования иерархического спектра,

подтверждаем его основополагающую роль в со-

ψ_L

Ψ_R

Ψ_L

ψ_R

здании специфических качественных форм МСС

кварков и лептонов. В то же время сами зер-

кальные фермионы должны быть много тяжелее

фермионов СМ. Это одно из условий возникнове-

Φ₂

Φ₁

ния правильных структур — масс частиц СМ и их

МСС.

Представляется, что именно такая система со-

1/M

ответствовала бы экспериментальному отсутствию

и исключительной малости влияния зеркальных

ψ_L

ψ_R

частиц на эффекты СМ и физику вне ее.

В работе [11] было замечено, что представление

Рис. 1. Механизм образования масс фермионов в

массовой матрицы суммой сепарабельных матриц с

настоящей работе (a) и в [10, 21] (б), φi — “хиггсовские

вакуумные средние”.

иерархией величин членов суммы не только приво-

дит к иерархическому спектру масс, но и позволя-

ет легко воспроизвести качественные черты МСС

обычном механизме see-saw (с тяжелыми майора-

кварков (матрицы CKM) как следствие одной толь-

новскими массами) приводит в [13] к неправиль-

ко слабой SU(2) симметрии без подбора величин

ным выводам (третья ссылка в [13] — исправление

параметров.

ошибки): легкие нейтрино тогда тоже оказываются

Сепарабельность означает отделение началь-

майорановскими. Без дополнительных, ниоткуда

ного состояния системы от конечного переходом

не следующих условий на константы, связываю-

через некоторое промежуточное состояние. Про-

щие легкие и тяжелые частицы, воспроизведение

межуточное состояние только массой отличается

свойств лептонной МСС (матрицы PMNS) ока-

от начального и конечного, сохраняя их квантовые

зывается здесь невозможным при любом характе-

числа. Это и есть зеркальные частицы, так как пря-

ре спектра нейтрино. При майорановской природе

мой скалярный переход фермиона в другой фер-

нейтрино в ЗС-модели не найти убедительный ка-

мион означает R ↔ L. При этом промежуточные

чественный принцип возникновения невыразитель-

состояния должны иметь массу, много большую

ных свойств матрицы PMNS.

начальных и конечных масс, чтобы в пропагаторах,

описывающих процесс (рис. 1), можно было прене-

Модель нарушения ЗС настоящей работы

брегать импульсами. Переходы (рис. 1a) из частиц

трактует систему нейтрино в полной аналогии с

СМ в тяжелые зеркальные состояния определя-

системой кварков и заряженных лептонов, т.е.

ются массовыми параметрами A, B-фермионов до

нейтрино также считаются дираковскими. В ЗС-

нарушения зеркальной симметрии (ЗС) (формула

лагранжиане отсутствуют майорановские члены.

(3), см. ниже), поэтому зеркальный механизм ока-

Массы нейтрино становятся малыми при очень

зывается более простым, чем переход с введением

больших массах их зеркальных партнеров. Только

юкавских связей и вакуумных средних скаляров

при инверсном спектре и дираковском характере

[10] (рис. 1б).

нейтрино система качественно воспроизводит не

Формулы масс легких кварков и лептонов (соот-

только малые²⁾ массы нейтрино, но и наблюдаемую

ветствующих состояниям СМ) описываются тогда

структуру матрицы PMNS прямо без дополнитель-

выражениями, аналогичными формулам see-saw-

ных подборов констант модели. Так же естественно

механизма [12]. Они возникают в результате спон-

возникает и находит объяснение сравнительная

танного нарушения первоначальной ЗС. Большие

малость синуса угла смешивания нейтринных

массы зеркальных частиц играют роль больших

флейворов sin θ₁₃ — единственной выделяющейся

майорановских масс see-saw. Дираковские массы

черты матрицы PMNS [15].

заменяются на параметры A, B-масс фермионов в

Вывод выражений для обеих МСС есть ос-

первоначальном ненарушенном ЗС-лагранжиане.

новное содержание настоящей статьи. Дополни-

В ряде работ автор развивал эту идею [13].

тельные проблемы, связанные с использованием

Применение ее к кваркам и заряженным лепто-

ЗС-механизмов, обсуждаются в предыдущих ра-

нам требует выполнения только воспроизведения

ботах автора и кратко в Заключении. В разд. 2

качественных условий — очень больших масс зер-

кальных частиц и слабой SU(2)-симметрии пол-

²⁾В работе [14] представлена современная эксперименталь-

ной ЗС-модели. Ошибка относительно возможно-

ная ситуация по определению характера спектра ней-

сти построения легких дираковских нейтрино при

трино.

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

322

ДЯТЛОВ

представлена общая схема введения ЗС. Раздел 3

A и B, вообще говоря, —матрицы 3 × 3 по индек-

представляет примерную схему нарушения ЗС, по-

сам поколений. Эти члены SU(2)-инвариантны, что

строенную в полной аналогии с нарушением слабой

означает:

симметрии в СМ. В разд. 4 получена массовая мат-

A(u) ≡ A

d),

B(u) = B

d).

(4)

рица системы кварков и соответствующая МСС.

В разд. 5 проводится анализ условий появления

В силу киральных свойств только член (3) с “мас-

в выбранном сценарии качественно близкой к на-

сами” A, B связывает компоненты ψ и Ψ друг с дру-

блюдаемой МСС лептонов. Приложение 1 пред-

гом (см. ниже формулу (18)). Очевидно, матрицы A

ставляет общий вывод массовой матрицы модели

и B должны быть эрмитовскими. Механизм разру-

и возможных здесь МСС. В Приложении 2 пред-

шения симметрии (2) строим в полной аналогии со

ложена гипотеза не зависящей от характера вза-

сценарием СМ.

имодействий причины появления иерархического

Задача ввести асимметрию ψ и Ψ, сохранив

спектра масс поколений всех фермионов.

полную тождественность других свойств, может

быть решена, только если у системы есть две сово-

купности состояний, различающиеся лишь R- и L-

2. ЗЕРКАЛЬНАЯ СИММЕТРИЯ

свойствами. Такой ситуации должны соответство-

В работах [11, 13] понимание ЗС предполагает

вать два возможных основных состояния (вакуума)

полную тождественность R- и L-систем до нару-

с разными слабыми свойствами. Это значит, что

шения симметрии. Такое понимание отличается от

после разрушения ψ ↔ Ψ-симметрии слабый ток

иных зеркальных систем, представленных в лите-

в одном из них, |L〉, окажется левым для легких

ратуре [3-7], где R- и L-системы порой имеют раз-

частиц ψ и правым для тяжелых Ψ. В другом состо-

ные взаимодействия, разные представления разных

янии, |R〉, свойства слабых токов противоположны.

групп, различные R-, L-векторные бозоны и даже

В рассматриваемой системе могут появиться

фотоны. С нашей точки зрения, тождественные

два типа вакуумных средних:

системы наиболее соответствуют первоначальной

〈R |ϕ₁| R〉 ≡ 〈L |ϕ₁| L〉,

(5)

идее Ли и Янга [2]. Различие только слабых свойств

(R ↔ L) и после нарушения ЗС положено в основу

равенство имеет место из-за предполагаемой тож-

предлагаемой модели.

дественности всех других свойств и



В ЗС-системе лагранжиан зависит лишь от пол-

|〈R |ϕ₂| L〉| =

^〈L

^ϕ⁺²

R〉.

(6)

ных дираковских операторов:

Очевидно, поле ϕ₁ — скаляр, а ϕ₂ — псевдоска-

Ψ_LR = ψ_L + Ψ_R (T_W = 1/2) ,

(1)

ляр. Надо иметь минимум два типа “хиггсовских”

Ψ_RL = ψ_R + Ψ_L (T_W = 0) ,

скаляров (псевдо-) и соответственных юкавских

связей, порождающих массы ψ- и Ψ-частиц. Раз-

— дублетов и синглетов слабого изоспина T_W .

личие их масс должно следовать из существования

В (1) мы опустили все другие квантовые числа:

различных минимумов потенциала V (ϕ₁, ϕ₂) ска-

флейворы u (up)

d (down), индексы поколений n,

лярных полей.

n^′ = 1, 2, 3 и др. Формула (1) представляет массив-

Прежде чем перейти к конкретному построению

ные дираковские фермионы — кварки и лептоны.

подходящей модели, остановимся на некоторых

Зеркальным преобразованием называем тож-

существенных особенностях выбранного стандарт-

дественную операцию, заведомо оставляющую

ного пути (положительных и отрицательных) спон-

лагранжиан инвариантным:

танного нарушения с помощью скалярных вакуум-

ных средних.

R ↔ L, ψ ↔ Ψ.

(2)

Задача сильной юкавской связи становится

Кинетическая часть и любое калибровочное взаи-

здесь основной: очень тяжелые фермионы есть

модействие СМ записываются через операторы (1)

неотъемлемая часть общей системы. Конечно, мы

и автоматически, благодаря киральным свойствам,

не можем ее решить. Более того, непосредственно

разделяются на Ψ- и ψ-части. Слабое взаимо-

в лагранжиане (см. далее (10)) только тяжелые

действие порождается векторным током дублетов

зеркальные Ψ взаимодействуют с наблюдаемым

Ψ_LR и тоже есть сумма Ψ_R и ψ_L токов. ЗС-

скаляром H. Но будет показано, что при этом

взаимодействия со скалярами, которые определя-

механизм образования масс (разд. 3) сохраняет

ют свойства спектров масс, рассматриваются в

для “легких” дираковских фермионов СМ обычное

разд. 3. Но сами массы состояний (1) непосред-

пертурбативное (при существующих массах и

ственно включаются в ЗС-лагранжиан:

вакуумном среднем η ≈ 246 ГэВ) взаимодействие

с хиггсовской частицей H (константа связи h ∼

L₀ = L_SM (Ψ_LR,Ψ_RL) + AΨLRΨ_LR +

(3)

∼ m/η). Это свойство является прямым след-

+BΨRLΨ_RL,

ствием инвариантности системы относительно

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

СТРУКТУРЫ МАТРИЦ СЛАБОГО СМЕШИВАНИЯ

323

(

)_n′

)

слабого изоспина SU(2) и не требует никаких

⁽Ψn

+ h(u)

γ₅,ϕc2

Ψ(u)RLn′ + c.c. +

дополнительных предположений.

(

)_n′

Получается, что, создав СМ, “природа” (в на-

)

⁽Ψn

+ h

,ϕ₁

Ψ(d)RLn′ +

шей модели) как бы отделила пертурбативную

часть большой общей системы³⁾. Все константы

(

)_n′

)

⁽Ψn

связи остаются здесь в пертурбативной области.

+ h

γ₅,ϕ₂

+ c.c.

RLn^′

Для этой цели частицы СМ следовало оторвать

от зеркальных состояний. Сильная взаимосвязь

В формуле (7) выписаны все значки состояний,

обеих частей должна отсутствовать. Это осуществ-

характеризующие использованную систему: флей-

ляется двумя важными наблюдаемыми особенно-

вор f = u

d, индексы поколений n, n^′ = 1, 2, 3.

стями СМ.

Круглые скобки (Ψ, ϕ) обозначают произведения

1. Хотя полная система — частицы СМ + зер-

изодублетов, ϕ^c = iσ_yϕ⁺. В дальнейшем, чтобы

кальные поколения (L, R-симметричная систе-

не загромождать формулы, большинство значков

ма) — не имеет киральных аномалий, [17], ее низ-

будем опускать. Матрицы h могут быть произволь-

коэнергетическая часть (СМ), как известно, сама

ными.

по себе лишена аномалий и поэтому перенорми-

Подставим в (7) выражения операторов (1) и

руема и может быть пертурбативной. Имеет место

получим:

сложное сокращение кварковых и лептонных ано-

]

мальных вкладов. Отсутствие низкоэнергетическо-

L^′ = h₁

^[(Ψ_R,ϕ₁) Ψ_L + (ψLϕ1)ψR

(8)

го сокращения означало бы сильную связь всех

[

]

+h₂

⁽Ψ_R,ϕ₂) Ψ_L + (ψL,ϕ2)ψR

+...=

этажей системы, при которой значительный разрыв

состояний не мог бы осуществиться.

⁽Ψ_R,[h₁ϕ₁ - h₂ϕ₂]⁾ Ψ_L +

2. Малая масса хиггсовского бозона (m_H ≈

)

ψ_L,[h₁ϕ₁ + h₂ϕ₂]

ψ_R + ...

≈ 126 ГэВ, [15]) не только сохраняет пертурба-

тивную унитарность в процессах с участием про-

Условием тождественности систем Ψ и ψ после

дольных векторных бозонов (m_H < 1 ТэВ), но и

нарушения зеркальной симметрии является равен-

обеспечивает пертурбативность самодействия ска-

ство матриц h_i:

ляров λ (V = λφ⁴, m_H < 0.5 ТэВ). Большие массы

h₁ ≡ h₂ = h.

(9)

бозона H также приводили бы к сильной связи с

состояниями высоких энергий.

В этом случае “миры” легких частиц, возникающих

В заключение этого раздела отметим, что вы-

в разных вариантах спонтанного нарушения ЗС,

бранная нами система ЗС отвечает на вопрос, не

действительно (см. (12)), абсолютно одинаковы

находящий ответа при других схемах [3], — дей-

(за исключением слабых свойств R ↔ L). Тогда

ствительно ли все зеркальные частицы тяжелее

лагранжиан (8) приобретает вид

частиц СМ. Прилагаемый механизм воспроизводит

)

МСС только при участии в процессе образования

L^′ = h

⁽Ψ_R,Φ₁) Ψ_L + h⁽ψL,Φ2

ψ_R + ... ,

(10)

массовых матриц СМ очень тяжелых зеркальных

Φ₁ = ϕ₁ - ϕ₂, Φ₂ = ϕ₁ + ϕ₂.

фермионов с массами, много большими масс ча-

стиц СМ.

В ЗС-мире операторы Φ₁ и Φ₂ не имеют опре-

Но происхождение иерархии масс дираковских

деленной четности. Но в разрешенной зеркальной

фермионов самой СМ, окончательный убедитель-

симметрии эта черта не вносит в свойства систе-

ный выбор причин этого явления остаются неопре-

мы ничего нового. Так же, как в СМ, одни и те

деленными (см. [10] и Приложение 2).

же бозоны Φ₁ и Φ₂ порождают юкавскую связь

и для кварков, и для лептонов. Это необходимо,

3. МОДЕЛЬ СПОНТАННОГО НАРУШЕНИЯ

чтобы не увеличивать число голдстоуновских фаз

ЗЕРКАЛЬНОЙ СИММЕТРИИ

бозонных SU(2) дублетов. Трех фаз одного из Φ₁-,

В соответствии с выводами разд. 2 рассмотрим

Φ₂-операторов, развивающего вакуумное среднее,

юкавские связи зеркально-симметричных опера-

достаточно для утяжеления всех трех слабых век-

торов (1) с комплексными изодублетами ϕ₁ (ска-

торных бозонов W_μ.

ляр) и ϕ₂ (псевдоскаляр). Имеем в полной аналогии

В качестве потенциала для скаляров V (Φ₁, Φ₂)

с СМ:

возьмем Φ₁, Φ₂ — симметричное выражение, по-

(

)_n′

)

(u)

строенное в полной аналогии с СМ:

⁽Ψn

L^′ = h(u)

,ϕc1

(7)

RLn^′

V (Φ₁, Φ₂) = κ|Φ₁|²|Φ₂|² -

(11)

³⁾Сильные взаимодействия кварков не играют роли в обра-

)

ρ² (

λ⁽

зовании фундаментальных масс. На очень малых рассто-

|Φ₁|² + |Φ₂|2

|Φ₁|⁴ + |Φ₂|4

яниях их роль незначительна.

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

324

ДЯТЛОВ

[

)

]

)1/2

При больших κ самые глубокие минимумы V раз-

∑

(( μ_ψ

ψ_μ =

ψ+O

Ψ .

деляют систему одновременно по Φ₁ и Φ₂ и по Ψ, ψ.

M_Ψ

Имеем решение (11) для вакуумных средних:

μ_ψ — величины порядка масс фермионов СМ μ_ψ ≪

〈Φ₂〉 = 0,

〈Φ₁〉² =

=η²,

(12a)

≪ M_Ψ. В правой части (15) подразумеваются сум-

мы по индексам поколений. Тогда взаимодействие

h_ψ

ψ_μψ_μΦ₁ появляется с константой связи, обыч-

〈Φ₁〉 = 0,

〈Φ₂〉² =

(12б)

ной для СМ. Имеем из формул (10) и (15):

)1/2 (

)1/2

⁽ μ

μ_ψ

h_ψ = h^ψ

∼

(16)

В интересном для СМ варианте (12а) оператор

M_Ψ1

M_Ψ2

Φ₁ представляет систему из одного нейтрального

M_Ψ μ_ψ

μ_ψ

скаляра H (хиггсовский бозон СМ) и голдстоунов-

∼

ских фаз, идущих на утяжеление W -бозонов. При

η M_Ψ

этом “древесная” масса другого бозона Φ₂, равная

Этот результат есть обязательное следствие сла-

бой SU(2)-симметрии.

ρ²

M^2Φ

=κ

(13)

Действительно, симметрия означает, что в попе-

речной части пропагатора векторных бозонов

может быть сделана при больших κ как угодно

большой:

g_μν - (q_μq_ν) /q²

Δ_μν =

M2W - q²

κη² ≫

(14)

полюс при q² = 0 должен сокращаться в инва-

Оператор Φ₂ создает четыре скалярных состояния:

риантной калибровке с голдстоуновскими вклада-

два заряженных (±) и два нейтральных, как это

ми, образуемыми фазами скаляра Φ₁. Сокращение

должно иметь место во вкладах любых диаграмм

происходит в случае K,^K-мезонов.

взаимодействия фермионов ψ с W , что и происхо-

Теперь обсудим не очень приятное обстоятель-

дит благодаря соотношениям (15) и (16).

ство, связанное с необходимым присутствием в

развиваемом сценарии непертурбативного юкав-

ского взаимодействия. Если Φ₁ отождествить с

4. МАССЫ И МАТРИЦА СЛАБОГО

хиггсовским скаляром H, то величина 〈Φ₁〉 = η

СМЕШИВАНИЯ КВАРКОВ

определяется массой W -бозона (M_W = g_W η/2,

Лагранжиан (10) и вакуумное среднее (12а) по-

η ≃ 246 ГэВ). (Обратим внимание, что при спон-

рождают дираковские массовые члены зеркальных

танном возникновении, даже в присутствии силь-

частиц

ных взаимодействий, массы W определяются, в

L^′ = M_Ψ Ψ_RΨ_L +

(17)

основном, полюсным голдстоуновским вкладом.

Другие вклады в массовый оператор представляют

Вместе с массовыми матрицами A и B ЗС-

собой слабые поправки, пропорциональные факто-

(

)

состояний Ψ_LR и Ψ_RL из первоначального лагран-

ру

k²g_μν - k_μk_ν

, не имеющие полюса при k² =

жиана (3), которые после нарушения зеркальной

= 0.) Большая масса частиц Ψ означает поэтому

симметрии осуществляют переходы Ψ ↔ ψ:

большие значения h ≃ M_Ψ/η ≫ 1. Это фактиче-

L′0 = AΨLRΨ_LR + BΨRLΨ_RL =

(18)

ски останавливает дальнейшее количественное ис-

пользование предлагаемой схемы (см. [18]).

ψ_LΨ_R +

ψ_RΨ_L + c.c

В то же время взаимодействие стандартного

Из (17), (18) можно получить систему уравнений

хиггсовского бозона H с легкими фермионами СМ,

для массовых матриц частиц ψ.

ψ, совпадает с тем, что мы имели в СМ. Дело в

Для этого одну из систем матриц (в простран-

том, что, хотя хиггсовский скаляр Φ₁ в уравнении

стве поколений) — h_i из формул (3), (10) или A, B

(10) взаимодействует непосредственно только с

из (3), (18), следует взять диагональной. Это всегда

зеркальными состояниями Ψ, диагонализация мас-

можно сделать без потери общности лагранжиана.

совых матриц полной системы ψ, Ψ приводит к

Простейшая и наглядная система уравнений для

собственным функциям массивных состояний Ψ_M -

масс ψ возникает при диагональной форме матриц

и ψ_μ-типа (см. разд. 7 работы [11]):

h_i, т.е. когда матрицы M_Ψ в (17) есть диагональные

[

)

]

)1/2

матрицы с собственными значениями M_n, n = 0, 1,

∑

(( μ_ψ

Ψ_M =

Ψ+O

ψ ,

(15)

2, близкими (при M ≫ |A|, [13]) к массам тяжелых

M_Ψ

зеркальных фермионов (формула (15)).

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

СТРУКТУРЫ МАТРИЦ СЛАБОГО СМЕШИВАНИЯ

325

Массовая матрица легких частиц ψ получается

В низшем приближении по (21) имеем для μ_ψ опять

тогда двумя различными способами.

сумму сепарабельных матриц (19) — матрицу, об-

1. Диаграмма рис. 1 позволяет написать выра-

ратную (B⁺)-1MA-1. При этом пренебрегаются

жение для древесного приближения в виде суммы

поправки к массам (19) и волновым функциям (15)

сепарабельных матриц

порядка

∑

)

(M(f)LR)_a =

Aⁿ

B+(f)bn.

(19)

⁽A

⁽A² 1)1/2

^aMnf)

≈

(23)

n=0

M M

Формула (19) возникает, когда все |M_n| велики,

)1/2

⁽B² 1)1/2

⁽m_ψ

и в пропагаторах Ψ можно пренебречь импуль-

≈

(A ∼ B).

сами |p| ≃ m_ψ ≪ M. Тензоры A и B образуются

M M

тремя векторами в пространстве поколений: Aⁿ =

= (An1, An2, An3), то же для B, a, b = 1, 2, 3.

Эти величины считаем меньшими отношений масс

самих m_ψ (отношений иерархии масс поколений).

2. Выражения (17), (18) для каждого f = u

Поправки в (19), связанные с иерархией масс

представляют матрицы шестого порядка компо-

нент Ψ, ψ

(m_i/m_k), будем учитывать. Они определяют струк-

туру МСС, величину ее малых элементов, в то

Ψ_L

(20)

ψ_L

время как m_ψ/M можно считать малыми при очень



больших |M| .



Диагонализация матрицы (19) при иерархиче-

B⁺

^M

^Ψ

M_LR =



ском порядке малости ее членов n = 0, 1, 2 выпол-

_A

ψR

нена в работе [11] и в существенной части повторе-

на в Приложении 1. Найдены собственные значе-

с диагональной матрицей M.

ния и функции состояний в пространстве поколе-

M_LR (20) есть прямое обобщение массовой

ний. Представлены коэффициенты МСС кварков

матрицы see-saw-механизма на случай трех поко-

(матрица ККМ). Собственные значения, т.е. мас-

лений фермионов, если выполняется условие

сы наблюдаемых поколений, образуют иерархиче-

|M| ≫ |A| , |B| .

(21)

ский спектр при последовательно уменьшающихся

Помимо трех больших собственных значений

вкладах членов n = 0, 1, 2.

M_n ≈ M_n имеем три малых массы μ_ψ. Чтобы их

получить, найдем матрицу, обратную (20) [19]:

В низшем приближении по иерархии масс имеем



для каждого из поколений I, II, III (I — старшее по



A-1



M-1LR =

^.

(22)

массе):



(B+)-1 - (B⁺)-1 MA-1



(

)

(

)

1/2

D₂

|A₀|², |A₁|2

D1/2

|B₀|², |B₁|2

|A₀||B₀|

m_I =

m_II =

(24)

M₀

|A₀||B₀|M₁

(

)

(

)

1/2

D₃

|A₀|², |A₁|², |A₂|2

D1/2

|B₀|², |B₁|², |B₂|2

m_III =

(

)

(

)

D1/22 |A0|2, |A1|2

D1/2

|B₀|², |B₁|2

M₂

A_n и B_n — векторы-столбцы, образующие столб-

≫ m_II ≫ m_III в (24) может быть представлена уже

цы матрицы A и B, |A_n|, |B_n| — длины векто-

иерархией параметров

ров, D — детерминанты, определяемые формулами

M₀ ≪ M₁ ≪ M₂.

(25)

Приложения 1; формулы (24) возникают из формул

(П.13)-(П.15).

Но параметры A и B, определяющие массы до

Очевидно, иерархия масс поколений m_I ≫ нарушения ЗС, могут следовать той же закономер-

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

326

ДЯТЛОВ

ности. Поскольку иерархический спектр поколений

m_s, m_III → m_u, m_d, и введем углы βn

m между

проявляется у всех фермионов СМ⁴⁾, он может

векторами Bnf) = (B1n, B2n, B3n)(f).

быть общим свойством фермионных спектров (см.

Имеем для элементов МСС кварков (формулы

Приложение 2).

(П.22) и (П.23)):

Для понимания структуры МСС кварков (мат-



md

(

)

(

)

m_u

рица ККМ) существенно, что в низшем приближе-



|V_cd| =

f β

f β(u)

(29)

,

нии иерархии, т.е. при вычислении с учетом (25),

^m_s

m_c

собственные функции левых состояний матрицы

cos β₁₂ - cos β₀₁ cos β₀₂

f (β) =

(19) определяются только не зависящими от флей-

sin β₁₂ cos β₀₁₂

вора f = u

d векторами A₀, A₁, A₂. Для поколений

sin² β₀₁₂ =

I, II, III имеем ортонормированные векторы в про-

странстве поколений (формулы (П.19)-(П.21)):

cos² β₀₁ + cos² β₀₂ - 2 cos β₁₂ cos β₀₁ cos β₀₂

sin² β₁₂

φ_I ≃

A₀,

(26)

|A₀|

Здесь β₀₁₂ — угол между β₀ и перпендикуляром к

плоскости B₁, B₂. Для V_ts получаем

φ_II ≃



^×



(A⁺⁰,A1)

ms



1 -

A₀



d)_-mc



^A

|A₁|²



|V_ts| =

ctg β₀₁)

(ctg β₀₁)^u

(30)

.

^m_b (

m_t

(

)

A⁺,A1

× A₁ -

A₀

Для принятых отношений масс кварков [15]

|A₀|2

главные члены (29) и (30) — первые слагаемые в

правых частях формул — есть величины порядка

[

]

φ_III ≃

[

]

A⁺⁰,A⁺¹

m_d



A⁺⁰,A⁺

|V_cd| ∼

> |V_ts| ∼

m_s ,

m_s

(A⁺⁰, A₁) и [A⁺⁰, A⁺¹] — скалярное и векторное про-

что и соответствует наблюдаемым значениям мат-

изведения векторов; поколение I — самое тяжелое.

рицы ККМ. Общие выражения для элементов V_td и

Матричные элементы МСС есть скалярные

V_ub приведены в Приложении 1 — формулы (П.24)

произведения собственных векторов

и (П.25). Они не равны друг другу, поскольку в них

(

)

нет асимметрии u

d, как в (29) и (30). Не выпи-

V_mn ≡ φ(u)m,φ

(27)

сывая для V_td и V_ub сложных формул, аналогичных

(29) и (30), можно найти величины этих элементов

В низшем приближении МСС кварков V оказы-

МСС, используя условие ортогональности первого

вается единичной матрицей. Учет следующих при-

и третьего столбцов найденной матрицы. Имеем

ближений приводит к малым изменениям диаго-

V_tsV+cd ≈ V_td + V+ub.

(31)

нальных членов и к появлению отличных от нуля

малых недиагональных. В Приложении 1 найде-

Из формул (П.24) и (П.25) видно, что V_td и V_ub есть

ны выражения матричных элементов V с учетом

величины одного порядка малости, поэтому из (31)

необходимых приближений и для произвольных

и (32)

комплексных векторов A, B (|A|, |B| ≪ M). Для

ясности представления иерархии элементов V для

|V_td| ∼ |V_ub| ≃

m_d ,

(32)

m_b

флейворов u

d пренебрежем комплексностями A и

B, т.е. возможными фазами CP-нарушения (что не

т.е. величину, много меньшую |V_cd| и |V_ts|. Меха-

имеет значения для иерархии).

низм нарушения ЗС приводит к правильной иерар-

хии матрицы СКМ. Качественные свойства МСС

Из формул (П.22), (П.23) имеем в рассматри-

воспроизведены без численного подбора констант.

ваемом приближении соотношения матрицы МСС

кварков, предложенной Вольфенштейном [20]:

Обилие свободных параметров в формулах (24)

((П.13)-(П.15)) и (29), (30) (β(u) и β

d)) создает

V_ud ≃ V_cs ≃ V_tb ≃ 1,

(28)

возможность воспроизведения любых нужных чис-

V_cd = -V_us, V_ts = -V_cb.

ленных значений масс и V_ik. Их подбор поэтому не

представляет особого интереса.

В формулах Приложения 1 для малых элементов V

выделим комбинации констант (24), представляю-

Механизм образования массовой матрицы в

щие массы кварков — m_I → m_t или m_b, m_II → m_c,

ЗС-модели (рис. 1a) значительно проще исполь-

зования механизма недиагональных по поколени-

⁴⁾Возможно, за исключением нейтрино, см. разд. 5.

ям вакуумных средних скаляров (рис. 1б, [10]).

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

СТРУКТУРЫ МАТРИЦ СЛАБОГО СМЕШИВАНИЯ

327

Присутствие в рассматриваемой схеме массовых

Ортонормированные левые собственные функ-

матриц A и B представляется совершенно есте-

ции сепарабельной матрицы (19) в низшем прибли-

ственным.

жении по иерархии зависят опять только от векто-

ров A_n. При иерархии состояний (33), инверсной

по отношению к массам заряженных лептонов, эти

5. МАТРИЦА СЛАБОГО СМЕШИВАНИЯ

функции для состояний 1-3 совпадают с выраже-

ЛЕПТОНОВ (МАТРИЦА PMNS)

ниями (26) с заменой A₀ ↔ A₂. Имеем:

Наблюдаемый спектр масс нейтрино — два

близких по массе состояния “1, 2”, одно — “3” —

φ⁽⁰⁾¹ =

A₂,

(34)

N₁

удалено от них. Величины масс всех нейтрино

(

)

(

)

много меньше

(≲10-6) массы электрона. До

A⁺,A1

φ⁽⁰⁾² =

A₁ -

A₂

сих пор достоверно не установлено, является ли

N₂

|A₂|2

нейтрино “3” самым легким или самым тяжелым

[

]

(“нормальный” или “инверсный” характер спектра

φ⁽⁰⁾³ =

A⁺²,A⁺¹

[14, 15]). При предпочтительном для зеркального

N₃

механизма инверсном характере спектр нейтрино

кардинально отличается от спектра фермионов

Нормальная иерархия (25) заряженных частиц

СМ — кварков и заряженных лептонов.

сохраняет для таких лептонов собственные функ-

В то же время иерархия масс поколений пред-

ции (26): III → e, II → μ, I → τ, с теми же не

ставляется свойством, присущим всем фермионам.

зависимыми от флейвора векторами A, что и в

Механизмы его образования тогда не зависят от

(34). Скалярные произведения (27) для функций

квантовых чисел или взаимодействий (см. Прило-

(26) и (34) дают для лептонов (33) МСС, абсо-

жение 2). Что касается спектра масс легких ней-

лютно отличную от матрицы СКМ. В новой матри-

трино, то объяснение его отличия может быть свя-

це отсутствуют диагональные единицы и иерархия

зано с тем, что механизм нарушения ЗС приводит

недиагональных элементов.

для этих масс к сложной сепарабельной формуле

типа (24) со своими константами A, B, M (причем,

Таким образом, задача о лептонной МСС в зер-

A(ν) ≡ A(e), формула (4)). Их выбором измененный

кальном подходе может быть решена рассмотре-

спектр может быть воспроизведен и при иерархии

нием характеристик только заряженных лептонов,

параметров A, B, M, которые сами являются мас-

не касаясь юкавских или майорановских свойств

сами фермионных состояний до нарушения ЗС и

самих нейтрино: векторы A_n не зависят от ν, e-

параметрами ее нарушения. Ясно, что M(ν) должны

флейвора.

быть очень большими.

Чтобы определить взаимное расположение век-

Абсолютно не похожа на МСС кварков (мат-

торов A_n в пространстве поколений, достаточ-

рица СКМ) и МСС лептонов (матрица PMNS)

но рассмотреть как можно более произвольную

[15]. В настоящем разделе будет показано, что

матрицу масс зеркальных аналогов заряженных

матрица PMNS качественно воспроизводится в

лептонов. Найти диагонализующие ее матрицы и

ЗС-модели, если спектр масс нейтрино СМ яв-

выяснить, во что переходят при таком действии

ляется инверсным — состояние “3” самое легкое

диагональные матрицы

A, описывающие массы

по массе. Матричные элементы PMNS при этом

фермионов до нарушения ЗС.

определяются только свойствами системы заря-

женных лептонов и в главном порядке по иерархии

Матрицы зеркальных заряженных лептонов μ,

масс заряженных частиц не зависят от параметров

определяемые факторами h формулы (10), можно

системы нейтрино.

взять эрмитовыми (сохранение четности до нару-

Рассмотрим сначала инверсный спектр нейтри-

шения ЗС) и соответствующими, согласно (25),

но с простой иерархией масс (ν опускаем):

иерархии, инверсной по отношению к спектру за-

m₁ ≫ m₂ ≫ m₃.

(33)

ряженных лептонов СМ.

Иерархическая малость m₃ окажется необхо-

Далее, в реальной МСС лептонов [15] вклад

димым условием для согласования свойств МСС

нарушающих CP комплексностей незначительно

лептонов. Путь к рассмотрению наблюдаемого ин-

влияет на основную структуру матрицы. Поэтому

версного спектра

для простоты и наглядности трактовки рассматри-

ваем опять вещественную симметричную матрицу

m₁ ≈ m₂ ≫ m₃

(33’)

зеркальных аналогов заряженных лептонов (A_n —

лежит через решение задачи (33).

вещественные трехмерные векторы).

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

328

ДЯТЛОВ

Такая матрица с иерархией собственных значе-

С точностью до (m_i/M)² имеем для обоих вари-

ний может быть построена обобщением известного

антов (38):

see-saw-механизма [12] на систему трех состоя-

ний. Имеем:

(a): μ₂ = M + m²¹²/M,

(39)



M m1 m2

M m2 m1

(b): μ₂ = M + m²¹²/M,



μ=



∼



 ,

(35)

(a): μ₁ = m - m²¹/M,

m₁

m₂



(b): μ₁ = -m²¹²/M + m(m²¹/m²¹²),

m2



m1



(a): μ₀ = -m²²/M,

M≫m_i.

(

)

(b): μ₀ =

m²²/m²¹²

Матрица (35) выбрана так, чтобы в ней при-

сутствовал лишь один большой элемент (энер-

гетический масштаб). В дальнейшем выясняется,

Следует иметь в виду, что в случае (b) из (39)

что это единственно важная и необходимая черта,

следует

обеспечивающая появление свойств МСС лепто-

нов. Единственность большого масштаба может

m²

m²¹²

оказаться и весьма реалистичной особенностью

(b): m =

(40)

механизма образования иерархии масс поколений

(см. Приложение 2). Изменяя индексы поколений

так что в наших формулах (b)-варианта m ≪

у Ψ_LR и Ψ_RL, этот элемент можно поместить в

положение (1, 1).

≪ (m²¹²/M). Как и в случае see-saw-механизма,

знак массы для данного рассмотрения не имеет

Элементы (35), равные нулю, могли бы обо-

значения. Отличие двух вариантов (a) и (b) друг от

значать несущественные, малые по сравнению с

друга проявляется при M → ∞. В случае (a), кроме

учитываемыми, величины. Их выбор определя-

M → ∞, в формулах остается еще один конечный

ется также еще одним, подсказанным see-saw-

механизмом, условием иерархии — определитель

масштаб m. В случае (b) все массы, кроме M → ∞,

не содержит большого масштаба M. Матрица (35)

обращаются в нуль. Здесь вариант (b) полностью

приводит к характеристическому уравнению:

соответствует see-saw-механизму.

(-μ)³ + (-μ)² (M + m) +

(36)

(

)

Находя собственные функции для каждого из

+ (-μ)

Mm-m²¹²

- mm²² = 0,

корней вариантов (a) и (b), построим диагона-

лизующие (35) ортогональные матрицы U (опять

m²¹² = m²¹ + m²².

/M)²):

точность (m_i

Как известно, его коэффициенты выражаются че-



рез корни μ_i и равны последовательно:



m₁

m₂



μ₂ + μ₁ + μ₀,μ₂ (μ₁ + μ₀) +

(37)

m

m₁m₂



(a): U =

-1

;

(41)

+μ₁μ₀,μ₂μ₁μ₀,μ₂ ≫ μ₁ ≫ μ₀.



m₂

m₁m₂



-1



При больших M корни легко находятся из (36)

M mM

и (37) с любой точностью. При иерархии соб-

ственных значений порядок их величин опреде-



m₁₂

mm₁m₂

ляется отношениями соседних последовательных



коэффициентов (36). Системы корней зависят от



m³¹²



соотношений между слагаемыми в коэффициенте



m₂

m₁



(b): U =



при (-μ):



m₁₂



m₁

m₂



Mm > m²¹² (a), Mm < m²¹² (b).

(38)



m₁₂

Дальнейшие формулы выписываем для случая,

Начинаем с диагональной формы матрицы масс

когда неравенства (38) обозначают “много боль-

изодублетов

A₁

A₂

A₃) (3), преобразуем ее

ше” или “много меньше”. Не меняя существа про-

цесса образования свойств матрицы PMNS, упро-

с матрицей U:

AU⁺. Для векторов-столбцов A₂,

щение формул облегчает понимание исследуемого

A₁, A₀, входящих в формулу (19), для массовых

ЗС-механизма.

матриц лептонов ℓ и ν, имеем:

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

СТРУКТУРЫ МАТРИЦ СЛАБОГО СМЕШИВАНИЯ

329

A₂, e

π/2

, τ

A₀

A₁

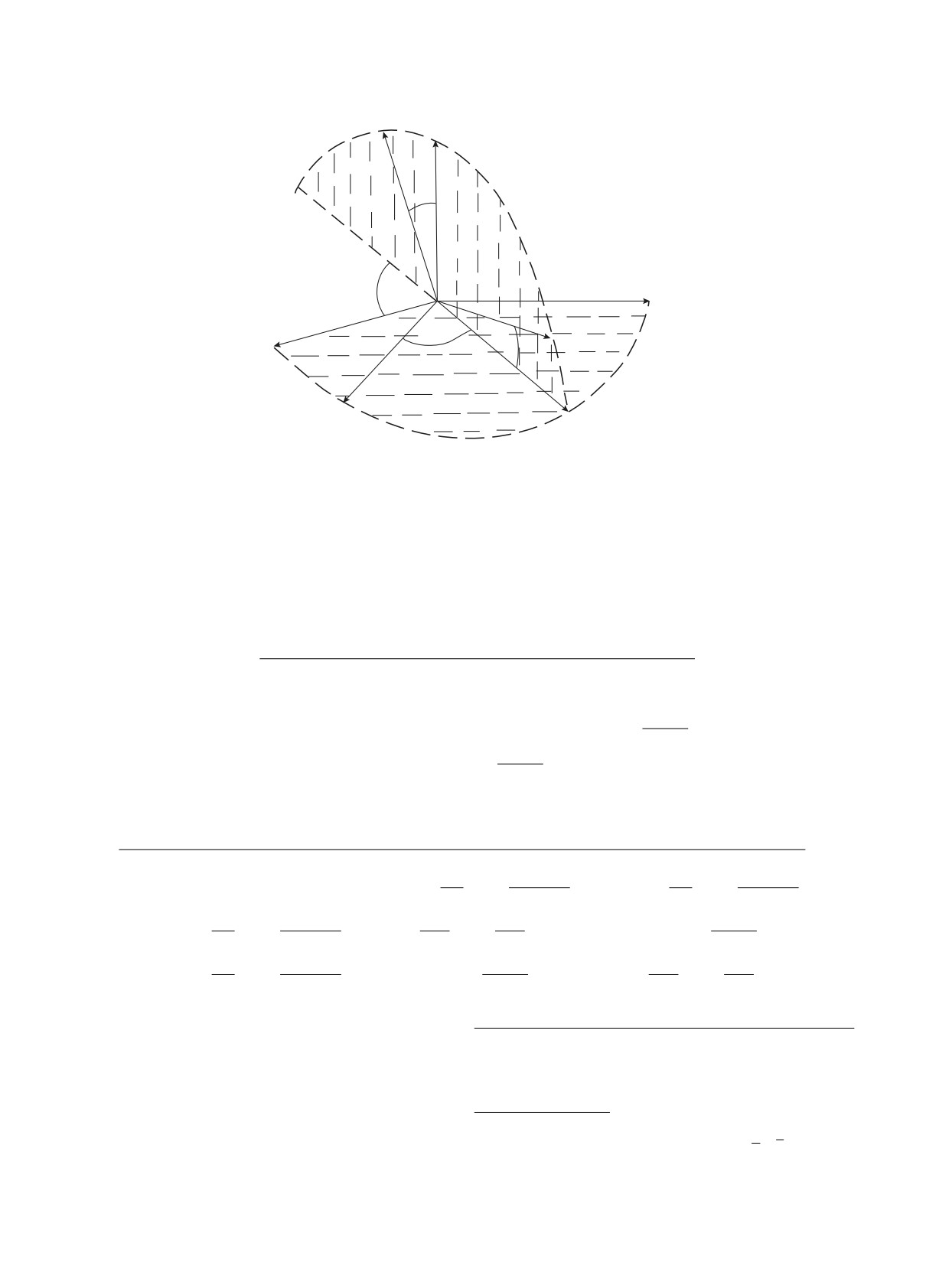
Рис. 2. Формирование “остова” МСС лептонов PMNS как поворота между осями, (46), в пространстве поколений:

A2⊥A0, A1, углы α, β — формулы (47), (48).

(а):



A₂

A₁

A₀



(

)

(

)



A₁

A₂

m₁/M

A₁

A₃

m₂/M



;

(42)

(

)

(



⁾m₁m₂



A₁

A₂

m₁/M

A₂

A₃

A₂



(

)

(



⁾m₁m₂



A₁

A₃

m₂/M

A₃

A₂

A₃



(b):



A₂

A₁

A₀



(



⁾m₂

m²¹m₂m

⁾m₁

m²²m₁m



A₁

A₂

+A˜₃

A₁

A₂

-A˜₃



m³¹²



(43)

(



⁾m₂

m²¹m₂m

m²¹

m²²

⁾m₁m₂



A₁

A₂

+A˜₃

+A˜₂

A₂

A₃



m³¹²

A₃ m²¹²

m²¹²



(



⁾m₁

m²²m₁m

⁾m₁m₂

m²²

m²¹



A₁

A₂

-A˜₃

A₂

A₃

+A˜₂



m³¹²

m²¹²

A₃ m²¹²

m²

В низшем приближении по иерархии масс для

единичной диагональной, что не подходит для об-

варианта (а) из формулы (42) имеем диагональную

разования матрицы PMNS⁵⁾

матрицу, т.е. ортогональные в пространстве индек-

⁵⁾Возможно, вариант (а) может иметь отношение к случаю

сов поколений векторы A_n. При любой иерархии

нормальной иерархии обоих флейворов u и d, т.е. к фор-

масс нейтрино МСС лептонов (27) оказывается

мированию матрицы СКМ у кварков.

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

330

ДЯТЛОВ

Для варианта (43) (b) в низшем приближении по иерархии получим матрицу



A2

A₁

A₀



A1



(



(44)



m²¹

m²²

⁾m₁m₂



+A˜₂

A₂

A₃



A₃ m²¹²

m²¹²



(



⁾m₁m₂

m²²

m²¹



A₂

A₃

+A˜₂



⁰



m²¹²

A₃ m²¹²

m²

Изобразим на рис. 2 векторы A_n из (44) и ор-

нулевого приближения. Результат хорошо изве-

тонормированные векторы (26) и (34), являющи-

стен — он сводится к повороту функций вырож-

еся в рассматриваемом приближении волновыми

денной задачи φ⁽⁰⁾¹ и φ⁽⁰⁾² на некоторый угол β₁₂ в

функциями частиц СМ. Напомним соответствие

их плоскости (рис. 2). В нашем случае эти функции

направлений (для разных иерархий масс у ν и ℓ):

совпадают с (34), они и для спектра (33’) не зависят

для ν :

(45)

от флейвора. Имеем:

ν₁ ∼ A₂, ν₂ ∼ A₁ - cosα₁₂A₂, ν₃ ∼ [A₁,A₂];

φ′1 = φ⁽⁰⁾¹ cos β₁₂ + φ⁽⁰⁾² sin β₁₂,

(47)

для l^± :

φ′2 = -φ⁽⁰⁾¹ sin β₁₂ + φ⁽⁰⁾² cos β₁₂.

τ ∼ A₀, μ ∼ A₁ - cosα₀₁A₀, e ∼ [A₀,A₁];

Угол β₁₂ есть функция параметров векторов A

α_ik есть углы между A_i и A_k. Согласно (44) вектор

и B(ν). Так что он зависит от флейвора ν. Но

A₂ ортогонален векторам A₀ и A₁, cos α₁₂ = 0. На

конкретный вид этой зависимости общую струк-

рис. 2 направим по A₂ ось Z.

туру матрицы V не изменяет и потому не имеет

Матрица смешивания есть матрица перехода от

здесь значения. После поворота (47) “остов” МСС

базиса ν к базису ℓ, (45). Очевидно, в рассматри-

лептонов приобретает вид

ваемом приближении имеем:



1



V =

(46)



0

cos α₀₁

sin α₀₁



cos β

sin β



V =



(48)



0 - sin α01 cos α01



− sin β cos α cos β cos α sin α



 μ



Формула (46) служила бы основной для МСС



 sin β sin α

- cos β sin α cos α

лептонов, если бы спектр нейтрино носил бы строго

иерархический порядок (33). Следующие прибли-

Здесь мы опустили индексы у углов α, β. Из (48)

жения приводили бы к малым величинам для эле-

видно, что элемент Ve3 = | sin θ₁₃| [15] будет отли-

ментов, равных нулю в (46), и малым изменениям

чен от нуля только при учете малых членов следую-

других элементов.

щих порядков иерархии масс. Оценка его величины

Для реального спектра (33’) необходимо сде-

требует учета не только известных отношений масс

лать еще один поворот координат на рис. 2 да-

заряженных лептонов [15]:

же для построения “основы” МСС в низшем по

m_l

m_μ

иерархии приближении. Дело в том, что ситуацию

≃

≃ 0.0018,

≃

≃ 0.056,

(49)

(33’) можно считать вырождением уровней “1, 2”

m_μ

207

m_τ

и решать задачу на снятие вырождения. Зада-

но и поправок к волновым функциям нейтрино (34)

ча исследовалась в первой работе [13], выяснены

условия на параметры A, B, которые приводят к

и (47), вызываемых неизвестной массой нейтри-

равенству масс m₁ ∼ m₂ в нулевом приближении

но m₃ ≪ m₁, m₂. Слишком малые поправки от

по иерархии, а также поправки, снимающие вы-

заряженных лептонов (49) могут оказаться недо-

рождение. Следующий шаг задачи — нахождение

статочными для описания наблюдаемого | sin θ₁₃| ∼

правильных волновых функций φ′1 и φ′2 опять-таки

∼ 0.14-0.16. Массы m₁, m₂ вычисляются здесь из

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

СТРУКТУРЫ МАТРИЦ СЛАБОГО СМЕШИВАНИЯ

331

наблюдаемых Δm2ik. Тогда:

Диагонализация массовых членов легких частиц

(19) практически не изменяет диагональности по

m₃

m₃ ≈ 0.01 эВ,

≲ 0.2,

(50)

поколениям электрослабых и других нейтральных

m1,2

по флейвору взаимодействий. Независимость ле-

m₁ ∼ m₂ ∼ 0.05 эВ,

вых функций (26) от флейвора в низших порядках

по иерархии масс и унитарность матриц преобра-

окажутся как раз подходящими. Остальные эле-

зований позволяет легко показать это.

менты V легко совмещаются с соответствующими

Хиггсовский бозон Φ₁(H) взаимодействует пря-

значениями элементов матрицы PMNS. Учет ма-

мо только с тяжелыми компонентами Ψ, а с лег-

лых поправок будет слабо влиять на остов (48).

кими ψ — через малые члены волновых функций

Малая величина m₃ ≪ m₁, m₂ является необ-

(15). Диагонализация юкавских констант (10) и

ходимым условием возникновения структуры (48).

матриц (19) приводит в низшем по иерархии масс

Отказ от малости потребовал бы включения в

приближении и к диагональному взаимодействию

волновые функции нейтрино (34) и членов (47),

легких СМ-состояний с хиггсовской частицей H.

определяемых не только факторами A. Экспери-

Недиагональные члены, а также правые токи могут

ментальная известность только разностей квадра-

и здесь появиться только в следующих порядках.

тов масс нейтрино оставляет такую возможность.

Второй хиггсовский бозон Φ₂ следует полагать

Но это означало бы и полное изменение результа-

очень тяжелым (выбор константы κ в форму-

тивной конструкции матрицы V .

ле (11)).

Недиагональные по поколениям связи зеркаль-

ных частиц с СМ-фермионами, появляющиеся в

6. ЗАКЛЮЧЕНИЕ

следующих порядках по иерархии масс, делают

зеркальные состояния нестабильными. В настоя-

Задача обсуждаемой модели — не развитие ди-

щее время дираковский и майорановский харак-

намики выбранной системы (3), (7), а подбор усло-

теры наблюдаемых нейтрино, нормальный или ин-

вий, способствующих появлению массовых матриц

версный тип их спектра окончательно не опреде-

фермионов, воспроизводящих как наблюдаемую

лены [14, 15]. Наше рассмотрение МСС лепто-

структуру спектров масс, так и свойства соответ-

нов представляет аргументы в пользу дираковского

ствующих МСС. Главная обычная причина вы-

нейтрино и инверсного спектра. Для майоранов-

бора ЗС-подхода — разрешение парадокса с воз-

ского нейтрино предлагаемый механизм образова-

можным физическим определением право-лево в

ния матрицы PMNS представляется невыполни-

СМ. Легкость воспроизведения свойств МСС при

мым, поскольку требует ряда дополнительных, ни

этом представляется весьма привлекательной. Для

откуда не следующих условий на константы модели

невыразительных характерных черт МСС лептонов

(в частности, одновременной совместной диагона-

трудно подобрать ответственные за их появление

лизации майорановской и дираковской частей масс

динамические механизмы. Сценарий спонтанно на-

зеркальных нейтрино, равенства матриц A = B(ν)

рушенной ЗС предлагает путь к пониманию их

и др.).

возникновения.

Для предложения действительно реальной ди-

Приложение 1

намической схемы, конечно, требуются дополни-

тельные обсуждения. Очень большие массы зер-

кальных аналогов частиц СМ, очевидно, могли бы

А. ВЫЧИСЛЕНИЕ СПЕКТРА МАСС

значительно уменьшать их влияние на процессы

СМ. В то же время в рассматриваемом механизме

Упростим написание суммы сепарабельных

нарушения ЗС (10) реальный хиггсовский бозон

матриц (19), включив величину 1/

n в параметр

H непертурбативно связан с зеркальными ферми-

Bnf). Массовую матрицу (19) рассмотрим в форме

онами: h = M/η ≫ 1, M ≫ η = 246 ГэВ. Но это же

сильное взаимодействие H позволяет надеяться,

∑

что их роль в рождении хиггсовского бозона (через

(M_LR)^ba = A^naB+bn.

(П.1)

петли виртуальных зеркальных фермионов) будет

n=0

существенно ослаблена [18]. Переходы легких СМ

Из произвольной матрицы M построим эрмитов-

частиц в зеркальные состояния (параметры A, B)

скую

должны оставаться пертурбативными.

(

)_a

′

(

)_a′

Все же механизм нарушения ЗС, предложенный

MM⁺

= (M_LR)^ba

M⁺

(П.2)

LR b

здесь, можно рассматривать как удобный механизм

∑

для наглядного представления заложенных в ЗС

= A^naB+bnBn′bA

′

n,n^′

(помимо главной цели) возможностей.

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

332

ДЯТЛОВ

Сепарабельная форма приводит к тому, что (П.2)

миноров) + det MM⁺ = 0,

есть произведение матриц, построенных на проек-

где след матрицы равен (располагаем вклады по

циях векторов A_n, B_n, n = 0, 1, 2, в пространстве

степеням малости в соответствии с (25) (|B₀| ≫

индексов поколений a, b = 1, 2, 3:

(

)

≫ |B₁| ≫ |B₂|):

MM⁺

= Δ3 (A₀,A₁,A₂) ×

(П.3)

(

)

×Δ₃

B⁺⁰,B⁺¹,B⁺²

Δ₃ (B₀,B₁,B₂) ×

Tr MM⁺ = |A₀|²|B₀|² +

(П.9)

(

)

[(

)(

)]

×Δ₃

A⁺⁰,A⁺¹,A⁺²

;

+ 2Re

A⁺¹,A₀

B⁺⁰,B₁

+ |A₁|²|B₁|² +

[(

)(

)]

здесь матрица Δ₃ равна

+ 2Re

A⁺²,A₀

B⁺⁰,B₂



[(

)(

)]



+ 2Re

A⁺²,A₁

B⁺¹,B₂

+ |A₂|²|B₂|².

A⁰¹ A¹¹ A²¹



Δ₃(A₀,A₁,A₂) =



A⁰² A¹² A²²

 ,

(П.4)

Сумма главных миноров равна:



∑

(

)

A0

A¹³ A²³



= D₂ |A₀|²,|A₁|2

(П.10)

(

)

(

)

Δ₃

A⁺⁰,A⁺¹,A⁺²

= Δ+3 (A₀,A₁,A₂).

× D₂ |B₀|2 ,|B₁|2

Любые миноры и определитель сепарабельной

[

(

))

матрицы, например, (П.1), есть опять произведе-

+ 2Re D₂

|A₀|²,

A⁺¹,A₂

ние определителей соответствующего порядка. Это

(

))]

следует из формулы для произвольного минора N-

× D₂ |B₀|²,

B⁺²,B₁

го порядка (с произвольным числом индексов)

[

((

)

(

))

+ 2Re D₂

A⁺⁰,A₁

A⁺¹,A₂

ε_aa′a′′ ... M^aMa′′ ...

εa1a₂a₃ ... M+a1b×(П.5)

((

)

(

))]

×D₂

B⁺¹,B₀

B⁺²,B₁

′

′′

×M

(

)

(

)

Так как все a, a^′, a^′′, . . . обязательно разные, то и

+ D₂ |A₀|²,|A₂|2

D₂

|B₀|² ,|B₂|2

b, b^′, b^′′, . . . (равно как и индексы n, n^′ из (П.2))

[

)

((

)

тоже разные. При сепарабельной структуре M

+ 2Re D₂

A⁺⁰,A₁

, |A₂|2

выражения (П.2) образуют произведения матриц

)]

((

)

Δ_N и, следовательно, соответствующих им де-

×D₂

B⁺¹,B₀

, |B₂|2

терминантов D_N . В M и M⁺ индексы b везде

(

)

(

)

одинаковы, по ним идет суммирование, поэтому

+ D₂ |A₁|2 ,|A₂|2

D₂

|B₁|² ,|B₂|2

результат вычислений будет содержать матрицы

или определители типа

(

)

В формуле (П.10) определитель D₂ от скалярных

Δ₃ (B₀,B₁,B₂)Δ₃

B⁺⁰,B⁺¹,B⁺²

= (П.6)

произведений четырех векторов задается формулой

(

)



= Δ₃ |B₀|²,|B₁|²,|B₂|2 ,



(a, b) (c, b)

D₂ ((a,b) ,(c,d)) =



^.

(П.11)

где матрица Δ₃(|B₀|², |B₁|², |B₂|²) построена на



(a,d)(c,d)

скалярных произведениях векторов (B+i, B_k):

(

)

Наконец, определитель MM⁺ равен (см. (П.2)):

Δ₃

|B₀|², |B₁|², |B₂|2

(П.7)

(

)



(

) (

)

det MM⁺

= D₃ |A₀|2 ,|A₁|2 ,|A₂|2

× (П.12)



|B₀|²

B⁺⁰,B₁

B⁺

,B₂



(

)

(

)

(

)



× D₃ |B₀|2 ,|B₁|2 ,|B₂|2

B⁺¹,B₀

|B₁|²

B⁺

,B₂



(

) (

)



B⁺²,B₀

B⁺²,B₁

|B₂|²



Очевидно, формула (П.12) симметрична R ↔ L.

В аргументах матриц мы будем выписывать лишь

Для подтверждения заявленных в тексте свойств

диагональные элементы. По такому же принципу

МСС необходимо вычисление величин ρ_I, ρ_II и

построены матрицы и детерминанты при других N.

ρ_III с различной точностью. Для старшей массы

После этого легко выписываются коэффициен-

ρ_I требуется вычисление трех последовательных

ты характеристического уравнения матрицы (П.1),

порядков по теории возмущений

(25), а для

ρ=m²

меньших масс ρ_II и ρ_III достаточно двух порядков.

(

)

(-ρ)³ + ρ²

Tr MM⁺

- ρ(сумма главных (П.8)

В результате, имеем:

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

СТРУКТУРЫ МАТРИЦ СЛАБОГО СМЕШИВАНИЯ

333

[(

)(

)]

[(

)(

)]

m^2I = |A₀|² |B₀|² + 2Re

A⁺⁰,A₁

B₀,B⁺¹

+ 2Re

A⁺⁰,A₂

B₀,B⁺²

(П.13)

(

)

(

)

D₂

|A₀|² , |A₁|2

D₂

|B₀|² |B₁|2

+ |A₁|² |B₁|² -

+...

|A₀|² |B₀|²

(

)

(

)

D₂

|A₀|² , |A₁|2

D₂

|B₀|² ,|B₁|2

m^2II =

(П.14)

|A₀|² |B₀|²

[

{

(

)

(

)]

}

[(

)(

)]

2Re D₂(|A₀|² ,

A⁺¹,A₂)

,D₂(|B₀|²,

B⁺²,B₁)

2Re

A⁺⁰,A₁

B⁺,B0

+...

|A₀|² |B₀|²

D₂(|A₀|² ,|A₁|²)D₂(|B₀|² ,|B₁|²)

(

)

(

)

D₃

|A₀|² , |A₁|², |A₂|2

D₃

|B₀|² , |B₁|² , |B₂|2

m^2III =

(

)

(

)

(П.15)

D₂

|A₀|² , |A₁|2

D₂

|B₀|² , |B₁|2

⎧

[

(

⎫

(

))(

(

))]

⎨

2Re D₂

|A₀|² ,

A⁺¹,A₂

D₂

|B₀|² ,

B⁺,B1

⎬

(

)

+...

^×⎩1-

⎭

D₂(|A₀|² ,|A₁|²)D₂

|B₀|² , |B₁|²

Выражения перед фигурными скобками в (П.14)

и аналогично для x₂, 1 ↔ 2. Чтобы определить

и (П.15) представляют собой низшие, отличные

зависимость от индексов в числителе и знаменателе

от нуля приближения для каждой из масс II, III.

(П.17) сразу в трех порядках теории возмущений,

Первый член (П.13) есть приближенный квадрат

приходится расписывать по компонентам A^na мат-

старшей массы I. Все квадраты масс больше нуля.

ричные элементы M, а они содержат много членов.

Формулы для их низших приближений выписаны

Например,

в (24).

[(

)

M₁₃ = A⁰¹

B⁺⁰,B₀

(П.18)

]

(

)

(

)

B. СОБСТВЕННЫЕ ФУНКЦИИ

B⁺⁰,B₁

A⁺³¹ +

B⁺⁰,B₂

A⁺³

МАТРИЦЫ (П.2)

[(

)

(

)

Чтобы найти МСС (формула (27)):

+A¹¹

B⁺¹,B₀

A⁺³⁰ +

B⁺¹,B₁

A⁺³¹ +

(

)

(

)

]

[(

)

V_TS = φ(u)LT,φ

TS = I, II, III, (П.16)

B⁺¹,B₂

A⁺³

+A²¹

B⁺²,B₀

A⁺¹⁰ +

]

(

)

(

)

где T , S — номера физических поколений, I — са-

B⁺²,B₁

A⁺³¹ +

B⁺²,B₂

A⁺³² .

мое тяжелое, т.е. третье в стандартной нумерации:

(tb), (cs), (ud), необходимо найти левые собствен-

В волновых функциях φ_LS необходимо найти

ные функции φ_l операторов (19) или (П.1). Это

значительно более громоздкая задача, чем спектр,

три члена иерархии для S = I и по два члена для II

поскольку функции есть векторы в пространстве

и III. Вычисления приводят к следующим сравни-

индексов a, b. Они зависят не только от скалярных

тельно простым формулам для векторов состояний:

произведений, но и непосредственно от компонент

{

(

)

B⁺,B0

векторов.

φ_I =

A₀ +

(П.19)

Уравнения с равным нулю детерминантом опре-

|A₀|

|B₀|²

деляют отношение компонент векторов решений

(

((

)(

)))

2Re

A₀,A⁺¹

B⁺,B1

(здесь M ≡ MM⁺):

A₁ +

x₁

|A₀|² |B₀|2

(П.17)

(

)

}

x₃

B⁺,B

ρM₁₃ - (M₁₃M₂₂ - M₁₂M₂₃)

A₂

;

|B₀|2

ρ² - ρ(M₁₁ - M₂₂) + (M₁₁M₂₂ - M₂₁M₁₂

)

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

334

ДЯТЛОВ

(

)

|A₀|

φ_II =

(П.20)

V+cd = φ(I)+I,φ

III

(П.23)

(

(

))1/2 ×



[

]

 D₂

|A₀|² , |A₁|²



|A₀|(A⁺⁰,

A⁺¹,A⁺²

)

{

(

)

A⁺,A1

D₂(|A₀|² ,|A₁|²)

× A₁ -

A₀ -

{(

)

|A₀|²

D₂(|B₀|² ,(B⁺¹,B₂))

(

)

(

)

D₂(|B₀|² ,|B₁|²)

D₂

|A₀|² , |A₁|2

B⁺,B1

(

)

}

−

A₀ -

D₂(|B₀|² ,(B⁺¹,B₂))

|A₀|4

|B₀|²

(

))

[

]}

D₂(|B₀|² ,|B₁|²)

D₂

|B₀|² ,

B⁺,B1

A⁺⁰ [A₀,A₂]

(

)

Коэффициенты V_ts и V_cd — величины первого

|A₀|2

D₂

|B₀|² , |B₁|²

порядка по иерархии. Коэффициент следующего

порядка малости V_td равен:

(

)

φ_III =



(

)1/2 ×

(П.21)



(П.24)

D₂

|A₀|² , |A₁|²



V_td = φ(u)+I,φ

III

(

{((

)

{

(

))

(

[

])

)

D₂

|B₀|² ,

B⁺,B2

A⁺⁰,

A⁺¹,A⁺

B⁺,B2

[

]

[

]

(

))1/2

× A⁺⁰,A⁺¹

(

)

A⁺⁰,A⁺²

|B₀|2

D₂

|B₀|² , |B₁|²

|A₀| D₂

|A₀|² , |A₁|

}

⎛

⎞

((

)(

))

((

)

(

))

D₂

B⁺,B1

B⁺,B2

[

]

D₂

B⁺⁰,B₁

B⁺,B2

(

)

⎠

A⁺¹,A⁺²

+^⎝

(

)

−

D₂

|B₀|² , |B₁|²

D₂

|B₀|² , |B₁|

⎛

(

⎞

((

)

(

))

}

Квадратные скобки определяют векторные произ-

)

D₂

|B₀|² ,

B⁺,B2

B⁺,B1

ведения.

−

⎝

(

)

⎠

В этих формулах нормировочные множители

|B₀|2

D₂

|B₀|² , |B₁|2

выписаны лишь в наинизшем приближении. Этого

достаточно для наших целей. Именно поэтому в

Элементы V+ub = V_td(u

d) отличаются от (П.24),

низшем, отличном от нуля порядке, множители и

все φ_T зависят только от векторов A_n. Их ортонор-

поскольку симметрия (анти) u

d здесь отсут-

ствует:

мированность при условии (4) A^u ≡

^d приводит

(

[

])

к диагональным элементам V_TT ≃ 1. Недиагональ-

A⁺⁰,

A⁺¹,A⁺

ные элементы относятся к следующим порядкам

V+ub =

(

))1/2 × (П.25)

иерархии: они определяются не основными члена-

|A₀| D₂

|A₀|² , |A₁|²

{((

)

ми φ_T , а поправками, зависящими от B^u =

^d. Так

)

B⁺,B2

из иерархии массовой матрицы возникает иерархия

МСС. Очевидно, условие (4) играет здесь ключе-

|B₀|2

вую роль.

⎛

⎞

((

)

(

))

D₂

B⁺⁰,B₁

,B₂

+^⎝

(

)

⎠

C. МАТРИЦА СЛАБОГО СМЕШИВАНИЯ

D₁

|B₀|² ,|B₁|2

Формулы (П.19)-(П.21) позволяют вычислить

⎛

(

))⎞

скалярные произведения (П.16), образующие мат-

((

))

}

D₂

|B₀|² ,

B⁺,B2

B⁺,B1

рицу СКМ. Напомним, что, благодаря (4), u

⎝

⎠

(

)

отличают только правые факторы B_n.

|B₀|2

D₂

|B₀|² , |B₁|2

Имеем для величин, входящих в формулу МСС:

(

)

Формулу (П.25) мы выписываем, чтобы было легко

(П.22)

V_ts = φ(u)+I,φ

видеть ортогональность столбцов найденной мат-

1/2

рицы V , т.е. формулу (32).

D₂(|A₀|² ,|A₁|²)

В сумме V_td + V+ub собираем члены, относящиеся

|A₀|²

{(

)

}

(

)

только к флейвору u и только к флейвору

d, и

,B₁)

(B⁺⁰, B₁)

расписываем детерминанты:

;

((

)

(

))

|B₀|2

D₂

B⁺⁰,B₁

B⁺¹,B₂

(П.26)

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

СТРУКТУРЫ МАТРИЦ СЛАБОГО СМЕШИВАНИЯ

335

(

)(

)

(

)

B⁺⁰,B₁

B⁺¹,B₂

- |B₁|² ,

B⁺⁰,B₂

Масштаб нарушения киральной симметрии в си-

(

)

стеме n-фермионов определяется Tr M, где M —

D₂

|B₀|² ,|B₁|2

их массовая матрица. В гипотетическом характе-

(

)(

)

ристическом уравнении для масс другие его инва-

= |B₀|² |B₁|² -

B⁺⁰,B₁

B⁺¹,B₀

рианты при иерархическом спектре не будут пред-

ставлять общего масштаба явления.

Получаем произведение выражений (П.22) на

Сумма квадратов масс

(П.23), т.е. равенство

(31). Очевидно, мы не

∑

подбирали ни фаз, ни модулей параметров.

m2n = (Tr M)² -

2m_nm_n′

(П.28)

Что касается фаз, то, конечно, в формулах

′

n =n

(П.19)-(П.21) мы выбрали фазы функций φ(u) и

максимальна при очень большой массе только од-

d), чтобы в низшем порядке диагональные эле-

ной из частиц:

менты (φ(u)+, φ

d)) равнялись единицам. Неесте-

m₁ ≃ Tr M,m₂,m₃ ... ≪ m₁.

(П.29)

ственно было бы в этом месте (хотя и без послед-

ствий для физики) нарушать SU(2)-симметрию.

В формуле (П.27) используются энергии сво-

Для формулы (31) можно было и данные фазы

бодных частиц, суммы расходятся, но рассуждение

оставить произвольными. Общее число остающих-

имеет отношение и к точному дираковскому ва-

ся параметров в представлении массовой матри-

кууму системы — расходимость означает наиболее

цы (19) позволяет воспроизводить любые МСС,

значимый вклад от частиц очень высоких энергий,

включая фазы нарушения CP . Правильная иерар-

а для них роль взаимодействий ослаблена.

хия элементов матрицы СКМ автоматически воз-

Конечно, буквальное установление связи глу-

никает из иерархии масс кварков и следствий

бины вакуума с характером спектра частиц пред-

слабой SU(2)-симметрии, без прямого численного

ставляется нерешаемой задачей. Формулы (П.27)-

подбора параметров.

(П.29) следует дополнить условиями, препятству-

ющими нулевыми значениям других масс. Иерар-

Приложение 2

хический характер отношений между этими мас-

сами может быть связан также с энергетическими

причинами.

Для существования общей, заведомо не зависи-

мой от характера взаимодействий причины возник-

Представляется важным, что возникающая при

новения иерархического характера спектра масс

этом связь вакуума и спектра не зависит от свойств

фермионов есть веское феноменологическое ос-

взаимодействий.

нование: все наблюдаемые фермионы СМ (может

быть, за исключением нейтрино) имеют иерархиче-

СПИСОК ЛИТЕРАТУРЫ

ские спектры масс поколений.

1. T. D. Lee and C. N. Yang, Phys. Rev. 102, 290 (1956).

Теоретически иерархия масс обсуждается мно-

2. T. D. Lee and C. N. Yang, Phys. Rev. 104, 254 (1956).

го десятилетий. Наиболее известное направление

3. J. Maalampi and M. Roos, Phys. Rep. 186, 53 (1990).

начиналось с работы Фроггатта и Нильсена [21]

4. L. B. Okun, hep-ph/0606202; Phys. Usp. 50, 380

и продолжено ими [10], так и многими другими

(2007).

авторами [22]. Обширный список литературы на-

5. A. B. Kaganovich, arXiv: 2105.03878 [hep-ph].

ходится в более новой статье [23]. Речь в них идет

6. G. Triantophyllou, arXiv: 1609.03404 [physics, gen-

об изобретении таких взаимодействий и подборе их

ph].

свойств, которые при нарушении киральной сим-

7. P. Q. Hung, Phys. Lett. B 649, 275 (2007); Pai-Hong

метрии безмассовой системы способны воспроиз-

Gu, Phys. Lett. B 713, 425 (2012).

водить наблюдаемые иерархии масс.

8. S. Chakdar, K. Gosh, S. Nandi, and S. K. Rai, arXiv:

Мы хотим обратить внимание на возможную

1305.2641 [hep-ph].

связь характера спектра масс фермионов с глу-

9. H. Fritzsch, Phys. Lett. B 70, 436 (1977); 73, 317

биной дираковского вакуума системы. Для n-фер-

(1978).

мионов при приобретении ими масс вакуум стано-

10. C. D. Froggatt, M. Gibson, H. B. Nielsen, and

вится ниже на

D. J. Smith, hep-ph/9706212; C. D. Froggatt and

∑(√

)

H. B. Nielsen, hep-ph/9905445.

p2n + m2n - |p_n|

≃

(П.27)

11. И. Т. Дятлов, ЯФ 77, 775 (2014) [Phys. At. Nucl. 77,

p,n

733 (2014)]; arXiv: 1312.4339 [hep-ph].

12. R. N. Mohapatra and A. Y. Smirnov, hep-

^∑m2n

∑

ph/0603118; S. F. King, A. Merle, S. Morisi,

≃-

|p|

Y. Shimizu, and M. Tanimoto, arXiv:

1402.4271

[hep-ph]; L. Maiani, arXiv: 1406.5503 [hep-ph].

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

336

ДЯТЛОВ

13. И. Т. Дятлов, ЯФ 78, 522 (2015); 78, 1015 (2015);

18. И. Т. Дятлов, ЯФ 80, 253 (2017) [Phys. At. Nucl. 80,

84, 460 (2021) [Phys. At. Nucl. 78, 485 (2015);

469 (2017)].

78, 956 (2015); 84, 773 (2021)]; arXiv: 1502.01501;

19. F. Bernard, arXiv: 1611.0859 [hep-ph].

1509.07280 [hep-ph].

20. L. Wolfenstein, Phys. Rev. Lett. 51, 1945 (1983).

14. S. Gariazzo, M. Gerbino, T. Brickmann, M. Lattanzi,

O. Mena, T. Shwetz, S. R. Chouldhury, K. Freese,

21. C. D. Froggatt and H. B. Nielsen, Nucl. Phys. B

S. Hannestad, C. A. Ternes, and M. Tortola, arXiv:

147, 277 (1979); C. D. Froggatt, G. Lowe, and

2205.02195v1 [hep-ph].

H. B. Nielsen, Nucl. Phys. B 414, 579 (1994).

15. R. L. Workman et al. (Particle Data Group), Prog.

22. M. Leurer, Y. Nir, and N. Seiberg, Nucl. Phys. B 398,

Theor. Exp. Phys. 2022, 083C01 (2022).

319 (1993); 420, 468 (1994); hep-ph/9212298; hep-

16. И. Т. Дятлов, ЯФ 80, 368 (2017) [Phys. At. Nucl. 80,

ph/9310320.

679 (2017)]; arXiv: 1703.00722 [hep-ph].

23. M. Fedele, A. Mastroddi, and M. Valli, arXiv:

17. S. L. Adler, Phys. Rev. 177, 2426 (1969); J. Preskill,

Ann. Phys. (N.Y.) 210, 323 (1991).

2009.05587 [hep-ph].

WEAK MIXING MATRIX STRUCTURES AS A CONSEQUENCE

OF BROKEN MIRROR SYMMETRY

I. T. Dyatlov¹⁾

¹⁾“Kurchatov Institute” — PNPI, Gatchina, Russia

A model of symmetry violation is described for a system that can spontaneously choose left-handed or

right-handed weak current. For the hierarchic structure of the fermion mass spectrum, such a mirror

symmetry system allows reproduction of all qualitative properties of weak mixing matrices for both quarks

(CKM matrix), and leptons (PMNS matrix), and at that, without additional numerical fitting of model

parameters. The hierarchy of CKM matric elements is directly linked with the hierarchical mass spectrum

of quark generation. The qualitative properties of the PMNS matrix arise for the inverse character of the

spectrum (m₃ is the smallest mass) and Dirac nature of SM neutrino. The comparatively small value of the

neutrino mixing angle θ₁₃ is a consequence of the smallness of m₃ and the smallness of the charged lepton

mass ratio m_e/m_μ.

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023