ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 2, с. 345-352

ЯДРА

ИСПОЛЬЗОВАНИЕ ГЛОБАЛЬНЫХ ПРОГНОЗОВ СКОРОСТЕЙ

БЕТА-РАСПАДА В АСТРОФИЗИЧЕСКИХ МОДЕЛЯХ

Поступила в редакцию 06.11.2022 г.; после доработки 06.11.2022 г.; принята к публикации 10.11.2022 г.

В настоящей работе проведены расчеты нуклеосинтеза тяжелых элементов для двух разных сценариев

слияния нейтронных звезд. В расчетах были использованы различные глобальные модели бета-

распада: случайной фазы (QRPA), релятивистского приближения случайной фазы (pn-RQRPA) и

метод конечных амплитуд (FAM). Показано, что использование в расчетах нуклеосинтеза разных

глобальных моделей приводит к формированию реалистичной структуры кривой распространенности

химических элементов. В отличие от нуклеосинтеза в сценарии слияния нейтронных звезд одинаковых

масс образование элементов в веществе внешней коры при взрыве маломассивной нейтронной звезды

в области от первого до второго пика слабо модельно-зависимо. Однако в сильном r-процессе за-

висимость распространенности элементов от модели бета-распада очень сильная. Систематического

влияния модели бета-распада на результаты нуклеосинтеза не обнаружено.

DOI: 10.31857/S0044002723020162, EDN: RJVULC

1. ВВЕДЕНИЕ

и положение третьего пика на кривой распростра-

ненности тяжелых элементов [3], что указывает на

В нуклеосинтезе тяжелых элементов при слия-

многоплановое влияние модели бета-распада на

нии нейтронных звезд [1] участвуют короткоживу-

нуклеосинтез.

щие не изученные экспериментально ядра. Поэто-

Процессы образования элементов тяжелее же-

му для моделирования их образования необходимы

лезного пика в результате захвата нейтронов и

прогнозы большого количества ядерных характе-

последующего бета-распада были предложены до-

ристик, среди которых скорость бета-распада яв-

статочно давно одновременно с классификацией и

ляется наиболее важной величиной. Моделирова-

других процессов образования новых элементов в

ние распространенности тяжелых ядер с разными

природе [4]. Процесс образования тяжелых эле-

прогнозами ядерных данных фактически являет-

ментов в быстром нуклеосинтезе, поддерживаемом

ся интегральным экспериментом, в котором воз-

многократным захватом нейтронов, был назван r-

можности теоретических моделей могут быть про-

процессом, а первые расчеты r-процесса были

анализированы, используя расчеты и результаты

сделаны позднее [5]. В отличие от s-процесса,

наблюдений распространенности тяжелых элемен-

проходящего в среде с малым количеством свобод-

тов.

ных нейтронов, r-процесс происходит в веществе

с избыточной концентрацией нейтронов за счет

Количество синтезируемых в r-процессе тяже-

их многократного захвата и последующих бета-

лых элементов зависит как от длительности ней-

распадов при относительно невысокой температуре

тронной экспозиции, так и от скорости движения

(T₉ < 2) и замораживании реакций с протонами и

волны нуклеосинтеза. А скорость нуклеосинтеза

альфа-частицами. В этом r-процессе образуется

зависит от условий и области r-процесса, опреде-

более половины ядер тяжелее железа, в том числе

ляемых астрофизическим сценарием, и от скорости

актиниды.

бета-распада ядер, вовлеченных в r-процесс. При

С момента классификации процессов нукле-

ускорении или замедлении движения волны нук-

осинтеза [4] было предложено много разных сце-

леосинтеза в область более тяжелых ядер траек-

нариев и моделей r-процесса, создающих условия

тория r-процесса на карте ядер меняется [2], как

для его протекания, однако взгляд на теорию r-

процесса стал принципиально меняться после на-

¹⁾Национальный исследовательский центр “Курчатовский

блюдений химического состава в спектрах очень

институт”, Москва, Россия.

старых звезд и открытия идентичности относитель-

²⁾Московский физико-технический институт (националь-

ный исследовательский университет), Долгопрудный,

ной распространенности r-элементов в солнечной

Россия.

системе и в старых звездах [6]. Еще один сильный

^*E-mail: Igor.Panov@itep.ru

аргумент в пользу изменения взгляда на r-процесс

345

346

ПАНОВ

появился после осознания невозможности дости-

Поскольку при исследовании влияния скорости

жения высокой плотности свободных нейтронов

бета-распада на скорость распространения нукле-

при взрыве и эволюции большинства коллапсиру-

осинтеза и на распространенность тяжелых ядер

ющих сверхновых [7]. В последние годы, спустя

в r-процессе была отмечена сильная модельная

много лет после первого предложения рассматри-

зависимость распространенности как от исполь-

вать слияние нейтронных звезд в тесной двойной

зуемой модели бета-распадов [24], так и от ско-

системе [8] в качестве сценария для образования

рости нуклеосинтеза в целом [3], мы продолжили

тяжелых элементов, пришло понимание, подтвер-

изучение влияния модели бета-распада на процесс

жденное многочисленными исследованиями (см.,

образования тяжелых ядер, используя увеличенное

например, обзор [9]) и наблюдениями [10], что в

количество глобальных прогнозов бета-распада:

джетах и в ветрах, образующихся в конце эво-

1) метода случайной фазы (QRPA) [23], 2) реля-

люции тесной двойной системы нейтронных звезд,

тивистской pn-RQRPA [22] и 3) метода конечных

создаются необходимые для развития r-процесса

амплитуд (FAM) [21].

условия. В процессе первой регистрации грави-

В новом глобальном прогнозе периодов бета-

тационных волн, возникающих при слиянии ней-

распада [22] для полностью согласованных рас-

тронных звезд, и определении химического состава

четов T1/2 для описания основных состояний

разлетающегося вещества после взрыва килоновой

ядер как с заполненными, так и незаполненны-

[10], были обнаружены r-элементы [10, 11]. И на

ми оболочками, использовалась релятивистская

сегодняшний день, хотя все возможности развития

модель Хартри-Боголюбова, а для описания

r-процесса в природе до конца не определены, про-

возбужденных состояний применялся метод pn-

цесс слияния нейтронных звезд считается одним

RQRPA. Остаточное взаимодействие вычислялось

из основных реальных сценариев, в которых идет

на основе того же релятивистского функционала

синтез тяжелых элементов.

плотности ядерной энергии (RNEDF) [22], что и

для расчета основных состояний (для согласования

Периоды полураспада и вероятности запазды-

результатов описания различных ядерных харак-

вающих процессов обычно рассчитываются на ос-

теристик). Другой новый прогноз значений T1/2

нове силовой функции бета-распада S_β (E), по-

основывался на зарядово-обменной версии метода

лучаемой из разных теоретических моделей, как

конечных амплитуд [21].

например, широко используемая для астрофизиче-

Все эти три глобальных прогноза величин T1/2

ских приложений модель случайной фазы (QRPA)

были использованы для моделирования нукле-

[12], или других моделей, использующих разный

осинтеза тяжелых элементов в двух разных сцена-

вид функционала плотности ядерной энергии [13,

риях эволюции тесных двойных систем нейтронных

14] (подробнее см. [15]). В большинстве расчетов

звезд.

r-процесса (см. [16, 17] и цитирование там) наибо-

лее часто использовались глобальные расчеты [12,

18], основанные на развитых в 1980-е гг. моделях

2. СЦЕНАРИИ И МОДЕЛЬ

[19, 20].

НУКЛЕОСИНТЕЗА

В последние годы шло интенсивное развитие

В условиях высокой концентрации нейтронов

моделей бета-распада, что привело к появлению

нуклеосинтез в r-процессе может идти достаточно

новых глобальных расчетов этих важных харак-

долго, сотни миллисекунд. За это время волна

теристик [21, 22], расширяющих возможность, с

нуклеосинтеза может достичь области актинидов,

одной стороны, изучить устойчивость результатов

где начинается интенсивное деление тяжелых ядер.

моделирования процесса нуклеосинтеза к ядер-

Деление изменяет линейный характер нуклеосин-

ным данным, а с другой, попытаться оценить с

теза и в ряде случаев приводит к зацикливанию

помощью наблюдений надежность той или иной

r-процесса [25], т.е. к вовлечению большого числа

ядерно-физической модели для прогнозирования

ядер-продуктов деления в качестве новых заро-

характеристик экзотических ядер.

дышевых ядер в нуклеосинтез и к образованию

большинства тяжелых элементов от второго пика

Расчеты на основе функционала плотности DF3

на кривой распространенности элементов до то-

[14, 15], неплохо описывающие характеристики

рия и урана. Соответствующее увеличение реак-

нейтроноизбыточных сферических ядер, пока про-

ций, используемых в расчетах, таких, как скоро-

ведены только для части ядер, участвующих в r-

сти вынужденного, запаздывающего и спонтанного

процессе, и существующего количества данных по-

деления, а также массового распределения ядер-

ка недостаточно для использования их в расчетах r-

продуктов деления и учет осколков деления как но-

процесса. В настоящей работе в качестве базовых

вых зародышевых ядер [25-27], усложняет систему

данных использовались расчеты скоростей бета-

уравнений и процесс моделирования и требует оп-

распада на основе модели QRPA [23].

тимизации численных схем и алгоритмов.

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

ИСПОЛЬЗОВАНИЕ ГЛОБАЛЬНЫХ ПРОГНОЗОВ

347

Применение в расчетах различных прогнозов

код SYNTHER реакциями слабого взаимодей-

бета-распада изменяет как продолжительность

ствия, банк которых [38] содержит данные для

нуклеосинтеза, так и его динамику. Изучение

изотопов элементов железного пика (20 < Z < 32).

влияния моделей бета-распада на распростра-

ненность образующихся элементов было про-

Скорости реакций перечисленных процессов,

ведено с использованием данных по периодам

определяющие собственные значения матрицы

бета-распада, полученных на основе трех разных

Якоби системы дифференциальных уравнений,

глобальных моделей. Однако продолжительность

различаются по абсолютному значению на по-

нуклеосинтеза зависит также и от сценария, в

рядки. Поэтому система уравнений нуклеосинтеза

котором реализуются необходимые для протекания

является жесткой и для ее численного интегри-

r-процесса условия. Поэтому мы рассмотрели

рования нами использовался метод Гира [39], для

влияние модели бета-распада на r-процесс в двух

реализации которого был использован разрабо-

реалистичных сценариях, которые могут развиться

танный ранее пакет программ [40, 41]. В основе

в конце эволюции тесной двойной системы ней-

алгоритма лежит метод предсказания и коррекции

тронных звезд.

(предиктор-корректор) с автоматическим выбо-

В большинстве проведенных до сих пор мно-

ром шага и порядка точности метода, который

гомерных гидродинамических расчетах эволюции

реализован в обоих используемых нами кодах,

двойных систем массы нейтронных звезд были

имеющих внутреннюю проверку на сохранение

близки и достаточно велики M₁ ∼ M₂ ≳ M_⊙, и

числа нуклонов и заряда.

результатом их взаимодействия являлось слияние

или столкновение с образованием одной массивной

В область нуклидов, участвующих в нукле-

нейтронной звезды, джетов и ветров (см., напри-

осинтезе, включались все элементы с зарядом от

мер, [28, 29] и цитирование там). В таких услови-

Z_min = 1 до Z_max = 110, а A_min и A_max опреде-

ях протекает сильный r-процесс с образованием

лялись согласно используемой массовой модели:

широкого спектра тяжелых элементов вплоть до

обобщенной модели Томаса-Ферми с интегралом

актинидов [30-32].

Струтинского [42]. Тем самым определялось пол-

ное число ядер, участвующих в нуклеосинтезе.

При сильном различии масс нейтронных звезд,

входящих в двойную систему, происходит погло-

Скорости ядерных реакций, являющиеся коэффи-

щение маломассивного компонента более массив-

циентами в дифференциальных уравнениях, были

ным — вещество перетекает на более массивную

рассчитаны с использованием тех же массовых

звезду, пока маломассивная нейтронная звезда не

моделей. В список учитываемых ядерных реакций

достигнет нижнего предела массы, при котором

входят все парные и другие основные реакции

она становится нестабильной и взрывается [33].

горения, как и реакции альфа-распада, деления и

При взрыве маломассивной нейтронной звезды [33,

слабые взаимодействия. Они включают: все пар-

34] во внешней коре MH3 развивается слабый r-

ные реакции с нейтронами, протонами, альфа-

процесс [35].

частицами и гамма-квантами; бета-распад и бета-

запаздывающие процессы, такие, как испускание

Для численных расчетов r-процесса в этих двух

нескольких нейтронов при бета-распаде и запаз-

сценариях нами был применен код SYNTHER

дывающее деление; вынужденное и спонтанное де-

(nucleoSYNThesis of Heavy Elements in the R-

ление; ряд других важных реакций, таких как 3-α-

process) [36], реализующий кинетическую схему,

развитую ранее [37] и позволяющую определить

реакция и реакции горения¹²O,¹⁶O,²⁸Si.

концентрации всех вовлеченных в нуклеосинтез

Примененная схема позволяет эффективно рас-

ядер. В этом коде реакции деления были допол-

считывать нуклеосинтез в различных сценариях

нены улучшенной моделью массового распределе-

ния ядер-продуктов деления, что обеспечило бо-

при T₉ < 7 и плотности ρ < 10¹² г/см³. Основ-

лее распределенный источник новых зародышевых

ные расчеты сделаны с использованием широко

ядер и улучшение установления квазистационарно-

использующихся скоростей бета-распада и запаз-

го тока ядер.

дывающих нейтронов [23, 43], альфа-распада [43],

скоростей термоядерных реакций [44] и деления

Поскольку этап нуклеосинтеза, предшествую-

[36, 45, 46]. Экспериментально измеренные скоро-

щий r-процессу, протекает в рассматриваемых сце-

нариях при высоких температурах и плотностях

сти бета-распада взяты из ядерной базы данных

и является фактически взрывным нуклеосинтезом,

NuDat2 (2009) [47]. Скорость захвата нейтронов

коды нуклеосинтеза были дополнены реакциями с

тяжелыми ядрами (для элементов с Z > 83), а

заряженными частицами, а также ранее не учи-

также скорости вынужденного и запаздывающего

тывавшимся взаимодействием нуклонов и ядер с

деления были рассчитаны ранее на основе стати-

электронами [17]. Мы дополнили используемый

стической модели [45, 46].

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

348

ПАНОВ

lgY_A

-2

-3

-4

-5

-6

-7

-8

100

120

140

160

180

200 A

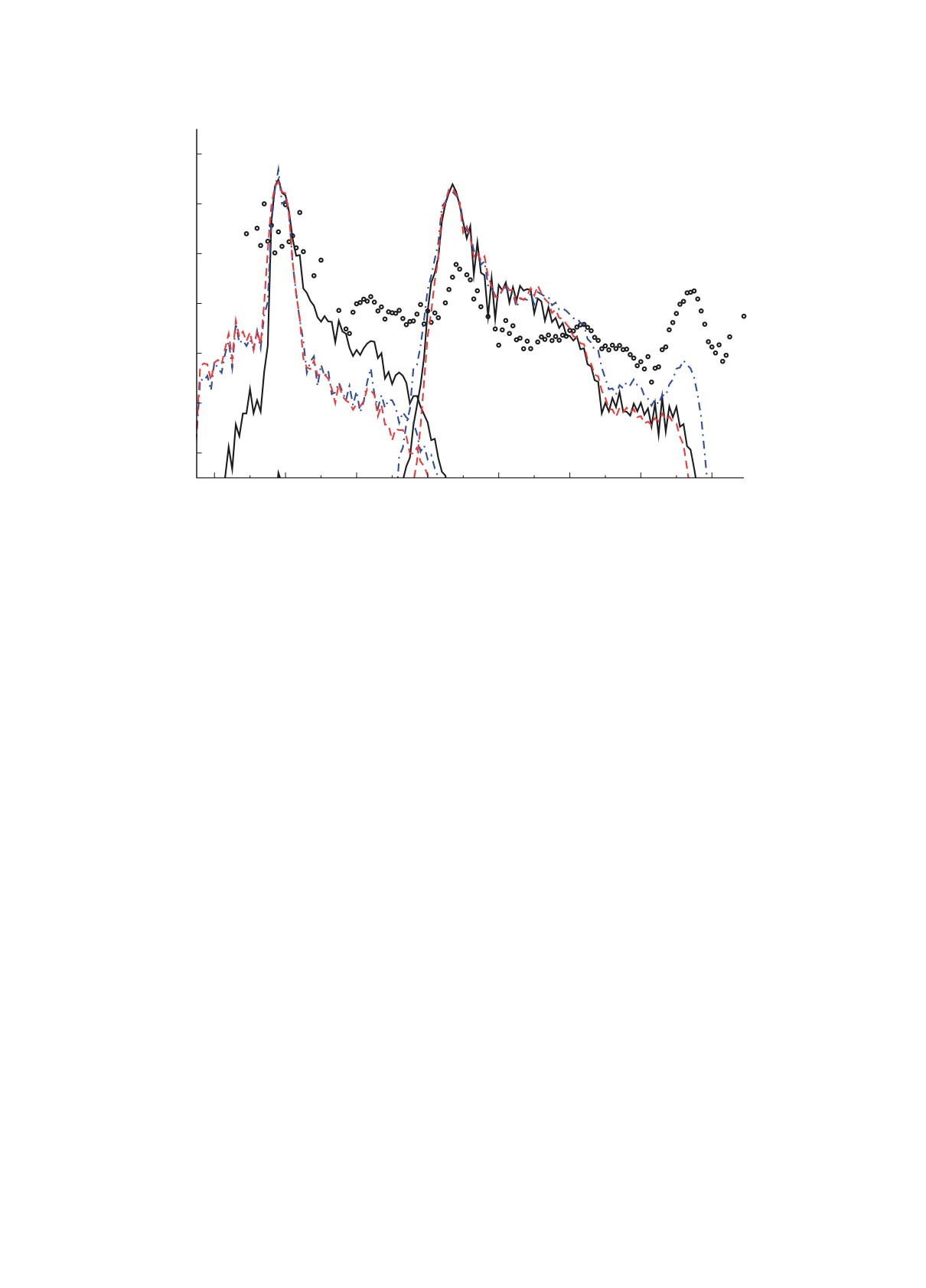
Рис. 1. Распространенность тяжелых элементов YA, образовавшихся в результате нуклеосинтеза при расширении

вещества внутренней коры взорвавшейся маломассивной нейтронной звезды, для вариантов № 1 (Ye = 0.297), № 9

(Ye = 0.359) с периодами бета-распада по прогнозам на основе метода случайной фазы (QRPA) [21] — сплошная кривая.

Значения Y (A), полученные в расчетах нуклеосинтеза с другими значениями периодов полураспада: релятивистского

приближения случайной фазы (pn-RQRPA) [22]

— штриховая кривая; метод конечных амплитуд (FAM) [21] —

штрихпунктирная. Шифр кривых — номер варианта.

3. ВЛИЯНИЕ ГЛОБАЛЬНЫХ ПАРАМЕТРОВ

чем вдоль траектории, бравшей начало в веществе

НА РЕЗУЛЬТАТЫ НУКЛЕОСИНТЕЗА

внешнего слоя (№ 1, Y0e = 0.350).

Рассмотрим сначала результаты расчетов r-

Кривые разных типов показывают результа-

процесса, использующие разные глобальные мо-

ты нуклеосинтеза — значения распространенности

дели бета-распада, полученные в сценарии взрыва

Y_A, полученные в расчетах, использующих различ-

маломассивной нейтронной звезды. Этот сценарий

ные прогнозы скоростей бета-распада. Видно, что

[33, 48] сейчас в развитии, и в настоящей работе

пики в области A ∼ 80, 130 почти не зависят от

мы рассмотрели нуклеосинтез только при разлете

глобальной модели, незначительное расхождение

внешней коры после взрыва нейтронной звезды. В

проявляется только в “хвостах” распространен-

веществе внешней коры реализовывается слабый

ности, в которых величина Y_A уменьшается на

r-процесс с образованием тяжелых элементов пре-

порядки.

имущественно в области от первого (A ∼ 80) до

Незначительность расхождения в величинах

второго (A ∼ 130) пиков. Результаты расчетов для

распространенности элементов становится понят-

наиболее удаленного от центра слоя внешней коры

ной из сравнения прогнозов периодов полураспада,

(№ 1) и самого внутреннего слоя внешней коры

представленных разными рассматриваемыми мо-

(№ 9) приведены на рис. 1. Рассмотренные слои,

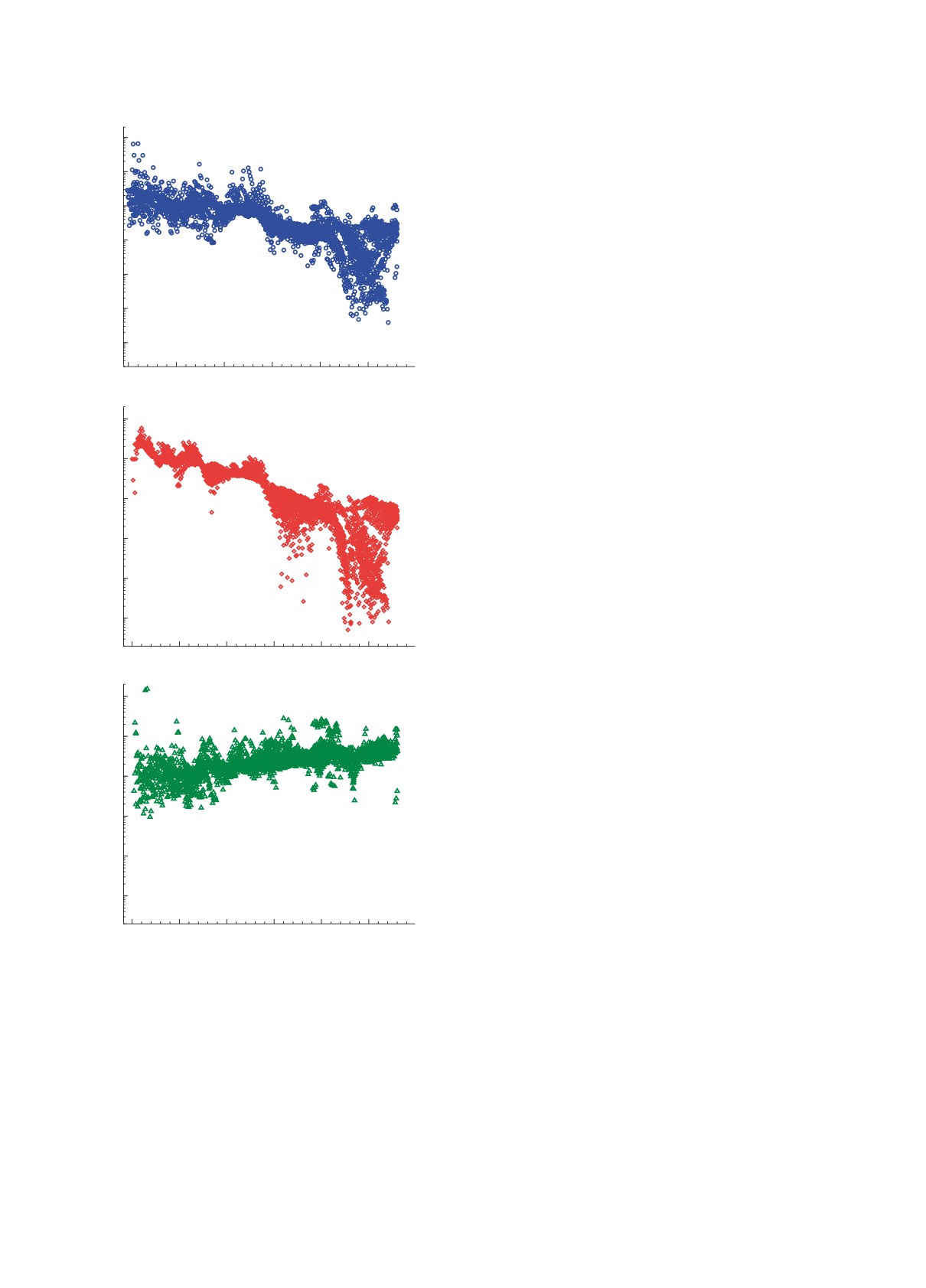
делями. Это видно из рис. 2, на котором приведены

согласно расчетам структуры нейтронной звезды,

отношения R_i периодов полураспада T1/2 для

перед взрывом [33, 35, 48] состояли из ядер одного

любых двух из трех рассмотренных прогнозов.

типа. Зародышевыми ядрами для нуклеосинтеза в

Значения T1/2 в основном различаются не более

слое № 1 был изотоп никеля⁸⁰Ni, а в слое № 9 —

чем в

раза для области ядер с массовыми

изотоп стронция¹²⁸Sr. Из-за большего различия в

числами от 80 до 150. Значения T1/2, полученные

составе зародышевых ядер в разных слоях (от № 1

в рамках модели pn-RQRPA [22], систематически

до № 9) атомный номер меняется от 78 до 128, а

становятся меньше прогнозов по другим моделям

заряд — от 28 до 38. В r-процессе, проходившем

с увеличением массового числа A, особенно в

при расширении самого внутреннего слоя (№ 9,

области A > 150. Скорость движения волны нук-

начальное отношение электронов к барионам Y0e =

леосинтеза в расчетах с этими данными ускоряется,

= 0.297), образовались более тяжелые элементы,

и появляется зародыш третьего пика (A ∼ 196).

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

ИСПОЛЬЗОВАНИЕ ГЛОБАЛЬНЫХ ПРОГНОЗОВ

349

R₁

При слиянии нейтронных звезд равных масс в

10²

одну массивную нейтронную звезду с выбросом в

окружающую среду образованных тяжелых эле-

10¹

ментов M_r(M_r ∼ 0.01-0.001 M_⊙) [49] зависимость

от модели бета-распада, как и отмечалось ранее

10⁰

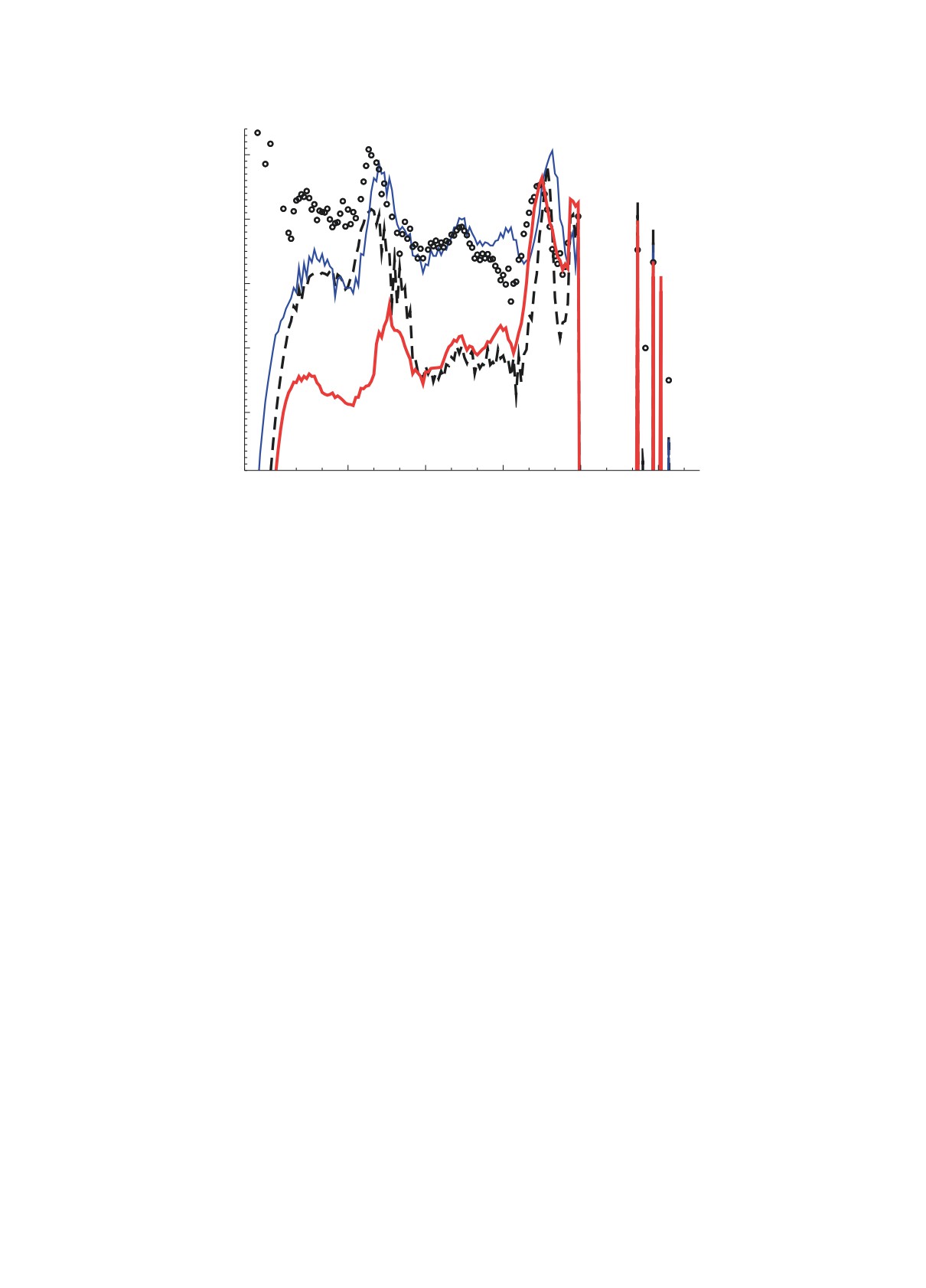
[24], очень сильная (рис. 3). Так, кривая 3 бы-

ла получена в случае применения модели FAM

10^-1

[21], прогнозирующей наибольшие значения T1/2. В

расчетах с такими данными после достижения вол-

10^-2

ной нуклеосинтеза области актинидов плотность

свободных нейтронов падает ниже минимально

10^-3

необходимой для поддержания r-процесса, а в ре-

10^-4

зультате деления образовавшихся актинидов обра-

зуется кадмиевый пик с распространенностью ядер

100

150

200

250

300

на три порядка меньше наблюдаемых значений. В

R₂

случае применения других ядерных данных [23],

прогнозирующих немного более короткие периоды

10¹

полураспада (см. рис. 2), выход элементов кад-

миевого пика увеличивается (кривая 1). И только

10⁰

в случае применения наиболее коротких периодов

бета-распада [22] устанавливается квазиравновес-

10^-1

ный ток ядер между кадмиевым и платиновым пи-

ками с вовлечением в нуклеосинтез ядер-продуктов

10^-2

деления как новых зародышевых ядер — кривая

2 на рис. 3. Закономерно, что различие между

10^-3

расчетными кривыми 3 и 1 на рис. 3 минимально,

поскольку и прогнозы периодов бета-распада для

10^-4

использовавшихся моделей очень близки (см. от-

ношение периодов полураспада R₃ на рис. 2в).

100

150

200

250

300

В результате сделанных расчетов проявился

R₃

еще один вопрос, обсуждавшийся ранее [50], — о

10²

возможной причине сдвига расчетного положения

третьего пика. Несовпадение положений наблюда-

емого и расчетного платинового пика отмечалось

10¹

разными авторами, изучающими процесс образо-

вания тяжелых элементов. Объяснения высказы-

10⁰

вались различные — от формирования отдельных

пиков в разных сценариях до недооценки величины

10^-1

эмиссии запаздывающих нейтронов или переоцен-

ки захвата нейтронов деления на стадии охлажде-

10^-2

ния [50]. Результаты данной работы подтверждают

наши предварительные выводы о зависимости по-

10^-3

ложения третьего теоретического пика от скорости

нуклеосинтеза [3]. Полученные в настоящей работе

100

150

200

250

300

результаты (см. рис. 3) также указывают на тенден-

Рис.

Отношения Ri прогнозов периодов

цию сдвига третьего пика в область больших атом-

бета-распада

короткоживущих (T1/2 < 1

с)

ных масс при уменьшении периодов бета-распада,

ядер, одной модели к другой: а

— R1 =

как было предположено ранее на основе парамет-

= T1/2(pn-RQRPA)/T1/2(QRPA) согласно гло-

рических расчетов с систематическим изменением

бальным данным на основе моделей pn-RQRPA

величин T1/2 [3].

[22] и QRPA

[23] соответственно; б

— R2 =

= T1/2(pn-RQRPA)/T1/2(FAM) согласно глобальным

данным на основе модели pn-RQRPA [22] и метода

4. ЗАКЛЮЧЕНИЕ

конечных амплитуд

[21] соответственно; в

—

R3 = T1/2(FAM)/T1/2(QRPA) согласно глобальным

Теоретические сценарии r-процесса [1], свя-

данным на основе метода конечных амплитуд [21] и

занные со слиянием нейтронных звезд в конце

модели QRPA [23] соответственно.

эволюции тесной двойной системы, недавно были

подтверждены наблюдениями спектров килоновой

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

350

ПАНОВ

lgY_A

-3

-4

-5

-6

-7

120

150

180

210

240

Рис. 3. Распространенность тяжелых элементов YA, образовавшихся в результате нуклеосинтеза при слиянии нейтрон-

ных звезд равных масс [49], полученных с использованием разных скоростей бета-распада. Кривые: 1 — QRPA [23], 2 —

[22], 3 — FAM [21].

после регистрации гамма-всплеска и гравитацион-

прогнозами периодов бета-распада показали су-

ных волн [10]. После многочисленных исследова-

щественно разную конечную распространенность

ний процесса слияния нейтронных звезд и реги-

элементов. Все полученные зависимости Y_A отра-

страции таких событий стало ясно, что сценарий

жают основные особенности интегральной кривой

слияния нейтронных звезд является основным для

распространенности тяжелых элементов, харак-

образования большинства тяжелых элементов в r-

терную для r-процесса, но скорость нуклеосинтеза

в каждом случае разная и поэтому накопление

процессе. Но эволюция нейтронных звезд в тесных

нуклидов происходит иначе. Различие в прогно-

двойных системах сильно зависит от их масс. Про-

зируемой распространенности Y_A возникает из-за

цесс слияния нейтронных звезд близких масс изу-

чен достаточно хорошо, но при сильном различии

больших различий в прогнозах разных глобальных

моделей для изотопов с массовым числом больше

масс нейтронных звезд сценарий слияния развива-

150, вклад которых в процесс нуклеосинтеза для

ется совсем иначе [33], приводя к иной динамике

сильного r-процесса очень значителен в том числе

развития нуклеосинтеза тяжелых элементов [34].

и из-за сильно различающегося вклада деления.

В настоящей работе влияние глобальных моде-

При использовании модели конечных амплитуд,

лей бета-распада на распространенность тяжелых

возможно, решается и проблема сдвига второго и

элементов было изучено для двух различных сцена-

третьего пиков, который присутствовал во многих

риев слияния нейтронных звезд — классического,

расчетах нуклеосинтеза разных авторов. Отсут-

рассматривающего слияние нейтронных звезд при-

ствие сдвига косвенно указывает на то, что периоды

мерно равных масс немного больше массы Солн-

бета-распада в области r-процесса должны быть

ца, и взрыва маломассивной нейтронной звезды,

немного длиннее, чем прогнозировалось ранее.

образующейся при эволюции тесной системы двух

Согласие между теоретической распространен-

нейтронных звезд существенно разных масс [33].

ностью, полученной с использованием глобальных

Для расчета распространенности элементов в этих

прогнозов скоростей бета-распада, при нуклеосин-

сценариях были использованы различные микро-

тезе во внешних слоях маломассивной нейтронной

скопические модели бета-распада: случайной фазы

звезды неплохое: все расчеты с разными глобаль-

(QRPA) [23], релятивистского приближения слу-

ными данными по T1/2 — pn-RQRPA, QRPA и

чайной фазы [22] (pn-RQRPA) и метод конечных

FAM — дают примерно одинаковую распростра-

амплитуд (FAM) [21].

ненность в области от первого до второго пиков.

Расчеты нуклеосинтеза в сценарии слияния

Это согласие закономерно, поскольку прогнозы

нейтронных звезд в веществе струй с различными

периодов полураспада для области образующихся

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

ИСПОЛЬЗОВАНИЕ ГЛОБАЛЬНЫХ ПРОГНОЗОВ

351

ядер с 60 < A < 150 очень близки. Показано, что

10.

N. R. Tanvir, A. J. Levan, C. Gonz ´alez-Fern ´andez,

использование в расчетах нуклеосинтеза разных

O. Korobkin, I. Mandel, S. Rosswog, J. Hjorth,

глобальных моделей бета-распада [21-23] при-

P. D’Avanzo, A. S. Fruchter, C. L. Fryer, T. Kangas,

B. Milvang-Jensen, S. Rosetti, D. Steeghs,

водит к формированию реалистичной структуры

кривой распространенности химических элементов

R. T. Wollaeger, Z. Cano, et al., Astrophys. J.

Lett. 848, L27 (2017).

в слабом r-процессе, проходящем во внешней коре

маломассивной нейтронной звезды при ее взрыве.

11.

D. Watson, C. J. Hansen, J. Selsing, A. Koch,

D. B. Malesani, A. C. Andersen, J. P. U. Fynbo,

И в отличие от нуклеосинтеза в сценарии слияния

A. Arcones, A. Bauswein, S. Covino, A. Grado,

нейтронных звезд образование элементов в обла-

K. E. Heintz, L. Hunt, C. Kouveliotou, G. Leloudas,

сти от первого до второго пика слабо модельно-

A. J. Levan, et al., Nature 574, 497 (2019).

зависимо.

12.

P. Moeller, J. R. Nix, and K.-L. Kratz, At. Data Nucl.

Сравнение расчетов T1/2 и P_n для различных

Data Tables 66, 131 (1997).

локальных групп ядер [51], важных для нуклеосин-

13.

I. N. Borzov, S. A. Fayans, and E. L. Trykov, Nucl.

теза, с использованием модели DF3a + CQRPA,

Phys. A 584, 335 (1995).

основанной на функционале Фаянса [15], показы-

14.

I. N. Borzov, Nucl. Phys. A 777, 645 (2006).

вает более высокую надежность расчетов ядерных

15.

И. Н. Борзов, ЯФ 83, 413 (2020) [I. N. Borzov, Phys.

характеристик по этому методу, и формирующаяся

At. Nucl. 83, 700 (2020)].

на его основе глобальная модель будет использо-

16.

K.-L. Kratz, K. Farouqi, and B. Pfeiffer, Prog. Part.

вана нами как в дальнейших расчетах нуклеосин-

Nucl. Phys. 59, 147 (2007).

теза в развиваемых сценариях, так и в оценках не

17.

И. В. Панов, ЯФ 81, 57 (2018) [I. V. Panov, Phys. At.

только модельной зависимости нуклеосинтеза, как

Nucl. 81, 68 (2018)].

в данной работе, но и для поиска групп ядер, наи-

18.

I. V. Panov, Yu. S. Lutostansky, and F.-K. Thi-

более сильно влияющих на образование элементов

elemann, J. Phys.: Conf. Ser. 665, 012060 (2016).

[52], что важно для планирования экспериментов

19.

В. Г. Алексанкин, Ю. С. Лютостанский, И. В. Па-

по изучению короткоживущих ядер.

нов, ЯФ 34, 1451 (1981).

Автор благодарит И.Н. Борзова, Ю.С. Люто-

20.

J. Krumlinde and P. Moeller, Nucl. Phys. A 417, 419

станского и А.В. Юдина за полезные обсуждения.

(1984).

Исследование применимости глобальных расчетов

21.

E. M. Ney, J. Engel, and N. Schunck, Phys. Rev. C

периодов бета-распада к расчетам r-процесса бы-

102, 034326 (2020).

ло выполнено при финансовой поддержке Россий-

22.

T. Marketin, L. Huther, and G. Martinez-Pinedo,

Phys. Rev. C 93, 025805 (2016).

ского научного фонда, грант № 21-12-00061.

23.

P. Moeller, B. Pfeiffer, and K.-L. Kratz, Phys. Rev. C

67, 055802 (2003).

СПИСОК ЛИТЕРАТУРЫ

24.

I. V. Panov, Book of Abstracts of the LXXI

International Conference “NUCLEUS-2021”, Ed.

1. J. J. Cowan, C. Sneden, J. E. Lawler, A. Aprahamian,

by V. N. Kovalenko and E. V. Andronov (VVM, Saint

M. Wiescher, K. Langanke, G. Mart

inez-Pinedo,

Petersburg, 2021), p. 269.

and F.-K. Thielemann, Rev. Mod. Phys. 93, 015002

25.

И. В. Панов, Ф.-К. Тилеманн, Письма в Аст-

(2021).

рон. журн.

29,

508

(2003)

[I. V. Panov and

2. И. В. Панов, Письма в Астрон. журн. 29, 163

F.-K. Thielemann, Astron. Lett. 29, 510 (2003)].

(2003).

26.

И. В. Панов, И. Ю. Корнеев, Ф.-К. Тилеманн,

3. И. В. Панов, Ю. С. Лютостанский, ЯФ 83, 349

Письма в Астрон. журн. 34, 213 (2008) [I. V. Panov,

(2020) [Phys. At. Nucl. 83, 613 (2020)].

I. Yu. Korneev, and F.-K. Thielemann, Astron. Lett.

4. E. M. Burbidge, G. R. Burbidge, W. A. Fowler, and

34, 189 (2008)].

F. Hoyle, Rev. Mod. Phys. 29, 547 (1957).

27.

И. В. Панов, И. Ю. Корнеев, Ф.-К. Тилеманн, ЯФ

5. P. A. Seeger, W. A. Fowler, and D. D. Clayton,

72, 1070 (2009) [I. V. Panov, I. Yu. Korneev, and

Astrophys. J. Suppl. 11, 121 (1965).

F.-K. Thielemann, Phys. At. Nucl. 72, 1026 (2009)].

6. C. Sneden, J. J. Cowan, I. I. Ivans, G. M. Fuller,

28.

S. Rosswog, U. Feindt, O. Korobkin, M.-R. Wu,

S. Burles, T. C. Beers, and J. E. Lawler, Astrophys.

J. Sollerman, A. Goobar, and G. Martinez-Pinedo,

J. 533, L139 (2000).

Class. Quant. Grav. 34, 104001 (2017).

7. L. H ¨udepohl, B. M ¨uller, H.-T. Janka, A. Marek, and

G. G. Raffelt, Phys. Rev. Lett. 104, 251101 (2010).

29.

S. Rosswog, T. Piran, and E. Nakar, Mon. Not. R.

8. С. И. Блинников и др., Письма в Астрон. журн.

Astron. Soc. 430, 2585 (2013).

10,

422

(1984)

[S. I. Blinnikov, I. D. Novikov,

30.

O. Korobkin, S. Rosswog, A. Arcones, and

T. V. Perevodchikova, and A. G. Polnarev, Astron.

C. Winteler, Mon. Not. R. Astron. Soc.

426,

Lett. 10, 177 (1984)].

1940 (2012).

9. F.-K. Thielemann, M. Eichler, I. V. Panov, and

31.

S. Rosswog, O. Korobkin, A. Arcones,

B. Wehmeyer, Ann. Rev. Nucl. Part. Sci. 67, 253

F.-K. Thielemann, and T. Piran, Mon. Not. R.

(2017).

Astron. Soc. 439, 744 (2014).

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023

352

ПАНОВ

32.

D. Martin, A. Perego, A. Arcones, F.-K. Thielemann,

43. P. Moeller, J. R. Nix, and K.-L. Kratz, At. Data Nucl.

O. Korobkin, and S. Rosswog, Astrophys. J. 813, 2

Data Tables 66, 131 (1997).

(2015).

44. T. Rauscher and F.-K. Thielemann, At. Data Nucl.

33.

С. И. Блинников, Д. К. Надежин, Н. И. Крама-

Data Tables 75, 1 (2000).

рев, А. В. Юдин, Астрон. журн. 98, 379 (2021)

45. I. V. Panov, E. Kolbe, B. Pfeiffer, T. Rauscher,

[S. I. Blinnikov, D. K. Nadyozhin, N. I. Kramarev, and

K.-L. Kratz, and F.-K. Thielemann, Nucl. Phys. A

A. V. Yudin, Astron. Rep. 65, 385 (2021)].

747, 633 (2005).

34.

И. В. Панов, А. В. Юдин, Письма в Астрон. журн.

46. I. V. Panov, I. Yu. Korneev, T. Rauscher, G. Martinez-

46, 552 (2020) [I. V. Panov and A. V. Yudin, Astron.

Pinedo, A. Kelic-Heil, N. T. Zinner, and F.-K. Thi-

Lett. 46, 518 (2020)].

elemann, Astron. Astrophys. 513, A61 (2010).

35.

И. В. Панов, А. В. Юдин, ЯФ 86,

(2023)

47. NuDat2,

2009, National Nuclear Data Center,

[I. V. Panov and A. V. Yudin, Phys. At. Nucl. 86, 1

http://www.nndc.bnl.gov/nudat2/

(2023)].

36.

И. Ю. Корнеев, И. В. Панов, Письма в Астрон.

48. А. В. Юдин, Т. Л. Разинкова, С. И. Блинников,

журн. 37, 930 (2011) [I. Yu. Korneev and I. V. Panov,

Письма в Астрон. журн. 45, 893 (2020) [A. V. Yudin,

Astron. Lett. 37, 864 (2011)].

T. L. Razinkova, and S. I. Blinnikov, Astron. Lett. 45,

37.

D. K. Nadyozhin, I. V. Panov, and S. I. Blinnikov,

847 (2020)].

Astron. Astrophys. 335, 207 (1998).

49. S. Rosswog et al., Astron. Astrophys. 341, 499

38.

K. Langanke and G. Martinez-Pinedo, Nucl. Phys. A

(1999).

673, 481 (2000).

50. M. Eichler, A. Arcones, A. Kelic, O. Korobkin,

39.

C. W. Gear, Numerical Initial Value Problems in

K. Langanke, T. Marketin, G. Martinez-Pinedo,

Ordinary Differential Equations (Englewood Cliffs,

I. Panov, T. Rauscher, S. Rosswog, C. Winteler,

New Jersey: Prentice-Hall, 1971).

N. T. Zinner, and F.-K. Thielemann, Astrophys. J.

40.

S. I. Blinnikov and O. S. Bartunov, Astron.

808, 30 (2015).

Astrophys. 273, 106 (1993).

51. P. Dimitriou, I. Dillmann, B. Singh, V. Piksaikin,

41.

S. I. Blinnikov and N. V. Dunina-Barkovskaya, Mon.

et al., Nucl. Data Sheets 3, 144 (2021).

Not. R. Astron. Soc. 266, 289 (1994).

42.

Y. Aboussir, J. M. Pearson, A. K. Dutta, and

52. M. R. Mumpower, R. Surman, G. C. McLaughlin,

F. Tondeur, At. Data Nucl. Data Tables 61, 127

and A. Aprahamian, Prog. Part. Nucl. Phys. 86, 86

(1995).

(2016).

IMPLEMENTATION OF GLOBAL BETA-DECAY RATE PREDICTIONS

TO ASTROPHYSICAL MODELS

I. V. Panov^1),2)

¹⁾NRC “Kurchatov Institute”, Moscow, Russia

²⁾Moscow Institute of Physics and Technology (National Research University),

Dolgoprudny, Russia

In the present work the nucleosynthesis calculations for 2 different scenarios of neutron star merger were

fulfilled. In calculations different global models of beta-decay: quasi-particle random phase approximation

(QRPA), relativistic approximation of RPA (pn-RQRPA), and final amplitude method (FAM) were applied.

It was shown that utilization of different beta-decay models in nucleosynthesis calculations leads to

formation of realistic structure of the chemical elements’ abundance curve. Opposite to the nucleosynthesis

in neutron star merger scenario, in which neutron masses are approximately equal, formation of heavy

elements in the matter of outer crust of neutron star during the explosion of low mass neutron star in

the region from the first to the second peak weakly depends on the model. But in strong r-process the

dependence of elements’ abundance on beta-decay model is very strong. Systematic influence of beta-decay

model on nucleosynthesis results was not found.

ЯДЕРНАЯ ФИЗИКА том 86

№2

2023