ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 3, с. 416-427
ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ
ПОИСК СВЯЗАННЫХ СОСТОЯНИЙ Ξ−nn-, Ξ−pn- И Ξ−pp-СИСТЕМ
© 2023 г. М. В. Егоров1)*
Поступила в редакцию 07.11.2022 г.; после доработки 12.12.2022 г.; принята к публикации 12.12.2022 г.
В работе осуществлен поиск связанных состояний систем Ξ-nn, Ξ-pn и Ξ-pp с использованием
решений связанных однородных интегральных уравнений Фаддеева, записанных относительно ком-
понент T-матрицы. В данных уравнениях вместо традиционного парциально-волнового разложения
используется прямое интегрирование по угловым переменным, с точным учетом связывания в фазовом
пространстве трехчастичных каналов в каждой из систем Ξ-nn-ΛΣ-n-Σ-Σ0n, Ξ-np-ΛΛn-ΛΣ0n и
Ξ-pp-ΛΛp-ΛΣ0p. Единственными ингредиентами представленного метода являются двухчастичные
t-матрицы, которые в случае парного Ξ-N-взаимодействия находились путем решения связанных
интегральных уравнений Липпмана-Швингера для систем ΞN-ΛΛ-ΣΣ в состоянии (I = 0,1S0),
ΞN в состоянии (I = 0,3S1), ΞN-ΛΣ в состоянии (I = 1,1S0) и ΞN-ΛΣ-ΣΣ в состоянии (I =
= 1,3S1). Для получения парных Ξ-N-, YY- и YN-взаимодействий, генерирующих t-матрицы,
используется обновленный вариант ESC16 микроскопической модели. Парное NN-взаимодействие
восстанавливалось на основе зарядово-зависимой Боннской модели. Прямые численные расчеты
энергий связи рассматриваемых систем ясно свидетельствуют о существовании по одному связанному
состоянию с энергиями связи 4.5 и 5.5 МэВ для Ξ-nn- и Ξ-np-систем соответственно и двух
состояний с энергиями связи 2.7 и 4.4 МэВ для системы Ξ-pp.
DOI: 10.31857/S004400272303008X, EDN: RKUYYC
1. ВВЕДЕНИЕ
ΞNN-состояний еще не увенчался успехом. Пер-
вое экспериментальное подтверждение существо-
Последние два десятилетия получило дальней-
вания связанных Ξ--ядерных состояний было по-
лучено в опыте E373 в KEK-PS [4] с помощью ре-
шее развитие направление ядерной физики, по-
священное исследованию барион-барионного вза-
акции Ξ- +14N →10ΛBe +5ΛHe. Эксперименталь-
имодействия в секторе со странностью S = -2.
ная оценка энергии отщепления Ξ--гиперона в эк-
Подверженные слабому распаду гипероны не могут
зотической14Ξ-N-системе составила SΞ- = 4.38 ±
выступать в роли бомбардирующих частиц и, также
± 0.25 МэВ с точностью до поправки на энергию
как в двухбарионном секторе S = -1, построение
возбуждения конечного Λ-гиперядра10ΛBe. В свя-
гиперон-нуклонных и гиперон-гиперонных взаи-
зи с указанным недостатком экспериментальных
модействий опирается, во многом, на теоретиче-
данных в двухбарионном секторе S = -2 большой
ские расчеты и опыты со вторичными пучками
интерес представляет планируемая коллаборацией
каонов в реакциях (K-, K+) и (K-, π±).
J-PARC [5] серия опытов по прецизионному поиску
экзотических гиперядерных состояний.
С экспериментальной точки зрения существует
крайне мало данных для двухбарионного сектора
Теоретические работы за последние пять
S = -2, ограниченных одной точкой полного сече-
лет демонстрируют определенный оптимизм от-
ния неупругих Ξ-p → ΛΛ и Ξ-p → Ξ0n процессов
носительно существования связанной ΞNN-
и упругого Ξ-p → Ξ-p рассеяния при лаборатор-
системы, характеризующейся различными спин-
ном импульсе Ξ--гиперона pЛАБΞ ≈ 0.5 ГэВ [1-3].
изоспиновыми квантовыми состояниями (I, JP ) =
В отличие от обнаруженного в 1968 г. в опытах
= (1/2, 1/2+ )
[6-8], (I, JP ) = (1/2, 3/2+ )
[9-
с эмульсиями связанного состояния S = -1 ги-
12], (I, JP ) = (3/2, 1/2+) [9, 10]. Существенный
пертритона3ΛH с энергией Λ отщепления SΛ =
скепсис ожиданию связанных состояний в системе
ΞNN придает тот факт, что величина энергии
= 0.13 МэВ экспериментальный поиск связанных
связывания Eb системы крайне чувствительна к
1)Томский государственный университет, физический фа-
выбору модели ΞN-взаимодействия. В результате
культет, Томск, Россия.
чего в одном и том же подходе с использованием
*E-mail: egorovphys@mail.ru
одного и того же вычислительного инструмента,
416
ПОИСК СВЯЗАННЫХ СОСТОЯНИЙ
417
но с разными моделями двухбарионного ΞN-
самого начала не позволяет рассматривать систему
взаимодействия можно получить как связанное,
Ξ-pn изолировано от канала ΛΛn. Аналогично
так и не связанное ΞNN-состояние. Иллюстра-
Ξ-nn устроено наполнение системы Ξ-pp. Учет
тивным примером являются расчеты с HAL QCD-
расширенного фазового пространства состояний
потенциалом [11, 12] системы ΞNN в состоя-
системы ΞNN на каналы YYN проводился только в
нии (I, JP ) = (1/2, 3/2+ ), которая оказывается
работах [6, 7] для состояния (I, JP ) = (1/2, 1/2+ ),
несвязанной. Расчеты с киральной составной
которое соответствует системе Ξ-np-ΛΛn. Было
кварковой моделью CCQM и с микроскопическим
показано, что влияние других неупругих каналов
ESC08c-потенциалом дают
[8] энергию связи
N ΛΣ и NΣΣ сводится к снижению энергии связи
системы ΞNN в обоих состояниях (I, JP ) =
системы Ξ-np-ΛΛn в среднем на 80-150 кэВ,
= (1/2, 3/2+ ) и (3/2, 1/2+). Можно отметить, на
оставляя при этом систему в связанном состоянии.
сегодняшний день только расчеты с киральной
В остальных теоретических работах система ΞNN
рассматривалась в микроскопических подходах
составной кварковой моделью [6, 7] приводят к
изолировано от влияния других трехчастичных
связанному состоянию ΞNN-системы в состоянии
каналов.
(I, JP ) = (1/2, 1/2+ ), тогда как такие же микро-
В настоящей работе проводятся микроско-
скопические расчеты с ΞN-потенциалом J ¨ulich
пические расчеты энергий связи систем Ξ-nn-
Ch-EFT [12] не дают связанного состояния в этом
ΛΣ-n-Σ-Σ0n, Ξ-pp-ΛΣ0p-Σ+Σ-p и Ξ-pn-
же состоянии. Расхождения между различными
микроскопическими расчетами можно связать не
ΛΛn-Σ0Λn. Данные трехчастичные системы ча-
столько с недостатком сведений о реалистичном
стиц описываются связанными по типам каналов
уравнениями Фаддеева [15]. Необходимость про-
поведении двухбарионного ΞN-потенциала (что
должения теоретических исследований в данной
отражается в постоянном обновлении барион-
области следует из недостатка эксперименталь-
барионных моделей, например, Nijmegen extended-
ных сведений и противоречивых теоретических
soft-core model2) от ESC08с [13] к ESC16 [14]
данных относительно существования связанных
и др.), но и со сложной динамической природой
состояний у системы ΞNN. В отличие от преды-
взаимодействия в системе ΞNN. Динамические
дущих микроскопических расчетов энергий связи
особенности можно условно разделить на те,
ΞNN-системы в данной работе решается система
которые связаны с двухбарионными взаимодей-
трехчастичных уравнений Фаддеева относительно
ствиями и те, которые продиктованы трехчастичной
компонент трехчастичных T -матриц без исполь-
природой системы ΞNN. Двухбарионное ΞN-
зования парциально-волнового разложения [16].
взаимодействие уже на пороге рождения Ξ ввиду
Данный подход к решению фаддеевских уравнений
его большой массы приводит к открытию неупругих
позволяет избавиться от дополнительного связы-
каналов ΛΛ, ΛΣ и ΣΣ. Причем переходы в
вания уравнений по орбитальным волнам путем
неупругие каналы устроены таким образом, что
прямого интегрирования по угловым переменным
вклады с I = 0 возникают в системе ΞN-ΛΛ-ΣΣ
в выбранной системе координат. Данный подход
в синглетной1S0-волне и только в системе ΞN
прямого численного интегрирования трехчастич-
в триплетных волнах3S1-3D1. Вклады с I = 1
ных уравнений обладает б ´oльшей предсказатель-
устроены иначе и возникают в системе ΞN-ΛΣ в
ной способностью, чем решения фаддеевских
синглетной1S0-волне и в системе ΞN-ΛΣ-ΣΣ в
уравнений в форме АГС (Альт-Грассбергер-
триплетных волнах3S1-3D1. Такие двухчастичные
Сандхас), поскольку задействует двухчастичные t-
особенности парных взаимодействий вместе с
матрицы без их трансформации в форму матричных
высокой массой Ξ-гиперона приводят к тому,
элементов операторов перехода, что позволяет
что система ΞNN уже на пороге рождения Ξ-
использовать локальные потенциалы в самой
гиперона представляет собой связанную систему
общей форме, не допускающие сепарабельного
целого ансамбля частиц. В представлении частиц
представления. Кроме того, в алгебраической мат-
ричной форме однородная система уравнений Фад-
ΞNN выглядит как связанные системы Ξ-nn-
деева относительно компонент T -матрицы в точке,
ΛΣ-n-Σ-Σ0n и Ξ-pn-ΛΛn-Σ0Λn-Σ+Σ-n.
соответствующей связанному состоянию E = Eb,
В обоих системах каналы с ΣΣ лежат примерно
имеет собственный вектор, компоненты которого
на 80 МэВ выше по энергии каналов с частицами
описывают связанное состояние системы. Поиск
ΣΛ и открываются последними. Канал с ΛΛ уже
таких собственных состояний на основе решения
является открытым в области порога Ξ-n, что с
уравнений Фаддеева относительно компонент T -
матриц без использования парциально-волнового
2)Отметим, что представленные в работах [13] и [14] па-
разложения положительно зарекомендовал себя
раметризации действительно отличаются, что несомненно
будет влиять на результаты цитируемых выше работ, в
в задачах о гиперон-ядерном и каон-ядерном
которых используется потенциал ESC08c.
взаимодействиях [17].
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
418
ЕГОРОВ
Работа построена следующим образом. В разд. 2
этого оператора сводится к перебору промежу-
приведены уравнения Фаддеева для трех тел разной
точных бра- и кет-состояний для Ψ и t-матрицы
массы и описана процедура нахождения энергий
соответственно
∫
связи трехчастичных систем без использования
〈qp|tP Ψ〉 = d3q′d3p′d3q′′d3p′′ pq |t| p′q′ ,
(2)
парциально-волнового разложения. В разд. 3 опи-
сана процедура получения двухчастичных t-матриц
для гиперон-нуклонного, гиперон-гиперонного и
p′q′ |P|p′′q′′ p′′q′′|Ψ
нуклон-нуклонного взаимодействий. В разд.
4
Для импульсных состояний в (2) системы трех
приведены численные значения энергий связи
частиц принята нормировка
всех рассмотренных систем и дано сравнение с
(
)
(
)
имеющимися в литературе данными. В Заключении
p′q′|p′q′
=δ3
p′ - p
δ3
q′ - q
(3)
кратко сформированы полученные в данной работе
Векторы p и p′ характеризуют относительное дви-
результаты.
жение в выделенных подсистемах взаимодейству-
ющих пар частиц. Частицы-спектаторы задаются
импульсами q и q′ в бра- и кет-фазовых про-
2. УРАВНЕНИЯ ФАДДЕЕВА
ДЛЯ T-МАТРИЦЫ БЕЗ ПАРЦИАЛЬНО-
странствах соответственно. Для того чтобы найти
ВОЛНОВОГО РАЗЛОЖЕНИЯ
матричные элементы оператора перестановки ча-
стиц, достаточно ввести набор переменных Якоби.
В операторной форме для компонент трехча-
Перестановка трех частиц с неравными в общем
стичной T -матрицы уравнения Фаддеева имеют
случае массами m1, m2, m3 приводит к появлению
вид
трех эквивалентных наборов переменных Якоби
для импульсов частиц-спектаторов и импульсов во
T |Ψ〉 = tP |Ψ〉 + tP R0T |Ψ〉 .
(1)
взаимодействующих парах:
⎧
Полная волновая функция трехчастичной си-
m3
m1
⎪p3 =
k1 -
k2;
стемы |Ψ〉 может быть найдена решением одно-
⎪
m1 + m2
m1 + m2
⎪
родного аналога уравнения (1) при фиксированной
⎪
m1 + m2
⎪
энергии E = Eb < 0, соответствующей связанному
⎪q3 =
k3 -
⎪
m1 + m2 + m3
состоянию системы. Взаимодействия между части-
⎪
m3
⎪
цами вводятся в систему (1) через двухчастичные
-
(k1 + k2) ;
⎪
⎪
m1 + m2 + m3
t-матрицы, поведение которых, как правило, хо-
⎪
m1
m3
рошо известно на массовой поверхности. Во вне
⎪
p2 =
k3 -
k1;
⎪
массовой поверхности, когда in- и out-импульсы
⎪
m3 + m1
m3 + m1
⎨
t-матрицы не совпадают с импульсом, диктуемым
m3 + m1
q2 =
k2 -
(4)
законом сохранения энергии для взаимодейству-
⎪
m1 + m2 + m3
ющей пары частиц, начинает играть роль анали-
⎪
⎪
m2
тическое продолжение данной t-матрицы. Наибо-
⎪-
(k3 + k1) ;
⎪
m1 + m2 + m3
лее естественно такое продолжение заложено в
⎪
⎪
m3
m2
кинематике трехчастичного уравнения (1), когда
⎪p1 =
k2 -
k3;
границы интервалов двухчастичных энергий z ∈
⎪
m2 + m3
m2 + m3
⎪
∈ [E, -∞) не могут принимать произвольных зна-
⎪
m2 + m3
⎪q1 =
k1 -
чений в каждой взаимодействующей паре частиц,
⎪
m1 + m2 + m3
⎪
что выгодно отличает [18] фаддеевский подход от
⎪
m1
⎩-
(k2 + k3) .
традиционных вариационных исчислений. Кроме
m1 + m2 + m3
того, без ограничения общности известные анали-
тические функции t-матриц, полученные, напри-
Нижний индекс у импульсов p и q слева обо-
мер, суммированием диаграмм Фейнмана, могут
значает выделенную подсистему частиц, где вза-
имодействие генерирует двухчастичную t-матрицу.
быть использованы в уравнении (1) без введения
Импульсы трех частиц в общей системе центра
сепарабелизующей процедуры (т.е. без преобразо-
масс обозначены как ki и k1 + k2 + k3 = 0. По-
вания уравнения (1) в форму АГС). Свободная от
скольку для каждой выделенной пары перемен-
взаимодействия резольвента R0 = (E + iϵ - H0)-1
ных Якоби существуют два эквивалентных способа
(где H0 — оператор кинетической энергии трех тел)
представления через оставшиеся две пары других
зависит только от текущей энергии системы E, пе-
переменных Якоби, то матричные элементы опе-
ребор значений которой задается. Трехчастичный
раторов перестановки имеют структуру, например,
аспект уравнения (1) возникает из-за операторов
для разбиения 1 (частицы 2 и 3):
циклической перестановки частиц P = P12P23 +
+ P13P23 [19]. В фазовом пространстве действие
p′q′ |P|p′′q′′
= p′q′|p′′q′′
+
(5)
2
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
ПОИСК СВЯЗАННЫХ СОСТОЯНИЙ
419
+ p′q′|p′′q′′
=
Две трехмерные δ-функции снимают шесть ин-
3
(
)
(
)
тегралов в (2) по переменным p′ и p′′. Интегри-
=δ3
q′ - q′′
δ3
p′ - p′′
+
2
2
рование по переменной q′ снимается δ-функцией,
(
)
(
)
+δ3
q′ - q′′
δ3
p′ - p′′
содержащейся в двухчастичных t-матрицах, дей-
3
3
ствующих в трехчастичном фазовом пространстве
Индексы в правой части
(5) указывают на
〈pq|t|p′q′〉 = 〈p|t|p′〉δ3(q - q′).
(8)
подсистему частиц, чьи импульсы (переменные
Якоби) определяют функциональные зависимости
В выбранной системе координат [16] явная зави-
q′1(q′2,p′2) и q′1(q′3,p′3). В явном виде такая
симость двухчастичных t-матриц от угловых пере-
функциональная форма имеет вид
менных имеет нетривиальный вид
(
)
⎧
m1
q2
⎪q1 = p3 - q3
;
t p, p′, E -
=
(9)
⎪
m1 + m2
2M
⎪
⎨
m3
(
√
p1 = -p3
-
m2 + m3
(6)
= t p,xp, κ21q2 + κ22q′′2 + 2κ1κ2qq′′xq′′,
⎪
(
)
⎪
m2 (m1 + m2 + m3)
)
⎪
q3
;
q2
⎩-
(m1 + m2) (m2 + m3)
xif,E -
,
2M
⎧
m1
⎪q1 = -p2 - q2
;
где xp, xq, xq′′ — косинусы углов, ассоциированных
⎪
m1 + m3
⎪
с импульсами p, q и q′′. Азимутальные углы, ассо-
⎨
m2
циированные с этими же импульсами, здесь и далее
p1 = -p2
+
m2 + m3
обозначены как φp, φq и φ′′. Проекция импульса
⎪
(
)
⎪
m3 (m1 + m2 + m3)
|κ1q + κ2q′′| на вектор p определяется косинусом
⎪
⎩+
q2
полярного угла разлета частиц:
(m1 + m3) (m2 + m3)
′′ypq′′
κ1qypq + κ2q
xif =
√
(10)
Аналогично можно получить выражения для функ-
κ21q2 + κ22q′′2 + 2κ1κ2qq′′xq′′
ций q2(q3, p3), p2(q3, p3), q2(q1, p1), p2(q1, p1),
q3(q1,p1), p3(q1,p1) и q3(q2,p2), p3(q2,p2). При-
Величины ypq и ypq′′ в (10) определяются соотно-
нимая во внимание формулу (6), можно получить
шениями
√
√
для (5) выражение
ypq = xpxq +
1-x2p
1 - x2q cos(φp - φq),
p′q′ |P|p′′q′′ =
(7)
(
)
(11)
m1
√
√
(
)
=δ3
-p′2 - q′
-q′′
×
2
ypq′′ = ypqxq′′ +
1-x2
1 - y2pq cos
φp - φ′′
m1 + m3
q′′
2
(
)
m2
Коэффициенты κ1, κ2 в (9), (10) определяются мас-
×δ3
q′′
+q′2
-p′′
+
сами m1-, m2- и m3-частиц. Обратим внимание,
m2 + m3
2
(
)
что энергия трехчастичной системы E связана с
m1
относительным импульсом q0 частицы-спектатора
+δ3
-p′3 - q′
3
-q′′
×
m1 + m2
в начальном состоянии
3
(
)
p2
q20
m3
E =
+
(12)
×δ3
-
+q′′ -q′3
-p′′
=
2μ
2M
m2 + m3
3
(
)
Приведенная масса частицы-спектатора и взаи-
m1
=δ3
p′ + q′
+q′′
×
модействующей пары частиц массой μ обозначена
m1 + m3
2
в (9) и (12) как M. Таким образом, из формулы
(
)
m2
(12) модуль импульса p не является независимой
×δ3
p′′ -
q′′ - q′
+
величиной.
m2 + m3
2
(
)
Для системы, допускающей один трехчастичный
m1
канал (например, ΛΛN), энергия связи Eb полу-
+δ3
p′ - q′
-q′′
×
m1 + m2
чается решением однородного уравнения Фаддеева
3
(
)
на численной сетке N × N импульсов (q0, q)
m3
⎡⎛
⎞
×δ3
p′′ + q′ +
q′′
m2 + m3
3
1N×N
0
0
⎢⎜
⎟
⎢⎜
⎟
В последнем равенстве (7) использовалась чет-
det⎢⎜
0
⎟
-
(13)
1N×N
⎣⎝0
⎠
ность δ-функции, и индекс подсистемы у импульс-
ных методов был вынесен за скобки.
0
0
1N×N
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
420
ЕГОРОВ
⎛
⎞⎤
суммированию в (2) по промежуточным состояни-
0
a12 a13
⎜
⎟⎥
ям
⎜
⎟⎥
∫
−
⎜
0
a23⎟⎥
= 0.
∑
21
⎝a
⎠⎦
〈qp|tP Ψ〉 =
d3q′d3p′d3q′′d3p′′ ×
(15)
a31 a32
0
α
E=Eb
× pq|t| p′q′α ,
Элементы aij получены из формулы (2) с исполь-
зованием приведенной выше процедуры получения
pq |P|p′′q′′α p′′q′′ |Ψα
матричных элементов оператора перестановки ча-
Полная волновая функция многоканальной трех-
стиц P . Матричные элементы aij имеют вид:
частичной системы распадается не только по типам
∫
m1
разбиений (индексы 1, 2, 3), но и по типам трехча-
a12
=
d3q′′ p,q|t1| - q
-q′′,q
×
стичных пространств (индекс α)
m1 + m3
∑
(14)
Ψ= Ψα =
(16)
(
)-1
2
α
q
q′′2
qq′′
∑
×
- |E| -
-
-
;
2μ23
2μ13
m3
= (φ12φ3 + φ23φ1 + φ31φ2)α .
∫
α
m1
a13
=
d3q′′ p,q|t1| - q
+q′′,q
×
Волновые функции взаимодействующих пар частиц
m1 + m2
в (16) обозначены как φij , частицы-спектатора —
(
)-1
2
φk, k = i, j. В действительности уже для ΛΛN-
q
q′′2
qq′′
×
- |E| -
-
-
;
канала, учитывая связь импульсов (12), при ко-
2μ23
2μ12
m2
[√(
)
)
∫
q20
m2
торой p ∈
2μ E -
,+∞ при достиже-
a21
=
d3q′′ p,q|t2| - q
+q′′,q
×
2M
m3 + m2
нии определенного значения импульса q в двух-
(
)-1
2
частичных подсистемах возможно открытие других
q
q′′2
qq′′
×
- |E| -
-
-
;
неупругих каналов. В данной работе для каждой
2μ31
2μ23
m3
из рассматриваемых систем Ξ-nn, Ξ-np, Ξ-pp в
∫
расчетах задействовались по три канала
m2
a23
=
d3q′′ p,q|t2| - q
-q′′,q
×
m1 + m2
Ξ-nn(3200.7) - ΛΣ-n(3252.7) -
(17)
(
)-1
2
- Σ-Σ0n(3329.6);
q
q′′2
qq′′
×
- |E| -
-
-
;
Ξ-np(3199.1) - ΛΛn(3170.7) - ΛΣ0n(3252.7);
2μ31
2μ12
m1
∫
Ξ-pp(3198.7) - ΛΛp(3169.9) - ΛΣ0p(3251.4).
m3
a31
=
d3q′′ p,q|t3| - q
-q′′,q
×
m3 + m2
В скобках в (17) указаны массы систем в МэВ. Для
(
)-1
определенности нумерация масс частиц организо-
2
q
q′′2
qq′′
вана по следующему принципу:
×
- |E| -
-
-
;
2μ12
2μ23
m2
1:
p Λ Σ+
1:
n Λ Σ0
∫
m3
a32
=
d3q′′ p,q|t3| - q
-q′′,q
×
2:
Ξ- Σ0 Σ-
2:
Ξ- Σ- Σ-
(18)
m1 + m3
(
)-1
3:
p p p
3: n n n
2
q
q′′2
qq′′
×
- |E| -
-
-
2μ12
2μ31
m1
1:
p Λ Λ,
Приведенные массы двухчастичных подсистем
в
2:
Ξ- Λ Σ0,
(14) введены символами μij , где i, j — номера
3:
n n n.
взаимодействующих частиц. Индекс у t-матрицы
определяет тип двухчастичной подсистемы, вза-
В каждом столбце (18) указана нумерация по ча-
имодействие в которой генерирует данную t-
стицам для систем Ξ-pp, Ξ-nn и Ξ-pn соответ-
матрицу.
ственно. Поскольку волновая функция для трех-
Появление трехчастичных неупругих каналов,
частичной системы с открытыми неупругими трех-
спровоцированное высокой массой рассматривае-
частичными каналами есть разложение по трехча-
мой системы ΞNN, приводит к дополнительному
стичным каналам (16), то уравнение Фаддеева для
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
ПОИСК СВЯЗАННЫХ СОСТОЯНИЙ
421
компонент T -матриц, соответствующих разбиени-
между энергиями zi(jk) двухчастичных подсистем
ям (18), на примере системы Ξ-np есть система
(jk) трехчастичного канала α с каналом β:
трехчастичных уравнений
(
)
(
)
⎛
⎞
zi(jk)α + (mj + mk)α -
(21)
zi(jk)β = α=
T1
⎜
⎟
− (mj + mk)β .
⎜
⎟
⎜
⎟
×
(19)
2
⎝T
⎠
Выполнение равенства
(21) соответствует от-
T3
крыванию трехчастичного канала β в уравнении
(
)
⎛
⎞
Фаддеева (19), когда при
zi(jk)α < 0 величина
(
)
(φ23φ1)Ξ-pn + (φ23φ1)ΛΛn + (φ23φ1)ΛΣ0n
zi(jk)α + (mj + mk)α - (mj + mk)β < 0 также
⎜
⎟
⎜
⎟
×
⎜
⎟
=
меньше нуля. В противном случае трехчастичный
φ31φ2)Ξ-pn + (φ31φ2)ΛΛn + (φ31φ2)ΛΣ0n
⎝(
⎠
канал β считается закрытым. Связь энергий
(
)
(φ12φ3)Ξ-pn + (φ12φ3)ΛΛn + (φ12φ3)ΛΣ0n
zi(jk)α с импульсами q гарантирует, что условие
⎛
⎞
(21) соответствует динамической связи импульсов
0
t1 t1
⎜
⎟
частиц-спектаторов в связанных трехчастичных
⎜
⎟
каналах.
=
⎜
⎟
×
2
0
t2
⎝t
⎠
Отличие изложенного выше подхода к построе-
t3 t3
0
нию и решению связанных трехчастичных уравне-
⎛
⎞
ний Фаддеева от работ [6, 7] заключается в том, что
в последних приводится нелинейная система фад-
(φ23φ1)Ξ-pn + (φ23φ1)ΛΛn + (φ23φ1)ΛΣ0n
⎜
⎟
⎜
⎟
деевских уравнений для связанной ΞNN-ΛΛN-
×
⎜
⎟
+
φ31φ2)Ξ-pn + (φ31φ2)ΛΛn + (φ31φ2)ΛΣ0n
системы. Решение такой нелинейной системы не
⎝(
⎠
может быть сведено на численной сетке к квад-
(φ12φ3)Ξ-pn + (φ12φ3)ΛΛn + (φ12φ3)ΛΣ0n
ратной матрице (13), что побуждает предположить
⎛
⎞
итеративный характер полученных в работах [6, 7]
0
t1R0T2 t1R0T3
⎜
⎟
решений.
⎜
⎟
+
⎜
⎟
×
Для используемого в данных расчетах зарядово-
2R0T1
0
t2R0T3
⎝t
⎠
зависимого Боннского NN-потенциала [20] ве-
t3R0T1 t3R0T2
0
рификация развиваемого метода решений одно-
⎛
⎞
родных интегральных уравнений Фаддеева
(13)
(φ23φ1)Ξ-pn + (φ23φ1)ΛΛn + (φ23φ1)ΛΣ0n
проводилась путем поиска связанных состояний
⎜
⎟
⎜
⎟
ядер3H и3He. Численные значения энергий связи
×
⎜
⎟
φ31φ2)Ξ-pn + (φ31φ2)ΛΛn + (φ31φ2)ΛΣ0n
⎝(
⎠
для тритона и гелия-3 составили [17] близкие к
экспериментальным значения 8.301 МэВ (экспе-
(φ12φ3)Ξ-pn + (φ12φ3)ΛΛn + (φ12φ3)ΛΣ0n
римент 8.480 МэВ) и 7.756 МэВ (эксперимент
Факторизованный вид функций Ψ в (16) и (19)
7.718 МэВ) соответственно. Кроме того, для энер-
следует понимать условно как иллюстрацию фак-
гий отщепления Λ-гиперона из ядра3ΛH решение
та кинематического отделения взаимодействующей
уравнения (13) с Боннским NN-потенциалом и
пары частиц от частицы-спектатора. Выделение
гиперон-нуклонным микроскопическим ESC16
взаимодействующей пары частиц отражено в ниж-
[21] и феноменологическим
[22] потенциалами
нем индексе у t- и T -матриц.
приводит к значениям SΛ = 0.32 МэВ и SΛ =
Появление трех конкурирующих каналов рас-
= 0.265 МэВ, что близко к современной экспе-
ширяет систему алгебраических уравнений (13) по-
риментальной оценке этой энергии SΛ = 0.41 ±
явлением дополнительных произведений вида
± 0.12 МэВ [23].
∀k = 1,2,3(tkR0) → (tkR0)Ξ-pn +
(20)
+ (tkR0)ΛΛn + (tkR0)ΛΣ0n .
3. ДВУХЧАСТИЧНЫЕ t-МАТРИЦЫ
Согласно (20) каждая из величин aij для связан-
Двухчастичные ингредиенты — t-матрицы —
ных трехчастичных каналов распадается на сумму
находились путем решения уравнений Липпмана-
интегралов от соответствующих парных t-матриц
Швингера в импульсном представлении для систем
и свободных от взаимодействия трехчастичных ре-
частиц ΞN-ΛΛ-ΣΣ (I = 0,
1S0), ΞN (I = 1,
зольвент R0, отличающихся для каждого канала
массами частиц разбиений (18). Естественное пе-
3S1), ΞN-ΛΣ (I = 1, 1S0), ΞN-ΛΣ-ΣΣ (I =
рераспределение энергии между частицами в двух-
= 1, 3S1). Потенциалы ΞN- и YY-взаимодействий
частичных подсистемах, характерное для фаддеев-
рассчитывались на основе результатов микро-
ских уравнений, сводится к простому соотношению
скопической модели ESC16 [14]. Недостаточно
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
422
ЕГОРОВ
подробное представление координатных потен-
В численных расчетах была выбрана сетка им-
циалов модели ESC16 [14] в области нуля ко-
пульсов (q0, q) размерностью 35 × 35. Число точек
ординат восстанавливалось с помощью сплайн-
в угловых направлениях в интеграле (14) составило
экстраполяции. С использованием разложения
7 × 7 единиц. Расчет одного матричного элемента
группы SU(3) по неприводимым представлениям
всех величин (14) для трех связанных трехчастич-
в изоспиновом базисе (см. табл. 26, 27 [14]) на
ных каналов на выбранной сетке с использовани-
основе приведенных на рис. 8-10 [14] диаго-
ем современного мобильного процессора занимает
нальных потенциалов были получены остальные
около 80 с. Параллельное заполнение элементов
недиагональные компоненты3). В качестве YN-
матрицы 35 × 35 с использованием навязанного
машинного распараллеливания позволяет в разы
потенциалов использовался результат расчета
снизить время заполнения таких матриц в зависи-
координатных гиперон-нуклонных потенциалов
мости от числа используемых параллельных пото-
по коду [21], соответствующему модели ESC16.
ков.
Дополнительно в расчетах использовался фе-
номенологический зарядово-независимый YN-
В зависимости от текущего значения трехча-
потенциал [22]. В качестве зарядово-зависимого
стичной энергии E определитель (13) принимает то
NN-потенциала использовалось сепарабельное
положительное, то отрицательное значение. Точ-
представление четвертого ранга Боннского NN-
ки, в которых определитель меняет знак, ассоци-
потенциала [20], хорошо зарекомендовавшее себя в
ируются с собственным значением системы (13),
описании NN-фазовых сдвигов вплоть до кинети-
характеризующим связанное состояние с энер-
гией E = Eb. Поведение определителя алгебра-
ческих энергий EЛАБ = 500 МэВ. Полученные на
ической системы связанных однородных уравне-
основе уравнений Липпмана-Швингера решения
ний Фаддеева в зависимости от энергии E пред-
для t-матриц после проверки использовались в
ставлено на рис. 2. В качестве двухчастичных
расчетах полных сечений процессов, представлен-
YN-взаимодействий в расчетах, представленных
ных на рис. 1. Отметим, что для упругого ΞN-
на данном рисунке, использовались координатные
рассеяния в области pЛАБ ≈ 380 МэВ открывается
функции, полученные на основе кода [21] и соот-
неупругий ΛΛ-канал, а в области pЛАБ ≈ 600 МэВ
ветствующие YN-модели ESC16. Замена данной
открывается канал ΛΣ. В целом поведение упругих
микроскопической модели YN-взаимодействия на
и неупругих процессов Ξ-N и YY согласуется с
простую феноменологическую [22] не приводит к
представленными в работе [14] результатами. Для
видимому изменению кривых рис. 2 в области
нуклон-нуклонного рассеяния в настоящей работе
|E| < 6 МэВ. Мнимые части определителя системы
использовался только сепарабельный вариант [20]
уравнений (13) возникают вполне естественным
Боннского NN-потенциала, который в достаточной
образом из парных t-матриц произведения парных
мере согласуется с парижским NN-потенциалом в
потенциалов и двухчастичных резольвент, в кото-
части описания фазовых сдвигов и отражает реаль-
рых содержат полюсные вклады благодаря тому,
ную картину поведения полного сечения упругого
что двухчастичная энергия z ∈ [E, -∞) в каж-
np-рассеяния. В секторе YN-рассеяния результат
дой паре пробегает нетривиальный полуинтервал.
использования микроскопической модели ESC16,
Численные значения энергий связи, полученные в
доступной по коду [21], и простой двухканальной
данной работе, представлены в табл. 1. Там же
феноменологической модели [22] также хорошо
приведены для сравнения известные в литературе
соответствует известным в литературе экспери-
значения энергий связи систем Ξ-NN для различ-
ментальным данным по полным сечениям.
ных спин-изоспиновых состояний. В цитируемой
литературе, как правило, приводятся значения для
энергий отщепления SΞ- гиперона из ядра. Срав-
4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
нение энергий связи Eb(A - 1Ξ- ) в табл. 1 для
Поиск энергий связи Eb рассматриваемых трех-
рассматриваемых гиперядерных систем AΞ- осу-
ществлялось в том числе с использованием связи
частичных систем Ξ-nn, Ξ-pn и Ξ-pp осуществ-
между энергиями связи и энергией отщепления
лялся с помощью решения алгебраической си-
стемы уравнений (13), записанной для связанных
SΞ- = Eb (A - 1Ξ-) - Eb (AΞ-) .
(22)
по трем трехчастичным каналам систем уравнений
Фаддеева (19).
Энергия связи Eb (A - 1Ξ- ) в (22) характеризует
систему, получаемую из исходной ядерной системы
3)В исходном виде разложения для “потенциалов” по
AΞ- путем удаления Ξ--гиперона. В численных
неприводимым представлениям не использовались, так
расчетах по формуле (22) для энергий связи Ξ-N-
как в этом случае линейные комбинации “потенциалов”
подсистем использовалось значение Eb(Ξ-N) =
V27, V8s, V8a и др. плохо соответствуют графической
информации рис. 8-10 [14].
= 1.67 МэВ [13, 28].
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
ПОИСК СВЯЗАННЫХ С
ОСТОЯНИЙ
423
σ, мбн
σ, мб
н
100
12
Ξ-p → Ξ-p
Ξ-p → ΛΛ
10
75
8
50
6
4
25
2
0
200
400
600
800
1000
0
200
400
600
800
1000
pЛАБ, МэВ
pЛАБ, МэВ
σ, мбн
σ, мбн
300
np → np
ΛN → ΛN
10
250
200
Bonn
150
1
ENDF
100
50
0.1
0
0.1
1
10
100
150
200
250
300
350
EЛАБ, МэВ
pЛАБ, МэВ
σ, мбн
σ, мбн
500
300
ΣN → ΣN
ΣN → ΛN
450
250
400
Egorov, 2021
350
200
300
ESC'16
250
150
200
100
150
100
50
50
0
0
50
100
150
200
250
300
50
100
150
200
250
300
pЛАБ, МэВ
pЛАБ, МэВ
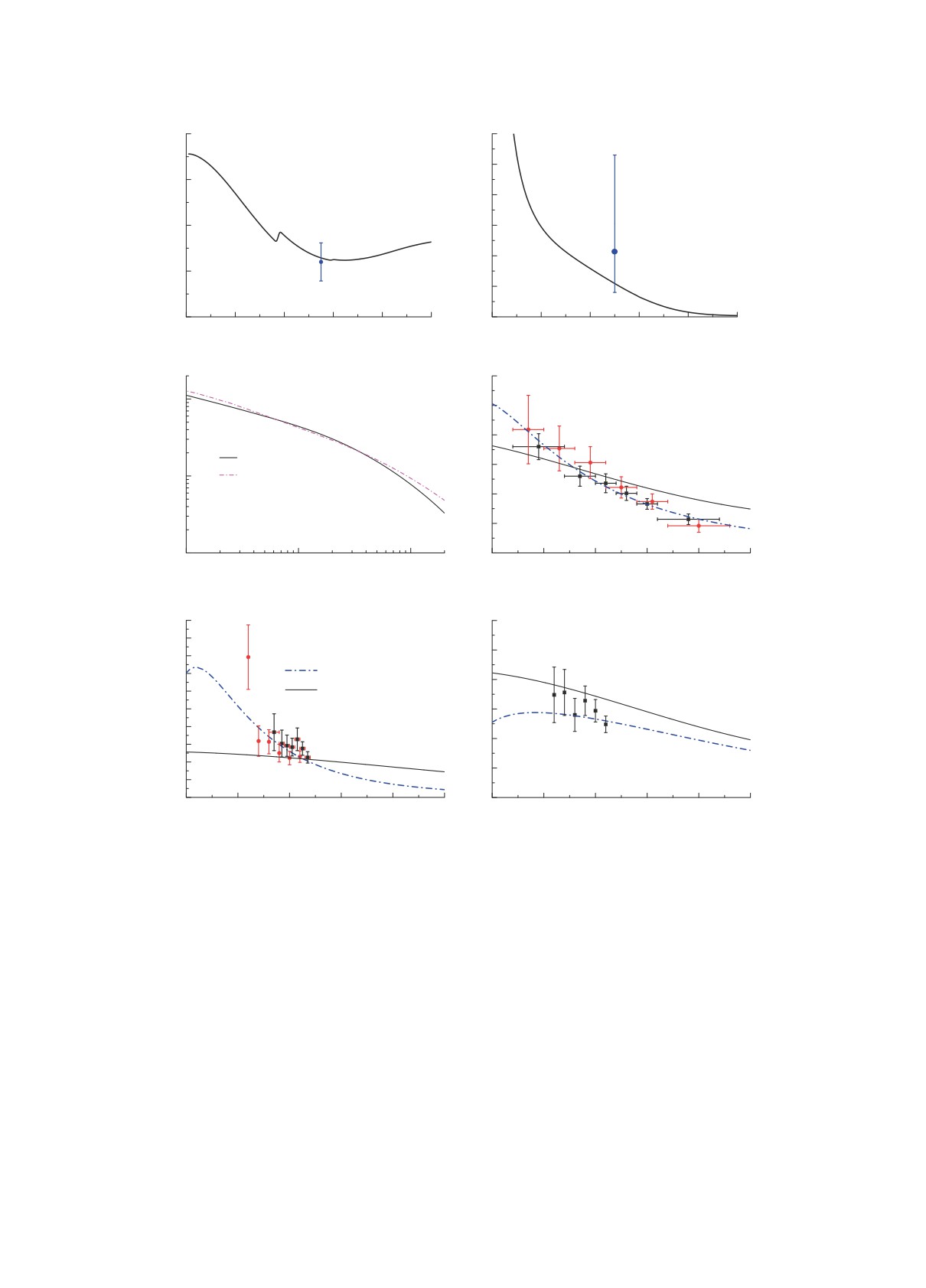
Рис. 1. Сверху: полные сечения процессов Ξ-p → Ξ-p, Ξ-p → ΛΛ, рассчитанные на основе модели ESC16 [14], в
сравнении с известными экспериментальными данными [1, 2]; полное сечение упругого np-рассеяния, рассчитанное по
Боннскоймодели[20] в сравнениис даннымибиблиотекиоцененныхядерныхданныхENDF. Снизу: полныесечения ΛN-,
ΣN-рассеяния и сечение конверсии ΣN → ΛN. Представлены расчеты с использованием микроскопической модели
ESC16, доступной по коду [21], и феноменологической модели [22]. Экспериментальные данные: ΛN [24, 25]; ΣN [26,
27]; ΣN → ΛN [26].
В данной работе не ставилась цель ассоци-
работе благодаря процедуре решения фаддеевских
ировать найденные связанные состояния систем
уравнений без парциально-волнового разложения
с полными двухчастичными t-матрицами есть воз-
Ξ-NN с конкретным спин-изоспиновым состоя-
можность получить весь спектр состояний рас-
нием. Тем не менее, можно отметить, что, посколь-
сматриваемых систем без необходимости выделе-
ку изоспин нейтрон-протонной пары равен нулю,
ния отдельных квантово-механических состояний в
система Ξ-np может находиться только в состоя-
двухчастичных ингредиентах модели. Тем не менее,
ниях (I,J+) = (1/2,1/2+), (1/2, 3/2+), тогда как
вес различных спин-изоспиновых конфигураций в
системы Ξ-NN с изоспином I = 3/2 — это либо
общей волновой функции систем Ξ-NN позволяет
Ξ-nn, либо Ξ-pp. Фактически только в данной
практически однозначно идентифицировать эти со-
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
424
ЕГОРОВ
Таблица 1. Известные в литературе результаты расчетов энергий связи Eb систем Ξ-NN, находящихся в
фиксированных спин-изоспиновых состояниях с использованием различных моделей ΞN-взаимодействия (здесь
же представлены результаты данной работы для систем Ξ-nn, Ξ-np и Ξ-pp без выделения отдельных спин-
изоспиновых состояний)
Eb, МэВ
(I, JP ), система
ΞN-модель
Литература
(
)
1
9.425
,32+ ,Ξ-np
ESC08c
E. Hiyama et al. [11]
2
(
)
1
не связана
,12+ ,Ξ-np
ESC08c
2
(
)
1
не связана
,32+ ,Ξ-np
HAL QCD
2
(
)
1
не связана
,12+ ,Ξ-np
HAL QCD
2
(
)
1
2.237
,12+ ,Ξ-np
ESC08c
H. Garcilazo [8]
2
(
)
3
2.886
,12+ ,Ξ-nn,Ξ-pp
s-волновая
I. Filikhin et al. [10]
2
(
)
1
17.205
,32+ ,Ξ-np
симуляция ESC08c
2
(
)
1
не связана
,12+ ,Ξ-np
J ülich Ch-EFT/HAL QCD
K. Miyagawa, M. Kohno [12]
2
(
)
1
не связана
,32+ ,Ξ-np
J ülich Ch-EFT/HAL QCD
2
(
)
1
3.05
,32+ ,Ξ-np
ESC08c
2
(
)
1
15.74
,32+ ,Ξ-np
ESC08c
H. Garcilazo, A. Valcarce [9]
2
(
)
3
2.89
,12+ ,Ξ-nn,Ξ-pp
ESC08c
2
(
)
1
3.37
,32+ ,Ξ-np
CCQM
2
(
)
3
5.23
,12+ ,Ξ-nn,Ξ-pp
CCQM
2
(
)
1
1.892-2.306
,12+ ,Ξ-np
CCQM
H. Garcilazo et al. [6]
2
(
)
1
1.814-2.153
,12+ ,Ξ-nn,Ξ-pp
CCQM
H. Garcilazo et al. [7]
2
4.50
Ξ-nn
ESC16
Настоящая работа
5.50
Ξ-np
ESC16
2.70; 4.40
Ξ-pp
ESC16
стояния с конкретным набором частиц. Например,
Наблюдение за поведением определителя с
для системы Ξ-np, в которой np-пара формиру-
энергией решаемой связанной системы однород-
ет подобное дейтрону состояние веса, составляют
ных уравнений Фаддеева показывает, что для
(
√
)
(
√
)
3-2
2
/9 и
6+2
2
/9 для состояний с J =
системы Ξ-np в области |E| < 20 МэВ имеется
только одно связанное состояние с энергией связи
= 1/2 и J = 3/2 соответственно. Поэтому с боль-
шой долей вероятности можно считать найденное в
Eb ≈ 5.5 МэВ. Эта энергия почти в 3 раза меньше,
данной работе связанное состояние системы Ξ-np
чем, например, предсказывается в работах [10,
как основное с (I, J+) = (1/2, 3/2+). Аналогичные
9] для состояния (1/2, 3/2+), которое можно
рассуждения для систем Ξ-nn и Ξ-pp позволяют
идентифицировать с системой Ξ-np. Других состо-
идентифицировать их собственные состояния с ве-
яний для системы Ξ-np в области |E| < 20 МэВ
(
√
)
(
√
)
совыми множителями
3-2
2
/9 и
6+2
2
/9
не прослеживается. Для системы Ξ-pp расчеты
для состояний с изоспинами I = 1/2 и I = 3/2
предсказывают существование двух состояний
с энергиями связи
2.7
и
4.4
МэВ в области
соответственно. Таким образом, с большой долей
вероятности системы Ξ-nn и Ξ-pp находятся в
|E| < 20 МэВ. Иными словами, в области энергий
состояниях с полным изоспином I = 3/2 и полным
5 < |E| < 20 система уравнений (13), записанная
угловым моментом, равновероятным между значе-
для системы частиц Ξ-pp, не имеет решения при
ниями J = 1/2 и J = 3/2.
используемом наборе двухчастичных t-матриц.
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
ПОИСК СВЯЗАННЫХ СОСТОЯНИЙ
425
50
50
Ξ-nn-ΛΣ-n-Σ0Σ-n
40
40
Мнимая
30
30
Вещественная
20
20
10
10
Ξ-pn-ΛΛn-ΛΣ0n
0
0
Вещественная
-10
-10
Мнимая
-20
-20
-30
-30
-40
-40
-50
-50
1.5
2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0
2
4
6
8
10
12
14
16
18
20
|E|, МэВ
|E|, МэВ
20
Ξ-pp-ΛΣ0p-Σ+Σ-p
15
Вещественная
10
Мнимая
5
0
-5
-10
-15
-20
1.5
2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0
|E|, МэВ
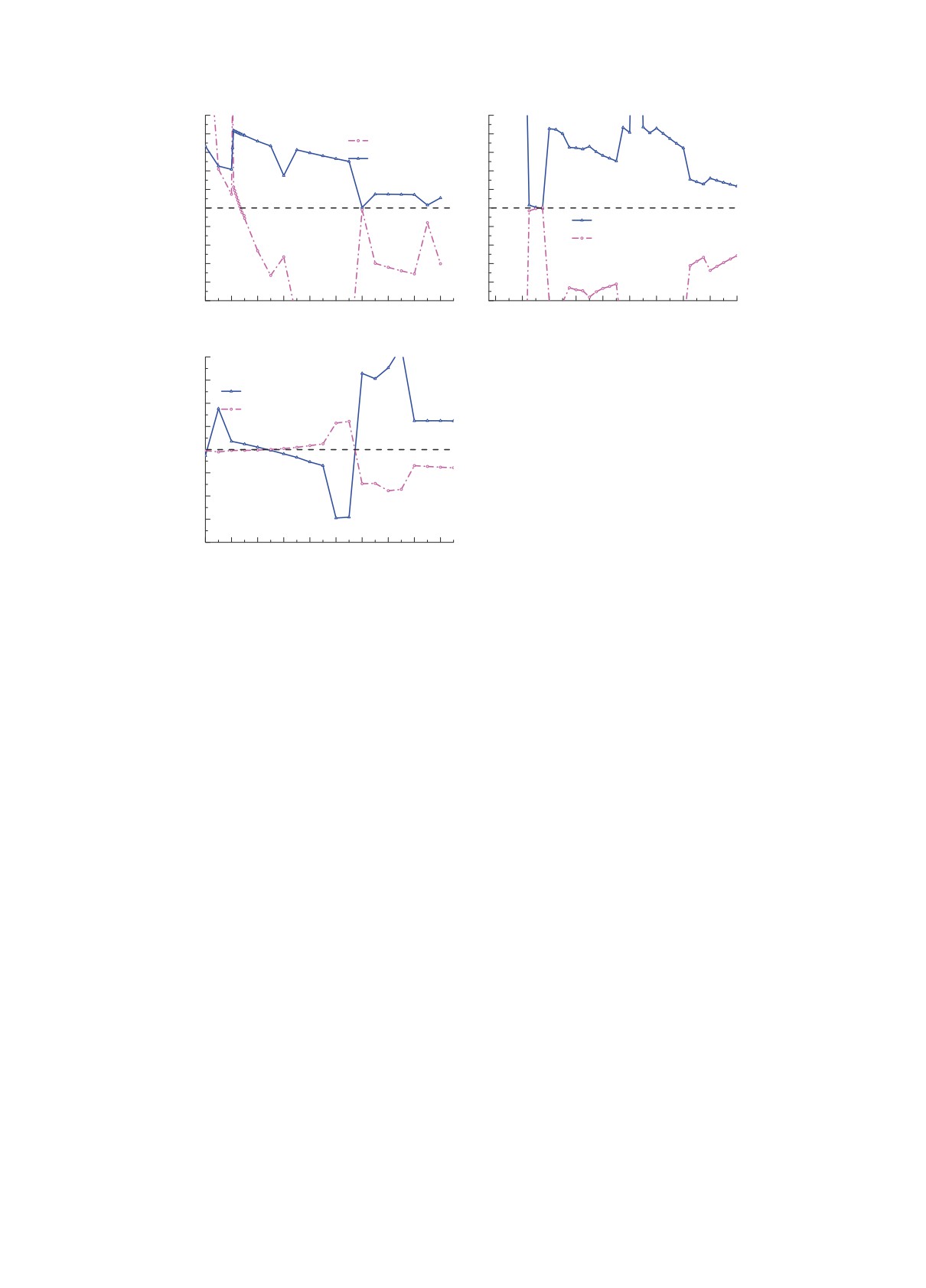
Рис. 2. Определители (масштаб произвольный) однородной системы уравнений Фаддеева для рассматриваемых систем
(указаны на рисунках) в зависимости от модуля кинетической энергии трех тел. Сплошная и штрихпунктирная кривые —
вещественная и мнимая части определителя соответственно. Точки пересечения вещественных частей определителя с
осью абсцисс соответствуют связанным состояниям систем с энергией |E| = |Eb|.
В отличие от системы Ξ-pp система Ξ-nn имеет
ESC16-модели Ξ-N-взаимодействия лучше соот-
только одно четко прослеживаемое состояние при
ветствуют кварковым расчетам CCQM работы [9].
Eb ≈ 4.5 МэВ. Как показали более подробные
В данной работе не обнаруживаются свидетельства
расчеты с шагом 20 кэВ в области |E| ≈ 2.17 МэВ,
существования резонансно-подобного состояния
только мнимая часть определителя (13) меняет
(I = 1/2, I = 1/2+) системы Ξ-NN в области
знак, тогда как вещественная часть не меняет
1.5 < |E| < 2.5 МэВ, найденного в работе [7].
знак. Учитывая зарядовую независимость pn- и
Следует отметить, что с точки зрения состава
nn-взаимодействий в Боннской параметризации
по частицам система Ξ-np (в отличие от систем
[20], притяжения в системе Ξ-n недостаточно
Ξ-nn и Ξ-pp c энергией связи Eb(Ξ-N) =
по сравнению с Ξ-p-системой для генерации
= 1.67 МэВ) не может иметь состояния с энергией
связанного состояния в системе Ξ-nn в области
связи Eb < 2.225 МэВ меньше, чем энергия связи
|E| ≈ 2.17 МэВ. Отметим, что решаемая система
дейтрона, поэтому привязку состояния (I = 1/2,
связанных однородных уравнений Фаддеева для
I = 1/2+) в табл. 1 к системе Ξ-np в области
системы Ξ-nn-ΛΣ-n-Σ-Σ0n является точной,
Eb < 2.225 МэВ следует понимать условной. Раз-
и ее решение в данной работе не включает
личие между значениями энергии связи системы
каких-либо приближений. Помимо этого, отличием
Ξ-NN в состоянии (I = 1/2, I = 1/2+), получен-
данной работы от результатов расчета работ [10,
ное в работах [6] и [7], как отмечалось во Введении,
9] является более современный вариант ESC-
связано только с влиянием трехчастичных каналов
модели Ξ-N-взаимодействия, а также использо-
ΛΣN и ΣΣN, которыми пренебрегалось в работе
вание соответствующей ESC микроскопической
[6]. С учетом уточненных данных работы
[7]
модели ΛN- и ΣN-взаимодействий
[21]. Как
резонансно-подобному состоянию (I = 1/2, I =
отмечалось во Введении, уже визуальный анализ
= 1/2+) системы Ξ-NN можно приписать как
потенциалов двух моделей ESC08c и ESC16
свидетельствует о различиях. Важно отметить,
систему Ξ-nn, так и систему Ξ-pp. Поскольку
что результаты данной работы с использованием
в работах [11, 8, 10, 12, 9], в отличие от работ
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
426
ЕГОРОВ
[6, 7], не проводился корректный учет связыва-
барион-барионном секторе со странностью S =
ния трехчастичных каналов Ξ-NN-ΛΣN-ΣΣN
= -2.
и Ξ-NN-ΛΛN-ΣΣN, то полученные в этих
Автор выражает благодарность Е.Б. Хитрук за
работах значения энергий связи не являются в
поддержку в подготовке рукописи. Работа выпол-
требуемой степени информативными. Как пока-
нена при финансовой поддержке фонда РФФИ,
зывают расчеты данной работы, пренебрежение
проект № 20-02-00004.
связыванием трехчастичных каналов при прочих
равных условиях существенно меняет положение
и факт наличия корней уравнения (13).
СПИСОК ЛИТЕРАТУРЫ
Дальнейший поиск связанных состояний си-
1.
J. K. Ahn, S. Aoki, K. S. Chung, M. S. Chung,
H. En’yo, T. Fukuda, H. Funahashi, Y. Goto,
стем Ξ-NN помимо уточнения парных Ξ-N-
A. Higashi, M. Ieiri, T. Iijima, M. Iinuma, K. Imai,
потенциалов должен сопровождаться сравнением
Y. Itow, J. M. Lee, S. Makino, et al., Phys. Lett. B
вкладов различных моделей гиперон-нуклонных
633, 214 (2006);
взаимодействий, неизбежно присутствующих в
расширенном трехчастичном фазовом простран-
2.
T. Tamagawa, J. K. Ahn, S. Ajimura, H. Akikawa,
стве системы Ξ-NN, возникающем из-за связы-
B. Bassalleck, A. Berdoz, D. Carman, R. E. Chrien,
вания трехчастичных каналов. Также представляет
C. A. Davis, P. Eugenio, H. Fischer, G. B. Franklin,
интерес влияние различных NN-моделей на энер-
J. Franz, T. Fukuda, L. Gan, L. Tang, et al., Nucl.
гию связи Ξ-NN-систем.
Phys. A 691, 234 (2001);
3.
Y. Yamamoto, T. Tamagawa, T. Fukuda, and
5. ЗАКЛЮЧЕНИЕ
T. Motoba, Prog. Theor. Phys. 106, 363 (2001);
В работе представлены результаты расчета
4.
K. Nakazawa, Y. Endo, S. Fukunaga, K. Hoshino,
энергий связи трехчастичных систем Ξ-nn, Ξ-np
S. H. Hwang, K. Imai, H. Ito, K. Itonaga, T. Kanda,
и Ξ-pp на основе решения связанных однородных
M. Kawasaki, J. H. Kim, S. Kinbara, H. Kobayashi,
интегральных уравнений Фаддеева относительно
A. Mishina, S. Ogawa, and H. Shibuya, Prog. Theor.
компонент трехчастичных T -матриц без исполь-
Exp. Phys. 2015, 033D02 (2015);
зования традиционной процедуры парциально-
волнового разложения. Точный учет связывания
5.
K. Aoki et al. (J-PARC Collab.), arXiv: 2110.04462
уравнений Фаддеева производился в каждой из
[nucl-ex].
рассматриваемых систем Ξ-nn-ΛΣ-n-Σ-Σ0n,
6.
H. Garcilazo, A. Valcarce, and T. F. Caram ´es, J. Phys.
G: Nucl. Part. Phys. 41, 095103 (2014);
Ξ-np-ΛΛn-ΛΣ0n и Ξ-pp-ΛΛp-ΛΣ0p. Двухча-
стичные t-матрицы для ΞN- и YY-взаимодействий
7.
H. Garcilazo, A. Valcarce, and T. F. Caram ´es, J. Phys.
находились путем решения связанных уравнений
G: Nucl. Part. Phys. 42, 025103 (2015);
Липпмана-Швингера для фиксированных спин-
изоспиновых состояний. Двухчастичные Ξ-N- и
8.
H. Garcilazo, Phys. Rev. C 93, 024001 (2016);
YY-потенциалы, генерирующие t-матрицы, на-
ходились с использованием микроскопической
9.
H. Garcilazo and A. Valcarce, Phys. Rev. C 93,
ESC16-модели. Рассчитанные по этим потен-
034001 (2016);
циалам полные сечения Ξ-p → Ξ-p и Ξ-p →
→ ΛΛ, а также ΛN → ΛN, ΣN → ΣN и ΣN →
10.
I. Filikhin, V. Suslov, and B. Vlahovic, Math. Model.
→ ΛN хорошо согласуются с немногочисленными
Geom. 5, 1 (2017);
экспериментальными данными. В качестве NN-
взаимодействия использовалось сепарабельное
11.
E. Hiyama, K. Sasaki, T. Miyamoto, D. Doi,
представление четвертого ранга Боннского NN-
T. Hatsuda, Y. Yamamoto, and Th. A. Rijken, Phys.
потенциала. Прямые численные расчеты энергий
Rev. Lett. 124, 092501 (2020);
связи рассматриваемых систем подтверждают
существование по одному связанному состоянию у
12.
K. Miyagawa and M. Kohno, Few Body Syst. 62, 65
систем Ξ-nn и Ξ-np с энергиями 4.5 и 5.5 МэВ
(2021).
соответственно. Кроме того, расчеты свидетель-
13.
M. N. Nagels, Th. A. Rijken, and Y. Yamamoto, arXiv:
ствуют о наличии двух связанных состояний
1504.02634 [nucl-th].
у системы Ξ-pp с энергиями 2.7 и
4.4
МэВ.
14.
M. N. Nagels, Th. A. Rijken, and Y. Yamamoto, Phys.
Данный результат можно считать опорным для
Rev. C 102, 054003 (2020);
последующей модификации ESC и последующих
моделей гиперон-нуклонных взаимодействий в
15.
L. D. Faddeev, Sov. Phys. JETP 12, 1014 (1961).
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023
ПОИСК СВЯЗАННЫХ СОСТОЯНИЙ
427
16.
H. Liu, Ch. Elster, and W. Glockle, Phys. Rev. C 72,
23. J. Adam et al. (STAR Collab.), Nat. Phys. 16, 409
054003 (2005);
(2020);
17.
M. Egorov, Phys. Rev. C 107, 014611(2023);
24. B. Sechi-Zorn, B. Kehoe, and J. Twitty, Phys. Rev.
также препринт:
175, 1735 (1968);
2021229/v1
18.
J. Revai and N. V. Shevchenko, Phys. Rev. C 90,
25. G. Alexander, U. Karshon, A. Shapira, and
034004 (2014);
G. Yekutiely, Phys. Rev. 173, 1452 (1968);
19.
W. Gl ¨ockle, H. Witała, D. H ¨uber, H. Kamada, and
J. Golak, Phys. Rep. 274, 107 (1996);
26. R. Engelmann, H. Filthuth, V. Hepp, and E. Kluge,
Phys. Lett. 21, 587 (1968);
20.
J. Haidenbauer, Y. Koike, and W. Plessas, Phys. Rev.
C 33, 439 (1986);
27. F. Eisele, H. Filthuth, W. Foehlisch, V. Hepp, and
21.
M. M. Nagels, Th. A. Rijken, and Y. Yamamoto,
G. Zech, Phys. Lett. B 37, 204 (1971);
Phys. Rev. C 99, 044003 (2019);
28. H. Garcilazo, A. Valcarce, and J. Vijande, Phys. Rev.
22.
M. Egorov and V. Postnikov, Nucl. Phys. A 1009,
C 94, 024002 (2016);
122172 (2021);
SEARCHING FOR THE BOUND STATES
IN THE Ξ−nn-, Ξ−pn-, AND Ξ−pp-SYSTEMS
M. V. Egorov1)
1)Physics department, Tomsk State University, Russia
Searching for the bound states in the systems Ξ-nn, Ξ-pn, and Ξ-pp was done with the usage of solution
of coupled homogeneous integral Faddeev equations written with respect to the T-matrix components.
In these equations direct integration over the angular variables with the precise consideration of the
three-body coupling in the phase space of the each systems Ξ-nn-ΛΣ-n-Σ-Σ0n, Ξ-np-ΛΛn-ΛΣ0n
and Ξ-pp-ΛΛp-ΛΣ0p is used instead of the traditional partial-wave decomposition. The only ingredients
of the presented method are two-body t-matrices, which were found by solving the coupled Lippmann-
Schwinger integral equations in the case of paired Ξ-N-interaction for systems ΞN-ΛΛ-ΣΣ in the state
(I = 0,1S0), ΞN in the state (I = 0,3S1), ΞN-ΛΣ in the state (I = 1,1S0), and ΞN-ΛΣ-ΣΣ in the state
(I = 1,3S1). To obtain two-body Ξ-N-, YY-, and YN-interactions generating t-matrices, an updated
version of the ESC16 microscopic model is used. Two-body NN-interaction was reconstructed on the
basis of the charge-dependent Bonn model. Direct numerical calculations of the binding energies of the
systems under consideration clearly indicate the existence of one bound state with binding energies of 4.5
and 5.5 MeV for Ξ-nn- and Ξ-np-systems, respectively, and two states with binding energies of 2.7 and
4.4 MeV for the system Ξ-pp.
ЯДЕРНАЯ ФИЗИКА том 86
№3
2023