ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 4, с. 452-460

ЯДРА

СПИН-ИЗОСПИНОВЫЙ ОТКЛИК ЯДРА

В РАМКАХ ФУНКЦИОНАЛА ФАЯНСА

Поступила в редакцию 18.01.2023 г.; после доработки 18.01.2023 г.; принята к публикации 20.01.2023 г.

Представлено эффективное приближение к полностью самосогласованным расчетам силовых функ-

ций β-распада. Оно базируется на описании основных состояний в рамках модифицированного

энергетического функционала плотности Фаянса (DF3-f) и квазичастичного приближения случайной

фазы в континууме (CQRPA). Уточнен изовекторный параметр h-2 объемной части функционала,

допустимый диапазон которого был определен нами ранее из ограничений на параметры уравнения

состояния ядерной материи — энергию симметрии и ее производную при равновесной плотности,

полученные из совместного анализа величины “нейтронной шубы” ΔRnp ядер²⁰⁸Pb и⁴⁸Ca, найденной

в экспериментах PREX-II, CREX, результатов ab initio расчетов свойств основных состояний ядер

с взаимодействием N3LO и систематики данных по массам нейтронных звезд из астрофизических

наблюдений. Проведены новые расчеты гамов-теллеровских силовых функций для дважды магических

ядер²⁰⁸Pb и¹³²Sn. Оценена точность глобальных DF3-a + CQRPA-расчетов периодов бета-

распада тяжелых (квази)сферических ядер с Z = 81-83 и T1/2 < 240 с в предложенной модели.

Экспериментальные времена жизни описываются с точностью до фактора 5.

DOI: 10.31857/S0044002723040098, EDN: EGAIAA

1. ВВЕДЕНИЕ

после появления первых теоретических оце-

нок, использовавших идеи вигнеровской SU(4)-

Спин-изоспиновые резонансы занимают важ-

симметрии [3] и аргументы о возможности на-

ное место в фундаментальных ядерно-физических

блюдения спиновых резонансов в ядрах, несмот-

исследованиях. Изучение их свойств играет за-

ря на наличие деструктивных факторов: спин-

метную роль в развитии современных микроско-

орбитального взаимодействия и сильной фрагмен-

пических моделей атомного ядра, прежде всего

тации из-за несохранения квантового числа полно-

мультиконфигурационной модели оболочек

[1]

го спина [4]. Несколько позже в микроскопических

и самосогласованной теории конечных ферми-

моделях — RPA с сепарабельным взаимодействи-

систем (ТКФС) А.Б. Мигдала [2]. К настоящему

времени наиболее изучены гигантский резонанс

ем [5] и упрощенной версии теории конечных

Гамова-Теллера (GTR) и пигми-резонансы в окне

ферми-систем [6] был дан более детальный, физи-

β-распада с квантовыми числами ΔL = 0, ΔS = 1,

чески адекватный прогноз полной силовой функции

ΔT = 1, спин-дипольные резонансы (SDR, ΔL =

β-распадного типа, включающей как низколежа-

= 1, ΔS = 1, ΔT = 1), возбуждаемые операторами

щие пигми-резонансы, так и новый гигантский

резонанс Гамова-Теллера. Эти предсказания были

στ^-, и изоспиновые моды фермиевского типа

подтверждены при обнаружении указанных мод

ΔL = 0, ΔS = 0, ΔT = 1 — изобар-аналоговые

резонансы (IAR), индуцируемые операторами

возбуждений в реакции перезарядки (p, n) при

промежуточных начальных энергиях и малых углах

изоспина τ^-.

рассеяния [7].

Интерес к зависящим от спина зарядово-

обменным возбуждениям ядер возник сразу же

В последнее время исследования фокусируются

на детальном изучении спектрального распределе-

¹⁾Национальный исследовательский центр “Курчатовский

ния силы гамов-теллеровских и спин-дипольных

институт”, Москва, Россия.

возбуждений в широком энергетическом интерва-

²⁾Лаборатория теоретической физики им. Н.Н. Боголюбо-

ле. Особый интерес представляют эксперименты

ва, ОИЯИ, Дубна, Россия.

на современных ускорителях радиоактивных ионов

³⁾Московский физико-технический институт (нацио-

(FRIB). До сих пор они касались, в основном, из-

нальный исследовательский университет), Долгопрудный,

Россия.

мерений масс сильно нейтронно-избыточных изо-

^*E-mail: Borzov_IN@nrcki.ru

топов и интегральных характеристик их β-распада.

^**E-mail: Tolokonnikov_SV@nrcki.ru

Зарядово-обменные реакции типа (p, n) [8] и (n, p)

452

СПИН-ИЗОСПИНОВЫЙ ОТКЛИК ЯДРА

453

[9] в обратной кинематике дают широкие возмож-

В настоящей работе самосогласованное опи-

ности спектроскопических исследований, включа-

сание свойств основных состояний базируется на

ющих измерения силовых функций нестабильных

новой версии энергетического функционала плот-

нейтронно-избыточных ядер, как в окне β-распада,

ности DF3-f, предложенного в нашей работе [26]

так и в области гигантских резонансов.

для описания изобар-аналогового резонанса. Кро-

ме экранировки обменного кулоновского члена за

Дополнительный анализ периодов полураспа-

да T1/2 и вероятностей запаздывающей мульти-

счет кулон-ядерного взаимодействия [27] “в игру

нейтронной эмиссии P_xn позволяет в некоторых

включен” изовекторный параметр h-2 объемной

случаях “реконструировать” значительную часть

части функционала. Раньше для его надежного

силовой функции спин-изоспиновых возбуждений

определения в [17] не имелось достаточного объема

в окне β-распада. Конкуренция силы переходов

данных. Теперь в [28] нами найден допустимый

Гамова-Теллера (GT) и переходов первого запрета

интервал значений h-2. Использованы ограничения

(FF) в окне β-распада определяет полные скорости

на параметры уравнения состояния ядерной мате-

β-распада сильно нейтронно-избыточных ядер. Их

рии — энергию симметрии и ее производную при

надежный прогноз исключительно важен и для мо-

равновесной плотности, полученные из совмест-

делирования временной шкалы процесса быстрого

ного анализа величины “нейтронной шубы” ΔRnp

астрофизического нуклеосинтеза и выходов произ-

ядер²⁰⁸Pb и⁴⁸Ca, найденной в экспериментах

водимых элементов [10]. Знание полных силовых

PREX-II, CREX [29, 30], ab initio расчетов EOS

функций спин-изоспиновых возбуждений неста-

и свойств основных состояний ядер с взаимодей-

бильных изотопов с большим избытком нейтронов

ствием N3LO и систематики данных по массам

дает ограничения на недостаточно хорошо извест-

нейтронных звезд из астрофизических наблюде-

ные спиновые компоненты ядерных функционалов

ний [31-35]. Учтены также данные, полученные в

плотности.

2017 г. коллаборацией LIGO-Virgo [36] при обна-

Объем новой информации по спин-изоспиновым

ружении гравитационных волн от слияния двойных

резонансам и β-распаду весьма значителен. Ос-

нейтронных звезд.

новные приближения, используемые в теоретиче-

Появление большого объема новых данных

ских подходах, обсуждались в ранних обзорах по

делает актуальным возвращение к проблеме спин-

GT-резонансам [11-14].

изоспинового отклика ядра. Цель работы — дать

более подробное описание формализма DF3-

Наиболее надежную экстраполяцию силовых

a + CQRPA и изучить влияние модификации

функций спин-изоспиновых возбуждений для

изовекторной объемной компоненты ЭФП DF3-a

экстремальных значений N/Z дают самосогласо-

на гамов-теллеровскую силовую функцию рефе-

ванные модели. Реалистичное описание распре-

деления силы спин-изоспиновых возбуждений в

рентных дважды магических ядер²⁰⁸Pb,¹³²Sn.

окне β-распада и в области гигантских резонансов

С уточненным параметром h-2 рассчитаны GT

обеспечивается моделью оболочек с взаимодей-

силовые функции дважды магического ядра¹³²Sn,

ствием [1]. Эти расчеты выполнялись вблизи за-

а также периоды β-распада (квази)сферических

мкнутых оболочек Z = 20, 28, 50 и N = 28, 50, 82.

нейтронно-избыточных ядер с Z = 81-83 и T1/2 <

Для более тяжелых ядер и ядер с незаполненными

240 с.

оболочками расчеты по мультиконфигурационной

оболочечной модели требуют ресурсов на пределе

возможностей современных суперкомпьютеров.

2. КРАТКОЕ ОПИСАНИЕ ФОРМАЛИЗМА

Для глобальных расчетов спин-изоспиновых

Опишем самосогласованный подход ЭФП к

резонансов и β-распадных характеристик для

свойствам основных состояний ядер со спарива-

нескольких тысяч ядер, необходимых для астро-

нием. Энергетический функционал зависит от нор-

физического моделирования, эффективен подход

мальной ρ и аномальной плотностей ν: E₀ [ρ, ν] =

∫

энергетического функционала плотности [15, 16].

E (ρ(r) ,ν (r))d³r. Гамильтониан среднего по-

Существует большое количество расчетов на осно-

ля h(1, 2) и потенциал спаривания Δ (r) находятся

ве новых нерелятивистских [17] и релятивистских

как вариации ЭФП по ρ и ν:

[18, 19] энергетических функционалов плотности, а

δE

также стандартного функционала Скирма [2]. Для

h(1,2) =

ядер со спариванием для таких расчетов широко

δρ(2,1)

использовались модели CQRPA [21, 22] и RQRPA

δE

[23], основные эффекты квазичастично-фононного

Δ (r) =

δν (r)

взаимодействия и сложных конфигураций эффек-

тивно учитывались в моделях FRSA [24] и QTBA

где 1 = (r₁, σ₁), 2 = (r₂, σ₂) — пространственные и

[25, 26].

спиновые координаты.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

454

БОРЗОВ, ТОЛОКОННИКОВ

Нами используется ЭФП Фаянса [17, 26, 28,

состояния ядерной материи — энергию симметрии

37] с более сложной зависимостью от ядерной

и ее производную при равновесной плотности —

плотности ρ, чем в ЭФП Скирма. Для объемной и

стало возможным найти допустимый интервал

поверхностной частей ЭФП эта зависимость симу-

значений h-2 = 1.0-1.5.

лируется дробно-линейным Паде-приближением,

Отклик ядра на внешнее зарядово-обменное

в схематической форме ее можно записать: ϵ (ρ) =

поле V₀ =^Q exp(-iωt) (+ эрмитово сопряженный

= (1 + h₁)ρ^α/(1 + h₂) ρ^σ, где h₁, h₂, α, σ — пара-

оператор) в самосогласованной теории конечных

метры. Как можно видеть, значение h-2 = 0 отве-

ферми-систем [2] описывается уравнением для эф-

чает более жесткой зависимости функционала от ρ,

фективного пол

V . Для ядер со спариванием в

как у ЭФП Скирма.

нейтронной и протонной системах оно имеет сле-

В настоящей работе мы применяем модифици-

дующий вид (в суперматричном представлении):

рованный ЭФП Фаянса DF3-f [27] с “активиро-

V (ω)

V₀ (ω)

FAˆ(ω

V (ω),

(3)

ванным” параметром h-2, согласованным с совре-

менными ограничениями, полученными из анализа

где

уравнения состояния ядерной материи, проведен-

⎛

⎞

⎛

⎞

ного в нашей работе [28]. Для функционала DF3-a

e_qV₀

⎜

⎟

⎜

⎟

уравнение состояния имеет вид

⎜

⎟

⎜

⎟

V =

⎜

⎟,

V₀ =

⎜

⎟,

(4)

⎝^d

⎠

⎝⁰

⎠

E (ρ,δ) /A = E (ρ_p,ρ_n) /ρ,

(1)

d₂

E (ρ,δ) /A =

(2)

⎛

⎞

)2/3 [

]

^{ 3⁽ρ

F F^ωξ F^ωξ

=ε_0F

(1 - δ)5/3 + (1 + δ)5/3 +

⎜

⎟

ρ₀

⎜

⎟

F =

⎜

^ξω F^ξ

⎟

(5)

)

⎝F

⎠

1 - h+1 (ρ/ρ₀)

⁽ρ

a₊

F^ξω

F^ξ

1 + h+2 (ρ/ρ₀)σ

ρ₀

)

}

1 - h-1 (ρ/ρ₀)

⁽ρ

Здесь^Q — зависящий от спина и изоспина одноча-

−

δ²

стичный оператор (^Q = σ_ατ_β, qτ_α, Pτ_α). Матрица

1 + h-2 (ρ/ρ₀) ρ0

A 4 × 4 состоит из интегралов по энергии ϵ от про-

Здесь εpF, ρ_p, εnF и ρ_n — энергия Ферми и плот-

изведений различных комбинаций функции Грина

ность протонов (нейтронов), ρ = ρ_p + ρ_n, δ =

G(ϵ) и функции Горькова F⁽¹⁾ (ϵ) и F⁽²⁾ (ϵ). Они

= (ρ_p - ρ_n) /ρ, ρ₀ = 2k^0F3/3π² = 0.164(7) фм-3 —

приведены в книге [2], и наиболее важный из них

равновесная плотность симметричной ядерной

имеет следующий вид:

материи, δ = (ρ_n - ρ_p) /ρ — параметр асимметрии,

∫

[

dε

ℏk^0F — импульс Ферми нуклонов одного сорта

G(ε) G(ε + ω) +

(6)

2πi

частиц, a+,- и h+,-1,2 — безразмерные параметры,

]

определяемые из сравнения с эксперименталь-

+ F(1) (ε)F(2) (ε + ω)

ными данными по основным состояниям; для

функционала DF3-a используется значение σ = 1,

Здесь знак “+” между двумя слагаемыми интеграла

C₀ = (dn/dε_F)¹ = 4ε_0F/3ρ₀ — обратная плотность

(6) соответствует t-нечетному полю.

состояний нуклонов одного сорта на поверхности

В стандартных обозначениях ТКФС для сило-

Ферми в точке равновесия симметричной материи.

вой функции имеем следующее выражение:

Уравнение состояния для чистой нейтронной

материи соответствует значению параметра изо-

S (ω,q) = -

Im P (ω,q) =

(7)

спиновой асимметрии δ = 1.

(

)

Энергия симметрии E_sym (ρ) = E (ρ, 1) /N -

Im e_q

V₀Aˆ(ω

V (ω, q)

- E (ρ,0)/A и ее производная по плотности

L(ρ) = 3ρ∂E_sym (ρ) /∂ρ определяются изовектор-

Элементы матрицы эффективного взаимодей-

ной частью функционала плотности. Как отмечено

ствия (5) являются различными вторыми вариа-

выше, в наших предыдущих расчетах изовекторный

ционными производными ЭФП в зависимости от

параметр h-2 принимался равным изоскалярному

нормальной ρ и аномальной плотности ν:

h⁺² ввиду недостатка в данных для фитирования.

δ²E

Однако, как показано в работе [28], из совре-

F =

;

F^ωξ = F^ξω =

;

F^ξ =

(8)

менных ограничений на параметры уравнения

δρ²

δρδν

δν²

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

СПИН-ИЗОСПИНОВЫЙ ОТКЛИК ЯДРА

455

Здесь F в (8) — спин-изоспиновая компонента

где m_π — пионная масса,

f_π — константа пион-

частично-дырочной (ph) амплитуды Ландау-

нуклонной связи, модифицированная в ядерной

Мигдала, которая входит в (3) в случае, когда

среде. В ТКФС обычно принимается, что она от-

внешнее поле V₀ зависит от спина. Fξ (1) —

личается от свободной константы f_π фактором

“аномальная” компонента обобщенной ампли-

f_π = (1 - 2ζ^πs) f_π.

(13)

туды, или, другими словами, эффективное NN-

взаимодействие в частично-частичном (pp) канале,

Введенный здесь новый квазичастичный заряд ζ^πs,

отвечающее за зависимость спаривательной части

вообще говоря, отличается от заряда ζ_s в (11)

функционала от нормальной плотности. Оно вхо-

[2], однако отличие это, по-видимому, невелико,

дит в уравнение для щели и включает смешанные

и можно использовать ζ^πs ≃ ζ_s. Π_Δ в знаменате-

ле (12) — это Δ-изобарная компонента пионно-

производные F^ωξ, F^ξω, обеспечивающие допол-

го массового оператора, которая берется в виде

нительную связь pp-канала с ph- и hh-каналами

[2, 38]:

амплитуды. (Изотопные индексы в отношениях

(3)-(8) для краткости опущены.)

0.9k²

Π_Δ = -

(14)

Для изоспиновых зарядово-обменных возбуж-

1 + 0.23k²/m2π

дений, в частности для IAR, уравнения для эф-

Далее, следуя [39], добавляется второй тензорный

фективного поля содержат амплитуду F^-, которая

член обмена ρ-мезоном:

определяется второй вариационной производной

того же ЭФП по изовекторной плотности ρ_- =

f2ρ (σ₁ × k)(σ₂ × k)

F_ρ =

(τ₁τ₂) .

(15)

= ρ_n - ρ_p:

m2ρ

m2ρ + k²

δ²E

F^- =

(9)

Здесь m_ρ — масса ρ-мезона, а

f_ρ — константа

(δρ_-)²

связи ρNN, модифицированная в ядерной сре-

де благодаря вкладу короткодействующих NN-

Для спин-изоспиновых возбуждений и β-

корреляций. Согласно

[38], этот вклад может

распада в модели DF3-a + CQRPA используется

быть приближенно учтен подавлением квадрата

эффективное приближение из нашей работы [22].

свободной константы f2ρ в два с половиной раза.

Характеристики основных состояний описываются

Вводя обозначения, аналогичные (13), имеем:

полностью самосогласованно с функционалом

Фаянса DF3-f [27]. Как показано в [37], пренебре-

f_ρ = (1 - 2ζ^ρs)f_ρ.

(16)

жение спиновыми компонентами в ЭФП вызывает

Нормируя тензорные константы соразмерно пара-

сравнительно небольшую ошибку в энергиях связи

метрам g, g^′ в (11), переобозначим коэффициенты в

(≈100 кэВ). Поэтому спин-изоспиновое эффек-

(12), (15) следующим образом:

тивное NN-взаимодействие в канале частица-

дырка (ph) не как вторая вариация ЭФП, а вво-

f2π

= C₀gtπ (1 - 2ζπs )2 ,

(17)

дится независимым образом — в виде контактного

m2π

NN-взаимодействия Ландау-Мигдала в канале

частица-дырка (ph), дополненного однопионным

f2ρ

π- и ρ-мезонным обменами, модифицированными

= C₀g^tρ (1 - 2ζ^ρs)² .

(18)

m2ρ

ядерной средой [38]:

В канале частица-дырка (pp) для расчета ос-

F^ω = F₀ + F_π + F_ρ.

(10)

новного состояния используется не зависящее от

Центральный, зависящий от спина и изоспина,

плотности изовекторное (T = 1) спаривание ну-

член (в импульсном представлении) имеет вид

левого радиуса с силой, зависящей от массового

[

]

числа A:

F₀ = C₀

g^′ (σ₁σ₂) (τ₁τ₂)

(11)

F^ξ

=C₀f_ξ.

(19)

где нормировочная постоянная C₀ = (dn/dε_F)-1 =

Предполагается также, что в QRPA-расчетах

= 300

МэВ фм-3, а g^′ — феноменологический

спин-изоспиновых возбуждений индуцированное

параметр, известный как

“константа Ландау-

изоскалярное (T = 0) протон-нейтронное эффек-

Мигдала”. Далее добавляется тензорный член,

тивное NN-взаимодействие в канале частица-

обусловленный однопионным обменом

[2]: π-

частица (динамическое спаривание) имеет анало-

мезонный член имеет вид

гичную форму. Такой anzats для эффективного

NN-взаимодействия применяется для анализа

f2π (σ₁k) (σ₂k)

F_π = -

(τ₁τ₂) ,

(12)

смягчения пионных мод в ядрах [12]. Он дает на-

m2π m2π + k² + Π_Δ

дежное описание спин-изоспиновых возбуждений,

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

456

БОРЗОВ, ТОЛОКОННИКОВ

), 1/МэВ

²⁰⁸Pb

GTR

S( )

2.0

= 1 МэВ

S₀(

), (h₂ = 3)

S( )

= 1)

S₀( ), (h2

1.5

1.0

0.5

, МэВ

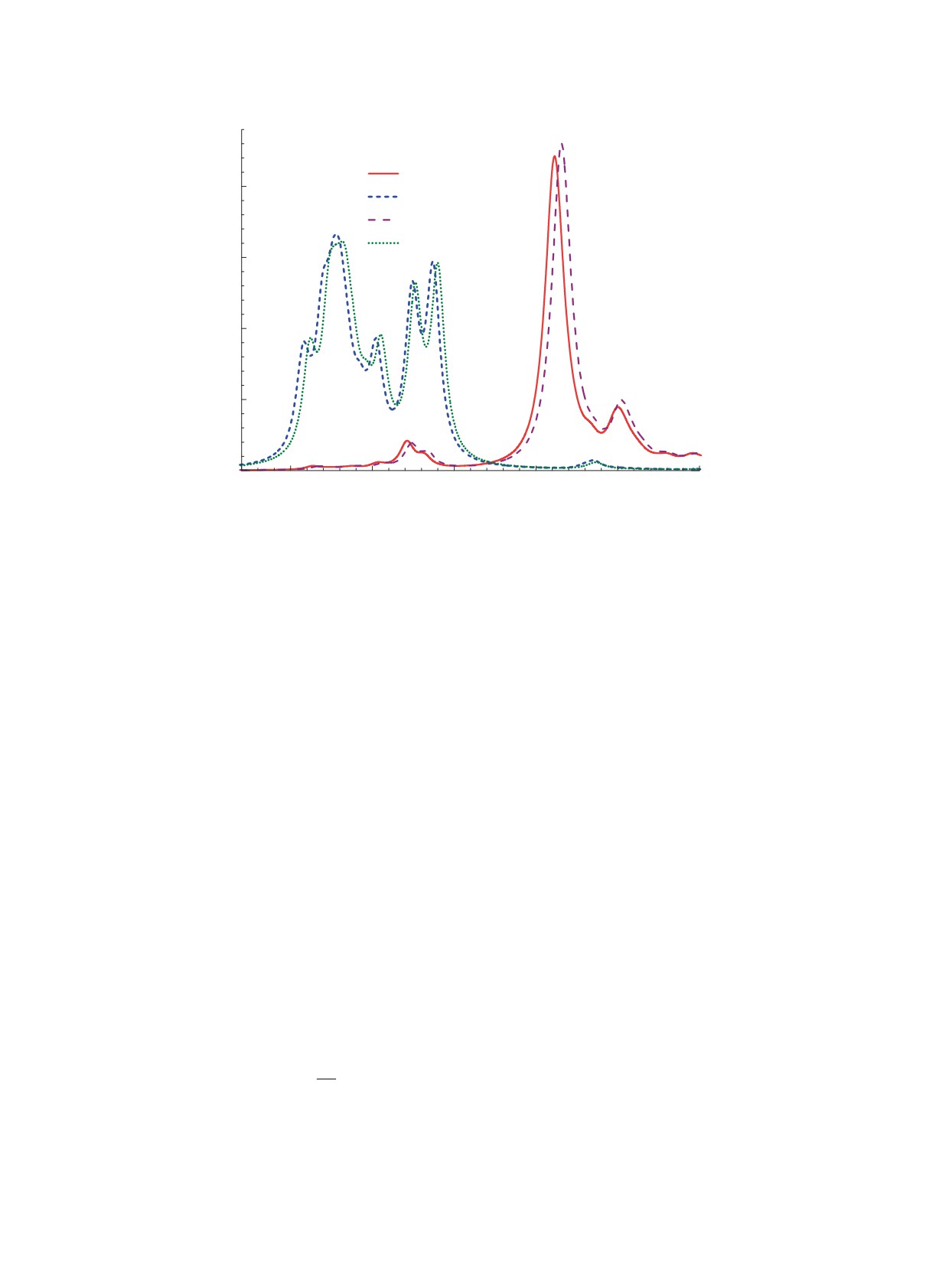
Рис. 1. Силовая функция²⁰⁸Pb. Расчет с функционалом DF3-f для двух значений h-2 = 1, 3 (детали см. в тексте).

низколежащих состояний аномальной четности и

При расчете силовых функций зарядово-

GT-резонансов [21], а также магнитных моментов

обменных спин-изоспиновых возбуждений, кроме

[40]. Важно, что используемое приближение (DF3-

естественной escape-ширины Γ^↑, связанной с

a + CQRPA) не меняет глобального характера са-

вылетом нуклона в континуум, можно добавить

мосогласованного подхода, поскольку параметры

спредовую ширину Γ^↓. С ее помощью полумик-

функционала и используемого NN-взаимодействия

роскопически учитывается фрагментация возбуж-

остаются универсальными (одинаковыми для всех

дений, связанная со сложными конфигурациями.

зарядовых и массовых чисел Z, A). Корреляции,

В рамках континуум-QRPA ширина линейно зави-

более сложные, чем в QRPA, включаются путем

сит от энергии возбуждения в дочернем ядре [41].

перенормировки спин-зависимых мультипольных

В настоящих расчетах для удобства представления

операторов с помощью не зависящего от энер-

результатов используются постоянные спредовые

гии возбуждения фактора подавления Q1/2 =

ширины Γ^↓ = 0.5 и 1 МэВ.

= (g_A/G_A). Таким образом, соответствующие

В расчетах использованы следующие значения

спин-изоспиновые вершины содержат дополни-

констант взаимодействия: g^′ = 1.1 и мезон-нуклон-

тельный фактор Q. Считается, что фактор по-

давления однопионной компоненты остаточного

ной связ

f_π = -1.45(1 - 2ζ^πs)

f_ρ = +2.64(1 -

взаимодействия также равен Q (хотя, в принципе,

− 2

ζρs) в нормировке C0 = 300 МэВ фм³, и фактор

он может быть выбран независимо).

подавления ζ_s = ζ^πs =

ζρs = 0.08. Следует отметить,

что все значения силовых констант определены

ранее из расчетов зарядово-обменных возбужде-

ний [42]. Они не зависят от массового числа A,

3. ОПИСАНИЕ GT-СИЛОВЫХ ФУНКЦИЙ

дают хорошее описание магнитных моментов [40]

В²⁰⁸Pb И¹³²Sn

и периодов β-распада [22] — в данных расчетах их

Силовые функции спин-мультипольных воз-

значения не изменяются.

буждений представляют отклик ядра на внешнее

На рис. 1 для референтного дважды магического

[

]

поле V₀τ_± =

(2L + 1)!!/q^L

j_L (qr) T^MJLS (n,σ) τ_±.

ядра²⁰⁸Pb приведены распределения GT-силы (ω

√

отсчитывается от основного состояния родитель-

При L = 0 и q → 0 величина 1/

4πV₀τ_± совпадает

ского ядра), рассчитанные с модифицированным

со стандартным оператором гамов-теллеровского

функционалом DF3-a для предельных значений

β-распада. Энергии GT-возбуждений, рассчи-

танные в CQRPA, отсчитываются от основного

изовекторного параметра: h-2 = 1.0, 3.0, опреде-

состояния родительского ядра.

ленных в [28]. Показаны силовые функции, полу-

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

СПИН-ИЗОСПИНОВЫЙ ОТКЛИК ЯДРА

457

S(E_x), 1/МэВ

¹³²Sn

GTR

3.0

)

S(E_x

2.5

S₀(E_x)

= 0.5 МэВ

2.0

1.5

1.0

0.5

E_x, МэВ

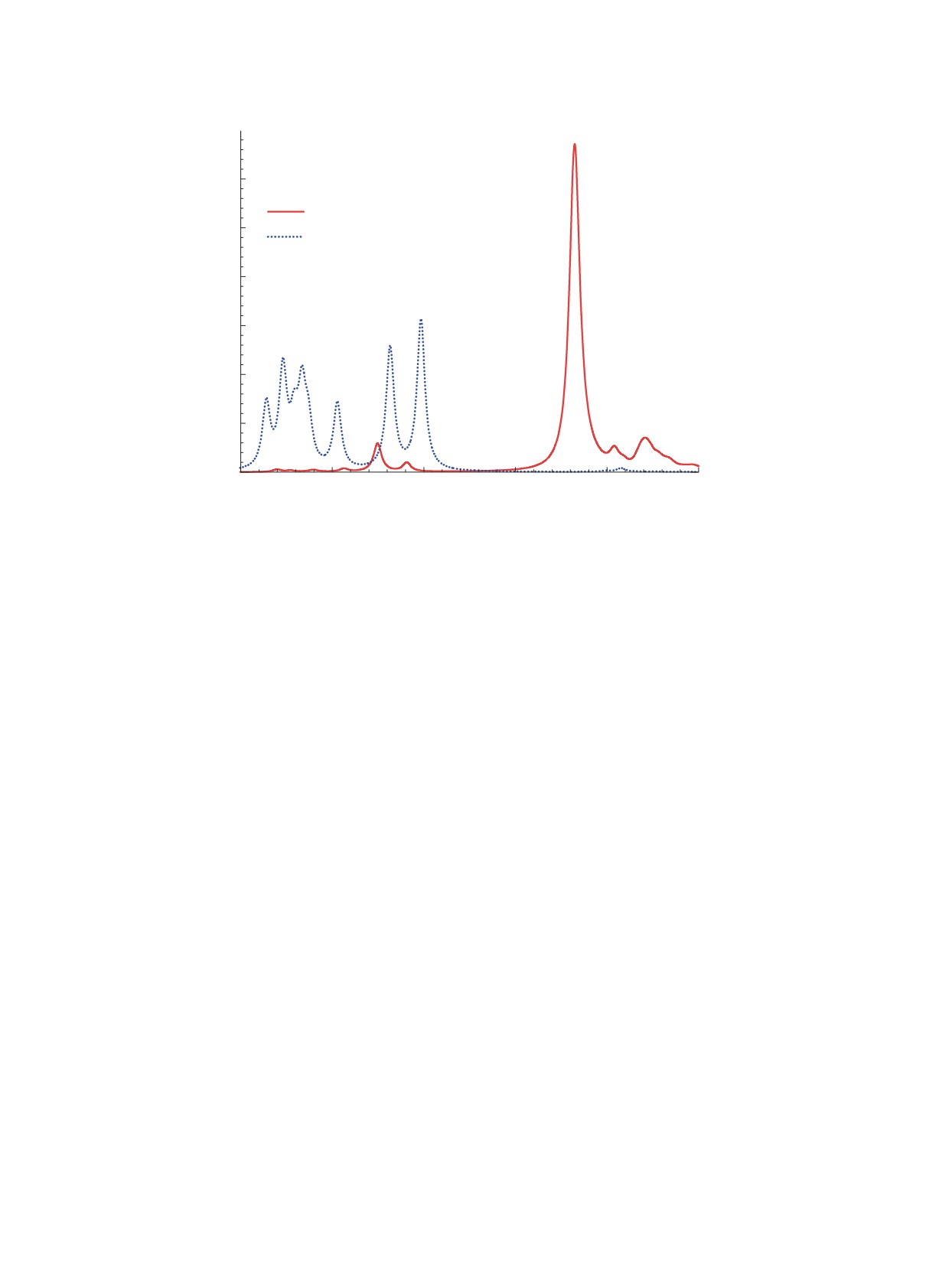
Рис. 2. Силовая функция¹³²Sn. Расчет с функционалом DF3-f для значения параметра h-2 = 3.

ченные как без, так и с включением эффективного

было показано в [12], это привело бы к нереа-

NN-взаимодействия. В распределении GT-силы

листичному смягчению спин-изоспинового отклика

выделяются низколежащие пигми-резонансы, свя-

ядра (так называемых пионных мод) из-за прибли-

занные в основном с переходами “поляризации

жения к точке π-конденсатной неустойчивости.

кора” j = l ± 1/2 → j = l ± 1/2 и “обратного спин-

Возможность понизить энергию GT-резонанса

флипа” j = l - 1/2 → j = l + 1/2, и основной пик

изучалась в рамках подхода релятивистского

гигантского GT-резонанса, преимущественно свя-

QRPA [19]. Без изменения константы g^′ этого мож-

занный с прямыми спин-флип переходами ти-

но достичь введением контактного изовекторно-

па j = l + 1/2 → j = l - 1/2, т.е. 1h11/2 → 1h9/2,

псевдовекторного взаимодействия в ph-канале:

1i13/2 → 1i11/2.

V_PV = -α_PV [γ₅γ^ντ]₁ [γ₅γ_ντ]₂. Для ядра 208Pb

Как видно, для значения свободного пара-

при достаточно сильном притяжении (большое

-α_PV ) получалось полное совпадение с экспери-

метра h-2 = 1 самосогласованный расчет дает

ментом, что вряд ли имело смысл, так как поправка

превышение энергии максимума GT-резонанса на

на квазичастично-фононное взаимодействие в [28],

2.30 МэВ, что типично для RPA-расчетов с явным

как и в нашем подходе, не учитывалась.

учетом только 1p1h-конфигураций и без учета

квазичастично-фононного взаимодействия. В то

На рис. 2 показана GT-силовая функция для

же время расчет в модифицированном ЭФП DF3-f

нестабильного дважды магического ядра¹³²Sn,

с найденным в [28] значением h-2 = 1.5 умень-

рассчитанная с модифицированным функционалом

шает расхождение до 1.80 МэВ. Исчерпывание

DF3-f для значения изовекторного параметра:

оболочечного правила сумм 3(N - Z) в расчете

h-2 = 1.5, из допустимого интервала, найденного в

составляет 13% для области энергий, включающей

[28] (здесь E_x — энергия возбуждения в дочернем

пигми-резонансы, и 62% до энергии E_x = 30 МэВ

ядре, даны силовые функции, полученные без и с

(экспериментальное значение S (E_x < 25 МэВ) =

эффективным NN-взаимодействием). Рассчитан-

= 64 ± 5% [43, 44]).

ная энергия максимума GTR, как и в²⁰⁸Pb, выше

Как известно, в схеме с учетом однопионного

(на 2.2 МэВ) экспериментальной энергии максиму-

обмена, используемой нами, значение силовой кон-

ма GT-резонанса E_x = 16.4 ± 0.4 ± 0.4 МэВ [45].

станты g^′ = 1.1 (надежно найденное в предыдущих

Таким образом, в¹³²Sn, как и в²⁰⁸Pb, масштаб

расчетах) не может быть уменьшено для улучшения

расхождения рассчитанной энергии GTR с экспе-

согласия с экспериментальным значением энергии

риментом близок к оценкам вклада квазичастично-

максимума GTR ω = 19.2 ± 0.2 МэВ [43, 44]. Как

фононной связи, получаемой в QTBA-расчетах

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

458

БОРЗОВ, ТОЛОКОННИКОВ

Z = 81 83, T < 240 c,

< 0.05

0.1

210

220

100

1000

exp

, c

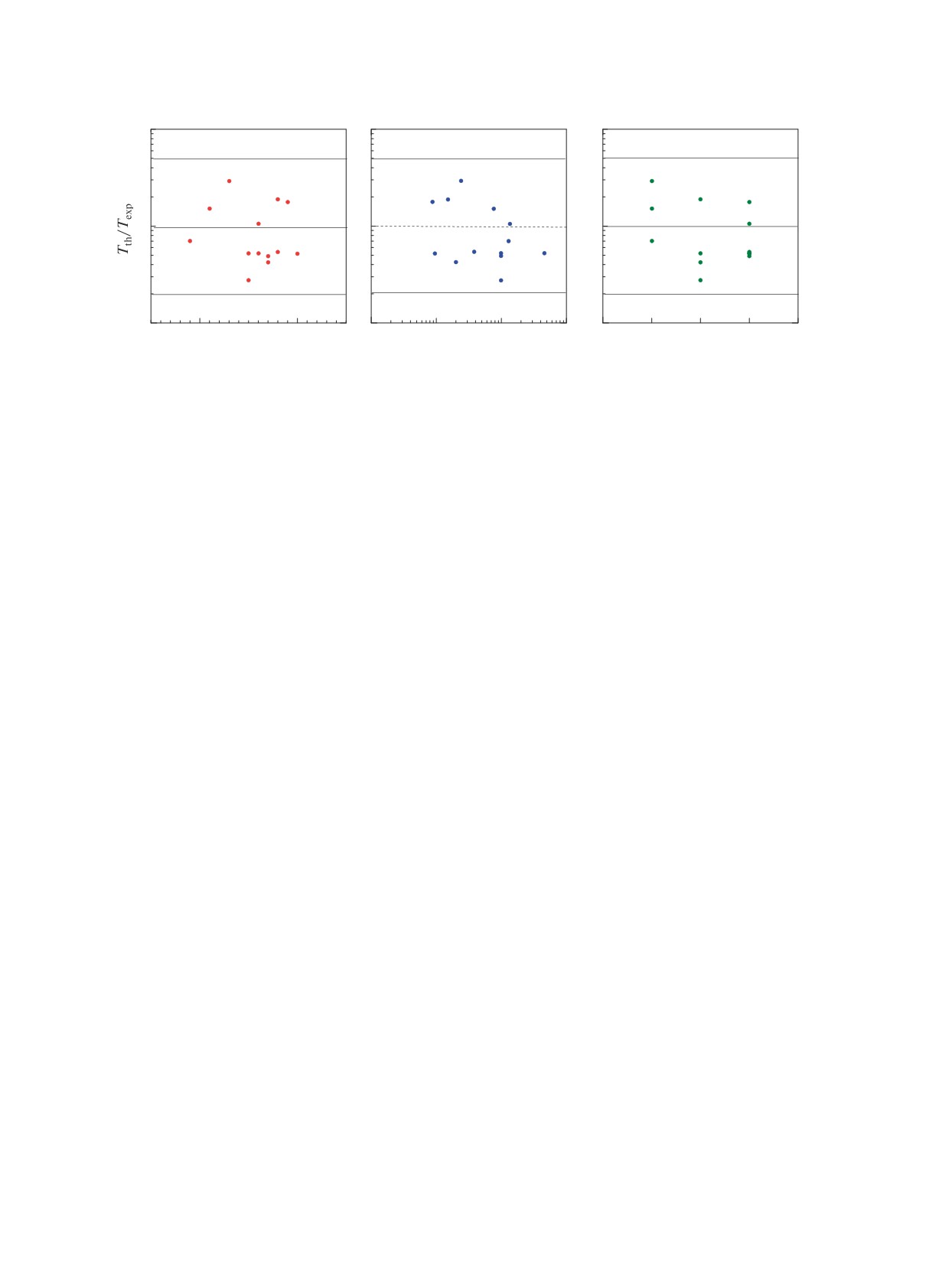
Рис. 3. Отношение рассчитанных в DF3-a + CQRPA к экспериментальным периодам полураспада для изотопов от Tl до

Bi (Z = 81-83) в зависимости от экспериментальных периодов полураспада, атомного массового числа и заряда.

[25]. Исчерпывание оболочечного правила сумм

важный параметр h-2 в изовекторной объемной

3(N - Z) до энергии E_x = 25 МэВ в расчете

компоненте функционала плотности энергии DF3-

составляет 60.5% (экспериментальное значение

a. Диапазон его значений найден ранее в [28].

S (E_x < 25 МэВ) = 53 ± 5 - 10 + 11% [45]).

В самосогласованных расчетах (без какого-либо

Относительное слабое влияние частично-

изменения других параметров функционала) полу-

частичного (pp) взаимодействия на характеристики

чено, что в¹³²Sn и в²⁰⁸Pb расхождение рассчи-

GTR хорошо известно, а также и его заметное

танной энергии GTR с экспериментом близко к

влияние на вклад пигми-резонансов в ядрах со

оценкам вклада квазичастично-фононной связи в

спариванием [42]. Как и в случае с притягатель-

QTBA-расчетах [25]. Для устранения переоценки

ным однопионным взаимодействием, увеличение

энергии GTR в полностью микроскопическом под-

константы эффективного NN-взаимодействия в

ходе представляет интерес применение модели с

pp-канале по сравнению с оценкой g^′ ≤ -0.3,

учетом взаимодействия Ландау-Мигдала, допол-

найденной в наших предыдущих расчетах [22], в

ненного π- и ρ-мезонным обменом, к расчетам в

данной модели невозможно из-за приближения к

рамках подхода QTBA. В качестве примера прак-

точке QRPA-неустойчивости.

тического применения нового варианта DF3-a +

Для тестирования модифицированной версии

+ CQRPA-модели рассчитаны периоды β-распада

функционала DF3-f рассчитаны периоды полурас-

(квази)сферических нейтронно-избыточных цепо-

пада для тяжелых ядер от Tl до Bi (Z = 81-83).

чек изотонов с Z = 76-83 и T1/2 < 240 с, важных

Эти величины чувствительны к распределению си-

для моделирования астрофизического r-процесса

лы GT- и FF-переходов в окне β-распада. Деталь-

нуклеосинтеза при слиянии нейтронных звезд в

ное описание теоретической модели расчета пери-

тесных двойных системах. Экспериментальные пе-

одов полураспада можно найти в наших работах

риоды β-распада [47] описываются с точностью

[22, 46].

до фактора 5, более высокой, чем в глобальных

На рис. 3 для тяжелых ядер Tl, Pb, Bi с

расчетах [48].

T1/2exp < 240 с показано отношение предсказан-

ных периодов полураспада к экспериментальным

Авторы благодарны В.И. Целяеву за плодо-

в зависимости от экспериментальных периодов,

творные обсуждения. Работа была поддержана

атомного массового числа и заряда. По мере при-

грантом Российского фонда фундаментальных ис-

ближения к замкнутой оболочке N = 126 ядра ли-

следований РФФИ-21-52-12035.

бо становятся сферическими, либо имеют неболь-

шую деформацию основного состояния. Видно, что

для ядер этой области разброс отношений перио-

СПИСОК ЛИТЕРАТУРЫ

дов полураспада составляет до 5 раз.

1. E. Caurier, G. Martinez-Pinedo, F. Nowacki,

A. Poves, and A. P. Zuker, Rev. Mod. Phys. 77, 427

4. ЗАКЛЮЧЕНИЕ

(2005).

Проведенные CRPA-расчеты гамов-теллеров-

2. А. Б. Мигдал, Теория конечных ферми-систем

ских силовых функций референтных дважды ма-

и свойства атомных ядер, 2-е изд. (Наука,

гических ядер²⁰⁸Pb,¹³²Sn позволяют уточнить

Москва, 1981).

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

СПИН-ИЗОСПИНОВЫЙ ОТКЛИК ЯДРА

459

P. Franzini and L. A. Radikati, Phys. Lett. 6, 322

28.

A. Bulgac and V. R. Shaginyan, Nucl. Phys. A 601,

(1963).

103 (1996).

29.

I. N. Borzov and S. V. Tolokonnikov, Phys. At. Nucl.

J.-I. Fujita and K. Ikeda, Nucl. Phys. 67, 145 (1965).

86, no. 3 (2023).

S. I. Gabrakov, A. A. Kuliev, and N. I. Pyatov, Phys.

30.

D. Adhikari et al. (PREX-II Collab.), Phys. Rev. Lett.

Lett. B 36, 275 (1971).

126, 172502 (2021).

Ю. В. Гапонов, Ю. С. Лютостанский, Письма в

31.

D. Adhikari et al. (CREX Collab.), Phys. Rev. Lett.

ЖЭТФ 15, 173 (1972).

129, 042501 (2022).

R. R. Doering, A. Galonsky, D. M. Patterson, and

32.

R. Essick, I. Tews, P. Landry, and A. Schwenk, Phys.

G. F. Dertsch, Phys. Rev. Lett. 35, 1691 (1975).

Rev. Lett. 127, 192701 (2021).

L. Shtul, in Proceedings of the 10th International

33.

R. Essick, P. Landry, A. Schwenk, and I. Tews, Phys.

Conference on Direct Reactions with Exotic Beams

Rev. 104, 065804 (2021).

(DREBS2018), p. 102.

34.

J. M. Lattimer, Nuclear Matter Symmetry Energy

R. Reifarth and Yu. A. Litvinov, Phys. Rev. ST Accel.

From Experiment, Theory and Observation, in

Beams 17, 014701 (2014).

Workshop at INT S@INT Seminar, Seattle,

10.

M. Arnould, S. Goriely, and K. Takahashi, Phys. Rep.

November 9, 2021.

450, 97 (2007).

35.

P.-G. Reinhard, X. Roca-Maza, and W. Nazarewicz,

11.

Ю. В. Гапонов, Ю. С. Лютостанский, ЭЧАЯ 12,

Phys. Rev. Lett. 127, 232501 (2022).

1324 (1981).

36.

B. P. Abbott et al. (LIGO Scientific Collab. and Virgo

12.

Н. И. Пятов, С. А. Фаянс, ЭЧАЯ 14, 953 (1983).

Collab.), Phys. Rev. Lett. 119, 161101 (2017).

13.

Ю. В. Наумов, А. А. Быков, И. Н. Изосимов, ЭЧАЯ

37.

J. Margueron, S. Goriely, M. Grasso, G. Col `o, and

14, 420 (1983).

H. Sagawa, J. Phys. G: Nucl. Part. Phys. 36, 125103

(2009).

14.

F. Osterfeld, Rev. Mod. Phys. 64, 491 (1992).

38.

A. B. Migdal, Rev. Mod. Phys. 50, 107 (1978).

15.

W. Kohn and L. J. Sham, Phys. Rev. 140, А1133

(1965).

39.

G. E. Brown, E. Osnes, and M. Rho, Phys. Lett. B

163, 41 (1985).

16.

Energy Density Functional Methods for Atomic

Nuclei, Ed. by Schunck (IOP Publ., Bristol, 2019).

40.

I. N. Borzov, E. E. Saperstein, S. V. Tolokonnikov,

G. Neyens, and N. Severijns, Eur. Phys. J. A 45, 159

17.

S. A. Fayans, S. V. Tolokonnikov, E. L. Trykov, and

(2010).

D. Zawischa, Nucl. Phys. A 676, 49 (2000).

41.

G. F. Bertsch and R. A. Broglia, Oscillations in

18.

T. Nik ˇsi ´c, D. Vretenar, P. Finelli, and P. Ring, Phys.

Finite Quantum Systems (Cambridge Univ. Press,

Rev. C 66, 024306 (2002).

Cambridge, 1994).

19.

D. Vale, Y. F. Niu, and N. Paar, Phys. Rev. C 103,

42.

I. N. Borzov, E. L. Trykov, and S. A. Fayans, Sov. J.

064307 (2021).

Nucl. Phys. 52, 627 (1990).

20.

J. Engel, M. Bender, J. Dobaczewski, W. Nazarewicz,

43.

D. J. Horen, C. D. Goodman, C. C. Foster,

and S. Surman, Phys. Rev. C 60, 014302 (1999).

C. A. Goulding, M. B. Greenfield, J. Rapaport,

21.

I. N. Borzov and S. Goriely, Phys. Rev. C 62, 035501

D. E. Bainum, E. Sugarbaker, T. G. Masterson,

(2000).

F. Petrovich, and W. G. Love, Phys. Lett. B 95, 27

22.

I. N. Borzov, Phys. Rev. C 67, 025802 (2003).

(1980).

23.

N. Paar, T. Nik ˇsi ´c, D. Vretenar, and P. Ring, Phys.

44.

A. Krasznahorkay, H. Akimune, M. Fujiwara,

Rev. C 69, 054303 (2004).

M. N. Harakeh, J. J ¨anecke, V. A. Rodin, M. H. Urin,

and M. Yosoi, Phys. Rev. C 64, 067302 (2001).

24.

A. P. Severyukhin, V. V. Voronov, I. N. Borzov,

N. N. Arsenyev, and N. Van Giai, Phys. Rev. C 90,

45.

J. Yasuda, V. Sasanj, R. G. T. Zegers, et al., Phys.

Rev. Lett. 121, 132501 (2018).

044320 (2014).

25.

V. I. Tselyaev, Phys. Rev. C 75, 024306 (2007).

46.

I. N. Borzov, Phys. At. Nucl. 83, 700 (2020).

26.

E. Litvinova, B. A. Brown, D.-L. Fang, T. Marketin,

47.

R. Caballero-Folch et al., Phys. Rev. Lett. 121,

and R. G. T. Zegers, Phys. Lett. B 730, 307 (2014).

012501 (2016).

27.

I. N. Borzov and S. V. Tolokonnikov, Phys. At. Nucl.

48.

T. Marketin, L. Huther, and G. Mart´ınez-Pinedo,

82, 560 (2020).

Phys. Rev. C 93, 025805 (2016).

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

460

БОРЗОВ, ТОЛОКОННИКОВ

NUCLEAR SPIN-ISOSPIN RESPONSE WITHIN

THE FAYANS FUNCTIONAL

I. N. Borzov^1),2), S. V. Tolokonnikov^1),3)

¹⁾National Research Center “Kurchatov Institute Moscow, Russia

²⁾Bogoliubov Laboratory of Theoretical Physics, JINR, Dubna, Russia

³⁾Moscow Institute of Physics and Technology (National Research University),

Dolgoprudny, Russia

An effective approximation to a fully self-consistent global description of the total force function of β-decay

within the framework of the theory of finite Fermi systems is presented, based on the calculation of ground

states within the framework of the modified energy density functional of Fayans et al. (DF3-f) and the

quasi-particle continuum random phase approximation (CQRPA). The isovector parameter h-2 of the

volumetric part of the functional has been refined, the permissible range of which was determined earlier

by us from restrictions on the parameters of the equation of state of nuclear matter — the symmetry energy

and its derivative at equilibrium density, obtained from a joint analysis of the value of the “neutron skin”

ΔRnp of nuclei²⁰⁸Pb and⁴⁸Ca, found in experiments PREX-II, CREX, results ab initio in calculations

of the properties of the ground states of nuclei with the interaction of N3LO and systematics of data on

the masses of neutron stars from astrophysical observations. New calculations of the Gamow-Teller force

functions for the reference double-magic nucleus²⁰⁸Pb, doubly magic nucleus¹³²Sn and nucleus with

developed neutron pairing¹³⁰Sn have been carriedout. In the proposed model, the global DF3-a + CQRPA

calculations of beta-decay half-lives of heavy (quasi) spherical nuclei with Z = 81-83 and T1/2 < 240 sec

is done. Experimental lifetimes are described with accuracy up to factor 5.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023