ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 4, с. 512-523

ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ

ЛЕПТОННЫЕ ШИРИНЫ РАСПАДОВ РЕЛЯТИВИСТСКОЙ

ДВУХФЕРМИОННОЙ СОСТАВНОЙ СИСТЕМЫ

Поступила в редакцию 15.12.2022 г.; после доработки 17.01.23 г.; принята к публикации 21.01.2023 г.

Получено новое релятивистское квазиклассическое выражение для лептонных ширин распадов

векторных мезонов как составной системы двух спиновых кварков произвольных масс, взаимодей-

ствующих посредством воронкообразного потенциала с кулоновским (хромодинамическим) взаимо-

действием. Проведено сравнение нового выражения с его релятивистским бесспиновым аналогом.

Изучено влияние спиновых параметров векторных мезонов (масс кварков) на поведение их лептонных

ширин распадов. Исследование проведено в рамках релятивистского квазипотенциального подхода,

основанного на ковариантной гамильтоновой формулировке квантовой теории поля, путем перехода

от импульсной формулировки в пространстве Лобачевского к трехмерному релятивистскому конфи-

гурационному представлению для случая составной системы двух релятивистских спиновых частиц

произвольных масс.

DOI: 10.31857/S0044002723040116, EDN: EGRURU

1. ВВЕДЕНИЕ

вым [2], а вся особенность, как и в нереляти-

вистской теории, которую вносит спин в волно-

Настоящая работа является продолжением ра-

вую РКП-функцию составной системы, является

боты [1] и посвящена описанию лептонных ширин

следствием зависимости квазипотенциала от спи-

распадов векторных мезонов на основе знания вол-

на. Кроме того, РКП-подход [2] для случая взаи-

новых функций составной системы двух реляти-

модействия двух релятивистских спиновых частиц

вистских фермионов (спинорных кварков) произ-

равных масс m₁ = m₂ = m позволяет перейти от

вольных масс. С этой целью мы будем использо-

импульсной формулировки в пространстве Лоба-

вать релятивистский квазипотенциальный (РКП)

чевского к трехмерному релятивистскому конфи-

подход, предложенный Кадышевским в работе [2],

гурационному представлению (r-представление),

основанный на ковариантной гамильтоновой фор-

введенному в [9]³⁾.

мулировке проблемы двух тел в квантовой теории

Для нахождения лептонных ширин распадов

поля [3] и совпадающий по форме с РКП-подходом

векторных мезонов V широко используют нере-

Логунова-Тавхелидзе [4], предложенным в рамках

лятивистскую формулу Матвеева, Струминского,

одновременного описания системы двух тел в кван-

Тавхелидзе [10] или Ван Роена-Вайскопфа [11]

товой теории поля. При этом важно, что в РКП-

(см. также работы [12-14])

подходе трехмерность заложена с самого начала,

а все частицы даже в промежуточных состояни-

Γn,ℓ=0(V → e⁺e^-) =

(1)

ях являются физическими, т.е. лежат на массо-

16πα²Q2V N_c

вых поверхностях. Тем самым двухчастичная за-

|ϕn,ℓ=0(0)|²,

3M2n

дача сводится к одночастичной, описание которой

ведется на языке волновой РКП-функции одной

где α — постоянная тонкой структуры, Q_V

—

релятивистской частицы, удовлетворяющей полно-

множители, обусловленные изотопической струк-

стью ковариантному трехмерному РКП-уравнению

турой векторных мезонов V и зарядами кварков,

в импульсном пространстве с квазипотенциалом

образующих их и выраженных в единицах элек-

(см., например, работы [5-8]). Квазипотенциал в

трического заряда e, M_n — полная энергия свя-

общем случае параметрически зависит от энер-

занного состояния двух спиновых кварков с чис-

гии составной системы и не является эрмито-

лом цветов N_c = 3, массами m₁, m₂ и относитель-

ным 3-импульсом q, т.е. e⁺e^-(или qq)-системы с

¹⁾Гомельский государственный технический университет

им. П.О. Сухого, Гомель, Беларусь.

³⁾Напомним, что в рамках рассматриваемого РКП-подхода

²⁾Международный центр перспективных исследований,

как модуль радиуса-вектора r, так и 3-импульс k реляти-

ГГТУ, Гомель, Беларусь.

вистской частицы являются релятивистскими инвариан-

^*E-mail: chyud@mail.ru;chern@gstu.by

тами [9].

512

ЛЕПТОННЫЕ ШИРИНЫ РАСПАДОВ

513

относительным орбитальным моментом ℓ = 0 для

был применен в работах [20], чтобы получить

данного уровня n, а ϕn,ℓ=0(0) — волновая функ-

в ВКБ-приближении выражения для лептонных

ция связанного состояния. Обычно в качестве нее

ширин распадов векторных и псевдоскалярных

используют нерелятивистскую волновую функцию

мезонов с относительным орбитальным моментом

ϕnrn,ℓ=0(r), отвечающую нерелятивистскому уравне-

ℓ ≥ 0, также заменяя функцию Бете-Солпитера

нию Шредингера для случая двух частиц равных

χBS,ℓ((0,r)) на волновую РКП-функцию ψMn,ℓ(r)

масс с несингулярным в нуле потенциалом запира-

в трехмерном релятивистском r-представлении [9],

ния V_conf(r) путем добавления к нему кулоновского

вычисленную в нуле. При этом авторы огра-

ничились предположением, что квазипотенциал

взаимодействия [15, 16]

является действительным и представляет собой

α_s

V_Coul(r) = -

(2)

сумму потенциала запирания V_conf(r) и куло-

новской части образа однобозонного обменного

где α_s — сильная константа связи.

потенциала V_c(r) = - cth(πmr)/r (ℏ = c = 1) в

Релятивистская модификация формулы (1) для

r-представлении, опуская функцию cth(πmr), т.е.

лептонной ширины распада векторного мезона в

заменяя потенциал V_c(r) = - cth(πmr)/r на куло-

s-состоянии (ℓ = 0) на лептон-антилептонную пару

новский (хромодинамический) потенциал (2), ко-

была выполнена в работе [17]. Развитый в [17] под-

торый в РКП-подходе в импульсном пространстве

ход базируется на решении релятивистским квази-

Лобачевского воспроизводит главное поведение

классическим (ВКБ) методом [18] модифицирован-

потенциала в КХД [21].

ного уравнения Бете-Солпитера, не зависящего от

относительного времени x₀. Это означает выпол-

Возможность применимости формулы (1) для

описания лептонных ширин распадов векторных

нение следующих предположений (одновременное

мезонов в рамках РКП-подхода [2, 9] обусловле-

взаимодействие): фоковское qq-состояние дает до-

минирующий вклад в функцию Бете-Солпитера

на тем, что функция Бете-Солпитера при x = 0

для случая взаимодействия двух релятивистских

двух заряженных частиц χ_BS(x) при x = (x₀, r) = 0

частиц равных масс m будет, в отличие от нере-

в области r > m-1 (ℏ = c = 1); qq-взаимодействие

лятивистского случая и релятивистского подхода,

адекватно описывается одновременным кулонов-

предложенного в работе [17], связана с волновыми

ским взаимодействием (2); возможные (дальнего

РКП-функциями в импульсном пространстве Ло-

порядка) спин-зависимые эффекты игнорируются.

бачевского, ΨMQ (k), и в трехмерном релятивист-

При этих предположениях доминирующий вклад

в функцию Бете-Солпитера для s-состояния при

ском r-представлении, ψMQ (r), не в нуле, как это

x₀ = 0 в области r ≫ m-1 дает решение одновре-

делалось в работах [19, 20], а в соответствии с

менного уравнения Солпитера для волновой функ-

преобразованиями Шапиро [22]

∫

ции Ψreln,ℓ=0(r) qq-системы, вычисленную в нуле, так

ψMQ(r) =

dΩ_k ξ(k, r)ΨMQ (k),

что χ_BS((0,r))|ℓ=0 = Ψreln,ℓ=0(r).

(2π)³

∫

Иной подход для нахождения лептонных ширин

ΨMQ(k) = drξ^∗(k,r)ψ_M

(r)

распадов векторных мезонов в s-состоянии осно-

ван на применении РКП-подхода [2]. В рамках

при r = iλ соотношением

этого РКП-подхода для случая составной систе-

∫

мы двух релятивистских бесспиновых частиц рав-

χ_BS(x = 0) =

dΩ_kΨMQ(k) =

(3)

ных масс m релятивистская модификация фор-

(2π)³

мулы (1) для лептонной ширины распада век-

= lim

ψMQ(r).

торного мезона в s-состоянии и с полной энер-

r→iλ

гией M_n < 2mc² на лептон-антилептонную пару

Здесь λ = ℏ/mc — комптоновская длина волны

была выполнена в работе [19] и состояла в за-

релятивистской частицы массы m, функции

мене функции Бете-Солпитера χ_BS((0, r))|ℓ=0 на

волновую РКП-функцию ψMn,ℓ=0(r) в трехмер-

⁽k₀ - ck · n)-1-ir/λ

ном релятивистском r-представлении [9], вычис-

ξ(k, r) =

mc²

ленную в нуле. Для этого РКП-уравнение для

волновой РКП-функции ψMn,ℓ=0(r) c потенциалом

образуют полную и ортогональную систему функ-

V (r) = -α_s/r + σr^s (σ, s > 0) было решено реля-

ций, соответствуют главной серии унитарных

тивистским аналогом модифицированного ВКБ-

неприводимых представлений группы Лоренца и

метода [18].

выполняют роль “плоских” волн в пространстве

РКП-подход [2] для случая составной системы

Лобачевского, а dΩ_k = mc²dk/E_k — релятивист-

двух релятивистских фермионов равных масс m

ский трехмерный элемент объема в пространстве

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

514

ЧЕРНИЧЕНКО

Лобачевского, которое реализуется на верхней

где μ = m₁m₂/(m₁ + m₂) — приведенная масса

пол ´е массового гиперболоида

двух частиц произвольных масс,

E2q - c²q² = m²c⁴,

u′rel =

√

(7)

√

1-u²

где E_q = q₀ = c

m²c² + q² — энергия реляти-

– относительная скорость эффективной реляти-

вистской частицы с массой m и 3-импульсом q

√

вистской частицы массы m^′, где скорость u дается

и связана с полной энергией M_Q =

(q₁ + q₂)² в

выражением

с.ц.и. соотношением [9]

√

4m′2c⁴

√s = M_Q = 2c^√m2c2 + q2 = 2E_q.

(8)

M² - (m₁ - m₂)²c⁴

Таким образом, соотношение (3) обеспечивает пра-

вильную связь между функцией Бете-Солпитера

а релятивистские бесспиновые кулоноподобные

и волновыми РКП-функциями в импульсном про-

ресуммирующие пороговые L- и S-факторы как

странстве Лобачевского и в трехмерном реляти-

функции быстроты χ^′, которые появляются в

вистском r-представлении.

рассматриваемом РКП-подходе, даются выраже-

ниями [26-29]⁴⁾

Выражение для релятивистской лептонной ши-

рины распада векторного мезона в состоянии с

L_RQP(χ^′) =

(9)

энергией M_Q = M_n для данного уровня n и с

[

]

(

)₂

относительным орбитальным моментом ℓ ≥ 0 на

∏

α_s

лептон-антилептонную пару было получено в ра-

S_RQP(χ^′),

2n sh χ^′

боте [23]. Развитый в [23] подход базируется на

n=1

РКП-подходе [2], обобщенном в работах [24, 25]

X_RQP(χ^′)

для случая составных систем двух релятивист-

S_RQP(χ^′) =

(10)

1 - exp[-X_RQP(χ^′)]

ских частиц произвольных масс m₁ и m₂. С этой

πα_s

целью РКП-уравнение в трехмерном релятивист-

X_RQP(χ^′) =

ском r-представлении для волновой РКП-функции

shχ^′

ψMQ(r) двух релятивистских бесспиновых частиц

Здесь

α_s = α_s/g^′ℏc, величина sh χ^′ выражается

произвольных масс m₁ и m₂, взаимодействующих

через относительную скорость в (7) как

посредством воронкообразного потенциала вида

α_s

shχ^′ = u′rel

/2g^′,

(11)

V (r) = V_conf(r) -

,α_s > 0,

(4)

а быстрота χ^′ связана с относительным

было решено релятивистским аналогом модифи-

импульсом q^′, энергией E_q′ эффективной реля-

цированного ВКБ-метода [18, 19]. Это решение

тивистской частицы массы m^′ и полной энергией

приводит, с учетом модификации формулы (1) со-

взаимодействующих частиц M_Q соотношениями

отношением (3), к следующему выражению для

q^′ = m^′csh χ^′n_q′ ,

|n_q′ | = 1,

лептонной ширины распада векторного мезона:

m′2c²

Γ_n,ℓ(V → e⁺e^-) =

(5)

E_q′ = m^′c² ch χ^′, M_Q =

ch χ^′.

(

)2ℓ+1

2α²Q2V (ℏc)³Γ²(ℓ + 1)

u^′

rel,n

Выражение (5) можно применять и при отсутствии

πλ′3g^′m^′c²Γ²(2ℓ + 2)M2n

g^′

кулоновского взаимодействия в потенциале (4), т.е.

(

) dM_n

при α_s

= 0. В частности, при ℓ = 0 выражение (5)

×L_RQP

u^′

rel,n

переходит в соотношение [33]

Здесь для бесспиновых кварков Q_V = e_q, где e_q —

Γn,ℓ=0(V → e⁺e^-) =

(12)

заряд кварка в единицах электрического заряда e,

2α²Q2V (ℏc)³u′rel,n

(

) dM_n

λ^′ = ℏ/m^′c

— комптоновская длина волны эф-

S_RQP

u^′

rel,n

πλ′3g′2m^′c²M2n

фективной релятивистской частицы массы m^′ =

√m₁m₂, выступающей в качестве двухчастичной

⁴⁾Напомним, что пороговые L- и S-факторы в (9) и (10)

связанной системы, фактор g^′ определяется выра-

имеют правильные релятивистские (u → 1) и ультрареля-

жением

тивистские (m^′ → 0) пределы, равные единице, в отличие

′

от релятивистских пороговых S-факторов, представлен-

m₁ + m₂

g^′ =

√

(6)

ных в работах [30-32] (подробности см. в работах [26-

2μ

m₁m₂

29]).

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ЛЕПТОННЫЕ ШИРИНЫ РАСПАДОВ

515

(

)

(

)]

План дальнейшего изложения следующий.

iλ^′

∂

λ′2

∂

sh iλ^′

Δ_θ,ϕ exp iλ^′

В разд.

полностью ковариантное конечно-

∂r

2r²

∂r

разностное РКП-уравнение в трехмерном реляти-

являющегося конечно-разностным оператором,

вистском r-представлении для радиальной волно-

построенным из операторов сдвига exp (±iλ^′∂/∂ r),

вой РКП-функции ϕ_ℓ(r, χ^′) двух релятивистских

в то время как Δ_θ,ϕ — его угловая часть, оператор

спиновых частиц произвольных масс m₁ и m₂,

полученное в [34] в рамках РКП-подхода [2, 24,

A определяется выражением

[

]

25], будет решено релятивистским ВКБ-методом.

(

)

(

)

Hrad

a^′

Hrad

² +b′ ,

Условие применимости ВКБ-приближения будет

0,ℓ

установлено. В разд. 3 в рамках применимости

ВКБ-приближения будет получено выражение для

в котором спиновые параметры a^′ и b^′ для вектор-

лептонных ширин распадов векторных мезонов

ных мезонов выражаются через фактор (6) форму-

в s-состоянии на лептон-антилептонную пару.

лой

Векторные мезоны рассматриваются как составная

система двух релятивистских спиновых кварков

a^′ =

g′2, b^′ =

g′2

(14)

произвольных масс m₁ и m₂, взаимодействую-

щих посредством воронкообразного потенциала,

при^Ô = γ_μ (вектор),

включающего в себя несингулярную чисто за-

причем значение спиновых параметров a^′ и b^′ в (14)

пирающую часть и сингулярную часть в виде

при m₁ = m₂ = m совпадает со значением их ана-

кулоновского (хромодинамического) потенциала.

логов a и b, которые были получены в [35] для

В разд. 4 будет выполнено исследование влияния

векторных мезонов; квазипотенциал V (r) является

спина и масс кварков (фактор g^′) на поведение

локальным в смысле геометрии Лобачевского и для

лептонных ширин распадов векторных мезонов.

простоты считается не зависящим от энергии M_Q, а

Для этого будет проведено сравнение поведения

нового спинового выражения для лептонных ширин

χ^′ — быстрота, которая параметризирует импульс

распадов векторных мезонов с их релятивистским

и энергию⁵⁾:

бесспиновым аналогом. В этом же разделе будут

Δ_q′,m′λ_Q = m^′csh χ^′nΔ

(15)

вычислены значения лептонных ширин распадов

q′,m′λQ

основного уровня s-состояния векторных ρ₀-, ω-

m^′

и φ-мезонов. В Заключении будет подведен итог

|nΔq′,m′λ

| = 1, M_Q =

Δ⁰

q^′,m^′λ_Q

проведенному исследованию.

Δ0q′,m′λ_Q = m^′c² ch χ^′.

2. КВАЗИКЛАССИЧЕСКОЕ РЕШЕНИЕ

Отметим, что для простоты рассмотрения в

РКП-УРАВНЕНИЯ

работе [34], как и в работах [36, 35], считалось,

Основой нашего рассмотрения является пол-

что квазипотенциал имеет биспинорную структуру

ностью ковариантное РКП-уравнение в r-пред-

вида

Ô ⊗ Ô, а вершинная функция также имеет

ставлении в конечно-разностной форме для ради-

спинорную структуру, пропорциональную матрице

альной волновой РКП-функции ϕ_ℓ(r, χ^′) состав-

^Ô, не зависящую от импульсных переменных, а

ной системы двух релятивистских спиновых ча-

шпур Sp[Ô+ Ô] = 0, где в качестве^Ô выбирались

стиц произвольных масс m₁, m₂ с относительным

матрицы Дирака γ₅, γ_μ, γ₅γ_μ (μ = 0, 1, 2, 3). Разло-

орбитальным моментом ℓ ≥ 0, взаимодействующих

жение же вершинной функции по полной системе

посредством сферически симметричных квазипо-

I,γ₅,γ_μ,γ₅γ_μ,σ_μνP^ν-матриц приводит к системе

тенциалов, которое имеет вид [34]

(

)

зацепляющихся уравнений. Такое представление

Hrad

- ch χ^′ ϕ_ℓ(r, χ^′) =

(13)

квазипотенциала и вершинной функции позволило,

0,ℓ

(

)

используя условия ортонормированности и полно-

Hrad

ты для дираковских спиноров, провести свертку

= -V (r

0,ℓ

ϕℓ(r, χ^′).

спиновых частей этих величин, а затем, применяя

Здесь

√

(

)

(

)

⁵⁾Напомним, что здесь λQ = (λ^Q; λQ) = Q/

Q²

—

λ′2ℓ(ℓ + 1)

4-вектор скорости составной частицы с 4-импульсом Q =

Hrad

= ch iλ^′

exp iλ^′

0,ℓ

2r(r + iλ^′)

= q1 + q2, причем все 4-импульсы принадлежат верхним

пол ´ам массовых гиперболоидов Δ

q^′,m^′λ_Q =

Δ0′

q ,m^′λ_Q

- радиальная часть оператора свободного гамиль-

− c²Δ2q′_,m′_λ

= m′2c⁴, где Δ0q′_,m′_λ

, Δ_q′_,m′λQ

—

тониана

[

(

)

временная и пространственная компоненты 4-вектора

∂

Λ-1q′ = Δq′,m′λQ из пространства Лобачевского

Ĥ₀

^λQ

= 2m^′c²

ch iλ^′

∂r

(подробности см. в работе [34]).

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

516

ЧЕРНИЧЕНКО

преобразование Лоренца, разделить временные и

где

пространственные переменные в аргументах четы-

∫

рехмерных δ-функций и выполнить интегрирова-

α^L,R±(r) =1

dr^′χ_±(r^′),

(20)

ние по этим переменным, что в конечном итоге

λ^′

и приводит к уравнению (13) (подробности см. в

r_L,R

работе [35]). Этот подход позволил найти точные

C_L,R — нормировочные константы, а левая r_L и

решения РКП-уравнения (13) с кулоноподобным

правая r_R точки поворота определяются как точки

(хромодинамическим) потенциалом (2), который в

ветвления корня в (20):

случае взаимодействия γ_μ ⊗ γ^μ является опреде-

X (r_L,R) = R(r_L,R).

(21)

ляющим [36, 37], а возможность его использова-

ния как образа кулоновской части фейнмановского

Условие применимости релятивистского ВКБ-

матричного элемента (квазипотенциала), содержа-

метода в спиновом случае, основанное на выраже-

щего все спиновые эффекты, была детально рас-

ниях в (17) для первых двух членов представле-

смотрена в работах [1, 20].

ния (16), дается неравенством



Решение уравнения (13) в ВКБ-приближении



ch χ_eff(r)

dχ₊(r)



λ^′

(22)

ищется в виде [1, 18-20, 23]

^≪

^χ₊(r)sh χ_eff(r) dr

[

]

где

ϕℓ(r, χ^′) = exp

g(r) ,

(16)

ℏ

χ_eff(r) = archX_eff(r) =

)₂

(

√

)

ℏ

(ℏ

= ln X_eff(r) + X^2eff(r) - 1 ,

g(r) = g₀(r) +

g₁(r) +

g₂(r) +

X (r)

X_eff(r) = ch χ_eff(r) =

Для первых двух членов представления (16) нахо-

R(r)

дим

∫

В случае ℓ = 0 условие (22) преобразуется в нера-

ℏ

g₀(r) = m^′c drχ_±(r) +

φ,

(17)

венство



ch χ_S (r) dχ_S (r)



λ^′

^≪

g₁(r) = -

ln([X²(r) - R²(r)] ×

^χ_S(r)shχ_S(r) dr

где величина

× [1 + a^′V (r)X(r)]) + c_±,

[

]

√

χ_S(r) = archX(r) = ln X(r) +

X²(r) - 1

где

[

√

]

имеет смысл быстроты эффективной релятивист-

χ_±(r) = ln X(r) ±

X²(r) - R²(r) ,

(18)

ской частицы массы m^′, движущейся в поле потен-

2X(r)

циала V (r), в терминах которой измеряется рас-

X (r) =

√

стояние между двумя точками импульсного про-

1 + a^′V (r)X(r)

странства Лобачевского.

′

В заключение этого раздела приведем условие

X(r) = ch χ^′ -

V (r),

квантования уровней энергий в ВКБ-приближе-

√

нии [38]

λ′2Λ

R(r) =

Λ = ℓ + 1/2.

∫

r²

dr [χ₊(r) - ln R(r)] =

(23)

Учет выражений в (17) для первых двух чле-

нов представления (16) позволяет получить ВКБ-

r_L

(

)

решения с левой r_L и правой r_R точками поворота

в области r_L ≤ r ≤ r_R:

= πλ^′ n +

ϕL,Rℓ(r, χ^′) =

(19)

n = 0,1,..., ℓ ≥ 0,

C_L,R

которое, как и в бесспиновом случае [23], нахо-

√

2⁴

[X²(r) - R²(r)][1 + a^′V (r)X(r)]

дится из условия совпадения волновых функций

{

[

в (19) в точке r ∈ (r_L; r_R). Для этого необходимо

× exp iαL,R+(r) ∓iπ]

положить

⎡

⎤

∫

}

[

C_L = C_ℓ exp^⎣-i

dr^′ ln R(r^′)⎦ ,

+ exp iα^L,R-(r) ± iπ]

λ^′

r_L

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ЛЕПТОННЫЕ ШИРИНЫ РАСПАДОВ

517

⎡

⎤

∫

в [11]). В случае релятивистских кварков формфак-

C_R = C_ℓ(-1)ⁿ exp ⎣-i

dr^′ ln R(r^′)⎦ ,

тор f₁(t) выберем в виде

λ^′

r_R

sh χ_Δ

f₁(t) =

(25)

где C_ℓ — произвольная постоянная. При a^′ = 0,

χ_Δ

b^′ = 2/g^′m^′c² ВКБ-условие квантования уровней

где χ_Δ/ sh χ_Δ — релятивистский геометрический

энергий (23) совпадает с аналогичным выражени-

фактор в РКП-подходе [2], который впервые обос-

ем, которое было получено в работе [23] для случая

нованно появился в работе [40] для инвариантного

двух бесспиновых частиц произвольных масс. В

описания пространственной структуры частиц в

случае равных масс m₁ = m₂ = m (g^′ = 1) выра-

трехмерном релятивистском r-представлении [9].

жение (23) переходит в ВКБ-условие квантования

Такой выбор формфактора f₁(t) имеет ясный фи-

уровней энергий, полученное в случае спиновых

зический смысл, поскольку, как было показано в

частиц равных масс в работе [39].

работе [40], фактор χ_Δ/ sh χ_Δ описывает величину

вклада в формфактор нуклона от его централь-

ной сферы, внутри которой движутся кварки с

3. ЛЕПТОННЫЕ ШИРИНЫ РАСПАДОВ

радиусом, равным его комптоновской длине волны

МЕЗОНОВ В РКП-ПОДХОДЕ

→

(r₀ = ℏ/Mc). В нерелятивистском пределе (χ_Δ

Релятивистская модификация формулы (1) в

→ 0) фактор χ_Δ/ sh χ_Δ → 1, что отвечает точеч-

РКП-подходе для лептонных ширин распадов век-

ной частице. Следовательно, в нерелятивистском

торных мезонов в s-состоянии и с энергией M_Q =

пределе формфактор f₁(t) не дает вклада в (24).

= M_n,(χ^′ = χ_n) как связанной системы двух реля-

Таким образом, фактор χ_Δ/ sh χ_Δ служит мерой

тивистских cпиновых кварков произвольных масс

вклада релятивистских эффектов, обусловленных

m₁ и m₂ состоит, согласно соотношению (3) и

динамикой кварков.

обоснованию к нему, в замене |χ_BS(x = 0)|²|ℓ=0 =

Отметим, что дополнительный фактор

= |ψMQ(r = iλ)|²|ℓ=0 и введения квадрата форм-

exp(-π ρ^′/2)Γ(1 + iρ^′) в формуле (24) обеспечивает

фактора кварка f₁(t), который в нерелятивистском

не только правильный релятивистский предел

случае в работе Ван Роена-Вайскопфа [11] прини-

порогового ресуммирующего S-фактора составной

мался равным 1. Тогда лептонная ширина распада

системы двух релятивистских спиновых кварков

векторного мезона в s-состоянии и с энергией

произвольных масс при χ^′ → +∞ (u → 1), равный

M_n определяется также, как и в случае связанной

1, но и переход к бесспиновому случаю при a^′ = 0

системы двух cпиновых кварков равных масс m [1],

через решение (19) равенством

и b^′ = 2/g^′m^′c² (подробности см. в работе [34]).

Таким образом, в рассматриваемом спиновом

Γn,ℓ=0(V → e⁺e^-) =

(24)

случае функция

16πα²Q2V f²¹(t)

ψ₀(r,χ^′) = e-πρ′/²Γ(1 + iρ^′)ϕL0(r,χ^′)

M2n



представляет собой физическую волновую РКП-



× lim

−πρ^′/2Γ(1 + iρ^′)ϕ0(r,χn)

функцию s-состояния составной системы двух

^e



r→iλ^′

релятивистских спиновых кварков произвольных

масс, взаимодействующих посредством воронко-

Здесь

образного потенциала вида (4).

′

α^′sa^′ ch χ

α_s

ρ′ =

α^′s =

Подчеркнем также, что формула (24) справед-

λ^′

лива (как это имело место и в работах [1, 17, 20, 23])

формфактор кварка f₁(t) в выражении оператора

в приближении одновременного взаимодействия,

тока кварка как функция квадрата 4-вектора пере-

ограничиваясь в дальнейшем учетом лишь обра-

дачи импульса t = (p^′ - p)² = 2M2Qc⁴(1 - ch χ_Δ),

за кулоновской части однобозонного обменного

квазипотенциала, V_c(r) = - cth(πmr)/r (ℏ = c =

где p, p′ — начальный и конечный импульсы, а

χ_Δ — соответствующая быстрота, зависит от ано-

= 1), опуская функцию cth(πmr), т.е. заменой

мального магнитного момента кварка μ_anom в от-

потенциала V_c(r) = - cth(πmr)/r на кулоновский

личие от формфактора кварка f₂(t), который не

(хромодинамический) потенциал

(2). В РКП-

дает вклада в магнитный момент кварка. В случае

подходе в импульсном пространстве Лобачев-

нерелятивистских кварков аномальный магнитный

ского потенциал (2) отвечает пропагатору, обла-

момент μ_anom в работе Ван Роена-Вайскопфа [11]

дающему КХД-подобным (хромодинамическим)

принимался равным нулю, а, следовательно, форм-

поведением [21]. Таким образом, внутри адрона

фактор f₁(t) выбирался равным 1 (подробности см.

взаимодействие двух релятивистских спиновых

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

518

ЧЕРНИЧЕНКО

кварков произвольных масс осуществляется в r-

Далее, поступая как, например, в работах [1,

представлении посредством сингулярного ворон-

15, 23], волновую РКП-функцию (26) полного

кообразного потенциала запирания (4), в котором

потенциала (4) при ℓ = 0 в области достаточно

V_conf(0) = 0. В поле такого потенциала уровни

больших ρ = r/λ^′, r ∈ (r_L; r_R), но таких, где все

энергии M_n = (m′2c²/μ) ch χ_n для данного уровня

же в потенциале

(4) доминирует кулоновское

n могут быть определены из ВКБ-условия кванто-

(хромодинамическое) взаимодействие (2), аппрок-

вания (23).

симируем радиальной s-волновой РКП-функцией

ϕCoul0(r, χ^′), отвечающей потенциалу (2), точный

В области r ∈ (r_L;r_R) ВКБ-решение (19) с ле-

вид которой можно представить через гипергеомет-

вой точкой поворота r_L и с данным фиксированным

рическую функцию в виде [34]

значением энергии M_n, отвечающее потенциалу

(4), запишем в виде

ϕCoul0(ρ, χ^′) =

(31)

ϕLℓ(r, χ_n) =

(26)

= 2πC^Coul0(χ^′)eiB′χ^′-χ′+i(ρ-ρ′)χ′ (ρ - ρ^′) ×

(

)

C_ℓ(χ_n)

×F

1 - iB^′,1 - i(ρ - ρ^′);2;1 - e-2χ′

√

[X²(r) - R²(r)][1 + a^′V (r)X(r)]

ρ = r/λ^′.

{

}

∫

[

]

Здесь C₀(χ^′) — произвольная функция от χ^′, пара-

× sin

dr^′ χ₊(r^′)- ln R(r^′) +

λ^′

метр B^′ определяется как

r_L

α^′s(a^′ ch² χ^′ + b^′)

где нормировочный множитель C_ℓ(χ_n) находится

B^′ =

(32)

4sh χ^′

из условия нормировки

причем параметр B^′ при χ^′ = iκ_n связан с условием

∫∞



квантования энергетических уровней в спиновом

4π dr

^ϕ^Lℓ(r, χ_n)2 = 1, ℓ ≥ 0.

(27)

случае для потенциала (2) выражением [34]

α^′s(a^′ cos² κ_n + b^′)

= n, ℓ = 0,

Заметим, что в области применимости ВКБ-

4sin κ_n

приближения (22) аргумент синуса в решении (26)

n = 1,2,...,

0 < κ_n < π/2.

является быстро осциллирующей функцией. По-

этому после подстановки решения (26) в условие

Сравнивая асимптотическое выражение для куло-

новской функции в (31)

нормировки (27) квадрат синуса, как обычно, мож-

но заменить его средним значением, равным 1/2 [1,



2πC^Coul0(χ_n)e-πB′/²



23]. Тогда вместо (27) имеем условие

ϕCoul0(ρ, χ_n)

∼

ρ≫1

shχ_n|Γ(1 - iB^′)|

[

]

2π|C_ℓ(χ_n)|² ×

(28)

× sin ρχ_n + δCoul,S0(χ_n) ,

r_R

√

= 1.

с асимптотикой ВКБ-решения в (26), взятого при

[X²(r) - R²(r)][1 + a^′V (r)X(r)]

ℓ = 0,

r_L



ϕL₀(ρ, χ_n)

∼

ρ≫1

Дифференцируя по полной энергии M_n =

[

]

C₀(χ_n)

= (m′2c²/μ) ch χ_n условие квантования (23) при

∼

√

sin ρχ_n + δCoul,WKB,S0(χ_n) ,

ℓ ≥ 0, где потенциал V_conf(r) не зависит от энергии

shχ_n

M_n, и принимая во внимание определения (18) и

находим связь между нормировочными множите-

условие (21) для точек поворота r_L,R, получим

лями



∫



2πC^Coul0(χ_n)2 =

(33)

√

(29)

[X²(r) - R²(r)][1 + a^′V (r)X(r)]

= shχ_neπB′ |Γ(1 - iB^′)|² |C₀(χ_n)|² ,

r_L

где

πλ^′m′2c

(

)

μ dM_n

δCoul,S0(χ^′) = B^′ ln

2ρ sh χ^′

- ρ^′χ^′ + arg Γ(1 - iB^′)

Из выражений (28) и (29) находим

– точная фаза волновой РКП-функции для куло-

новского потенциала (2), а

dM_n

|C_ℓ(χ_n)|² =

(30)

(

)

2π²λ^′m′2c² dn

δCoul,WKB,S0(χ^′) = B^′ ln

2ρ sh χ^′

- ρ^′χ^′ - B^′ ln B^′

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ЛЕПТОННЫЕ ШИРИНЫ РАСПАДОВ

519

– ее выражение в ВКБ-приближении [38].

при α_s = 0, а при a^′ = 0, b^′ = 2/g^′m^′c² и f₁(t) =

= 1 оно переходит в выражение (12) для бесспино-

Наконец, принимая во внимание определение

вого случая. Соответствующие нерелятивистские

(24) и соотношения (30), (31) и (33), получим ВКБ-

или релятивистские пороговые L- и S-факторы

выражение для лептонной ширины распада вектор-

появляются и в других выражениях для лептонных

ного мезона в s-состоянии и с энергией M_n как

ширин распадов векторных мезонов как составных

составной системы двух спиновых кварков про-

систем двух спиновых (или бесспиновых) частиц

извольных масс, взаимодействующих посредством

равных масс m. Однако не все пороговые L- и

воронкообразного потенциала (4) с кулоновским

S-факторы, появляющиеся в лептонных ширинах

(хромодинамическим) взаимодействием (2):

распадов векторных мезонов, имеют правильные

Γn,ℓ=0(V → e⁺e^-) =

(34)

релятивистские пределы [26-29], что существенно

влияет на поведение лептонных ширин распадов

4α²Q2V f²¹(t)(ℏc)³ sh χ_n

dM_n

SRQP,S (χ_n)

векторных мезонов в этой области. Этот вопрос

πλ′3g^′m^′c²M2n

для случая двух частиц равных масс был подробно

исследован в работе [1].

Здесь

XRQP,S(χ^′)

SRQP,S(χ^′) =

[

] ×

(35)

4. ИССЛЕДОВАНИЕ ВЛИЯНИЯ

1 - exp

-XRQP,S(χ^′)

СПИНОВЫХ ПАРАМЕТРОВ ВЕКТОРНЫХ



²

МЕЗОНОВ НА ПОВЕДЕНИЕ ИХ

×e-πρ′Γ(2 + iρ′)F (1 + iB′, -iρ′; 2; 1 - e-2χ′ )

ЛЕПТОННЫХ ШИРИН РАСПАДОВ

- релятивистский кулоноподобный ресуммирую-

Для исследования влияния спина и масс квар-

щий пороговый S-фактор для случая составной

ков на поведение лептонных ширин распадов век-

системы, состоящей из двух релятивистских спи-

торных мезонов в s-состоянии были построены

новых частиц произвольных масс m₁ и m₂ [34].

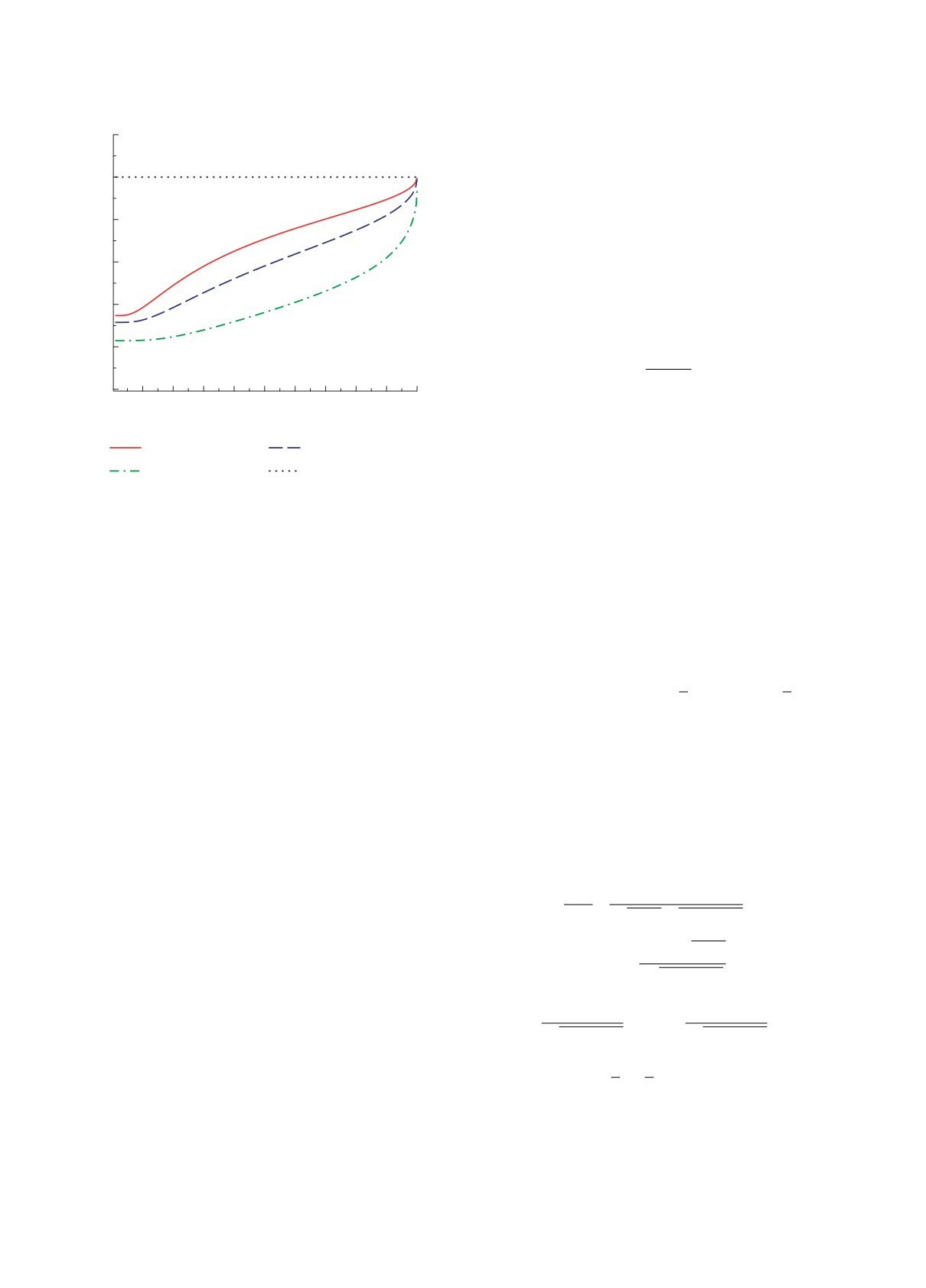
графики функции R = R(u) (рис. 1) как функции

В рассматриваемом РКП-подходе S-фактор (35)

скорости u, определенной как отношение реля-

воспроизводит как известный нерелятивистский

тивистской спиновой лептонной ширины распада

результат в нерелятивистском пределе (v ≪ 1) в

векторного мезона в s-состоянии, представленной

бесспиновом случае, когда m₁ = m₂ = m, a^′ = a =

выражениями (34), (35) и (36), к ее релятивистско-

= 0 и b^′ = b = 2/mc², так и ожидаемые реляти-

му бесспиновому аналогу, представленному выра-

вистский (u → 1) и ультрарелятивистский (m^′ →

жениями (10) и (12), которые берутся при f₁(t) = 1,

→ 0) пределы для значения параметров a^′ и b^′

Q_V = e_q, ℏ = c = 1, α_s = α^′s = α_s = 0.2 и отвечают

в (14) (подробности см. в работах [34, 41, 42]).

различным значениям фактора g^′: g^′ = 1 — сплош-

Величина XRQP,S(χ^′) связана с параметром B^′ в

ная кривая, g^′ = 1.5 — штриховая кривая и g^′ =

(32) выражением

= 2.5 — штрихпунктирная кривая; точечная кривая

соответствует значению α_s = 0. При построении

πα^′s(a′ ch2 χ^′ + b^′)

графиков функции R были также использованы

XRQP,S(χ^′) = 2πB^′ =

2sh χ^′

соотношения (7) и (11) как функции скорости u

′

и учтены выражения для спиновых параметров a

которое может быть представлено с помощью (11)

и b^′ для векторных мезонов в (14) как функции

в терминах скоростей (7) и (8) в виде

фактора g^′.

XRQP,S(u) =

(36)

Из рис. 1 видно, что в нерелятивистской области

√

[

]

значений скорости u (u ≪ 1) значение функции

πα^′s

1-u

a^′u²

g′2(a^′ + b^′) +

R < 0.4. Следовательно, в этой области значений

2g^′u

1-u²

скорости u учет спина и масс кварков, форми-

[

]

πα^′s

a^′

рующих спиновые параметры a^′ и b^′ векторных

g′2(a^′ + b^′) +

u′2

rel

g^′u′rel

мезонов, существенно влияет на поведение функ-

ции R, а значит, и на поведение лептонных ширин

Подчеркнем, что выражение (34) для реляти-

распадов векторных мезонов. Этот эффект связан

вистской лептонной ширины распада векторного

с влиянием значений спиновых параметров a^′ и b^′

мезона в s-состоянии включает в себя спиновый

как функций фактора g^′ на поведение порогового

S-фактор (35), а его бесспиновый аналог

(12)

S-фактора (35) в области малых зачений скорости

содержит бесспиновый S-фактор (10), поведение

u по сравнению с его релятивистским (10) бесспи-

которых было детально исследовано в работах [34,

новым аналогом. Это влияние спиновых парамет-

41-43] и [26-29] соответственно. При этом вы-

ров на поведение порогового S-фактора в области

ражение (34) можно применять и при отсутствии

малых зачений скорости u было детально исследо-

кулоновского взаимодействия в потенциале (4), т.е.

вано в работах [34, 41-43]. Это так называемый

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

520

ЧЕРНИЧЕНКО

Массы векторных ρ₀-, ω- и φ-мезонов были

1.2

выбраны равными [46]: Mρ0 = 775.26 МэВ, M_ω =

= 782.65 МэВ и M_φ = 1019.461 МэВ. Значения

1.0

фактора g^′, который определяется формулой (6)

через отношения масс m_u, m_d, m_s кварков, образу-

ющих векторные ρ₀-, ω- и φ-мезоны, принимаются

0.8

равными: g′ρ0 = g^′ω = 1.0012 (как и в работе [38]

для π^±-мезона), а g^′φ = 1 (из-за равных масс).

0.6

Значения масс m_u, m_d, m_s для u-, d-, s-кварков

были найдены в работе [38] при исследовании

0.4

спектра масс псевдоскалярных π^±-, K^±- и K₀-

мезонов: m_u = 62.57 МэВ, m_d = 69.00 МэВ, m_s =

0.2

= 262.29 МэВ. Тогда, принимая во внимание опре-

√m

деление массы m^′ =

1m2 эффективной реляти-

вистской частицы, были вычислены массы m′ρ0 =

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

= m^′ω = 65.71 МэВ (как и в работе [38] для π^±-

′

мезона) и m

= m_s = 262.29 МэВ для векторных

g' = 1, _s = 0.2

g' = 1.5, _s = 0.2

ρ₀-, ω- и φ-мезонов. Значения быстроты χ^′ = χ,

g' = 2.5, _s = 0.2

= 0

соответствующие выбранным значениям масс M,

m^′ и фактора g^′ для ρ₀-, ω- и φ-мезонов, находятся

Рис. 1. Поведение функции R как функции скорости

u, равной отношению релятивистского выражения (34)

согласно формулам (6) и (15) из выражений

для лептонных ширин распадов векторных мезонов

Mρ0 = 2m^′ρ

g^′ρ

ch χρ0 ,

(37)

к его релятивистскому бесспиновому аналогу (12),

взятых при f1(t) = 1, QV = eq, ℏ = c = 1, αs = α^s =

M_ω = 2m^′ωg^′ω ch χ_ω, M_φ = 2m^′φg^′φ ch χ_φ.

= αs = 0.2 и отвечающих различным значениям фак-

тора g^′. Кривые: сплошная — g^′ = 1, штриховая —

Значения множителя Q_V , обусловленные изо-

g^′ = 1.5, штрихпунктирная — g^′ = 2.5, точечная —

топической структурой векторных мезонов V и

αs = 0.

зарядами кварков, образующих их и выражен-

ных в единицах электрического заряда e, для

векторных ρ₀-, ω- и φ-мезонов были взяты из

эффект Зоммерфельда [44, 45]. Однако с ростом

√

скорости u влияние значений спиновых параметров

работ [10, 11]: Qρ0 = 1/

2, Q_ω = 1/3

2,Q_φ = -

a^′ и b^′ на поведение функции R уменьшается, но

−1/3. Значения линейной (σ^′ = σ) и кулоновской

продолжает зависеть, и достаточно существенно,

(α^′s = α_s) констант взаимодействия для основного

от значений фактора g^′ ≥ 1. В релятивистском пре-

уровня ρ₀-, ω- и φ-мезонов в s-состоянии, а так-

деле (u → 1), как видно из рис. 1, функция R →

же значения спектральной плотности dM_n/dn =

→ 1 для всех трех значений фактора g^′, т.е. это

= 2m^′g^′ sh χ^′ndχ^′n/dn для них были вычислены с

влияние становится исчезающе малым. Такое по-

помощью условия квантования уровней энергий

ведение функции R в релятивистском пределе (u →

для векторных мезонов (a^′ = g′2/2, b^′ = 3/4 -

→ 1) обусловлено тем, что релятивистские порого-

- a^′) [38]

вые S-факторы (10) и (35) имеют правильный ре-

[

лятивистский предел, равный 1 (см. соответственно

ch χ^′

√

(38)

работы [26-29] и [34, 41-43]). В заключение дан-

a^′σ^′

b^′/a^′

1 + b^′/a^′

ного абзаца подчеркнем, что различие масс квар-

(

)

√

ков (фактор g^′), образующих составную систему,

th χ^′

b^′/a^′

× arth

√

существенно влияет на поведение функции R, а

1 + b^′/a^′

значит, и на поведение лептонных ширин распадов

(

)]

векторных мезонов.

shχ^′

√

arctg

√

В качестве примера применения выражения

1 + b^′/a^′

(34), где ℏ = c = 1, проведем вычисление леп-

(

)

тонных ширин распадов основного уровня (n =

ℓ

=π n+

- δCoul,WKB,Sℓ(χ^′),

= 1) s-состояния (ℓ = 0) векторных ρ₀-, ω- и

φ-мезонов, образованных соответствующими па-

n = 0,1,..., ℓ ≥ 0,

рами релятивистских u-, d- и s-кварков, взаи-

модействующих посредством суммы линейного и

используя выбранные значения фактора g^′ и най-

кулоновского (хромодинамического) потенциалов.

денные значения быстроты χ^′ посредством соотно-

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ЛЕПТОННЫЕ ШИРИНЫ РАСПАДОВ

521

Таблица 1. Значения лептонных ширин распадов и параметров ρ₀-, ω- и φ-мезонов

Мезоны M, МэВ m_u, МэВ m_d, МэВ m_s, МэВ

m^′, МэВ

g^′

χ^′

Q_V

α_s

√

ρ₀

775.26

62.57

69.00

65.71

1.0012

2.4595

5.3135

0.3290

√

782.65

62.57

69.00

65.71

1.0012

2.4691

1/3

5.3806

0.3261

1019.461

262.29

1.2836

-1/3

0.7517

0.7793

Мезоны

χ_Δ

-t, ГэВ²

Γ_теор, кэВ

Γ_эксп, кэВ

ρ₀

3.2042

13.63

0.9855

7.04

7.04 ± 0.06

3.0081

11.21

0.9858

0.60

0.60 ± 0.02

2.4054

9.53

0.8574

1.251

1.251 ± 0.021

шений (37), где

ЗАКЛЮЧЕНИЕ

(

)

′

2ρ₊ sh χ

δCoul,WKB,Sℓ(χ^′) = B^′ ln

√

-χ^′ρ^′

В настоящей работе в рамках РКП-подхода в

Λ² + B′2

релятивистском квазиклассическом приближении

получено новое релятивистское выражение для

- фаза релятивистской кулоновской волновой

лептонных ширин распадов векторных мезонов

РКП-функции в ВКБ-приближении, взятой в

в s-состоянии на лептон-антилептонную пару.

точке поворота ρ₊ = 4(ch χ^′ - 1)/σ^′(a^′ + b^′).

Рассмотрение проводится для случая, когда ре-

Значения быстроты χ_Δ, параметризирующей

лятивистские спиновые кварки произвольных

масс m₁, m₂, составляющие векторные мезоны,

формфактор f₁(t) в (25), были выбраны равными:

взаимодействуют посредством воронкообразного

χΔρ0 = 3.2042, χΔω = 3.0081 и χΔφ = 2.4054. Они

соответствуют теоретическим значения лептонных

потенциала, включающего в себя несингуляр-

ширин распадов основного уровня s-состояния

ную чисто запирающую часть и сингулярную

векторных ρ₀-, ω- и φ-мезонов, которые принад-

часть в виде кулоновского (хромодинамического)

лежат доверительным интервалам их эксперимен-

потенциала. Для этой цели было использова-

тальных значений [46].

но полностью ковариантное конечно-разностное

РКП-уравнение в трехмерном релятивистском r-

Значения всех величин для основного уровня s-

представлении, полученное в [34] в рамках РКП-

состояния векторных ρ₀-, ω- и φ-мезонов, включая

подхода [2, 24, 25] для случая взаимодействия двух

значения линейной и кулоновской констант взаи-

релятивистских спиновых частиц произвольных

модействия кварков, скорости u, быстроты χ_Δ и

масс. РКП-уравнение решено релятивистским

квадрата 4-вектора передачи импульса t, а так-

ВКБ-методом. Установлено условие применимости

же теоретические и экспериментальные значения

ВКБ-приближения. Проведено сравнение нового

лептонных ширин распадов для них, приведены в

выражения с его релятивистским бесспиновым

табл. 1. Из табл. 1 видно, что кварки, образующие

аналогом. Исследовано влияние спина и масс

основной уровень s-состояния векторных ρ₀-, ω-

кварков на лептонные ширины распадов векторных

и φ-мезонов, являются релятивистскими (для них

мезонов в s-состоянии. Выполнено вычисление

скорость u > 0.85).

лептонных ширин распадов основного уровня s-

Подчеркнем, что результаты вычислений учи-

состояния векторных ρ₀-, ω- и φ-мезонов.

тывают релятивистский характер связанной си-

стемы, поскольку как лептонные ширины распа-

Показано, что новое выражение для лептонных

дов векторных мезонов (34), так и условие кван-

ширин распадов векторных мезонов (34) при a^′ =

тования уровней энергий (38) были получены в

= 0, b^′ = 2/g^′m^′c² и f₁(t) = 1 переходит в его реля-

рамках полностью ковариантного РКП-подхода в

тивистский бесспиновый аналог. Для исследования

квантовой теории поля. При этом остается неод-

влияния спина и масс кварков на лептонные ши-

нозначность определения параметров взаимодей-

рины распадов векторных мезонов в s-состоянии

ствия. Для устранения этой неоднозначности необ-

были построены графики функции R как функции

ходимо использовать другие физические характе-

скорости u, определенной как отношение нового

ристики для рассматриваемых связанных систем,

выражения для релятивистской лептонной ширины

либо зафиксировать некоторые параметры взаи-

распада векторного мезона в s-состоянии, к ее

модействия, например, мы фиксировали значения

релятивистскому бесспиновому аналогу (рис. 1).

фактора g^′ (см. табл. 1).

Поведение функции R на рис. 1 показывает, что

ЯДЕРНАЯ ФИЗИКА том 86

2023

№4

522

ЧЕРНИЧЕНКО

учет спина и масс кварков влияет на поведение леп-

В. Г. Кадышевский, ЖЭТФ 46, 654, 872 (1964) [Sov.

тонных ширин распадов векторных мезонов. Это

Phys. JETP 19, 443, 597 (1964)]; Докл. АН СССР

влияние особенно существенно в нерелятивистской

160, 573 (1965) [Sov. Phys. Dokl. 10, 46 (1965)].

области значений скорости u (u ≪ 1), где значение

A. A. Logunov and A. N. Tavkhelidze, Nuovo Cimento

29, 380 (1963).

функции R < 0.4, и обусловлено различным пове-

дением в области малых значений скорости u реля-

R. N. Faustov, Ann. Phys. (N.Y.) 78, 176 (1973).

N. B. Skachkov and I. L. Solovtsov, Preprint

тивистских бесспиновых и спиновых пороговых S-

No. E2-11727, JINR (Dubna, 1978); Н. Б. Скачков,

факторов, параметризирующих лептонные ширины

И. Л. Соловцов, ЯФ 30, 1079 (1979) [Sov. J. Nucl.

распадов векторных мезонов.

Phys. 30, 562 (1979)].

Поведение функции R, а значит, и лептон-

N. B. Skachkov and I. L. Solovtsov, Preprint

ных ширин распадов векторных мезонов также

No. E2-11678, JINR (Dubna, 1978); Н. Б. Скачков,

существенно зависит от поведения пороговых S-

И. Л. Соловцов, ТМФ 41, 205 (1979) [Theor. Math.

факторов в релятивистской области значений ско-

Phys. 41, 977 (1979)].

рости u (u → 1). Установлено, что с ростом скоро-

А. Д. Линкевич, В. И. Саврин, Н. Б. Скачков, ТМФ

сти u влияние спина и масс кварков, формирующих

53, 20 (1982) [Theor. Math. Phys. 53, 955 (1982)].

спиновые параметры a^′ и b^′ векторных мезонов,

V. G. Kadyshevsky, R. M. Mir-Kasimov, and

на поведение функции R (рис. 1) уменьшается

N. B. Skachkov, Nuovo Cimento A 55, 233 (1968).

и в релятивистском пределе (u → 1) это влияние

10.

В. А. Матвеев, Б. В. Струминский, А. Н. Тавхелид-

становится исчезающе малым (R → 1), поскольку

зе, Препринт Р-2524, ОИЯИ (Дубна, 1965).

11.

R. Van Royen and W. F. Weisskopf, Nuovo Cimento A

релятивистские бесспиновые и спиновые порого-

50, 617 (1967).

вые S-факторы (10) и (35) в R имеют правильный

12.

R. Barbieri, R. Gatto, R. K ¨ogerler, and Z. Kunszt,

релятивистский предел, равный 1.

Phys. Lett. B 57, 455 (1975).

Полученная в настоящей работе формула (34)

13.

R. Barbieri, R. Gatto, R. K ¨ogerler, and Z. Kunszt,

может быть использована для описания лептонных

Nucl. Phys. B 105, 125 (1976).

ширин распадов векторных мезонов в s-состоянии,

14.

E. Etim and L. Sch ¨ulke, Nuovo Cimento A 77, 347

в частности, она была применена к вычислению

(1983).

лептонных ширин распадов основного уровня s-

15.

J. S. Bell and J. Pasupathy, Z. Phys. C 2, 183 (1979).

состояния векторных ρ₀-, ω- и φ-мезонов, значе-

16.

N. Fr ¨oman and P. O. Fr ¨oman, J. Phys. France 42,

ния которых находятся в доверительном интервале

1491 (1981).

их экспериментальных значений.

17.

B. Durand and L. Durand, Phys. Rev. D 30, 1904

Выражение для релятивистских квазиклассиче-

(1984).

ских лептонных ширин распадов векторных мезо-

18.

А. Д. Донков, В. Г. Кадышевский, М. Д. Матеев,

Р. М. Мир-Касимов, в сб. : Труды IV международ-

нов было получено в рамках полностью ковариант-

ного симпозиума по нелокальным теориям по-

ного метода и имеет правильную связь с функцией

ля, Алушта, 20-28 апреля 1976, Д2-9788, ОИЯИ

Бете-Солпитера, а следовательно, можно ожи-

(Дубна, 1976), с. 36.

дать, что оно более полно учитывает как реляти-

19.

Н. Б. Скачков, И. Л. Соловцов, ЯФ 31, 1332 (1980)

вистский характер частиц, образующих векторные

[Sov. J. Nucl. Phys. 31, 686 (1980)].

мезоны, так и их массы и спины.

20.

А. В. Сидоров, Н. Б. Скачков, ТМФ 46, 213

Автору приятно выразить искреннюю благодар-

(1981) [Theor. Math. Phys. 46, 141 (1981)]; Пре-

ность О.П. Соловцовой за обсуждение полученных

принт Р2-80-45, ОИЯИ (Дубна, 1980); V. I. Savrin,

результатов, ценные замечания и техническую под-

A. V. Sidorov, and N. B. Skachkov, Hadronic J. 4,

держку, Ю.А. Курочкину и В.В. Андрееву за об-

1642 (1981).

суждение полученных результатов, их комментарии

21.

V. I. Savrin and N. B. Skachkov, Lett. Nuovo Cimento

и стимулирующие дискуссии.

29, 363 (1980).

22.

И. С. Шапиро, Докл. АН СССР 106, 647 (1956)

Работа выполнена при поддержке програм-

[Sov. Phys. Dokl. 1, 91 (1956)]; ЖЭТФ 43, 1727

мы международного сотрудничества Республи-

(1963) [Sov. Phys. JETP 16, 1219 (1963)].

ки Беларусь с ОИЯИ и Государственной про-

23.

В. В. Кондратюк, Ю. Д. Черниченко, ЯФ 81, 40

граммы научных исследований на 2021-2025 гг.

(2018) [Phys. At. Nucl. 81, 51 (2018)].

“Конвергенция-2025”, подпрограмма “Микромир,

24.

В. Г. Кадышевский, М. Д. Матеев, Р. М. Мир-

плазма и Вселенная”.

Касимов, ЯФ 11, 692 (1970) [Sov. J. Nucl. Phys. 11,

388 (1970)].

25.

В. Г. Кадышевский, Р. М. Мир-Касимов, Н. Б. Ска-

СПИСОК ЛИТЕРАТУРЫ

чков, ЭЧАЯ 2, 635 (1972) [Sov. J. Part. Nucl. 2, 69

1. Ю. Д. Черниченко, ЯФ 85, 159 (2022) [Phys. At.

(1972)].

Nucl. 85, 205 (2022)].

26.

Ю. Д. Черниченко, Изв. НАН Беларуси. Сер. физ.-

2. V. G. Kadyshevsky, Nucl. Phys. B 6, 125 (1968).

мат. наук 4, 81 (2009).

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ЛЕПТОННЫЕ ШИРИНЫ РАСПАДОВ

523

27.

О. П. Соловцова, Ю. Д. Черниченко, ЯФ 73, 1658

37. Н. Б. Скачков, ТМФ 22, 213 (1975) [Theor. Math.

(2010) [Phys. At. Nucl. 73, 1612 (2010)].

Phys. 22,

149

(1975)]; Preprint No. Р2-12152,

28.

О. П. Соловцова, Ю. Д. Черниченко, ТМФ 166, 225

ОИЯИ (Дубна, 1979).

(2011) [Theor. Math. Phys. 166, 194 (2011)].

38. Ю. Д. Черниченко, ЯФ 85, 353 (2022) [Phys. At.

29.

Ю. Д. Черниченко, Релятивистский квазипо-

Nucl. 85, 488 (2022)].

тенциальный подход в задачах рассеяния,

39. Ю. Д. Черниченко, ЯФ 83, 270 (2020) [Phys. At.

(Изд. центр УО ГГТУ им. П. О. Сухого, Гомель,

Nucl. 83, 488 (2020)].

2011).

40. Н. Б. Скачков, ТМФ 25, 313 (1975) [Theor. Math.

30.

A. H. Hoang, Phys. Rev. D 56, 7276 (1997).

Phys. 25, 1154 (1975)].

31.

J.-H. Yoon and Ch.-Y. Wong, Phys. Rev. C 61,

41. Yu. D. Chernichenko, O. P. Solovtsova, and L. P. Kap-

044905 (2000); J. Phys. G: Nucl. Part. Phys. 31, 149

(2005).

tari, Nonlin. Phen. Compl. Syst. 23, 449 (2020).

32.

A. B. Arbuzov, Nuovo Cimento A 107, 1263 (1994).

42. Yu. D. Chernichenko, L. P. Kaptari, and O. P. Solov-

33.

Yu. D. Chernichenko and O. P. Solovtsova, in

tsova, Eur. Phys. J. Plus. 136, Art. 132 (2021) [arXiv:

Proceedings of the XI International School-

2012. 13128v1 (hep-ph)].

Seminar on the Actual Problems of Microworld

43. Yu. D. Chernichenko, O. P. Solovtsova, and

Physics, August

1-12,

2011, Gomel, Belarus,

L. P. Kaptari, in Proceedings of the XXVIII

Preprint No. E1,2-2013-23, JINR (Dubna, 2013), p.

Anniversary Seminar

“Nonlinear Phenomena

61.

in Complex Systems”, NPCS’2021, May 18-21,

34.

Ю. Д. Черниченко, ЯФ 84, 262 (2021) [Phys. At.

2021, Minsk, Belarus (Nonlinear Dynamics and

Nucl. 84, 339 (2021)].

Applications, Minsk, 2021), Vol. 27, p. 101.

35.

Ю. Д. Черниченко, ЯФ 80, 396 (2017) [Phys. At.

44. A. Sommerfeld, Atombau und Spektrallinien

Nucl. 80, 707 (2017)].

(Vieweg, Braunschweig, 1939), Vol. 2.

36.

N. B. Skachkov and I. L. Solovtsov, Preprint No. E2-

45. G. Gamov, Z. Phys. 51, 204 (1928).

81-760, JINR (Dubna,

1981); Н. Б. Скачков,

И. Л. Соловцов, ТМФ 54, 183 (1983) [Theor. Math.

46. K. A. Olive et al . (Particle Data Group), Chin. Phys.

Phys. 54, 116 (1983)].

C 38, 090001 (2014).

LEPTONIC DECAY WIDTHS FOR THE COMPOSITE SYSTEM

OF TWO RELATIVISTIC FERMIONS

Yu. D. Chernichenko^1),2)

¹⁾ Sukhoi State Technical University of Gomel, Belarus

²⁾ International Center for Advanced Studies, Gomel, Belarus

The new relativistic semiclassical leptonic decay widths of vector mesons as the relativistic systems of two

quarks with arbitrary masses interacting by means of the funnel-type potentials with Coulomb interaction

are obtained. The behavior of the relativistic leptonic decay widths of vector mesons was investigated.

Comparison of the behavior for new expression with its relativistic spinless analog is given. Consideration

is conducted within the framework of completely covariant quasipotential approach in the Hamiltonian

formulation of quantum field theory via a transition to the relativistic configurational representation in the

case of two relativistic spin particles of arbitrary masses.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023